On inferior inputs and marginal returns

Abstract

An input is inferior if and only if an increase in its price raises all marginal productivities. A sufficient condition for input inferiority under quasi-concavity of the production function is then that there are increasing marginal returns with respect to the other input and a non-positive marginal productivity cross derivative. Thus, contrary to widespread opinion, input “competitiveness” is not needed. We discuss these facts and illustrate them by introducing a class of simple production function functional forms. Our results suggest that the existence of inferior inputs is naturally associated with increasing returns, and possibly strengthen the case for inferiority considerably.

1 Introduction

An “inferior” input is one the demand for which decreases with output, at given prices. Clearly, this feature is a property of the cost-minimizing “conditional” demand system, $\varvec{x}(\varvec{w}, y)$, where $\varvec{x}$ is a vector of $n$ inputs whose positive prices are given by $\varvec{w}$, and $y$ indicates the output level.¹ We will discuss the case for an inferior input by assuming that the production function $y=f(\varvec{x})$ is twice differentiable, strictly increasing and (locally) strongly quasi-concave. Accordingly (see e.g. Avriel et al. 1988, paragraph 4.3), at any interior solution $\varvec{x}(\cdot )$ is differentiable, and input $i$ is (locally) inferior if and only if $x_{iy} = \partial x_{i}/\partial y\,<\,0$.

In spite of its simple definition, the case for an inferior input has not yet (as far as we know) received a convincing interpretation in terms of the underlying technology. For a given level of output, at an interior solution the optimal input mix will equate the Marginal rates of technical substitution (MRTSs, which are given by the ratios of marginal productivities) to the corresponding price ratios. Accordingly, the question of the existence of an inferior input concerns the way these rates change across isoquants (i.e., for changes in the output level). It is easy to make a graphical argument for inferiority in the two-input case (see e.g. Katz and Rosen 1998, chapter 10, Figure 10.16), but surprisingly difficult to relate it to properties of the production function.

However, it has long been known (see Hicks 1946, chapter VII; Samuelson 1947, chapter IV; Puu 1971) that, under (strong) concavity of the production function, an input is inferior if and only if it is “regressive”, i.e., if a rise in its price increases the profit-maximizing level of output $y(p, \varvec{w})$, where $p$ is the output price. The simple reason is that an input is inferior if and only if a rise in its price decreases the marginal cost. This fact is easily established by Shephard’s Lemma, whereby the derivative of the cost function $c(\varvec{w}, y)$ with respect to input prices is equal to the demand system, i.e., in matrix terms,

$$\begin{aligned} \varvec{D}_{\varvec{w}} c(\varvec{w},y)=\varvec{x}(\varvec{w},y) \end{aligned}$$

(1)

(the operator $\varvec{D}$ stands for the set of first derivatives), and thus it must be the case that

$$\begin{aligned} \varvec{D}_{\varvec{w}} c_y (\varvec{w},y)=\varvec{D}_y \varvec{x}(\varvec{w},y), \end{aligned}$$

(2)

where $c_{y} = \partial c/ \partial y$ is marginal cost.

The result given in (2) is a nontrivial implication of cost minimization. Its simple economic intuition is that an increase in the price of an input will actually raise the marginal cost if and only if that input l is not substituted away upon increases in output. As a further consequence, under (strong) concavity of the production function, all inputs must be “normal” (that is, their demand must increase with respect to output) if they are not “competitive”,² i.e. if all the cross derivatives of the production function are non-negative (technically, this property is equivalent to the requirement of supermodularity of the production function, if this is twice differentiable: see e.g. Quah 2007).³ This comes from the fact that the Jacobian of the profit-maximizing demand system, $\tilde{\varvec{x}}(p, \varvec{w})$, with respect to input prices, is given by:

$$\begin{aligned} \varvec{D}_{\varvec{w}} \tilde{\varvec{x}} (p,w)=\frac{1}{p}\varvec{D}^2f(\tilde{\varvec{x}}(p,w))^{-1}, \end{aligned}$$

(3)

where $\varvec{D}^{2}f(\varvec{x})$ is the Hessian of the production function and $p$ the output price. Now, if all the off-diagonal elements of $\varvec{D}^{2}f(\cdot )$ are non-negative, a clear-cut conclusion concerning the substitutability properties of $\tilde{\varvec{x}}(\cdot )$ follows. In fact, it is well known that in that case its inverse $\varvec{D}^{2}f(\cdot )^{-1}$ must be a non-positive matrix (see e.g. Takayama 1985, chapter 4, and in particular Theorem 4.D.3, p. 393). That is, according to terminology introduced by Hicks (1956), under concavity all inputs must be gross $p$-complements (i.e., $\partial \tilde{x}_i /\partial w_{j}\,<\, 0,\; i,j = 1, {\ldots }, n)$ if they are all gross $q$-complements ($f_{ij}=\frac{\partial ^2f}{\partial x_i x_j } \ge 0, i, j = 1, {\ldots }, n, i \ne j$, where $f_{ij}$ is the cross derivative of the production function with respect to inputs $i$ and $j)$: see e.g. Bertoletti (2005).

Since

$$\begin{aligned} \varvec{D}_{\varvec{w}} y(p,\varvec{w})=\varvec{D}f(\tilde{\varvec{x}}(p,w))^{\prime } \varvec{D}_{\varvec{w}} \tilde{\varvec{x}}(p, \varvec{w}), \end{aligned}$$

(4)

it follows that if no cross derivative of the marginal products is negative, then $\varvec{D}_{\varvec{w}}y(\cdot )\,<\, \mathbf 0$ and no input can be regressive. In other words, any regressive input $j$ must have at least a gross $p$-substitute (i.e., there must exist an input $i$ such that $\partial \tilde{x}_i /\partial w_{j}\,>\,0$), otherwise the profit-maximizing level of output could not increase. This result is often, and to some extent misleadingly, stated through the assertion that a necessary but not sufficient condition for an input to be inferior is that (some) inputs are competitive (see e.g. Epstein and Spiegel 2000, Proposition 1, p. 505). This assertion has apparently shaped the search for technologies that exhibit inferior inputs: see Epstein and Spiegel (2000) and Weber (2001).

In the next section, we will discuss the conditions for obtaining an inferior input under the assumption (which is standard for analyzing cost-minimizing behavior) of bare (strong) quasi-concavity of the production function. This weaker assumption is necessary because we want to focus on the case of increasing marginal returns, which seems, as far as we know, to have attracted no attention in the literature. Intuitively, an input is inferior if at a larger productive scale it should be economically substituted. From (2), this can be interpreted as requiring that the marginal productivities of all inputs be raised by an increase in the inferior input price, subsequent to input adjustment. We will illustrate the case for inferiority without “competitiveness” among inputs (meaning negative cross derivatives of marginal productivities) by considering a simple class of additive functional forms for the production function in the case of two inputs, with the normal input (there must be at least one) exhibiting increasing marginal returns. The point we make also applies to the case of many inputs, on condition that the input with increasing returns enters the production function additively, and in the two-input case to any sign of the cross derivative under certain restrictions. These results provide an economically meaningful rationale for the existence of inferior inputs, namely their association with the existence of increasing returns with respect to another input, and suggest that the case for inferiority could be stronger than is commonly thought.

2 Marginal productivities and inferiority

Our starting point is the well-known identity:⁴

$$\begin{aligned} c_y (\varvec{w},y)\equiv \frac{w_i }{f_i (\varvec{x}( \varvec{w},y))} \end{aligned}$$

(5)

$i = 1, {\ldots }, n$, where $f_{i}=\partial f/\partial x_{i}$ is the marginal productivity of input $i$. Assume that input $j$ is (locally) inferior and that its price $w_{j}$ increases: the conditional demand system has to vary such that it increases all the marginal productivities. That is, the following necessary and sufficient condition must hold:

$$\begin{aligned} \varvec{D}^2f(\varvec{x}(\varvec{w},y)) \varvec{d}_j \varvec{x}(\varvec{w},y)=\varvec{a}>0, \end{aligned}$$

(6)

where $\varvec{d}_{j} \varvec{x}(\varvec{w}, y) = \varvec{D}_{w} \varvec{x}(\varvec{w},y) \varvec{e}_{j} \textit{dw}_{j}$ is the change in demand induced by an increase in $w_{j}$, and $\varvec{e}_{j}$ is the jth natural unit vector.

(6) provides a simple alternative explanation of why, in the case of (strong) concavity of the production function, if all cross derivatives of the production function are non-negative no inferior input can exist. In fact, in such a case (6) would be equivalent to:

$$\begin{aligned} \varvec{d}_j \varvec{x}(\varvec{w},y)=\varvec{D}^2f(\varvec{x}(\varvec{w},y))^{-1}\varvec{a}<0, \end{aligned}$$

(7)

which says that all the changes $d_{j}x_{i}$ should be negative. But this is impossible, since the output has to remain constant, i.e., $\varvec{D}f^{\prime }\varvec{d}_{j}\varvec{x} = 0$. In fact, one net $p$-substitute for input $j$ ought to exist;⁵ that is, there must be an input $i$ such that $x_{ij} = \partial x_{i}/\partial w_{j}\,>\,0$ (again, see e.g. Bertoletti 2005 for this terminology). An intuition for this result can be grasped by consideration of the two-input case. Clearly, in such a setting, under decreasing marginal returns (an implication of concavity), the productivity of the normal input substitute (whose use increases after the rise in the inferior input price) cannot increase unless the production function cross derivative is negative.

Before proceeding, let us briefly discuss the case for an inferior input under the perspective we are considering. Is there any reason why we should expect the marginal productivities to decrease monotonically with respect to prices (along the path of the conditional demand system)? A cost-minimizing behavior implies that the cost has to rise after an input price increase (or that the output that can be produced at a given cost should decrease).⁶ But there seem to be no general argument for expecting a rise in marginal cost too. When the price of a factor rises, its demand decreases, and this is compatible with either an increase or a decrease in its so-called “weighted marginal productivity” (the reciprocal of the right-hand-side of (5)). According to (6), what happens to the marginal productivities of the other inputs depends on the second order derivatives of the production function and (endogenously) on their net $p$-substitutability relationships with the input whose price has increased. However, since the price ratios of these inputs (and thus the corresponding MRTSs) remain unchanged, their productivities must move together. Notice that, in general, at least one net $p$-substitute ought to exist for the input whose price rose, and to some extent it would be natural to expect a decrease in the productivity of this input. However, as we have seen above, even under concavity its productivity might on the contrary increase, unless the cross derivatives of the production function are all non-negative. Besides this case, there is actually a class of well-known technologies with the previously alleged property. If the technology is homothetic, it is easily seen that the marginal cost is proportional to the cost, and in particular that the vector $\varvec{D}_{\varvec{w}}c_{y}$ and $\varvec{D}_{\varvec{w}}c$ are related by a positive scalar multiplication. However, as Tönu Puu (1971, p. 243) wrote forty years ago: “[homotheticity]⁷ is assumed for mathematical simplicity in exemplifications and in econometric applications.” and “I cannot see anything to make the case [of an inferior input]⁸ unlikely”.

Let us consider the special case in which there are only two inputs, and let us assume that the inferior input is 1 (so that 2 is a normal input). We can then uniquely characterize the differential $\varvec{d}_{1}\varvec{x}$, since:

$$\begin{aligned} d_1 x_2 (\varvec{w},y)=-\frac{f_1 (x(\varvec{w},y))}{f_2 (x(\varvec{w},y))}d_1 x_1 (\varvec{w},y)>0. \end{aligned}$$

(7’)

Accordingly, condition (6) is equivalent to the system:

$$\begin{aligned} \begin{aligned}&\left[ {f_{11} (x(\varvec{w},y))-f_{12} (x(\varvec{w},y))\frac{f_1 (x(\varvec{w},y))}{f_2 (x(\varvec{w},y))}} \right]<0, \\&\left[ {f_{21} (x(\varvec{w},y))-f_{22} (x(\varvec{w},y))\frac{f_1 (x(\varvec{w},y))}{f_2 (x(\varvec{w},y))}} \right]<0, \end{aligned} \end{aligned}$$

(8)

and it is easily interpreted as requiring that the movement along the relevant isoquant increases the productivity of input $i$, either “directly” through $d_{1}x_{i}$, or “indirectly” through $d_{1}x_{j}$ $(i, j = 1, 2, i \ne j).$ It is equivalent to the condition that the elasticities of the marginal products, $\varepsilon _{ij}=f_{ij}x_{j}/f_{i}$, are ordered in such a way that $\varepsilon _{21} \,>\, \varepsilon _{11}$ and $\varepsilon _{22}\,>\,\varepsilon _{12}$: in other words, both inputs 1 and 2 have a larger proportional impact on $f_{2}$ than on $f_{1}$. Notice that, in contrast, homotheticity requires that the sums of the elasticities of each marginal product with respect to all inputs should be equal (i.e., $\Sigma _{j}\varepsilon _{ij}$ should be independent from $i)$, to keep the MRTSs constant with respect to any proportional input change.

Condition (8) can be written compactly as:

$$\begin{aligned} f_{22} (x(\varvec{w},y))\frac{f_1 (x(\varvec{w},y))}{f_2 (x( \varvec{w},y))}>f_{12} (x(\varvec{w},y))>\frac{f_2 (x(\varvec{w},y))}{f_1(x(\varvec{w},y))}f_{11} (x(\varvec{w},y)). \end{aligned}$$

(8’)

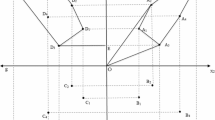
Consider the relevant “iso-marginal-productivity curves” given by $f_{i}$ $=$ constant ($i$ $=$ 1,2). Notice that the curve of input $i$ increases if $f_{ii}$ and $f_{ij}$ do not agree in sign, and that they are orthogonal if $f_{12}$ $=$ 0 (this requires $f_{22}> 0 > f_{11}$ to satisfy (10)). Geometrically, (8$^\prime$) says that these curves are (locally) “steeper” than the isoquant if $f_{12}$ is negative (see Puu 1971, p. 247, Figure 2.c, for the case in which both $f_{11}$ and $f_{22}$ are negative), and (locally) “flatter” if $f_{12}$ is positive (see Fig. 1 for the case in which $f_{22} > 0 >f_{11})$. Also note that (8$^\prime$) cannot hold under concavity unless $f_{12}$ is negative. But even if $f_{12}$ is non-negative, the existence of an inferior input cannot actually be ruled out if the other input exhibits increasing marginal returns. In fact, local (strong) quasi-concavity only requires that:

$$\begin{aligned}&f_{21} ({\varvec{x}}({\varvec{w}},y))-f_{22} ({\varvec{x}}({\varvec{w}},y))\frac{f_1 ({\varvec{x}}({\varvec{w}},y))}{f_2 ({\varvec{x}}({\varvec{w}},y))}+f_{12} ({\varvec{x}}({\varvec{w}},y))\nonumber \\&\quad -f_{11} ({\varvec{x}}({\varvec{w}},y))\frac{f_2 ({\varvec{x}}({\varvec{w}},y))}{f_1 ({\varvec{x}}({\varvec{w}},y))}>0. \end{aligned}$$

(9)

Notice, however, that (9) implies that the second inequality in (8$^\prime$) will be satisfied if the first holds. This is summarized for the case of two inputs in the following Proposition 1 (under strong quasi-concavity of the production function).

Fig. 1

Isoquant and iso-marginal-productivity curves: the case with $f_{12} \,>\,0$ and $f_{22}\,>\,0\,>\, f_{11}$

Proposition 1

(Necessary and sufficient conditions) Input i is inferior if and only if $\varepsilon _{jj} > \varepsilon _{ij} (i \ne j)$, where $\varepsilon _{ij} = \partial lnf_{i}/\partial lnx_{j}.$

As far as we know, Proposition 1 was first proved under (strong) concavity by Bilas and Massey (1972), and by Bear (1972), who pointed out the redundancy of the condition $\varepsilon _{ji}$ > $\varepsilon _{ii}$ and noted that the result applies to the case of (strong) quasi-concavity as well.⁹ Here, we are interested in the fact that the assumption of increasing (marginal) returns in the other input naturally satisfies the requirement that a price increase raises marginal productivities, if quasi-concavity can be guaranteed. The following Proposition 2 summarizes.

Proposition 2

(Sufficient conditions) One input is inferior if there are strictly increasing returns with respect to the other input and a non-positive marginal productivity cross derivative.

The intuition for Proposition 1 is simple: if an increase in both inputs affects the productivity of one input more than the other, it is impossible that (locally) the “isocline” (that is, the locus of point $\varvec{x}$ such that the MRTS is constant) curve is increasing. For what concerns Proposition 2, simply notice that if one input exhibits increasing returns, a rise in the price of the other input must raise its productivity, unless the production function cross derivative is positive.¹⁰ To illustrate, consider the following functional form for the production function:¹¹

$$\begin{aligned} g(\varvec{x})=\ln (x_1 +1)+e^{x_2 }-1. \end{aligned}$$

(10)

$g(\cdot )$ is a strictly increasing, additive, (at least) twice differentiable function which is also strongly quasi-concave (but not concave) for positive input quantities, with $g$(0) $=$ 0. Notice that the MRTS is given by:

$$\begin{aligned} \frac{g_1 (\varvec{x})}{g_2 (\varvec{x})}=\frac{1}{(x_1 +1)e^{x_2 }}, \end{aligned}$$

(11)

and that as a consequence the isoclines invariably decrease. Also notice that the strictly decreasing isoquants intercept the horizontal axis at $x_{1}=e^{y}$ – 1, where their slope is $e^{- y}$, and the vertical axis at $x_{2}$ = ln($y$ + 1), with slope $y$ + 1. A typical isoquant is depicted in Fig. 2, together with an interior solution and the relevant isocline. At any interior solution,¹² the conditional demand system moves continuously along the relevant isoquant for changes in the input price ratio, and along the relevant isocline for changes in the output level, thus confirming that input 1 is inferior. Of course, the marginal cost will decrease with respect to output.

Fig. 2

Isoquant, isocline and optimal input choice for the $g(\cdot )$ p.f

Finally, notice that while complexity is compounded if the cross derivatives of the marginal productivities are not null, a continuity argument allows sufficiently small cross derivatives of any given sign not to alter the previous results. In other words, input competitiveness is by no means necessary to produce input inferiority (formally, the validity of the contrary result that can be found e.g. in Bear 1972, pp. 412–3, does not extend from the concavity case to quasi-concavity). For example, it is easy to see that the functional form:

$$\begin{aligned} \tilde{g}(\varvec{x})=\ln (x_1 +1)+e^{x_2 }(x_1 +1)-1, \end{aligned}$$

(12)

which generalizes (10) to the case of a strictly positive cross derivative, does indeed satisfy both conditions (8$^\prime$) and (9).

Let us now return to the case of $n>2$. Again, let us assume that the production function is additive, and that at an interior solution at which the production function is (locally) quasi-concave there is one¹³ input with increasing marginal returns. Now let us suppose that the price of this factor, say input 2, rises, thereby decreasing its marginal productivity and raising the marginal cost. Call input 1 a net $p$-substitute of input 2: the former input must be inferior, since when its price increases it symmetrically increases the demand for input 2 and its productivity. Thus, at least one inferior input will exist in the given case. Moreover, for an additive production function it must be that ($i \ne j)$:

$$\begin{aligned} \begin{aligned} x_{iy} (\varvec{w},y)&=-\frac{c_{yy} (\varvec{w},y)f_i (x_i ( \varvec{w},y))}{c_y (\varvec{w},y)f_{ii} (x_i (\varvec{w},y))},\\ x_{ij} (\varvec{w},y)&=\frac{x_{iy} (\varvec{w},y)x_{jy} ( \varvec{w},y)}{c_{yy} (\varvec{w},y)}, \end{aligned} \end{aligned}$$

(13)

where $c_{yy} = \partial c_{y}/\partial y$, as can easily be proved by differentiation of the identity (5). It follows that in fact all the inputs with decreasing marginal returns will be inferior, net $p$-substitutes with respect to 2 (i.e., $x_{2j}>0, j \ne 2$) and net $p$-complements each others (i.e., $x_{ij} < 0, i, j \ne 2$). Notice that the marginal cost must decrease with respect to output, and that conditions (6) are a fortiori satisfied whenever dw $_{j} \, >\, 0, j \ne 2$.

Now note that the previous arguments for the existence of inferior inputs generalize to the case in which the production function is additive exclusively with respect to the input that exhibits increasing returns, i.e., to the case in which $f(\varvec{x}) = f^{-2} (\varvec{x}_{-2})+f^2(x_{2})$, where $\varvec{x}_{-2}$ is the vector of all inputs but 2 and $f^{2\prime \prime }(\cdot ) \, >\, 0$ (whereby the results given by (12) hold for $i$ = 2). This is stated in the following Proposition 3 (under strong quasi-concavity of the production function).

Proposition 3

(Sufficient conditions) If there are strictly increasing returns with respect to an input which enters additively the production function, all the other inputs are inferior.

In summary, the net $p$-substitute of an input exhibiting increasing marginal returns tends (it depends on the cross derivatives of the production function) to be an inferior input. Accordingly, our results have uncovered an association between the existence of inferior inputs and that of increasing returns. We additionally observe that it would be natural to think of an additive technology as referring to the use of many different plants by the firm. Indeed, our results apply to the case in which a single firm owns $n$ plants, and each quantity $x_{i}$ is actually internally produced at plant $i$ by means of $m_{i}$ inputs $\varvec{z}^{i}$ within a sub-production function $x_{i}=h^{i}(\varvec{z}^{i})$, where each $h^{i}(\cdot )$ is monotonically increasing, concave and linearly homogenous (accordingly, an appropriate version of “two-stage budgeting” applies, with the “price” of input $i$ being computable as a well-defined index of the $\varvec{z}^{i}$ prices: see e.g. Deaton and Muellbauer 1980, Section 5.2). Following such an interpretation, let us suppose that there is a single plant $i$ where the output $y$ is produced by means of $x_{i}$ with increasing (marginal) returns, while all the others exhibit decreasing returns at the plant level. An increase in total output will then be associated with a decrease in the production in the latter plants, whose underlying inputs are inferior if the ones used in the former plant are specific to it. Thus, in our examples it is the occurrence of increasing returns that, as output increases, creates an opportunity for input substitution.

We conclude this section by reminding the attentive reader that any twice-differentiable, strong quasi-concave function $f(\cdot )$ is a so-called “transconcave” entity, i.e., it can be transformed into a concave function by means of a monotonically increasing function of one variable $G(\cdot )$: see e.g. Avriel et al. (1988, Theorem 8.25, p. 278). This implies that our production functions (10) and (12) are concavifiable, and that their concavized versions could then be used to describe profit-maximizing behavior that exhibits regressive inputs (of course, the process of concavification would generate negative cross derivatives for the production function $F(\varvec{x}) = G(f(\varvec{x}))$. What matters more is that our “increasing returns story” would still apply to the inner productive stage described by $f(\cdot )$, while $G(\cdot )$ could then be interpreted as an outer stage of production that exhibits decreasing (marginal) returns. Notice that, conversely, with a (two-input) concave technology exhibiting an inferior input as a starting point, one should always be able to de-concavize it by taking a monotonically increasing convex transformation of the associate production function. While preserving both its quasi-concavity and the satisfaction of (8$^\prime$), this operation will leave increasing marginal returns with respect to the normal input to emerge once the second order cross derivative of the resulting production function is turned from negative into positive.

3 Concluding remarks

In this note we have revisited the case for the existence of inferior inputs. We have argued that to assume the underlying technology is concave, as is common in the literature, is restrictive and possibly misleading.¹⁴ In particular, by assuming bare (strong) quasi-concavity of the underlying technology, we have shown that inferior inputs ought to exist if the underlying technology is additive with respect to another input exhibiting increasing marginal returns (a result which admits an interpretation in terms of returns to scale at the plant level): see Proposition 3 above. In the two-input case, we have similarly shown that a negative cross derivative of the production function is sufficient, but not necessary, to make an input inferior if there are increasing marginal returns with respect to the other (see Propositions 1 and 2 above). As a corollary to these results, we can assert that competitiveness among inputs is not needed to deliver input inferiority. Thus, in addition to presenting a class of (simple) functional forms that exhibit inferior inputs (according to Weber 2001, only a few examples were already known in the literature), we have uncovered what we believe to be a novel and economically meaningful reason for their existence, namely their association with the presence of increasing returns. We believe that this should considerably strengthen the case for inferiority, which is widely held to be dubious: see e.g. Cowell (2006, p. 32).

Let us now return to the correspondence between the inferiority of inputs and of consumption goods (see Footnotes 1 and 3 above). It is an interesting paradox that while they are formally identical, the latter seem to be much more popular (see any microeconomic textbook, in which the case of inferior inputs is usually not even mentioned).¹⁵ Moreover, the paradox deepens if one considers that to provide an intuitive economic explanation of the existence of a normal commodity, it is necessary to refer to the somehow exotic result that a rise of its price decreases the marginal utility of income, with utility held constant: see Fisher (1990).¹⁶ The point is, of course, that in production theory the reciprocal of the latter quantity is well known as the marginal cost. In particular, notice that in consumption theory inferior commodities are usually but informally interpreted as “low-quality goods” (see e.g. Varian 1996, p. 96: “examples might include gruel [ ${\ldots }$ ], or nearly any kind of low-quality good.”). Our results, which relate the input substitution associated to inferiority to the existence of increasing returns, appear to provide only a partial support to the extension of the previous interpretation (inferior inputs as “poor inputs”, e.g. some kind of unskilled work) to production theory.

Finally, we have to mention that, as we discovered after having completed the first draft of this paper, although the property of the additive technology we exploited in the previous section is already known in consumer theory, it is considered “very peculiar” (Deaton and Muellbauer 1980, Section 5.3) or even “clearly pathological” (Barten and Bohn 1982, Section 15), apparently because strictly speaking it implies that only one commodity will be normal. However, we cannot see any special difficulty in our production story of plants with different returns to scale. In particular, while it corresponds to economic commonsense that at any interior solution only a single plant with increasing returns is operated, notice that there can actually be many normal inputs (all those uniquely associated to that plant).¹⁷ Might this be yet another instance of the aforementioned paradox?