Effects of grain size, texture and grain growth capacity gradients on the deformation mechanisms and mechanical properties of gradient nanostructured nickel

Abstract

Developing a complete understanding of the structure–property relationship of gradient nanostructured metals is crucial to the technological advancement that will overcome the barriers to the engineering applications of this novel class of materials with superior mechanical properties. To this end, the individual effects of three unique structural features, namely the grain size gradient, texture gradient and grain growth capacity gradient, on the deformation mechanisms and mechanical properties of gradient nanostructured nickel are investigated using a dislocation-density-based crystal plasticity finite element model. It is revealed that increasing the grain size gradient, which increases the relative fraction of coarse grains, leads to limited variations in statistically stored dislocation (SSD) density yet significant declines in geometrically necessary dislocation (GND) density due to the distinct origins of these two kinds of dislocations, resulting in significantly weakened back stress hardening in contrast to moderate changes in forest dislocation hardening. Increasing the texture gradient, which increases the average Schmid factor of the sample, leads to consistent decreases in SSD density, GND density, back stress as well as yield and flow stresses. The decrease in SSD density is attributed to decreasing average shear strain rate as a result of the Schmid effect, whereas the Schmid effect and decreasing intergranular misorientation both contribute to the decreases in GND density and back stress. Furthermore, increasing the grain growth capacity gradient leads to an increase in SSD density due to diminished dislocation recovery, as well as decreases in GND density and back stress due to diminished strain gradient intensity. Last but not least, strain localization decreases with increasing grain size gradient and texture gradient. These conclusions are instrumental to optimizing the mechanical properties of gradient nanostructured metals as well as designing new heterostructured materials with exceptional properties and performance.

1 Introduction

Traditionally, most metals and alloys for structural applications are characterized by homogeneous microstructures where the average grain sizes in different parts are more or less uniform. According to the classic Hall–Petch relationship [1], a homogeneous, polycrystalline metal can be strengthened by decreasing the average grain size, as an increase in the volume fraction of grain boundaries will further impede dislocation motion. Nevertheless, decreasing the grain size will inevitably lead to diminished ductility and deformability of the material due to restricted dislocation mobility, thereby creating the dilemma known as “strength-ductility tradeoff,” which limits the application of many metallic materials. In recent years, however, gradient nanostructured (GNS) metals have emerged as a novel class of structural materials with the promising potential of breaking through the strength-ductility tradeoff. These materials, characterized by a gradient of grain sizes typically spanning three or four orders of magnitude from the surface to the core, possess an outstanding combination of strength and ductility superior to their homogeneous counterparts [2,3,4,5,6,7,8,9,10,11].

The exceptional mechanical properties and performance of GNS metals can be attributed first and foremost to the existence of grain size gradients. Experimental and theoretical investigations indicate that a grain size gradient introduces structural heterogeneity into the material, which leads to deformation heterogeneity where the coarse grains plastically yield first and sustain higher plastic strain during deformation than the fine grains, giving rise to the layer-by-layer elastic–plastic transition as well as strain partitioning [12, 13]. As a result, strain gradients are developed inside the material, and geometrically necessary dislocations (GNDs) are generated and increase rapidly in density in order to fulfill strain continuity [14,15,16,17]. The GNDs not only impede dislocation motion and thus contribute to strain hardening, but also pile up in the vicinity of interfaces such as grain boundaries, producing a long-range internal stress toward the dislocation source known as the back stress, which further strengthens and hardens the material [5, 18, 19]. The extra strengthening and strain hardening induced by GNDs enhance both the strength and ductility, hence endowing GNS metals with extraordinary mechanical properties [20,21,22,23]. In addition, it has been revealed that the mechanical properties of GNS metals, such as strength, ductility, fracture resistance and damage tolerance, can be tuned and optimized by introducing different grain size gradients into the materials [24,25,26,27,28].

Despite the valuable insights gained from previous research efforts concerning the origin of the superb mechanical properties of GNS metals, few studies have looked into the effects of different grain size gradients, i.e., a change in the grain size distribution profile, on the underlying deformation mechanisms in these materials. Questions such as how a change in grain size gradient affects the evolution of dislocation density and back stress, how it influences the various strengthening and hardening mechanisms in GNS metals, and how they are further manifested in the mechanical behaviors of these materials under deformation, remain unanswered. Investigations into these important questions are crucial to forming a complete picture of the structure–property relationship of GNS metals for scientists and researchers, and thus, to overcoming the technological barriers that limit their industrial applications. Therefore, exploring the effects of grain size gradient on the deformation mechanisms and mechanical properties of GNS metals stands as the first goal of this work.

Despite the importance of grain size gradient, it is by no means the only factor that influences the mechanical properties of GNS metals. An often overlooked yet significant feature is the texture gradient. Different processing methods for GNS metals such as surface mechanical attrition treatment or electrodeposition will produce different texture gradients in the samples, where the texture, i.e., the preferred crystallographic orientations of the gains, changes gradually along the depth [29,30,31]. By adjusting processing parameters such as current density, additive content, texture gradients can be tuned just like grain size gradients [24, 32,33,34]. Although very few studies, if any, have focused on the effects of texture gradient on GNS metals under deformation, earlier research work has clearly demonstrated that textures play a significant role in the mechanical properties of metals and alloys, especially those with nanocrystalline grains [35, 36]. Hence, the present work also strives to reveal the effects of texture gradient on the deformation mechanisms and mechanical behaviors of GNS metals.

Finally, grain growth capacity gradient is yet another factor that governs the structure–property relationship of GNS metals and influences their mechanical behaviors. It has been reported that significant grain growth occurs in gradient nanograined copper during tensile deformation, which is a mechanically driven grain boundary migration process that endows the material with exceptional plasticity [37]. In contrast, both grain coarsening and refinement occur concomitantly in GNS nickel under tension. The coarsening of the grains smaller than 280 nm is caused by stress-induced grain boundary migration and rotation, whereas the refinement of the grains larger than 280 nm is ascribed to the formation of dislocation substructures [32]. In addition, concomitant grain coarsening and refinement have also been observed in samples of nanocrystalline nickel and NiCo alloy [38]. Moreover, different grain size gradients will induce different grain growth capacities and reducing the temperature to 200 K will also lead to a significant change in grain growth capacity [32]. Few studies, to the author’s knowledge, have considered the aspect of grain growth capacity gradients in GNS metals, which have been shown to significantly impact the mechanical properties of these materials. Therefore, discovering the effects of grain growth capacity gradient is another objective of this work.

One of the reasons that the effects of grain size, texture and grain growth capacity gradients on the deformation mechanisms and mechanical properties of GNS metals have yet to be revealed lies in the fact that these gradients are often coupled together, i.e., a change in one will often lead to changes in the others, and it is challenging, if not infeasible, to decouple them and study each effect individually via experiments alone [8]. In this regard, computational modeling and simulation can play an important role. For instance, Li et al. [39] developed a dislocation density-based continuum plasticity model and investigated the origin of extra strain hardening in gradient interstitial-free (IF) steel. The model not only successfully reproduced the experimentally observed surface non-uniform deformation, but also revealed that the strain hardening, which arose from the generation of GNDs and back stress, could be as high as that of its coarse-grained counterpart. Zhao et al. [40] developed a multiple mechanism-based constitutive model accounting for GNDs and back stress at both sample and grain levels, which was incorporated into a finite element framework to study the contributions by different hardening mechanisms in gradient IF steel. It was found that the sample-level GNDs and back stress had little effect on the mechanical properties of the gradient material, whereas the grain-level GNDs and back stress contributed significantly to its strain hardening. Lu et al. [41] investigated the mechanical properties of GNS aluminum and the associated dislocation structure and evolution via a dislocation dynamics model considering dislocation-grain boundary interactions, which demonstrated the sequential yielding of the grains under plastic deformation as well as the non-uniform distribution of the strain gradient and GND density. Yu [42] developed a constitutive model capable of predicting the overall mechanical behaviors of GNS materials such as gradient IF steel and GNS nickel under plastic deformation based on grain size gradient profile. It was found that strain gradient in GNS metals was dependent on both the grain size gradient and the accumulated strain gradient. Xu et al. [43] explored the differences in the deformation mechanisms and mechanical properties of GNS copper, aluminum and nickel via large-scale molecular dynamics simulations, which highlighted the metal-type dependence of GNS metals in terms of dislocation and grain boundary mediated plasticity. In addition to GNS metals, significant progress has also been made in recent years in the investigation of the relationship between dislocation-mediated plasticity and the mechanical properties of structural materials in general. Jiang et al. [44] developed a governing relationship between surface GND density and the associated long-range internal stress of polycrystalline metals, which was incorporated into a CPFE framework to explore the grain size effects of polycrystalline copper. The calculated Hall–Petch effect demonstrated good agreement with experimental data, highlighting the effect of dislocation densities on the mechanical properties of polycrystalline metals. Li and coworkers [45,46,47] developed an atomistically informed multiscale crystal defect dynamics (MCDD) method, which is a higher-order, strain gradient-based crystal plasticity finite element theory and formulation, to study the crystal plasticity and the dynamics of dislocation patterns in single BCC crystals. The MCDD method is capable of capturing geometrically compatible dislocation pattern distribution and evolution in BCC crystals as well as the size effects in nanoscale plasticity with minimal empiricism and high computational efficiency. Moreover, a temperature-dependent higher-order Cauchy–Born rule was incorporated into the MCDD framework, which further enables the model to capture dislocation cross slip in single BCC crystal at low temperature and dislocation cell structures at high temperature. Li et al. [48] established a micromechanical model for heterogeneous nanograined metals considering the pileup of GNDs, which demonstrated that the strength-ductility tradeoff can be overcome by altering the shape, size and fraction of inclusions. Therefore, by creating dislocation density-based, mechanistically informed models of GNS metals and altering one of the gradients while controlling the others, the individual effects of each factor can be investigated, which serves as the basic methodology of this work.

In this work, a crystal plasticity finite element (CPFE) model is developed incorporating the evolution of statistically stored and geometrically necessary dislocation densities as well as back stress to explore the individual effects of grain size, texture and grain growth capacity gradients of GNS nickel. The model is described briefly in Sect. 2, and the results obtained from the simulations are presented and discussed in Sect. 3, followed by the major conclusions drawn from this study in Sect. 4.

2 Crystal plasticity finite element model

2.1 Constitutive equations

At the center of the CPFE model are the constitutive equations, which account for the mechanical behaviors of a material. As a starting point, a deformation gradient tensor F, which describes the deformation of a material, is defined as:

$${\mathbf{F}} = \frac{{\partial {\mathbf{x}}}}{{\partial {\mathbf{X}}}}$$

(1)

where X and x are vectors representing the original, undeformed position and the current, deformed position of a material point, respectively. It is well known that the deformation of metals and alloys can be classified into elastic and plastic stages [49, 50]. The elastic deformation can be further classified into two consecutive steps: a rotation of the crystal lattice followed by an elastic stretch [51]. Accordingly, the deformation gradient is decomposed into an elastic component and a plastic one, and the elastic component is further decomposed into an elastic stretch tensor and a lattice rotation tensor:

$${\mathbf{F}} = {\mathbf{F}}_{{\text{e}}} {\mathbf{F}}_{{\text{p}}} ,\quad {\mathbf{F}}_{{\text{e}}} = {\mathbf{V}}_{{\text{e}}} {\mathbf{R}}_{{\text{e}}}$$

(2)

where ${\mathbf{F}}_{{\text{e}}}$ and ${\mathbf{F}}_{{\text{p}}}$ are the elastic and plastic deformation gradient tensors, respectively, and ${\mathbf{V}}_{{\text{e}}}$ and ${\mathbf{R}}_{{\text{e}}}$ are the elastic stretch tensor and the lattice rotation tensor, respectively. Accordingly, four configurations of the crystal lattice emerge from such a decomposition scheme: the original, undeformed configuration, denoted by ${\mathcal{B}}_{0}$; an intermediate configuration where the undeformed crystal lattice undergoes plastic deformation ${\mathbf{F}}_{{\text{p}}}$, denoted by ${\overline{\text{B}}}$; another intermediate configuration where the lattice is further rotated by ${\mathbf{R}}_{{\text{e}}}$, denoted by ${\hat{\text{B}}}$; and the current configuration where the lattice is further stretched elastically by ${\mathbf{V}}_{{\text{e}}}$, denoted by ${\mathcal{B}}$. In this work, the constitutive equations are formulated with respect to the intermediate configuration ${\hat{\text{B}}}$.

The elastic Green–Lagrange strain tensor in configuration ${\hat{\text{B}}}$, denoted by ${\hat{\mathbf{E}}}_{{\text{e}}}$, can be formulated with respect to the elastic stretch tensor ${\mathbf{V}}_{{\text{e}}}$ as follows:

$${\hat{\mathbf{E}}}_{{\text{e}}} = \frac{1}{2}\left( {{\mathbf{V}}_{{\text{e}}}^{{\text{T}}} {\mathbf{V}}_{{\text{e}}} - {\mathbf{I}}} \right)$$

(3)

where ${\mathbf{I}}$ is the second-order identity tensor. The elastic Green–Lagrange strain tensor ${\hat{\mathbf{E}}}_{{\text{e}}}$ is further related to the second Piola–Kirchhoff stress tensor ${\hat{\mathbf{S}}}$ in configuration ${\hat{\text{B}}}$ via the generalized Hooke’s law:

$${\hat{\mathbf{S}}} = \hat{\mathbb{C}}{ }:{\hat{\mathbf{E}}}_{{\text{e}}}$$

(4)

where $\hat{\mathbb{C}}$ is the fourth-order elastic stiffness tensor. Equation (4) describes the stress–strain relationship of the material under elastic deformation.

The deformation gradient ${\mathbf{F}}$, on the other hand, forms the basis for the definition of the velocity gradient tensor ${\mathbf{L}}$:

$${\mathbf{L}} = {\dot{\mathbf{F}}\mathbf{F}}^{ - 1} = {\dot{\mathbf{V}}}_{{\mathbf{e}}} {\mathbf{V}}_{{\text{e}}}^{ - 1} + {\mathbf{V}}_{{\text{e}}} {\hat{\mathbf{L}}}_{{\text{p}}} {\mathbf{V}}_{{\text{e}}}^{ - 1}$$

(5)

where ${\dot{\mathbf{F}}} = \frac{{\partial {\mathbf{F}}}}{\partial t}$. ${\hat{\mathbf{L}}}_{{\text{p}}}$ is the plastic velocity gradient in configuration ${\hat{\text{B}}}$, which can be written as:

$${\hat{\mathbf{L}}}_{{\text{p}}} = \mathop {{\hat{\mathbf{F}}}}\limits^{.}_{{\text{p}}} {\hat{\mathbf{F}}}_{{\text{p}}}^{ - 1} = {\dot{\mathbf{R}}}_{{\text{e}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}} + {\mathbf{R}}_{{\text{e}}} {\overline{\mathbf{L}}}_{{\text{p}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}}$$

(6)

where ${\hat{\mathbf{F}}}_{{\text{p}}}$ and ${\overline{\mathbf{L}}}_{{\text{p}}}$ are the plastic deformation gradient and plastic velocity gradient in configuration ${\hat{\text{B}}}$ and ${\overline{\text{B}}}$, respectively.

In the crystal plasticity framework, slip systems of a single crystal are modeled explicitly, and the plastic velocity gradient of a single crystal can be calculated as the sum of the shear strain rate in each slip system induced by dislocation slip:

$${\overline{\mathbf{L}}}_{{\text{p}}} = {\dot{\mathbf{F}}}_{{\text{p}}} {\mathbf{F}}_{{\text{p}}}^{ - 1} = \mathop \sum \limits_{\alpha = 1}^{{{\text{N}}_{{{\text{slip}}}} }} \dot{\gamma }^{\alpha } {\overline{\mathbf{p}}}^{\alpha } ,\quad {\overline{\mathbf{p}}}^{\alpha } = {\overline{\mathbf{m}}}^{\alpha } \otimes {\overline{\mathbf{n}}}^{\alpha }$$

(7)

where $\alpha$ is the index of a slip system, $N_{{{\text{slip}}}}$ is the total number of slip systems, $\dot{\gamma }^{\alpha }$ is the shear strain rate in slip system $\alpha$, and ${\overline{\mathbf{p}}}^{\alpha }$ is the Schmid tensor associated with slip system $\alpha$ in configuration ${\overline{\text{B}}}$ [52]. ${\overline{\mathbf{p}}}^{\alpha }$ is expressed as the dyadic product of ${\overline{\mathbf{m}}}^{\alpha }$ and ${\overline{\mathbf{n}}}^{\alpha }$, the slip direction vector and the slip plane normal vector of slip system $\alpha$ in configuration ${\overline{\text{B}}}$, respectively.

The velocity gradients ${\mathbf{L}}$, ${\overline{\mathbf{L}}}_{{\text{p}}}$ and ${\hat{\mathbf{L}}}_{{\text{p}}}$ can be decomposed into their symmetric and skew symmetric parts:

$${\mathbf{L}} = {\mathbf{D}} + {\mathbf{W}},\quad {\overline{\mathbf{L}}}_{{\text{p}}} = {\overline{\mathbf{D}}}_{{\text{p}}} + {\overline{\mathbf{W}}}_{{\text{p}}} ,\quad {\hat{\mathbf{L}}}_{{\text{p}}} = {\hat{\mathbf{D}}}_{{\text{p}}} + {\hat{\mathbf{W}}}_{{\text{p}}}$$

(8)

where ${\mathbf{D}}$, ${\overline{\mathbf{D}}}_{{\text{p}}}$ and ${\hat{\mathbf{D}}}_{{\text{p}}}$, which are the symmetric parts of ${\mathbf{L}}$, ${\overline{\mathbf{L}}}_{{\text{p}}}$ and ${\hat{\mathbf{L}}}_{{\text{p}}}$, respectively, are termed the rate of deformation tensors, while ${\mathbf{W}}$, ${\overline{\mathbf{W}}}_{{\text{p}}}$ and ${\hat{\mathbf{W}}}_{{\text{p}}}$, which are the skew symmetric parts of ${\mathbf{L}}$, ${\overline{\mathbf{L}}}_{{\text{p}}}$ and ${\hat{\mathbf{L}}}_{{\text{p}}}$, respectively, are termed the spin tensors. Using Eqs. (6)–(8), ${\hat{\mathbf{D}}}_{{\text{p}}}$ and ${\hat{\mathbf{W}}}_{{\text{p}}}$ can be formulated as:

$${\hat{\mathbf{D}}}_{{\text{p}}} = {\mathbf{R}}_{{\text{e}}} {\overline{\mathbf{D}}}_{{\text{p}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}} = \mathop \sum \limits_{\alpha = 1}^{{N_{{{\text{slip}}}} }} {\dot{\gamma }}^{\alpha } {\text{sym}}\left( {{\hat{\mathbf{p}}}^{\alpha } } \right) = \mathop \sum \limits_{\alpha = 1}^{{N_{{{\text{slip}}}} }} \dot{\gamma }^{\alpha } {\text{sym}}\left( {{\hat{\mathbf{m}}}^{\alpha } \otimes {\hat{\mathbf{n}}}^{\alpha } } \right)$$

(9a)

$${\hat{\mathbf{W}}}_{{\text{p}}} = {\dot{\mathbf{R}}}_{{\text{e}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}} + {\mathbf{R}}_{{\text{e}}} {\overline{\mathbf{W}}}_{{\text{p}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}} = {\dot{\mathbf{R}}}_{{\text{e}}} {\mathbf{R}}_{{\text{e}}}^{{\text{T}}} + \mathop \sum \limits_{\alpha = 1}^{{N_{{{\text{slip}}}} }} \dot{\gamma }^{{\upalpha }} {\text{skew}}\left( {{\hat{\mathbf{m}}}^{\alpha } \otimes {\hat{\mathbf{n}}}^{\alpha } } \right)$$

(9b)

where

$${\hat{\mathbf{m}}}^{\alpha } = {\mathbf{R}}_{{\text{e}}} {\overline{\mathbf{m}}}^{\alpha } ,\quad {\hat{\mathbf{n}}}^{\alpha } = {\mathbf{R}}_{{\text{e}}} {\overline{\mathbf{n}}}^{\alpha }$$

(10)

The shear strain rate arises from the motion of dislocations; hence, it can be related to the competition between the driving force and the resistance of dislocation slip, namely the resolved shear stress (RSS) and the critical resolved shear stress (CRSS), respectively, via the following rate-dependent formulation [49]:

$$\dot{\gamma }^{\alpha } = \dot{\gamma }_{0}^{\alpha } \left( {\frac{{\left| {\tau^{\alpha } } \right|}}{{\tau_{c}^{\alpha } }}} \right)^{\frac{1}{m}} {\text{sign}}\left( {\tau^{\alpha } } \right)$$

(11)

where $\dot{\gamma }_{0}^{\alpha }$ is a reference shear strain rate, $\tau^{\alpha }$ and $\tau_{c}^{\alpha }$ are the RSS and CRSS associated with slip system $\alpha$, respectively, and $m$ is a strain-rate sensitivity exponent. From Eq. (11), it is seen that plastic yielding and dislocation slip occur only when the RSS is significant in comparison with the CRSS.

The RSS associated with a slip system, as its name suggests, can be derived by resolving the second Piola–Kirchhoff stress tensor ${\mathbf{S}}$ into the slip system. The CRSS, on the other hand, arises from several contributing factors as a result of different hardening mechanisms. In the present work, the CRSS is formulated as:

$$\tau_{c}^{\alpha } = \tau_{0}^{\alpha } + \tau_{{{\text{GB}}}}^{\alpha } + \tau_{{{\text{for}}}}^{\alpha } + \tau_{b}^{\alpha }$$

(12)

where $\tau_{0}^{\alpha }$, $\tau_{{{\text{GB}}}}^{\alpha }$, $\tau_{{{\text{for}}}}^{\alpha }$ and $\tau_{b}^{\alpha }$ are the lattice friction stress, restriction on dislocation slip imposed by grain boundaries, forest dislocation hardening and back stress hardening, respectively. The lattice friction stress $\tau_{0}^{\alpha }$ is usually considered as a constant at a given temperature [39, 53]. The grain boundary effect on dislocation motion, $\tau_{{{\text{GB}}}}^{\alpha }$, is described by the Hall–Petch relation [54, 55]:

$$\tau_{{{\text{GB}}}}^{\alpha } = \frac{{k_{{{\text{HP}}}} }}{\sqrt d }$$

(13)

where $k_{{{\text{HP}}}}$ is the Hall–Petch coefficient and $d$ the grain size. Forest dislocation hardening results from the entanglement and storage of both statistically stored dislocations (SSDs) and GNDs, and can be expressed via the Taylor equation [48, 56]:

$$\tau_{{{\text{for}}}}^{\alpha } = \chi \mu b\sqrt {\rho_{{{\text{ssd}}}}^{\alpha } + \rho_{{{\text{gnd}}}}^{\alpha } }$$

(14)

where $\chi$, $\mu$ and b are a dislocation interaction parameter, the shear modulus of the material and the magnitude of the Burgers vector of the dislocations, respectively. $\rho_{{{\text{ssd}}}}^{\alpha }$ and $\rho_{{{\text{gnd}}}}^{\alpha }$ are the SSD and GND densities associated with slip system $\alpha$, respectively, the evolution equations of which will be presented in the succeeding subsections.

2.2 Statistically stored dislocation density evolution

The SSDs, as their name suggests, are statistical in nature and have no geometric consequence, and their evolution depends on the competition between dislocation storage due to entanglement and annihilation due to dynamic recovery, as expressed by a modified Kocks–Mecking–Estrin (KME) equation as follows [57, 58]:

$$\frac{{\partial \rho_{{{\text{ssd}}}}^{\alpha } }}{{\partial \gamma^{\alpha } }} = \frac{{k_{3} }}{{{\text{bd}}}} + k_{1} \sqrt {\rho_{{{\text{ssd}}}}^{\alpha } } - k_{2} \rho_{{{\text{ssd}}}}^{\alpha } - \left( {\frac{{d_{c} }}{d}} \right)^{2} \rho_{{{\text{ssd}}}}^{\alpha }$$

(15)

where $k_{1}$, $k_{2}$, and $k_{3}$ are three coefficients. In Eq. (15), the partial derivative of SSD density with respect to shear strain represents the accumulation rate of SSDs. The first two terms on the right-hand side denote the increase in SSD density due to athermal storage, where the dislocation mean free path is determined by the grain size and by the average spacing between the dislocations, respectively [48]. The third and fourth terms represent the decrease in SSD density resulting from the dynamic recovery of dislocations. The fourth term stands for an intensified dynamic recovery effect significant only when the grain size is comparable to or below a critical grain size $d_{c}$, at which point the dislocation mean free path is governed by the grain boundaries of the fine grains [48]. The coefficients $k_{1}$ and $k_{2}$ are temperature and strain-rate sensitive and are related to each other via the following equation [59,60,61]:

$$\frac{{k_{2} }}{{k_{1} }} = \frac{\chi b}{g}\left( {1 - \frac{{{\text{kT}}}}{{{\text{Db}}^{3} }}\ln \left( {\frac{{\dot{\varepsilon }}}{{\dot{\varepsilon }_{0} }}} \right)} \right)$$

(16)

where $g$, $k$, $T$, $D$, $\dot{\varepsilon }$ and $\dot{\varepsilon }_{0}$ are an effective activation enthalpy, the Boltzmann’s constant, the temperature, a dislocation drag stress, the applied strain rate and a reference strain rate, respectively. Together, the first and fourth terms on the right-hand side of Eq. (15) are grain-size-dependent, whereas the other two are not.

2.3 Geometrically necessary dislocation density evolution

GNDs are generated in order to maintain strain continuity at polycrystal interfaces; therefore, their evolution is correlated with strain gradient. In conventional strain gradient plasticity theory, GND density is linearly proportional to the strain gradient [62,63,64]. Nevertheless, recent experimental evidence suggests that such a theory may need revision [65, 66], since it does not take the dynamic evolution of dislocation sources into consideration. TEM observation indicates that as plastic deformation continues, dislocation density increases rapidly, leading to an increasing probability of a gliding dislocation cutting across another dislocation loop bowing out of a dislocation source on a different slip plane. The interaction of the two dislocations will lead to the formation of a jog, immobilizing the looping dislocation, hence deactivating the source. As a result, although the intensity of strain gradient increases linearly with increasing strain, the formation and deactivation of dislocation sources gradually reach a dynamic equilibrium as deformation goes on, leading to a gradual slowdown and saturation of GND density [65, 66].

In light of the newly discovered scenario involving dislocation dynamics, a modified strain gradient plasticity formulation is adopted in this work to account for the evolution of GND density with respect to strain gradient [67]:

$$\dot{\rho }_{{{\text{gnd}}}}^{\xi } = \left[ { - \frac{1}{b}\mathop \sum \limits_{\alpha } d_{e}^{\alpha \xi } \left( {\nabla \dot{\gamma }^{\alpha } \cdot m^{\alpha } } \right) + \frac{1}{b}\mathop \sum \limits_{\alpha } d_{s}^{\alpha \xi } \left( {\nabla \dot{\gamma }^{\alpha } \cdot p^{\alpha } } \right)} \right]\left( {1 - \frac{{\rho_{{{\text{gnd}}}}^{\xi } }}{{\rho_{{{\text{gnd}}}}^{{{\text{sat}},\xi }} }}} \right)$$

(17)

where the superscript $\xi$ is an index referring to one of the 12 edge and 6 screw types of GNDs in face-centered cubic (FCC) metals. $d_{e}^{\alpha \xi }$ and $d_{s}^{\alpha \xi }$ are two multipliers with the values of − 1, 0 or 1 according to the spatial relationship between the slip system $\alpha$ and the dislocation index ${\upxi }$ [63, 64]:

$$d_{e}^{\alpha \xi } = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {{\text{for}}\;\; \alpha = \xi = 1, 2, \ldots , 12} \hfill \\ 0 \hfill &\quad {{\text{for}}\;\;{\text{all}}\;{\text{other}}\;{\text{cases}}} \hfill \\ \end{array} } \right.$$

(18a)

and

$$d_{s}^{\alpha \xi } = \left\{ {\begin{array}{*{20}l} { - 1} \hfill &\quad {{\text{for}}\;\;d_{s}^{{\left( {4,13} \right)}} , d_{s}^{{\left( {6,18} \right)}} , d_{s}^{{\left( {8,17} \right)}} , d_{s}^{{\left( {9,15} \right)}} , d_{s}^{{\left( {10,16} \right)}} , d_{s}^{{\left( {11,14} \right)}} } \hfill \\ 1 \hfill &\quad {{\text{for}} \;\;d_{s}^{{\left( {1,16} \right)}} , d_{s}^{{\left( {2,17} \right)}} , d_{s}^{{\left( {3,18} \right)}} , d_{s}^{{\left( {5,14} \right)}} , d_{s}^{{\left( {7,13} \right)}} , d_{s}^{{\left( {12,15} \right)}} } \hfill \\ 0 \hfill &\quad {{\text{for}} \;\;{\text{all}}\;{\text{other}}\;{\text{cases}}} \hfill \\ \end{array} } \right.$$

(18b)

The relationship between the slip system $\alpha$ and the dislocation index $\xi$ is listed in Table 1. $\rho_{{{\text{gnd}}}}^{\xi }$ and $\rho_{{{\text{gnd}}}}^{{{\text{sat}},\xi }}$ are the current and the saturated GND densities, respectively. According to Eq. (17), the increase rate of GND density is dependent on the spatial gradient of the strain rate, and it gradually slows down as the GND density approaches its saturated value, consistent with the aforementioned experimental observation. A procedure for the numerical implementation of Eq. (17) is presented in Appendix A. Once the strain rate gradient in a slip system is calculated, it is substituted into Eq. (17) to calculate the GND densities associated with that slip system.

Table 1 Relationship between Slip System α and Dislocation Index ξ [63, 64]

2.4 Back stress evolution

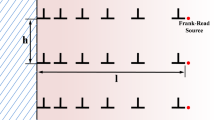
After emission from dislocation sources, the GNDs pile up at grain boundaries, producing long-range back stresses in the opposite direction of the RSS, i.e., toward the dislocation sources, which strengthen and harden the GNS material, as indicated by Eq. (12). The GND pileups are predominantly concentrated in a pileup zone in close proximity to the grain boundaries [21, 68, 69], as illustrated in Fig. 1. Before deriving the equation governing the evolution of back stress, it is necessary to distinguish between the characteristics of edge and screw dislocations. Most GND pileups consist of edge dislocations [70]. This is because unlike an edge dislocation which has a unique slip plane, a screw dislocation can cross slip on multiple slip planes. It has been observed that screw dislocations tend to cross slip out of a GND pileup, leading to the disappearance of the pileup as well as the associated back stress [66]. Therefore, this model only considers the back stress produced by edge dislocation pileups.

Fig. 1

Schematic illustration of geometrically necessary dislocation (GND) pileups in proximity to grain boundaries as well as the produced back stress. $h$, $l$ and $\tau_{b}$ denote the average distance between two GND pileups, the average length of the pileups and the back stress, respectively

Denoting the average spacing of the GND pileups by $h$, the average number of GNDs in a single pileup by $n$, and the total number of GNDs in the pileup zone by $N$, they can be related as follows:

$$N = n\left( \frac{d}{h} \right)$$

(19)

where $d$ is the grain size. The density of GNDs in the pileup zone, on the other hand, by its definition, can be approximated as the number of GND lines threading a surface of unit area, i.e., the number of GNDs lines divided by the area of the pileup zone that they intersect [70]:

$$\rho_{{{\text{gnd}}}}^{\alpha } = \frac{N}{{{\text{dl}}}}$$

(20)

where $l$ is the average length of the GND pileups, as shown in Fig. 1. The back stress generated by a single pileup can be calculated as [53, 71]:

$$\tau_{b}^{\alpha } = \frac{\mu bn}{{\pi \left( {1 - \nu } \right)l}}$$

(21)

where $\nu$ is the Poisson’s ratio of the material. Finally, combining Eqs. (19)–(21), the back stress can be related to the GND density through

$$\tau_{b}^{\alpha } = \frac{{\mu bh\rho_{{{\text{gnd}}}}^{\alpha } }}{{\pi \left( {1 - \nu } \right)}}$$

(22)

which is the governing equation for the evolution of back stress used in this work.

2.5 Grain growth model

As stated in Sect. 1, grain coarsening and refinement occur simultaneously in GNS nickel under tensile deformation, where the nanocrystalline and ultrafine grains smaller than 280 nm undergo coarsening while those larger than 280 nm refinement, both of which are termed “grain growth” in this work for simplicity. To study the effects of grain growth capacity gradients, a grain growth model must be incorporated into the CPFE framework. An earlier experimental investigation on gradient-nanograined copper suggests a linear grain growth behavior of the material under deformation [37]. In addition, previous numerical investigations have demonstrated that linear grain growth models are sufficient to capture the grain-size-dependent behaviors of GNS copper and nickel with the FCC crystal structure [54, 55, 72]. Therefore, a linear grain growth model is adopted in this work, where a change in grain size is proportional to the corresponding change in the applied strain [72]:

$$d = d_{0} + \frac{{\varepsilon - \varepsilon_{0} }}{{\varepsilon_{f} - \varepsilon_{0} }}\left( {d_{f} - d_{0} } \right)$$

(23)

In Eq. (23), $d$, $d_{0}$ and $d_{f}$ are the current, the initial and the final grain sizes with respect to the tensile deformation, respectively; $\varepsilon$, $\varepsilon_{0}$ and $\varepsilon_{f}$ are the current, the initial and the final applied engineering strain, respectively.

2.6 Finite element model

The constitutive equations as well as the governing equations for the evolution of SSD density, GND density and back stress are incorporated into a user-defined material subroutine originally developed by Marin et al. [51], which is loaded into the finite element software Abaqus, where a finite element model is created and serves as the numerical solver for these aforementioned equations, as illustrated in Fig. 2.

Fig. 2

Finite element models of the three gradient nanostructured nickel samples a Sample I, b Sample II and c Sample III with different grain size gradients under study, along with schematic illustrations of their microstructures. Each model consists of 10,000 C3D8 elements. Sample I possesses the mildest grain size gradient, whereas Sample III the steepest. The three illustrations of the GNS nickel samples below the three finite element models are only schematic and symbolic in nature. They do not bear any one-to-one correspondence with the models above them in terms of the shape, size and location of each grain. d Boundary conditions applied to the models. The nodal degrees of freedom (d.o.f.) on the RD-, TD- and ND- faces are constrained along the RD, TD and ND, respectively. Uniaxial tension is applied on the RD+ face along RD at a constant strain rate of 3 × 10^–4 s⁻¹

The size of the dog-bone shaped tensile bar and that of the finite element model are shown in Fig. 2. The tensile bar has a gauge length of 6 mm, and a cross section of 0.5 × 1.2 mm² [24, 32]. The most important dimension of the GNS nickel sample is that along the depth of the sample, i.e., the thickness of the tensile bar, since it determines the gradients of the grain size, the texture and the grain growth capacity, which will affect the effects of GNDs and back stress. Therefore, the dimension along the depth of the sample, i.e., along the normal direction (ND), must be based on the actual thickness of the tensile bar. Hence, the dimension of the finite element model along the ND is set as the thickness of the tensile bar, i.e., 0.5 mm, as shown in Fig. 2.

When it comes to the dimensions of the finite element models in the other two directions, i.e., the rolling direction (RD) and the transverse direction (TD), only a fraction of the tensile bar needs to be modeled, since the sizes of the grains at a given depth along these two directions are uniform, and the dimensions along these two directions will not significantly affect the deformation mechanisms and mechanical properties of the samples provided that they are sufficiently large. Nevertheless, as commonly known, the results of finite element analyses are subject to change with a change in the model size and the discretization method, i.e., the size of the model and the number of elements in the mesh will affect the analysis results. To determine the size of the model and the number of elements along the RD and TD, a convergence analysis is performed, where the deformations of two finite element models, one with a dimension of 0.05 × 0.05 × 0.5 mm³ consisting of 10 × 10 × 100 elements and the other 0.075 × 0.075 × 0.5 mm³ consisting of 15 × 15 × 100 elements, are simulated, as discussed in Appendix B. The convergence analysis indicates that the finite element model with a dimension of 0.05 × 0.05 × 0.5 mm³ consisting of 10 × 10 × 100 elements is sufficiently large to provide accurate results for the study, and there is no need to further increase the size of the model. Therefore, this model is used throughout this work. The C3D8-type elements are used to mesh the model, with each element having 8 integration points. Each integration point represents a single grain and has multiple attributes, including its grain size, crystallographic orientation and grain growth capacity.

Since the focus of this work is on the effects of grain size, texture and grain growth capacity gradients, the entire sample along the depth, i.e., from the surface to the core, must be modeled. Due to the multitude of grains and a large discrepancy in grain sizes spanning three orders of magnitude, representing one grain with many elements is not computationally feasible. On the other hand, when one integration point in an element is used to represented multiple grains, a homogenization scheme must be used where the collective behaviors of a cluster of grains are averaged and represented by an integration point [55]. The shortcoming of this homogenization method is that all these grains in the cluster, represented by a single integration point, will have the same displacement and strain values at any given time step, making the calculation of strain gradient and thus, the GND density impossible. In other words, such a homogenization scheme will smear out the intergranular information that is crucial to the calculation of GND density at the grain level. Therefore, the most feasible way to model the GNS nickel samples is to represent each grain with an integration point in a C3D8 finite element, which contains 8 integration points. In this way, the strain rate gradient and thus, the GND density can be calculated by interpolating the values of the strain rate at the 8 integration points in the element using their respective interpolation functions, as presented in Appendix A.

In the CPFE framework, grain size is treated as a parameter or an attribute associated with each grain. As described in Appendix A, instead of representing each grain with an identically sized finite element, the same element size is used throughout the finite element model. This allows for the decoupling of grain size and element size. As a result, grain growth can be implemented by simply changing the size of each grain as a parameter based on the linear grain growth model, i.e., Eq. (23), whereas the shape of the element evolves according to the displacements of the finite element nodes based on the elastic and plastic deformation of the element in the finite element software. When it comes to calculating displacement-dependent variables such as the GND density, the displacement of each integration point in the element is scaled down based on the ratio of the size of the grain to the size of the element, as indicated by Eq. (A7). In this way, the GNS nickel samples studied in this work, which consist of numerous grains with grain sizes spanning three orders of magnitude, can be modeled with an acceptable number of elements, the deformation of which can then be simulated with manageable computational costs.

A Cartesian coordinate system is established for the finite element model, where the three orthogonal directions are the normal direction (ND), the transverse direction (TD) and the rolling direction (RD), respectively. The grain size gradient of the GNS nickel under study is introduced into the model along the ND, as shown in Fig. 2. As illustrated in Fig. 2d, the finite element model has six faces, which are termed RD+, RD−, TD+, TD−, ND+ and ND−, respectively, according to the normal direction and the relative position of each face. The translational degrees of freedom of the nodes on the RD−, TD− and ND− faces are constrained along the RD, TD and ND, respectively, so that rigid body motion of the model is restricted, whereas the nodes on the TD+ and ND+ faces are not constrained. Uniaxial tension is applied on the RD+ face along the RD at a constant strain rate of 3 × 10^–4 s⁻¹, identical to the experimental testing condition.

Three GNS nickel samples with different grain size gradients are under study in this work, as shown in Fig. 3a. These three grain size gradients, represented by the solid symbols in the figure, are extrapolated from three samples in previous studies where the grain size gradients were experimentally determined and represented by the hollow symbols [24, 32]. All three samples have similar grain sizes in the top layer (25 nm) and at the bottom (4 μm), yet the grain size gradient, i.e., the transition in grain size with respect to the normalized distance of the samples, is the mildest in Sample I and the steepest in Sample III, which is also illustrated in Fig. 2. As a result, there is a much higher volume fraction of fine grains in Sample I than in Sample II, and in Sample II than in Sample III.

Fig. 3

a Grain size gradients, b texture gradients and c grain growth capacity gradients of gradient nanostructured nickel Sample I, II and III, respectively. The experimental data are represented by hollow symbols, while their extrapolated values, which are used in the simulations, are displayed as solid ones. In Fig. 3b, the solid lines represent the texture gradients of the samples determined by fitting the experimental data, whereas the dashed lines their extrapolations. The texture gradient of Sample III is obtained by calculating the mean values of those of Sample I and II due to the absence of experimental data. The inset of Fig. 3c is a magnified view of the grain growth capacity gradients of Sample I and II where the grain sizes are below 280 nm. All experimental data are obtained from References [24, 32]

In addition to the grain size gradient, these three samples also differ in the texture gradient. Experimentally measured XRD intensity data for (111) and (200) textured grains in Sample I and II are converted into the percentage or ratio of these two textures and presented in Fig. 3b [32]. These experimental data are then fitted, and (111) and (200) crystallographic orientations are randomly assigned to the grains in each layer based on the fitting results. For instance, in the 9th layer of Sample I, the percentage of (200) textured grains is 48%; hence, a total of 10 × 10 × 8 × 48% = 384 grains are randomly assigned the (200) orientation, while the other 416 grains have the (111) orientation. When it comes to the 62nd layer, where the percentage of (200) textured grains increases to 82.5%, there are a total of 660 grains with the (200) orientation and those with the (111) orientation decrease to 140. In this way, the texture gradients of the samples are incorporated into the CPFE model. For Sample III, the experimental XRD intensity data are unavailable. As a workaround, the mean value of the fitted curves representing the texture gradients of Sample I and II is used for Sample III, as shown in Fig. 3b.

Finally, the grain growth capacity gradients of Sample I and II are taken into consideration by extrapolating the grain coarsening ability data for grains smaller than 280 nm, as well as the measured changes in grain sizes before and after the tensile deformation for those larger than 280 nm, respectively, as shown in Fig. 3c [32]. Again, the experimental grain growth data for Sample III are unavailable. Considering that the grain size gradient of Sample III is similar to that of Sample II in the sense that both are much steeper than that of Sample I, as shown in Fig. 3a, the grain growth capacity of Sample III is expected to be similar to that of Sample II. Therefore, the grain growth capacity of Sample II is also adopted for Sample III in this work, due to a lack of experimental data.

As grain size decreases into the nanoscale, dislocation activities are increasingly confined by the limited space within the grain interior, leading to a gradual transition in deformation mechanism from full dislocation slip to partial dislocation-mediated plasticity [73, 74]. For GNS nickel, plastic deformation is dominated by partial dislocation activities below a critical grain size of 50 nm at room temperature [32]. The transition from full-dislocation-mediated deformation to partial-dislocation dominated processes leads to diminished grain coarsening ability, the critical grain size of which corresponds to the inflection points of the grain growth capacity curves shown in Fig. 3c. Accordingly, in this study, partial dislocation slip is considered as the dominant deformation mechanism for grains smaller than 50 nm, whereas plastic deformation is accommodated by full dislocations for grains larger than the critical grain size. These two types of dislocations not only differ in their respective slip systems, as shown in Table 2, but in the magnitudes of their Burgers vectors as well, as shown in Table 3. These differences are taken into consideration by the model.

Table 2 Slip systems associated with partial and full dislocations in Nickel

Table 3 Material and model parameters

2.7 Material and model parameters

The material and model parameters used in this work are listed in Table 3, most of which are either adopted directly from the literature or calculated based on literature values. For instance, the elastic moduli $C_{11}$, $C_{12}$ and $C_{44}$, the Poisson’s ratio $\nu$, the shear modulus $\mu$, the strain-rate sensitivity exponent $m$, the dislocation interaction parameter $\chi$, etc., are based on their literature values, where the references are given in Table 3. For other parameters, the reference shear strain rate $\dot{\gamma }_{0}^{\alpha }$ is usually at the same order of magnitude as the applied tensile strain rate, which is 3 × 10^–4 s⁻¹. Hence, a $\dot{\gamma }_{0}^{\alpha }$ value of 1 × 10^–4 s⁻¹ is used in this work. The value of the dislocation storage coefficient $k_{1}$ is usually in the range of 10⁸–10¹⁰ m⁻¹ in the literature [60, 75]. Accordingly, a $k_{1}$ value of 1 × 10¹⁰ m⁻¹ is adopted here. Similar to the dislocation storage coefficient, the literature value of the effective activation enthalpy $g$ is in the range of 10^–3–10^–2 [60, 75], and that of the dislocation drag stress $D$ is around 700 MPa [76, 77]. Hence, a value of 2.3 × 10^–2 is used for $g$ and 750 MPa for $D$ in this study, respectively. The saturated GND density $\rho_{{{\text{gnd}}}}^{{{\text{sat}},\xi }}$ adopts an estimated value of 1 × 10¹⁵ m⁻², since it is revealed that in heavily cold rolled nanocrystalline nickel the saturated dislocation density can reach a magnitude of 10¹⁵ m⁻² below a strain level of 10% [78]. Finally, parameters including the lattice friction stress $\tau_{0}^{\alpha }$, the Hall–Petch coefficient $k_{{{\text{HP}}}}$ and the dislocation geometric coefficient $k_{3}$ are determined by fitting the model predictions with experimental data [24, 32]. For example, the lattice friction stress $\tau_{0}^{\alpha }$ and the Hall–Petch coefficient $k_{{{\text{HP}}}}$ are determined by fitting the yield stresses of the three samples. Similarly, the dislocation geometric coefficient $k_{3}$ is determined by fitting the flow stresses of the three samples after yielding. In other words, the fitting is done with respect to multiple engineering stress–strain data and to different parts of these data, which ensures the validity of the parameters used in this study.

3 Results and discussion

3.1 Model validation

In order for the predictive capability of the model to take effect, it must be validated against experimental data first. The mechanical responses of GNS nickel Sample I, II and III under uniaxial tension predicted by the CPFE model are compared with the corresponding experimental data in the form of engineering stress–strain curves, presented in Fig. 4 [24]. The reasonable agreement between the model predictions and the experimental data substantiates the validity of the model. In addition, the model is further validated by applying it to simulate the uniaxial compression of the three samples, as discussed in Appendix C. In the following, the model will be used to explore the individual effects of grain size, texture and grain growth capacity gradients on the deformation mechanisms and mechanical properties of GNS metals.

Fig. 4

Engineering stress–strain curves of gradient nanostructured nickel Sample I, II and III under uniaxial tension predicted by the model in comparison with experimental data [24, 32]

3.2 Effect of grain size gradient

To reveal the individual effects of the grain size gradient, they must be isolated by controlling the other two types of gradients: the texture gradient and the grain growth capacity gradient. Therefore, three different grain size gradients are adopted in this section, corresponding to those of Sample I, II and III illustrated in Fig. 3a, which are named GSG I, II and III, respectively. As stated in Sect. 2.6, GSG I is the mildest of the three whereas GSG III the steepest. Hence, the sample with GSG I has the highest volume fraction of fine grains and the lowest of coarse grains, and vice versa. Furthermore, all three GNS nickel samples possessing these three grain size gradients have exactly the same texture gradient as well as grain growth capacity gradient, which are those associated with Sample I in Fig. 3b and c, respectively, so as to eliminate the impact of these two types of gradients.

The evolution of the average SSD density, GND density and back stress per slip system with respect to engineering strain in the three samples with GSG I, II and III is displayed in Fig. 5a–c, respectively. It is seen that increasing the grain size gradient from GSG I to GSG II initially leads to a decline in the average SSD density, when the applied strain is smaller than 2.44%. Nevertheless, due to the higher rate of increase in the average SSD density in the sample with GSG II compared to that with GSG I, the former surpasses the latter beyond a strain value of 2.44%. In addition, further increasing the grain size gradient from GSG II to GSG III leads to a slightly diminished SSD density throughout the deformation process. Overall, the average SSD density manifests only limited changes with the grain size gradient. In contrast, the average GND density presented in Fig. 5b decreases sharply with an increase in grain size gradient from GSG I to GSG II, and from GSG II to GSG III. Since the back stress produced as a result of GND pileups is proportional to the GND density, as reflected by Eq. (22), the average back stress per slip system also decreases significantly with increasing grain size gradient, as shown in Fig. 5c. Altogether, Fig. 5 indicates that the two types of dislocations, i.e., SSDs and GNDs, evolve distinctly in response to a change in the grain size gradient of GNS nickel.

Fig. 5

a The average SSD density, b The average GND density and c The average back stress per slip system as a function of engineering strain in gradient nanostructured nickel samples with Grain Size Gradient I, II and III, respectively

To study the effects of grain size gradient in detail, it is not only necessary to look at the average values of the SSD and the GND densities as well as the back stress, but also the statistical distributions of these internal variables. Figure 6a–c demonstrates the distribution of the average SSD density as a function of the three grain size gradients at engineering strain levels of 1%, 4% and 6%, respectively. At 1% strain, i.e., the early stage of deformation, for GSG II and GSG III, the SSD densities in most grains are narrowly concentrated around a relatively low value of 1 × 10¹⁴ m⁻², while there are far more grains with higher SSD densities in GSG I. As a result, the average SSD density in GSG I is greater than those in GSG II and III at this stage of deformation, as shown in Fig. 5a. When it comes to 4% strain, however, the number of grains with relatively high SSD densities in GSG II and III surpasses that in GSG I, as illustrated in Fig. 6b, leading to higher average SSD density values in GSG II and III compared to that in GSG I, as shown in Fig. 5a. This trend continues as the strain further increases to 6%, with even more grains having high SSD densities in GSG II and III compared to those in GSG I, further enlarging the discrepancy in the average SSD density values between the former and the latter, as seen in Fig. 5a.

Fig. 6

a–c Statistical distribution of the average SSD density as a function of the three grain size gradients at engineering strain levels of 1%, 4% and 6%, respectively. d–f Distribution of the average GND density as a function of the three grain size gradients at engineering strain levels of 1%, 4% and 6%, respectively. g–i Distribution of the average back stress per slip system as a function of the three grain size gradients at engineering strain levels of 1%, 4% and 6%, respectively

The distributions of the average GND density and the average back stress per slip system with respect to the grain size gradient at strain levels of 1%, 4% and 6% are presented in Fig. 6d–i, respectively. Consistent with the results presented in Fig. 5b and c, an increase in the grain size gradient of GNS nickel gives rise to significant declines in the GND density and back stress, manifested by a sharp decrease in the fraction of grains with high GND densities and back stresses and an increase in the fraction of grains with low GND densities and back stresses at all strain levels.

Several factors, including lattice friction, grain boundary strengthening embodied by the Hall–Petch effect, forest dislocation hardening and back stress hardening, contribute collectively to the mechanical behaviors of GNS nickel under deformation, as indicated by Eq. (12). To figure out the effects of grain size gradient on the mechanical properties of GNS metals, the stress contribution by each individual factor must be revealed, which is shown in Fig. 7a–c for samples with GSG I, II and III, respectively, and the percentage of the contribution to the flow stress by each factor at engineering strain levels of 1%, 4% and 6% is presented in Fig. 7d–f. For GSG I, the Hall–Petch effect contributes most to the flow stress at the early stage of deformation, whereas forest dislocation hardening takes over and plays a dominant role at higher strain levels. For example, the Hall–Petch effect and forest dislocation hardening account for 40.8% and 32.9% of the flow stress at 1% strain, respectively, which become 26.8% and 39.7% at 6% strain. Back stress hardening is also significant in the sample with GSG I, accounting for 17.9% of the flow stress at 6% strain. As the grain size gradient increases from GSG I to GSG III, the effect of forest dislocation hardening increases in significance, whereas the contributions by the Hall–Petch effect and back stress hardening diminish. For example, for GSG I, back stress hardening accounts for 6.1%, 15.8% and 17.9% of the flow stress at 1%, 4% and 6% strain, respectively, which decrease to 0.9%, 2.6% and 3.2% at the corresponding strain levels in the sample with GSG III. In contrast, the percentage of the contribution by forest dislocation hardening is 39.7% at 6% strain in GSG I, which increases to 62.0% at the same strain level in GSG III. From Fig. 7, the individual effects of grain size gradient on each deformation mechanism can be derived, which are presented in Fig. 8a–d. It is clear that increasing the grain size gradient from GSG I to GSG III leads to significant declines in the Hall–Petch effect and back stress hardening, whereas the forest dislocation hardening only exhibits moderate changes.

Fig. 7

a–c Contribution to the overall stress by lattice friction, the Hall–Petch effect, forest dislocation hardening and back stress hardening in gradient nanostructured nickel samples with Grain Size Gradient I, II and III, respectively. d–f Percentage of the contribution to the overall stress by each mechanism at 1%, 4% and 6% strain in each of the three samples with a different grain size gradient, respectively

Fig. 8

Effects of grain size gradient on a lattice friction, b the Hall–Petch effect, c forest dislocation hardening and d back stress hardening as a function of engineering strain, respectively

The distinct patterns of evolution concerning SSDs and GNDs with respect to changes in the grain size gradient of GNS nickel can be attributed to their different origins. With an increase in the grain size gradient from GSG I to GSG II, the fraction of fine grains in the sample decreases while that of coarse grains increases, leading to an increase in the average grain size. As indicated by Eq. (15), this increase in the average grain size will lead to a diminished athermal storage rate of SSDs, reflected by the term $\frac{{k_{3} }}{{{\text{bd}}}}$, as well as a decline in the dynamic recovery of SSDs through the term $\left( {\frac{{d_{c} }}{d}} \right)^{2} \rho_{{{\text{ssd}}}}^{\alpha }$. At the early deformation stage, the SSD density $\rho_{{{\text{ssd}}}}^{\alpha }$ is low; hence, the decrease in SSD density due to the diminished athermal storage is greater than the increase in SSD density resulting from the reduced dynamic recovery, leading to a decrease in the overall SSD density when the grain size gradient increases from GSG I to GSG II at strain levels lower than 2.44%, as shown in Fig. 5a. As plastic deformation continues, the steady increase in SSD density gives rise to continuously enhanced dynamic recovery. Due to the much higher fraction of fine grains in GSG I compared to that in GSG II, the intensified dynamic recovery is much stronger in GSG I than it is in GSG II, thereby suppressing the growth of SSD density in GSG I more strongly than it does in GSG II, leading to a higher rate of increase in the average SSD density of GSG II. As a result, it surpasses the average SSD density of GSG I at 2.44% strain, exhibiting the crossover shown in Fig. 5a, and the difference between the two further increases with increasing strain. Moreover, increasing the grain size gradient from GSG II to GSG III will lead to a further increase in the fraction of coarse grains and hence, a further decrease in both dislocation athermal storage and dynamic recovery. Nevertheless, because the samples with GSG II and III mostly consist of coarse grains, where the effect of the intensified dynamic recovery, i.e., the fourth term on the right-hand side of Eq. (15) is insignificant, the decrease in dislocation storage is more impactful than that in dynamic recovery. As a result, the average SSD density in GSG III is consistently lower than that in GSG II, as shown in Fig. 5a. From the above analysis, it can be concluded that the growth of SSD density is influenced by the competition between grain-size-dependent dislocation athermal storage and dynamic recovery. The simultaneously diminished dislocation storage and recovery arising from an increase in the grain size gradient of GSG metals will partially offset each other, giving rise to only limited changes of SSD density with respect to the grain size gradient.

The GND density, on the other hand, depends on the strain gradient inside the material under deformation, as manifested by Eq. (17). Previous studies indicate that strain gradient is most intense in the vicinity of interfaces such as grain boundaries [15, 69], since the microstructural heterogeneity between two neighboring grains, i.e., the large discrepancy in grain size, hardness, crystallographic orientation et al. on either side of the grain boundary, will lead to pronounced strain discontinuity and hence, intense strain gradient across the interface, which needs to be accommodated by the generation of GNDs [15, 69, 79]. Given the same level of intergranular heterogeneity, i.e., the same strain intensity, the strain gradient near a grain boundary will increase with decreasing grain size, since the variation distance of the strain is restricted by the grain size. As a result, the average GND density will increase with decreasing average grain size, which is supported by experimental and numerical investigations [72, 79, 80]. That is why in this study, decreasing the grain size gradient from GSG III to GSG I, which amounts to increasing the volume fraction of smaller grains, leads to a significant increase in the average GND density, as shown in Fig. 5b.

The above analysis on the difference between the evolution of SSD and GND densities with grain size gradient highlights their distinct origins, which are manifested in the mechanical properties of GNS nickel. As the grain size gradient increases from GSG I to GSG III, the volume fraction of fine grains decreases while that of coarse grains increases, leading to marked declines in both the Hall–Petch effect and the back stress hardening, as shown in Fig. 8b and d, respectively. In contrast, the variation in forest dislocation hardening is more complicated and nuanced. As indicated by Eq. (14), forest dislocation hardening depends on the total dislocation density, i.e., the sum of SSD and GND densities. On one hand, the average SSD density only exhibits moderate changes with grain size gradient owing to the competition between dislocation athermal storage and intensified dynamic recovery, as shown in Fig. 5a. On the other hand, the average GND density decreases significantly with increasing grain size gradient, as shown in Fig. 5b. Hence, the total dislocation density should also exhibit significant declines as the grain size gradient increases from GSG I to GSG III. Nevertheless, as stated in Sect. 2.6, partial dislocations dominate the plastic deformation of nanograins smaller than 50 nm. Since the volume fraction of fine grains decreases with increasing grain size gradient, the number of nanograins with sizes below 50 nm, the plastic deformation of which is mediated by partial dislocations, also decreases from GSG I to GSG III. Partial dislocations, owing to their smaller magnitude of Burgers vector, do not contribute to strain hardening as effectively as full dislocations [72]. Therefore, although the total dislocation density in GSG I is notably higher than those in GSG II and III, the less effective hardening ability associated with GSG I due to a higher fraction of partial-dislocation-mediated nanograins limits the forest dislocation hardening of GSG I and reduces the differences in hardening between the three samples, leading to moderate changes in forest dislocation hardening with grain size gradient, as shown in Fig. 8c.

In conclusion, with an increase in grain size gradient, although forest dislocation hardening only exhibits moderate changes, it increases in significance and becomes the dominant strain hardening mechanism, whereas back stress hardening is only significant when a large volume fraction of fine grains is present in the sample, i.e., with a mild grain size gradient.

3.3 Effect of texture gradient

In this section, the effects of texture gradient on the deformation mechanisms and mechanical behaviors of GNS nickel are investigated. To do so requires controlling the grain size gradient and the grain growth capacity gradient, while systematically modifying the texture gradient of the sample. Therefore, the grain size gradient and grain growth capacity gradient associated with sample I are adopted in this section, as shown in Fig. 3a and c, respectively. Furthermore, four texture gradients, namely TG I, II, III and IV, are adopted in this section, as displayed in Fig. 9a. It is worth noting that TG III is identical to the texture gradient of Sample I in Fig. 3b, which is obtained by fitting the converted experimental data [32]. As the texture gradient increases from TG I to TG IV, the percentage of the (200) textured grains increases while that of the (111) textured ones decreases consistently. Because the average Schmid factor of the 12 FCC slip systems associated with a [200] oriented grain is about 0.272, greater than the average Schmid factor of 0.136 associated with a [111] oriented grain, the average Schmid factor associated with the texture gradient increases consistently from TG I to TG IV, as presented in Table 4.

Fig. 9

a Four texture gradients used in this study where the percentage of (200) textured grains increases from Texture Gradient I to Texture Gradient IV at a given grain size. The hollow triangles represent the experimental data converted from XRD intensity [32]. b Engineering stress–strain curves of gradient nanostructured nickel samples with these four different texture gradients under uniaxial tension

Table 4 Average Schmid factors associated with the texture gradients

The engineering stress–strain responses of GNS nickel samples with TG I, II, III and IV under uniaxial tension are illustrated in Fig. 9b, respectively. The yield and flow stresses decrease consistently from TG I to TG IV, i.e., with an increasing texture gradient. To reveal the deformation mechanisms underlying the observed mechanical behaviors, the average SSD density, GND density and back stress per slip system in the four samples are presented in Fig. 10a–c, respectively. Similar to the trend demonstrated by the stress–strain relationship, the average SSD density, GND density and back stress per slip system all decrease as the texture gradient increases from TG I to TG IV. As a result, both the effects of forest dislocation hardening and back stress hardening decline from TG I to TG IV, as shown in Fig. 11c and d, respectively. In addition, the contributions to the overall flow stress by the lattice friction and the Hall–Petch effect also decrease with increasing texture gradient, as shown in Fig. 11a and b, respectively.

Fig. 10

a The average SSD density, b The average GND density and c The average back stress per slip system as a function of engineering strain in gradient nanostructured nickel samples with Texture Gradient I, II, III and IV, respectively

Fig. 11

Effects of texture gradient on a lattice friction, b the Hall–Petch effect, c forest dislocation hardening and d back stress hardening as a function of engineering strain, respectively

The variation of the macroscopic stresses contributed by the lattice friction and the Hall–Petch effect, respectively, can be easily explained by the Schmid effect: as the lattice friction stress $\tau_{0}^{\alpha }$ is a constant in Eq. (12), and the slip resistance arising from the Hall–Petch effect, $\tau_{{{\text{GB}}}}^{\alpha }$, is identical in all four samples at a given strain level due to the identical grain size gradient and grain growth capacity gradient, the sample with a lower Schmid factor will exhibit a higher contribution to the flow stress and vice versa. Hence, the contributions to the flow stress by the lattice friction and the Hall–Petch effect decrease with an increasing average Schmid factor resulting from an increasing texture gradient. What is not obvious is why the average SSD and GND densities also decrease with an increase in texture gradient, as indicated in Fig. 10a and b, giving rise to similar variations in terms of the forest dislocation hardening and back stress hardening seen in Fig. 11c and d.

The evolution of SSD density and GND density is based on Eqs. (15 and 17), respectively. In both equations, the densities of these two types of dislocations are dependent on the shear strain or the shear strain rate in a slip system. The variations in the average shear strain and the average shear strain rate per slip system with respect to the texture gradient are presented in Fig. 12a and b, respectively. It is seen that the average shear strain rate decreases with increasing texture gradient, leading to the same trend for the average shear strain. The reason underlying the above observation can also be attributed to the Schmid effect: In Eq. (7), the plastic velocity gradient tensor, which is a measure of how fast a grain deforms plastically, is formulated as the sum of the product of the shear strain rate in each slip system and the Schmid tensor associated with that slip system. Equation (7) is expressed in a tensorial format, but its scalar expression should also hold true. Therefore in this work, it is proposed that a similar relationship stands between the total strain rate of a grain and the shear strain rate of each slip system:

$$\dot{\gamma }_{{{\text{total}}}} = \mathop \sum \limits_{\alpha = 1}^{{N_{{{\text{slip}}}} }} \dot{\gamma }^{\alpha } s^{\alpha }$$

(24)

where $\dot{\gamma }_{{{\text{total}}}}$ is the total strain rate of a grain under tensile or compressive deformation, and $s^{\alpha }$ is the Schmid factor associated with slip system $\alpha$. Since the applied macroscopic tensile strain rate on each sample during deformation is constant and identical, i.e., 3 × 10^–4 s⁻¹, as stated in Sect. 2.6, it can be postulated that the average total strain rate per grain in the four samples with different texture gradients should also be similar. Figure 12c shows the average tensile strain rate per grain as a function of engineering strain for these four samples. And it is indeed the case that the grain-averaged total strain rates are identical in these four samples, the value of which is close to 3 × 10^–4 s⁻¹ in a steady state of plastic flow, as seen in Fig. 12c. It then follows that since the average Schmid factor increases with increasing texture gradient from TG I to TG IV, yet the average total strain rate in each sample remains the same, the average shear strain rate in each sample will decrease with increasing texture gradient based on Eq. (24), which is exactly what is observed in Fig. 12b. As a result, the average SSD density, GND density and back stress per slip system also decrease with increasing texture gradient, as shown in Fig. 10a–c, leading to the diminished forest dislocation hardening and back stress hardening with increasing texture gradient from TG I to TG IV seen in Fig. 11c and d, respectively. In sum, the Schmid effect is responsible for the variation in forest dislocation hardening and back stress hardening of GNS nickel with texture gradient as well.

Fig. 12

a The change in the average shear strain and b the change in the average shear strain rate of the slip systems in gradient nanostructured nickel samples with Texture Gradient I, II, III and IV. c The average tensile strain rate per grain as a function of engineering strain in these four samples

While the effect of texture gradient on SSD density can be explained based on the Schmid effect alone, there may be another more subtle yet perhaps equally important factor responsible for the effect of texture gradient on the evolution of GND density and back stress, namely the intergranular misorientation. The statistical distribution of the intergranular misorientation angles in samples with initial texture gradients TG I, II, III and IV is shown in Fig. 13a–d, respectively. By comparing the four figures, it is seen that as the texture gradient increases, the fraction of grains with high misorientation angles, for example those greater than 40°, gradually decreases, whereas the fraction of grains with low misorientation angles increases. Grains with low intergranular misorientation can deform in a more concerted fashion, thereby inducing less deformation incompatibility and strain discontinuity, giving rise to lower strain gradients and thus, lower GND densities inside the sample. In contrast, high intergranular misorientation will lead to more pronounced strain heterogeneity and higher GND densities [67]. Accordingly, as the fraction of grains with high intergranular misorientation decreases and that with low intergranular misorientation increases with increasing texture gradient, the strain gradient will diminish in intensity, leading to decreasing GND density and back stress, which are also responsible for the decrease in the average GND density and back stress per slip system with increasing texture gradient seen in Fig. 10b and c, respectively.

Fig. 13

Statistical distribution of the intergranular misorientation angles in samples with Texture Gradient a I, b II, c III and d IV, respectively

In conclusion, as the increase in texture gradient leads to an increase in the average Schmid factor, the average SSD density decreases as a result of decreasing shear strain rate due to the Schmid effect, while the Schmid effect and the decrease in intergranular misorientation both contribute to the declines in the average GND density and back stress, leading to decreasing forest dislocation hardening and back stress hardening with increasing texture gradient.

3.4 Effect of grain growth capacity gradient

This section focuses on the effects of grain growth capacity gradient on the deformation mechanisms and mechanical properties of GNS metals. The grain size gradient and texture gradient associated with Sample I in Fig. 3a and b, respectively, are adopted in this section, whereas the effects of three grain growth capacity gradients are systematically investigated, namely GGC I, II and III, as shown in Fig. 14a. GGC II is identical to the grain growth capacity gradient of Sample I shown in Fig. 3c. For the fine grains smaller than 280 nm which undergo grain coarsening during tensile deformation, the grain growth capacity gradient increases consistently from GGC I to III, as shown in Fig. 14a. For the grains larger than 280 nm which undergo refinement, the three grain growth capacity gradients are set to be identical to that of Sample I in Fig. 3c.

Fig. 14

a Three grain growth capacity gradients used in this study where the coarsening abilities of the nanocrystalline and ultrafine grains smaller than 280 nm increase from Grain Growth Capacity I to Grain Growth Capacity III at a given grain size. The refining capacities of the grains larger than 280 nm due to the formation of dislocation substructures are set to be identical in all gradients. b Engineering stress–strain curves of gradient nanostructured nickel samples with these three different grain growth capacity gradients under uniaxial tension

The engineering stress–strain curves of the samples with these three grain growth capacity gradients are illustrated in Fig. 14b. It is seen that the stress decreases as the grain growth capacity gradient increases from GGC I to III. Furthermore, the average SSD density, GND density and back stress per slip system with respect to the grain growth capacity gradient are presented in Fig. 15a–c, respectively. The SSD density and GND density exhibit the opposite behaviors in terms of their variations: the SSD density increases yet the GND density decreases with increasing grain growth capacity gradient. Because the average back stress per slip system is linearly dependent on the GND density, as indicated by Eq. (22), it also decreases with an increase in the grain growth capacity gradient.

Fig. 15

a The average SSD density, b the average GND density and c the average back stress per slip system as a function of engineering strain in gradient nanostructured nickel samples with Grain Growth Capacity I, II and III, respectively. d Variation in the coefficient of the intensified dynamic recovery of statistically stored dislocations with the three grain growth capacity gradients

The contributions to the overall flow stress by lattice friction, the Hall–Petch effect, forest dislocation hardening and back stress hardening are shown in Fig. 16a–d, respectively. As the grain growth capacity gradient increases from GGC I to III, the Hall–Petch effect decreases significantly, especially at higher strain levels, the forest dislocation hardening remains largely unchanged, and the back stress hardening manifests moderate decreases. In other words, the decrease in the flow stress of GNS nickel under tension with increasing grain growth capacity gradient seen in Fig. 14b is mostly caused by decreasing Hall–Petch effect and to a lesser extent by decreasing back stress hardening.

Fig. 16

Effects of grain growth capacity gradient on a lattice friction, b the Hall–Petch effect, c forest dislocation hardening and d back stress hardening as a function of engineering strain, respectively

Similar to the discussion on the variations in the average SSD and GND densities in Sect. 3.2, the opposite trends of evolution concerning these two types of dislocations also arise from their distinct origins. The coefficient of the intensified dynamic recovery term, i.e., $\left( {\frac{{d_{c} }}{d}} \right)^{2}$ in Eq. (15), as a function of strain for GGC I to III is illustrated in Fig. 15d. It is seen that this coefficient decreases with increasing strain as a result of grain growth. With increasing grain growth capacity gradient, the nanocrystalline and ultrafine grains smaller than 280 nm can grow to larger sizes at a given strain level. Based on Eq. (15), which governs the evolution of SSD density inside the grains, both dislocation storage embodied by the grain-size-dependent term $\frac{{k_{3} }}{{{\text{bd}}}}$ and intensified dynamic recovery reflected by the term $\left( {\frac{{d_{c} }}{d}} \right)^{2} \rho_{{{\text{ssd}}}}^{\alpha }$ will diminish as a result of larger grain sizes, giving rise to the opposite effects on the net accumulation rate of SSDs. Nevertheless, due to the extremely fine grain sizes, the decrease in the intensified dynamic recovery of dislocations far exceeds the decrease in their storage, leading to a net increase in dislocation athermal storage rate, and thus, a higher SSD density. Hence, the average SSD density increases with increasing grain growth capacity gradient, as shown in Fig. 15a. In contrast, as the fine grains grow to larger sizes, the strain gradient intensity will decrease, resulting in consistently lower average GND density and back stress as the grain growth capacity gradient increases, as shown in Fig. 15b.

In terms of the mechanical properties, since the fine grains can grow to increasingly large sizes as the grain growth capacity gradient increases, the restriction on the motion of dislocations by grain boundaries manifested by the Hall–Petch effect will decrease based on the Hall–Petch relationship, as shown in Fig. 16b. Moreover, because the average SSD and GND densities demonstrate the opposite trends with respect to the grain growth capacity gradient, as shown in Fig. 15a and b, respectively, their variations will partially offset each other, giving rise to only slight changes in the total dislocation density. Hence, the forest dislocation hardening is largely unaffected by changes in the grain growth capacity gradient, as shown in Fig. 16c. Finally, as the average back stress per slip system decreases with increasing grain growth capacity gradient, its contribution to the flow stress exhibits the same trend, as shown in Fig. 16d.

3.5 Effects of structural gradients on strain localization

Nanocrystalline metals are known for their propensity of non-uniform plastic deformation and strain localization due to their limited strain hardening capability, which culminates in the formation of shear bands that lead to catastrophic shear fracture [81,82,83]. In contrast, in GNS and laminated metals consisting of both nanocrystalline and coarse grains, although strain localization still occurs during deformation and leads to the formation of shear bands in the nanostructured layer, the formed shear bands are dispersive and stabilized by strain delocalization due to the constraining effects of the coarse grained layer, resulting in delayed fracture failure and enhanced uniform elongation of the nanostructured layer [83,84,85]. In addition, constitutive modeling of shear band formation in GNS Cu indicates that the number of shear bands in the nanostructured layer increases with increasing grain size gradient, decreasing thickness of the grain size gradient region and increasing surface grain size [86].

Because of the correlation between localized deformation and shear banding, the propensity for strain localization and shear band formation in GNS metals can be revealed through an analysis of the localized strain distribution [87]. The probability density distribution of the granular equivalent plastic strain in GNS nickel samples at 6% tensile strain with respect to the three different grain size gradients, four texture gradients and three grain growth capacity gradients studied in the previous sections are presented in Fig. 17a–c, respectively. The dispersion in the equivalent plastic strain distribution decreases with an increasing grain size gradient or an increasing texture gradient, as shown in Fig. 17a and b, respectively, indicating that plastic strain distribution becomes more uniform, strain heterogeneity is reduced, and the tendency for strain localization is decreased. Furthermore, when it comes to the effects of grain growth capacity gradient, Fig. 17c demonstrates that increasing the grain growth capacity gradient only leads to slight decreases in the dispersion of the plastic strain distribution, i.e., strain localization is only slightly reduced by an increase in the grain growth capacity gradient. To sum up, strain localization in GNS nickel during tensile deformation decreases with increasing grain size gradient and texture gradient, and it is less sensitive to grain growth capacity gradient. These conclusions are consistent with the results from a previous modeling study [86].

Fig. 17

Probability density distribution of the equivalent plastic strain of the grains in GNS nickel samples with a Grain Size Gradient I, II and III; b Texture Gradient I, II, III and IV; and c Grain Growth Capacity Gradient I, II and III, respectively, at 6% strain during tensile deformation

As shown in Fig. 6c, f and i, the distributions of the average SSD density, the average GND density and the average back stress per slip system at 6% tensile strain all decrease in dispersion and increase in uniformity with an increase in the grain size gradient. This indicates that plastic deformation of the coarse grains is more uniform than that of the fine grains. Therefore, an increase in the grain size gradient of the samples, which leads to an increase in the volume fraction of the coarse grains and a decrease in that of the fine grains, will lead to lower strain heterogeneity and localization, as illustrated in Fig. 17a. A decrease in strain localization with respect to an increasing texture gradient, on the other hand, may be attributed to a decrease in the percentage of the (111) oriented grains. It has been reported that strain localization is dependent on local grain interaction [88] and is facilitated by plastically harder neighboring grains [89]. As illustrated in Fig. 9a, an increase in texture gradient leads to an increase in the percentage of the (200) textured grains relative to that of the (111) textured grains. The (111) textured grains have lower Schmid factors than those of the (200) textured grains and are thus plastically harder to deform. Therefore, as the texture gradient increases, the percentage of the plastically harder (111) textured grains decreases, leading to diminished strain localization in the samples. The above analysis highlights the significance of structural gradients on the deformability of GNS metals.

As reviewed in Sect. 1, the MCDD method is an atomistically informed multiscale crystal plasticity finite element method. In comparison with the CPFE model proposed in this work, the MCDD method possesses several significant advantages: to begin with, it is capable of capturing geometrically compatible dislocation pattern distribution and evolution in FCC and BCC single crystals, which the CPFE model, due to its higher length scale based on continuum mechanics, is unable to simulate. Secondly, the MCDD method can model crystal plasticity without or with minimal empiricism, since it is an atomic-level first principle method that does not require any physical parameters to be fitted. In addition, the MCDD method is capable of simulating temperature-dependent dislocation substructures, such as dislocation cross slip in single BCC crystal at low temperature and dislocation cell structures at high temperature, whereas the proposed CPFE model does not take the effects of temperature on dislocation substructures into consideration. In terms of disadvantages, firstly, due to its multiscale nature, the MCDD method is more computationally intense and expensive compared with the CPFE model. Furthermore, despite its greatly expanded time and length scale as well as improved computational efficiency in comparison with conventional molecular dynamics method, the MCDD method is limited to studying crystal plasticity at micrometer or submillimeter scale. In contrast, the CPFE model proposed in this work, which is rooted in continuum mechanics, can capture the mechanical behaviors of materials at macroscopic length scale and at quasi-static experimental strain rate, which allows the model predictions to be compared directly with experimental results under laboratory conditions.

As a final remark, the three prominent features of GNS metals under investigation in this work, i.e., the grain size gradient, texture gradient and grain growth capacity gradient, can all be tuned by altering or adjusting the methods, routes and parameters used in their synthesis and processing. For instance, grain size gradient can be tuned by adjusting the processing time in surface mechanical attrition treatment [90, 91], as well as the current density and additive content in electrodeposition [24]. Texture gradient can be tuned by modifying the nominal rolling strain during cold rolling [33], the processing time in surface mechanical attrition treatment [34], as well as the current density, additive content and pulse parameters in electrodeposition [32, 36]. Grain growth capacity gradient can be tuned by adding alloying elements to selected areas of the sample, the pinning effect of which reduces grain boundary mobility and thus, retards grain growth [92], by altering experimental temperature [32], and by adjusting annealing parameters [93]. Developing a complete understanding of the structure–property relationship of GNS metals and alloys is crucial to optimizing the properties and performance of this class of materials, as well as to designing novel and superior heterostructured materials for engineering applications. The author hopes that the conclusions made in this work will be helpful to that end.

4 Conclusion

In this study, a crystal plasticity finite element model is created incorporating the formulations for the evolution of statistically stored and geometrically necessary dislocations as well as back stress resulting from dislocation pileups to reveal the individual effects of grain size, texture and grain growth capacity gradients on the deformation mechanisms and mechanical properties of gradient nanostructured metals. It is found that:

• Increasing the grain size gradient, which increases the volume fraction of the coarse grains at the expense of the fine grains, leads to only limited changes in the average SSD density due to the competition between simultaneously diminished dislocation storage and dynamic recovery. The average GND density, on the hand, decreases consistently due to decreasing strain gradient intensity, giving rise to a similar trend in the variation of the average back stress. As a result, there is a pronounced decrease in the back stress hardening, in contrast to the moderate changes manifested by the forest dislocation hardening. Together with a significantly weakened Hall–Petch effect, an increase in the grain size gradient of GNS metals lowers the overall strength of the materials.

• Increasing the texture gradient, which increases the average Schmid factor of the sample, leads to consistent declines in the average SSD density, GND density and back stress. The decrease in the average SSD density is attributed to decreasing average shear strain rate of the slip systems as a result of the Schmid effect, whereas the Schmid effect and decreasing intergranular misorientation are both responsible for the decrease in the average GND density and back stress with increasing texture gradient. Together, the yield and flow stresses of GNS metals decrease with an increase in texture gradient.

• Increasing the grain growth capacity gradient, which increases the average grain size at a given strain level, leads to an increase in the average SSD density due to diminished dynamic recovery of dislocations, as well as decreases in the average GND density and back stress, which arise from a reduced strain gradient intensity. As a result, the Hall–Petch effect and back stress hardening decrease with increasing grain growth capacity gradient, whereas the forest dislocation hardening is largely unaffected due to the opposite patterns of variation in SSD and GND densities, leading to a decrease in the strength of GNS metals.

• Strain localization decreases with increasing grain size gradient and texture gradient, and it is less sensitive to grain growth capacity gradient.

Appendices

Appendix A: Procedure for the numerical implementation of GND density evolution

In Eq. (17), the increase rate of GND density is dependent on the spatial gradient of the strain rate. Therefore, the first step in the numerical implementation of Eq. (17) is calculating the strain rate gradient, which is calculated by modifying a numerical procedure developed in [94] and adopted in [95]. To begin with, the gradient of shear strain rate in slip system $\mathrm{\alpha }$ in the global Cartesian coordinate system, $\nabla \dot{\gamma }^{\alpha }$, is written as:

$$\nabla \dot{\gamma }^{\alpha } = \frac{{\partial \dot{\gamma }^{\alpha } }}{\partial x}{\mathbf{e}}_{{\mathbf{x}}} + \frac{{\partial \dot{\gamma }^{\alpha } }}{\partial y}{\mathbf{e}}_{{\mathbf{y}}} + \frac{{\partial \dot{\gamma }^{\alpha } }}{\partial z}{\mathbf{e}}_{{\mathbf{z}}}$$

(A1)

where (${\mathbf{e}}_{{\mathbf{x}}}$, ${\mathbf{e}}_{{\mathbf{y}}}$, ${\mathbf{e}}_{{\mathbf{z}}}$) are unit vectors along the TD, RD and ND, respectively, as shown in Fig. 2.

The value of a field variable at a given point in an element can be calculated by interpolating the values at the Gaussian integration points using the interpolation functions. Hence, the shear strain rate can be calculated as:

$$\dot{\gamma }^{\alpha } = \mathop \sum \limits_{i = 1}^{8} N_{i} \dot{\gamma }_{i}^{\alpha }$$

(A2)

where i is an index referring to one of the eight integration points in a C3D8 finite element, as shown in Fig. 18. $N_{i}$ and $\dot{\gamma }_{i}^{\alpha }$ are the interpolation function and shear strain rate in slip system $\alpha$ at the ith integration point, respectively.

Fig. 18

Schematic illustration of the finite element C3D8, which contains 8 integration points

It then follows that the strain rate gradient can be calculated by calculating the partial derivative of the interpolation function with respect to the displacement at each integration point in the element:

$$\begin{array}{*{20}r} \hfill {\frac{{\partial \dot{\gamma }^{\alpha } }}{\partial x} = \mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} }}{\partial x}\dot{\gamma }_{i}^{\alpha } } \\ \hfill {\frac{{\partial \dot{\gamma }^{\alpha } }}{\partial y} = \mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} }}{\partial y}\dot{\gamma }_{i}^{\alpha } } \\ \hfill {\frac{{\partial \dot{\gamma }^{\alpha } }}{\partial z} = \mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} }}{\partial z}\dot{\gamma }_{i}^{\alpha } } \\ \end{array}$$

(A3)

The partial derivative of the interpolation function with respect to displacement at an integration point, $\frac{{\partial N_{i} }}{\partial x}$, $\frac{{\partial N_{i} }}{\partial y}$ and $\frac{{\partial N_{i} }}{\partial z}$, can be calculated using the chain rule:

$$\begin{array}{*{20}r} \hfill {\frac{{\partial N_{i} }}{\partial x} = \frac{{\partial N_{i} }}{\partial g}\frac{\partial g}{{\partial x}} + \frac{{\partial N_{i} }}{\partial h}\frac{\partial h}{{\partial x}} + \frac{{\partial N_{i} }}{\partial r}\frac{\partial r}{{\partial x}}} \\ \hfill {\frac{{\partial N_{i} }}{\partial y} = \frac{{\partial N_{i} }}{\partial g}\frac{\partial g}{{\partial y}} + \frac{{\partial N_{i} }}{\partial h}\frac{\partial h}{{\partial y}} + \frac{{\partial N_{i} }}{\partial r}\frac{\partial r}{{\partial y}}} \\ \hfill {\frac{{\partial N_{i} }}{\partial z} = \frac{{\partial N_{i} }}{\partial g}\frac{\partial g}{{\partial z}} + \frac{{\partial N_{i} }}{\partial h}\frac{\partial h}{{\partial z}} + \frac{{\partial N_{i} }}{\partial r}\frac{\partial r}{{\partial z}}} \\ \end{array}$$

(A4)

where g, h and r are the counterparts of x, y and z, respectively, in the isoparametric space, i.e., coordinates in the local coordinate system. Equation (A4) can be further written in a matrix form:

$$\left[ {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial x}} \\ {\frac{{\partial N_{i} }}{\partial y}} \\ {\frac{{\partial N_{i} }}{\partial z}} \\ \end{array} } \right] = J^{ - 1} \left[ {\begin{array}{*{20}c} {\frac{{\partial N_{i} }}{\partial g}} \\ {\frac{{\partial N_{i} }}{\partial h}} \\ {\frac{{\partial N_{i} }}{\partial r}} \\ \end{array} } \right]$$

(A5)

where $J$ is the Jacobian matrix:

$$J = \left[ {\begin{array}{*{20}c} {\frac{\partial x}{{\partial g}}} & {\frac{\partial y}{{\partial g}}} & {\frac{\partial z}{{\partial g}}} \\ {\frac{\partial x}{{\partial h}}} & {\frac{\partial y}{{\partial h}}} & {\frac{\partial z}{{\partial h}}} \\ {\frac{\partial x}{{\partial r}}} & {\frac{\partial y}{{\partial r}}} & {\frac{\partial z}{{\partial r}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}z_{i} } \hfill \\ {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}z_{i} } \hfill \\ {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}z_{i} } \hfill \\ \end{array} } \right]$$

(A6)

where $x_{i}$, $y_{i}$ and $z_{i}$ are the coordinates of the ith integration point in the global coordinate system.

Equation (A6) indicates that the calculated strain rate gradient is dependent on the displacements of integration points, and thus, on element size. Therefore, in theory, the size of each element in the finite element model should be identical to the actual size of the grain it represents. However, due to the large difference in grain sizes in the GNS nickel, which span three orders of magnitude from 25 to 4 μm, it is infeasible to model the material using such a modeling scheme, since the numerous fine grains would make the simulation computationally intractable. Instead, the same element size is used throughout the sample, as shown in Fig. 2, and the displacement of each integration point in an element is scaled down based on the ratio of the size of the grain that the element represents to the size of the element. Accordingly, Eq. (A6) is rewritten as:

$$J = \frac{d}{l}\left[ {\begin{array}{*{20}l} {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial g}z_{i} } \hfill \\ {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial h}z_{i} } \hfill \\ {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}x_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}y_{i} } \hfill & {\mathop \sum \limits_{i = 1}^{8} \frac{{\partial N_{i} \left( {g, h, r} \right)}}{\partial r}z_{i} } \hfill \\ \end{array} } \right]$$

(A7)

where d and l are the grain size and the size of the finite element, respectively.

Once the gradient of shear strain rate, $\nabla \dot{\gamma }^{\alpha }$, is calculated, it is substituted into Eq. (17) to calculated the rate of GND density evolution, i.e., $\dot{\rho }_{{{\text{gnd}}}}^{\xi }$. Finally, the GND density at the end of the current time step can be calculated as:

$$\rho_{{{\text{gnd}}}}^{\xi , n} = \rho_{{{\text{gnd}}}}^{\xi , n - 1} + \dot{\rho }_{{{\text{gnd}}}}^{\xi } \cdot \Delta t$$

(A8)

where $\rho_{{{\text{gnd}}}}^{\xi , n}$ and $\rho_{{{\text{gnd}}}}^{\xi , n - 1}$ are the GND densities at the end of the current time step and the previous time step, respectively. $\Delta t$ is the time increment during a time step.

Appendix B: Convergence analysis for the determination of model size and element numbers along the rolling and transverse directions

A convergence analysis is performed to determine the size of the model and the number of elements along the RD and TD. The deformations of two finite element models, one with a dimension of 0.05 × 0.05 × 0.5 mm³ consisting of 10 × 10 × 100 elements and the other 0.075 × 0.075 × 0.5 mm³ consisting of 15 × 15 × 100 elements, are simulated, as shown in Fig. 19a. The engineering stress–strain responses of Sample I, II and III, respectively, predicted by these two models are shown in Fig. 19b, while the average SSD density, GND density and back stress per slip system are shown in Fig. 20, respectively. It is seen that the results calculated with these two models are almost completely identical to each other, indicating that the analysis results have converged with respect to both models, and that a finite element model with a dimension of 0.05 × 0.05 × 0.5 mm³ consisting of 10 × 10 × 100 elements is sufficiently large to provide accurate results for the study, and there is no need to further increase the size of the model. Therefore, a finite element model with a dimension of 0.05 × 0.05 × 0.5 mm³ consisting of 10 × 10 × 100 elements is used throughout this work.

Fig. 19

a Two finite element models consisting of 10 × 10 × 100 elements and 15 × 15 × 100 elements, respectively, used in the convergence analysis. b Engineering stress–strain curves of Sample I, II and III, respectively, predicted by these two models

Fig. 20

a The average SSD density, b the average GND density and c the average back stress per slip system as a function of engineering strain in gradient nanostructured nickel samples I, II and III, respectively, calculated using the two models with different dimensions and meshes shown in Fig. 19a

Appendix C: Gradient nanostructured nickel samples under uniaxial compression as further validation of the model

To further validate the model by demonstrating that it can also be applied to deformation modes other than uniaxial tension, the uniaxial compression of Sample I, II and III is simulated at a constant strain rate of 3 × 10^–4 s⁻¹. The engineering stress–strain responses of the three samples under uniaxial compression are illustrated in Fig. 21a, while the average SSD density, the average GND density and the average back stress per slip system as a function of engineering strain in these three samples are presented in Fig. 21b–d, respectively. The CPFE model proposed in this work successfully predicted the evolution of deformation mechanisms and the mechanical behaviors of the samples under uniaxial compression, further substantiating its validity and applicability. In addition, it is seen that the predicted flow stresses of the samples under compression are higher than those under tension, as shown in Fig. 4, especially near the points of uniform elongation, which is consistent with previous studies [96,97,98].

Fig. 21

a Engineering stress–strain curves of gradient nanostructured nickel Sample I, II and III under uniaxial compression, respectively, predicted by the model. b The average SSD density, c the average GND density and d the average back stress per slip system as a function of engineering strain in these three samples under uniaxial compression