Upscaling of Diffusion–Reaction Phenomena by Homogenisation Technique: Possible Appearance of Morphogenesis

Abstract

The main objective of this work is to describe reaction–diffusion of two species in a porous medium. We aim at finding the macroscopic model equivalent to the description of the physics at the pore scale, with a peculiar attention to possible shape morphogenesis as introduced in Turing’s seminal article in 1952 (Turing in Philos Trans R Soc Lond Ser B 237:37, 1952). The upscaling process makes use of the method of asymptotic expansions which takes advantage of the presence of the small parameter of separation of scales $\varepsilon = l/L$, where l and L are the characteristic sizes of the pores and the sample or the diffusion wavelength, respectively. Two different situations are investigated here: large reaction–diffusion and large diffusivity ratios. Among all possibilities, we investigate three orders of magnitude of the reaction terms and two orders of magnitude of the diffusivity ratio. In each of the situations, we demonstrate, if it exists, the macroscopic equivalent model at a scale $L \gg l$, at the first order of approximation. Hence, we obtain a catalogue of macroscopic models for each considered case, their domain of validity, and the expression of the macroscopic properties. We underline the adequate conditions to account for the appearance of morphogenesis.

1 Introduction

The main objective of this work is to describe reaction–diffusion of two chemical substances, called morphogens, in a porous medium. Citing the introduction of Murray (2002), “Mathematics is required to bridge the gap between the level on which most of our knowledge is accumulating and the macroscopic level of the patterns we see. [...] Even if the mechanisms were well understood, mathematics would be required to explore consequences of manipulating the various parameters associated with any particular scenario. [...] The goal is to develop models which capture the essence of various interactions allowing their outcome to be more fully understood”. We aim here at finding the macroscopic equivalent model to the description of the physics at the pore scale, with a peculiar attention to possible morphogenesis. Morphogenesis is a mechanism which produces spatial patterning. Let us note that morphogenesis could be also present in the absence of separation of scales, when considering a periodic sample of a porous medium. Patterns appear, for example, on coat mammals, on butterfly’s wings, or on flowers. Morphogenesis may result from eventual instabilities of species concentrations (Turing 1952), as in the present work. Morphogenesis is also present in geology, for example, in hornfels, metamorphic rocks formed by contact metamorphism and heat diffusion. A nice example of such hornfels can be found in the Milliau Island, France (Barriere 1977). Other examples may be found in Kessler and Werner (2003).

For examples of morphogenesis in the nano-micro-technologies, the interested reader may refer to Grzybowski et al. (2005). Some authors addressed the problem at stake by using homogenisation techniques such as Panfilov (2010) for an example of such patterns in porous media, but he did not introduce dimensionless parameters, Allaire [8] by considering only one particular case or Valdes-Parada et al. (2017) by using another technique of homogenisation.

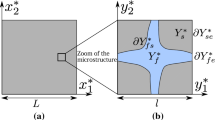
The existence of macroscopic equivalent model is here determined by using the method of asymptotic expansions (Auriault 1991; Auriault et al. 2009). The equations describing the physical phenomena at the pore scale are first set in a dimensionless form, based on characteristic physical values. Dimensionless parameters are hence obtained explicitly as ratios of characteristic quantities. Considering these dimensionless parameters, at different orders of magnitude, leads to different macroscopic behaviours in the case of homogenisable situations. If the situation cannot be homogenised, no macroscopic equivalent model exists. Hence, we obtain a catalogue of macroscopic models for each considered case, their domain of validity, and the expression of the macroscopic property. For the sake of clarity, we will limit the development to the first order of approximation. In order to illustrate our methodology, we consider here a porous media as the fluid holder. For the sake of simplicity, we assume a rigid periodic porous medium with a large number of periods $\Omega$ with a characteristic size l: the size of the porous sample is $L\gg l$. $\varepsilon = l/L \ll 1$ is the small parameter of separation of scales. The boundary of the pores $\Omega _l$ is denoted $\delta \Omega _l$. Two species of concentration $c_1$ and $c_2$ are diffusing and reacting with each other in a fluid at rest which saturates the periodic porous medium. We also assume that the process is isotropic. The reaction–diffusion process is described at the pore scale by the following two coupled equations:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial X_i\partial X_i} + f(c_1, c_2), \end{aligned}$$

(1)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial X_i\partial X_i} +g(c_1, c_2), \end{aligned}$$

(2)

The boundary $\delta \Omega _l$ is assumed as impervious to the solutes:

$$\begin{aligned} D_p{\partial c_p\over \partial X_i}n_i =0 \quad \text{ on }\ \delta \Omega _l,\quad p=1,2, \end{aligned}$$

(3)

where $\mathbf n$ is the unit normal to $\Omega _l$. In the above equations, $D_1$ and $D_2$ are the molecular diffusion coefficients of the two species 1 and 2, respectively. We will see that the structures of functions f and g have no influence on the upscaling process. In contrast to the upscaling process, the structures of f and g play an important role when investigating morphogenesis. Different f and g yield different patterns. Therefore, for the sake of simplicity of the presentation, we will consider linear reaction terms, since the upscaling results will remain valid for nonlinear f and g

$$\begin{aligned} f(c_1, c_2)= & {} R_{11}c_1 + R_{12}c_2 + R_{10}, \\ g(c_1, c_2)= & {} R_{21}c_1 + R_{22}c_2 + R_{20}. \end{aligned}$$

The above reaction terms are such that positive (negative) $R_{11}$ and $R_{22}$ correspond to auto-production (auto-degradation) and positive (negative) $R_{12}$ and $R_{21}$ correspond to cross-production (cross-degradation). An example of such system may be found in Turing (1952) p. 70. The assumption of linearity is based on the idea that any reaction terms may be linearised as a first approximation, as suggested by Segel and Jakson (2012). This system was also presented in Cross and Hohenberg (1993).

Let us recall that, in the framework of the upscaling process in use, two quantities A and B are related by $A =\mathcal{O}(\varepsilon ^p B)$ if

$$\begin{aligned} \varepsilon ^{p+1}\ll {A\over B} \ll \varepsilon ^{p-1}. \end{aligned}$$

Then the domain of validity of $A= \mathcal{O}(B)$ is generally quite large. For the sake of simplicity, all the coefficients in the above equations are assumed as constant over $\Omega _f$ and we consider $c_1/c_2= \mathcal{O}(\varepsilon ^0)$ and $f/g= \mathcal{O}(\varepsilon ^0)$. The aim of the paper is to investigate transient diffusion with reaction at scale $L\gg l$. Therefore, at least one species, say species 1, verifies

$$\begin{aligned} {c_1 \over t_c} =\mathcal{O}\left( D_1{ c_1\over L^2 }\right) , \end{aligned}$$

where $t_c$ is the characteristic time of the process. And $c_2$ will verify

$$\begin{aligned} {c_2 \over t_c} =\mathcal{O}\left( \varepsilon ^q D_2{ c_2\over L^2 }\right) , \end{aligned}$$

where $q=0$ shows that transient diffusion with reaction is also present for $c_2$ at scale L, and $q = 1, 2$ correspond to high diffusivity contrasts.

In the case of linear f and g, we assume for simplicity

$$\begin{aligned} R_{11}= \mathcal{O}(R_{12})= \mathcal{O}(R_{21})= \mathcal{O}(R_{22}). \end{aligned}$$

We will also consider cases where $f=0$ and $g=0$ intersect, which corresponds to the following condition in the case of linear f and g :

$$\begin{aligned} R_{11} R_{22} - R_{12}R_{21} \ne 0. \end{aligned}$$

Note that the model (1, 2, 3) may be seen itself as a macroscopic equivalent model at scale l to a model at a lower scale, the diffusing particle scale. Therefore, (1, 2, 3) is an approximate model. However, this approximation has no influence on the upscaling process from scale l to scale L to be addressed since we will limit the present analysis to the first-order macroscopic model (Auriault 2017).

The aim of the paper is twofold:

1. To determine a macroscopic equivalent model, if it exists, at scale L from the description at the pore scale l. Length L is either the characteristic size of the macroscopic porous sample or the pseudo-wavelength of the solute concentrations (that supposes a sufficiently small excitation time). The upscaling process is conducted by using the technique of double-scale expansions (Auriault et al. 2009; Bensoussan et al. 1978; Keller 1977; Sanchez-Palencia 1974, 1980). It consists in first rendering dimensionless system (1, 2, 3) and evaluating the dimensionless numbers in function of the integer powers of the small parameter of separation of scale $\varepsilon$ (Auriault 1991; Auriault et al. 2009). This is generally done by using either l or L for the characteristic length. In this paper, we consider the “macroscopic point of view”, i.e. we choose L. Therefore, the dimensionless space variable is $\mathbf{x}= \mathbf{X} / L$. However, as physical quantities are also varying at the pore scale l, we introduce a second dimensionless variable $\mathbf{y}= \mathbf{X} / l = \mathbf{x}/\varepsilon$. Physical dimensionless quantities, say $\phi$, depend on both $\mathbf{x}$ and $\mathbf{y}$ and on the dimensionless time $t^*$, defined as the ratio of the time to a characteristic time. They are in the following form:

$$\begin{aligned} \phi = \phi ^{(0)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon \phi ^{(1)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon ^2 \phi ^{(2)} (\mathbf{x},\mathbf{y},t^*)+ \cdots ,\quad {\mathbf{y}=\mathbf{x}/ \varepsilon .} \end{aligned}$$

(4)

Due to the assumed periodic character of the porous medium, the $\phi ^{(i)}$’s are $\mathbf{y}$-periodic. After introducing such expansions for $c_1$ and $c_2$ into (1, 2, 3), the method consists in investigating $\phi ^{(0)}$ and its successive correctors: $\varepsilon \phi ^{(1)}$, $\varepsilon ^2 \phi ^{(2)}$, etc. The approximate nature of the equations (1, 2, 3) plays no role since we only need here the three first terms in the expansion (Auriault 2017). Indeed, the upscaling process yields the equivalent macroscopic model, if it exists.

Shortly speaking, non-homogenisable situations correspond to the absence of a separation of scales: $L = \mathcal O$(l).

2. To look for possible morphogenesis, which could occur in two different situations:

• When the diffusivity ratio is ${D_1/D_2 = \mathcal O}(\varepsilon ^0)$, a morphogenesis process appears under two conditions as presented in Turing (1952); Murray (2002, 2003); Garikipati (2017).

  Firstly, the reaction terms f and g in (1, 2) cancel out during the reaction–diffusion process as t goes to infinity :

  $$\begin{aligned} f(c_1, c_2)= & {} 0, \end{aligned}$$

  (5)
  $$\begin{aligned} g(c_1, c_2)= & {} 0, \end{aligned}$$

  (6)

  which means that $c_1$ and $c_2$ are constant. These values may be obtained by considering a macroscopic boundary value problem with time-independent boundary values of $c_1$ and $c_2$. Then, as time t goes to infinity, the concentrations reach locally constant values.

  Secondly, the values of $c_1$ and $c_2$ given by (5, 6) should correspond to an unstable equilibrium. The interested reader may refer for details to Murray (2003) page 87. The induced diffusion process then yields patterns.

• A large diffusivity ratio, ${(D_1/D_2) = \mathcal O}(\varepsilon ^{-2})$, could yield a pore scale concentration $c_2(\mathbf{y})$ which describes patterns.

The dimensionless form of the diffusion–reaction system is presented in Sect. 2. When the diffusivity ratio is ${D_1/D_2 = \mathcal O}(\varepsilon ^0)$, we are left with a single dimensionless number which measures the ratio of the reaction term to the diffusion term. This dimensionless number is to be evaluated in function of the small parameter of separation of scales, $\varepsilon$. This number introduces a third characteristic length, the diffusion–reaction length $l_{DR} = \sqrt{D/R}$, where D and R are diffusion and linear reaction constants, respectively (Garikipati 2017). Then, in Sect. 3 we investigate the upscaling process in the case ${D_1/D_2 = \mathcal O}(\varepsilon ^0)$, for different estimations of $l_{DR}$, in particular: $l_{DR}=\mathcal{O}(L)$, the intermediate case where $l_{DR}=\mathcal{O}(\varepsilon ^{-1/2}l)= \mathcal{O}(\varepsilon ^{1/2}L)$, and $l_{DR}=\mathcal{O}(\varepsilon ^0)= \mathcal{O}(\varepsilon L)$. The possible appearance of morphogenesis is investigated. Finally Sect. 4 is devoted to the investigation of large diffusivity ratios, $D_1/D_2=\mathcal{O}(\varepsilon ^{-1})$ and $D_1/D_2=\mathcal{O}(\varepsilon ^{-2})$, respectively. All the different macroscopic models of reaction–diffusion are presented in Table 1.

Table 1 Synthesis of the different first-order macroscopic models of reaction–diffusion in porous media

2 Dimensionless Diffusion–Reaction System

The solute concentrations $c_1(\mathbf{X},t)$ and $c_2(\mathbf{X},t)$ verify

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial X_i\partial X_i} + f(c_1, c_2), \end{aligned}$$

(7)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial X_i\partial X_i} +g(c_1, c_2), \end{aligned}$$

(8)

$$\begin{aligned} D_p{\partial c_p\over \partial X_i}n_i= & {} 0 \quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(9)

Remember that we assume both solute concentrations of similar orders of magnitude, as well as the different terms in the definitions of f and g.

As above mentioned, the main results of the following upscaling analysis will remain valid for nonlinear reaction terms, such as the Schnakenberg model (Schnakenberg 1976).

$$\begin{aligned} \begin{aligned} f(c_1, c_2)= R_{10} +R_{11}c_1 + R_{12}c_1^2 c_2, \\ g(c_1, c_2)=R_{20}+ R_{21}c_1 + R_{22}c_1^2 c_2. \end{aligned} \end{aligned}$$

(10)

However, for simplicity, we consider here only linear expressions of both f and g.

We consider a periodic-time excitation which generates concentration pseudo-wavelengths $\mathcal{O}(L)$. We use L as the characteristic length to make dimensionless the diffusion–reaction system. The dimensionless space variable is $\mathbf{x}= \mathbf{X} / L$. Therefore, we have at constant frequency $\omega$

$$\begin{aligned} \mathcal{B}_1={\vert {\partial c_1 \over \partial t} \vert \over \vert D_1{\partial ^2 c_1\over \partial X_i\partial X_i} \vert } ={\omega L^2 \over D_1}, \quad \mathcal{B}_2={\vert {\partial c_2 \over \partial t} \vert \over \vert D_2{\partial ^2 c_2\over \partial X_i\partial X_i} \vert } ={\omega L^2 \over D_2}, \quad \mathcal{D}= {\mathcal{B}_2 \over \mathcal{B}_1} ={D_1 \over D_2}. \end{aligned}$$

On the other hand, since $f = \mathcal O$ (g), we have:

$$\begin{aligned} \mathcal{A}_1={ \vert f \vert \over \vert D_1{\partial ^2 c_1\over \partial X_i\partial X_i} \vert } = {R L^2 \over D_1 } ={ L^2 \over l^2_{DR_1}}, \quad \mathcal{A}_2={ \vert g \vert \over \vert D_2{\partial ^2 c_2\over \partial X_i\partial X_i} \vert } ={ R L^2 \over D_2 } ={ L^2 \over l^2_{DR_2}}, \end{aligned}$$

with $l_{RD_i}=\sqrt{D_i/R}$, $i=1,2$, and $R = \mathcal{O}(R_{11})= \mathcal{O}(R_{12})= \mathcal{O}(R_{21})= \mathcal{O}(R_{22})$.

The dimensionless system becomes:

$$\begin{aligned} \mathcal{B}_1{\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \mathcal{A}_1f(c_1, c_2), \end{aligned}$$

(11)

$$\begin{aligned} \mathcal{B}_2{\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} +\mathcal{A}_2\,g(c_1, c_2), \end{aligned}$$

(12)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0 \quad \text{ on }\ \delta \Omega _l,\quad p=1,2, \end{aligned}$$

(13)

where, for the sake of simplicity, notations are kept unchanged, with the exception of the space variable which is now $\mathbf {x}$.

Among all possibilities, we focus on two classes of situations, either $D_1/D_2=\mathcal{O}(\varepsilon ^0)$ or large ratio $D_1/D_2$.

2.1 Diffusivity Ratio $(D_1/D_2)=\mathcal{O}(\varepsilon ^0)$, $\mathcal{A}=\mathcal{A}_1=\mathcal{A}_2=\mathcal{O}(\varepsilon ^{-p})$, $p=0, 1, 2$

(Presented in Sect. 3)

As $D_1/D_2=\mathcal{O}(\varepsilon ^0)$, we have $\mathcal{B}_1=\mathcal{B}_2=\mathcal{O}(\varepsilon ^0)$. We are left with a single dimensionless number, namely $\mathcal{A}=\mathcal{A}_1=\mathcal{A}_2$. Three estimations of $\mathcal{A}$ are of peculiar interest in order to take into account the coupling between the species: $\mathcal{A}= \mathcal{O}(\varepsilon ^0)$, i.e. $l_{RD}= \mathcal{O}(L)$, $\mathcal{A}= \mathcal{O}(\varepsilon ^{-1})$, i.e. $l_{RD}= \mathcal{O}(\varepsilon ^{1/2}L)$, and $\mathcal{A}= \mathcal{O}(\varepsilon ^{-2})$, i.e. $l_{RD}= \mathcal{O}(l)$, for models I, II, and III, respectively. The corresponding dimensionless systems are successively investigated in Sect. 3. For the sake of simplicity, dimensionless notations are left unchanged, with the exception of the space variable. The dimensionless diffusion–reaction system is in the form:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \mathcal{A} \ f(c_1, c_2), \end{aligned}$$

(14)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} +\mathcal{A} \ g(c_1, c_2), \end{aligned}$$

(15)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(16)

2.2 Large Diffusivity Ratios $\mathcal{D}=D_1/D_2=\mathcal{O}(\varepsilon ^{-p})$, $p=1, 2$

(Presented in Sect. 4)

We consider $\mathcal{D}=D_1/D_2=\mathcal{O}(\varepsilon ^{-p})$, $\mathcal{A}_1 =\mathcal{O}(\mathcal{B}_1) = \mathcal{O}(\varepsilon ^0)$ and $\mathcal{A}_2 =\mathcal{O}(\mathcal{B}_2)=\mathcal{O}(\varepsilon ^p)$, $p=1, 2$.

The dimensionless system then becomes:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \ f(c_1, c_2), \end{aligned}$$

(17)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} \varepsilon ^p D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \ g(c_1, c_2), \end{aligned}$$

(18)

$$\begin{aligned} D_q{\partial c_q\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad q=1,2. \end{aligned}$$

(19)

The two cases $q=1,2$ of large diffusivity ratio, models IV and V, are investigated in Sects. 4.1 and 4.2, respectively.

The estimations of the dimensionless numbers for the different investigated models are shown in Table 1.

3 Diffusivity Ratio $(D_1/D_2)=\mathcal{O}(\varepsilon ^0)$

3.1 Low reaction–diffusion: $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^0)$: Model I

Model I is for $\mathcal{B}_1 = \mathcal{O}(\mathcal{B}_2)= \mathcal{O}(\mathcal{A}_1)= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^0)$. We have ${l_{RD}}= \mathcal{O}(L)$.

The dimensionless diffusion–reaction system becomes:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \ f(c_1, c_2), \end{aligned}$$

(20)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \ g(c_1, c_2), \end{aligned}$$

(21)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(22)

$c_1$ and $c_2$ are in the following form:

$$\begin{aligned} c_1= & {} c_1^{(0)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon c_1^{(1)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon ^2 c_1^{(2)} (\mathbf{x},\mathbf{y},t^*)+ \cdots \end{aligned}$$

(23)

$$\begin{aligned} c_2= & {} c_2^{(0)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon c_2^{(1)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon ^2 c_2^{(2)} (\mathbf{x},\mathbf{y},t^*)+ \cdots ,\quad {\mathbf{y}=\mathbf{x}/ \varepsilon ,} \end{aligned}$$

(24)

where the $c^{(i)}$ ’s are $\mathbf{y}$-periodic. The upscaling process is similar to the one presented in previous works (Auriault 1991; Auriault et al. 2009). After introducing the two above ansatz into (20, 21, 22), and extracting like powers of $\varepsilon$, we successively obtain boundary value problems to be investigated.

• At the lower-order $\varepsilon ^{-2}$, it becomes:

  $$\begin{aligned}&D_1{\partial ^2 c^{(0)}_1\over \partial y_i\partial y_i} =0, \end{aligned}$$

  (25)
  $$\begin{aligned}&D_2{\partial ^2 c^{(0)}_2\over \partial y_i\partial y_i} =0, \end{aligned}$$

  (26)
  $$\begin{aligned}&D_p{\partial c^{(0)}_p\over \partial y_i}n_i =0 \text{ on }\ \delta \Omega _l, \quad c^{(0)}_p \ \text{ y-periodic }, p=1,2. \end{aligned}$$

  (27)

  The solution is:

  $$\begin{aligned} c^{(0)}_1=c^{(0)}_1(\mathbf{x},t), \quad c^{(0)}_2=c^{(0)}_2(\mathbf{x},t). \end{aligned}$$

• At the next-order $\varepsilon ^{-1}$, it becomes:

  $$\begin{aligned}&D_1{\partial \over \partial y_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right) =0, \end{aligned}$$

  (28)
  $$\begin{aligned}&D_2{\partial \over \partial y_i}\left( {\partial c^{(1)}_2\over \partial y_i }+ {\partial c^{(0)}_2\over \partial x_i}\right) =0, \end{aligned}$$

  (29)
  $$\begin{aligned}&D_p\left( {\partial c^{(1)}_p\over \partial y_i} + {\partial c^{(0)}_p\over \partial x_i}\right) n_i =0 \text{ on }\ \delta \Omega _l,\quad c^{(1)}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

  (30)

  From the above, $c^{(1)}_1$ and $c^{(2)}_1$ will be in the following form:

  $$\begin{aligned} c^{(1)}_1= & {} \xi _{1i} (\mathbf{y}) {\partial c^{(0)}_1\over \partial x_i} + {\bar{c}}^{(1)}_1(\mathbf{x},t), \\ c^{(1)}_2= & {} \xi _{2i} (\mathbf{y}) {\partial c^{(0)}_2\over \partial x_i} + {\bar{c}}^{(1)}_2(\mathbf{x},t). \end{aligned}$$

• Finally, the first-order equivalent macroscopic model is obtained by considering the order $\varepsilon ^0$:

  $$\begin{aligned} D_1{\partial \over \partial y_i}\left( {\partial c^{(2)}_1\over \partial y_i }+ {\partial c^{(1)}_1\over \partial x_i}\right)= & {} {\partial c^{(0)}_1 \over \partial t} - D_1{\partial \over \partial x_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right) -f^{(0)}, \end{aligned}$$

  (31)
  $$\begin{aligned} D_2{\partial \over \partial y_i}\left( {\partial c^{(2)}_2\over \partial y_i }+ {\partial c^{(1)}_2\over \partial x_i}\right)= & {} {\partial c^{(0)}_2 \over \partial t} - D_2{\partial \over \partial x_i}\left( {\partial c^{(1)}_2\over \partial y_i }+ {\partial c^{(0)}_2\over \partial x_i}\right) -g^{(0)} \end{aligned}$$

  (32)
  $$\begin{aligned} D_p\left( {\partial c^{(2)}_p\over \partial y_i} + {\partial c^{(1)}_p\over \partial x_i}\right) n_i= & {} 0, \text{ on }\ \delta \Omega _l,\quad c^{(2)}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

  (33)

  The Fredholm alternative imposes to the averages of the right-hand members of (31) and (32) to cancel out. This gives the equivalent macroscopic model at the first order of approximation

  $$\begin{aligned} {\partial c^{(0)}_1 \over \partial t}= & {} D^{(eff)}_{1ij}{\partial ^2 c^{(0)}_1\over \partial x_i\partial x_j} + {f^{(0)}(c^{(0)}_1,c^{(0)}_2)}, \end{aligned}$$

  (34)
  $$\begin{aligned} {\partial c^{(0)}_2 \over \partial t}= & {} D^{(eff)}_{2ij}{\partial ^2 c^{(0)}_2\over \partial x_i\partial x_j} +{g^{(0)}{(c^{(0)}_1,c^{(0)}_2)}}. \end{aligned}$$

  (35)

  The effective diffusion tensors $D^{(eff)}_{1ij}$ and $D^{(eff)}_{2ij}$ are:

  $$\begin{aligned} D^{(eff)}_{1ij}= & {} D_1<I_{ij} +{\partial \xi _{1i} \over \partial y_j}>,\\ D^{(eff)}_{2ij}= & {} D_2<I_{ij} +{\partial \xi _{2i} \over \partial y_j}>, \end{aligned}$$

  where $< .>$ stands for the pore volume averaging symbol

  $$\begin{aligned} <\phi > = {1 \over \Omega _l}\int _{\Omega _l} \phi \ \text{ d } \Omega . \end{aligned}$$

Model I is a “classical” macroscopic equivalent model. Note that morphogenesis is generally absent, unless very peculiar cases, for example, when considering a ring of size L, which imposes periodic condition at the boundary of the sample $X \in [0,L]$ (Turing 1952).

3.2 Large Diffusion–Reaction: $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-1})$: Model II

We investigate $\mathcal{B}_1 = \mathcal{O}(\mathcal{B}_2)= \mathcal{O}(\varepsilon ^0)$ and $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-1})$. We have here ${l_{RD}}= \mathcal{O}(\varepsilon ^{1/2}L)$.

The dimensionless diffusion–reaction system now takes the form:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \varepsilon ^{-1}\ f(c_1, c_2), \end{aligned}$$

(36)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \varepsilon ^{-1} \ g(c_1, c_2), \end{aligned}$$

(37)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(38)

At the order $\varepsilon ^{-2}$, we recover the same system as for model I. Therefore, we have:

$$\begin{aligned} c^{(0)}_1=c^{(0)}_1(\mathbf{x},t), \quad c^{(0)}_2=c^{(0)}_2(\mathbf{x},t). \end{aligned}$$

At the order $\varepsilon ^{-1}$, the system becomes:

$$\begin{aligned} D_1{\partial \over \partial y_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right)= & {} - f^{(0)}, \quad f^{(0)}=R_{11}c^{(0)}_1 + R_{12}c^{(0)}_2 + R_{10}, \end{aligned}$$

(39)

$$\begin{aligned} D_2{\partial \over \partial y_i}\left( {\partial c^{(1)}_2\over \partial y_i }+ {\partial c^{(0)}_2\over \partial x_i}\right)= & {} - g^{(0)}, \quad g^{(0)}=R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}, \end{aligned}$$

(40)

$$\begin{aligned} D_p\left( {\partial c^{(1)}_p\over \partial y_i} + {\partial c^{(0)}_p\over \partial x_i}\right) n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad c^{(1)}_p \ \text{ y-periodic },\quad p=1,2. \end{aligned}$$

(41)

Integration of (39) and (40) over the period yields

$$\begin{aligned}<f^{(0)}>=0, \quad <g^{(0)}>=0. \end{aligned}$$

However, since $c^{(0)}_1$ and $c^{(0)}_2$ are $\mathbf{y}$ independent, we obtain

$$\begin{aligned} \begin{aligned} f^{(0)}=R_{11}c^{(0)}_1 + R_{12}c^{(0)}_2 + R_{10}=0,\\ g^{(0)}=R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}=0. \end{aligned} \end{aligned}$$

(42)

The above system stands for the first-order approximation of the equivalent macroscopic model. Since $R_{11} R_{22} - R_{12}R_{21} \ne 0$, $c^{(0)}_1$ and $c^{(0)}_2$ are well defined. Note that they are $\mathbf{y}$, $\mathbf{x}$, and t independent.

3.2.1 Morphogenesis

Values of the concentrations given by (42) may be unstable (Turing 1952). Possible morphogenesis then occurs with a pattern wavelength $l_{DR} = \sqrt{D/R}=\mathcal{O} (\varepsilon ^{1/2} L)$. The $\varepsilon ^{-1/2} \Omega$-periodic increments ${\tilde{c}}_1$ and ${\tilde{c}}_2$, defined as

${\tilde{c}}_i = c^{(0)}_i - <c^{(0)}_i>$ (i = 1, 2), towards a morphologic pattern, if it exists, are described by:

$$\begin{aligned} {\partial {\tilde{c}}_1 \over \partial t}= & {} D_1{\partial ^2 {\tilde{c}}_1\over \partial z_i\partial z_i} + R_{11}{\tilde{c}}_1 + R_{12}{\tilde{c}}_2, \end{aligned}$$

(43)

$$\begin{aligned} {\partial {\tilde{c}}_2 \over \partial t}= & {} D_2{\partial ^2 {\tilde{c}}_2\over \partial z_i\partial z_i} + R_{21}{\tilde{c}}_1 + R_{22}{\tilde{c}}_2, \end{aligned}$$

(44)

$$\begin{aligned} D_p{\partial {\tilde{c}}_p\over \partial z_i}n_i= & {} 0\quad \text{ on } \text{ the } \text{ pore } \text{ surface }, \quad {\tilde{c}}_p \ \text{ y-periodic }, \quad p=1,2, \end{aligned}$$

(45)

where $\mathbf{z}= \mathbf{X} / \varepsilon ^{1/2}L$.

The general solution of this system takes the form, in the 1D case to simplify the presentation (Garikipati 2017)

$$\begin{aligned} {\tilde{c}}_p=\sum _k U_{pk} \exp ^{i kz}\exp ^{\omega _k t}, \quad p=1,2. \end{aligned}$$

(46)

After introduction in the above system, we obtain

$$\begin{aligned} U_{1k} \omega _k= & {} - D_1 U_{1k}\vert k \vert ^2 + R_{11} U_{1k}+ R_{12} U_{2k}, \end{aligned}$$

(47)

$$\begin{aligned} U_{2k} \omega _k= & {} - D_2 U_{2k}\vert k \vert ^2 + R_{21} U_{1k}+ R_{22} U_{2k}. \end{aligned}$$

(48)

For non-trivial values of the $U_{pk}$, one must have

$$\begin{aligned} \omega _k= & {} {-((D_1+ D_2)\vert k \vert ^2 - R_{11} - R_{22} )\over 2} \nonumber \\&\quad \pm {\sqrt{((D_1 + D_2)\vert k \vert ^2 - R_{11} - R_{22})^2 + 4 R_{12}R_{21}} \over 2}. \end{aligned}$$

(49)

Unstable situations are for $\text{ Re }(\omega _k)>0$, which gives morphogenesis. Model II is possibly a morphogenesis model with $c_1$ and $c_2$ patterns.

3.2.2 Correctors

Remember that $c^{(0)}_1$ and $c^{(0)}_2$ are time-independent values of the concentrations. Equations (39), (40), and (41) for the first $\Omega$-periodic correctors $c^{(1)}_1$ and $c^{(1)}_2$ are simplified to

$$\begin{aligned}&D_1{\partial ^2 c^{(1)}_1\over \partial y_i\partial y_i} =0 \end{aligned}$$

(50)

$$\begin{aligned}&D_2{\partial ^2 c^{(1)}_2\over \partial y_i\partial y_i} = 0 \end{aligned}$$

(51)

$$\begin{aligned}&D_p {\partial c^{(1)}_p\over \partial y_i} n_i =0 \quad \text{ on }\ \delta \Omega _l, \quad { c}^{(1)}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

(52)

From the above,

$$\begin{aligned} c^{(1)}_1=c^{(1)}_1(\mathbf{x},t), \quad c^{(1)}_2=c^{(1)}_2(\mathbf{x},t). \end{aligned}$$

At the next order, we obtain

$$\begin{aligned} D_1{\partial \over \partial y_i}\left( {\partial c^{(2)}_1\over \partial y_i }+ {\partial c^{(1)}_1\over \partial x_i}\right)= & {} - f^{(1)}, \quad f^{(1)}=R_{11}c^{(1)}_1 + R_{12}c^{(1)}_2 , \end{aligned}$$

(53)

$$\begin{aligned} D_2{\partial \over \partial y_i}\left( {\partial c^{(2)}_2\over \partial y_i }+ {\partial c^{(1)}_2\over \partial x_i}\right)= & {} - g^{(1)}, \quad g^{(1)}=R_{21}c^{(1)}_1 + R_{22}c^{(1)}_2 , \end{aligned}$$

(54)

$$\begin{aligned} D_p\left( {\partial c^{(2)}_p\over \partial y_i} + {\partial c^{(1)}_p\over \partial x_i}\right) n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad { c}^{(2)}_p \ \text{ y-periodic },\quad p=1,2. \end{aligned}$$

(55)

Integration over the period of (53) and (54) yields

$$\begin{aligned}<f^{(1)}>=0, \quad <g^{(1)}>=0. \end{aligned}$$

The above system stands for the first corrector of the equivalent macroscopic model. We see that $c^{(1)}_1 =0$ and $c^{(1)}_2 =0$. It is easy to check that this property stands for all successive correctors $c^{(i)}_1=0$ and $c^{(i)}_2=0$, $i\ge 2.$

3.3 Very Large Diffusion–Reaction: $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-2})$: Model III

We now consider $\mathcal{B}_1 = \mathcal{O}(\mathcal{B}_2)= \mathcal{O}(\varepsilon ^0)$ and $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-2})$. We have ${l_{RD}}= \mathcal{O}(l)$.

The dimensionless diffusion–reaction system takes now the form

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \varepsilon ^{-2}\ f(c_1, c_2), \end{aligned}$$

(56)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \varepsilon ^{-2} \ g(c_1, c_2), \end{aligned}$$

(57)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(58)

After introducing ansatz (23) and (24), we obtain at the order $\varepsilon ^{-2}$

$$\begin{aligned} D_1{\partial ^2 c^{(0)}_1\over \partial y_i\partial y_i}= & {} - f^{(0)}, \quad f^{(0)}=R_{11}c^{(0)}_1 + R_{12}c^{(0)}_2 + R_{10}, \end{aligned}$$

(59)

$$\begin{aligned} D_2{\partial ^2 c^{(0)}_2\over \partial y_i\partial y_i}= & {} - g^{(0)}, \quad g^{(0)}=R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}, \end{aligned}$$

(60)

$$\begin{aligned} D_p{\partial c^{(0)}_p\over \partial y_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad { c}^{(0)}_p \ \text{ y-periodic },\quad p=1,2. \end{aligned}$$

(61)

The Fredholm alternative imposes

$$\begin{aligned}<f^{(0)}>=0, \quad <g^{(0)}>=0. \end{aligned}$$

From the above, constant values of $<c^{(0)}_1>$ and $<c^{(0)}_2>$ that are independent of x and t are obtained. Let

$$\begin{aligned} c^{(0)}_1 =<c^{(0)}_1> + {\tilde{c}}_1, \quad c^{(0)}_2 = <c^{(0)}_2> + {\tilde{c}}_2. \end{aligned}$$

${\tilde{c}}_1$ and ${\tilde{c}}_2$ verify

$$\begin{aligned} D_1{\partial ^2 {\tilde{c}}^{(0)}_1\over \partial y_i\partial y_i}= & {} - R_{11}{\tilde{c}}^{(0)}_1 - R_{12}{\tilde{c}}^{(0)}_2 , \end{aligned}$$

(62)

$$\begin{aligned} D_2{\partial ^2 {\tilde{c}}^{(0)}_2\over \partial y_i\partial y_i}= & {} -R_{21}{\tilde{c}}^{(0)}_1 - R_{22}{\tilde{c}}^{(0)}_2 , \end{aligned}$$

(63)

$$\begin{aligned} D_p{\partial {\tilde{c}}^{(0)}_p\over \partial y_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad {\tilde{c}}^{(0)}_p \ \text{ y-periodic },\quad p=1,2. \end{aligned}$$

(64)

The solution is

$$\begin{aligned} {\tilde{c}}_1 =0, \quad {\tilde{c}}_2 =0. \end{aligned}$$

$c^{(0)}_1$ and $c^{(0)}_2$ are constants independent of $\mathbf{x}$ and t as in model II.

Model III is therefore described as:

$$\begin{aligned} R_{11} c^{(0)}_1 + R_{12} c^{(0)}_2 + R_{10}= & {} 0, \end{aligned}$$

(65)

$$\begin{aligned} R_{21} c^{(0)}_1 + R_{22} c^{(0)}_2 + R_{20}= & {} 0. \end{aligned}$$

(66)

3.3.1 Morphogenesis

When the values given by the above system (65), (66) are unstable, a periodic instability of period $\Omega$ arrises which yields a pattern wavelength $l_{DR} = l$.

The $\Omega$-periodic increments ${\tilde{c}}_1 = c^{(0)}_1 - <c^{(0)}_1>$ and ${\tilde{c}}_2 = c^{(0)}_2 - <c^{(0)}_2>$ towards a morphologic pattern are described by

$$\begin{aligned} {\partial {\tilde{c}}_1 \over \partial t}= & {} D_1{\partial ^2 {\tilde{c}}_1\over \partial y_i\partial y_i} + f({\tilde{c}}_1, {\tilde{c}}_2), \end{aligned}$$

(67)

$$\begin{aligned} {\partial {\tilde{c}}_2 \over \partial t}= & {} D_2{\partial ^2 {\tilde{c}}_2\over \partial y_i\partial y_i} + \ g({\tilde{c}}_1, {\tilde{c}}_2), \end{aligned}$$

(68)

$$\begin{aligned} D_p{\partial {\tilde{c}}_p\over \partial y_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad {\tilde{c}}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

(69)

Model III may yield morphogenesis with $c_1$ and $c_2$ patterns.

3.3.2 Correctors

We assume now the stability at the first order. After taking into account the properties of $c^{(0)}_1$ and $c^{(0)}_2$, the first correctors $c^{(1)}_1$ and $c^{(1)}_2$ verify

$$\begin{aligned} D_1{\partial ^2 c^{(1)}_1\over \partial y_i \partial y_i}= & {} - f^{(1)}, \quad f^{(1)}=R_{11}c^{(1)}_1 + R_{12}c^{(1)}_2 , \end{aligned}$$

(70)

$$\begin{aligned} D_2{\partial ^2 c^{(1)}_2\over \partial y_i \partial y_i}= & {} - g^{(1)}, \quad g^{(1)}=R_{21}c^{(1)}_1 + R_{22}c^{(1)}_2 , \end{aligned}$$

(71)

$$\begin{aligned} D_p{\partial c^{(1)}_p\over \partial y_i} n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad { c}^{(1)}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

(72)

It becomes

$$\begin{aligned} c_1^{(1)}= c_2^{(1)} =0. \end{aligned}$$

It is easy to check that all further correctors cancel out.

3.4 Other Estimations of the Diffusion–Reaction Term

To complete the analysis of the present section, let us shortly consider the two following limit cases.

3.4.1 Extremely Large Diffusion–Reaction: $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-3})$

The dimensionless diffusion–reaction system takes now the form

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \varepsilon ^{-3}\ f(c_1, c_2), \end{aligned}$$

(73)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \varepsilon ^{-3} \ g(c_1, c_2), \end{aligned}$$

(74)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(75)

After introducing ansatz (23) and (24), we obtain at the order $\varepsilon ^{-3}$

$$\begin{aligned} R_{11} c^{(0)}_1 + R_{12} c^{(0)}_2 + R_{10}= & {} 0, \end{aligned}$$

(76)

$$\begin{aligned} R_{21} c^{(0)}_1 + R_{22} c^{(0)}_2 + R_{20}= & {} 0. \end{aligned}$$

(77)

We recover the result (65) and (66) which describes model III. It is clear that $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{-p})$, $p>3$ yields the same result.

3.4.2 Extremely Small Diffusion–Reaction: $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon )$

The dimensionless diffusion–reaction system takes now the form

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \varepsilon \ f(c_1, c_2), \end{aligned}$$

(78)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \varepsilon \ g(c_1, c_2), \end{aligned}$$

(79)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(80)

Introducing again ansatz (23) and (24), it is easy to check that the upscaling process yields at the first order of approximation, two non-coupled diffusion equations for $c_1$ and $c_2$, respectively. In model VI (see Table 1), the reaction–diffusion and morphogenesis are absent at the first order of approximation. This result remains valid for $\mathcal{A}_1= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{p})$, $p>1$. The models associated with different evaluations of $\mathcal{A}$ are shown in Fig. 1.

Fig. 1

Different macroscopic models for $\mathcal{D} = \mathcal{D}_1 /\mathcal{D}_2 = \mathcal{O}(\varepsilon ^0)$ and $\mathcal{A} = \mathcal{A}_1 = \mathcal{A}_2 = \mathcal{O}(\varepsilon ^p)$. Models with possible morphogenesis are shown by a “$^{*}$”

4 Large Diffusivity Ratio, $D_1 / D_2$

4.1 Large Diffusivity Ratio, $D_1 / D_2= \mathcal{O}(\varepsilon ^{-1})$: Model IV

We investigate in this section the case where the diffusivity ratio is large, $D_1 / D_2=\mathcal{O} (\varepsilon ^{-1})$. We have $\mathcal{B}_1 = \mathcal{O}(\mathcal{A}_1)= \mathcal{O}(\varepsilon ^0)$ and $\mathcal{B}_2= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon )$. The dimensionless system now becomes:

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \ f(c_1, c_2), \end{aligned}$$

(81)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} \varepsilon D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \ g(c_1, c_2), \end{aligned}$$

(82)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(83)

The concentrations are in the following form (23–24).

• At the lower order, it becomes:

  $$\begin{aligned}&D_1{\partial ^2 c^{(0)}_1\over \partial y_i\partial y_i} =0, \end{aligned}$$

  (84)
  $$\begin{aligned}&D_2{\partial ^2 c^{(0)}_2\over \partial y_i\partial y_i} =0, \end{aligned}$$

  (85)
  $$\begin{aligned}&D_p{\partial c^{(0)}_p\over \partial y_i}n_i =0\quad \text{ on }\ \delta \Omega _l, \quad c^{(0)}_p \ \text{ y-periodic }, \quad p=1,2. \end{aligned}$$

  (86)

  The solution is:

  $$\begin{aligned} c^{(0)}_1=c^{(0)}_1(\mathbf{x},t), \quad c^{(0)}_2=c^{(0)}_2(\mathbf{x},t). \end{aligned}$$

• At the next order, $c^{(1)}_1$ is given by:

  $$\begin{aligned}&D_1{\partial \over \partial y_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right) =0, \end{aligned}$$

  (87)
  $$\begin{aligned}&D_1\left( {\partial c^{(1)}_1\over \partial y_i} + {\partial c^{(0)}_1\over \partial x_i}\right) n_i =0 \text{ on }\ \delta \Omega _l,\quad c^{(1)}_1 \ \text{ y-periodic }. \end{aligned}$$

  (88)

  As in Sect. 3, $c^{(1)}_1$ will be in the form:

  $$\begin{aligned} c^{(1)}_1= \xi _{1i} (\mathbf{y}) {\partial c^{(0)}_1\over \partial x_i} + {\bar{c}}^{(1)}_1(\mathbf{x},t). \end{aligned}$$

• Now, $c^{(2)}_1$ verifies

  $$\begin{aligned} D_1{\partial \over \partial y_i}\left( {\partial c^{(2)}_1\over \partial y_i }+ {\partial c^{(1)}_1\over \partial x_i}\right)= & {} {\partial c^{(0)}_1 \over \partial t} - D_1{\partial \over \partial x_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right) -f^{(0)}, \end{aligned}$$

  (89)
  $$\begin{aligned} D_1\left( {\partial c^{(2)}_p\over \partial y_i} + {\partial c^{(1)}_p\over \partial x_i}\right) n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad c^{(2)}_p \ \text{ y-periodic }. \end{aligned}$$

  (90)

  The Fredholm alternative imposes to the averages of the right-hand members of (89) to cancel out. This gives the equivalent macroscopic model at the first order of approximation similar to Model I

  $$\begin{aligned} {\partial c^{(0)}_1 \over \partial t}= & {} D^{(eff)}_{1ij}{\partial ^2 c^{(0)}_1\over \partial x_i\partial x_j} + f^{(0)}, \nonumber \\ f^{(0)}= & {} R_{11}c^{(0)}_1 + R_{12}c^{(0)}_2 + R_{10}. \end{aligned}$$

  (91)

• $c^{(1)}_2$ is given by

  $$\begin{aligned} D_2{\partial \over \partial y_i}\left( {\partial c^{(1)}_2\over \partial y_i }+ {\partial c^{(0)}_2\over \partial x_i}\right)= & {} {\partial c^{(0)}_2 \over \partial t} -g^{(0)} \end{aligned}$$

  (92)
  $$\begin{aligned} D_2\left( {\partial c^{(1)}_2\over \partial y_i} + {\partial c^{(0)}_2\over \partial x_i}\right) n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad c^{(1)}_2 \ \text{ y-periodic }, p=1,2. \end{aligned}$$

  (93)

  The Fredholm alternative imposes to the averages of the right-hand members of (92) to cancel out. This gives the equivalent macroscopic model for $c_2$ at the first order of approximation

  $$\begin{aligned} {\partial c^{(0)}_2 \over \partial t} = g^{(0)}, \quad g^{(0)}=R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}. \end{aligned}$$

  (94)

• Finally model IV is given by (91, 94). Model IV is model I when species 2 does not diffuse.

4.2 Very Large Diffusivity Ratio, $\mathcal{D}=D_1 / D_2= \mathcal{O}(\varepsilon ^{-2})$: Model V

We investigate in this section the case where the diffusivity ratio is very large, $D_1 / D_2= \mathcal{O}(\varepsilon ^{-2})$. We have $\mathcal{B}_1 = \mathcal{O}(\mathcal{A}_1)= \mathcal{O}(\varepsilon ^0)$ and $\mathcal{B}_2= \mathcal{O}(\mathcal{A}_2)= \mathcal{O}(\varepsilon ^{2})$. The dimensionless system now becomes

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \ f(c_1, c_2), \end{aligned}$$

(95)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} \varepsilon ^2 D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \ g(c_1, c_2), \end{aligned}$$

(96)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(97)

The concentrations are in the following form

$$\begin{aligned} c_1= & {} c_1^{(0)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon c_1^{(1)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon ^2 c_1^{(2)} (\mathbf{x},\mathbf{y},t^*)+ \cdots \end{aligned}$$

(98)

$$\begin{aligned} c_2= & {} c_2^{(0)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon c_2^{(1)}(\mathbf{x},\mathbf{y},t^*) + \varepsilon ^2 c_2^{(2)} (\mathbf{x},\mathbf{y},t^*)+ \cdots \end{aligned}$$

(99)

4.2.1 Macroscopic Equivalent Behaviour of $c_1$

We first introduce the above two ansatz into (95) to (97), and extract like powers of $\varepsilon$. We successively obtain boundary value problems to be investigated. The route is quite similar to the one in Sect. 3.

The lower-order $\varepsilon ^{-2}$ yields

$$\begin{aligned} c^{(0)}_1=c^{(0)}_1(\mathbf{x},t). \end{aligned}$$

And at the next-order $\varepsilon ^{-1}$, it becomes

$$\begin{aligned} c^{(1)}_1= \xi _{1i} (\mathbf{y}) {\partial c^{(0)}_1\over \partial x_i} + {\bar{c}}^{(1)}_1(\mathbf{x},t). \end{aligned}$$

Finally, the first-order equivalent macroscopic model is obtained by considering the order $\varepsilon ^0$ of (95)

$$\begin{aligned} D_1{\partial \over \partial y_i}\left( {\partial c^{(2)}_1\over \partial y_i }+ {\partial c^{(1)}_1\over \partial x_i}\right)= & {} {\partial c^{(0)}_1 \over \partial t} - D_1{\partial \over \partial x_i}\left( {\partial c^{(1)}_1\over \partial y_i }+ {\partial c^{(0)}_1\over \partial x_i}\right) -f^{(0)}, \end{aligned}$$

(100)

$$\begin{aligned} D_p\left( {\partial c^{(2)}_1\over \partial y_i} + {\partial c^{(1)}_1\over \partial x_i}\right) n_i= & {} 0\quad \text{ on }\ \delta \Omega _l, \quad { c}^{(2)}_1 \ \text{ y- } \text{ periodic }. \end{aligned}$$

(101)

The average of the right-hand members of (100) cancels out due to Fredholm alternative, leading to the equivalent macroscopic model at the first order of approximation

$$\begin{aligned} {\partial c^{(0)}_1 \over \partial t}= & {} D^{(eff)}_{1ij}{\partial ^2 c^{(0)}_1\over \partial x_i\partial x_j} +<f^{(0)}>,\nonumber \\<f^{(0)}>= & {} R_{11}c^{(0)}_1 + R_{12}<c^{(0)}_2 >+ R_{10}, \end{aligned}$$

(102)

where $< .>$ stands for the pore volume averaging symbol

$$\begin{aligned} <\phi > = {1 \over \Omega _l}\int _{\Omega _l} \phi \ \text{ d } \Omega . \end{aligned}$$

The effective diffusion tensor $D^{(eff)}_{1ij}$ is as in Sect. 3

$$\begin{aligned} D^{(eff)}_{1ij} = D_1<I_{ij} +{\partial \xi _{1i} \over \partial y_j}>. \end{aligned}$$

4.2.2 Investigation of $c_2$

Equation (96) at the order $\varepsilon ^0$ becomes

$$\begin{aligned} {\partial c^{(0)}_2 \over \partial t} = D_2{\partial ^2 c^{(0)}_2\over \partial y_i\partial y_i} + R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}, \end{aligned}$$

(103)

with

$$\begin{aligned} D_2{\partial { c}^{(0)}_2\over \partial y_i}n_i =0\quad \text{ on }\ \delta \Omega _l, \quad { c}^{(0)}_2 \ \text{ y- } \text{ periodic }. \end{aligned}$$

(104)

By averaging (103) over the pore volume, we have

$$\begin{aligned} {\partial<c^{(0)}_2> \over \partial t} = R_{21}c^{(0)}_1 + R_{22} <c^{(0)}_2> + R_{20}. \end{aligned}$$

(105)

Now, subtracting member to member the above relation (105) to (103) and noting the increment ${\tilde{c}}_2$ as ${\tilde{c}}_2 = c^{(0)}_2 - <c^{(0)}_2>$ yields

$$\begin{aligned} {\partial {\tilde{c}}_2 \over \partial t} = D_2{\partial ^2 {\tilde{c}}_2\over \partial y_i\partial y_i} + R_{22}{\tilde{c}}_2, \end{aligned}$$

(106)

with

$$\begin{aligned} D_2{\partial { \tilde{c}}_2\over \partial y_i}n_i =0 \quad \text{ on }\ \delta \Omega _l, \quad { \tilde{c}}_2 \ \text{ y- } \text{ periodic }. \end{aligned}$$

(107)

Let us introduce the eigenfunctions $\phi _n$ and the corresponding eigenvalues $\lambda _n$, $n=0,1,2,...$ of the following problem

$$\begin{aligned} D_2{\partial ^2 \phi _n\over \partial y_i\partial y_i}= & {} - \lambda _n\phi _n \\ D_2{\partial \phi _n\over \partial y_i}n_i= & {} 0 \quad \text{ on }\ \delta \Omega _l, \quad \phi _n \ \text{ y- } \text{ periodic }. \end{aligned}$$

We have $\lambda _0=0<\lambda _1<\lambda _2<...$, $\phi _0=0$ and the $\phi _n^{'s}$ are orthogonal. The solution of (106, 107) are in the following form

$$\begin{aligned} {\tilde{c}}_2= \sum _{n=1}^{\infty } A_n \exp ^{-(\lambda _n-R_{22})t}\phi _n. \end{aligned}$$

Instabilities and corresponding $c_2$ patterns will be present if $R_{22} >\lambda _1$.

4.3 Different Estimations of the Diffusivity Ratio

It is clearly sufficient to investigate ratios $D_1 / D_2 \ge \mathcal{O}(\varepsilon ^0)$, as ratios $D_1 / D_2 <\mathcal{O}(\varepsilon ^0)$ are obtained by reversing $c_1$ and $c_2$. On the other hand, $D_1 / D_2 =\mathcal{O}(\varepsilon ^0)$ was already investigated in Sec 3.1 and corresponds to model I.

Let us consider $D_1 / D_2 = \mathcal{O}(\varepsilon ^{-3})$. The dimensionless systems now becomes

$$\begin{aligned} {\partial c_1 \over \partial t}= & {} D_1{\partial ^2 c_1\over \partial x_i\partial x_i} + \ f(c_1, c_2), \end{aligned}$$

(108)

$$\begin{aligned} {\partial c_2 \over \partial t}= & {} \varepsilon ^3 D_2{\partial ^2 c_2\over \partial x_i\partial x_i} + \ g(c_1, c_2), \end{aligned}$$

(109)

$$\begin{aligned} D_p{\partial c_p\over \partial x_i}n_i= & {} 0\quad \text{ on }\ \delta \Omega _l,\quad p=1,2. \end{aligned}$$

(110)

The macroscopic equivalent behaviour of $c_1$ is obtained as in Sect. 4.2.1 and becomes (102)

$$\begin{aligned} {\partial c^{(0)}_1 \over \partial t}= & {} D^{(eff)}_{1ij}{\partial ^2 c^{(0)}_1\over \partial x_i\partial x_j} +<f^{(0)}>,\nonumber \\<f^{(0)}>= & {} R_{11}c^{(0)}_1 + R_{12}<c^{(0)}_2 >+ R_{10}, \end{aligned}$$

(111)

where $< .>$ stands for the pore volume averaging symbol

$$\begin{aligned} <\phi > = {1 \over \Omega _l}\int _{\Omega _l} \phi \ \text{ d } \Omega . \end{aligned}$$

The effective diffusion tensor $D^{(eff)}_{1ij}$ is as in Sect. 3

$$\begin{aligned} D^{(eff)}_{1ij} = D_1<I_{ij} +{\partial \xi _{1i} \over \partial y_j}>. \end{aligned}$$

Now, Equation (109) at the order $\varepsilon ^0$ becomes

$$\begin{aligned} {\partial c^{(0)}_2 \over \partial t} = R_{21}c^{(0)}_1 + R_{22}c^{(0)}_2 + R_{20}. \end{aligned}$$

(112)

By averaging (112) over the pore volume, we have as in Sect. 4.2.2

$$\begin{aligned} {\partial<c^{(0)}_2> \over \partial t} = R_{21}c^{(0)}_1 + R_{22} <c^{(0)}_2> + R_{20}. \end{aligned}$$

(113)

Now, diffusion of $c_2$ is absent: Subtracting member to member the above relation (113) to (112) and noting ${\tilde{c}}_2 = c^{(0)}_2 - <c^{(0)}_2>$ yields

$$\begin{aligned} {\partial {\tilde{c}}_2 \over \partial t} = R_{22}{\tilde{c}}_2. \end{aligned}$$

(114)

Model VII is similar to model V (Fig. 2), but an eventual morphogenesis is possible only for $c_1$.

The models associated with different evaluations of $\mathcal{D}$ are shown in Table 1.

Fig. 2

Different macroscopic models for $\mathcal{A} = \mathcal{A}_1 = \mathcal{A}_2 = \mathcal{O}(\varepsilon ^0)$ and $\mathcal{D} = \mathcal{D}_1 /\mathcal{D}_2 = \mathcal{O}(\varepsilon ^p)$. Models with possible morphogenesis are shown by a “$^{*}$”

5 Conclusion

The equivalent macroscopic model to be considered to describe the evolution of chemical species which diffuse and react in a given porous medium is strongly sensitive to the size L of the macroscopic sample or of the concentration pseudo-wavelength. Increasing L, with a given l, decreases $\varepsilon =l/L$ and, as a consequence, could change the estimations of the dimensionless numbers in function of the small parameter of separation of scales $\varepsilon$. Thus the equivalent macroscopic model could change, as well as the patterns in case of morphogenesis. In the paper, the investigations to obtain the macroscopic description, if it exists, are limited to two main categories of estimations. In the first one, Sect. 3, the relative weight of the diffusion–reaction terms is varying from $\varepsilon ^0$ to $\varepsilon ^{-3}$ and over. In the second one, the diffusivity ratio is varying from $\varepsilon ^0$ to $\varepsilon ^{-3}$. Each case yields different macroscopic equivalent models presented in Table 1. It is noticeable that these first-order models are valid whatever the structures of the source terms f and g.

Morphogenesis is present when the diffusion–reaction term enables instabilities. However, the patterns wavelength $l_{RD}$ is sensitive to the macroscopic equivalent model into consideration. It is shown in the paper that $l_{RD}$ is $\mathcal{O}(l)$, $\mathcal{O}(L\varepsilon ^{1/2})$, or $\mathcal{O}(L)$, depending on the value of the size of the macroscopic sample, L.

We considered here only the case of linear reaction terms. The main results of the above analysis will, however, remain valid for polynomial reaction terms.

This study allows considering many cases in the huge literature dedicated to morphogenesis model. We underline the idea that from the same microscopic description of the physical phenomena, we obtained different macroscopic models, as well as their domains of validity, and the expression of the macroscopic properties, which is very important for the identification of their values.