1 Introduction

The climatic changes, observed over the last decades, have led to many upheavals on a global scale with consequences for the environment and human well-being. Given the nature of its climate, Algeria is among the countries most affected by these climatic changes whose indicators, such as temperature and rainfall, are easily detectable. This is indeed what has been shown by many studies carried out in recent years, some of which were done in the Chéliff watershed which is the area of our investigation (Meddi et al. 2007; Amrani 2011).

The availability of a climate database is a fundamental prerequisite for modeling and mapping hydrological and environmental processes. Whatever the nature and structure of these models, most of them need a complete and reliable dataset on a temporal and spatial basis. Unfortunately, the measurement of hydrological variables (rainfall, flow, etc.) may suffer from systematic errors and data gaps and random data (Vieux 2001). In addition, these data are only available for few and very limited meteorological stations widely dispersed in space. In the face of these problems, many statistical methods of spatial interpolation have been proposed and some authors have tried to identify the most appropriate method that is able to describe the rainfall resource at any point for a given time scale and a particular spatial domain.

The methods of spatial interpolation differ according to their assumptions (deterministic/stochastic or probabilistic) and the scope of the study (global/local) (Isaaks and Srivastava 1989). Deterministic methods assume that the way in which the phenomenon was generated is known in detail and empirical equations can be used, whereas the probabilistic methods assume that there is a large number of processes with complex interactions that generated the phenomenon; therefore, we cannot describe them quantitatively, but we must assume that there is an uncertainty that we are going to model by probability laws. Global methods use all data for all points to be estimated, whereas local methods only use neighborhood data for each point to estimate.

Spatial interpolation methods are used for any phenomenon that is distributed in space whether it is environmental, economic, or social (Goovaerts 1997). Currently, there is no comprehensive literature review that summarizes all the spatial interpolation algorithms used for rainfall, but most of the more than 50 interpolation algorithms listed by Li and Heap (2011) have been applied to the spatial estimate of rainfall. For climatology in particular, there are reference documents such as Hartkamp et al. (1999) and Dobesch et al. (2007). These methods have been applied to different climatic parameters such as temperature (Boer et al. 2001), evapotranspiration (Cadro et al. 2019), solar radiation (Pons and Ninyerola 2008), wind speed (Luo et al. 2008), and rainfall.

With particular reference to rainfall, the time scales range from the hour (Erdin et al. 2012; Chen et al. 2017), to the day (Ly et al. 2011; Chen et al. 2017), the month (Frazier et al. 2016; Adhikary et al. 2017), the season (Diodato 2005; Borges et al. 2016), and the year (Bajat et al. 2013; Borges et al. 2016). Spatial extent ranges from local like watershed (Ly et al. 2011; Adhikary et al. 2017), then regional (Subyani 2004), national (Lloyd 2005; Schiemann et al. 2011), and finally global (Agnew and Palutikof 2000; De Wit et al. 2008). These research works used deterministic methods such as Thiessen polygon (Ly et al. 2011), inverse distance weighting (Ly et al. 2011; Borges et al. 2016), and spline (Hutchinson 1995; Borges et al. 2016) as well as probabilistic methods such as regression (Diodato and Ceccarelli 2005; Borges et al. 2016), geostatistics (Ly et al. 2011; Frazier et al. 2016), and hybrid or mixed methods integrating deterministic and probabilistic approaches or using auxiliary information (Dahri et al. 2016).

It is well-known that rainfall generally increases with altitude (Singh and Kumar 1997) or with the proximity of a water body (Agnew and Palutikof 2000). Naturally, this auxiliary information, as well as others such as satellite images, has been used to improve the quality of the results of spatial interpolation methods. Chua and Bras (1982) and Dingman et al. (1988) were among the first researchers to include elevation in geostatistical methods for interpolation of annual rainfall. Goovaerts (2000) used geostatistical algorithms to include elevation in the interpolation procedure in southern Portugal. Ninyerola et al. (2000) used a linear regression equation that included several climatic, topographic, and geographic variables (cloud factor, altitude, latitude, and continentality) with correctors modeled by inverse distance weighting (IDW) estimators and kriging in the Catalonia region (Spain). Diodato and Ceccarelli (2005) compared linear regression and ordinary cokriging (OCK) method for the Sannio Mountains (Southern Italy), obtaining the best results for cokriging. More recently, Pellicone et al. (2018) evaluated a deterministic method (IDW) and several stochastic methods (geostatistics) to predict monthly precipitation in a region in southern Italy. Also, Amini et al. (2019) compared several deterministic and stochastic spatial interpolation methods to map monthly and annual rainfall and temperature in a watershed in Iran.

The review of the literature on the application of spatial interpolation methods to rainfall shows that there are many published studies at different spatial and temporal scales. With the abundance of these applications, a relevant question arises regarding their accuracy and precision for a given set of conditions (Hartkamp et al. 1999). The performance of spatial interpolation methods would depend on several factors such as the type and nature of the interpolation surface, the quality and quantity of input data, the type of rain, the strength of correlation between rain and auxiliary variables, sampling density, spatial distribution of samples, clustering of samples, variance of data, normality of data, quality of secondary information, stratification, and size or resolution of the grid, as well as interactions between these factors (Vicente-Serrano et al. 2003; Li and Heap 2011; Ly et al. 2011; Berndt and Haberlandt 2018). Therefore, these factors will influence the choice of the interpolation method and the accuracy of the results. The choice among the wide range of interpolation techniques to be used in the estimation of meteorological data is a complex and sensitive process. There are no consistent results on the impact of these factors on the performance of spatial interpolators. There is no optimal method in all circumstances. Thus, any method of interpolation of rainfall has its own advantages and disadvantages. Consequently, it is always difficult to identify the best method of spatial interpolation. It is therefore strongly recommended to select interpolation methods of quality according to the purpose of the application, the geographical conditions of the study area, the climatic regime, and the density of the meteorological stations as well as the spatial and temporal scales. Subsequently, it is important to compare the results obtained using alternative methods applied to the same set of data. In addition, the utility of the auxiliary information would depend on the time scale and spatial extent. For example, the integration of altitude improved the spatial interpolation of monthly and annual rainfall (Goovaerts 2000; Lloyd 2005), but this was not the case for daily rainfall (Ly et al. 2011). Similarly, Berndt and Haberlandt (2018) concluded that incorporating altitude into KED improved interpolation performance at the annual time scale while this improvement was slightly lower for the monthly time scale; on the other hand, the advantage was minor for the weekly scale and, even worse, for the daily time scale, the performances are already slightly lower than those of the univariate geostatistical method (OK). Indeed, “the correlation between rainfall and topography increases with the length of the time interval” (Bardossy and Pegram 2013) because the rainfall fields are spatially discontinuous on shorter time scales and more continuous on longer ones (New et al. 2001).

Most studies, in their comparison of several methods, have found that geostatistical methods yield more accurate predictions than deterministic methods (Kisaka et al. 2016). However, other authors have found that the results depend on the sampling density of meteorological stations (Dirks et al. 1998) and, in some cases, the accuracy of complex methods is not greater than that of simple algorithms and may even be less than this (Dirks et al. 1998; Lloyd 2005; Moral 2010).

With particular reference to geostatistical approaches, univariate methods (simple kriging or ordinary kriging) tend to smooth the interpolated variable and thus have difficulty in accurately reproducing spatial variability. Multivariate methods (cokriging, regression-kriging, and kriging with external drift) use additional spatial information from static covariates such as altitude or dynamic variables such as weather radar to improve interpolation performance (Kumari et al. 2017; Pellicone et al. 2018).

More specifically for multivariate geostatistical methods using auxiliary information, several authors compared different methods and found that KED generally provided the best estimates (Goovaerts 2000; Hengl et al. 2003; Li and Heap 2011; Dahri et al. 2016). Also, it was found that RK (Moral 2010) and KED (Bardossy and Pegram 2013) performed better than OCK. In addition, for the OCK, it is necessary to evaluate the variogram of the rainfall and the altitude as well as their cross-variogram by jointly modeling a dynamic quantity (rainfall) and a static one (altitude), which is more delicate.

Based on the elements of the literature review above, it was decided to exclude deterministic methods and to be limited to geostatistical methods only. For the latter, we chose the univariate approach (OK) that uses only rainfall data as a reference to which we would compare two multivariate approaches, i.e., regression-kriging (RK) and kriging with external drift (KED) which are able to integrate, in addition to rainfall, auxiliary information such as elevation; cokriging has been excluded for the reasons mentioned above.

The novelty of this research work can be summarized in five points. First of all, there are very limited published case studies from North Africa and specifically none from Algeria. As each study area has its own climatological and topographical features, we need to find out the most appropriate spatial interpolation method for making maps. In addition, the impact of not considering snow water equivalent (station 1) on interpolating rainfall and how geostatistical methods attenuated differently this impact were evaluated. Moreover, although the comparison of geostatistical methods for rainfall was extensively assessed, there are very few examples in the literature that compared specifically RK to KED (Feki et al. 2012; Cantet 2017). Both algorithms are apparently similar since they try to detrend rainfall data before interpolating residuals; however, there are subtle differences between these two kriging algorithms (Hengl et al. 2003, 2004, 2007). KED is better if rainfall and elevation are related locally, whereas RK performs better if the two variables have a global relationship (Feki et al. 2012). Also, conventionally, geostatistical studies would be done using at least 100 samples (Webster and Oliver 2007; Oliver and Webster 2014, 2015); however, our sample size is small. The aim was to check how auxiliary information (elevation) would improve the interpolation of scarce data (rainfall). Finally, the three kriging algorithms were compared by an in-depth assessment of cross-validation results.

The objective of this work is to find out what is the most appropriate geostatistical method for the mapping of mean annual rainfall in a sub-watershed in northwestern Algeria, typical of a Southern Mediterranean climate.

2 Geographic location

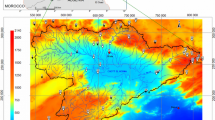
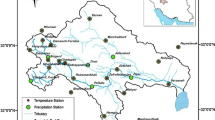
The study area is located in northwestern Algeria (Fig. 1). It is part of the large Chéliff-Zahrez watershed and occupies its northern part with 18 of its 36 sub-watersheds and an area of 18,000 km2. Only this part of the watershed was kept because of the availability and reliability of rainfall data; on the other hand, the southern part of the basin is characterized by the lack of rainfall data, especially during the 1990s when most of the hydrometric stations went out of operation.

Fig. 1
figure 1

Geographic location of rainfall stations with the digital elevation model (DEM)

Full size image

The study area stretches 136 km from south to north and 267 km from west to east. The geography of the region of this area is quite heterogeneous, it occupies the plains of Chéliff and Mina in the center, with the mouth of Oued Chéliff northwest to the Mediterranean Sea where the altitude is the lowest (4 m), and the highland areas to the north and south, where the highest altitudes in the study area are about 1968 m. The coordinates of this zone, according to the UTM projection (WGS 1984, zone number 31), are 241,000 and 508,000 m for longitude and 3,899,000 and 4,035,000 m for latitude.

Overall, the general distribution of land in the study area is characterized by a very significant useful agricultural area (UAA). This UAA is mainly concentrated in the center of the watershed, as well as in the mid-mountain areas and a low reforestation rate. Forest is mainly concentrated in the mid-mountain areas (south and north of the watershed). The importance of UAA per area decreases as altitude increases. The occupation of the UAA is dominated by cereals, fruit trees, and vegetable crops.

3 Material and methods

3.1 Rainfall and topographic data

The spatial and temporal representativeness of rainfall stations in the study area has a major influence on the reliability of the final map. Rainfall data were collected directly from the National Agency of Hydraulic Resources (ANRH). Then we proceeded to their filtering. The selected 58 meteorological stations, with a density of about one station per 310 km2, have rainfall data spanning 40 years (1972–2012), which is a sufficient series length to carry out this study, which is greater than 30 years, as recommended by the World Meteorological Organization (WMO). Some stations have gaps that will be filled using the linear regression method on a monthly scale with full baseline pluviometric data having a high correlation, the same altitude and orientation similar to the North and South mountain ranges (Peterson and Easterling 1994; Laborde and Mouhous 1998; Peterson et al. 1998; Aguilar et al. 2003). The correlation coefficient between the rain gauges and the corresponding reference rain gauges was in all cases greater than 0.75 for the stations close to the massifs, and greater than 0.85 in the Chéliff and Mina plains. The topographic information was extracted from a digital elevation model (DEM) with a resolution of 30 × 30 m to establish the elevation grid of the study area.

3.2 Transformation of rainfall data

The geostatistical approach of spatial interpolation, kriging, is considered the best unbiased linear predictor (BLUP) if the data obey the conditions of normality, homogeneity of variances, and stationarity (Isaaks and Srivastava 1989). However, spatial data, particularly climate data, violate these conditions. For example, rainfall is generally asymmetrical. High asymmetry and outliers have an undesirable impact on variogram structure and kriging estimates (Gringarten and Deutsch 2001). For spatial data that follow a normal distribution, spatial variability is easier to model, since the effects of extreme values are reduced resulting in more stable variograms (Goovaerts 1997).

Data transformation may be required before kriging to standardize data distribution, delete outliers, and improve stationarity of data (Deutsch and Journel 1998). The most frequently used data transformation methods are square root (Foehn et al. 2018) and logarithm (Subyani 2004; Pellicone et al. 2018). These two types are only special cases of a much more general form called Box–Cox transformation (Box and Cox 1964). It is characterized by a parameter which is equal, in particular, to 0.5 for the square root and 0 for the logarithm. It has been used in spatial analysis of climate variables (Erdin et al. 2012). We have adopted this transformation in our research work.

Normality of rainfall data was checked graphically using tools such as the histogram and the boxplot as well as numerically by comparing the mean and median, the symmetry (skewness), and flattening (kurtosis) coefficients with those of a normal distribution and also through the Shapiro–Wilk formal statistical test (Royston 1982).

3.3 Spatial interpolation algorithms

Three geostatistical spatial interpolation methods will be used: ordinary kriging (OK), regression-kriging (RK), and kriging with external drift (KED). The last two methods (RK and KED) use the secondary information (elevation) in addition to the main information (rainfall). We will compare the results obtained with those calculated using the OK method which considers only rainfall.

Kriging is a generalized least squares regression technique that takes into account the spatial dependence between observations, as revealed by the variogram, in spatial prediction. Each measure z (uα) is interpreted as a particular realization of a random variable Z (uα). Geostatistical interpolation is used to estimate the unknown value of rainfall z at the unsampled location u0 as a linear combination of neighboring observations:

$$ \hat{Z}\left({u}_0\right)=\sum \limits_{\alpha }{\lambda}_{\alpha }Z\left({u}_{\alpha}\right) $$
(1)

\( \hat{Z}\left({u}_0\right) \) being the value to be estimated of the variable of interest (rainfall) at the unsampled target location u0 and Z(uα) being the observed values of the rainfall at the sampled locations in the vicinity of u0.

The weights λα are calculated in such a way that this estimator is optimal, that is to say without bias and error variance is minimal. The weights are determined from the theoretical model of the variogram fitted to the experimental variogram calculated from the data.

The three methods differ in the way of calculating these weights and also if they take into account auxiliary information like elevation or not. By the way, all kriging estimators are variants of the linear regression basic estimator \( \hat{z}\left({u}_0\right) \), defined as follows (Goovaerts 1997; Moral 2010; Portalés et al. 2010):

$$ \hat{z}\left({u}_0\right)-m\left({u}_0\right)=\sum \limits_{\alpha =1}^{N\left({u}_0\right)}{\lambda}_{\alpha}\left({u}_0\right)\left[z\left({u}_{\alpha}\right)-m\left({u}_{\alpha}\right)\right] $$
(2)

where N(u0) is the number of neighboring observations at the location u0 and λα(u) is the weight attributed to z(uα) interpreted as a realization of the random variable Z(uα). The values m(u0) and m(uα) are the expected values of the random variables Z(u0) and Z(uα). Several kriging variants can be distinguished according to the model considered for the trend m(u0) (Deutsch and Journel 1998; Goovaerts 1997).

3.3.1 Variogram

The three kriging methods require models of the function that characterize spatial variability, the variogram, as well as its main characteristic parameters such as the nugget effect, the sill, and the range (Goovaerts 1997). The experimental variogram is calculated from the observed data according to the following equation:

$$ \hat{\gamma}(h)=\frac{1}{2N(h)}\sum \limits_{\alpha =1}^{N(h)}{\left(Z\left({u}_{\alpha}\right)-Z\left({u}_{\alpha }+h\right)\right)}^2 $$
(3)

with Z(uα) and Z(uα + h) being the values observed at the locations uα and uα + h separated by the distance h and N(h) being the number of such pairs. Here, isotropic (experimental and theoretical) variograms were considered ignoring the separation direction because the size of the sample (58) is limited and would not possibly detect anisotropy, i.e., spatial variability that would differ from one direction to another (Haberlandt 2007; Schuurmans et al. 2007; Moral 2010).

Then, a theoretical model must be adjusted to this experimental variogram. Different models can be adjusted like spherical, exponential, Gaussian, etc. The model parameters are estimated using the weighted least squares method (Cressie 1993; Goovaerts 2000; Cantet 2017)) with the weights being the inverse of the number of pairs of points separated by a given distance. The choice of a model is based on cross-validation, discussed in Section 3.4, which gives a mean error of 0 (unbiased) and a minimal square root of the mean squared error.

3.3.2 Ordinary kriging

For OK, the most commonly used form of kriging, m(u0), in Eq. (2), is considered unknown and fluctuates locally, which makes it possible to maintain stationarity in the local neighborhood. OK is an example of univariate kriging, considering only one variable at a time. Weights (λα) of OK are obtained by solving a system of linear equations known as the OK system, consisting of N(h) + 1 equations (Goovaerts 1997). The only information required by OK system are the values of variograms corresponding to different spatial lags. These are easily obtained once a variogram model has been fitted to experimental values.

3.3.3 Regression-kriging

In RK, instead of directly interpolating rainfall, as for OK, the analysis is done in two separate steps (Goovaerts 2000; Hengl et al. 2007; Alsamamra et al. 2009; Feki et al. 2012; Agou et al. 2019): estimation of the trend and then kriging of residuals. These two components are added to give the final predictions. In the first step, a simple linear regression analysis is performed between rainfall and the external variable (elevation) at a given sampled location. The regression parameters (intercept and slope) are estimated from the pairs of rainfall and elevation of the sample data which are, then, used to estimate rainfall values. The estimate can be done using the ordinary least squares (OLS) or the generalized least squares (GLS) method. The results do not differ significantly if there is no significant spatial clustering of sampling points (Odeh et al. 1995). The residuals are then calculated as the difference between the observed and the estimated rainfall values. The new variable, residuals, retains the spatial variability of rainfall (Odeh et al. 1995), but some of the variability has been suppressed as a result of the external information (elevation) used in the regression model. In the second step, the spatial variability of the residuals is described by the experimental variogram and then modeled by adjusting a theoretical variogram. This makes it possible to estimate the residuals by simple kriging (SK) at any location, including sampled and unsampled locations by considering m(u0) in Eq. (2) as a constant for the entire study area. The SK system for residuals with N(u0) equations (Goovaerts 1997; Webster and Oliver 2007) can be solved. The final estimates are obtained by combining the trend estimates and residuals on the kriging grid.

3.3.4 Kriging with external drift

KED (Hudson and Wackernagel 1994; Goovaerts 1997) considers that m(u0), in Eq. (2), varies regularly within each local neighborhood and is modeled as a linear combination of secondary data, such as elevation. KED is an example of multivariate kriging, considering simultaneously two or more variables at a time. The trend is modeled as a linear function of auxiliary information, elevation in our case, which is considered to be another random variable, in addition to rainfall, and is interpreted as the drift or general trend that can follow the behavior of rainfall in the study area.

Rainfall is modeled as a non-stationary random variable whose expected value is variable and is a linear function of locally evaluated elevation (Goovaerts 2000). This method requires that the external variable gradually vary in space and be known at each location to be estimated. It also assumes a linear relationship between the target variable and the drift variable (Deutsch and Journel 1998; Webster and Oliver 2007). With KED, the deterministic and stochastic components are adjusted simultaneously, so that the drift variable is integrated into the kriging system (Webster and Oliver 2007).

The analysis is carried out in several steps (Tapsoba et al. 2005; Feki et al. 2012). First, the coefficients of the external drift (constant and slope) are estimated, locally around each rain gauge, from the OLS rainfall–elevation data pairs and external trend or drift, representing m(u0) in Eq. (2), is estimated. The external drift is thus estimated at the sampled locations as well as at all the nodes of the interpolation grid. Then, the estimated residuals are calculated, at the sampled locations, as the difference between the observed and the estimated (external drift) values of rainfall. In a third step, the experimental variogram of the residuals is calculated and a theoretical model is adjusted to it. Theoretically, the variogram should be estimated from the residuals. However, this is not usually a simple procedure because neither the residuals nor the trend are known a priori. As was also done by Hudson and Wackernagel (1994), Lloyd (2005), and Berndt and Haberlandt (2018), experimental variograms were deduced from a simplified approach, that is, using only the observed values of rainfall. In addition, Moges et al. (2007) found that the spatial variation of rainfall does not depend entirely on the parameters controlling the shape of the variogram model (nugget effect, sill or range) and is sensitive to the type of kriging method used. Moreover, this simplification does not modify the predicted value, but only overestimates the variance of its error (Ahmed and De Marsily 1987; Pardo-Iguzquiza 1998). Finally, rainfall is estimated at the nodes of the interpolation grid using the variogram values at these nodes and the simple kriging algorithm.

KED and RK appear to be similar but lead to different results (Hengl et al. 2003). With KED, the equations are solved immediately while RK explicitly separates the estimation of trends from the spatial prediction of the residuals. For RK, there is no risk of instability, unlike the KED system (Goovaerts 2000). Moreover, in theory, regression requires independent residuals, but kriging relies on dependent residuals. For this reason, generalized linear models can be an alternative. The advantage of KED is that the equations are solved only once. Therefore, with KED, there is a joint estimate of the prediction variance, but with RK, the parts of the regression and kriging variances are estimated separately and must be summed.

The spatial interpolation, using the three kriging methods (OK, RK, and KED), was done on the transformed data using the natural logarithm, Y(u), following the Box–Cox method. The final results are presented in the original scale by making a back-transformation (Diggle and Ribeiro Jr 2007; Yamamoto 2007; Hengl et al. 2018).

3.4 Cross-validation

The increasing application of interpolation methods raises concerns about their accuracy and precision (Hartkamp et al. 1999). Rainfall interpolation studies often involve a comparison of theoretical models fitted to experimental variograms as well as different spatial interpolation methods. When data sample size is very small, as in our case with only 58 rain gauges, the comparison of methods is done by cross-validation (Isaaks and Srivastava 1989; Cressie 1993) which is a common method for validating the accuracy of interpolation techniques (Tapsoba et al. 2005; Adhikary et al. 2017).

In general, differences between observed and predicted values are used to evaluate model performance. In cross-validation, information about a sampled point is temporarily deleted and is estimated from the remaining data points and the difference between the actual value and the estimated value is calculated. This operation is repeated for the rest of the measured points. Thus, the quality of the estimate, resulting from the model, can be statistically controlled by means of a scatterplot between the actual and estimated data and the analysis of errors. Thus, graphical tools such as scatterplots, histograms, boxplots, and maps can be used. Similarly, different numerical indices were used such as Pearson correlation coefficient (r), coefficient of determination (r2), Spearman correlation coefficient (rs), mean error or bias (ME), mean absolute error (MAE), square root of the mean squared error (RMSE), Nash–Sutcliffe efficiency coefficient (EF), Willmott agreement index (d), and concordance coefficient of Lin (CC).

Quality criteria based on correlation measures such as r, r2, and rs are considered sensitive to extreme values and insensitive to additive and proportional differences between observations and predictions based on regression (Moore 1991). The mean error (ME), the mean absolute error (MAE), and the square root of the mean squared error (RMSE) are the best overall measures of model performance (Willmott 1982; Vicente-Serrano et al. 2003) because they summarize the average difference in units of observed and predicted values. Therefore, the ME and MAE measure bias or systematic error whereas the RMSE is considered a reliable measure of accuracy (Johnston et al. 2003). RMSE is considered more important in cases where important errors are particularly undesirable. It must be minimal. The Willmott agreement index (d) (Willmott 1982; Kumari et al. 2017) assesses the extent to which estimated values approach observed values. It overcomes the lack of sensitivity of r2 and EF to systematic under- and overestimates by the model (Legates and McCabe 1999).

3.5 Software

The SPSS statistical software was used to check graphically and numerically normality. The SAS statistical software was used to determine the optimal parameter to use in the Box–Cox transformation. To calculate the values of the experimental variograms as well as the theoretical models that were adjusted to them, we used the VarioWin 2.2 software (Pannatier 1996; Portalés et al. 2010; Frazier et al. 2016) for two main reasons: it is a software dedicated exclusively to computing and fitting variograms and it uses a goodness-of-fit (IGF) criterion which is a standardized weighted residual sum of squares between observed and estimated values of the variogram for each spatial lag (Pannatier 1996; Webster and Oliver 2007). This IGF is considered as an advantage (Lamhamedi et al. 2006). Although RK can be done in ArcGIS (Moral 2010; Portalés et al. 2010; Batista et al. 2017), KED cannot be done in it. We used GSLib (Deutsch and Journel 1998) since it is able to do the three kriging algorithms (OK, RK, and KED). The maps for the three geostatistical interpolation methods were produced using ArcGIS 9.2 while the cross-validation indicators and graphs were produced with the SPSS software.

4 Results and discussion

4.1 Exploratory data analysis

Rainfall data collected from 58 rainfall stations were explored to understand the distribution pattern of the data. Graphs (Fig. 2) and standard descriptive statistics (Table 1) were used to describe the data. The application of the Box–Cox method gave a coefficient lambda = 0, which corresponds to the use of logarithm as the optimal data transformation.

Fig. 2
figure 2

Histogram of rainfall at the original scale (top) and after log-transformation (bottom). Curve represents the fitting of a normal distribution

Full size image
Table 1 Descriptive statistics for mean annual rainfall (mm) and elevation (m) for original and log-transformed (Ln) data
Full size table

The histogram of the original data shows an asymmetry towards the right (some stations have abundant rainfall) indicating the non-normality of the distribution whereas that of the data having undergone the logarithmic transformation have a better symmetry which possibly signifies the normality of the distribution. In fact, rainfall has a significantly different mean (395.0 mm) and median (369.7 mm) while these two statistical parameters are almost equal (6.0 and 5.9 mm, respectively) for the transformed data. Moreover, the asymmetry (skewness) and flattening (kurtosis) coefficients are clearly different from zero for the original data (0.8 and 0.6, respectively), whereas they are close to zero for the transformed data (0.3 and − 0.3, respectively). Finally, the Shapiro–Wilk test confirms the non-normality of the original data (p = 0.010 < 0.05) and the normality of the transformed data (p = 0.424 > 0.05).

The rainfall has an average value of 395 mm which is recorded in almost all the Chéliff and the Mina plains, where the altitude is less than 80 m. It is moderately variable with a coefficient of variation of 22% and minimum and maximum values of 251.1 and 644.8 mm, respectively. Regarding the elevation, it varies from 54 m (corresponding to the mouth of the Cheliff River on the Mediterranean Sea) to 1162 m (corresponding to the mountain ranges of Wersenisse where the mean annual rainfall is among the highest in our study area) with an average of 390.3 m and a coefficient of variation of 80%. The distribution is not normal and its logarithmic transformation follows a normal distribution.

Using ArcGIS, the relative coverage area of the different elevation classes was calculated (Table 2). Comparing these percentages to those for the 58 weather stations, we note that the low elevations are more represented than the high elevations (67.3% of stations have elevations less than 400 m, 17.2% have elevations between 400 and 800 m and 15.5% of stations have elevations greater than 800 m while these percentages throughout the whole study area are 40.5%, 39.2%, and 20.3%, respectively). This is a disadvantage in an area where 59.5% of the land is more than 400 m (Table 2 and Fig. 1). It is therefore clear that there is an over-representation of low elevations and an under-representation of high elevations.

Table 2 Classes of elevations of rainfall stations and of the whole study area
Full size table

4.2 Rainfall–elevation relationship

The strength of the linear relationship between rainfall and elevation was analyzed using the scatterplot (Fig. 3) as well as the regression line and the Pearson (r) and Spearman rank linear correlation coefficients (rs) (Table 3). In general, there is a good relationship between rainfall and elevation (Fig. 3) with two distinct ranges corresponding, on the one hand, to low and medium altitudes and, on the other hand, to high altitudes. The regression equations are as follows:

Fig. 3
figure 3

Scatterplot representing the relationship between rainfall and elevation. Figures show the number of the rainfall stations

Full size image
Table 3 Coefficients of correlation and of regression linking mean annual rainfall (mm) to elevation (m) for original and log-transformed data
Full size table

Rainfall = 318.052 + 0.197 × Elevation

Ln (Rainfall) = 5.773 + 0.0005 × Elevation

The rainfall–elevation relationship is strong and positive as indicated by the Pearson correlation coefficients (0.71 and 0.70 for the original and the transformed data, respectively). The high value of the Spearman rank correlation coefficient (0.69) shows that there is a good correlation between ranks of rainfall and of elevation: in general, low rainfall corresponds to low altitudes and high rainfall to high altitudes, with a few exceptions as for stations number 1, 28, and 52. The coefficient of determination (r2) is around 0.5, indicating that taking elevation into account as the sole source of auxiliary information, one can explain half of the change in rainfall. It seems reasonable then to take into account the exhaustive information on the elevation, included as a random variable, in rainfall mapping. All the correlation coefficients as well as the regression coefficients were significant at the 0.1% level.

The relationship between rainfall and elevation can also be evaluated in space (Fig. 1). Thus, the clear relationship between rainfall and elevation is clearly visible: the plains (e.g., stations 48, 49, 53, 55, 56, and 57) record the lowest rainfall while the abundant rainfall is in the highlands (example of the stations 2, 3, 7, 13, 25, and 27). We can also expect the maritime influence of the Mediterranean Sea, combined with the effect of the elevation: the typical example is the station 25 which, even if it does not have the highest altitude (850 m compared to 1162 m), it has the highest rainfall (645 mm). In addition, there is a very clear increasing gradient in rainfall from the west to the east and also from the center of the study area to the north and south ends. This gradient generally follows the pattern of elevations, with the exception of station 1, which has an unusually low rainfall (311 mm at an elevation of 656 m) compared to its vicinity and also with respect to this gradient. Stations 15 and 16 have approximately the same altitude (650 and 637 m, respectively) as station 1 but much higher rainfall (449 and 411 mm, respectively). This could be explained by the fact that, on the one hand, observers only take into consideration precipitations in the form of rain and ignore those in the form of snow which is quite important and, on the other hand, station 1 is located on the south side of the Ksar El Boukhari plateau containing stations 2 and 12 (with an elevation of 1085 and 1074 m, respectively) while stations 15 and 16 are on the north side. As a result, the Ksar El Boukhari region would act as a natural barrier between the highlands to the south and the Chéliff plain upstream to the north.

Station 24 has a low elevation (280 m) while its rainfall is among the highest (the 7th with 507 mm) because it is located in the west foot of Djebel Zaccar and upstream of the Wadi watershed Ebda which is characterized by a high density of vegetation cover; Jebel Zaccar plays the foehn phenomenon.

4.3 Structural analysis of data

The variogram models fitted to mean annual rainfall and their parameters are shown in Table 4 and Fig. 4. For OK and KED, the variogram was fitted using an exponential model with a nugget effect of 150 mm2, a partial sill of 6600 mm2 and a range of 50.8 km. For RK, a spherical model was fitted to the variogram with a nugget effect of 1500 mm2, a partial sill of 4700 mm2 and a span of 69.3 km.

Table 4 Model and parameters of theoretical variograms fitted to experimental variograms for mean annual rainfall
Full size table
Fig. 4
figure 4

Experimental (points) and fitted theoretical (curve) variograms of mean annual rainfall for OK and KED (left) and RK (right)

Full size image

Elevation, as secondary information, has reduced semi-variances. It can be seen that the total sill of the variogram is higher for OK and KED (6750 mm2) than for RK (6100). This is expected because the covariate, elevation which was considered for RK but not for OK variogram, partly explains the variability of the rainfall data.

It should also be noted that the relative nugget effect is lower for OK and KED (2.2%) than for RK (24.2%), indicating that the spatially structured variability is lower for rainfall residuals (RK) than for rainfall themselves (OK).

4.4 Rainfall mapping

Different descriptive statistical parameters of the measured rainfall as well as those of the predicted by the three geostatistical interpolation methods are given in Table 5. One of the characteristics of the geostatistical methods is the smoothing in the sense that the predicted values are less variable than the measured values; in other words, the predicted minimal values are larger than those measured while the maximal predicted values are smaller than those measured. This smoothing phenomenon is the least for KED followed by OK while it is the most accentuated for RK which has 298.7 and 565.8 mm as minimal and maximal values compared to 251.1 mm and 644.8 mm for the measured values. This phenomenon is confirmed by the standard deviations, in particular by the reduction of the estimation variances with respect to the measured data variance of 55.2, 50.5, and 35.2% for RK, OK, and KED, respectively, and also by the coefficient of variation which is minimal for RK (14.8%) followed by OK (15.7%) and KED (17.6%) compared to measured values (22%).

Table 5 Descriptive statistics of measured and predicted mean annual rainfall (mm) using 3 geostatistical methods (OK, RK, and KED)
Full size table

Figure 5 shows the maps obtained by the three methods of geostatistical interpolation (OK, RK, and KED) at the nodes of a grid of 4 km × 4 km, i.e., 16 km2 with a neighborhood defined by 10 as number of neighbors and 18,500 m as neighborhood radius. The three maps show the fundamental differences between the three approaches.

Fig. 5
figure 5

Maps of mean annual rainfall estimated by OK (top), RK (middle), and KED (bottom)

Full size image

OK only uses primary data (rainfall values). It can therefore be considered as a reference for evaluating the real gain of taking elevation data into account. The rainfall estimates by OK (Fig. 5 top) show fairly smooth zonal profiles, with minimal low-level rainfall in the western and central plains of the East side of the study area, and increasing rainfall from the center to the north and south ends, again for the eastern part of the study area, generally following the pattern of elevation previously noted for the measured values (Fig. 1), although the elevation at the kriging estimation points was not taken into account with this method. This is the result of the physical relationship between rainfall and elevation. There is also a marked influence of the unusually low rainfall of station 1 (southeast of the study area) on the rainfall estimates of its vicinity.

RK derives the rainfall value directly from the orography through an overall linear correlation between the primary data and the elevation for the determination of the general trend followed by the local interpolation of the residuals. A smooth pattern was observed for RK (Fig. 5, middle), quite similar to, but much clearer than, that observed for OK (Fig. 5, top), with some important differences. Thus, in the western part, there is much more detail in the rainfall values for RK, whereas these values are much smoother and summary for OK. The opposite phenomenon is noted for the central part of the east side of the study area and the southeast around station 1 which recorded abnormally low rainfall. In the western part (stations 49 to 58), the rainfall is very uniform (minimum 251.1 mm, maximum 352.5 mm, and CV = 9.1%). As OK only uses rainfall, the map looks smooth. On the other hand, since RK also uses the elevation which is not at all uniform (minimum 54 m, maximum 590 m and CV = 114.4%), the map is more nuanced. On the east side (stations 1 to 7 and 12), rainfall is twice as variable as in the west (minimum 311.0 mm, maximum 623.1 mm, and CV = 18.9%), mainly because of the abnormally low value from station 1 (311 mm). As a result, the OK map is more contrasted than the west side. In contrast, the integration of the elevation into RK softened the influence of the abnormal value of station 1, especially since the elevation is much more uniform (minimum 435 m, maximum 1085 m, and CV = 36.8%) by comparison with the western part. Overall, estimates of RK were slightly higher than those of OK (Table 5), with RK and OK mean values of 393.1 and 389 mm and median values of 395.6 and 383.5 mm, respectively. The same remark applies to the minimal and maximal values and the different percentiles. Although RK takes elevation into account, it incorporates an average regional effect of elevation into an interpolation by kriging rainfall data in the search neighborhood.

KED incorporates the elevation point in the calculation of the estimate, as does RK; however, KED takes into account local elevation variations while RK considers a single global model. As a result, it is noted that there is a very great similarity in the patterns of rainfall maps for KED (Fig. 5 bottom) and OK (Fig. 5 top), unlike RK (Fig. 5 middle). This is mainly due to the use of the same variogram (experimental and fitted theoretical model) of the initial rainfall data (Hengl et al. 2004). Also, the map for KED is noticeably less smooth but rather much more broken, quite complex visually and contains much more detail than the map for OK because of the multitude of local models linking rainfall to elevation and thus a more consistent correspondence between rainfall at one point and local orographic factors. Similarly, the influence of the unusually low rainfall of station 1 is relatively attenuated: in the vicinity of this station, the rainfall obtained by KED is greater than 300 mm, while values between 254 and 300 mm are found for OK. Finally, the comparison of the maps for RK and KED shows that the areas with rainfall greater than 500 mm are much smaller for RK and only appear in the southern central part, whereas for KED, they are found in addition to this part, in other parts as in the east of this southern central part as well as in the north and especially in the north center and east. This is the consequence of the nature of the rainfall–elevation trend which is global and creates an accentuated smoothing for RK, whereas it is local and keeps the details for KED.

Rainfall contour lines have the appearance of DEM curves in areas with very low density of stations (e.g., areas around stations 1, 52, and 58) and in areas where rainfall and elevation are slightly correlated (example of the zone of stations 50 and 53 to 57 with r = 0.10). In these regions, the KED model allows the dominance of the external drift (elevation). In the undersampled regions, the spatial organization of rainfall values reflects, to varying degrees, that of topography (Tapsoba et al. 2005) and KED maps are similar to those of OK. Rossiter (2005, 2007) confirms this result by mentioning that, although the main and auxiliary variables are not highly correlated, KED estimate is similar to drift.

4.5 Quality of the interpolation algorithms

To deepen the comparative study of geostatistical interpolation methods, the performance indicators for cross-validation are given in Figs. 6 and 7 and Table 6. The errors of the three methods are symmetrically distributed with a single peak around zero (Fig. 6). The normal distribution of cross-validation errors would indicate a good predictive model for kriging (Isaaks and Srivastava 1989). The results in Fig. 6 therefore imply that the variogram models are relatively accurate for the three kriging methods. We also note the impact of the abnormally low value of the rainfall of the station 1 which was clearly overestimated by OK and KED which resulted in the presence of the bar corresponding to 200 mm.

Fig. 6
figure 6

Histogram of rainfall prediction errors by OK (top), RK (middle), and KED (bottom)

Full size image
Fig. 7
figure 7

Boxplots of mean annual rainfall prediction errors using OK (left), RK (middle), and KED (right)

Full size image
Table 6 Coefficients of regression linking predicted and observed mean annual rainfall (mm) with some fitting quality indicators for 3 kriging methods using errors from cross-validation
Full size table

The boxplots of rainfall prediction errors (Fig. 7) show that, generally, the three kriging methods correctly predicted rainfall for the 58 stations; the perfect correspondence between the predicted and the measured values is represented by the horizontal line corresponding to 0 (dashed line) in Fig. 7. However, the degree of underestimation (numbers below line 0 in Fig. 7) or overestimation (numbers above line 0 in Fig. 7) has varied according to the method. Thus, the largest overestimation was recorded for the station 1, a well-insulated station and for which an abnormally weak rainfall was registered compared to its neighborhood, for OK and KED with respectively 177.6 and 179.4 mm, which represents 57.1 and 57.7% compared to the measured value (311 mm), whereas this overestimation is much smaller for RK (121 mm recorded at the station 28 having an average elevation of 376 m, which represents 38.9% compared to the measured value). On the other hand, OK gave the highest number of stations (6) with the highest underestimates (exceeding 100 mm): in descending order, stations 25, 7, 27, 38, 13, and 2 with 201.7, 172.5, 142.8, 130.5, 105, and 101.8 mm, respectively, which represents 31.3, 27.7, 24.1, 26.4, 19.5, and 19.5% compared to the measured values. All these stations, except 38, have the highest elevations (ranked from 1st to 9th) (Fig. 1). Station 38, although it has an average elevation (320 m, ranked 26th), experienced the 4th highest underestimation of rainfall; this could be due to the fact that the effect of the Mediterranean Sea (this station is close to the coast, with a distance of 19 km, Figs. 1 and 5) and the effect of the vegetation cover (high density represented by the Bessa-Chlef forest) were not considered. RK gave the highest underestimates for 3 of the 6 previous stations: 27, 7, and 38 with 156.7, 136.1, and 112.2 mm, respectively, which represent 26.5, 21.8, and 22.7% compared to the measured values whereas the minimum of strong underestimates were recorded for KED for stations 25 and 38 (102.8 and 100 mm representing 15.9 and 20.3%). Comparing the three methods, one notices the very clear reduction, on the one hand, of the overestimation of the rainfall of the station 1 which was of 177.6 and 179.4 mm for OK and KED, respectively, and which was reduced by almost half (94.4 mm) for RK and, on the other hand, the underestimation of the rainfall of station 25 which was the strongest with OK (201.7 mm) and then it was reduced by half for KED (102.8 mm), whereas it is only 79 mm for RK. These results show that KED is the best interpolator according to the limited number of large underestimates (2) or overestimates (1) or the relative importance of this strong underestimation (20.3%) or overestimation (57.7%) followed by RK (3 underestimates with the highest representing 26.5% of the measured value) and finally the OK (6 underestimates with the highest representing 31.3% of the measured value and an overestimation of 57.1%).

A first quantitative approach to evaluate the accuracy of the models is using the correlation coefficient (r) and the coefficient of determination (r2) between the measured values and those predicted by each of the three interpolation methods (Table 6). The best match is obtained for KED (r = 0.82 and r2 = 67%) followed by RK (r = 0.79 and r2 = 62%) while OK is far from these last two (r = 0.70 and r2 = 49%). These correlation and determination coefficients are the consequences of the number of significant underestimations and overestimations and their relative importance (Fig. 7). The second approach, strongly related to the first, concerns the regression coefficients (intercept and slope); moreover, the slopes and the coefficients of determination are almost equal (Table 6). In principle, a perfect agreement between the measured values and those predicted would imply an intercept = 0 and a slope = 1. The best model would be the one with the smallest intercept and the largest slope. This is the case for KED (intercept = 136.6 mm and slope = 0.66) followed by RK (intercept = 184.9 mm and slope = 0.53) and finally OK (intercept = 193.5 mm and slope = 0.50).

KED can be considered the best model in statistical terms (Table 6) because it gives the lowest values of ME, MAE, and RMSE (− 1.9, 35.4, and 49.5 mm, respectively) and the highest values of d, CC, and EF (0.89, 0.80, and 0.67, respectively). The results of RK are intermediate while those of OK are the worst. There is clearly a marked improvement in the estimation performance taking into account the elevation, in particular by KED: the average error goes from 6 mm for OK to − 1.9 mm indicating a minimal or almost absent systematic error or bias. The mean absolute error decreased from 40 to 35.4 mm and the RMSE decreased from 61.4 to 49.5 mm (Table 6).

5 Conclusion

The objective of this study was to compare three geostatistical interpolation methods based on the univariate kriging algorithm (OK) and the multivariate kriging which takes into account the altitude of 58 rain gauges for regression-kriging (RK) and kriging with external drift (KED), to obtain the best distribution of mean annual rainfall (1972–2012) in a region centered in the main watershed in Algeria.

The results showed a good correlation between rainfall and elevation (r = 0.71) and that the introduction of elevation information improves the performance of covariate kriging methods, especially KED followed by RK, in areas with complex morphology like the Chéliff watershed. Overall, the cross-validation statistical indicators show that the KED interpolation method is the best, for unbiasedness and accuracy, when rainfall data are heterogeneous and many local rainfall–elevation relationships are considered as opposed to a unique global rainfall–elevation relationship as in the case of RK; the two methods using the auxiliary information are better than the one that does not use this secondary information (OK). Finally, the study showed that, using the kriging algorithm carried out with the best method, it is possible to develop a rainfall map, of good quality, in the northern part of the Chéliff watershed, especially with an auxiliary variable. The performance of the geostatistical rainfall interpolation methods, RK and KED, could be improved by considering other sources of auxiliary information such as distance to the sea and the importance of vegetation cover (e.g., forest).