1 Introduction

Nowadays, investigation on air temperature has achieved relevant importance because of its influence on all natural systems and human activities, such as crop growth (Verdoodt et al. 2004; Bechini et al. 2006), agro-ecological zoning (Caldiz et al. 2001; Ye et al. 2008), and food security assessment (Ye and Van Ranst 2009, 2002; Ye et al. 2013). Moreover, high temperatures can cause an increase of death rates, especially when the data rise above critical values (Kunst et al. 1993; Curriero et al. 2002; Hajat et al. 2002; Keellings and Waylen 2012).

Stochastic modeling and simulation of daily meteorological data is a prominent subject in literature since several decades. A classical approach for the analysis of temperature data, based on the procedures presented by Yevjevich (1972), was proposed by Richardson (1981), who considered maximum and minimum temperatures as continuous multivariate stochastic processes. Generally, the stochastic models, used to reproduce climatic and hydrological series, are the autoregressive (AR), the moving average (MA), the autoregressive moving average (ARMA), and the autoregressive integrated moving average (ARIMA) models (Box and Jenkins 1976; Grimaldi et al. 2005). A limitation of these models is that they can only capture the short-range dependence, thus presenting a lack of flexibility in reproducing the combined effect of short- and long-memory (Box and Jenkins 1976). Since Hurst (1951) detected the presence of long-term persistence in data series studying the Nile River levels, the need of long memory in time series modeling has been pointed out. In fact, long-range dependence has been encountered in various hydrological data (Lye and Lin 1994; Pelletier and Turcotte 1997; Koscielny-Bunde et al. 2006; Ehsanzadeh and Adamowski 2010). Doukhan et al. (2003) evidenced that long-range dependent processes are characterized by a hyperbolic decrease of the autocorrelation function and are closely related to self-similarity. Recently, Prass et al. (2012) found that long-range dependence may affect the performance of time series models with a short time step. Moreover, incorporating long-range dependence into time series modeling is also conceptually important, since the model should capture the behavior of the data as realistically as possible. To this aim, Granger and Joyeux (1980) and Hosking (1981) proposed the fractionally differenced ARIMA models (FARIMA or ARFIMA) as an extension of the ARIMA models. The differencing order of the FARIMA models can be fractional, thus providing flexibility in that they can capture both short- and long-memory behavior, by varying the autoregressive and moving average components and using few parameters (Lohre et al. 2003; Montanari et al. 1997; Prass et al. 2012). This is an advantage of the FARIMA modeling framework because other long-memory models, capable of reproducing the Hurst phenomenon, such as the fractional Gaussian noise, have no flexibility in the choice of the short-memory autocorrelation structure (Koutsoyiannis 2002). In fact, it is shown that the fractionally integrated time series models are much more accurate than the traditional autoregressive models employing a similar number of parameters (Caballero et al. 2002).

Many studies have been developed on FARIMA models in literature. Bisaglia and Grigoletto (2001) proposed a bootstrap-based method to construct prediction intervals for FARIMA processes. Rupasinghe and Samaranayake (2012) and Rupasinghe et al. (2014) introduced a simpler alternative method, based on the sieve bootstrap approach of Alonso et al. (2002) and Alonso et al. (2003). Several contributions have been proposed in hydrology (e.g., Hosking 1984), climatology (e.g., Baillie and Chung 2002), and temperature (e.g., Smith 1993). As regards in particular hydrological studies, Montanari et al. (1997) proposed a FARIMA model for the analysis of monthly and daily inflows of Lake Maggiore (Italy). Montanari et al. (2000) applied a special form of the generalized FARIMA process to the Nile River monthly flows at Aswan. They combined the generalized FARIMA approach with a multiplicative ARIMA approach, which allowed to model seasonal and non-seasonal long and short memory. Sheng and Chen (2011) developed a new model, based on FARIMA with stable innovations, to analyze the data and predict the future elevation levels of Great Salt Lake. Yang and Bowling (2014) used a FARIMA model to estimate the long memory in daily stream flow for basins in the Upper Great Lakes region.

In this paper, a stochastic model which adopts the FARIMA approach is proposed for the analysis of daily temperature. Specifically, the different steps of the proposed model concern the data deseasonalization, by means of a truncated Fourier series expansion; the data normalization, through the transformations introduced by Johnson (1949); and the analysis of the correlation structure through a FARIMA model. The model was applied to a maximum temperature series and verified on other four southern Italian gauges. As an example of the possible model applications, some features of the maximum daily temperature have been evaluated by means of a Monte Carlo simulation procedure.

2 Stochastic modeling of daily temperature

Let us indicate with i = 0 , 1 , 2 ,  .  . . the days from a generic starting point, and let us define T(i) as the temperature characterizing the generic i-day. The T(i) values can be the maximum, T max(i), or the minimum, T min(i), or even the mean temperature, T mean(i), of the day. A sequence of T(i) observations can be explained as a realization of a discrete parameter stochastic process which shows a cyclostationarity condition, with period D equal to a year (D = 365.25 days).

2.1 Deseasonalization

The temperature is not a stationary variable (Jewson and Caballero 2003; Campbell and Diebold 2005), where the non-stationarity can be caused by a deterministic seasonal component or by a monotonic trend. Assuming the trend component equal to zero, the T(i) process can be reduced to a weakly stationary standardized process, Y(i), through the transformation (Grimaldi 2004; Montanari et al. 1997, 2000; Prass et al. 2012)

$$ Y(i)=\frac{T(i)-{\mu}_T(i)}{\sigma_T(i)} $$
(1)

where μ T (i) and σ T (i) are the mean and the standard deviation functions of the T(i) process, respectively. The mean and the variance functions can be described by means of the truncated Fourier series

$$ {\mu}_T(i)=\frac{1}{2}{a}_{\mu, 0}+{\displaystyle \sum_{j=1}^{n_{h,\mu }}\left[{a}_{\mu, j} \cos \left(\frac{2\pi\;j}{D}i\right)+{b}_{\mu, j} \sin \left(\frac{2\pi\;j}{D}i\right)\right]} $$
(2)
$$ {\sigma}_T^2(i)=\frac{1}{2}{a}_{\sigma^2,0}+{\displaystyle \sum_{j=1}^{n_{h,{\sigma}^2}}\left[{a}_{\sigma^2,j} \cos \left(\frac{2\pi\;j}{D}i\right)+{b}_{\sigma^2,j} \sin \left(\frac{2\pi\;j}{D}i\right)\right]} $$
(3)

in which n h , μ and \( {n}_{h,{\sigma}^2} \) are the number of harmonics, while a μ , 0 , a μ , j  , b μ , j and \( {a}_{\sigma^2,0},{a}_{\sigma^2,j},{b}_{\sigma^2,j} \) are the coefficients of the Fourier expansion of the mean and the variance functions, respectively.

Given a sample of observed temperature, t(i k ), with k = 1 , 2 ,  .  .  . K which corresponds to the days i 1 , i 2 ,  .  .  .  , i k , the functions μ T (i) and \( {\sigma}_T^2(i) \) can be estimated through their analogous sample values, m T (i) and \( {s}_T^2(i) \).

By using the least squares method, the Fourier coefficients of the mean function can be estimated by minimizing the following function:

$$ {S}_{\mu}^2\left({a}_{\mu, 0},{a}_{\mu, 1},{b}_{\mu, 1},\dots \right)={\displaystyle \sum_{k=1}^K{\left\{t\left({i}_k\right)-\frac{1}{2}{a}_{\mu, 0}-{\displaystyle \sum_{j=1}^{n_{h,\mu }}{f}_{\mu}\left({i}_kj;{a}_{\mu, j},{b}_{\mu, j}\right)}\right\}}^2} $$
(4)

where f μ (i k j; a μ , j , b μ , j ) = a μ , j  cos (2π i k j/D) + b μ , j  sin (2π i k j/D).

Analogously, the coefficients of the Fourier expansion of the variance function can be estimated using the same sample, by minimizing the following function:

$$ {S}_{\sigma^2}^2\left({a}_{\sigma^2,0},{a}_{\sigma^2,1},{b}_{\sigma^2,1},\cdots \right)={\displaystyle \sum_{k=1}^K{\left\{{\left[t\left({i}_k\right)-{\mu}_T\left({i}_k\right)\right]}^2-\frac{1}{2}{a}_{\sigma^2,0}-{\displaystyle \sum_{j=1}^{{}^nh,{\sigma}^2}{f}_{\sigma^2}\left({i}_kj;{a}_{\sigma^2,j},{b}_{\sigma^2,j}\right)}\right\}}^2} $$
(5)

where \( {f}_{\sigma^2}\left({i}_kj;{a}_{\sigma^2,j},{b}_{\sigma^2,j}\right)={a}_{\sigma^2,j} \cos \left(2\pi\;{i}_kj/D\right)+{b}_{\sigma^2,j} \sin \left(2\pi\;{i}_kj/D\right) \).

If the temporal span of the sample is a multiple of the period D, and the series does not have any missing days, the trigonometric interpolation theory provides the estimation of the coefficients in explicit form (Prass et al. 2012). The number of harmonics (\( {\widehat{n}}_{h,\mu } \) and \( {\widehat{n}}_{h,{\sigma}^2} \)) must be estimated by assuring the absence of the periodicity of the process Y(i), with respect to the criterion of the parameter parsimony. The Y(i) data obtained through the deseasonalization of t(i k ) are generally correlated, but the tests employed for the estimation of the number of harmonics require a random sample. Therefore, for each prefixed couple n h , μ and \( {n}_{h,{\sigma}^2} \), a transformed random subsample of y(i k ), namely, \( y\left({i}_{k_{*}}\right)=\left[t\left({i}_{k*}\right)-{\mu}_T\left({i}_{k*}\right)\right]/{\sigma}_T\left({i}_{k*}\right) \) with k * = 1 , 2 ,  .  .  .  , K *, can be created. This subsample can be obtained by extracting values sampled every δ days (temporal span), with δ long enough to limit the stochastic dependence effect, however assuring a reliable sample length. The subsample is subdivided into M classes, assigning to each generic m th class the N m values of \( y\left({i}_{k_{*}}\right) \) for which it holds

$$ \left(m-1\right)/M\le \left({i}_k \mod D\right)/D<m/M\kern0.5em m=1,2,\ldots M $$
(6)

Indicated as μ Y , m and \( {\sigma}_{Y,m}^2 \) the mean and the variance values of each class, it is possible to test the hypotheses H 0 , μ  : μ Y , 1 = μ Y , 2 =  .  .  .  = μ Y , M  = μ Y and \( {H}_{0,{\sigma}^2}:{\sigma}_{Y,1}^2={\sigma}_{Y,2}^2=\ldots ={\sigma}_{Y,M}^2={\sigma}_Y^2 \). The hypothesis H 0 , μ is tested through the statistics \( {S}_V^2 \), approximately distributed according to a Fisher variance-ratio law v 2(f 1, f 2). The hypothesis \( {H}_{0,{\sigma}^2} \) is tested through the Barlett’s test (Snedecor and Cochran 1989) based on the statistics \( {S}_B^2 \) approximately distributed according to a χ 2(f 1) law. Both the procedures are detailed in Appendix 1.

2.2 Gaussianization procedure

The Gaussianization procedure (e.g., Chen and Gopinath 2000; Hólm et al. 2002; Servidio et al. 2011) is a necessary condition to respect the coherence of the linear stochastic model. In this case, the sample values y(i k ) of the random variable Y have a null mean value, m Y  = 0, and a unit variance, \( {s}_Y^2=1 \), but generally show skewness (g 1 , Y ) and kurtosis (g 2 , Y ) coefficients, which significantly differ from the theoretical values expected for a Gaussian variable (γ 1 , Y  = 0 and γ 2 , Y  = 3, respectively). In this case, it is possible to transform the original variable, Y, into a standardized Gaussian variable, Z = f(Y). For this purpose, the transformation functions introduced by Johnson (1949) are well suited,

$$ Z=\eta +\theta \ln \left[{f}_Y^{(.)}\left(y;\alpha; \beta \right)\right] $$
(7)

where − ∞  < η <  + ∞, θ > 0, − ∞  < α <  + ∞, and β > 0 are the parameters of the transformation and \( {f}_Y^{\left(\cdot \right)}\left(y;\alpha, \beta \right) \) can take one of the following forms:

$$ \begin{array}{cc}\hfill {f}_Y^{(U)}\left(y;\alpha, \beta \right)=\left(y-\alpha \right)/\beta +\sqrt{1+{\left(y-\alpha \right)}^2/{\beta}^2}\hfill & \hfill -\infty <y<+\infty \hfill \end{array} $$
(8)
$$ \begin{array}{cc}\hfill {f}_Y^{(L)}\left(y;\alpha, \beta \right)=\left(y-\alpha \right)/\beta \hfill & \hfill y>\alpha \hfill \end{array} $$
(9)
$$ \begin{array}{cc}\hfill {f}_Y^{(B)}\left(y;\alpha, \beta \right)=\left(y-\alpha \right)/\left(\alpha +\beta -y\right)\hfill & \hfill \alpha <y<\alpha +\beta \hfill \end{array} $$
(10)

Specifically, Eqs. (8) and (10) are known as unbounded and bounded Johnson transformations, respectively, while Eq. (9) implies that the random variable y is distributed according to a log-normal law with three parameters. The choice of the function \( {f}_Y^{\left(\cdot \right)}\left(y;\alpha, \beta \right) \) to be adopted depends on the sample values of the skewness coefficient, g 1 , Y , and the kurtosis coefficient, g 2 , Y . In fact, given that

$$ {R}_1=\sqrt[3]{1+{g}_{1,Y}^2/2+\sqrt{g_{1,Y}^2\left(1+{g}_{1,Y}^2/4\right)}} $$
(11)
$$ {R}_2=\sqrt[3]{1+{g}_{1,Y}^2/2-\sqrt{g_{1,Y}^2\left(1+{g}_{1,Y}^2/4\right)}} $$
(12)
$$ {G}_2=6\left({R}_1^2+{R}_2^2\right)+\left({g}_{1,Y}^2-8\right)\left({R}_1+{R}_2\right)-2{g}_{1,Y}^2+7 $$
(13)

Equation (8) has to be used if g 2 , Y  > G 2, Eq. (10) if g 2 , Y  < G 2, while Eq. (9) concerns only the special case g 2 , Y  = G 2.

The different techniques used for the estimation of the transformation parameters are based on the method of moments. In the proposed model, only the parameters η and θ have to be effectively estimated, since α and β are linked to the former through analytical expressions, being μ Y  = 0 and \( {\sigma}_Y^2=1 \).

If the unbounded Johnson transformation must be adopted, in order to estimate the parameters η and θ, the following equation in the variable ω =  exp (0/θ 2) has to be numerically resolved (Tuenter 2001):

$$ \left[\omega -{\omega}_{*}\right]{\left[2\omega +{\omega}_{*}+3\right]}^{\;2}-4{g}_{1,Y}^2=0 $$
(14)

where

$$ {\omega}_{*}=2\left[\sqrt{1+\frac{1}{2}\left({\omega}^2-\frac{g_{2,Y}+3}{\omega^2+2\omega +3}\right)}-1\right] $$
(15)

Otherwise, if the bounded Johnson transformation must be applied, the parameter estimation is less simple. In fact, for the estimation of the parameters η and θ, the following non-linear system should be numerically resolved:

$$ \left\{\begin{array}{l}{\gamma}_{1,Y}\left(\eta, \theta \right)={g}_{1,Y}\hfill \\ {}{\gamma}_{2,Y}\left(\eta, \theta \right)={g}_{2,Y}\hfill \end{array}\right. $$
(16)

in which also the values of the functions γ 1 , Y (η, θ) and γ 2 , Y (η, θ) should be numerically evaluated.

2.3 Correlation structure

The sample data series z(i k ) of the random variable Z, obtained from the Johnson transformations applied to the sample y(i k ), usually shows a correlation structure characterized by a marked persistence, with values of autocorrelation coefficients slowly decreasing for growing lags. Assuming that the zero mean process z(i) can be described by a FARIMA (p,d,q) model, the following relationship holds:

$$ {\varPhi}_p(B){\left(1-B\right)}^dz(i)={\varPsi}_q(B)\varepsilon (i) $$
(17)

where B is the backward operator, Φ p (B) is the p-order polynomial of the autoregressive component, Ψ q (B) is the q-order polynomial of the mean average component, ε(i) is a sequence of i.i.d. random variables with mean zero, and d is the fractional order of differentiation. In other terms, the FARIMA (p,d,q) model can be considered as a composition between a fractional filter d and an ARMA (p,q) process

$$ {\left(1-B\right)}^dz(i)=u(i) $$
(18)
$$ {\varPhi}_p(B)u(i)={\varPsi}_q(B)\varepsilon (i) $$
(19)

Equation (19) shows that the intermediate process u(i) is an ARMA (p,q) process, which for Ψ 0 = 1 is

$$ u(i)={\displaystyle \sum_{k_p=1}^p{\varphi}_{k_p}}u\left(i-{k}_p\right)+{\displaystyle \sum_{k_q=0}^q{\psi}_{k_q}}\varepsilon \left(i-{k}_q\right) $$
(20)

By employing the series expansion of (1 − B)d, Eq. (18) can be described as

$$ u(i)=\varGamma \left(d+1\right){\displaystyle \sum_{s=0}^{\infty}\frac{{\left(-1\right)}^s}{\varGamma \left(d-s+1\right)s!}}z\left(i-s\right) $$
(21)

It is well known that the maximum likelihood estimation of the variance-covariance matrix of a multivariate normal distribution is the sample variance-covariance matrix (Anderson and Olkin 1985). By using a FARIMA model, the correlation structure depends on the model parameters. Thus, through a weighted least squares method, we find the best fitting of the maximum likelihood estimation of the variance-covariance matrix.

The estimation of the parameters d, \( {\varphi}_{k_p} \), and \( {\psi}_{k_q} \) can be obtained following a trial-and-error procedure. Through Eq. (21), for each assigned value of the parameter d, it is possible to transform the sample z(i k ) in a sample u(i k ), which can be considered as a realization of the ARMA (p,q) process. Thus, once the sample autocorrelation values r U , λ (d) of u(i k ) for λ = 1 ,  .  .  .  , p + q are evaluated, the estimated values \( {\widehat{\varphi}}_1(d),\ldots,{\widehat{\varphi}}_p(d) \), \( {\widehat{\psi}}_1(d),\dots, {\widehat{\psi}}_q(d) \) can be obtained, by considering

$$ \begin{array}{cc}\hfill {\rho}_{U,\lambda}\left[{\widehat{\varphi}}_1(d),\dots, {\widehat{\varphi}}_p(d),{\widehat{\psi}}_1(d),\dots, {\widehat{\psi}}_q(d)\right]={r}_{U,\lambda }(d)\hfill & \hfill \lambda =1,\dots, p+q\hfill \end{array} $$
(22)

where ρ U , λ are the theoretical autocorrelation values of the ARMA (p,q) process.

The actual value \( \widehat{d} \) of d can be estimated by minimizing the weighted mean square deviation

$$ {S}_{\rho}^2={\displaystyle \sum_{l=1}^{N_r}{\omega}_l{\left\{{r}_{Z,l}-{\rho}_{Z,l}\left[{\widehat{\varphi}}_1(d),\dots, {\widehat{\varphi}}_p(d),{\widehat{\psi}}_1(d),\dots, {\widehat{\psi}}_q(d),d\right]\right\}}^2} $$
(23)

where r Z , l are the sample correlogram values derived by the sample z(i k ); ρ Z , l are the theoretical autocorrelation values of the FARIMA (p,d,q) model; N r is the maximum lag to which the calculation for the deviation can be extended; and ω l , with l = 1 ,  .  .  .  , N r and \( {\displaystyle {\sum}_{l=1}^{N_r}{\omega}_l}=1 \), are the weighting coefficients which allow to distribute the quality of the data fit at varying of the lag l.

The estimated values \( \widehat{p} \) and \( \widehat{q} \) must be fixed by respecting the principle of parametric parsimony (Box and Jenkins 1976). Akaike (1974) suggests a mathematical formulation of the parsimony criterion of model building, known as Akaike information criterion (AIC), for the purpose of selecting an optimal model fits to a given data. In this work, the Akaike information criterion in the correct form (AICc) has been used (Sugiura 1978; Burnham and Anderson 2002). The model showing the minimum value of the AICc can be considered as the one which better matches both the fitting to the observed data and the principle of parametric parsimony. Before applying the AIC criterion, it has been verified that the residuals were white noise through the application of the Anderson-Darling test (Anderson and Darling 1952).

3 Application

3.1 Database

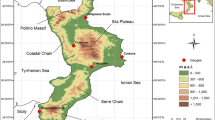
The proposed stochastic model has been applied to the maximum daily temperatures, T(i) = T max(i), of the Cosenza gauge and verified on other four southern Italian gauges, managed by the Centro Funzionale Multirischi of the Calabria region (Fig. 1). The gauges are located in an area characterized by high climatic variability due to its geographic location and mountainous nature (Coscarelli and Caloiero 2012). Summers are typically dry, denoting a subtropical Mediterranean climate. The coastal areas present mild winters and hot summers with little precipitation. The Ionian side, influenced by air masses coming from Africa, records high temperatures and intense precipitation; on the Tyrrhenian side, influenced by western air currents, milder temperatures and considerable orographic precipitation are observed. The internal areas are characterized by colder winters, sometimes snowy, and fresher summers with some precipitation (Ferrari et al. 2013; Buttafuoco et al. 2015; Caloiero et al. 2015a).

Fig. 1
figure 1

Localization of the temperature gauges on a DEM

Full size image

The main features of the selected gauges are presented in Table 1. The gauges are located at different altitudes, namely, from a few meters to about 800 m above sea level (a.s.l.). Moreover, considering an observation period spanning from 1951 to 2010, the temperature gauges have less than 9 % missing days. Previous regional studies on the temperature data series of Calabria region (Caloiero et al. 2015b, c) did not show significant trends in maximum temperature data for the gauges used in this study. As a further analysis, in this study, the Mann-Kendall test (Mann 1945; Kendall 1962) has been applied to investigate the existence of monotonic trend in maximum daily temperature, as suggested also by Prass et al. (2012). Results confirmed that no statistical significant trends exist for the selected gauges.

Table 1 Gauges used for the application
Full size table

3.2 Parameter estimation

The absence of trends in the data series considered in this study allows the use of Eqs. (2) and (3). Since the series of the maximum daily temperature, t max(i k ), show some missing data, the estimation of the coefficients of the truncated Fourier expansion referred to the mean, μ T (i), and to the variance functions, \( {\sigma}_T^2(i) \), has been performed by minimizing Eqs. (4) and (5).

With reference to the Cosenza gauge, Table 2 shows the results of the tests used for the identification of the minimum number of harmonics of the Fourier expansion, for which both the hypotheses \( {H}_{0,{\sigma}^2} \) and H 0 , μ cannot be rejected (significant level = 0.05). The tests employed data sampled every 8 days (δ = 8) and indicated that two harmonics are required for both the mean and the variance functions in order to remove the periodicity in the first- and second-order statistics of the observed series. The results of the same tests applied also to the other gauges confirm that two harmonics are needed for all the stations to remove the periodicity in the mean function (Table 3). Moreover, differently from the Cosenza gauge, for three series, the periodicity of the variance function can be removed with only one harmonic. In Table 3, for each station, the estimated values of the coefficients of the truncated Fourier expansion for the mean and the variance functions are also reported. Figure 2 shows, for the Cosenza gauge, the comparisons between sample and estimated values of the mean and the standard deviation functions, respectively. In particular, the estimated values have been obtained for zero, one, and two harmonics for each day of the year. The same comparisons are shown for the Catanzaro gauge in Fig. 3. In Fig. 4, the comparison among the ACFs of the observed and the deseasonalized values (for a lag range centered to 365 days) is shown.

Table 2 Identification of the number of harmonics for the Cosenza gauge
Full size table
Table 3 Coefficients of the truncated Fourier expansions for the mean and the variance functions
Full size table
Fig. 2
figure 2

Cosenza gauge: a comparison between the observed m T (i) and the estimated μ T (i) functions of the mean, averaged for each day of the year, and b comparison between the sampling s T (i) and the estimated σ T (i) functions of the standard deviation, averaged for each day of the year

Full size image
Fig. 3
figure 3

Catanzaro gauge: a comparison between the observed m T (i) and the estimated μ T (i) functions of the mean, averaged for each day of the year, and b comparison between the sampling s T (i) and the estimated σ T (i) functions of the standard deviation, averaged for each day of the year

Full size image
Fig. 4
figure 4

Comparison among the autocorrelation values of the observed and the deseasonalized data (one and two harmonics) for a lag range centered to 365 days

Full size image

The Gaussianization procedure applied to the deseasonalized data series of Cosenza, \( y\left({i}_k\right)=\left[{t}_{\max}\left({i}_k\right)-{\widehat{\mu}}_T\left({i}_k\right)\right]/{\widehat{\sigma}}_T\left({i}_k\right) \), was performed through the unbounded version of the Johnson transformations. Operatively, the parameters η and θ of the Johnson transformation have been estimated by numerically solving Eq. (14), thus allowing also the estimation of the derived parameters α and β (Table 4). The application to the other gauges evidenced that only the data series of the Potenza gauge has been transformed into a Gaussian process by means of the bounded function, thus requiring the numerical solution of the non-linear system (Eq. (16)). For all the gauges, Table 4 presents the sample values of the skewness and the kurtosis coefficients of the y(i k ) series (g 1 , Y , g 2 , Y ) and the set of the estimated values of the Johnson transformation parameters \( \left(\widehat{\alpha},\widehat{\beta},\widehat{\eta},\widehat{\theta}\right) \).

Table 4 Parameter estimation of the Johnson transformation
Full size table

The achievement of the Gaussian feature of the series z(i k ) is evidenced by the comparison of the sampling values with the theoretical values of the standard normal variable on probabilistic plot, as shown for the Cosenza and the Villapiana gauges in Fig. 5.

Fig. 5
figure 5

Comparison between observed values and theoretical cumulative distribution function of the Z variable for two gauges (Cosenza and Villapiana Scalo)

Full size image

The identification of the FARIMA (p,d,q) process aimed at describing the correlation structure of the Gaussian series. Specifically, the procedure, based on the AICc index, identified the orders \( \widehat{p} \) and \( \widehat{q} \), which better fitted the observed data and preserved the parametrical parsimony criterion. The results of this procedure for the Cosenza gauge are presented in Table 5. Namely, for increasing values of the orders p and q, the differential fractional order, d, was identified by minimizing the weighted mean square function, \( {S}_{\rho}^2 \) (Eq. (23)). In this equation, a maximum lag N r  = 50 has been fixed, and the weighting coefficients, \( {\omega}_j={\omega}_j^{\ast }/{\displaystyle \sum {\omega}_j^{\ast }} \), j = 1 , 2 ,  .  .  .  , N r with \( {\omega}_j^{\ast }=1-{\left[\left(j-1\right)/{N}_r\right]}^c \) and c = 1/2, have been adopted. The final results for all the gauges are summarized in Table 6. Globally, for three stations, a FARIMA (1, \( \widehat{d} \),0) model was identified, while for the other two stations, a FARIMA (1, \( \widehat{d} \),1) model was detected. The comparisons between sampling and theoretical correlograms evidenced the ability of the proposed FARIMA model to reproduce the long-term memory (Fig. 6).

Table 5 Identification of the FARIMA model for the Cosenza gauge
Full size table
Table 6 Identification of the FARIMA models for the all gauges used in the application
Full size table
Fig. 6
figure 6

Comparison between sampling and theoretical autocorrelations values for Cosenza gauge

Full size image

3.3 Analysis of maximum daily temperatures

The proposed model, through the application of a Monte Carlo simulation procedure (Appendix 2), can be useful for assessing various features of the temperature database. Specifically, the synthetic world simulation concerned 105 years, corresponding to a total generation of about L s  = 4 × 107 values.

In this study, first, the proposed model has permitted the estimation of the probability F W(τ)[w(τ)] = P[W(τ) ≤ w(τ)] of the annual maximum of the sequences of days, W(τ), with maximum daily temperature over a threshold, τ. Figure 7 shows, on a probabilistic Gumbel graph, the return periods T W(τ) of the random variable W(τ), defined as T W(τ) = 1/{1 − F W(τ)[w(τ)]}, corresponding to different threshold values for the Cosenza station (altitude 242 m a.s.l.). In particular, for increasing threshold values, high return periods can be reached also for short-day sequences. As an example, considering the threshold τ = 40°, the values of W(τ) shift from 2 to 5 days for return periods ranging from 10 to 100 years. Differently, for higher-elevation gauges, such as Potenza (811 m a.s.l.), the same range of values is observed for a lower threshold value of temperature (about 35°). This behavior can be clearly connected to the influence of the gauge altitude on the variable W(τ).

Fig. 7
figure 7

Return periods T W(τ) of the variable W(τ) for different values of the threshold τ for the Cosenza and Potenza gauges (red linear tendency lines)

Full size image

As a further application, the probability values \( {p}_{I_{W\left(\tau \right)}}\left({i}_{W\left(\tau \right)}\right)=P\left[{I}_{W\left(\tau \right)}={i}_{W\left(\tau \right)}\right] \) that such exceedances start in a specified day, i w , were also evaluated. The probability values \( {p}_{I_{W\left(\tau \right)}}\left({i}_{W\left(\tau \right)}\right) \) of the yearly temporal occurrence I W(τ) of W(τ) are shown in Fig. 8 for various threshold values always for the Cosenza gauge. The maximum probability values have been detected in summer around the 210th day of the year.

Fig. 8
figure 8

Probability values p IW(τ) of the temporal occurrence in the year I W(τ) for different threshold values of temperature for the Cosenza gauge

Full size image

Finally, the probability values F W(κ)[w(κ)] = P[W(κ) ≤ w(κ)], associated to the annual maximum of sequences of days W(κ), with maximum daily temperature greater their expected value μ T (i) plus κ-times the standard deviation, have been estimated. The return periods T W(κ) of the variable W(κ), for different values of parameter κ, are presented in Fig. 9 for the Cosenza and the Crotone gauges. As a result, for fixed values of the return period and the parameter κ, the annual maxima values W(κ) were greater for the Crotone gauge than for the Cosenza gauge. In particular, this behavior was more evident for the lower threshold values. For example, the W(κ) values obtained for κ = 0, which corresponds to a return period T W(κ) = 100 years, were 53 days for Cosenza and 80 days for Crotone, respectively.

Fig. 9
figure 9

Return periods T W(κ) of the variable W(κ) for different values of κ for the Cosenza and Crotone gauges (red linear tendency lines)

Full size image

4 Conclusion

In this paper, a stochastic model developed to simulate daily maximum temperature series, coherently with observed time series, is proposed. The model was based on three different steps. The first step was data deseasonalization, obtained by means of a truncated Fourier series expansion. Subsequently, a normalization technique was performed through the Johnson transformation. Finally, a FARIMA model was applied for the analysis of the correlation structure of the normalized data, characterized by a marked persistence. The procedure has been first applied to the Cosenza gauge and then tested to a set of maximum temperature series registered in four gauges located in southern Italy. The model satisfactorily reproduced the long-term memory of the temperature series, also allowing the parametric parsimony criterion.

Moreover, through the application of a Monte Carlo simulation procedure, the proposed model allowed the evaluation of various features of the temperature database. First, the empirical probability distribution of the annual maximum of the sequences of days, with maximum daily temperature over fixed thresholds, has been obtained. Results showed high return periods also for short-day sequences at increasing threshold values. Successively, the probability values that such sequences can start in a specified day have been also evaluated, showing that the highest occurrence probabilities fall in summer periods. Finally, the return period values associated to annual maximum of sequences of days, characterized by maximum daily temperature greater than their expected value plus κ-times the standard deviation, have been obtained.

An important criterion for stochastic modeling is the reproducibility of the statistical characteristics of observed data (Lee 2015). Effectively, the proposed model allowed the prediction of the statistical properties of temperatures, with few data required as input. Moreover, the stochastic model, not depending on station altitude and climatic zone, had the advantage of being applicable in a certain area, aiming to estimate occurrence probabilities and return periods associated with high-temperature events at any day of the year and/or at any gauge. This ability to extrapolate findings is particularly important when seeking to determine the risks of extremely rare events. For these reasons, the model is an attractive tool for management decision-making, and its basic structure can easily be applied to larger areas with spatially differentiated data.