Copula-based risk evaluation of droughts across the Pearl River basin, China

Abstract

Daily precipitation data for the period of 1960–2005 from 42 precipitation gauging stations in the Pearl River basin were analyzed using the Mann–Kendall trend test and copula functions. The standardized precipitation index method was used to define drought episodes. Primary and secondary return periods were also analyzed to evaluate drought risks in the Pearl River basin as a whole. Results indicated that: (1) in general, the drought tendency was not significant at a 95 % confidence level. However, significant drought trends could be found in November, December, and January and significant wetting trends in June and July. The drought severity and drought durations were not significant at most of the precipitation stations across the Pearl River basin; (2) in terms of drought risk, higher drought risk could be observed in the lower Pearl River basin and lower drought risk in the upper Pearl River basin. Higher risk of droughts of longer durations was always corresponding to the higher risk of droughts with higher drought severity, which poses an increasing challenge for drought management and water resources management. When drought episodes with higher drought severity occurred in the Pearl River basin, the regions covered by higher risk of drought events were larger, which may challenge the water supply in the lower Pearl River basin. As for secondary return periods, results of this study indicated that secondary return periods might provide a more robust evaluation of drought risk. This study should be of merit for water resources management in the Pearl River basin, particularly the lower Pearl River basin, and can also act as a case study for determining regional response to drought changes as a result of global climate changes.

1 Introduction

Droughts have strong social and economic impacts. Droughts can have a devastating effect on agriculture, water supply, and the economy, causing deleterious impacts on human society. It is estimated that the global economic losses caused by droughts are as high as 6 to 8 billion US dollars each year, being far more than other meteorological disasters (Wilhite 2000). Drought, as a prolonged status of water deficit, is perceived as one of the most expensive and least understood natural disasters (Kao and Govindaraju 2010). Thus, occurrences, changing characteristics, and risk evaluation of droughts have been receiving increasing attention in recent decades (e.g., Zhang 2004; Calanca 2007; Husak et al. 2007; Lioyd-Hughes 2010; Cancelliere and Salas 2010; Lei and Duan 2010). In order to quantify drought risk, it is important to determine space and time changes in drought.

A drought is a period dominated by abnormally dry weather that lasts long enough to produce a serious imbalance in the water cycle. Mishra and Singh (2010) thoroughly reviewed the fundamental concepts of drought, classification of droughts, drought indices, historical droughts using paleoclimatic studies, and the relation between droughts and large-scale climate indices. There are a mount of drought indices defined to monitor the drought conditions at a regional or global scale. Various drought indices and related strength and weakness of each drought index can be referred to Mishra and Singh (2010). By definition, environmental droughts generally include: (a) meteorological drought; (b) hydrological drought; and (c) agricultural drought (e.g., Livada and Assimakopoulos 2007). This study focuses on the meteorological drought which is defined as a lack of precipitation over a region for a period of time. The factors devoted to defining this kind of drought are rainfall amount, vegetation condition, agricultural productivity, soil moisture, reservoir level, stream flow change, and economic impact. Besides, Wu et al. (2001) compared Standardized Precipitation Index (SPI), Palmer Drought Index, China-Z Index, and the statistical Z score and their applications in the monitoring of drought conditions over China, indicating that the China-Z Index and Z score can provide results similar to the SPI for all time scales. However, SPI has been widely used for studying different aspects of droughts (e.g., Zhang et al. 2008; Mishra and Singh 2009). Thus, SPI technique will be used in this study to monitor the drought conditions over the Pearl River basin.

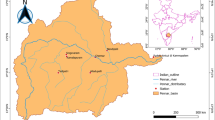
The Pearl River basin involves the West River (Xijiang, in Chinese), the North River (Beijiang), the East River (Dongjiang), and the rivers within the Pearl River Delta (PRD), with a total drainage area of 453,690 km². The PRD is the integrated delta composed of West River delta, North River delta, and East River delta. The area of the PRD is about 9,750 km², wherein the West River delta and the North River delta account for about 93.7 % of the total area of the PRD. Figure 1 shows the location of the study region. A detailed account of the Pearl River basin can be found in Zhang et al. (2008, 2009a). Using nonparametric trend tests, Gemmer et al. (2011) showed that only a few stations experienced trends in precipitation indices on an annual basis. On a monthly basis, significant positive and negative trends above the 90 % confidence level appeared in all months except December. Investigating regionalization of precipitation extremes using the L-moments approach and also stationarity test and serial correlation check, Yang et al. (2010) indicated that the entire Pearl River basin could be categorized into six regions, based on topography and spatial patterns of mean precipitation. They also discussed characteristics of precipitation extremes for different return periods over the Pearl River basin and analyzed related causes.

Fig. 1

Sketch map showing the locations of the study region and the precipitation stations. The numbers and related precipitation stations are listed as the follows: 1 Weining, 2 Zhanyi, 3 Yuxi, 4 Luxi, 5 Mengzi, 6 Anshun, 7 Xingyi, 8 Wangmo, 9 Luodian, 10 Dushan, 11 Rongjiang, 12 Rongan, 13 Guilin, 14 Nanxiong, 15 Fengshan, 16 Hechi, 17 Du'an, 18 Liuzhou, 19 Mengshan, 20 Xindu, 21 Lianzhou, 22 Shaoguan, 23 Fogang, 24 Lianping, 25 Xunwu, 26 Napo, 27 Baise, 28 Jingxi, 29 Laibin, 30 Guiping, 31 Wuzhou, 32 Guangning, 33 Gaoyao, 34 Guangzhou, 35 Heyuan, 36 Zengcheng, 37 Huizhou, 38 Longzhou, 39 Nanning, 40 Luoding, 41 Taishan, and 42 Shenzhen

In investigations, Zhang et al. (2009a) focused on precipitation concentration (CI), on precipitation extremes (2009b), and on wetness and dryness variations (2008). Moisture flux analysis based on the NCAR/NCEP datasets indicated stronger intensity of water vapor transport in rainy season than that in winter (dry season), showing considerable influence of water vapor flux on dry and wet conditions of the Pearl River basin (Zhang et al. 2008). This finding was further corroborated by high correlations between moisture budget, moisture content, and number of wet months in winter. Besides, Zhang et al. (2009a) indicated an increasing CI after the 1990s when compared to that before the 1990s. It was tentatively concluded that these CI changes in the Pearl River basin were likely associated with the consequences of global warming.

In general, the Pearl River basin is characterized by abundant precipitation. However, intensifying hydrological cycle tends to alter the precipitation process (e.g., Zolina et al. 2010; Zhang et al. 2010), which has the potential to cause higher frequencies of droughts and floods (e.g., Zhang et al. 2011). It should be emphasized that the Pearl River basin plays an important role in the socioeconomic development of China. Taking the PRD as an example, on less than 0.5 % of the country’s territory, the PRD region produces about 20 % of the national GDP, attracts about 30 % of foreign direct investment, and contributes about 40 % of the export (therefore called “World Factory”). The Pearl River basin is also an important source of water supply. The East River, one of the tributaries of the Pearl River, bears the heavy responsibility for the water supply for large cities in the vicinity of the lower Pearl River basin, such as Hong Kong, Macau, Shenzhen, and Guangzhou. About 80 % of the water supply of Hong Kong is from the East River basin (e.g., Wong et al. 2010).

Despite the significance of the Pearl River basin, limited work has been done on addressing the changing characteristics of droughts or evaluation of drought risks across this basin. Besides, the copula functions are used in this study to investigate joint probability of drought behaviors within the Pearl River basin; furthermore, the concept of the secondary return periods is accepted and analyzed in this study. All these are the novel points when compared to previous research, particularly such reports have not been found in the Pearl River basin, which can well justify the significance and scientific merits of this study. In this case, the objectives of this study therefore were: (1) to analyze probabilistic behavior of SPI-based drought events and (2) to evaluate the risk of droughts using the theory of runs, Mann–Kendall trend test, copula functions, and L-moment method.

2 Data

Daily precipitation data for 1960–2005 were collected from 42 national standard rain stations in the Pearl River basin (Fig. 1). These data were obtained from the National Climate Center of the China Meteorological Administration (CMA). There are a few missing values in the daily precipitation data sets. Of the 42 stations, 7 stations had some missing values; in total the missing values were less than 0.01 % of the total values. The missing values were filled in using the average value of its neighboring days. The gap filling-in method would have no influence on long-term temporal trends. Checking the data consistency by the double-mass method, it was found that all data were consistent. Based on the CMA classification, a rain day was considered if at least 0.1 mm day⁻¹ was measured (Gemmer et al. 2011).

3 Methodology

3.1 Standardized precipitation index

McKee et al. (1993) proposed SPI for evaluation of drought conditions in Colorado. They defined SPI for each of the time scales as the difference between precipitation on a time scale (x _i ) and the mean value ($\bar{x}$), divided by the standard deviation (s):

$$ {\hbox{SPI}} = \frac{{{x_i} - \bar{x}}}{s} $$

(1)

Different probability distributions have been used to model precipitation time series at various time scales and in different climate regions (e.g., Zhang et al. 2008). In this study, the gamma distribution function was employed, based on the recommendation by McKee et al. (1993). Assume that x is the precipitation series considered, the probability density function of the gamma function is:

$$ g(x) = \frac{1}{{^{{\beta^\partial }\tau \left( \partial \right)}}}{x^{\partial - 1}}{e^{ \frac{{ - x}}{\beta } }}x \geqslant 0 $$

(2)

$$ \tau (x) = \int\limits_0^\infty {{x^{\partial - 1}}{e^{ - x}}dx} $$

(3)

wherein α is the shape parameter, β is the scale parameter, x is the precipitation amount, and Г(x) is the gamma function. The gamma parameters were estimated by the maximum likelihood estimation method. The cumulative probability distribution function for a given time scale can be computed as:

$$ G(x) = \int\limits_0^x {g(x)dx} = \frac{1}{{^{{\beta^\partial }\tau \left( \partial \right)}}}\int\limits_0^x {{x^{\partial - 1}}{e^{ \frac{{ - x}}{\beta } }}} dx $$

(4)

Note that precipitation can be 0 mm but the gamma function does not include x = 0. Therefore, the cumulative probability distribution function was computed as:

$$ H(x) = q + \left( {1 - q} \right)G(x) $$

(5)

where q represents the probability of the zero-rain events.

Then the SPI was obtained as:

$$ {\hbox{SPI}} = {\Phi^{ - 1}}\left( {H(x)} \right) $$

(6)

where Φ⁻¹ is the inverse function of the standardized normal distribution.

Persistence is common within hydro-meteorological series which may negatively impact the fit of the probability function. Kao and Govindaraju (2010) suggested being shy away from this point by computing the SPI for different months. The computation of SPI was based on a certain time scale, such as 3 or 6 months. The months were classified into 12 months and SPI for each month was computed. The time scale of the SPI computation was 6 months, for the drought duration or the period with precipitation deficit is usually long, being about half a year (Zhang et al. 2011). The drought severity adopted in this study is defined in Table 1.

Table 1 Drought level by SPI value

3.2 Theory of runs

Drought events were defined by the theory of runs (Yevjevich 1967). In general, in a finite sequence, a series of the same symbol that satisfies certain conditions is called a “Run”. Run-length is the number of the same symbols in a run. Shiau and Shen (2001) indicated that drought events defined by SPI < 0 caused serious water resources supply and drought-induced loss. In this study, we took 0 as the cutoff level of the run-length and the lengths of run were defined by drought durations (D). The drought severity was defined as the absolute value of SPI₆. In addition, if SPI₆ of an individual month was <0 between two drought events (drought duration and drought severity were d ₁, d ₂, and s ₁, s ₂), the two droughts would be categorized into a subordinate drought and can be combined into one drought (Fleig et al. 2006). The combined drought duration would be D ₃ = d ₁ + d ₂ + 1 and drought severity would be S ₃ = (s ₁ + s ₂)/2 (Fig. 2).

Fig. 2

Definition of drought events using the theory of runs

3.3 Mann–Kendall trend test

Nonparametric trend detection methods are less sensitive to outliers than are parametric statistics. In addition, the rank-based nonparametric M-K test (Mann 1945; Kendall 1975) can test trends without requiring normality or linearity. Therefore, this method has been recommended for general use by the World Meteorological Organization (Mitchell et al. 1966). This study also used the M-K test method to analyze trends in drought series represented by SPI values. It should be noted that results of the M-K test are affected by the serial correlation of time series. von Storch and Navarra (1995) suggested eliminating the persistence effect in the meteor-hydrological series before Mann–Kendall analysis. Following Zhang et al. (2001), a statistically significant trend in precipitation series (x ₁, x ₂, x ₃,…, x _n ) was detected using the following steps: (1) compute lag-1 serial correlation ρ ₁; (2) if ρ ₁ < 0.1, the Mann–Kendall test was applied to the time series directly; otherwise (3) the M-K test was applied to the preprocessed time series, i.e., x ₂ − ρ ₁ x ₁, x ₃ − ρ ₁ x ₂,…, x _n  − ρ ₁ x _n−1. The 95 % confidence level was used to evaluate the significance of trends. The significance level used in this study was 0.05.

3.4 Marginal distribution

Six probability distribution functions (PDFs) were chosen for candidates: General Extreme Value distribution (three parameters); General Pareto distribution (three parameters); Pearson type III distribution (three parameters); log normal distribution (three parameters); Wakeby distribution (five parameters); and Gamma distribution. These six PDFs are commonly used in hydrologic extreme value analysis. Parameters of these distribution functions were estimated by the L-moment method proposed by Hosking (1990). The goodness-of-fit of the probability function was evaluated by Kolmogorov–Smirnov’s statistic D (K-S D) (Frank and Masse 1951). In this paper, 95 % confidence level was accepted to reject or accept a fit. Based on the K-S D, the probability distribution function with the highest goodness-of-fit was selected for each station.

3.5 Copula functions

Copulas have been used in the analysis of hydro-meteorological extremes (Zhang and Singh 2006, 2007; Kao and Govindaraju 2010). In this study, the Archimedean copula family (details can be referred to the Appendix section) was used to analyze the joint probability of drought events (Zhang and Singh 2007); because it can be easily constructed, a large variety of copulas belong to this family, and it can be applied when the correlation among extreme hydro-meteorological variables is positive or negative (Zhang and Singh 2007).

3.6 Evaluation of copulas

Copulas were evaluated using the procedure proposed by Huard et al. (2006). Assume that ζ is the entire set of copula functions, we sample a limited subset ζ _Q ⊂ζ. The copula function in the subset ζ _Q can be represented by C _l , l = 1,…,Q. We have the following assumption, i.e.,

H _l : The test data are from copula function C _l , l = 1,…,Q.

We computed the probability Pr(H _l │D) for a given dataset. Based on the Bayes theorem, we computed the following probability for each copula function, i.e.,

$$ \Pr \left( {{H_l}|D,I} \right) = \frac{{\Pr \left( {D|{H_l},I} \right)\Pr \left( {{H_l}|I} \right)}}{{\Pr \left( {D|I} \right)}} $$

where Pr(H _l │D,I) is the probability that the copula function can fit the given data set well; Pr(H _l │I) is the priority weight of a copula function; and Pr(D│I) is the constant standardized by the standard normal distribution. The copula function with the highest Pr(H _l │D,I) is the right candidate. The matlab script can be downloaded from http://code.google.com/p/copula/.

3.7 Determination of the generating function and the resulting copula

The first step in determining a copula was to obtain its generating function from bivariate observations. The procedure to obtain the generating function and the resulting copula was introduced by Genest and Rivest (1993) which was followed in this study. The two variables here are (X, Y): (x ₁, y ₁), (x ₂, y ₂),…, (x _N , y _N ). X and Y are drought index series analyzed in this study. The procedure can be described here:

• 1. Kendall’s τ was determined, based on observed series:

  $$ {\tau_N} = {\left( {\matrix{ N \\ 2 \\ }<!end array> } \right)^{ - 1}}\sum\limits_{i < j} {{\hbox{sign}}\left[ {\left( {{x_i} - {x_j}} \right)\left( {{y_i} - {y_j}} \right)} \right]} $$

  where N is the length of the series; sign = 1 when x _i  ≤ x _j and y _i  ≤ y _j , otherwise, sign = −1; i, j = 1, 2, …, N; and τ _N is the estimate of τ from the observed series.

• 2. The copula parameter, θ, was estimated based on the copula generator of each copula family and Kendall’s τ based on Eq. (17) of the Appendix.

3.8 Bivariate return periods

Salvadori and De Michele (2004) performed bivariate frequency analysis and summarized eight possible joint events, see Table 1 in Salvadori and De Michele (2004), where $E_{U,u}^< = \left\{ {U \leqslant u} \right\}$, $E_{U,u}^> = \left\{ {U < u} \right\}$, $E_{V,v}^< = \left\{ {V \leqslant v} \right\}$, and $E_{{V,v}}^{ > } = \left\{ {V > v} \right\}$; ∧ denotes “and”, and ∨ denotes “or”. These eight joint events mostly correspond to the extreme events that are critical. The two variables describing droughts features are drought duration and drought severity. Drought events with long duration and large severity may exercise a considerable influence on human society. In this case, the joint events considered in this study are:

$$ \left\{ {U > u} \right\} \vee \left\{ {V > v} \right\}\quad {\text{and}}\quad \left\{ {U > u} \right\} \wedge \left\{ {V > v} \right\} $$

Let U denote drought severity and V drought duration, then joint return periods related these two events were computed as:

$$ {T_{\left\{ {U > u\; \vee \;V > v} \right\}}} = \frac{{{\mu_t}}}{{P\left( {U > u\; \vee \;V > v} \right)}} = \frac{{{\mu_t}}}{{1 - F\left( {u,v} \right)}} $$

(7)

$$ {T_{\left\{ {U > u \wedge V > v} \right\}}} = \frac{{{\mu_t}}}{{P\left( {U > u \wedge V > v} \right)}} = \frac{{{\mu_t}}}{{1 - F(u) - F(v) + F\left( {u,v} \right)}} $$

(8)

where F(u) = P(U ≤ u), F(v) = P(V ≤ v), and F(u,v) is the joint distribution; u _t denotes the time interval, e.g., if the series studied is the annual maximum streamflow, then u _t is 1 year. Based on the theory of runs and Markov theorem, u _t was computed as (Shiau and Shen 2001):

$$ {\mu_t} = \frac{1}{{{P_{DW}}}} + \frac{1}{{{P_{WD}}}} $$

wherein ${{p}_{{WD}}} = p\left( {{\text{SP}}{{{\text{I}}}_{t}} \leqslant 0\left| {{\text{SP}}{{{\text{I}}}_{{t - 1}}} > 0} \right.} \right)$ and ${{p}_{{DW}}} = p\left( {{\text{SP}}{{{\text{I}}}_{t}} > 0\left| {{\text{SP}}{{{\text{I}}}_{{t - 1}}} \leqslant 0} \right.} \right)$. In this study, the unit of u _t is month.

3.9 Secondary return periods

For a given return period, the same copula function with different variable combinations can probably produce the same quantiles, e.g., C(u, v) = q and C(u _* ,v _* ) = q. Salvadori and De Michele (2004) proposed the secondary return periods by which, instead of considering a particular joint distribution F _XY with well-specified marginals F _X and F _Y , return periods of the events of interest were calculated using a suitable copula. Besides, they also stressed that, in some cases, it may be even possible to derive analytical expressions of the isolines of return periods. They also implied that the secondary return period provided a precise indication for performing risk analysis and may also yield useful hints for doing numerical simulations (Salvadori and De Michele 2004). In this study, we also accepted the secondary return period for evaluation of drought risk within the Pearl River basin and compared with the joint return periods computed based on the routine computation procedure.

For computation of the secondary return periods, the occurrence probability should be computed first. The Kendall distribution K _C (Nelsen 2006) was used to define this probability as ${K_C}(q) = P\left[ {C{u_1}{u_2}\left( {{u_1},{u_2}} \right) \leqslant q} \right]$. The Kendall distribution K _C related to each copula function can be referred to Table 2. The bivariate K _C can be seen in Fig. 3 which used the Gumbel–Hougaard copula with parameter θ = 2. In this figure, the curves show C(u, v) = q, and the probability of the area covered by C(u, v) ≤ q is K _C (q) . It can then be seen that the probability of the region covered by C(u,v)≤0.2 is 0.36, and the probability of the regions covered by C(u,v)≤0.6 is 0.75. The analytical form of K _C , for tϵ(0,1], was computed as (Nelsen 2006):${K_C}(t) = t - \frac{{\varphi (t)}}{{\varphi \prime \left( {{t^{+} }} \right)}}$, wherein φ′(t ⁺) denotes the right integral.

Table 2 The Kendall distribution K _C related to each copula function

Fig. 3

Kendall distribution function K _C for Gumbel–Hougaard copulas with parameter θ = 2. K _C shows the probability when C(u,v) ≤ q, e.g., the K _C (0.4) = 0.58 for C(u,v) ≤0.4

Input of the copula generator can produce the K _C function for each copula function. The secondary return periods were computed as:

$$ T = \frac{{{\mu_t}}}{{P\left[ {C{u_1}{u_2}\left( {{u_1},{u_2}} \right) \leqslant q} \right]}} = \frac{{{\mu_t}}}{{{K_C}(q)}} $$

With respect to ${{T}_{{\left\{ {U > u\: \vee \:V > v} \right\}}}}$ of this study, ${C^*}\left( {u,v} \right) = 1 - C\left( {u,v} \right) = 1 - t$ and the related probability of the secondary return period would be $P\left[ {{C^*}{u_1}{u_2}\left( {{u_1},{u_2}} \right) \leqslant 1 - t} \right] = 1 - P\left[ {{C}{u_1}{u_2}\left( {{u_1},{u_2}} \right) \leqslant t} \right]$. In this case, the K _C function was computed as (Salvadori and De Michele 2004) ${\bar{K}_C}(t) = 1 - {K_C}(t)$. The related secondary return period was obtained via: $T = \frac{{{\mu_t}}}{{1 - {K_C}(t)}}$.

For ${T_{\left\{ {U > u \wedge V > v} \right\}}}$, the analytical form of K _C is not available and which was resolved using Monte Carlo simulation: (1) we generated 1,000 points, (u, v), corresponding to a certain copula function and (2) we then counted the frequency when C(u,v) ≤ q. The probability of K _C would be the ratio of the frequency to 1,000, i.e.,

$$ {\hat{K}_C}\left( {\hbox{q}} \right) = \frac{{\hat{C}\left( {u,v} \right) \leqslant q}}{{10,000}} $$

$$ \hat{C}\left( {u,v} \right) = 1 - u - v + C\left( {u,v} \right) $$

In this case, the secondary return period was:

$$ T = \frac{{{\mu_t}}}{{{{\hat{K}}_C}(q)}} $$

4 Results and discussions

4.1 Drought analysis by taking the Fogang station as a case study

We took the Fogang station as a case study with the aim to clarify the computation procedure used in this study. Trends of drought series for each month were tested by the Mann–Kendall trend test and results are shown in Table 3. A significant drought tendency was identified for October but no significant drought trends were found for other months (Table 3). Besides, the Mann–Kendall trends for the SPI-based drought episodes were negative for most of the months, about 83 % of the total months, showing that most of the months were tending to be dry. Results of trend analysis showed increasing drought duration and drought severity but were not significant at > 95 % confidence level.

Table 3 Mann–Kendall trends in the SPI-based drought episodes for each month

The drought duration series was fitted by the six candidate probability distribution functions (left panel of Fig. 4) and the drought severity series was fitted and is shown in the right panel of Fig. 4. There were 28 drought episodes, so the 95 % confidence level of K-S D was 0.257 (Brinbaum 1952). Statistically speaking, these six probability distribution functions performed well in fitting the observed drought duration series (Table 4). However, the Wakeby function performed better when compared to other five probability functions (Table 4). Based on the relations between Kendall τ and the parameter θ of each copula function, the parameter of each copula function was computed as 8.07 for the Clayton, 18.33 for the Frank, and 5.04 for the Gumbel. After the selection of the right marginal distribution functions, the copula-based risk evaluation of droughts was done, and results are illustrated in Fig. 5. It can be seen from Fig. 5a that the Frank copula was the right one. Figure 5b–d shows contours of drought duration vs. drought severity, the Kendall distribution K _C computed by the analytical method, and the Kendall distribution K _C obtained by Monte Carlo simulation, respectively.

Fig. 4

Observed and theoretical probability curves for the drought duration (a) and drought severity (b)

Table 4 The goodness-of-fit based on K-S D statistics for the drought severity at the Fogang station

Fig. 5

a Selection results for the copula functions based on the Bayesian method at the Fogang station; b Contour-based Frank copula; c Kendall distribution function K _C (t) based on numerical analysis results; d Kendall distribution function K _C (t) based on Monte Carlo numerical simulation analysis technique

Based on the SPI series at the Fogang station, we obtained p _WD = 0.2311 and p _WD = 0.2182. Thus the average time elapsed between drought episodes was ${\mu_t} = \frac{1}{{{P_{DW}}}} + \frac{1}{{{P_{WD}}}} =$ 8.9 months or about 0.7 years. The joint return periods and the secondary return periods of droughts with different drought durations and drought severity were computed under two scenarios: (1) the drought duration was 6 months and the drought severity was 7.5; (2) the drought duration was 9 months and the drought severity was 13.5. Results are given in Table 5. It is seen that ${T_{\left\{ {U > u \wedge V > v} \right\}}}$ was longer than ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$. This point is easy to understand. The probability that two cases occur simultaneously is relatively smaller than that when one of the two cases occurs. Moreover, it can be observed from Table 5 that the secondary return period of ${T_{\left( {U > u \wedge V > v} \right)}}$ is shorter than ${T_{\left( {U > u \wedge V > v} \right)}}$, and the secondary return period of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ is longer than ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$. It should be because the secondary return periods include more possible scenarios which are represented by isolines. However the joint return period only includes one of the scenarios. In this sense, the secondary return periods should be more robust when compared to the joint return periods. The same analysis procedure was followed in the analysis of the drought episodes at other precipitation stations across the Pearl River basin.

Table 5 The ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ and ${T_{\left\{ {U > u \wedge V > v} \right\}}}$ and their corresponding secondary return periods

4.2 Mann–Kendall trends of the drought episodes

For the economy of presentation of results, results of the Mann–Kendall trends in drought episodes for each precipitation station are illustrated in Fig. 6. The numbers along the x-axis denote precipitation, which are listed in the caption of Fig. 1. Blue color denotes drought tendency, and red color wet tendency. It can be seen from Fig. 6 that the drought tendency in most months at most stations is not significant. However, drought tendency is evident at the Weining, Zhanyi, Yuxi, Anshun, Wuzhou, and Guangning stations. It can be seen from Fig. 1 that four of these stations are located in the upper Pearl River basin and two stations in the lower Pearl River basin. Thus, the drought tendency is observed mainly in the upper Pearl River basin. Besides, drought episodes are found mainly in November, December, and January but the wetting tendency in June and July. Results of the Mann–Kendall trend analysis of the drought duration and drought severity are shown in Fig. 7. It can be seen from Fig. 7a that most of the precipitation stations are characterized by not significant changes in drought duration. Drought severity also does not experience significant changes. Moreover, Fig. 7a, b shows that the distributions of changes in drought duration and drought severity are spatially consistent.

Fig. 6

Trends in droughts for precipitation stations considered in this study across the Pearl River basin. The numbers along the x-axis denote names of the precipitation stations and these stations are displayed in the caption of Fig. 1. The spatial distribution of these precipitation stations can be found in Fig. 1

Fig. 7

Trends of the drought duration (a) and trends of drought severity (b) across the Pearl River basin. Significance of the trends is tested at >95 % confidence level

4.3 Return periods

Following the computation procedure as shown for the Fogang station, return periods of droughts were analyzed for each station. The average duration elapsed between two successive drought episodes is shown in Table 6. It can be seen that the waiting time between two successive drought episodes was more than half a year. Besides, the spatial patterns of return periods are illustrated in Fig. 8. Two scenarios were also considered for the analysis of joint return periods and related secondary return periods, i.e.: (1) drought duration was 6 months with a drought severity of 7.5; and (2) drought duration was 9 months with a drought severity of 13.5.

Table 6 The average time elapsed between drought episodes, μ _t , with unit of 1 year

Fig. 8

Joint return periods of droughts with duration of 6 months and drought severity of 7.5. a ${T_{\left\{ {U > u \wedge V > v} \right\}}}$; b ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$; c the secondary return periods of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$, and d the secondary return periods of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$

The spatial distribution of return periods for the first scenario is shown in Fig. 8. Figure 8a shows the spatial distribution of ${T_{\{ U > u \wedge V > v\} }}$; Fig. 8b shows the spatial patterns of ${T_{\{ U > u\; \vee \;V > v\} }}$; Fig. 8c shows the spatial distribution of the secondary return periods of ${T_{\{ U > u \wedge V > v\} }}$; and Fig. 8d illustrates the spatial distribution of secondary return periods of ${T_{\{ U > u\; \vee \;V > v\} }}$. It can be observed from Fig. 8a, c that a higher risk of droughts characterized by a duration of 6 months and a drought severity of 7.5 can be found in the northwestern parts, the northern and southern parts, and also in the southeastern parts of the Pearl River basin. Particularly, the southeastern parts of the Pearl River basin include the Pearl River delta, being the populous place with highly developed socioeconomy. A high risk of droughts may have considerable impacts on the sustainable development of socioeconomy. As for the return periods of drought episodes with a duration of 6 months or drought severity of 7.5 (Fig. 8b, d), larger regions, when compared to the spatial distribution of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$, are featured by higher risk of droughts. Specifically, the southern, southeastern, western, and northern parts of the Pearl River basin are dominated by higher risk of droughts with a duration of 6 months or drought severity of 7.5.

Figure 9 illustrates the spatial distribution of return periods, including secondary return periods, of drought episodes with a longer duration of 9 months and a higher drought severity of 13.5 than that shown in Fig. 8. Similarly, Fig. 9a shows the spatial distribution of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$; Fig. 9b shows the spatial patterns of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$; Fig. 9c shows the spatial distribution of secondary return periods of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$; and Fig. 9d illustrates the spatial distribution of secondary return periods of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$. It can be seen from Fig. 9 that ${T_{\left\{ {U > u \wedge V > v} \right\}}}$ is about 14 years (Fig. 9a), ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ about 5.4 years (Fig. 9b), the secondary return period of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$ about 10 years (Fig. 9c), and the secondary return period of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ about 7 years (Fig. 9d). Similar features can be identified for the spatial distribution of return periods of droughts with longer durations and higher severities. A higher drought risk can be observed in the southeastern, northern, northwestern, and southern parts of the Pearl River basin. The main stream of the Pearl River basin is dominated by lower drought risk.

Fig. 9

Joint return periods of droughts with duration of 9 months and drought severity of 13.5. a ${T_{\left\{ {U > u \wedge V > v} \right\}}}$; b ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$; c the secondary return periods of ${T_{\left\{ {U > u \wedge V > v} \right\}}}$, and d the secondary return periods of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$

Figures 8 and 9 show similar properties in terms of the spatial patterns of return periods of drought episodes with different durations and severities. A higher drought risk can be detected in the eastern parts of the Pearl River basin and also in the northeastern parts. These regions are important for water supply, particularly the East River. About 80 % of the annual water demand of Hong Kong is from the East River. Higher drought risk of this region may definitely give rise to new challenges for water resources management and conservation of the ecological environment.

5 Closing remarks and conclusions

Evaluation of drought risk based on copula functions and Mann–Kendall trend test method is conducted over the Pearl River basin based on daily precipitation data sets from 42 rain stations covering a period of 1960–2005. The following conclusions are drawn from this study:

• 1. In general, the drought tendency is not statistically significant. However, significant drought tendencies can be found at the Weining, Zhanyi, Yuxi, Anshun, Wuzhou, and Guangning stations. But a majority of these stations are located in the western parts of the Pearl River basin and two stations in the lower Pearl River basin. Besides, drought tendency is evident in November, December, and January, but June and July have a wet tendency. The Mann–Kendall trends of drought duration and drought severity are consistent in their spatial distribution.

• 2. Two scenarios of drought events are investigated in this study: (1) the drought duration is 6 months with a drought severity of 7.5 and (2) the drought duration is 9 months with a drought severity of 13.5. Results of analysis of joint return periods and related secondary return periods indicate a higher risk of droughts in the western, northern, southern, and southeastern parts of the Pearl River basin. Relatively a lower drought risk is detected along the main stream of the Pearl River basin. Nevertheless, a comparatively higher risk of droughts is observed in the eastern parts of the Pearl River basin than in the western parts. Moreover, the spatial distributions of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ and ${T_{\left\{ {U > u\; \wedge \;V > v} \right\}}}$ are relatively consistent, implying higher probability of concurrence of droughts with longer duration and higher severity. This result means serious challenges in the water resources management and human mitigation of drought hazards. Results of this study also indicate that when droughts of higher severity occur, the regions in the eastern parts of the Pearl River basin have a higher drought risk increase. The eastern parts of the Pearl River basin are mostly populous and are characterized by highly developed socioeconomy. What is more is the fact that the East River is located in this region which bears a heavy responsibility for the water supply for Hong Kong, Macau, and also other megacities in the vicinity of or within the Pearl River Delta. Higher risk of droughts may enhance threats to water supply for these megacities.

• 3. Properties of the spatial distributions of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$, ${T_{\left\{ {U > u\; \wedge \;V > v} \right\}}}$, and their secondary return periods are similar. However, the secondary return period of ${T_{\left\{ {U > u\; \wedge \;V > v} \right\}}}$ is smaller than that of ${T_{\left\{ {U > u\; \wedge \;V > v} \right\}}}$; the secondary return period of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$ is larger than that of ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$. Computation of the secondary return period involves all possible scenarios; thus, the secondary return periods may provide indications for risk analysis. In this sense, the drought risk may be larger than that deduced by ${T_{\left\{ {U > u\; \wedge \;V > v} \right\}}}$; similarly, the drought risk should be smaller than that deduced by ${T_{\left\{ {U > u\; \vee \;V > v} \right\}}}$.

Appendix

The Copula family is described as the follows.

• 1. Gumbel–Hougaard (GH) family

  The GH family can be formulated as:

  $$ C\left( {u,v} \right) = \exp \left\{ { - {{\left[ {{{\left( { - \ln u} \right)}^\theta } + {{\left( { - \ln v} \right)}^\theta }} \right]}^{1/\theta }}} \right\},\theta \in \left[ {1,\infty } \right) $$

  (9)

  where u and v are the marginal distribution functions of two hydrological variables; θ is the parameter of the GH family; C is the copula having the function of capturing the essential features of the dependence among random variables. Parameters u, v, and θ in the following equations have the same meaning as those in Eq. (9), so no further explanations are provided thereafter. The copula generator of the GH family (Zhang and Singh 2007) is:

  $$ \phi (t) = {\left( { - \ln t} \right)^\theta } $$

  (10)

  t is the u ₁ or v ₁, being specific values of u and v in Eq. (9) varying from 0 to 1. The relationship between parameter, θ, and Kendall’s coefficient of correlation, τ, between X and Y is τ = 1 − θ ⁻¹. The GH copula performs well in the description of the correlation structure of two variables characterized by a positive correlation.

• 2. Clayton family

  The Clayton family can be formulated as:

  $$ C\left( {u,v} \right) = {\left( {{u^{ - \theta }} + {v^{ - \theta }} - 1} \right)^{ - 1/\theta }},\theta \in \left( {0,\infty } \right) $$

  (11)

  The copula generator of Clayton family is

  $$ \varphi (t) = \left( {{t^{ - \theta }} - 1} \right)/\theta, \theta \in \left( {0,\infty } \right) $$

  (12)

  The relation between parameter, θ, and Kendall’s coefficient of correlation, τ, between X and Y is:

  $$ \tau = \frac{\theta }{{2 + \theta }},\theta \in \left( {0,\infty } \right) $$

  (13)

  The Clayton family is good for describing two variables with a positive correlation.

• 3. Frank family

  The Frank family can be formulated as:

  $$ C\left( {u,v} \right) = - \frac{1}{\theta }\ln \left[ {1 + \frac{{\left( {{e^{ - \theta u}} - 1} \right)\left( {{e^{ - \theta v}} - 1} \right)}}{{\left( {{e^{ - \theta }} - 1} \right)}}} \right],\theta \in R $$

  (14)

  The copula generator of the Clayton family is

  $$ \varphi (t) = - \ln \frac{{{e^{ - \theta t}} - 1}}{{{e^{ - \theta }} - 1}},\theta \in R $$

  (15)

  The relation between parameter, θ, and Kendall’s coefficient of correlation, τ, between X and Y is:

  $$ \tau = 1 + \frac{4}{\theta }\left[ {\frac{1}{\theta }\int\limits_0^\theta {\frac{t}{{{e^t} - 1}}dt - 1} } \right],\theta \in R $$

  (16)

  The Frank family performs well for describing two variables with a positive correlation.

• 4. t copula family

  The t family can be formulated as:

  $$ C_{v,R}^t\left( {u,v} \right) = {\int_{ - \infty }^{t_v^{ - 1}(u)} {\int_{ - \infty }^{t_v^{ - 1}(v)} {\frac{1}{{2\pi {{\left( {1 - {\theta^2}} \right)}^{\frac{1}{2}}}}}\left[ {1 + \frac{{{s^2} - 2\theta st + {t^2}}}{{v\left( {1 - {\theta^2}} \right)}}} \right]} }^{ - \frac{{\left( {v + 2} \right)}}{2}}}dsdt $$

  (17)

  $t_{v,R}^n$ is the R-dimensional standard t distribution with degree of freedom of v. $t_v^{ - 1}$ is the inverse function of $t_{v,R}^n$.

  The relation between parameter, θ, and Kendall’s coefficient of correlation, τ, between X and Y is:

  $$ \theta = \sin \left( {\frac{{\pi \tau }}{2}} \right) $$

  (18)

Conditional copula

Let X and Y be random variables with marginal distribution as u = F _X (x) and v = F _Y (y). The conditional distribution function of X given Y = y can be expressed by the copula method as:

$$ \begin{array}{*{20}{c}} {H\left( {X < x\left| {Y = y} \right.} \right) = {{C}_{\theta }}\left( {u\left| {v = {{v}_{1}}} \right.} \right) = \mathop{{\lim }}\limits_{{\Delta v \to 0}} \frac{{{{C}_{\theta }}\left( {u,v + \Delta v} \right) - {{C}_{\theta }}\left( {u,v} \right)}}{{\Delta v}}} \\ { = \frac{\partial }{{\partial v}}{{C}_{\theta }}\left( {u,v} \right)\left| {v = {{v}_{1}}} \right.} \\ \end{array} $$

(19)

An equivalent formula for the conditional distribution function for Y given X = x can be obtained. The conditional distribution function of X given Y ≥ y can be expressed by the copula method as

$$ {{C}_{\theta }}\left( {u\left| {v < {{v}_{1}}} \right.} \right) = \frac{{{{C}_{\theta }}\left( {u,v} \right)}}{v} $$

(20)

Similarly, an equivalent formula for the conditional distribution function for Y given X < x can be obtained.