1 Introduction

Forecasting of time series is an important mathematical aspects and it spans along many fields including water resources, economics and social demography (Granger and Newbold 2014; Salas 1980; Yaffee and McGee 2000). Understanding and analysis of the existing time series is required for future forecasting of the time series. The subject of long-term rainfall series analysis has received a great deal of attention recently, especially with regard to expected climate changes (Goyal 2014; Moyo et al. 2017; Murphy et al. 2017; Smit et al. 2000; Trenberth 1998). The study of long rainfall time series permits creating quantitative judgments of the potential boundaries of stationary hypothesis. The statistical studies of rainfall time series data were found to be useful in water resources planning and management and usually carried out at the spatio-temporal scales (Loucks et al. 2005; Vicente-Serrano 2006).

While examining any rainfall time series, one of the important tasks is to identify and summarize the time series data in classes by expressing their significant features (Hipel and McLeod 1994; Sethi et al. 2015; Tiwari et al. 2015). Trend analysis and homogeneity test are primary tasks of time series studies (Wilks 2011). Mann–Kendall analysis is the usually practised methodology for the trend detection for any time series (Sang et al. 2013; Yue et al. 2002). It suggests the polarity of trend (positive or negative) at different significance levels. Mann–Kendall test is non-parametric and does not consider any assumption on the distribution of the time series data. The Mann–Kendall test provides a single value for the one time series and is not able to extract the nonlinearity of the trend. Sequential Mann–Kendall Test was applied to detect nonlinear trend of the rainfall time series, i.e., temporal scale of the rainfall time series. Innovative trend analysis is one of the recently applied techniques to establish the general trend of the time series.

Homogeneity is a fundamental characteristic for the time series. von Neumann ratio test and cumulative deviation test are accepted techniques for homogeneity check. Singular spectrum analysis was suggested to observe the order of departure signature from homogeneity. Singular spectrum analysis is a strong tool to analyze the univariate time series in multidimensional spatial dimension.

Mann–Kendall and Sen’s tests were applied to long-term annual and seasonal rainfall series of India for trend analysis. West Peninsular India showed a positive trend for the annual rainfall series. Sequential Mann–Kendall test was applied to get the nonlinear trend of the rainfall time series and the result was validated using Mann–Kendall test. Partial cumulative deviation test was carried out in the study to get the nonlinear trend of the time series and was found to be in coherence with sequential Mann–Kendall test. Innovative trend analysis results could be useful to get trend in an easy way and to describe the number of temporal clusters available in the time series; therefore, it will be useful for soft computing analysis. Innovative trend analysis methodology was also able extract the monotonicity of the time series and hence useful to detect the number of available change points in the time series. In that way, it will be helpful to classify the rainfall series temporally. von Neumann ratio test and cumulative deviation test were applied to get the homogeneity of the long-term rainfall time series (1851–2006). Singular spectrum analysis was proposed and then successfully verified (from von Neumann ratio test and cumulative deviation test statistics) to detect the non-homogeneity character for the rainfall time series.

2 Study area

The country is situated north of the equator between 8°4′ and 37°6′ north latitude and 68°7′ and 97°25′ east longitude. It is the seventh largest country in the world, with a total area of 3,166,414 km2. India measures 3214 km from north to south and 2933 km from east to west. It has a land frontier of 15,200 km and a coastline of 7517 km.

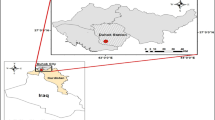
For the study, seven regions in India were categorized, considering the seasonal and annual rainfall (Fig. 1). These regions are as follows: North Mountainous India (NMI), North Central India (NCI), Northwest India (NWI), East Peninsular India (EPI), West Peninsular India (WPI), South Peninsular India (SPI) and Northeast India (NEI) and are shown in Fig. 1 (Li et al. 2014; Sontakke et al. 2008). North Mountainous India (MNI) is the Great Himalayan Mountain of topography elevation more than 7000 m and mean annual rainfall about 1500 mm, of which nearly 72% is from the monsoon season.

Fig. 1
figure 1

Study area description (regions and rain gauges locations)

Full size image

Northwest India (NWI) region is an arid and semi-arid climate zone of India. In this region, the ‘Thar’ Desert is located. The mean annual rainfall of this region is 800 mm and 88% is contributed by the monsoon season. North Central India (NCI) is the Indo-Gangetic Plains, a humid sub-tropical climatic region. The mean annual rainfall is 1212 mm, with the monsoon contributing 85% of it. The mean annual rainfall for the WPI, EPI and SPI regions is 1103, 1162 and 1555 mm, with nearly 85, 73 and 60% falling in the monsoon season, respectively (Li et al. 2014; Parth Sarthi et al. 2015).

The presented case study comprises a very large area, of about 3.288 million km2. Available data consist of annual and monthly rainfall time series for 316 rain gauges categorized into seven homogeneous zones, from 1851 to 2006, analyzed to detect potential trends from different methodologies and their significance (Kumar et al. 2010). Long-term (1851–2006) instrumental area-averaged monthly rainfall series of seven homogeneous zones and the whole India were taken from the Indian Institute of Tropical Meteorology (http://www.tropmet.res.in/) for the study. The monthly data of rainfall series were prepared in five parts named as annual (AN), January–February (JF) March–April–May (MM), June–July–August–September (JS) and October–November–December (OD).

2.1 General statistical analysis

As a prelim step of time series analysis, statistics of the data were investigated. Some robust statistics like coefficient of variation, quartile skew coefficient and percentile coefficient of kurtosis were used in the present study including mean, maximum, minimum and standard deviation (Eqs. 1–3), where CV values of 0–15, 16–35 and > 36 indicate little, moderate and high variability, respectively. Italic values of Table 3 indicate the high variability of the rainfall series. Table 1 shows higher seasonal variation rather than annual variation for rainfall time series. Non-monsoon seasons show a higher variability than the monsoon season for all seven zones. Quartile skew coefficient was based on a comparison of distances of the third and the first quartile to the median:

$${\text{CV}} = \frac{\sigma }{{\bar{x}}} \times 100,$$
(1)
$${\text{qs}} = \frac{{(P_{75} - P_{50} ) - (P_{50} - P_{25} )}}{{(P_{75} - P_{25} )}},$$
(2)
$${\text{PCK}} = \frac{1}{2}\left( {\frac{{P_{75} - P_{25} }}{{P_{90} - P_{10} }}} \right),$$
(3)

where CV is the coefficient of variation, σ the standard deviation of the dataset, \(\bar{x}\) the mean of the dataset, qs the quartile skew coefficient, P10 the 10th percentile of the dataset, P25 the 25th percentile of the dataset, P50 the 50th percentile of the dataset, P75 the 75th percentile of the dataset, P90 the 90th percentile of the dataset and PCK the percentile coefficient of kurtosis.

Table 1 Statistical measures for rainfall time series (1851–2006)
Full size table

3 Trend analysis

Identification of meteorological regimes of India is an important subject in stochastic hydrology under climate change conditions. Generally, parametric and non-parametric techniques have been employed to get the regime changes; the latter has been widely used mainly because of a fewer number of assumptions involved in their implementation (Khaliq et al. 2009). In any sign investigation study, mostly it is vital to estimate hydrological trends at local scales, that is, point estimates. In the current study, the MK and the SRC rank-based tests and CS test were used for identifying temporal changes in observational records. Most of these tests are based on the assumption of independent and identically distributed variables.

3.1 Mann–Kendall test

Mann (1945) presented a non-parametric test for randomness against time, which constitutes a particular application of Kendall’s test for correlation commonly known as the ‘Mann–Kendall’ test (Hamed 2008; Hamed and Rao 1998). Letting P1, P2, …, Pn be a sequence of rainfall measurements over time, Mann proposed to test the null hypothesis, H0, that the data come from a population where the random variables were independent and identically distributed. The alternative hypothesis, H1, is that the data follow a monotonic trend over time. Under H0, the Mann–Kendall test statistic (S) is (Eqs. 4– 7):

$$S = \sum\limits_{i = 1}^{n - 1} {\sum\limits_{j = i + 1}^{n} {\text{sgn} (P_{j} - P_{i} )} } ,$$
(4)

where

$$\text{sgn} (\theta ) = \left\{ {\begin{array}{*{20}c} { + 1 \ldots \theta > 0} \\ { - 1 \ldots \theta < 0} \\ {0 \ldots \theta = 0} \\ \end{array} } \right..$$
(5)

Under the hypothesis of independent and randomly distributed random variables, when n ≥ 8, the S statistic is approximately normally distributed, with zero mean and variance as follows:

$$\sigma^{2} = \frac{n(n - 1)\,\,(2n + 5)}{18},$$
(6)

where σ is the standard deviation of the dataset. Therefore, the standardized Z statistics follow a normal standardized distribution:

$$Z = \left\{ {\begin{array}{*{20}c} {\frac{S - 1}{\sigma } \ldots S 0} \\ \begin{aligned} \frac{S + 1}{\sigma } \ldots S 0 \\ 0 \ldots S = 0 \\ \end{aligned} \\ \end{array} } \right.,$$
(7)

where S is the Mann–Kendall statistic.The hypothesis is that no trend is rejected when the Z value computed by the equation is greater in absolute value than the critical value Zα, at a chosen level of significance α.

3.2 Theil–Sen estimator (TS)

Theil–Sen estimator is a non-parametric statistics to calculate the median slope among all lines through pairs of two-dimensional sample points (Eq. 8). It is an unbiased estimator of the true slope in simple linear regression. Theil–Sen estimator is a widely used methodology after MK test to validate the results:

$${\text{TS}} = {\text{median}}\left( {\frac{{P_{j} - P_{i} }}{j - i}} \right)\quad {\text{For }}i{\, <\, }j.$$
(8)

3.3 Changes in mean (%)

To calculate the percentage change in mean annual rainfall, mean trend applying Sen’s slope was used:

$${\text{Mean Changes (\% ) = }}\frac{{\beta \, *\,{\text{length of year}}}}{\text{mean}}*100,$$
(9)

where β is Sen’s slope.

3.4 Sequential Mann–Kendall test

To detect the nonlinear trend with time, Sneyers (1990) introduced sequential or partial values, z(t), from the progressive analysis of the Mann–Kendall test. Herein, z(t) is a standardized variable that has zero mean and unit SD. The following steps are applied to calculate z(t) (Eqs. 10–13):

  1. 1.

    The values of Pj mean time series (j = 1,…,n) are compared with Pi, (i = 1,…, j−1). At each comparison, the number of cases Pj > Pi is counted and denoted by nj.

  2. 2.

    The test statistic t is then calculated by the equation

$$t_{j} = \sum\limits_{1}^{j} {n_{j} } .$$
(10)
  1. 3.

    The mean (E) and variance of the test statistics (Var) are

$$E(t_{j} ) = \frac{j(j - 1)}{4},$$
(11)
$${\text{Var}}(t_{j} ) = \frac{{j(j - 1)\,\left( {2j + 5} \right)}}{72}.$$
(12)
  1. 4.

    The sequential values or partial values of the statistics z(t) are then calculated as

$$z(t) = \frac{{t_{j} - E(t_{j} )}}{{\sqrt {Var(t_{j} )} }}.$$
(13)

3.5 Partial cumulative deviation test (PS)

Cumulative deviations from the mean are rescaled using partial standard deviation of the series (Eqs. 14–16) and then it used to detect the nonlinear trend of the rainfall time series.

$$PS_{k} = \sum\limits_{t = 1}^{k} {\left( {P_{t} - \overline{P} } \right)} ,$$
(14)
$$SD_{k} = \frac{1}{k}\sum\limits_{t = 1}^{k} {\left( {P_{t} - \overline{P} } \right)}^{2} ,$$
(15)

where k = 1, 2,……, n.

$${\text{PCD}} = \frac{{{\text{PS}}_{k} }}{{{\text{SD}}_{k} }}.$$
(16)

Pt is the rainfall sequence in time and n the total number of rainfall records.

3.6 Innovative trend analysis

Innovative trend analysis is a new technique proposed by Sen in 2011 (Şen 2011). The applicability of the analysis is very simple and applied to verify the results of MKT. The first half of the time series in the X-axis was plotted against the second half of the series in the Y-axis. It becomes obvious that the monotone increasing (decreasing) trend in the given time series fall above (below) the 1∶1 line. This idea was used to quantify the results of MKT. It is very much handy to use the ITA method to extract the trend information from the available rainfall time series.

4 Homogeneity test

4.1 von Neumann ratio test

The von Neumann ratio (N) is the commonly used test to check the absence or presence of homogeneity in the time series. It is directly associated with the first-order serial correlation coefficient. It is defined as follows:

$$N = {{\sum\limits_{t = 1}^{n - 1} {\left( {P_{t} - P_{t + 1} } \right)}^{2} } \mathord{\left/ {\vphantom {{\sum\limits_{t = 1}^{n - 1} {\left( {P_{t} - P_{t + 1} } \right)}^{2} } {\sum\limits_{t = 1}^{n} {\left( {P_{t} - \overline{P} } \right)} }}} \right. \kern-0pt} {\sum\limits_{t = 1}^{n} {\left( {P_{t} - \overline{P} } \right)} }}^{2} ,$$
(17)

where Pt is the rainfall sequence in time and n the total number of rainfall records.

4.2 Cumulative deviation test

Cumulative deviations from the mean are rescaled using standard deviation of the series (Eqs. 18–22) and then used to detect the nonlinear trend of the rainfall time series.

$${\text{PS}}_{k} = \sum\limits_{t = 1}^{k} {\left( {P_{t} - \bar{P}} \right)} ,$$
(18)
$${\text{SD}} = \frac{1}{n}\sum\limits_{t = 1}^{n} {\left( {P_{t} - \bar{P}} \right)}^{2} ,$$
(19)

where k = 1, 2… n.

$$PCD = \frac{{PS_{k} }}{SD},$$
(20)
$$RCD = \hbox{max} \;(PCD) - \hbox{min} \;(PCD),$$
(21)
$$CD_{s} = \frac{RCD}{\sqrt n }.$$
(22)

Pt is the rainfall sequence in time and n the total number of rainfall records.

5 Singular spectrum analysis

The singular spectrum analysis technique is a very new and powerful technique to analyze time series in hydrology (Sivapragasam et al. 2010). It has the capacity to perform multivariate component analysis from a single time series. In this method, singular spectrum analysis decomposes the original time series into different components of the series, and each series represents the trend, periodicity and noise of the series (Vitanov et al. 2008). This tool is very helpful in finding trends, smoothing of the time series, deriving the seasonality components, identifying periodicity at varying amplitudes and detecting shifting or change point in the series (Solow and Patwardhan 1996).

It is assumed that the any dynamic system satisfies for the set of k first-order differential equations for variables xi. The following sequential methodology was adopted to analyze the time series data using singular spectrum analysis.

  1. 1.

    Conversion of univariate time series (xi) where “i” lies between 1 and n to multivariate characteristic matrix (X) using Eq. 23. Here, n represents the length of the time series and k is defined as the degree of freedom of the dynamic system. The degree of freedom k can vary from 2 to n − 1.

$$X = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt n }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt n }$}}\left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \ldots & {x_{k} } \\ {x_{2} } & {x_{3} } & \ldots & {x_{k + 1} } \\ \vdots & \vdots & \ldots & \vdots \\ \vdots & \vdots & \ldots & \vdots \\ {x_{n - k + 1} } & {x_{n - k + 2} } & \ldots & {x_{n} } \\ \end{array} } \right].$$
(23)
  1. 2.

    Characteristic matrix (X) is transformed to decomposed vector (S) using Eq. 24. Basically, it is the multiplication of transpose characteristic matrix (X′) to characteristics matrix (X).

$$S = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt n }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt n }$}}\left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \ldots & {x_{n - k + 1} } \\ {x_{2} } & {x_{3} } & \ldots & {x_{n - k + 2} } \\ \vdots & \vdots & \ldots & \vdots \\ \vdots & \vdots & \ldots & \vdots \\ {x_{k} } & {x_{k + 1} } & \ldots & {x_{n} } \\ \end{array} } \right]{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt n }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt n }$}}\left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \ldots & {x_{k} } \\ {x_{2} } & {x_{3} } & \ldots & {x_{k + 1} } \\ \vdots & \vdots & \ldots & \vdots \\ \vdots & \vdots & \ldots & \vdots \\ {x_{n - k + 1} } & {x_{n - k + 2} } & \ldots & {x_{n} } \\ \end{array} } \right].$$
(24)
  1. 3.

    Eigenvalues and eigenvector of the decomposed vector (S) is calculated. Eigenvalues of the decomposed time series are hereby used to derive the order of homogeneity for the rainfall time series.

6 Results and discussions

6.1 Rainfall trends

The results of the trend analysis using Mann–Kendall and Sen’s tests are presented in Tables 2 and 3. The rainfall data from seven zones were used, which had instrumental observed datasets with adequate record length (1851–2006). It was observed that only WPI had a positive trend under 95% significance level for the annual time series. Some seasonal variations were also observed for monsoon (NMI (negative trend) and WPI (positive trend)) and post-monsoon season (AI (positive trend) and NEI (positive trend)). Using same datasets, we adopted the Sen’s T test to identify the trend and observed that its results seemed to be quite coherent with the Mann–Kendall test. The results of the Sen’s T test seemed to be similar to those obtained from the Mann–Kendall test.

Table 2 Z values for the rainfall time series under Mann–Kendall test
Full size table
Table 3 Sen’s slope for the rainfall time series
Full size table

6.2 Changes in mean (%)

Using Eq. 9, long-term changes in mean value were estimated. It is noticed that the seasonal maximum positive and negative changes in the mean value are 27.49% (OD) and − 16.38 (JS) for the NWI and NMI rainfall zones, respectively, during 1851–2006. No significant changes were found in the mean values for the region NWI (JF), NCI (JF) and NEI (JF), corresponding to the season. In the annual analysis for different zones of India, it was found that the maximum change in the mean rainfall was 11.53% for WPI, whereas the maximum fall in the mean rainfall was 7.8% for the NMI region (Fig. 2).

Fig. 2
figure 2

Percentage changes in mean (1851–2006)

Full size image

6.3 Sequential Mann–Kendall test

The above described tests are the total estimators of the time series. They are unable to extract any idea about the local temporal changes. To get these temporal changes, sequential MK was carried out. The sequential MK values were computed for the rainfall time series from the beginning to end of the study period (1851–2006). The sequential MK values are presented as line graphs, and when the line crosses the upper or lower confidence limits it is an indication that there is a significant trend because the calculated MK value is greater than the absolute value of the normal standard Z value (at the 5% significance level). The intention of conducting the sequential MK tests and charting the results is to check how the trends fluctuated over the whole study period (1851–2006). Figure 3 shows that the sequential MK test method was able to detect nonlinear trend for the rainfall time series, whether it is annual or seasonal.

Fig. 3
figure 3

SQMKT for selected rainfall series [negative (NMI_JS), no trend (NCI_JF) and positive (WPI_AN)]

Full size image

The applications of the partial cumulative deviation test were also presented for different types of rainfall series recorded at various zones and seasons (Fig. 4). It was found to be similar to the SQMKT test results and the nonlinear trend of the rainfall series could be observed.

Fig. 4
figure 4

PCD for selected rainfall series [negative (NMI_JS), no trend (NCI_JF) and positive (WPI_AN)]

Full size image

The applications of the innovative trend analysis methodology were also presented for different types of rainfall series (for positive trend—Fig. 5, for negative trend—Fig. 6 and for no trend—Fig. 7) recorded at various zones and seasons. It was found to be in coherence with and Sen’s T test results.

Fig. 5
figure 5

ITA graph for WPI_AN

Full size image
Fig. 6
figure 6

ITA graph for NMI_JS

Full size image
Fig. 7
figure 7

ITA graph for NCI_JF

Full size image

6.4 Homogeneity test

von Neumann ratio and cumulative deviation test were performed for the rainfall time series (Tables 4 and 5). The expected value of the von Neumann ratio is 2. However, it tends to be greater or less than 2 for the non-homogenous time series. Cumulative deviation test statistics was calculated from partial cumulative deviation and rescaled with standard deviation for the whole time series.

Table 4 von Neumann ratio for the rainfall time series
Full size table
Table 5 Cumulative deviation test statistics for the rainfall time series
Full size table

Rainfall time series for seven zones were decomposed by applying Eqs. 23 and 24. Univariate matrix was converted to multivariate matrix with variable degree of freedom. The eigenvalues of the decomposed matrix for monsoon time series were plotted against the degree of freedom (Fig. 8). Figure 8 presents the order of non-homogeneity existing in the time series. Singular spectrum analysis of univariate rainfall series successfully extracts the homogeneous character of the time series. The monsoon season (JS) of the NMI and WPI zones showed higher departure from homogeneity (Tables 4 and 5) and singular spectrum analysis showed the results to be in coherence with the same (Fig. 8).

Fig. 8
figure 8

Eigenvalue graph for JS season for different zones

Full size image

7 Conclusions

Eight statistical methods such as Mann–Kendall test, Theil–Sen slope estimation, sequential Mann–Kendall test, partial cumulative deviation test, innovative trend analysis, von Neumann ratio test and singular spectrum analysis were used to characterize the long-term rainfall time series of India. Mann–Kendall test and Theil–Sen slope estimation were used here to estimate the global trend of the time series. From the above tests, one cannot determine the local trend of the long-term rainfall time series. To address the problem stated above, the authors have utilized sequential Mann–Kendall test and partial cumulative deviation test for the same rainfall series. For example, annual time series for the WPI zone has the highest increasing trend as per MKT statistics (2.71). The same value did not represent any local changes happening during 1851–2006. Figure 3 addresses the problem of global trend of the time series and also represents the local trend. Innovative trend analysis is a unique graphical representation to find the trend of time series. The benefit of using this method is that it classifies the trend analysis at the minima or maxima level, which cannot be predicted using the first four methods. This will be helpful for planning purposes of watershed management, where the trend of lower range of rainfall is important for the drought-prone region. Subsequently, higher range rainfall statistics iss important for flood-affected zones. von Neumann ratio test and singular spectrum analysis were used to estimate the order of non-homogeneity in the time series.