Introduction

In recent years, the effects of climate change and its effects have become increasingly prominent around the world, resulting in climate hazards, such as severe storms, floods, forest fires, heatwaves, droughts, and strong winds (Chibuike et al. 2014; Hajani and Rahman 2017; Hajani 2020). Unfortunately, the potential for extreme increases in rainfall intensity often leads to climatic and environmental hazards, increasing the risk of flooding in most parts of the world (Joshua and Ekwe 2013). To reduce the risk of climate change, it is necessary to understand the impact of climate change on the rainfall data of flood control measures (IPCC 2014). The relationship between rainfall and flood runoff probability is important from both practical and theoretical perspectives (Breinl et al. 2021). Floods usually occur when it rains for several days, when it rains for a short period, or when rivers and streams flood the area due to the accumulation of ice and debris (Packman and Kidd 1980). The most common cause of floods is stormwater. Stormwater collects faster than the soil absorbs, or the river carries it away (Pilgrim and Cordery 1975). About 75% of all presidential disaster statements are related to floods. The extreme rainfall distribution depends on the climatological conditions of each interesting location (Barbero et al. 2019).

According to the IPCC report, the frequency and depth of rainfall events will increase worldwide (IPCC 2014). In this regard, the assessment of changes in rainfall data series by applying various statistical tests is very important and has been studied by many researchers around the world (Yue et al. 2003; Chowdhury and Al-Zahrani 2013; Gao et al. 2016; Ongoma and Chen 2017; Hajani et al. 2017; Hajani and Rahman 2018; Nashwan et al. 2019; Tarekegn et al. 2021). For example, Mamoon and Rahman (2017) investigated the trends from 29 rainfall stations covering the period of 1962–2010 in Qatar. Two nonparametric trend tests [i.e. Mann–Kendall (MK) and Spearman’s Rho (SR) tests] were adopted to identify trends in the rainfall data series. Both increasing and decreasing were observed for most of the rainfall series. In another study, Nashwan et al. (2019) used seasonal and annual rainfall data over Egypt and the Nile river basin to estimate the statistical significance of trends throughout 1948–2010. The MK and Modified MK tests were used to find trends in rainfall data series. The results showed a significant difference between the trends obtained with both the modified MK test and the MK test. Meena (2020) detected a trend in rainfall in the Udaipur district of Rajasthan state, India between 1957 and 2016. The Modified MK test and Sen’s slope were used at a 5% significance level. The results showed that rainfall in the study area tended to increase over the study period.

Several studies in neighboring countries (e.g., Iran, Turkey, and Syria) have been conducted on the trend of rainfall on various time scales to evaluate the impacts of climatic changes. For example, Modarres and Sarhadi (2009) assessed trends in the total annual rainfall and 24-h maximum rainfall intensity data for the period of 1951–2000 at 145 rainfall stations in Iran. The MK test was used to assess trends in rainfall data. The study shows that the decreasing trends of annual rainfall are mostly observed in northern and north-western regions of Iran, while the increasing trends of 24-h maximum rainfall are mostly located in arid and semi-arid regions of Iran. In addition, Güçlü (2018) evaluated trends in annual rainfall data at 24 stations from 1931 to 2010 in different regions of Turkey. In this study, partial MK test and innovative trend analysis (ITA) method were adopted. It was found that about two-thirds of the stations in the study area showed an increasing trend. Furthermore, Güçlü (2020) used 50-year rainfall records in the Mediterranean, the Black Sea, and Continental climate regions in Turkey. It has been observed that Mediterranean stations are showing a complete upward trend. On the other hand, the stations in the Black Sea area are decreasing at low and high values, and the stations in the continental climate area are increasing.

The climate of the Kurdistan region has been identified according to the Koppen classification as a semi-arid climate. In this region, a comprehensive understanding of the rainfall pattern is greatly needed as it will significantly affect the balance among these natural features. Unfortunately, only very few studies have evaluated changes in rainfall data in the Kurdistan region. For example, Al Salihi et al. (2014) adopted the MK test to determine trends in rainfall data over 30 years from 36 stations in different parts of Iraq. The results show that rainfall levels in Iraq are declining on various time and spatial scales, especially in northern Iraq (i.e., the Kurdistan Region). It was also found that from 1989 to 1999, most of the changes were in the northern region. In another study, AL-Lami et al. (2014) investigated the homogeneity of 36 rainfall stations throughout Iraq between 1981 and 2010. The Pettit, Standard Normal Homogeneity, Buishand Range, and Von Neumann Rate tests were adopted at a significance level of 0.05. Based on the monthly and annual data series, the results of the above four homogeneity tests showed that most of the data series from 36 stations were found to be homogeneous. In addition, Agha et al. (2017) used the similar four homogeneity tests of AL-Lami et al. (2014) and investigated the homogeneity of 9 rainfall stations throughout northern Iraq. Based on the seasonal and annual series, the results show that most of the data series were found to be homogeneous.

Rainfall studies are very helpful in understanding the nature of climate change and, therefore, behaviour and impact. Rainfall time series is a series of rainfall observations recorded at specific times, usually at regular intervals. Therefore, time-dependent data sets are called time series (e.g., monthly, seasonal, and annual time series). In general, time series analysis is useful for comparing actual performance and analyzing the causes of variation (Maragatham 2012). In addition, Sen (2012) introduced an ITA method implemented on water resources. Many researchers used the ITA method to analyze time-series data along with the MK method. For example, monthly rainfall trends in different parts of the world were analyzed using the ITA method (Wang et al. 2020). Thus, the ITA method is widespread and is an applicable method compared to the MK method (Alashan 2020). No study has been done so far over any area in the Kurdistan Region using the Modified MK test and ITA method to analyze the trends of rainfall data, especially on monthly, seasonal, and annual rainfall variability. In this regard, the purpose of this study is devoted to examining the trends in rainfall time series at site locations in the Kurdistan region, Iraq for the period 1976–2017. Besides, this study is with five specific objectives: (1) to detect the outlier of rainfall data series to check the quality control of the rainfall data series. (2) to examine trends in rainfall data series in detail using the ITA method and comparing its results with the MK and modified MK tests.; (3) to quantify the significance of changes after removing the effects of serial correlation on the results of trend analysis from the time series; (4) to detect the occurrence of abrupt changes in rainfall; and (5) to explore homogeneity in rainfall time series. The results of the present study will help the researchers to understand the characteristics of rainfall data in Duhok city, also, it will be a reference for future studies on the water resources, hydrological processes, and climate change fields in Duhok city, Kurdistan region, north Iraq.

Study area and data

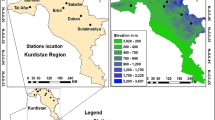
The study area of the current study is Duhok city in the Kurdistan Region, Iraq. Duhok city is the capital city of Duhok prefecture (governorate) and it is one of the main cities in the Kurdistan Region. The study area extends approximately between latitudes 36° 50′ 00″ and 36° 54′ 40″ N, and longitudes 42° 52′ 00″ and 43° 04′ 44″ E in the north–west of Iraq, as shown in Fig. 1, at 430–450 m above the sea level and it covers about 107 km2, near the Syrian–Turkish border (Othman 2008). Duhok city is located in a flat area between the two mountain ranges of Bekhair in the north and northeast and Zawa in the southeast (Othman 2008; Mustafa et al. 2012). A flat area with a tourist environment was seen on the west side (Duhok Province 2015).

Fig. 1
figure 1

Location of the selected Duhok station in Duhok city, Kurdistan Region, Iraq

Full size image

Depending upon temperature variation in a whole year, there are four seasons, namely, Summer—June, July, and August (JJA); Autumn—September, October, and November (SON); Winter—December, January, and February (DJF); and Spring—March, April and May (MAM). It rains and is cold in winter, with temperatures ranging from 2 to 16 °C. While summers are dry and hot, with temperatures above 43 °C during July and August (WCG 2019). Rainfall is very seasonal, occurring in the winters of October–April (Othman 2008; AL-Lami et al. 2014). The average annual rainfall ranges from 236.5 to 909.7 mm, indicating a very seasonal runoff regime with runoff peaking mainly in early spring (April) due to snowmelt (Abbasa et al. 2016). In the current study, the historical monthly rainfall data series of 43 years (1976–2017) at site location (i.e., Duhok station) were used (Fig. 1). The time series analysis of rainfall data was done on a monthly, seasonally, and yearly basis. Monthly rainfall data series is obtained by adding up daily data every month. The monthly rainfall data of this station had less than 5% gaps. The gaps in the rainfall data of a particular station were filled by regression analysis. Historical records of monthly rainfall data series have been provided from the Directorate of Duhok Dam in the Kurdistan Region.

Methods

In this study, different statistical methods were applied to the rainfall data series. A brief description of each of these statistical techniques used in this paper is presented below.

Moving average method

A moving average is a time series formed by averaging several consecutive values from another time series. It's a kind of mathematical convolution (Hyndman 2011). If we represent the original time-series by X1, …, Xn, then a moving average of the time series is written as

$$\overline{T}_{t} = \frac{1}{2k + 1}\mathop \sum \limits_{i = - k}^{k} X_{t + i} .$$
(1)

That is, the trend-cycle estimate at time t is obtained by averaging the time series values within the k period of t. Observations that are close in time may have similar values.

Quality control of the rainfall data series

The quality control method used was the outlier detection for rainfall data series using Mandel’s k method (Wilrich 2013; Jaafar and Al-Lami 2019). The k statistic detects differences between variances. The Mandel’s k statistic (Mandel 1985, 1991) can be found by

$$K_{j} = \frac{{S_{j} }}{{\overline{S}^{2} }} \,\,j = 1, 2, 3, \ldots ,p,$$
(2)
$$\overline{S}^{2} = \frac{1}{p}\mathop \sum \limits_{i = 1}^{p} S_{i}^{2} ,$$
(3)

where \({S}_{j}\) is a series of (p) sample variances, each being based on observed value (n). To identify the amount of variance that is probably not normal, the statistic h can be used to calculate critical values and confidence violations for a particular level of importance (Wilrich 2013). The formula for the critical value is given by the following formula:

$$K_{p,n,1 - \alpha } = \sqrt {p/(1 + \left( {p - 1} \right)F_{v1,v2;\alpha } } ,{\mkern 1mu} {\mkern 1mu} \nu 1 = \left( {p - 1} \right)\left( {n - 1} \right);{\mkern 1mu} {\mkern 1mu} \nu 2 = n - 1,$$
(4)

where \(F_{v1,v2;\alpha }\) the quantity (α) of the distribution (F) for the freedom degrees (v1 and v2).

Mann–Kendall (MK) test

The MK trend test (Mann 1945; Kendall 1975) is based on the correlation between time series ranks and sequences. For a given time series {Xi, i = 1, 2, 3, …, n}, the null hypothesis (H0) assumes it is assumed to be independently distributed (no trend), and the alternative hypothesis (H1) suppose it is a monotonous tendency. The MK test statistic calculated as follows:

$$S = \mathop \sum \limits_{i = 1}^{n - 1} \mathop \sum \limits_{j = i + 1}^{n} {\text{sgn}}\left( {X_{j} - X_{i} } \right),$$
(5)

where X is a univariate time-series, i and j are the time indices associated with individual values, n is the number of data points and the sgn is determined as follows:

$${\text{sgn}}\left( {X_{j} - X_{i} } \right) = \left\{ {\begin{array}{*{20}c} { + 1} \\ 0 \\ { - 1} \\ \end{array} } \right. {\text{if}} \begin{array}{*{20}c} {\left( {X_{j} - X_{i} } \right) > 0} \\ {\left( {X_{j} - X_{i} } \right) = 0} \\ {\left( {X_{j} - X_{i} } \right) < 0} \\ \end{array} .$$
(6)

As documented in Mann (1945) and Kendall (1975), the statistic S under the null hypothesis is approximately normally distributed for n ≥ 8 with mean and variance as follows:

$$E\left( S \right) = 0,$$
(7)
$${\text{Var}}\left( S \right) = \frac{{n\left( {n - 1} \right)\left( {2n + 5} \right) - \mathop \sum \nolimits_{i = 1}^{q} t_{i} \left( i \right)\left( {i - 1} \right)\left( {2i + 5} \right)}}{18},$$
(8)

where t represents tie and q represents the number of tied groups. The standardised test statistic (Z) can be specified by the following equation:

$$Z_{S} = \left\{ {\begin{array}{*{20}c} {\frac{S - 1}{{\sqrt {{\text{Var}}\left( S \right)} }} {\text{ for }} S > 0} \\ {\frac{S + 1}{{\sqrt {{\text{Var}}\left( S \right)} }} {\text{for}}\, S < 0} \\ {0 {\text{for}}\,S = 0} \\ \end{array} } \right..$$
(9)

The null hypothesis is rejected at a significance level (α) if \(\left| {Z_{s} } \right| > Z_{{{\text{crit}}}}\), where \(Z_{{{\text{crit}}}}\) is the value of the standard normal distribution with an exceedance probability of α/2, where α is the statistical significance level concerned. In this study levels of significance at 10%, 5%, 1%, were adopted.

Modified Mann–Kendall test

A modified MK test was adopted to reduce the effect of serial correlation on the trend results of the MK test. The median slope (Ti) of the trends was estimated using the Sen Approach (Steven-Brauner 1997) as recommended by Hamed and Rao (1998) and Yue and Wang (2004), the data series are de-trended by Eq. 10. The amended variance of the MK test statistic is obtained from the following equation:

$$Y_{i} = X_{i} - T_{i} \times i,$$
(10)
$$\mathop {{\text{Var}}\left( S \right)}\limits^{*} = CF \times {\text{Var}}\left( S \right).$$
(11)

The degree of tendency is predicted by Sen’s estimator (Sen 1968). Here, the slope (Ti) of all data pairs is computed as median slope Ti of the identified trend, i.e., the Sen’s estimator of the slope is the median of these N values of Xi data series (Steven-Brauner 1997), and the Sen`s estimator is given by

$$T_{i} = \frac{{X_{i} - X_{j} }}{i - j}\;{\text{for}}\; i = \, 1, \, 2, \, 3, \ldots , \, N.$$
(12)

The \({\text{Var}}\left( S \right)\) is the variance of the MK test statistic based on the original data. The modified standardized MK test statistic by Hamed and Rao (1998) can be written as

$$Z_{S} = \left\{ {\begin{array}{*{20}c} {\frac{S - 1}{{\sqrt {V^{*} \left( S \right)} }}\,\, S > 0} \\ {\frac{S + 1}{{\sqrt {V^{*} \left( S \right)} }} \,\,S < 0} \\ {0 \,\,S = 0} \\ \end{array} } \right..$$
(13)

The correction factor (CF) introduced by Hamed and Rao (1998) is given by

$${\text{CF}} = 1 + \frac{2}{{n\left( {n - 1} \right)\left( {n - 2} \right)}}\mathop \sum \limits_{i = 1}^{n - 1} \left( {n - i} \right)\left( {n - i - 1} \right)\left( {n - i - 2} \right)r_{k} ,$$
(14)

where n is the actual number of observations. The slope of the trends was estimated using the Sen Approach (Eq. 12) as recommended by Hamed and Rao (1998) and Yue et al. (2002), among many others. \(r_{k}\) is calculated by replacing the sample data \(X_{i}\) by the respective ranks \(X_{i}\) in the below equation (Salas et al. 1980):

$$r_{k} = \frac{{\frac{1}{n - i}\sum\nolimits_{i = 1}^{n} {[X_{i} - \overline{X}][X_{i + 1} - \overline{X})]} }}{{\frac{1}{n}\sum\nolimits_{i = 1}^{n} {[X_{i} - \overline{X}]^{2} } }}\;{\text{where}}\;\overline{X} = \frac{1}{n}\sum\limits_{i = 1}^{n} {[X_{i} ]} .$$
(15)

In addition, the continuous independence hypothesis is tested by the lag-1 autocorrelation coefficient as H0: r1 = 0 against H1: |r1|> 0. The t test statistic has a t-distribution with (n − 2) degrees of freedom (Cunderlik and Burn 2004). In the case of |t|≥ tα/2, the null hypothesis of continuous independence at the significance level α is rejected.

Innovative trend analysis (ITA) method

In the ITA method, the data series were divided into two equal sub-series from the first time series to the end-time series, and both parts (i.e. sub-series) were separately sorted in ascending order. Then, depending on the method of the 2D Cartesian coordinate system, the first part was plotted on the horizontal axis (X-axis) and the second part was plotted on the vertical axis (Y-axis). If the data points in the scatter plot were on the 1:1 (i.e. 45°) line, it indicates that the data have no trend. If the data points accumulate below the 1:1 line, it indicates that there is a negative (i.e. a decreasing) trend present in the data series. If the data points are above the 1: 1 line, this indicates a positive (i.e., increasing) trend in the data series (Sen 2012). In addition, this study used two confidence intervals (± 10%) to help readers better understand the difference between rainfall datapoints and trendless lines without statistical effects (Alifujiang et al. 2020).

Pettitt change point test

The Pettitt change point test is a nonparametric approach developed by Pettitt (1979) to detect change points in time series data. This test can detect when time (t) may have occurred in the time series data. The null hypothesis of this test is that there is no shift in the time series at the time (t), and the alternative hypothesis is that there is a change point at a time (t). The test statistic is calculated as follows:

$$D_{ij} = \left\{ \begin{gathered} + 1 \hfill \\ 0 \hfill \\ - 1 \hfill \\ \end{gathered} \right.\begin{array}{*{20}c} {} \\ \end{array} {\text{if}}\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {(X_{i} - X_{j} ) > 0} \\ {(X_{i} - X_{j} ) = 0} \\ {(X_{i} - X_{j} ) < 0} \\ \end{array} ,$$
(16)

where Xi and Xj are the magnitudes of the rainfall data series at the time i and j, respectively, and Xi precedes Xj in time. To evaluate the test over the entire study period (T) these D statistics are summarized as follows:

$$U_{t,T} = \sum\limits_{i = 1}^{t} {\sum\limits_{j = t + 1}^{T} {D_{ij} } } .$$
(17)

If the two samples X1, …, Xt and Xt + 1, …, XT are from the same population, the statistics Ut,T are considered. The test statistic Ut,T, is evaluated for all possible values of t in the range 1 to T. Identify the point in time t (year) when a sudden shift occurs in the time series. The following statistic is used:

$$K_{T} = \mathop {\max }\limits_{1 \le t < T} \left| {U_{t,T} } \right|.$$
(18)

If the KT is significantly different from zero, a change point will occur in t years. This corresponds to the time when the absolute values of Ut,T are obtained. This is done by a hypothesis test based on the resampling method.

Testing the homogeneity of trends

In the current study, six homogeneity tests (Van Bell and Hughes, Runs, Pettit, SNH, BR, and VNR tests) have been adopted on the rainfall data series. It is worth mentioning that none of these six homogeneity tests have been previously applied to Duhok station from 1976 to 2017 and on rainfall data series separately. The details of each of these six tests have been explained below:

Van Belle and Hughes (Chi-square) test is a nonparametric approach that was developed by Van Belle and Hughes (1984). In this test the statistic (i.e. \(\chi_{{{\text{homogeneous}}}}^{2}\)) is calculated as

$$\chi_{{{\text{homogeneous}}}}^{2} = \chi_{{{\text{total}}}}^{2} - \chi_{{{\text{trend}}}}^{2} = \sum\limits_{i = 1}^{k} {(Z_{i} )^{2} - k(\overline{Z})^{2} } .$$
(19)

The values of \((Z_{i} )\) and \((\overline{Z})\) are computed by

$$Z_{i} = \frac{{S_{i} }}{{\sqrt {{\text{Var}}(S_{i} )} }}.$$
(20)
$$\overline{Z} = \frac{1}{k}\sum\limits_{i = 1}^{k} {Z_{i} } \;\left( {k = \, 12 \, \,{\text{for\,monthly\,rainfall\,data}}} \right),$$
(21)

where Si is the MK statistic for month i, and the χ2homogenous has a Chi-square distribution. The χ2homogenous between months is compared with the critical value for the Chi-square (χ2) distribution with m − 1 df. If χ2homogenous is not significant, then a valid test of the general trend is possible by referring to the assumed α = 0.05 for the Chi-square (χ2) distribution with 1 df. If χ2homogenous is significant the null hypothesis of homogeneous monthly trend direction must be rejected.

Runs test was developed by Swed and Eisenhart (1943). The estimated Zc statistic value (Eq. 22) is compared to the Z-test value of the two-sided hypothesis test at a significance level of 5%. If the Zc statistic value is greater than the z-test value, Ho is rejected, so the H1 hypothesis is accepted and the time series under investigation is a statistically significant inhomogeneous series:

$$Z_{{\text{c}}} = \frac{{r - \frac{{2 \times N_{i} \times N_{j} }}{{N_{i} + N_{j} }} - 1}}{{\sqrt {\frac{{2 \times N_{i} \times N_{j} (2 \times N_{i} \times N_{j} - N)}}{{N^{2} (N - 1)}}} }}.$$
(22)

In Eq. 22, Zc is the test value. N is the number of data. Ni is the number of data smaller than the median. Nj is the number of data greater than the median. and r is the number of runs of the data that are above and below the critical value. The runs test rejects the null hypothesis if |Zc| is greater than Z1-α/2. For a large sample runs tests (that is, both Ni and Nj are greater than 10), the test statistic is compared to the standard normal table (that is, Z1-α/2). That is, at the 5% significance level, a test statistic with an absolute value greater than 1.96 at a significance level of 5% indicates non-randomness. For a small sample runs test, there are tables for determining critical values that depend on the values of Ni and Nj (Mendenhall and Reinmuth 1982).

Pettitt test is a nonparametric rank test developed by Pettitt (1979). The time-s analysis of the homogeneity test provides information according to the level of significance used. The Pettitt test rejects the null hypothesis (H0: no break, homogeneous) if the year was a significant break in a trend for a corresponding station. The rank of the data series is used to calculate the test statistic and ignore the normality of the data series (Pettitt 1979). Below is a brief description of the Pettitt test:

$$X_{k} = 2\sum\nolimits_{i = 1}^{k} {r_{i}^{{}} - k(n + 1)} ,\;k = 1, \ldots ,n,$$
(23)
$$X_{K} = \max_{1 \le \, k \le \, n} \left| {X_{K} } \right|,$$
(24)

where ri is the ranks of the data series. If there is a break in year K, the statistics will be maximum or minimum near the year k = K. Critical values for \(X_{K}\) at the 5% significance level depending on the sample size is given in Table 1.

Table 1 Critical values for the homogeneity tests at 5% significance level for a 42-year sample size m taken from Wijngaard et al. (2003)
Full size table

Standard normal homogeneity (SNH) test is a parametric test which was proposed by Alexanderson (1986). The null hypothesis is the same for the Pettitt test. Alexnderson (1986) describes statistics for comparing the average of the first year of a record with the average of the last year. The test statistic Tk is computed as

$$T_{k} = k\overline{z}_{1}^{2} + (n - k)\overline{z}_{2}^{2} ,\;k = {\mathbf{1}}, \, {\mathbf{2}}, \, {\mathbf{3}}, \ldots ,n,$$
(25)

where

$$\overline{z}_{1}^{{}} = \frac{1}{k}\frac{{\sum\nolimits_{i = 1}^{k} {(y_{i}^{{}} - } \overline{y} )}}{s},$$
(26)
$$\overline{z}_{2}^{{}} = \frac{1}{n - k}\frac{{\sum\nolimits_{i = k + 1}^{n} {(y_{i}^{{}} - } \overline{y} )}}{s},$$
(27)
$$S = \frac{1}{n}\sum\limits_{i = 1}^{n} {(y_{i}^{{}} - } \overline{y} ).$$
(28)

If there is a change point in the data series, Tk reaches its maximum near of k = K. The test statistic To is computed as follows:

$$T_{o} = {\text{ max }}\left( {T_{k} } \right),{ 1 } \le k < n.$$
(29)

If To is greater than the critical value, the null hypothesis is rejected. The critical value of To is based on the sample size reported by Alexanderson (1986), as shown in Table 1.

Buishand range (BR) test is a parametric test that was developed by Buishand (1982). The null hypothesis is the same as the Pettitt test. This test is based on the adjusted partial sums calculated by the following equation:

$$S_{k}^{*} = \frac{{n\sum\nolimits_{i = 1}^{k} {(y_{i}^{{}} - \overline{y} )} }}{{\sum\nolimits_{i = 1}^{n} {(y_{i}^{{}} - \overline{y} )^{2} } }},\;k = 1, \, 2, \ldots ,n,$$
(30)

where \(\overline{y}\) is the average of the data time series, the test statistic is defined as

$$Q = \mathop {\max }\limits_{0 \le k \le n} S_{k}^{*} .$$
(31)

The null hypothesis is accepted, when the value is less than the critical values based on sample size (n) given by Buishand (1982), as shown in Table 1.

Von Neumann rate (VNR) test is a nonparametric test which is developed by Von Neumann (1941). It uses the ratio of the mean square successive (year to year) difference to the variance. The VNR ratio (N) is calculated as

$$N = \sum\limits_{i = 1}^{n - 1} {\left( {y_{i}^{{}} - y_{i + 1}^{{}} } \right)^{2} } /\sum\limits_{i = 1}^{n} {\left( {y_{i}^{{}} - \overline{y} } \right)^{2} } .$$
(32)

The critical values based on sample size (n) can be taken from Buishand (1982), as shown in Table 1.

In a hypothesis test, the critical value is a point on the test distribution that is compared to the test statistic to determine if the null hypothesis is rejected (Statistics Online 2021). The critical values of the six adopted homogeneity tests (Table 1) mentioned above were used to test the hypothesis of the rainfall time series (i.e. monthly, seasonal and annual data series) during the period 1976–2020 (42-year data length; i.e. 42-year sample size) at α = 5% significance level.

Results and discussion

Moving average rainfalls

The average annual rainfall (AAR) with 3 years moving average annual rainfalls (MAAR) for the data period ranging between 1976 to 2017 for the Duhok station considered in this study is shown in Fig. 2. It can be observed in Fig. 2 that the AAR ranges between 19.7 mm for the years 1978 and 75.8 mm for the year 1994. While the average annual rainfall value equals 44.6 mm for the study period of 1976–2017. In Fig. 2, by considering moving AAR of 3 years, it shows that the MAAR is ranging between 15.2 mm and 68.4 mm for the monthly duration data. It is worth mentioning that the highest monthly rainfall of 330.4 mm occurred in January 2013.

Fig. 2
figure 2

Average annual rainfall (AAR) with 3-year moving average annual rainfalls (MAAR) for Duhok station in Kurdistan region, Iraq during 1976–2017

Full size image

Results of quality control of the rainfall data series

The quality control of monthly, seasonal and annual rainfall data series of Duhok station were tested using Mandel’s k statistic method to detect the outlier, as described in “Methods”. The results of Mandel’s k method in Fig. 3 showed that no outlier was detected in the rainfall data series of Duhok station. The most common reasons for outliers to appear in climate data are equipment errors related to incorrect data entry related to observers, or equipment relocations, changes, or rare equipment maintenance delays (Jaafar and Al-Lami 2019). The rainfall data measurements and the availability of each station play a major role in identifying the causes of outliers in the results due to the detailed information in the station data. This information is not available at Duhok station. Therefore, there is no evidence of the reason for the outliers of the station under study.

Fig. 3
figure 3

Detected outliers for the Duhok station (alpha = 0.05)

Full size image

Trend in rainfall data series by ITA method, MK test and Modified MK test

This study used the ITA method to determine trends in monthly, seasonal, and annual rainfall data series for the study period from 1976 to 2017, as described in “Methods”. In general, the results of applying the ITA method (Figs. 4, 5, 6) show that most data points fall under the 1:1 line, implying an overall downward trend. However, the characteristics of patterns in different rainfall data series are quite different. On a monthly scale, as shown in Fig. 4, concerning the two confidence interval bands (10% and -10%), the results show a clear increasing trend of all the values (i.e., low, medium, and high) in January with data generally falling above the 10% relative band. In February and March, most of the rainfall points below 110 mm per month have no trend, while, from 110 and up to 180 mm per month shows a decreasing trend, and the precipitation above 200 mm per month shows an increasing trend.

Fig. 4
figure 4

Results of applying the ITA method for monthly rainfall data at Duhok station (1976–2017)

Full size image
Fig. 5
figure 5

Results of applying the ITA method for seasonal rainfall data at Duhok station (1976–2017)

Full size image
Fig. 6
figure 6

Results of applying the ITA method for AAR at Duhok station (a) non-monotonic trends (b) the trends of each cluster (low, medium and high)

Full size image

Decreasing trends were detected in both April, May and October. In general, the low rainfall values show a steady decrease in the first subseries more than the second subseries in April. The same situation is evident in October, except for the low values. While, in May the rainfall data points in low values change more abruptly than the medium and high values. In June, July and August the rains are very rare and sporadic almost every year. In September an increasing trend is indicated inside the 10% bands, but there are not many rainfall data points. Most rainfall data points show decreasing trend areas in November outside the 10% bands of all the values (i.e., low, medium, and high). Finally, in December, the low rainfall points in the upper triangular show an increasing trend. This means that there is an increase in the low rainfall in the second halves of the observed data (1997–2017) compared to that in the first halves (1976–1996). However, there are not many rainfall data points in the middle and high categories, a decreasing trend is obvious.

On a seasonal scale, as shown in Fig. 5, the results show that most of the rainfall points below 75 mm per month have no trend, while, from 75 mm up to 120 mm per month show a decreasing trend with data generally falling under the 10% relative band in Spring. In the Summer season (i.e., June, July and August), the region is dry. Most rainfall data points indicate a decreasing trend area in Autumn, outside the 10% bands of low and medium values. In Winter an increasing trend is observed inside the 10% bands for most of the rainfall points.

The results on an annual scale as shown in Fig. 6 show an increasing trend for low values of the rainfall points below 30 mm per month. Also, the rainfall points from 30 to 40 mm per month show a decreasing trend with data generally falling under the 10% relative band. For the medium values, a steady decreasing trend is observed for all the annual rainfall data points inside the 10% bands. Even though there are not many rainfall data points in high values, most of the data points indicate a decreasing trend outside the 10% bands.

The results of the MK test for the case of non-autocorrelated rainfall series for trend detection in monthly, seasonal and annual rainfall series are shown in Fig. 7. It can be observed in Fig. 7, that the trend results of the MK test at monthly, seasonal and annual rainfall scales are statistically insignificant at three levels of significance (i.e., 10%, 5%, and 1%) except for the January and Winter series. The increase in rainfall trends in January and Winter were statistically significant at a 10% significance level (Fig. 7). Even though most of the trends were non-significant at the 10%, 5% and 1% significance levels, more than half of the total monthly series show an upward trend. In the case of seasonal rainfall data series, Summer and Winter seasons have rising trends, whereas falling trends are observed in both Spring and Autumn seasons. In addition, there was an increasing trend of annual precipitation in 42 years (study period of 1976–2017).

Fig. 7
figure 7

MK trend test result of rainfall in Duhok station (1976–2017)

Full size image

The results of the Modified MK test for the autocorrelated series for trend detection in the monthly, seasonal and annual series are shown in Table 2. Sen’s slope estimator and CF are also shown in Table 2. Depending on the correlation factor (i.e., r1 > ± 0.278), the five series are autocorrelated out of 17 series at the 10% and 5% significance levels. On the monthly scale, it has been found that the highest magnitude of Sen’s slope estimator is 1.134 (in January) and the lowest magnitude of Sen’s slope is -0.413 (in November). Furthermore, on the seasonal scale, it has been found that the highest value of Sen’s slope estimator is 0.446 (in Winter). On an annual scale, it was found that the value of Sen’s slope estimator (i.e., 0.181) is higher than the monthly and seasonal scales.

Table 2 Results of the modified MK trend tests for different rainfall data series
Full size table

Tables 3 and show a comparison among the results of the trend tests (i.e., MK test, Modified MK test and 42 years the ITA method) for monthly, seasonal and annual rainfall data over a 42-year study period. The results in both Table 3 and provide information on the evolution of the patterns of the rainfall time series in terms of the evaluation of the low and high values. Moreover, the ITA method is another aspect of the MK and Modified MK tests. As shown in Table 3, the low and high values of all rainfall series were evaluated individually according to the ITA method. The results in Table 3 show that according to both MK and Modified MK trend tests, an increasing trend for 8 of the 12 months at selected stations in the study area and a decreasing trend for the remaining 4 months. In addition, depending on the trend slope, the results of the ITA method show, an increasing trend is apparent in 6 of the 12 months.

Table 3 Zc statistics of the MK and modified MK trend tests, also trend slope of the ITA method for different rainfall data series
Full size table

In the case of seasonal time series, the results of the three trends tests (i.e., MK test, Modified MK test and the ITA method) show that Summer and Winter seasons have rising trends, whereas falling trends are observed in both Spring and Autumn seasons. Also, it has been found that the trend results on the annual scale (i.e., AAR) showed an increasing trend for the three trends tests. In general, it can be observed in Table 3 that using the TFPW approach, which considers the effect of serial correlation on trend results, resulted from a slight increase in the range of trends and its statistical significance in rainfall data series (i.e., Zc statistics). Table 3 also shows that the trend slope of the ITA method is higher for the data series which significantly increase (e.g., January and Winter) than those which insignificantly increase or decrease (e.g., February to December).

It can be observed in Table 4 that according to both the MK test and Modified MK test, there is no significant trend in most of the rainfall series (i.e., monthly, seasonal and annual) except for January and Winter, where the rainfall time series have increased significantly. Whereas the results of the ITA method indicate that increasing trends exist in 3 months (i.e., January, October and December) out of 12 months for high rainfall series. According to the low rainfall series, 1 month (i.e., January) shows an increasing trend, and the November and Winter series show a decreasing trend.

Table 4 Comparison of the MK test, modified MK test and the ITA method for analyzing the rainfall data series in the Duhok station between 1976 and 2017
Full size table

Depending on both the MK test and Modified MK test, it can be observed in Table 4 that 11 out of 17 rainfall series (i.e., monthly, seasonal andr annual rainfall series) show an increasing trend, and 4 of the 17-rainfall series are showing a decreasing trend. This outcome is compatible with Sen’s Slope values in Table 2. In the case of applying the ITA method, for high values, 8 out of 17 rainfall series show an increasing trend and 5 show a negative trend at low values.

Abrupt shift in rainfall data

The Pettitt change-point test is used to identify abrupt changes (shift) in the average rainfall time series in Duhok station. The direction of the shift in the average is determined by comparing the average of the subseries before the shift and after the shift. Figure 8 of the Pettitt test shows that there has been a significant positive shift occurred after 1990. The Pettitt test shows that the Duhok station has positive trends at the 10% significance level. In addition, it is found that the mean of the AAR data after the change point is higher (i.e., 46.89) than the mean prior to the change point (i.e., 41.30) with a rate of change of 13%. Furthermore, the MK test statistics prior to and after the change point (i.e., Zc = 0.274 and Zc = − 0.896, respectively) are smaller compared to the MK test statistic for the complete data series (i.e., Zc = 0.542). The observed AAR is characterized by quick transitions that can be described as "jumps" of the same year, but these jumps are not significant except in 1990 which shows a significant positive shift jump (see Fig. 8). The AAR data show that since the year 1990 (i.e., change point year), the high increasing change in AAR is sudden and prolonged happened in 3 years (1992, 1993, and 1994). However, unlike it was expected by previous scenarios based on 1992, 1993 and 1994, the AAR data since 1995 shows a decrease and after 1995 the AAR data series return nearly to the same level prior to 1990. Indeed, trends of AAR, are obtained by MK and Modified MK trend tests, also the ITA method showed increasing changes within the period 1976–2017 in Duhok station, which indicates an increasing trend (see Table 3). The AAR analysis (Fig. 8) suggests a rainfall increase in the upcoming years. Moreover, the rainfall data indicate that a high probability of sudden and prolonged changes in the rainfall data series.

Fig. 8
figure 8

Pettit change point test results for Duhok station showing a positive shift in the mean of the AAR data (circle represents change point)

Full size image

Homogeneity of trends in rainfall data series

As stated in “Methods”, the homogeneity of the rainfall data of the Duhok station in the Kurdistan region, Iraq was tested using each of Van Bell and Hughes homogeneity, Runs, Pettit, SNH, BR, and VNR tests. In the application of homogeneity tests, the rainfall time series (monthly, seasonal and annual time series) were considered separately. The results of each method were evaluated for a significance level of 95% and the inhomogeneities were detected. The critical values obtained from each of the above-mentioned homogenous tests are shown in Table 1. The data of the months June to August have been neglected due to very limited rainfall, hence all statistical parameters of the adopted homogeneity tests are close to zero. In the current study, the methods for testing the homogeneity of the series may be classified into two groups:

Group 1: Van Belle and Hughes (1984) test was applied to monthly and seasonal rainfall data. The computed χ2homogenous value (i.e. χ2homogenous = 3.51) for Van Belle and Hughes (1984) test was found to be less than the critical value of the χ2homogenous at α = 0.05 (that is 19.68 for df = 11). The calculated χ2homogenous value was not significant, so the χ2trend value was then compared to the critical value of the χ2trend at α = 0.05. Since Duhok station had χ2trend value (i.e., χ2trend = 0.082) less than the critical value of the χ2trend (that is 3.84 for df = 1) its monthly rainfall trends were inhomogeneous, which indicates that the trends in all months had a different direction. For seasonal data (i.e., Spring, Summer, Autumn and Winter), the computed χ2homogenous value (i.e., χ2homogenous = 1.218) for the Van Belle and Hughes (1984) test was found to be less than the critical value of the χ2homogenous at α = 0.05 (which is 7.81). Since the calculated χ2homogenous value was not significant, the χ2trend value was compared to the critical value of the χ2trend at α = 0.05. Since Duhok station had a χ2trend value (i.e., χ2trend = 0.001) was below than the critical value of the χ2trend (that is 3.84 for df = 1), its seasonal rainfall trends were inhomogeneous, indicates that the trends in all seasons had a different direction.

Group 2: Runs, Pettitt, SNH, BR and VNR tests were applied to the monthly seasonal and annual rainfall data series. In Table 5, it can be observed that most of the rainfall time series pass the critical test values (Table 1) of the five adopted tests at the 95% significance level. The results of the Runs test show that non-homogeneous was detected only in September (significant negative shifts). The results of the Pettitt, SNH and BR tests show that the inhomogeneity is generally detected between the years 1994 and 2007. It can also be observed in Table 5, that the inhomogeneity is detected in September using Pettitt, SNH and VNR tests, while Table 2 shows that rainfall data series on January and September was found to be inhomogeneous by applying the BR test at a significance level of 95%. The outcome of the Pettitt, SNH, BR and VNR tests homogeneity tests in the current study is similar to the outcome of the studies by AL-Lami et al. (2014) and Agha et al. (2017) who analyzed rainfall data and found the homogeneity for all stations located in northern Iraq. It should be noted that AL-Lami et al. (2014) used data for the period 1980 to 2010, while Agha et al. (2017) used data for the period 1943 to 2010 and our data period covers 1976 to 2017.

Table 5 Results of homogeneity tests for different rainfall data series
Full size table

Conclusion

In this study, quality control, trend tests and homogenous tests were applied to monthly, seasonal and annual data series for a study period of 1976–2017 at site location in Duhok city, Kurdistan Region, Iraq. The quality control technique used was the outlier detection using Mandel’s K methods at 5ioa n% significance level. The Mann–Kendall (MK), Modified MK tests and Innovative Trend Analysis (ITA) trend tests have been applied to identify trends in the rainfall data series at the 10%, 5% and 1% significance levels. Pettitt Change Point test has been employed to determine the direction and timing of a change point. The homogeneity of the data times series at the selection station has been examined using the Van Bell and Hughes homogeneity, Runs, Pettit, standard normal homogeneity, Buishand Range, and Von Neumann rate tests.

The results of the Mandel k method show that no outliers were found in the monthly, seasonal, and annual rainfall data series of the selected station. The results of the MK test show that the number of positive trends is greater than the number of negative trends, especially in the time series the individual rainfall. The statistical Zc value of the MK test represent both an increasing and a decreasing trend in the study area, but this increase or decrease is not significant, except for the January and Winter series. The increase in rainfall trends in January and Winter was statistically significant with the 10% significance level. The use of the Modified MK test, which accounts for the impacts of serial correlation on-the results, has resulted in a slight increase in the magnitude of trend and its statistical significance in rainfall data series. Monthly time series were found to have the most significant trend in January with a significance level of 5%, and the seasonal time series were found to have the most significant trend in Winter. Sen's slope also shows positive and negative slope values according to the MK test value and the modified MK trend test. There are 11 out of 17 rainfall series with a positive trend and Zc and increasing Sen’s slope magnitude, and there are 4 out of 17 rainfall series with negative Zc value and Sen’s Slope.

The results of the ITA method indicated that increasing trends were observed in January, October and December for the high rainfall series, while according to the low rainfall series, January shows an increasing trend and November show a decreasing trend. The difference between the MK test and Modified MK test in the monthly, seasonal and annual rainfall series was small. The Pettit test results showed that there was a significant positive shift since 1990. In the case of homogeneity of the rainfall data series, the entire time series (most of monthly, seasonal and annual series) is homogeneous. Finally, the present study concluded that there is evidence of some change in the trend of rainfall data series during the 1976–2017 study period at Duhok station in the Kurdistan Region, Iraq.