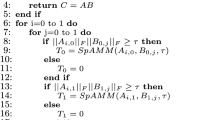1 Introduction

Matrix multiplication is one of the most fundamental linear algebra operations, and it is widely employed as an essential tool for various applications, including machine learning, scientific computations, and data analysis. Recently, the data size in various domains has increased continuously, and the demand for rapid matrix multiplication of large matrices also has increased sharply.

Recent graphics processing units (GPUs) exploit massive parallelism for general-purpose computing, not only for graphics applications. To meet the demands for fast matrix multiplication, GPUs have been employed as accelerators, and the state-of-the-art GPU-based matrix multiplication library (i.e., CUBLAS [5, 20]) shows up to hundreds or thousands times higher performance than using a central processing unit (CPU) alone. However, the matrix size a GPU can handle efficiently is limited by the relatively small GPU memory (i.e., device memory) compared with the CPU-side (i.e., host memory). To handle a large matrix better with limited memory space, we could employ a divide-and-conquer approach. Some of the well-designed divide-and-conquer matrix multiplication algorithms have even lower asymptotic complexity than a classical \(O(N^3)\) method [7, 29]. However, it is hard to get dramatic improvement in performance, such as what is achieved with a GPU for matrices of adequate size. This is because divide-and-conquer methods lead to much data communication between host and device memories. Such data transfer overhead is a well-known performance bottleneck for GPU-based algorithms [4, 10, 11, 26, 32].

One recent computing trend is the presence in most systems of both CPU-like and GPU-like cores [15, 25]. For example, recently, a workstation or a PC has both multiple CPU cores and a GPU (or multiple GPUs). Now, not only workstation but also even an embedded system (e.g., NVIDIA’s Jetson series [17] and AMD’s Ryzen embedded family [1]) has both CPU and GPU chips.

However, prior GPU-based matrix multiplication algorithms do not fully utilize the available computing power in such heterogeneous computing environments.

1.1 Contributions

In this paper, we present a novel Heterogeneous Parallel Matrix multiplication (\(\times \)) (HPMaX) framework that handles large matrix multiplication efficiently by utilizing both multiple GPUs and multi-core CPUs, which are also powerful computing resources (Sect. 3.2). We first divide the matrix multiplication work into a set of matrix addition and multiplication tasks based on Strassen’s matrix multiplication method (Sect. 3.1). Then, we propose a heterogeneous parallel Strassen algorithm (Sect. 4.1). This allows distribution of the tasks across multi-core CPUs and GPUs, in ways that minimize the data communication overhead and fully utilize the available computing power. Based on the divide-and-conquer strategy of Strassen’s method, our heterogeneous parallel Strassen algorithm can handle a matrix up to four times larger than with the prior GPU-only method at once. To handle a matrix so large that our heterogeneous parallel Strassen algorithm cannot handle it at once due to the device memory limit, we propose a block-based work decomposition method (Sect. 4.2). Then, we figure out the disjoint workspace property among the decomposed tasks, and further improve the performance of our method by maximally overlapping computations and data transfers with multiple streams to a GPU (Sect. 4.3). Finally, we extend our framework to utilize multiple GPUs (Sect. 4.4).

We implemented our HPMaX framework on five different machine configurations consisting of two octa-core CPUs and one or two GPUs. Then, we applied our framework to various sizes of matrices (up to 131,072 \(\times \) 131,072 in single and double precisions) and compared the performance with four alternative methods based on prior work (Sect. 5). Overall, our method showed higher performance than prior methods, including GPU-based algorithms. Moreover, compared with the state-of-the-art GPU-based matrix multiplication library (i.e., CUBLAS), our method achieves up to 1.97 times higher performance when we use the same GPUs with multi-core CPUs. Furthermore, in some cases, our method using a low-performance GPU (e.g., GTX 1060, 3 GB) achieved performance comparable with that of CUBLAS using a high-performance GPU (e.g., RTX 2080, 8 GB). We could achieve such high performance by utilizing fully the capacities of the given heterogeneous computing systems while employing Strassen’s method to provide lower asymptotic complexity. We also found that HPMaX continually achieves better performance as we use more computing resources. These results demonstrate the efficiency and robustness of our approach.

2 Related work

Accelerating matrix multiplication has been widely studied for a long time, and we can divide the most popular approaches into two categories: reduction of the number of floating-point operations and employment of parallel computing architectures.

2.1 Lower asymptotic complexity

In 1969, Strassen first introduced a matrix multiplication algorithm with lower asymptotic complexity \(O(N^{2.81})\) than with the classical \(O(N^{3})\) method [29]. This work led to several following works, which further reduced the k of \(O(N^{k})\) [23, 24, 28, 30], such as with the Coppersmith-Winograd algorithm with \(O(N^{2.38})\) [7]. However, we could utilize the benefits of those algorithms only with a large matrix because the constant coefficients of the big O-notation are too big. Thus, Strassen’s method is still the most widely used matrix multiplication acceleration algorithm in practice. Our method employs Strassen’s approach, and in addition, we propose an efficient parallel algorithm for use in heterogeneous computing environments.

2.2 Parallel matrix multiplication algorithms

The recent trend for improving computing power is to put more cores in a chip rather than to increase the clock frequency of a core. Current commodity CPUs have four or eight cores, and the high-end CPUs have up to sixty-four cores (e.g., AMD’s Threadripper). Moreover, hardware accelerators such as GPUs have thousands of processing cores. Along with this architectural trend, researchers have proposed parallel matrix multiplication algorithms. Some of them employ multi-core CPUs [13, 27], and others take advantage of the massive parallelism of GPUs [2, 9, 19, 31, 33, 35]. Generally, GPU-based methods for matrix multiplication show much higher performance than multi-core CPU-based algorithms because such multiplication is computation-intensive, and GPU architecture is suited for it. Volkov and Demmel [33] showed that a highly optimized matrix multiplication algorithm on a GPU achieved much higher performance than with a CPU. This is known as the state-of-the-art GPU matrix multiplication algorithm and is widely used as part of the CUBLAS library [5, 20].

Our HPMaX framework can benefit from such well-optimized GPU libraries because it uses a classical matrix multiplication method for a multiplication task between sub-matrices smaller than a threshold size (Sect. 3.2).

2.3 Parallel strassen algorithms

Lai et al. [16] proposed an efficient implementation of the Strassen algorithm on a GPU. It achieved better performance than with the CUBLAS library and demonstrated that a well-designed Strassen algorithm could improve matrix multiplication performance on a GPU. They also proposed a method for prediction of threshold size (i.e., cutoff-size) at which Strassen algorithm starts to show better performance than the classical method. Ray et al. [25] compared the results of Strassen algorithm and the classical matrix multiplication method run on both CPU and GPU. The results also showed that a GPU with Strassen algorithm showed better performance for a large matrix (e.g., 4000 \(\times \) 4000).

One of the common points found in previous work is that the classical \(O(N^{3})\) method shows better performance with a small matrix, and the threshold varies depending on the hardware. With our method, we also noted this observation and employed a cutoff-size to define the block size that is the basic work unit of our heterogeneous parallel Strassen algorithm.

Although GPU-based algorithms show impressive performance, the relatively small memory of such devices (e.g., 2–24 GB) limits the maximum size of the matrix it can handle efficiently at once, compared with the CPU-side memory (e.g., 16 GB-1 TB). A feasible solution for the limited device memory problem is to use a divide-and-conquer strategy that includes using host memory [26]. Yugopuspito et al. [34] proposed a GPU-based Strassen algorithm that utilizes the host memory as auxiliary space. Based on Strassen’s method, it divides the input matrices into sub-matrices recursively with addition and subtraction kernels until it meets the threshold size. Then, it launches multiplication kernel for the sub-matrices. The whole matrices are maintained in the host memory, and it sends the required region of the matrices for the current kernel to the GPU at each time. Therefore, it could handle four times larger matrices with the classical matrix multiplication method since only the required data for a kernel is maintained in the device memory. However, such an out-of-core approach requires much data communication between host and device memories, and we found that it limits the performance improvement. But, they did not give much study on minimizing data communication overhead. In addition, it does not fully utilize the available computing capability of the CPU.

Like Yugopuspito et al., our method bases on Strassen’s method and mainly utilizes GPU for computation. However, our heterogeneous parallel framework handles a large matrix by using not only a GPU but also multi-core CPUs to reduce data communication overhead while exploiting the computing power of the CPUs at the same time. To efficiently utilize both computing resources and handle large matrices, we use block-based work decomposition method instead of recursive work decomposition used in Yugopuspito et al. We also extend our method to utilize multiple GPUs different from the prior work that used a single GPU.

Computing clusters were also employed to get more processing power for matrix multiplication [6], and many of them also employed Strassen algorithm [3, 12, 18, 22]. Karunadasa et al. [12] proposed a distributed parallel algorithm running on a small GPU cluster. In their work, a master node divides the input matrices and sends the sub-matrices to slave nodes having a GPU. Then, each slave node performs matrix multiplication for given sub-matrices and returns the result to the master node. Finally, the master node generates the final result. Peng et al. [35] gave investigation on the benefit of using multiple GPUs for two matrix multiplication algorithms, including classical and Strassen’s methods. They partitioned the result matrix into tiles and distributed them to GPUs. Then, each GPU performed matrix multiplication for the given tile. In their implementation of Strassen algorithm, it handles a tile by one-level Strassen’s method. For both algorithms, they performed matrix additions on CPU cores and multiplication operations on GPUs. They reported that, with a single GPU, the Strassen algorithm achieved a little better performance than the classical method. On the contrary, it showed lower performance than the classical one when using multiple GPUs. They found that the Strassen algorithm requires a large number of matrix additions at the beginning, and it becomes the performance bottleneck since GPUs stay idle until CPU finished the addition operations.

Our algorithm also employed both multi-core CPUs and GPUs while giving dedicated tasks to them, similar to Karunadasa et al. and Peng et al. However, we aim to design an efficient algorithm for heterogeneous computing environments in a node, different from the prior work that targeted computing cluster. Also, our method exploits the concurrent execution ability of heterogeneous computing systems intensively, different from prior work that takes serialized steps among computing resources. As a result, our method shows higher performance than the classical algorithm robustly with a single GPU and multiple GPUs.

3 Overview

In this section, we provide background on Strassen algorithm and then briefly describe our HPMaX framework.

3.1 Strassen algorithm

Strassen algorithm runs in a divide-and-conquers manner [29]. Let \(C=AB\) where A, B, and C are \(2^n\times 2^n\) matrices. If A and B are not of type \(2^n\times 2^n\), the missing rows and columns are filled with zeros. The three matrices are partitioned into equally sized block matrices as in Eq. (1) with \(A_{ij},B_{ij},C_{ij} \in {\mathbb {R}}^{2^{n-1}\times 2^{n-1}}\)

$$\begin{aligned} A = \begin{bmatrix} A_{11} &{}\quad A_{12}\\ A_{21} &{}\quad A_{22}\\ \end{bmatrix} , B = \begin{bmatrix} B_{11} &{}\quad B_{12}\\ B_{21} &{}\quad B_{22}\\ \end{bmatrix} , C = \begin{bmatrix} C_{11} &{}\quad C_{12}\\ C_{21} &{}\quad C_{22}\\ \end{bmatrix} \end{aligned}$$
(1)

Then, \(C_{ij}\)s are computed by

$$\begin{aligned} C_{11}= & {} A_{11}B_{11}+A_{12}B_{21} \quad C_{12} = A_{11}B_{12}+A_{12}B_{22} \nonumber \\ C_{21}= & {} A_{21}B_{11}+A_{22}B_{21} \quad C_{22} = A_{21}B_{12}+A_{22}B_{22} \end{aligned}$$
(2)

In Strassen algorithm, new matrices are defined as follows

$$\begin{aligned} M_1= & {} (A_{11}+A_{22})(B_{11}+B_{22}) \nonumber \\ M_2= & {} (A_{21}+A_{22})B_{11} \qquad M_5 = (A_{11}+A_{12})B_{22} \nonumber \\ M_3= & {} A_{11}(B_{12}-B_{22}) \qquad M_6 = (A_{21}-A_{11})(B_{11}+B_{12}) \nonumber \\ M_4= & {} A_{22}(B_{21}-B_{11}) \qquad M_7 = (A_{12}-A_{22})(B_{21}+B_{22}) \end{aligned}$$
(3)

Finally the \(C_{ij}\) are expressed in terms of \(M_k\) like

$$\begin{aligned} C_{11}= & {} M_1 + M_4 - M_5 + M_7 \qquad C_{21} = M_2 + M_4 \nonumber \\ C_{12}= & {} M_3 + M_5 \qquad C_{22} = M_1 - M_2 + M_3 + M_6 \end{aligned}$$
(4)

As a result, we need only seven multiplications instead of the eight with the classic method. This division process is repeated recursively until the sub-matrices degenerate into numbers, and the time complexity becomes \(O(N^{log7})\), which is approximately \(O(N^{2.8074})\), where \(N = 2^n\).

3.2 HPMaX framework

As figured out in several previous works [16, 34], we also found that the classical \(O(N^3)\) method works similar to or better than the Strassen algorithm for matrices with a size equal to or smaller than a given threshold (i.e., cutoff-size). Therefore, when the input matrices were equal to or smaller than the cutoff-size, we use a GPU with the classical method. We determined the cutoff-size for the target GPU according to the device memory size and the number of streams (Sects. 5 and 5.4). If the size of the input matrices exceeded the cutoff-size, our HPMaX framework takes on the matrix multiplication work.

Fig. 1
figure 1

Overview of our HPMaX framework

Full size image

Figure 1 shows an overview of our HPMaX framework. It consists of three main components: (1) master worker, (2) slave workers, and (3) GPU(s). The master worker manages the HPMaX framework. For given matrix multiplication work, the master worker divides the input matrices and generated \(T(C_{ij})\) tasks, which represent computation for \(C_{ij}\) in Eq. (2). This process is based on our block-based work decomposition method (Sect. 4.2). Each slave worker has two separate queues, incoming and outgoing queues (\(Q_\mathrm{in}\) and \(Q_\mathrm{out}\)), by which to communicate with the master worker. The master worker allocates the generated \(T(C_{ij})\)s by pushing them to the incoming queues of the slave workers evenly in a round-robin manner. Since the workspaces of \(T(C_{ij})\)s are independent, slave workers can process them concurrently without any synchronization operations such as a locking mechanism (Sect. 4.3). A slave worker takes a \(T(C_{ij})\) from the incoming queue and computes \(C_{ij}\). According to our heterogeneous parallel Strassen algorithm (Sect. 4.1), slave workers cooperate with the given the GPU(s). When multiple GPUs are available, slave workers are evenly mapped to the GPUs. Otherwise, all slaves share a GPU. Each slave worker has a dedicated stream to a GPU, and all slaves run in parallel to utilize the computing capability of the heterogeneous computing systems maximally. Once a slave worker gets the result of a \(T(C_{ij})\), it is put into its outgoing queue. Finally, the result collector gathers the computed \(C_{ij}\)s from slave workers and then creates the output matrix C.

4 Heterogeneous parallel matrix multiplication

In this section, we first explain our heterogeneous parallel Strassen algorithm (Sect. 4.1). Then, we propose a work decomposition method for handling a matrix so large that our heterogeneous parallel Strassen algorithm cannot handle it at once due to lack of device memory (Sect. 4.2). Also, we explain how we maximize the parallelism of our method with multiple streams (Sect. 4.3). Finally, we extend our method to utilize multiple GPUs (Sect. 4.4).

4.1 Heterogeneous parallel strassen algorithm

When a slave worker takes a \(T(C_{ij})\) from the incoming queue, it generates two matrix multiplication tasks according to Eq. (2). For example, it generates \(T(A_{11}B_{11})\) and \(T(A_{12}B_{21})\) for \(T(C_{11})\). If the size of \(C_{ij}\) is smaller than the cutoff-size, two multiplication tasks are processed on the GPU using with the classical method, and the slave worker sums them. Otherwise, a slave worker manages these tasks with its task queue (\(Q_\mathrm{task}\)) and processes them one-by-one with our heterogeneous parallel Strassen algorithm. Then, the slave worker gathers all the results and makes the final \(C_{ij}\).

When a slave worker takes a task from \(Q_\mathrm{task}\), it decomposes that into seven \(T(M_k)\)s, \(k \in \{1,2,\ldots , 7\}\) representing the computation in Eq. (3). Each \(T(M_k)\) consists of two sub-tasks, \(T_\mathrm{add}(M_k)\) and \(T_\mathrm{mul}(M_k)\). In this case, \(T_\mathrm{add}(M_k)\) includes one or two matrix addition(s) and makes two temporal matrices for \(T_\mathrm{mul}(M_k)\). Then, \(T_\mathrm{mul}(M_k)\) multiplys the two temporal matrices and generates the final output (\(M_k\)).

A straightforward way to handle a large matrix using limited device memory is to employ the host memory as auxiliary memory space, as done by Yugopuspito et al. [34]. In this approach, the GPU performs both \(T_\mathrm{add}(M_k)\) and \(T_\mathrm{mul}(M_k)\) while maintaining only the necessary sub-matrices for each task in the device memory. Therefore, it can handle a matrix four times larger than when using the classical method. However, it requires much data communication between the host and the device memories (forty-seven data transactions), and the total size is \(O(\frac{47}{4}N^2)\), compared with the classical method requiring only three data transactions of which the total size is \(O(3N^2)\). This communication overhead is a typical performance bottleneck that occurs when using GPUs. In addition to the communication overhead, this approach wastes the computing power of the multi-core CPUs, which are also powerful computing resources.

Table 1 Required device memory space and data communication overhead for three different methods when the input matrix size is \(N \times N\)
Full size table

To reduce such data transfer overhead while fully utilizing the computing power of multi-core CPUs as well, we let multi-core CPUs process \(T_\mathrm{add}(M_k)\). And, we send only two temporal matrices to the GPU instead of four (or three) sub-matrices, and then the GPU performs \(T_\mathrm{mul}(M_k)\). This work distribution strategy is based on a well-known architectural difference between CPU and GPU [14]. Taking additional memory space for the temporal matrices is less burdensome for the host memory, which usually has sufficient space compared with the device memory. In addition, the CPU architecture has advanced features that support irregular memory access patterns, like a well-organized cache hierarchy. This helps to access sub-matrices efficiently independent of the data layout for the input matrices. On the other hand, although a GPU has limited memory, it outperforms multi-core CPUs for matrix multiplication computation since a GPU has a highly optimized architecture for regular streaming floating-point operations. With this work distribution approach, we decrease data transfer overhead to twenty-one data transactions, of which the total size is \(O(\frac{21}{4}N^2)\). Moreover, it requires only 1/4 of the device memory space needed with the classical method (Table 1).

Fig. 2
figure 2

Timeline that shows overlapping among computation of CPU and GPU and the data communications. The last task of the CPU (yellow box) is the merge step in Eq. (4) (colour figure online)

Full size image

To further improve the performance of our method, we also exploit the concurrent execution ability of the heterogeneous parallel systems. Recent GPUs support asynchronous processing with CPUs, and data transfer between host and device memories also can be executed concurrently while CPUs and GPUs are doing their computations [21]. Based on these concurrent execution capabilities, we increase the utilization efficiency of the heterogeneous parallel computing resources. We found that the workspace of \(T_\mathrm{mul}(M_k)\) is independent from that of \(T_\mathrm{add}(M_{k+l, l > 0})\). Furthermore, getting back the \(T_\mathrm{mul}(M_k)\) result from the device to the host memory can be overlapped with transferring two temporal matrices for \(T_\mathrm{mul}(M_{k+l, l > 0})\) from the host to the device memory. Based on these observations, we overlap computations of the CPUs and the GPU and data communication as much as possible. As a result, the computation time of the GPU hides most of the CPU processing time. Figure 2 is an example time-line, and it shows overlaps among the computations of CPU and GPU and the data communication.

4.2 Block-based work decomposition

When the input matrices are too large to process using the heterogeneous parallel Strassen algorithm (e.g., \(\frac{3}{4}N^2 \times 4~(or~8)~bytes > device~memory~size\)), we adapt a divide-and-conquer strategy. To do that, we first divide the matrices by a unit of block. Each block is a sub-matrix of an input or output matrix, and we use (\(2~\times \) cutoff-size) as the length and height of a block. Then, we can represent the input and out matrices as follows,

$$\begin{aligned} \begin{aligned} \begin{bmatrix} A_{11} &{} \dots &{} A_{1p}\\ \vdots &{} \ddots &{} \vdots \\ A_{n1} &{} \dots &{} A_{np} \end{bmatrix} \times \begin{bmatrix} B_{11} &{} \dots &{} B_{1m}\\ \vdots &{} \ddots &{} \vdots \\ B_{p1} &{} \dots &{}B_{pm} \end{bmatrix} = \begin{bmatrix} C_{11} &{} \dots &{} C_{1m}\\ \vdots &{} \ddots &{} \vdots \\ C_{n1} &{} \dots &{} C_{nm} \end{bmatrix}, \end{aligned} \end{aligned}$$
(5)

where

$$\begin{aligned} C_{ij} = \displaystyle \sum _{k=1}^{p} A_{ik}B_{kj}. \end{aligned}$$
(6)

Now, our problem is reduced to a set of \(T(C_{ij})\)s in Eq. (6). The master worker distributes them to slave workers evenly, and each slave worker treats the given \(T(C_{ij})\)s with our heterogeneous parallel Strassen algorithm. The only change from the algorithm in Sect. 4.1 is that a \(T(C_{ij})\) includes p multiplication tasks (i.e., \(T(A_{ik}B_{kj})\)) instead of two. Finally, Algorithm 1 summarizes the detailed workflow of our heterogeneous parallel Strassen algorithm.

figure a

With our block-based decomposition method, we can handle any large-scale matrices with \(O(\frac{3}{4}(|block|)^2)\) device memory space. In our experiments, 8192–16,384 is a generally good choice for the block size, and this requires only 192–768 MB for matrices with single-precision floating-point numbers (0.38–1.5 GB for double-precision). Please note that recent entry-level GPUs also have more than 2 GB device memory, and our method efficiently utilizes such GPUs for matrix multiplication.

4.3 Maximizing parallelism with streams

Although we overlap computations and data communications as much as possible in our heterogeneous parallel Strassen algorithm, there is still idle time on both the CPUs and the GPU since it processes \(T(M_k)\) sequentially from \(M_1\) to \(M_7\). To minimize idle time and improve the performance even more, we employ multiple slave workers with multiple streams. A stream is a kind of work queue for utilizing a GPU, and operations (e.g., kernel launch or data transfer) in different streams can be launched simultaneously on a GPU [21].

Disjoint property among \(T(C_{ij})s\) To compute \(C_{ij}\), we access the sub-matrices of A and B. Then, we write the results to the sub-region of C. Read operations do not change the data, and there is no problem even if multiple threads read the same region on a matrix. Although write operations modify the data, accessing regions on C for writing the results of each \(T(C_{ij})\) are totally independent. Therefore, the workspace among \(T(C_{ij})s\) are disjoint, and we can process them asynchronously.

Based on this disjoint property, multiple slave workers process \(T(C_{ij})\)s in parallel. Each slave worker runs independently on its dedicated threads. To process \(T(C_{ij})\)s in parallel, each slave worker has a private workspace on both the host memory and the device memory for processing \(T(M_k)\) (e.g., space for \(A_\mathrm{tmp}\), \(B_\mathrm{tmp}\), and \(M_{k}\)). Consequently, the required device memory space is \(O(\frac{3}{4}|block|^2) \times (\#~of~slave~workers)\). Each slave worker also has a dedicated stream to a GPU and puts in requests for processing \(T_\mathrm{mul}(M_k)\) through the stream. The GPU fetches a request from one of the streams when it has room to launch another kernel. Depending on the capability of the GPU, one request from a stream or \(n~(>1)\) requests from multiple streams can be processed simultaneously [21]. With multiple slave workers and a dedicated stream for each worker, we can utilize the computing resources more intensively, and it boosts the performance of our HPMaX framework.

Maximizing parallelism for a small matrix When the matrix size was smaller than (2 \(\times \) cutoff-size), we had only one \(T(C_{ij})\) (i.e., \( T(C_{11}) = T(C)\)). In this case, the master worker distributes \(T(M_k)\)s in \(T(C_{11})\) to slave workers instead of \(T(C_{ij})\)s. Each slave worker handles the given \(T(M_k)\)s with the heterogeneous parallel Strassen algorithm in Sect. 4.1 while using its own stream. Because the workspaces among \(T(M_k)\) are also disjoint, we could process them in parallel. Each slave worker returns \(M_k\) through \(Q_\mathrm{out}\), the master worker collects and make the final result C depending on Eq. (4).

4.4 Multi-GPU extention

When multiple GPUs are available, we can simply extend our HPMaX framework to utilized them simultaneously. Based on disjoint properties among \(T(C_{ij})\)s, slave workers can work with different GPU each other. Therefore, we can utilize multiple GPUs by mapping slave workers to available GPUs, which means making streams between them. More specifically, we map the same number of slave workers to available GPUs. Also, we select the number of slave workers according to the following criterion. We use two slave workers for each GPU if there are only four or fewer blocks, which means that the matrix size is equal or less than (2 \(\times \) cutoff-size). Otherwise, we employ four slave workers per GPU while halving the number of threads for each slave worker. This criterion bases on two underline observations. At first, although we can generate more than four blocks by decreasing the cutoff-size for small size matrices, such a small block is not enough to fully exploit the computing power of a GPU and makes the communication overhead increase too. Second, using more workers (streams) to a GPU leads to more overlapping between computation and communication. Therefore, when the matrix size is large enough to meet the required block size to utilize GPUs efficiently, using four slave workers achieved higher performance (e.g., up to 19%) than two slave workers per GPU, even though the number of threads per worker decreases.

5 Results and analysis

figure b

We implemented our HPMaX framework in five different heterogeneous systems consisting of two octa-core CPUs and one or two GPU(s) (Table 2). We used OpenMP [8] to implement the master and slave workers, including the parallel processing module for \(T_\mathrm{add}(M_k)\) on multi-core CPUs. Since the master and slaves act synchronously, we implemented it as a simple structure like Algorithm 2. Also, we implemented the matrix multiplication kernel for \(T_\mathrm{mul}(M_k)\) on GPU by using CUDA runtime API and CUBLAS 9.0 library. Generally, we used four slave workers for each GPU, and each of them had a dedicated stream to a GPU. The data communication between a slave worker and a GPU is performed through the dedicated stream, and we handled it explicitly with CUDA runtime APIs, including cudaMalloc(), cudaMallocHost(), and cudaMemcpyAsync(). For single-precision, we used 4096, 8192, and 16,384 as the cutoff-size for GTX 1060 (Machine 1), RTX 2080 (Machine 2&3), and RTX Titan (Machine 4&5), respectively. They requires 192 MB, 768 MB, and 3 GB device memory per stream, respectively. Because each stream requires independent memory space, Machine 1, Machine 2&3, and Machine 4&5 use 768 MB, 3 GB, and 12 GB device memory space, respectively. Please note that we have two GPUs for Machine 3 and 5, and each GPU on the machines uses 3 GB and 12 GB device memory, respectively. For double-precision, we used 8192 as the cutoff-size for RTX Titan (Machine 4&5) since it exceeds the device memory size when the cutoff-size is 16,384. For other GPUs, we use the same cutoff-size with the single-precision case. Therefore, the required device memory sizes are 1.5 GB for Machine 1 and 6 GB for others. To fully utilize the computing power of the multi-core CPUs, we generally made the \(T_\mathrm{add}(M_k)\) module utilize (\(p/(4*g)\)) threads on each slave worker, where p (e.g., 16 in our experiments) is the number of physical cores in the systems and g is the number of GPUs. As we describe in Sect. 4.4, we used two slaver workers per GPU for matrices whose size is equal or smaller than (2 \(\times \) cutoff-size), and each slaver worker utilizes (\(p/(2*g)\)) threads.

Table 2 Configurations of the five heterogeneous computing systems used in our experiments
Full size table

To check the efficiency and robustness of our heterogeneous parallel algorithm, we also implemented four alternative methods:

  • \({{ CPU}}_{{ classic}}\) is a parallel version of the classical \(O(N^3)\) matrix multiplication method. In this method, it divides the region of the output matrix evenly depending on the number of threads and distributes them to each thread. It utilizes p threads (i.e., CPU cores).

  • CUBLAS-Ext (\({{ GPU}}_{{ classic}}\)) is an extended version of the CUBLAS library [20]. When the matrix is small enough to process in the device memory at once, it uses CUBLAS directly. If the matrix is larger than the capability of the device memory or there are multiple GPUs, it divides them with our block-based work distribution method. However, different from our method, it performs \(A_{ik}B_{kj}\) in Eq. (6) by CUBLAS while adding the results to \(C_{ij}\) in the GPU too. Because this requires four times larger memory space, we used a single stream per GPU for this method.

  • \({ CPU}_{{ strassen}}\) is an implementation of a CPU-based Strassen algorithm that processes both \(T_\mathrm{add}(M_k)\) and \(T_\mathrm{mul}(M_k)\) on the multi-core CPUs.

  • \(GPU_\mathrm{strassen}\) is an extended implementation of Yugopuspito et al. [34]. In this method, the basic work-flow is similar to our method, and it uses multiple streams. However, it performs all the computations on the GPU(s). Instead of sending two temporal matrices (i.e., \(A_\mathrm{tmp}\) and \(B_\mathrm{tmp}\)), it sends four (or three) sub-matrices for computing \(M_k\) (Eq. (3)) and performs both \(T_\mathrm{add}(M_k)\) and \(T_\mathrm{mul}(M_k)\) on the GPU(s). When the matrix is small enough (e.g., 8192  \(\times \)  8192) to handle it in the device memory, it sends all the input matrices to the device memory. And, it performs one-level Strassen’s matrix multiplication without any communication with the host.

CUBLAS-Ext with multiple streams We also implemented another version of CUBLAS-Ext that used four streams while halving the block size to hide the data transfer time. However, it showed performance lower or similar to that with the single-stream version of CUBLAS-Ext. We found that the multiple stream version incurred more data transactions, which led to higher data transfer overhead. We also found that the CUBLAS library shows better performance with larger blocks, from the perspective of the elements per time for matrix multiplication.

Optimization for sub-matrix transfer on CUBLAS-Ext and \({ GPU}_{{ strassen}}\) Because the memory layout of a sub-matrix (e.g., \(A_{ik}\) or \(B_{kj}\)) is not continuous, special care is required to send the sub-matrices to the GPU efficiently. We tested three versions of sub-matrix transfer methods. (1) The first method was a row-by-row transfer. We found that this method required a large number of API calls (i.e., the number of rows), and each of them had a specific amount of calling cost. Therefore, it became a bottleneck for sending the sub-matrices. (2) As the second approach, we employed a special memory copy API in CUDA, cudaMemcpy2D(), designed to transfer a sub-matrix by an API call. It showed much better performance (e.g., 3–7 times higher) than the manual row-by-row transfer. (3) The final one was making a copy of the sub-matrix in the host memory so that it has a fully continuous memory layout and then sending it by one data transfer API. Although this approach requires an additional copy step in the host memory, it showed up to two times faster performance compared with using the cudaMemcpy2D(). Therefore, we used the third method when we measured the performance of CUBLAS-Ext and \({{ GPU}}_{{ strassen}}\).

Benchmarks To measure the performance of different methods, we generated a set of matrices having different sizes and densities. We randomly generated floating-point numbers for each element of the matrices in single- and double-precision. The size of the input matrices varied from 8192  \(\times \)  8192 to 131,072  \(\times \)  131,072, and we also differentiate the ratio of zeros (e.g., 10%, 40%, and 70%) for each matrix size. Since we found that the ratio of zeros had little effect on the processing time, we focused on the size of the matrix for performance analysis. As the input matrices, we used eight different combinations of those matrices, including non-square matrices.Footnote 1 For each combination, we ran test ten times, then average the results for comparison and analysis.

Table 3 This table shows the matrix multiplication time (seconds) of five different algorithms on five machine configurations
Full size table

5.1 Results

Table 3 shows the processing time of five different algorithms, including ours, on five machine configurations (Table 2) for eight different matrix sizes. For the CPU-based algorithms, \(CPU_\mathrm{strassen}\) took less processing time about 15% for single-precision and 16% for double-precision on average independent of the matrix size, respectively. This result validates the benefit of Strassen’s method from the perspective of computational cost. However, both CPU algorithms showed a considerable gap in performance (e.g., up to about a thousand times) with other methods that use a GPU.

Fig. 3
figure 3

These graphs show the processing time of three different algorithms on the five machine configurations for eight different combinations of matrices, in single- and double-precision. The matrix sizes are marked as \(n \times k \times m\) where sizes of the matrices A, B, and C are \(n \times k\), \(k \times m\), and \(n \times m\), respectively (\(AB = C\))

Full size image

Single-precision matrix multiplication Figure 3a compares the performance of two GPU-based methods and our heterogeneous parallel algorithm on single-precision matrix multiplication. For matrices small enough to handle in an in-core manner with a GPU (e.g., up to 8192  \(\times \)  8192 for Machine 1, 16,384 \(\times \) 16,384 for Machine 2, and 32,768 \(\times \) 32,768 for Machine 4), \(GPU_\mathrm{strassen}\) showed about 25% (on average) higher performance than CUBLAS-Ext. On the other hand, CUBLAS-Ext showed about 14% (on average) higher performance on average for large matrices processed in an out-of-core manner. This is because, although \(GPU_\mathrm{strassen}\) has low asymptotic complexity, it requires additional data communication to compute \(T_\mathrm{add}(M_k)\).

Our HPMaX generally showed better performance than the other two GPU-based algorithms. On Machine 1, 2, and 4, our method achieved up to 1.61, 1.76, and 1.97 times (1.39, 1.55, and 1.53 times on average) higher performance than CUBLAS-Ext. Our method has less computational cost than CUBLAS-Ext since it bases on Strassen’s method, and it utilizes both multi-core CPUs and a GPU, distinct from other GPU-based methods. Moreover, our method requires less data transfer between host and device memories (different from \(GPU_\mathrm{strassen}\)) while efficiently hiding the communication overhead with multiple streams. As a result, we achieved such impressive performance, and these results demonstrate the benefit of our approach.

Interestingly, our method using a low-performance GPU (GTX 1060, 3GB) achieved comparable performance with that of CUBLAS-Ext using a high-performance GPU (RTX 2080, 8GB) for relatively small matrices (e.g., up to 16,384 \(\times \) 16,384). Also, our method on Machine 2 having an RTX 2080 generally showed similar or rather higher performance compared with CUBLAS-Ext on Machine 4 having the high-end GPU (Titan RTX, 24GB). We found that the scalability for a high-performance GPU is relatively low for small matrices compared with large matrices. On the other hand, the contribution of multi-core CPUs is stable, independent of the problem size. Therefore, we were able to get such interesting results, and it demonstrates the robustness of our heterogeneous parallel computing approach.

Double-precision matrix multiplication Figure 3b shows the processing time of three different GPU-based algorithms on double-precision matrix multiplication. Similar to the single-precision case, our HPMaX generally shows higher performance than the other two GPU-based methods. Compared with CUBLAS-Ext, our method achieved up to 1.18, 1.24, and 1.24 times (1.13, 1.17, and 1.19 times on average) higher performance on Machine 1, 2, and 4, respectively.

On the other hand, different from the single-precision case, \(GPU_\mathrm{strassen}\) showed up to 1.27 times (1.12 times on average) higher performance than CUBLAS-Ext and achieved a compatible performance with HPMaX. We found that \(T_\mathrm{mul}(M_k)\) has an overwhelming workload than \(T_\mathrm{add}(M_k)\) and data communication time in double-precision matrix multiplication. Therefore, \(T_\mathrm{add}(M_k)\) computation and data communication overhead affect just a little to the entire performance. Also, the processing time of \(T_\mathrm{mul}(M_k)\)s hides most of the data communication overhead. Please see Sect. 5.2 for the detailed analysis. Nonetheless, HPMaX showed up to 10% (5% on average) higher performance than \(GPU_\mathrm{strassen}\), and this validates the robustness of our approach.

Using multiple GPUs To check the scalability of our HPMaX framework, we added one more identical GPU to Machine 2 and 4, then set Machine 3 and 5. With the additional GPU, all the GPU-based algorithms achieve almost two times of performance improvement (Fig. 3a, b). However, for small size (e.g., less than 16,384  \(\times \)  16,384) and single-precision matrices, they got performance improvement lower than two times since the workload is not enough to utilize two GPUs fully. Independent of the matrix size and precision, HPMaX generally showed the best performance among three GPU-based algorithms, like up to 1.35 and 1.23 times (1.22 and 1.15 times on average) higher performance than CUBLAS-Ext in the single and double precision cases, respectively. These results demonstrate the high scalability of our HPMaX framework for additional GPUs.

5.2 Performance analysis

To check the benefit of employing multi-core CPUs over \(GPU_\mathrm{Strassen}\), we measured the processing times for \(T_\mathrm{add}(M_k)\) and \(T_\mathrm{mul}(M_k)\), and data transfer times, using \(GPU_\mathrm{Strassen}\) and our HPMaX framework. For this profiling, we used the 65,536  \(\times \)  65,536 matrix and Machine 4. Also, we ran each task one-by-one synchronously to check the workload of each of them. Figure 4 are the stacked column charts that show the total time consumed for processing each task type. Since \(GPU_\mathrm{Strassen}\) performs \(T_\mathrm{add}(M_k)\) on the GPU, it has to get sub-matrices for \(T_\mathrm{add}(M_k)\) from the host memory and requires much more data communication between host and device memories. As mentioned in the paragraph of optimization for sub-matrix transfer, this process also includes generating a copy of the sub-matrix in the host memory (the gray region in Fig. 4) to minimize the communication overhead. On the other hand, HPMaX performs \(T_\mathrm{add}(M_k)\) on the CPUs, and only sends two temporal matrices for \(T_\mathrm{mul}(M_k)\) to the device memory. Therefore, HPMaX had much less communication overhead and took less time overall than \(GPU_\mathrm{Strassen}\) even though processing \(T_\mathrm{add}(M_k)\) is much faster on the GPU than on the multi-core CPUs.

As shown in Table 3, our method took 35.93 s for the 65,536  \(\times \)  65,536 single-precision matrix, while the summation of times for all tasks was 64.33 s (Fig. 4a). This means that our HPMaX framework made about half of the whole process overlap. For double-precision (Fig. 4b), the summation time is 1036.50 s, while our method took 916.02 s. Although there is less overlap than the single-precision case due to the dominant portion of \(T_\mathrm{mul}(M_k)\), we found that 13% of the whole process overlaps in the double-precision case too. These results demonstrate that our approach takes advantage of the concurrent execution ability of the heterogeneous computing systems well.

Fig. 4
figure 4

These figures show the total processing time for each task type and data communication time on \(GPU_\mathrm{Strassen}\) and our method. For this analysis, we used Machine 4 and 65,536  \(\times \)  65,536 matrices in single- and double-precision

Full size image

5.3 The number of CPU threads

To check the benefit of using additional CPU cores, we measured the processing time of our method with different numbers of CPU threads. We varied the number of threads from four to sixteen because we used four streams, and our systems have two octa-core CPUs. As shown in Table 4, it generally took less time when using more CPU threads. One interesting observation is that the effect of employing more threads dropped considerably after a specific point (e.g., after eight threads). We found that the workloads of the CPUs (i.e., \(T_\mathrm{add}(M_k)\)) and the GPU (i.e., \(T_\mathrm{mul}(M_k)\)) for the overlapping region almost match at that point. From this point, the processing time of CPUs becomes shorter than the processing time of the GPU. It means that the processing time of the GPU determines the total running time, and that contribution of the additional CPU threads becomes invisible. Nonetheless, more CPU threads achieved better performance since they reduced processing time for the non-overlapping region such as \(T_\mathrm{add}(M_1)\) and for the result collecting process. In the double-precision case, it also shows a similar trend with the single-precision case. However, the effect of using more threads is less noticeable because the workload on the \(T_\mathrm{mul}(M_k)\) is dominant. We found that using sixteen threads improves the performance of double-precision matrix multiplication by up to 3% (1% on average) compared with using four threads.

Table 4 This table shows the single-precision matrix multiplication time (in seconds) of HPMaX with different numbers of CPU threads
Full size table

5.4 Cutoff-size and the number of streams

Since each stream requires an independent workspace in the device memory, the maximum cutoff-size is decreased as the number of streams (or # of slave workers) increased. Table 5 shows the matrix multiplication time when using different combinations of the number of streams and cutoff-sizes. Generally, using multiple streams achieved better performance than using single-stream since more than one stream is needed to exploit the concurrent execution ability of heterogeneous computing systems. However, more streams did not always guarantee better performance. This is because the smaller cutoff-size leads to more data communication between the host and device memories even though this could increase the concurrency with more streams. We found that the combination of four streams and the associated largest cutoff-size generally showed a good performance while using less memory space than other configurations showing comparable performance. This conclusion is consistent with the observation of Sunitha et al. that four-way concurrency is the best in most cases [32].

Table 5 This table shows the processing time and device memory usage with the different configurations for the number of streams and cutoff-sizes
Full size table

6 Conclusions

We presented a novel heterogeneous parallel matrix multiplication (HPMaX) framework that efficiently handles a large matrix by utilizing both multi-core CPUs and GPUs. Based on Strassen’s method and our block-based work decomposition, we represented the work of matrix multiplication for a large matrix as a set of matrix addition and multiplication tasks among its sub-matrices. Then, depending on the characteristics of each task type and computing resources, our method processes them by allocating the addition tasks to CPUs and multiplication tasks to GPUs. Moreover, our HPMaX framework exploits the concurrent execution ability of heterogeneous computing systems for further performance improvement. We implemented our method on five different heterogeneous systems and applied it to various sizes of matrices. Overall, our method achieved higher performance than prior GPU-based approaches, including CUBLAS, which is the state-of-the-art GPU matrix multiplication library. More interestingly, our HPMaX using a lower-performance GPU and multi-core CPUs achieved performance comparable with that of CUBLAS using a higher-performance GPU. Also, our HPMaX framework showed better performance continually when employing more computing resources like CPU cores and GPUs. These results validate the advantages of our approach.

6.1 Limitations and future work

We achieved impressive performance gains by employing multi-core CPUs compared with GPU-only methods. However, after a specific point, the benefit of employing more CPU cores is less noticeable due to the workload imbalance between CPUs and GPUs (Sect. 5.3). Such workload balancing problems should become more critical in a system having higher heterogeneity, such as a workstation having multiple different GPUs. In this direction, we have a plan to design a scheduling algorithm that finds optimal work distribution achieving the best performance for an arbitrary combination of computing resources. Based on the scheduling algorithm, we would like to extend our framework so that it is generally applicable to various types of heterogeneous parallel computing environments. At second, we targeted large-scale matrices, and we designed it to handle matrices smaller than the cutoff-size with the classical method on a GPU. As future work, we would like to improve our HPMaX frame to utilize heterogeneous computing resources for small matrices too. Finally, we would like to apply our HPMaX framework to various applications like machine learning and computer-generated holography.