Dynamic behaviour of competing memes’ spread with alert influence in multiplex social-networks

Abstract

This study elucidates the dynamic behaviour of the two competing mutually exclusive epidemic (meme) spreading model with the alert of memes over multiplex social networks. Each meme spreads over a distinct contact networks $(CN_1,CN_2)$ of an undirected multiplex social network. The behavioural responses of agents (alerts) to the spread of competing memes is disseminated through information dissemination network (IDN). Here, IDN has the same nodes but different links with respect to the respective $CN_i(i=1,2)$. The analytical treatment of this model is analysed through the mean field approximation of the epidemic process. Also, it has been shown through numerical illustrations that a node in the alert state is less probable to become infected than a node in the susceptible state. Moreover, co-existence of both the memes, the survival threshold, the absolute dominance threshold of the two competitive memes and the alert threshold for minimizing the severity of meme spread are analytically explored and numerically illustrated.

1 Introduction

Myriad research efforts in capturing the dynamics of epidemic spreading process of diseases (or ideas, computer viruses, product adoption) and in controlling the outbreak of the epidemic spreading have attracted the biologists, social scientists and communication engineers in the recent years. These overwhelming research efforts have led to develop and study the dynamic behaviour of the various epidemic models. These models have been successful in providing insights and in understanding the phenomenon of epidemic process which leads to the successful conclusion of both the prevention and prediction of epidemics. With the advent of the network science, complex epidemic models were analysed to capture the dynamics of epidemic spread through real networks.

The theory of epidemics over a network can be applied to the spread of email worms (ex. News, rumors, meme, brand awareness and marketing new products), epidemic dissemination or/and routing occurring in ad-hoc and peer to peer networks. However, most of the earlier works in epidemic models with regard to the contact patterns among the individuals within a population were suitable for a well mixed homogeneous population rather than the heterogeneous population. In particular, Moreno et al. [1] have presented the results for heterogeneous networks. Pastor et al. [2] studied the epidemic spread in scale free networks, showing that in these networks, the epidemic threshold disappears with consequent concerns for the robustness of many real complex systems. Moreover, node based epidemic models were analysed by Wang et al. [3] and Ganesh et al. [4]. Further, Deepayan et al. [5] proposed the general epidemic threshold condition for the non-linear dynamical system which proved that the epidemic threshold for a network is exactly the inverse of the largest eigenvalue of its adjacency matrix. Later, Van Mieghem et al. [6] proved that the epidemic threshold $\tau _c$ is equal to the inverse of the spectral radius of the adjacency matrix of a contact graph. However, Poletti et al. [7] developed a population based model where susceptible nodes could choose between the two behaviour responses to the presence of infection. In [8], they proved that the size of epidemic outbreak reduced when individuals had the awareness of the disease. Faryad et al. [10] discussed the epidemic threshold in the case of spontaneous behavioural responses, and assessed the capability of the human behavioural responses to influence the epidemic spreading in networks. Later, Faryad et al. [9] extended the SIS model to SAIS model, which incorporates the reaction agents to spread the infection. Based on this model, they studied how dissemination of information can help to strengthen the resilience of the population of agents against the propagation. Furthermore, the problem of finding the cost-optimal distribution of resources throughout the nodes of the network was studied by Preciado et al. [11]. Afterwards, Nowzari et al. [12] proposed a generalized epidemic model over arbitrary directed graphs with heterogeneous nodes and also derived the necessary and sufficient conditions for global exponential stability. Recently, Watkins et al. [13] have developed a robust economic model predictive controller for the containment of stochastic continuous time SEIV epidemic processes which had driven the process quickly to extinction, while minimizing the rate at which control resources were used. Moreover, it addressed the problem of efficiently controlling the general stochastic epidemic systems without relying on the mean-field approximation, which is an important issue in the theory of stochastic epidemic processes.

In the competitive memes spreading scenario, highly challenging efforts are taken to study the dynamic behaviour of the distinct memes spreading over the network layers. Funk and Jansen [14] extended the bond percolation analysis of the two competitive viruses in the case of the two layer network and investigated the effects of overlapping layers. Granell [15] investigated a two layer network where one layer helps in spreading the disease of physical contact network and the other propagating the information to stop the disease of a virtual overlay network. They identified a meta critical point for the epidemic onset leading to disease suppression. Moreover, the value of the critical point depended on the awareness of the dynamics and the overlay of the network structure. Wei et al. [16] studied the SIS spreading of two competitive viruses on an arbitrary two layer network, deriving sufficient conditions for exponential die out for both the viruses. They also introduced a statistical tool Eigen Predict, to predict the viral dominance of one competitive virus over the other. Shouhuai et al. [17] analyzed a general model of multivirus spreading dynamics in arbitrary networks and also discussed the analytical results that made a fundamental connection between the defence capability and the network connectivity. On the other hand, Weng et al. [18] proposed the competition among the memes with limited attention of agent based social network model. Further,the epidemic model of two exclusive, competitive viruses over a two-layer network with generic structure and also proved the long term coexistence of the two competitive viruses in non-trivial multilayer networks which was extended by Faryad et al. [19]. Liu et al. [20] analysed a distributed continuous-time bi-virus model for a system of groups of individuals. Additionally, they have explored the equilibria of a continuous-time bi-virus model. Aresh et al. [21] derived analytically generic switching thresholds at which the extinction, co-existence, and absolute-dominance equilibria transpire in multiplex social network. Multiple competing viruses over static and dynamic graph structures, and an antidote control technique for stability analysis were discussed by Philip et al. [22]. Later, Liu et al. [23] examined the effect of human awareness on a distributed continuous-time bi-virus model and compared their stability with those of the model without human awareness. Recently, Watkins et al. [24] have developed an optimization program for determining the optimal-cost parameter distributions. Moreover, a heuristic design was performed in the case of a fixed budget $SI_1SI_2S$ spreading model of the two competing behaviours over a bilayer network.

All the above mentioned competing epidemic spreading models assume infection rates that are linear in the virus occupancy probabilities of the individuals in a population. As the linear infection rates are the overestimation of the real infection rates, in some situations these models cannot accurately predict the process of spreading of the multiple competing viruses. Yang et al. [25] proposed a continuous-time bilayer-network-based bi-virus competing spreading model with generic infection rates. Recently, Liu et al. [26] extended their work to limit the behaviour of the network characterized by analyzing the equilibria of the system and its stability of continuous-time bi-virus model in which two competing viruses spread over a network. Table 1 summarizes the consolidated view of the existing research works which inherently describes the models over specific network topology for spread of meme. Furthermore, this table shows how the proposed work differs from the other existing models in literature. The advancements in networking technologies require a robust analytic framework for modeling epidemic spreading process which has been recently addressed by many researchers in the field of communication networking. In order to model the on-line informative propagation for meme spreading through media (IDN) and contact networks (likeFacebook, Twitter, Whatsapp, etc.), the competitive meme spreading model over two CNs and IDN can be considered. Although, many epidemic models over social networks have been developed, the model of competing memes spread over contact and information dissemination networks have not been studied yet. Hence, the proposed work uses the competitive meme spread model over CNs and IDN. The following are the main contributions in this model: (i) The proof of long term co-existence of competitive meme spreading over two CNs and IDN. (ii) The mathematical framework of survival threshold shows the survival of $\hbox {meme}_k$ while the spreading severity of competing $\hbox {meme}_l$ is reduced. (iii) Analytical derivation for the alert threshold of $\hbox {meme}_k$, at which the spreading probability of the alert of $\hbox {meme}_k$ is increased and the spreading probability of alert of $\hbox {meme}_l$ is reduced.

Table 1 Summary of the models over specific network topology studied in recent literature

The rest of the paper is organised as follows: Sect. 2 describes the preliminary notions, presents the mathematical model of $SA_1I_1SA_2I_2S$, with steady state analysis and compares the mathematical model with SAIS model. Section 3 illustrates the numerical results. Finally, Sect. 4 discusses the concluding remarks of the proposed work and presents the scope for future enhancements.

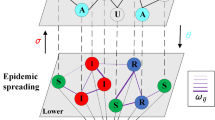
2 Alert influence behaviour of competitive spreading memes in multiplex social networks

This section develops a continuous time $SA_1I_1SA_2I_2S$ model for the two competitive memes propagating on the two contact networks with the alerts of memes propagation over information dissemination network.

2.1 Preliminaries

Consider a population having N individuals (nodes) in which two memes can spread through the different transmission routes on $CN_1$, $CN_2$ and the alert information about the memes through IDN. In these layers, the individuals are identical and the link of the nodes are distinct based on the connectivity of both the layers.

Mathematically, the multiplex network is represented as $G(V,E_{C_1},E_{C_2},E_I)$ where $V(= 1,2,\ldots ,N)$is the set of vertices, $E_{C_1}, E_{C_2}, E_I$ are the set of edges of $CN_1, CN_2$ and IDN layers respectively. Let us consider $A=(a_{ij})$ which represents the adjacency matrix

$$\begin{aligned} a_{ij} =\left\{ \begin{array}{ll} 1, &{}\quad (i,j)\in E_{C_1}, \\ 0, &{}\quad otherwise \end{array} \right. \end{aligned}$$

of $CN_1$ and $B=(b_{ij})$ which represents the adjacency matrix

$$\begin{aligned} b_{ij} =\left\{ \begin{array}{ll} 1, &{}\quad (i,j)\in E_{C_2}, \\ 0, &{}\quad otherwise \end{array} \right. \end{aligned}$$

of $CN_2$ whose nodes are undirected and connected. Similarly, $C=(c_{ij})$ which represents the adjacency matrix

$$\begin{aligned} c_{ij} =\left\{ \begin{array}{ll} 1, &{}\quad (i,j)\in E_I,\\ 0, &{}\quad otherwise \end{array} \right. \end{aligned}$$

of IDN, where the nodes are directed and not connected.

2.2 $SA_1I_1SA_2I_2S$ model for two competing meme

The $SA_1I_1SA_2I_2S$ model is an extension of the SAIS model of a single meme propagation to the competitive meme propagation scenario of CN and IDN layers. Initially, the proposed model considers all the N nodes that are in any one of the following states: S-susceptible, $I_1$-infected (infected by $\hbox {meme}_k$), $I_2$-infected (infected by $\hbox {meme}_l$), $A_1$-alert of $\hbox {meme}_k$ or $A_2$-alert of $\hbox {meme}_l$. For each individual $i \in {1,2,\ldots ,N}$, let us define a random variable $X_i(t)$ as state of ith node at time t. Here, $\{X_i(t), t\ge 0\}$ is CTMC representing $SA_1I_1SA_2I_2S$ model.

The following are the five states in the continuous time Markov process representing the $SA_1I_1SA_2I_2S$ model

$$\begin{aligned} X_i(t) =\left\{ \begin{array}{ll} 0, &{}\quad \text {node-i is susceptible},\\ 1, &{}\quad \text {node-i is infected by }meme_k,\\ 2, &{}\quad \text {node-i is infected by }meme_l,\\ 3, &{}\quad \text {node-i has alert of } meme_k,\\ 4, &{}\quad \text {node-i has alert of }meme_l \end{array} \right. \end{aligned}$$

Fig. 1

Transition rate diagram according to the $SA_1I_1SA_2I_2S$ model

Figure 1 depicts the transition diagram of the $SA_1I_1SA_2I_2S$ model

• (i) The transition diagram represents the curing time of the infected nodes that follow exponential distribution with curing rate $\delta _1$ for $\hbox {meme}_k$ and $\delta _2$ for $\hbox {meme}_l$.

• (ii) $\beta _1$ is the rate at which susceptible state S becomes $I_1$ infected with $\hbox {meme}_k$. Similarly, the transition from state S to $I_2$, happens with rate $\beta _2$ per link and has an influence of state $I_2$.

• (iii) Alerted nodes infected with rate $\beta _{a_1}$ at which the alert state $A_1$ becomes $I_1$ with $\hbox {meme}_k$. Similarly the transition from state $A_2$ to $I_2$, happens with infection rate $\beta _{a_2}$ per link. An alert individual for $\hbox {meme}_k$ and $\hbox {meme}_l$ is assumed to be the reduced version of $\beta _1$ and $\beta _2$ respectively. That is $r_1\beta _1$ and $r_2\beta _2$ with $0 <r_1\le 1$, $0<r_2\le 1$.

• (iv) The alert information about $\hbox {meme}_k$ spreads through $CN_1$ with rate $m_1$ and propagates through IDN with rate $\mu _1$. Similarly the alert about $\hbox {meme}_l$ spreads through $CN_2$ with rate $m_2$ and also through IDN with rate $\mu _2$.

  $$\begin{aligned}&Pr\left( X_i(t+\varDelta t)=1\mid X_i(t)=0\right) =\beta _1Y_i(t)\varDelta t+o(\varDelta t)\\&\qquad \qquad \text {for} \quad i\in \left\{ 1,2,\ldots ,N\right\} , Y_i(t)=\sum \limits _{j=1}^{N}a_{ji}1_{\left\{ X_j(t)=1\right\} } \\&Pr\left( X_i(t+\varDelta t)=2\mid X_i(t)=0\right) =\beta _2Q_i(t)\varDelta t+o(\varDelta t)\\&\qquad \qquad \text {for} \quad i\in \left\{ 1,2,\ldots ,N\right\} , Q_i(t)=\sum \limits _{j=1}^{N}b_{ji}1_{\left\{ X_j(t)=2\right\} } \\&Pr\left( X_i(t+\varDelta t)=1\mid X_i(t)=3\right) = \beta _{a_1}Y_i(t)\varDelta t+o(\varDelta t) \\&Pr\left( X_i(t+\varDelta t)=2\mid X_i(t)=4\right) = \beta _{a_2}Q_i(t)\varDelta t+o(\varDelta t) \\&Pr\left( X_i(t+\varDelta t)=3\mid X_i(t)=0\right) = (m_{1}Y_i(t)+\mu _1 Z_i(t))\varDelta t +\,o(\varDelta t),\\&\qquad \qquad \text {for} \quad i\in \left\{ 1,2,\ldots ,N\right\} , Z_i(t)=\sum \limits _{j=1}^{N}c_{ji}1_{\left\{ X_j(t)=3\right\} }\\&Pr\left( X_i(t+\varDelta t)=4\mid X_i(t)=0\right) = (m_2Q_i(t)+\mu _2 Z_i(t))\varDelta t +\, o(\varDelta t)\\&Pr(X_i(t+\varDelta t)=0\mid X_i(t)=1)=\delta _1\varDelta t+o(\varDelta t)\\&Pr(X_i(t+\varDelta t)=0\mid X_i(t)=2)=\delta _2\varDelta t+o(\varDelta t) \end{aligned}$$

The evolution of system is represented in the following differential equations. The state probabilities are defined as follows: $P_{ki}(t)=P_r(X_i(t)=k), k = 0,1,2,3,4$ for node i and also, $\sum \nolimits _{k=0}^{4}P_{ki}(t)=1$.

By theorem of total probability, the evolution of infection probability of $\hbox {meme}_k$ is determined.

$$\begin{aligned} Pr\left( X_i(t+\varDelta t)=1\right)= & {} \Pr \left( X_i(t+\varDelta t)=1\mid X_i(t)=0\right) Pr\left( X_i(t)=0\right) \\&\quad +\,Pr\left( X_i(t+\varDelta t)=1\mid X_i(t)=3\right) Pr\left( X_i(t)=3\right) \\&\quad +\,Pr\left( X_i(t+\varDelta t)=1\mid X_i(t)=1\right) Pr\left( X_i(t)=1\right) \end{aligned}$$

This implies that

$$\begin{aligned}&P_{1i}(t+\varDelta t)= \beta _1 Y_i(t)\varDelta t P_{0i}(t)+\beta _{a_1}Y_i(t)P_{3i}(t)\varDelta t+P_{1i}(t)(1-\delta _1 \varDelta t) \\&\frac{P_{1i}(t+\varDelta t)-P_{1i}(t)}{\varDelta t}=\beta _1 Y_i(t) P_{0i}(t)+\beta _{a_1}Y_i(t)P_{3i}(t)-P_{1i}(t)\delta _1 \ \ \ \ \ \ \ \ \ (I) \end{aligned}$$

Based on the mean field approximation [35], the dynamics of node-i infected by $\hbox {meme}_k$ is derived by taking limit $\varDelta t \rightarrow 0$ and expectation on both the sides in (I), we have

$$\begin{aligned} \frac{dI_i^1(t)}{dt}=\beta _1 S_i(t) \sum \limits _{j=1}^{N}a_{ji}I_j^1 +\beta _{a_1}\zeta _i^1(t)\sum \limits _{i=1}^{N}a_{ji}I_j^1-I_i^1(t)\delta _1 \end{aligned}$$

(1)

where $E(X_i(t)=0)=S_i(t)$, $E(X_i(t)=k)=I_i^k(t)(k=1,2),E(X_i(t)=3)=\zeta _i^1(t)$ and $E(X_i(t)=4)=\zeta _i^2(t)$.

Similarly, the following mean field approximations for the state of node-i infected by $\hbox {meme}_l$, node alerted for $\hbox {meme}_k$ and node-i alerted for $\hbox {meme}_l$ are obtained.

$$\begin{aligned} \dot{I}^2_i= & {} \beta _2\left( 1-I_i^1-I_i^2-\zeta _i^1-\zeta _i^2\right) \sum \limits _{j=1}^{N}b_{ji}I_j^2+ \beta _{a_2}\zeta _i^2\sum \limits _{j=1}^{N}b_{ji}I_j^2-\delta _2I_i^2 \end{aligned}$$

(2)

$$\begin{aligned} \dot{\zeta }^1_i= & {} \left( 1-I_i^1-I_i^2-\zeta _i^1-\zeta _i^2\right) \left( m_{1}\sum \limits _{j=1}^{N}a_{ji}I_j^1+\mu _1\sum \limits _{j=1}^{N}c_{ji}I_j^1\right) -\beta _{a_1}\zeta _i^1\sum \limits _{j=1}^{N}a_{ji}I_j^1\nonumber \\ \end{aligned}$$

(3)

$$\begin{aligned} \dot{\zeta }^2_i= & {} \left( 1-I_i^1-I_i^2-\zeta _i^1-\zeta _i^2\right) \left( m_2\sum \limits _{j=1}^{N}b_{ji}I_j^2+\mu _2\sum \limits _{j=1}^{N}c_{ji}I_j^2\right) -\beta _{a_2}\zeta _i^2\sum \limits _{j=1}^{N}b_{ji}I_j^2\nonumber \\ \end{aligned}$$

(4)

The competitive meme propagation model reveals that the dynamic behaviour is dependent on the epidemic parameter and the contact network layer structure. The effective infection rate of both the memes is defined as the ratio of the infection rate over the curing rate which measures the expected number of attempts of an infected node to infect its neighbors before recovery. In this model, if transmission of both the memes is without alert, then the model will be reduced to the $SI_1SI_2S$ model. Therefore, the system exhibits a threshold for the effective infection rate $\tau _1=\beta _1/\delta _1$ and $\tau _2=\beta _2/\delta _2$, under which the infection dies out exponentially and also the inverse of the largest eigenvalue of the adjacency matrix A and B are $\tau _1=1/\lambda _{1}(A)$, $\tau _2=1/\lambda _{1}(B)$ respectively.

2.3 Steady state analysis

In the proposed model, the healthy equilibrium establishes the exponential extinction of $\hbox {meme}_k$ and $\hbox {meme}_l$. Wei et al. [30] showed that an initial infection dies out exponentially, under the conditions $\tau _1<\frac{1}{\lambda _{1}(A)}$ and $\tau _2<\frac{1}{\lambda _{1}(B)}$. A meme with lower effective infection rate is very weak to spread in the population, even in the absence of any meme competition.

The competitive memes do not affect the no-spreading thresholds, $\tau _1^m=\frac{1}{\lambda _{1}(A)}$ and $\tau _2^m=\frac{1}{\lambda _{1}(B)}$ for meme k and l respectively. If any one of these meme’s effective infective rate is less than no spreading threshold, then the competitive scenario reduces to a single meme problem.

In $SA_1I_1SA_2I_2S$ model, Eqs. (1–4) yield the following equilibrium equations

$$\begin{aligned}&\frac{\bar{I}_i^1}{1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2}\nonumber \\&\quad =\frac{\tau _1\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\tau _{a_1}\left( \bar{m}_{1}\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1 \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) }{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1} \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1 \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\bar{I}_i^2}{1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1}\nonumber \\&\quad =\frac{\tau _2\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\tau _{a_2}\left( \bar{m}_2\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\bar{\mu }_2\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2\right) }{(1+\bar{m}_2)\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\bar{\mu }_2\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2}\sum \limits _{j=1}^{N}b_{ji}\bar{I}_j^2 \end{aligned}$$

(6)

$$\begin{aligned}&\bar{\zeta }_i^1=\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2 \right) \frac{\bar{m}_1\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1}{(1+\bar{m_1})\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1} \end{aligned}$$

(7)

$$\begin{aligned}&\bar{\zeta }_i^2=\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1 \right) \frac{\bar{m}_2\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\bar{\mu }_2\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2}{(1+\bar{m_2})\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\bar{\mu _2}\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2} \end{aligned}$$

(8)

where $\bar{I}_i^1$, $\bar{I}_i^2$ are equilibrium infectious probabilities and $\bar{\zeta }_i^1$, $\bar{\zeta }_i^2$ are steady state probabilities of ith node being alerted for $\hbox {meme}_k$ and $\hbox {meme}_l$. The normalized alertness rates are $\tau _{a_1}=r_1\tau _1 (0<r_1\le 1)$; $\tau _{a_2}=r_2\tau _2 (0<r_2\le 1)$; $\bar{m}_1=m_1/\beta _{a_1}$; $\bar{m}_2=m_2/\beta _{a_2}$; $\bar{\mu }_1=\mu _1/\beta _{a_1}$ and $\bar{\mu }_2=\mu _2/\beta _{a_2}$. Equations (5) and (6) can be rewritten as

$$\begin{aligned} \frac{\bar{I}_i^1}{1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2} = \tau _1 Q_i\sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1 \end{aligned}$$

(9)

where $Q_i=\frac{(1+r_1\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+r_1\bar{\mu }_1 \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1}{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1 \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1}$

and

$$\begin{aligned} \frac{\bar{I}_i^2}{1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1} = \tau _2 R_i\sum \limits _{j=1}^{N}b_{ji}\bar{I}_j^2 \end{aligned}$$

(10)

where $R_i=\frac{(1+r_2\bar{m}_2)\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+r_2\bar{\mu }_2 \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2}{(1+\bar{m}_2)\sum \nolimits _{j=1}^{N}b_{ji}\bar{I}_j^2+\bar{\mu }_2 \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^2}$.

Next the discussion is about the equilibrium of the analysis for the case of disease free, the absolute dominance for $\hbox {meme}_k$ and also for $\hbox {meme}_l$.

Case (i): In disease free equilibrium, all the individuals are healthy and so the infection probability does not exist for both the memes.

Case (ii): In case of the absolute dominance of $\hbox {meme}_k$ (nodes are only infected by $\hbox {meme}_k$), $\bar{I}_i^1=u_i$, $\bar{I}_i^2=0$ and $\bar{\zeta }_i^2=0$, $i=1,2,\ldots ,N$. The equilibrium equation (9) becomes

$$\begin{aligned} \frac{u_i}{1-u_i}=\tau _1Q_i\sum \limits _{j=1}^{N}a_{ji}u_j \end{aligned}$$

(11)

where $u_i$ is the steady state infection probability of $\hbox {meme}_k$ satisfying (11) [33].

Case (iii): Absolute dominance of $\hbox {meme}_l$ (nodes are only infected by $\hbox {meme}_l$), $\bar{I}_i^1=0$, $\bar{I}_i^2=v_i$ and $\bar{\zeta }_i^1=0$, $i=1,2,\ldots ,N$. The equilibrium equation (10) becomes

$$\begin{aligned} \frac{v_i}{1-v_i}=\tau _2R_i\sum \limits _{j=1}^{N}b_{ji}v_j \end{aligned}$$

(12)

where $v_i$ is the steady state infection probability of $\hbox {meme}_l$ satisfying (12). From [19], the survival and absolute dominant threshold are defined as follows:

Definition 1

Given $\hbox {meme}_l$ effective infection rate $\tau _2>1/\lambda _{1}(B)$, the survival threshold $\tau _{1s}$ is the critical point such that $\hbox {meme}_k$ steady-state infection probability of each node is zero for $\tau _1<\tau _{1s}$ and is positive for $\tau _1>\tau _{1s}$. i.e.,

$$\begin{aligned} \bar{I}_i^1=0, \ \ \ \text {for}\ \ \tau _1<\tau _{1s}\\ \bar{I}_i^1>0, \ \ \ \text {for}\ \ \tau _1>\tau _{1s} \end{aligned}$$

for all $i\in \{1,\ldots ,N\}$.

Definition 2

Given $\hbox {meme}_l$ effective infection rare $\tau _2>1/\lambda _{1}(B)$, the absolute dominance threshold $\tau _1$ is the critical point such that not only $\hbox {meme}_k$ survives but also it removes the other meme. In other words, $\hbox {meme}_l$ steady-state infection probability of each node becomes zero for $\tau _1>\tau _{1}^{*}$; i.e.,

$$\begin{aligned} \bar{I}_i^2>0, \ \ \ \text {for} \ \ \tau _1<\tau _1^*\\ \bar{I}_i^2=0, \ \ \ \text {for}\ \ \tau _1>\tau _1^* \end{aligned}$$

for all $i\in \{1,\ldots ,N\}$.

The mean field stability analysis of the proposed model is discussed in the following theorem.

Theorem 1

Let $\bar{I}=(\bar{I}^1,\bar{I}^2)^T$ be the equilibrium vector of mean field dynamics of $meme_k$ and $meme_l$. Here, let $\bar{I}^j=(\bar{I}_1^j,\bar{I}_2^j,\ldots , \bar{I}_N^j)^T$, $j=1,2$; $\bar{\zeta }^1=(\bar{\zeta }_1^1, \bar{\zeta }_2^1, \ldots , \bar{\zeta }_N^1)^T$ and $\bar{\zeta }^2=(\bar{\zeta }_1^2, \bar{\zeta }_2^2,\ldots ,$$\bar{\zeta }_N^2)^T$. Assuming $\bar{I}_i^1=0$, for all i, $\bar{I}_i^2$ is (locally) exponentially stable iff $J_{11}$ is Hurwitz,

$$\begin{aligned} J_{11}=\beta _1 diag((1-\bar{I^2}-\bar{\zeta ^1}-\bar{\zeta ^2})A)+\beta _{a_1} diag(\bar{\zeta ^1}A)-\delta _1I, \end{aligned}$$

$\delta _1$ is the recovery rate of $meme_k$, I is the identity matrix of order N and $\beta _1$, $\beta _{a_1}$ is the infection rate without alert and with alert of $meme_k$ respectively.

Proof

Assuming that the contact networks $CN_1$ and $CN_2$ are strongly connected and irreducible, $\bar{I}=(\bar{I}^1,\bar{I}^2)^T$ be the equilibrium vector of mean field dynamics of $meme_k$ and $meme_l$ which is defined as $\bar{I}^j=(\bar{I}_1^j, \bar{I}_2^j,\ldots , \bar{I}_N^j)^T, \ j=1,2$. Also assume, $\bar{\zeta }^1=(\bar{\zeta }_1^1, \bar{\zeta }_2^1, \ldots , \bar{\zeta }_N^1)^T$ and $\bar{\zeta }^2=(\bar{\zeta }_1^2, \bar{\zeta }_2^2, \ldots , \bar{\zeta }_N^2)^T$.

The nonlinear system can be defined by $\dot{X}=JX$ where, $J= \left( \begin{array}{cc} J_{11}&{}\quad J_{12}\\ J_{21}&{}\quad J_{22} \end{array} \right)$, $\dot{X}=(\dot{I^1},\dot{I^2})^T$ and, $X=(I^1,I^2)^T$.

First, the nonlinear systems (1) and (2) are linearized about $\bar{I}$ where $\bar{I}_i^2$ is a solution of (10) with $\bar{I}_i^1=0$, for all i. After linearization the resulting system is,

$$\begin{aligned} J= \left( \begin{array}{cc} J_{11}&{}\quad 0\\ J_{21}&{}\quad J_{22} \end{array} \right) \end{aligned}$$

(13)

where

$$\begin{aligned} J_{11}= & {} \beta _1 diag\left( \left( 1-\bar{I^2}-\bar{\zeta }^1-\bar{\zeta }^2 \right) A \right) +\beta _ {a_1} diag\left( \bar{\zeta }^1A \right) -\delta _1I,\\ J_{21}= & {} -\,\beta _2 diag\left( B^T\bar{I^2}\right) ,\\ J_{22}= & {} -\,\beta _2 diag\left( B^T\bar{I^2}\right) +\beta _2 diag\left( \left( 1-\bar{I^2}-\bar{\zeta }^1-\bar{\zeta }^2 \right) B \right) \\&+\beta _{a_2}diag\left( \bar{\zeta }^2B \right) -\delta _2I. \end{aligned}$$

By [36], the nonlinear dynamics given by (1) and (2) are (locally) exponentially stable if and only if the linearized system J is exponentially stable, since the Jacobian matrix of the system is bounded and Lipshitz.

Subsequently to prove that J is Hurwitz, it is enough to prove that $J_{22}$ is Hurwitz. Since in the Jacobian matrix J, the eigenvalues are $J_{11}$ and $J_{22}$. Here, $J_{22}$ matrix is exactly the same matrix of the single meme, single layer SAIS system. Using proposition [37], $\bar{I^2}$ is locally exponentially stable equilibrium point of the single layer model. So $J_{22}$ must be Hurwitz as it is component wise bounded and Lipshitz. Hence, J is Hurwitz. $\square$

Fig. 2

The steady state infection fraction of $\hbox {meme}_k$ in the $SA_1I_1SA_2I_2S$ model becomes non zero at the survival threshold $\tau _{1s}$, it coincides with the single meme propagation at the absolute dominance threshold $\tau _1^*$ for increasing $\tau _1$. In the steady state infection fraction of $\hbox {meme}_k$ is zero for $\tau _1\le \tau _{1s}$, and extinction region for $\hbox {meme}_k$. For the case $\tau _1>\tau _1^*$ the competitive meme propagation is identical to the single meme scenario

Fig. 3

Coexistence of $\hbox {meme}_k$ and $\hbox {meme}_l$ of $SA_1I_1SA_2I_2S$ model in multiplex networks

2.4 Comparison of SAIS model and $SA_1I_1SA_2I_2S$ model

This section addresses the problem to identify the following critical values such as survival threshold $(\tau _{1s})$, absolute dominance threshold $(\tau _1^*)$ and coexistence for the effective infection rate of memes. Moreover, it has to be analyzed for which values of $\tau _1$, the $\hbox {meme}_k$ will survive or completely remove the other competing meme. Finally, the proposed model is compared with the SAIS model. Figure 2, depicts the two critical values $\tau _{1s}$ and $\tau _{1}^{*}$ in the dynamic of an epidemic spread. Case (i) when $\tau _1<\tau _{1s}$ the initial infection dies out exponential. Case (ii) When $\tau _1>\tau _{1}^{*}$ the infection persists steady state. Case (iii) Between the two threshold both the memes will be persevered in the population. For $\tau _1<\tau _{1s}\simeq 4*1/\lambda _{1}(A)$, the steady state infection fraction of $\hbox {meme}_k$ is zero and $\tau _1>\tau _{1}^{*}\simeq 12*1/\lambda _{1}(A)$ the competitive meme reduces to single meme as shown in Fig. 2. Moreover, the coexistence of memes will exist for $\tau _1$ that lies within the region of $(\tau _{1s},\tau _{1}^{*})$ which is depicted in Fig. 3. Assuming the two contact network layers to be identical, the multiplex network is reduced into a single layer network. So the survival and absolute dominance thresholds coincide. The stability analysis of the identical layers are discussed in [19]. The survival threshold of the equilibriums by using bifurcation analysis can be determined. The disease free equilibrium is unstable for $\tau _1>\frac{1}{\lambda _{1}(A)}$ and also unstable in the case of the absence of one of the memes. The stability will exist only for the case of coexistence equilibrium. Given the fixed value of $\tau _2$, the survival threshold of $\hbox {meme}_k$ is the critical value where the coexistence equilibrium exist. Survival threshold of $\hbox {meme}_k$ is analytically identified by the following theorem.

Theorem 2

If $\bar{I}_i^1=0$, $\bar{I}_i^2=v_i$, $\frac{\partial \bar{I}_i^1}{\partial \tau _1}>0$, $\frac{\partial \bar{I}_i^2}{\partial \tau _1}=0$ and $\frac{\partial \bar{\zeta }_i^2}{\partial \tau _1}=0$ at $\tau _1=\tau _{1s}$, then the non-linear eigenvalue problem can be obtained from $\varTheta =\tau _{1s}(1-v_i)\varphi _i\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j$ which has the possible solution as survival threshold

$$\begin{aligned} \tau _{1s}=\frac{1}{\lambda _{1}(diag(1-v_i)\varphi _i A)}, \end{aligned}$$

where $\varphi _i=\frac{\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\tau _{a_1}\left( \bar{m}_1\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j \right) }{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\bar{\mu }_1 \sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j}$ for which non trivial solution exist for $\varTheta =(\varTheta _1, \varTheta _2, \ldots , \varTheta _n)^T$, $\varTheta _i>0$ for $i=1, 2, \ldots , N$.

Proof

Taking the derivative of the equilibrium equation (5) with respect to $\tau _1$ and defining $\frac{\partial \bar{I}_i^1}{\partial \tau _1}\mid _{\tau _1=\tau _{1s}}=\varTheta _i$, $\bar{I}_i^2=v_i\mid _{\tau _1=\tau _{1s}}$.

This implies that

$$\begin{aligned}&\frac{(1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2)\frac{\partial \bar{I}_i^1}{\partial \tau _1}+\bar{I}_i^1\left( \frac{\partial \bar{I}_i^1}{\partial \tau _1}+\frac{\partial \bar{I}_i^2}{\partial \tau _1}+\frac{\partial \bar{\zeta }_i^2}{\partial \tau _1}\right) }{(1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2)^2}\\&\quad =\sum \limits _{j=1}^{N}a_{ji}\frac{\partial \bar{I}_j^1}{\partial \tau _1}\frac{(\tau _1+\tau _{a_1}\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\frac{\partial \bar{I}_j^1}{\partial \tau _1}+\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\tau _{a_1}\bar{\mu }_{1}\sum \nolimits _{j=1}^{N}c_{ji}\frac{\partial \bar{I}_j^1}{\partial \tau _1}}{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\frac{\partial \bar{I}_j^1}{\partial \tau _1}+\bar{\mu }_{1}\sum \nolimits _{j=1}^{N}c_{ji}\frac{\partial \bar{I}_j^1}{\partial \tau _1}}\\&\frac{(1-v_i)\varTheta _i}{(1-v_i)^2}=\frac{(\tau _{1s}+\tau _{a_1}\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\tau _{a_1}\bar{\mu }_{1}\sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j}{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\bar{\mu }_{1}\sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j}\sum \limits _{j=1}^{N}a_{ji}\varTheta _j\\&\varTheta _i=(1-v_i)\frac{(\tau _{1s}+\tau _{a_1}\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\tau _{a_1}\bar{\mu }_{1}\sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j}{(1+\bar{m}_1)\sum \nolimits _{j=1}^{N}a_{ji}\varTheta _j+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\varTheta _j}\sum \limits _{j=1}^{N}a_{ji}\varTheta _j \end{aligned}$$

By Perron–Frobenius theorem [19], the dominant eigen vector of the matrix $diag(1-v_i)\varphi _iA$ has all positive entries when $\varTheta _i>0$. Hence, the survival threshold $\tau _{1s}$ with $\varTheta _i>0$ has a coexistence equilibrium. Similar, to the SIS epidemic threshold [6], the survival threshold is the inverse of the spectral radius of the adjacency matrix A, but scaled by the reduced susceptibility factor $(1-v_i)\varphi _i$ for each node.

Similarly, the survival threshold for $\hbox {meme}_l$ can be derived. All other equilibrium is unstable and exists only for $\bar{I}_i^1\ge 0$ and $\bar{I}_i^2\ge 0$, for all $i=1,2,\ldots ,N$ and the coexistence equilibrium will exist for $\tau _1>\tau _{1s}$ and $\tau _2>\tau _{2s}$. $\square$

The following theorem identifies the promoting alert threshold for $\hbox {meme}_k$. While increasing the alert rate of $\hbox {meme}_k$, the promoting rate of $\hbox {meme}_k$ is also increased. The widespread occurring at the threshold value $(m_{1c})$, helps in promoting the behaviour of the infection $\hbox {meme}_k$. The same could be followed for $(m_{2c})$.

Theorem 3

If $\bar{I}_i^1,\bar{I}_i^2>0$, $\frac{d\bar{\zeta }_i^1}{d\bar{m}_1}= \frac{d\bar{\zeta }_i^2}{d\bar{m}_1}=0$ and $\bar{\zeta }_i^2=0$ at $m_{1c}$, then the promoting alert (influencer) threshold for $\hbox {meme}_k$ is given by

$m_{1c}=\frac{\left\{ \begin{array}{l}\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1 \right) \left( \sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\phi _j \right) \\ -\,\bar{\mu }_1(\phi _i+\psi _i)\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1\end{array}\right\} }{(\phi _i+\psi _i)\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1-\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1 \right) \sum \nolimits _{j=1}^{N}a_{ji}\phi _j}$, where $\phi _i=\frac{d\bar{I}_i^1}{d\bar{m}_1}$ and $\psi _i=\frac{d\bar{I}_i^2}{d\bar{m}_1}$.

Proof

Equilibrium equation (7) can be written as,

$$\begin{aligned}&\bar{\zeta }_i^1\left( \left( 1+\bar{m}_1\right) \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \\&\quad =\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2\right) \left( \bar{m}_1\sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \end{aligned}$$

Differentiate with respect to $\bar{m}_1$ we get

$$\begin{aligned}&\bar{\zeta }_i^1\left( \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\left( 1+\bar{m}_1\right) \sum \limits _{j=1}^{N}a_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}+\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}\right) \\&\quad \quad +\,\frac{d\bar{\zeta }_j^1}{d\bar{m}_1}\left( \left( 1+\bar{m}_1\right) \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \\&\quad =\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^2\right) \left( \bar{m}_1\sum \limits _{j=1}^{N}a_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}+\sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1\right. \\&\quad \quad \left. +\,\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}\right) +\left( \bar{m}_1\sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu _1}\sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \left( -\frac{d\bar{I}_i^1}{d\bar{m}_1}-\frac{d\bar{I}_i^2}{d\bar{m}_1}-\frac{d\bar{\zeta }_i^2}{d\bar{m}_1}\right) \\&\quad \frac{d\bar{\zeta }_i^1}{d\bar{m}_1}=\frac{\left\{ \begin{array}{l} \left( \bar{m}_1\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu _1}\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \left( -\frac{d\bar{I}_i^1}{d\bar{m}_1}-\frac{d\bar{I}_i^2}{d\bar{m}_1}-\frac{d\bar{\zeta }_i^2}{d\bar{m}_1}\right) +\left( 1-\bar{I}_i^1\right. \\ \qquad \left. -\,\bar{I}_i^2-\bar{\zeta }_i^1-\bar{\zeta }_i^2\right) \left( \sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{m}_1\sum \nolimits _{j=1}^{N}a_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\frac{d\bar{I}_j^1}{d\bar{m}_1}\right) \end{array}\right\} }{\left( 1+\bar{m}_1\right) \sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1} \end{aligned}$$

At $\bar{m_1}= m_{1c}$, $\bar{I}_i^1, \bar{I}_i^2>0$, $\frac{d\bar{\zeta }_i^1}{d\bar{m}_1}=\frac{d\bar{\zeta }_i^2}{d\bar{m}_1}=0$ and $\bar{\zeta }_i^2=0$.

$$\begin{aligned}&\left( m_{1c}\sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1\right) \left( \phi _i+\psi _i\right) \nonumber \\&\quad =\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1\right) \left( \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+ m_{1c}\sum \limits _{j=1}^{N}a_{ji}\phi _j+\bar{\mu _1}\sum \limits _{j=1}^{N}c_{ji}\phi _j\right) \nonumber \\&\qquad \qquad m_{1c}\left( \left( \phi _i+\psi _i\right) \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1-\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1\right) \sum \limits _{j=1}^{N}a_{ji}\phi _j\right) \nonumber \\&\quad =\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1\right) \left( \sum \limits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu _1}\sum \limits _{j=1}^{N}c_{ji}\phi _j\right) \nonumber \\&\qquad \qquad -\,\bar{\mu _1}\left( \phi _i+\psi _i\right) \sum \limits _{j=1}^{N}c_{ji}\bar{I}_j^1 \end{aligned}$$

(14)

This implies that,

$$\begin{aligned} m_{1c}=\frac{\left\{ \begin{array}{l}\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1\right) \left( \sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1+\bar{\mu }_1\sum \nolimits _{j=1}^{N}c_{ji}\phi _j\right) \\ -\bar{\mu }_1\left( \phi _i+\psi _i\right) \sum \nolimits _{j=1}^{N}c_{ji}\bar{I}_j^1\end{array}\right\} }{(\phi _i+\psi _i)\sum \nolimits _{j=1}^{N}a_{ji}\bar{I}_j^1-\left( 1-\bar{I}_i^1-\bar{I}_i^2-\bar{\zeta }_i^1\right) \sum \nolimits _{j=1}^{N}a_{ji}\phi _j} \end{aligned}$$

To corroborate the theoretical results, the following section illustrates the simulation numerically. $\square$

3 Numerical simulations

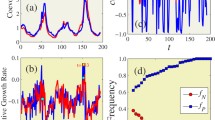
This section discusses the numerical results of the competitive $SA_1I_1SA_2I_2S$ model with alert influence over CN and IDN networks. Numerical results are further validated with stochastic simulations using GEMFSim framework [27]. Stochastic simulation of all state probabilities are depicted in Fig. 4, using the values of the following parameters $m_1=0.1, m_2=10, \delta _1=0.005*m_1, \delta _2=0.5*m_2, \beta _1=10/\lambda _1, \beta _2=90/\lambda _2, \beta _{a_1}=1/3* \beta _1, \beta _{a_2}=1/3* \beta _2,$ and $\mu _1=\mu _2=1/\lambda _3$.

Time dependent stochastic simulations are shown in Fig. 5 for varying alert rates to validate our analytical findings. In Fig. 5a, the results are obtained for the same parameter values as in Fig. 4, when $m_1=10, m_2=0.1 (m_1 > m_2)$. Figure 5a also shows that the infection probability of $\hbox {meme}_k$ is decreasing as the infection probability of competing $\hbox {meme}_l$ is increasing . That is, the increase in alert rate of $\hbox {meme}_k$ prevents spread of $\hbox {meme}_k$. A similar scenario with the contrasting effect is depicted in Fig. 5b, when $m_1=0.1, m_2=8(m_2 > m_1)$. Figure 6 represents the dynamic behaviour of both the memes for each node in the contact networks of 100 individuals. Particularly, the red color trajectory path indicates the infection probability of $meme_k$, while blue color trajectory path represents infection probability of $meme_l$ using the same parameter values as discussed above.

Fig. 4

Stochastic simulation of all state probabilities

Fig. 5

a Stochastic simulation of fraction of infected nodes when $m1>m2$, b stochastic simulation of fraction of infected nodes when $m1<m2$

Fig. 6

Trajectory path for 100 nodes representing the behaviour of $meme_k$ and $meme_l$

Moreover, the model shows the coexistence of competitive memes, survival threshold and dominant threshold of multiplex networks. Based on the identification of the competitive threshold, the threshold values could be either stable or extinct. In this regard, the real network data of Facebook, Twitter, and Flickr each having 100 nodes and the corresponding adjacency matrices A, B and C are generated for the numerical simulation. The spectral radius of the adjacency matrix A and B are 6.93488 and 4.0781 respectively. Initially, the coexistence of both the memes with the given fixed value of $\beta _2 = 5.1,m_2 = 2$ and varying $\tau _1$ are shown in Fig. 5. At $\tau _1=9.2*1/\lambda _1(A)$ both the memes, $\hbox {meme}_k$ and $\hbox {meme}_l$ will exist.

The graphical visualization of survival and absolute dominance threshold of $\hbox {meme}_k$ are shown in Figs. 7 and 8. By using theorem 2, at $\tau _1=0.2*1/\lambda _1(A)$, $\hbox {meme}_k$ starts to survive for the alert rate of $\hbox {meme}_k (m_1=8)$ and has been compared without alert for $\hbox {meme}_k$ as shown in Fig. 7. It also shows that the survival threshold of $\hbox {meme}_k$ is concise at a given alert rate than the case of no alert. In Fig. 8, the dominant threshold with alert and without alert cases are analyzed. Since, the infection rate of alert individual is less than the infection probability of $\hbox {meme}_l$ ($\beta _2$), the simulation parameter values are chosen as $\beta _2= 5.7, m_1 = 2, m_2 = 8$, $\mu _1=\mu _2 = 4$, $\delta _1=6.9348, \delta _2 = 3.8741$ and the alert infection rate as $\beta _{a_2}=r_2\beta _2$ with $r_2\le 1$.

Fig. 7

Illustration of survival threshold of $\hbox {meme}_k$ on a multiplex networks.The effective infection rate $\hbox {meme}_l$ constant at $\tau _2=6*1/\lambda _1(B)$. The steady state infection fraction of $\hbox {meme}_k$ with alert rate $m_1=8$ and no alert of survival threshold in multiplex networks

Fig. 8

Illustration of absolute-dominance threshold of $\hbox {meme}_k$ on a multiplex networks. The effective infection rate $\hbox {meme}_l$ constant at $\tau _2=6*1/\lambda _1(B)$. The steady state infection fraction of $\hbox {meme}_l$ with alert rate $m_1=8$ and no alert of absolute dominance threshold in multiplex networks

Using various alert rates, the alert probability of $\hbox {meme}_k$ and $\hbox {meme}_l$ are obtained. Figure 9 shows that the wide spread of $\hbox {meme}_k$ has occurred where as the $\hbox {meme}_l$ becomes extinct at the alert threshold ($m_{1c}$) of $\hbox {meme}_k$.

Fig. 9

$m_1$ versus alert probability of both memes

4 Conclusion and future work

The proposed model presents the extension of the single virus SAIS model to competitive meme propagation model. The major contributions of this work are identification of coexistence, extinction of both the memes, absolute dominant threshold of memes and alert threshold in multiplex social networks. Also, comparing the alert behaviour of single meme to competitive memes, the infection fraction of $\hbox {meme}_k$ and $\hbox {meme}_l$ is significantly reduced to the case of no-alert. The proposed alert influencer threshold helps in promoting the behaviour of the meme like advertisements promoting new products in marketing. It is applicable for competitive products like Iphone vs Android or spreading a disease through the physical contact or vector host population. The competitive meme with promoting alert over multiplex social network topology is highly challenging and adoptable for promoting new products in the field of marketing. Optimizing the threshold of alert rate of a meme which controls the corresponding meme’s propagation in competing scenario will be the scope for future research.