Adaptive-Multilevel BDDC and its parallel implementation

Abstract

We combine the adaptive and multilevel approaches to the BDDC and formulate a method which allows an adaptive selection of constraints on each decomposition level. We also present a strategy for the solution of local eigenvalue problems in the adaptive algorithm using the LOBPCG method with a preconditioner based on standard components of the BDDC. The effectiveness of the method is illustrated on several engineering problems. It appears that the Adaptive-Multilevel BDDC algorithm is able to effectively detect troublesome parts on each decomposition level and improve convergence of the method. The developed open-source parallel implementation shows a good scalability as well as applicability to very large problems and core counts.

1 Introduction

The Balancing Domain Decomposition by Constraints (BDDC) was developed by Dohrmann [7] as a primal alternative to the Finite Element Tearing and Interconnecting-Dual, Primal (FETI-DP) by Farhat et al. [8]. Both methods use constraints to impose equality of new ‘coarse’ variables on substructure interfaces, such as values at substructure corners or weighted averages over edges and faces. Primal variants of the FETI-DP were also independently proposed by Cros [5] and by Fragakis and Papadrakakis [9]. It has been shown in [24, 38] that these methods are in fact the same as BDDC. Polylogarithmic condition number bounds for FETI-DP were first proved in [28] and generalized to the case of coefficient jumps between substructures in [15]. The same bounds were obtained for BDDC in [20, 21]. A proof that the eigenvalues of the preconditioned operators of both methods are actually the same except for the eigenvalues equal to one was given in [21] and then simplified in [3, 19, 24]. FETI-DP, and, equivalently, BDDC are quite robust. It can be proved that the condition number remains bounded even for large classes of subdomains with rough interfaces in 2D [13, 44] as well as in many cases of strong discontinuities of coefficients, including some configurations when the discontinuities cross substructure boundaries [29, 30]. However, the condition number does deteriorate in many situations of practical importance and an adaptive method is warranted.

Adaptive enrichment for BDDC and FETI-DP was proposed in [22, 23], with the added coarse functions built from eigen problems based on adjacent pairs of substructures in 2D formulated in terms of FETI-DP operators. The algorithm has been developed directly in terms of BDDC operators and extended to 3D by Mandel, Sousedík and Šístek [27, 35], resulting in a much simplified formulation and implementation with global matrices, no explicit coarse problem, and getting much of its parallelism through the direct solver used to solve an auxiliary decoupled system. The only requirement for all these versions of the adaptive algorithms is that there is a sufficient number of corner constraints to prevent rigid body motions between any pair of adjacent substructures. This requirement has been recognized in other contexts [4, 18], and in the context of BDDC by Dohrmann [7], and recently by Šístek et al. [33].

Moreover, solving the coarse problem exactly in the original BDDC method becomes a bottleneck as the number of unknowns and, in particular, the number of substructures gets too large. Since the coarse problem in BDDC, unlike in the FETI-DP, has the same structure as the original problem, it is straightforward to apply the method recursively to solve the coarse problem only approximately [7]. The original, two-level, BDDC has been extended into three-levels by Tu [41, 42] and into a general multilevel method by Mandel, Sousedík and Dohrmann [25, 26]. Recently the BDDC has been extended into three-level methods for mortar discretizations [12], and into multiple levels for saddle point problems [37, 43]. The abstract condition number bounds deteriorate exponentially with increasing number of levels.

Here we combine the adaptive and multilevel approaches to the BDDC method in order to develop its variant that would preserve parallel scalability with an increasing number of subdomains and also show its excellent convergence properties. The adaptive method works as previously. It selects constraints associated with substructure faces, obtained from solution of local generalized eigenvalue problems for pairs of adjacent substructures, however this time on each decomposition level. Because of the multilevel approach, the coarse problems are treated explicitly (unlike in [27, 35]). The numerical examples show that the heuristic eigenvalue-based estimates work reasonably well and that the adaptive approach can result on each decomposition level in the concentration of computational work in a small troublesome parts of the problem, which leads to a good convergence behavior. The developed open-source parallel implementation shows a good scalability as well as applicability to very large problems and core counts.

The theoretical part of this paper presents a part of the work from the thesis [36] in a shorter, self-contained way. Also some results by the serial implementation of the algorithm from [36] are reproduced here for comparisons. The two-dimensional version of the algorithm was described in conference proceedings [39]. The main original contribution of this paper is the description of the parallel implementation of the method, and numerical study of its performance.

The paper is organized as follows. In Sect. 2 we establish the notation and introduce problem settings and preliminaries. In Sect. 3 we recall the Multilevel BDDC originally introduced in [26]. In Sect. 4, we describe the adaptive two-level method in terms of the BDDC operators with an explicit coarse space. In Sect. 5 we discuss a preconditioner for LOBPCG used in the solution of the local generalized eigenvalue problems in the adaptive method. Section 6 contains an algorithm for the adaptive selection of components of the Multilevel BDDC preconditioner. Numerical results are presented in Sect. 8, and Sect. 9 contains summary and concluding remarks.

2 Notation and substructuring components

We first establish notation and briefly review standard substructuring concepts and describe BDDC components. See, e.g., [17, 34, 40] for more details about iterative substructuring in general, and in particular [7, 20, 24, 26] for the BDDC. Consider a bounded domain $\Omega \subset \mathbb R ^{3}$ discretized by conforming finite elements. The domain $\Omega$ is decomposed into $N$ nonoverlapping subdomains $\Omega ^{i},\,i=1,\dots N$, also called substructures, so that each substructure $\Omega ^{i}$ is a union of finite elements. Each node is associated with one degree of freedom in the scalar case, and with three displacement degrees of freedom in the case of linear elasticity. The nodes contained in the intersection of at least two substructures are called boundary nodes. The union of all boundary nodes of all substructures is called the interface, denoted by $\Gamma$, and $\Gamma ^{i}$ is the interface of substructure $\Omega ^{i}$. The interface $\Gamma$ may also be classified as the union of three different types of sets: faces, edges and corners. We will adopt here a simple (geometric) definition: a face contains all nodes shared by the same two subdomains, an edge contains all nodes shared by same set of more than two subdomains, and a corner is a degenerate edge with only one node; for a more general definition see, e.g., [14].

We identify finite element functions with the vectors of their coefficients in the standard finite element basis. These coefficients are also called variables or degrees of freedom. We also identify linear operators with their matrices, in bases that will be clear from the context.

Here, we find it more convenient to use the notation of abstract linear spaces and linear operators between them instead of the space $\mathbb R ^{n}$ and matrices. The results can be easily converted to matrix language by choosing a finite element basis. The space of the finite element functions on $\Omega$ will be denoted as $U$. Let $W^{s}$ be the space of finite element functions on substructure$~\Omega ^{s}$, such that all of their degrees of freedom on $\partial \Omega ^{s}\cap \partial \Omega$ are zero. Let

$$\begin{aligned} W=W^{1}\times \cdots \times W^{N}, \end{aligned}$$

and consider a bilinear form $a\left( \cdot ,\cdot \right)$ arising from the second-order elliptic problem such as Poisson’s equation or a problem of linear elasticity.

Now $U\subset W$ is the subspace of all functions from $W$ that are continuous across the substructure interfaces. We are interested in the solution of the problem

$$\begin{aligned} u\in U:a(u,v)=\left\langle f,v\right\rangle ,\quad \forall v\in U, \end{aligned}$$

(1)

where the bilinear form $a$ is associated on the space $U$ with the system operator$~A$, defined by

$$\begin{aligned} A:U\mapsto U^{\prime },\quad a(u,v)=\left\langle Au,v\right\rangle , \quad \forall u,v\in U, \end{aligned}$$

(2)

and $f\in U^{\prime }$ is the right-hand side. Hence, (1) is equivalent to

$$\begin{aligned} Au=f. \end{aligned}$$

(3)

Define $U_{I}\subset U$ as the subspace of functions that are zero on the interface $\Gamma$, i.e., the ‘interior’ functions. Denote by $P$ the energy orthogonal projection from $W$ onto $U_{I}$,

$$\begin{aligned} P:w\in W\longmapsto v_{I}\in U_{I}:a\left( v_{I},z_{I}\right) =a\left( w,z_{I}\right) ,\quad \forall z_{I}\in U_{I}. \end{aligned}$$

Functions from $\left( I-P\right) W$, i.e., from the nullspace of $P,$ are called discrete harmonic; these functions are $a$-orthogonal to $U_{I}$ and energy minimal with respect to increments in $U_{I}$. Next, let $\widehat{W}$ be the space of all discrete harmonic functions that are continuous across substructure boundaries, that is

$$\begin{aligned} \widehat{W}=\left( I-P\right) U. \end{aligned}$$

(4)

In particular,

$$\begin{aligned} U=U_{I}\oplus \widehat{W},\quad U_{I}\perp _{a}\widehat{W}. \end{aligned}$$

(5)

The BDDC method [7, 24] is a two-level preconditioner characterized by the selection of certain coarse degrees of freedom, such as values at the corners and averages over edges or faces of substructures. Define $\widetilde{W}\subset W$ as the subspace of all functions such that each coarse degree of freedom has a common value for all relevant substructures and vanishes on $\partial \Omega ,$ and $\widetilde{W}_{\Delta }\subset \widetilde{W}$ as the subspace of all functions such that their coarse degrees of freedom vanish. Next, define $\widetilde{W}_{\Pi }$ as the subspace of all functions such that their coarse degrees of freedom between adjacent substructures coincide, and such that their energy is minimal. Clearly, functions in $\widetilde{W}_{\Pi }$ are uniquely determined by the values of their coarse degrees of freedom, and

$$\begin{aligned} {\widetilde{W}}_{\Delta }\perp _{a}{\widetilde{W}}_{\Pi },\quad \text{ and}\quad {\widetilde{W}}={\widetilde{W}}_{\Delta }\oplus {\widetilde{W}}_{\Pi }. \end{aligned}$$

(6)

The component of the BDDC preconditioner formulated in the space ${\widetilde{W}}_{\Pi }$ is called the coarse problem and the components in the space $\widetilde{W}_{\Delta }$ are called substructure corrections.

We assume that

$$\begin{aligned} a \text{ is} \text{ positive} \text{ definite} \text{ on} {\widetilde{W}}. \end{aligned}$$

(7)

This will be the case when $a$ is positive definite on the space $U$ and there are sufficiently many coarse degrees of freedom [26]. We further assume that the coarse degrees of freedom are zero on all functions from $U_{I}$, that is,

$$\begin{aligned} U_{I}\subset {\widetilde{W}}_{\Delta }. \end{aligned}$$

(8)

In other words, the coarse degrees of freedom depend on the values on substructure boundaries only. From (6) and (8), it follows that the functions in $\widetilde{W}_{\Pi }$ are discrete harmonic, that is,

$$\begin{aligned} {\widetilde{W}}_{\Pi }=\left( I-P\right) {\widetilde{W}}_{\Pi }. \end{aligned}$$

(9)

Next, let $E$ be a projection from $\widetilde{W}$ onto $U$, defined by taking some weighted average on substructure interfaces. That is, we assume that

$$\begin{aligned} E:{\widetilde{W}}\rightarrow U,\quad EU=U,\quad E^{2}=E. \end{aligned}$$

(10)

Since a projection is the identity on its range, it follows that $E$ does not change the interior degrees of freedom,

$$\begin{aligned} EU_{I}=U_{I}, \end{aligned}$$

(11)

since $U_{I}\subset U$. Finally, we recall that the operator $\left( I-P\right) E$ is a projection [26].

3 Multilevel BDDC

We recall Multilevel BDDC which has been introduced as a particular instance of Multispace BDDC in [26]. The substructuring components from Sect. 2 will be denoted by an additional subscript $_{1},$ as $\Omega _{1}^{s},\,s=1,\ldots N_{1}$, etc., and called level $1$. The level $1$ coarse problem will be called the level $2$ problem. It has the same finite element structure as the original problem (1) on level $1$, so we put $U_{2}={\widetilde{W}}_{\Pi 1}$. Level $1$ substructures are level $2$ elements and level $1$ coarse degrees of freedom are level $2$ degrees of freedom. Repeating this process recursively, level $i-1$ substructures become level $i$ elements, and the level $i$ substructures are agglomerates of level $i$ elements. Level $i$ substructures are denoted by $\Omega _{i}^{s},\,s=1,\ldots ,N_{i},$ and they are assumed to form a conforming triangulation with a characteristic substructure size $H_{i}$. For convenience, we denote by $\Omega _{0}^{s}$ the original finite elements and put $H_{0}=h$. The interface$~\Gamma _{i}$ on level$~i$ is defined as the union of all level$~i$ boundary nodes, i.e., nodes shared by at least two level$~i$ substructures, and we note that $\Gamma _{i}\subset \Gamma _{i-1}$. Level $i-1$ coarse degrees of freedom become level $i$ degrees of freedom. The shape functions on level $i$ are determined by minimization of energy with respect to level $i-1$ shape functions, subject to the value of exactly one level $i$ degree of freedom being one and the other level $i$ degrees of freedom being zero. The minimization is done on each level $i$ element (level $i-1$ substructure) separately, so the values of level $i-1$ degrees of freedom are in general discontinuous between level $i-1$ substructures, and only the values of level $i$ degrees of freedom between neighbouring level $i$ elements coincide.

The development of the spaces on level $i$ now parallels the finite element setting in Sect. 2. Denote $U_{i}={\widetilde{W}}_{\Pi , i-1}$. Let $W_{i}^{s}$ be the space of functions on the substructure $\Omega _{i}^{s}$, such that all of their degrees of freedom on $\partial \Omega _{i}^{s}\cap \partial \Omega$ are zero, and let

$$\begin{aligned} W_{i}=W_{i}^{1}\times \cdots \times W_{i}^{N_{i}}. \end{aligned}$$

Then $U_{i}\subset W_{i}$ is the subspace of all functions from $W_{i}$ that are continuous across the interfaces $\Gamma _{i}$. Define $U_{Ii}\subset U_{i}$ as the subspace of functions that are zero on$~\Gamma _{i}$, i.e., the functions ‘interior’ to the level$~i$ substructures. Denote by $P_{i}$ the energy orthogonal projection from $W_{i}$ onto $U_{Ii}$,

$$\begin{aligned} P_{i}:w_{i}\in W_{i}\longmapsto v_{Ii}\in U_{Ii}:a\left( v_{Ii},z_{Ii}\right) =a\left( w_{i},z_{Ii}\right) ,\quad \forall z_{Ii}\in U_{Ii}. \end{aligned}$$

Functions from $\left( I-P_{i}\right) W_{i}$, i.e., from the nullspace of $P_{i},$ are called discrete harmonic on level $i$; these functions are $a$-orthogonal to $U_{Ii}$ and energy minimal with respect to increments in $U_{Ii}$. Denote by $\widehat{W}_{i}\subset U_{i}$ the subspace of discrete harmonic functions on level$~i$, that is

$$\begin{aligned} \widehat{W}_{i}=\left( I-P_{i}\right) U_{i}. \end{aligned}$$

(12)

In particular, $U_{Ii}\perp _{a}\widehat{W}_{i}$. Define ${\widetilde{W}}_{i}\subset W_{i}$ as the subspace of all functions such that each coarse degree of freedom on level$~i$ has a common value for all relevant level$~i$ substructures, and ${\widetilde{W}}_{\Delta i}\subset {\widetilde{W}}_{i}$ as the subspace of all functions such that their level $i$ coarse degrees of freedom have zero value. Define ${\widetilde{W}}_{\Pi i}$ as the subspace of all functions such that their level $i$ coarse degrees of freedom between adjacent substructures coincide, and such that their energy is minimal. Clearly, functions in ${\widetilde{W}}_{\Pi i}$ are uniquely determined by the values of their level $i$ coarse degrees of freedom, and

$$\begin{aligned} {\widetilde{W}}_{\Delta i}\perp _{a}{\widetilde{W}}_{\Pi i},\quad \quad {\widetilde{W}}_{i}={\widetilde{W}}_{\Delta i}\oplus {\widetilde{W}}_{\Pi i}. \end{aligned}$$

(13)

We assume that the level$~i$ coarse degrees of freedom are zero on all functions from $U_{Ii}$, that is,

$$\begin{aligned} U_{Ii}\subset {\widetilde{W}}_{\Delta i}. \end{aligned}$$

(14)

In other words, level $i$ coarse degrees of freedom depend on the values on level$~i$ substructure boundaries only. From (13) and ( 14), it follows that the functions in ${\widetilde{W}}_{\Pi i}$ are discrete harmonic on level$~i$, that is

$$\begin{aligned} {\widetilde{W}}_{\Pi i}=\left( I-P_{i}\right) {\widetilde{W}}_{\Pi i}. \end{aligned}$$

(15)

Let $E$ be a projection from $\widetilde{W}_{i}$ onto $U_{i}$, defined by taking some weighted average on $\Gamma _{i}$

$$\begin{aligned} E_{i}:{\widetilde{W}}_{i}\rightarrow U_{i},\quad E_{i}^{2}=E_{i}. \end{aligned}$$

Since projection is the identity on its range, $E_{i}$ does not change the level$~i$ interior degrees of freedom, in particular

$$\begin{aligned} E_{i}U_{Ii}=U_{Ii}. \end{aligned}$$

(16)

The Multilevel BDDC method is now defined recursively [7, 26] by solving the coarse problem on level $i$ only approximately, by one application of the preconditioner on level $i+1$. Eventually, at the top level $L-1$, the coarse problem, which is the level $L$ problem, is solved exactly. A formal description of the method is provided by the following algorithm.

Algorithm 1

(Multilevel BDDC, [26, Algorithm 17]) Define the preconditioner $r_{1}\in U_{1}^{\prime }\longmapsto u_{1}\in U_{1}$ as follows:

for $i=1,\ldots ,L-1$ ,

Compute interior pre-correction on level $i$,

$$\begin{aligned} u_{Ii}\in U_{Ii}:a\left( u_{Ii},z_{Ii}\right) =\left\langle r_{i},z_{Ii}\right\rangle ,\quad \forall z_{Ii}\in U_{Ii}. \end{aligned}$$

(17)

Get an updated residual on level $i$,

$$\begin{aligned} r_{Bi}\in U_{i},\quad \left\langle r_{Bi},v_{i}\right\rangle =\left\langle r_{i},v_{i}\right\rangle -a\left( u_{Ii},v_{i}\right) ,\quad \forall v_{i}\in U_{i}. \end{aligned}$$

(18)

Find the substructure correction on level $i$:

$$\begin{aligned} w_{\Delta i}\in W_{\Delta i}:a\left( w_{\Delta i},z_{\Delta i}\right) =\left\langle r_{Bi},E_{i}z_{\Delta i}\right\rangle ,\quad \forall z_{\Delta i}\in W_{\Delta i}. \end{aligned}$$

(19)

Formulate the coarse problem on level $i$,

$$\begin{aligned} w_{\Pi i}\in W_{\Pi i}:a\left( w_{\Pi i},z_{\Pi i}\right) =\left\langle r_{Bi},E_{i}z_{\Pi i}\right\rangle ,\quad \forall z_{\Pi i}\in W_{\Pi i}. \end{aligned}$$

(20)

If $\ i=L-1$, solve the coarse problem directly and set $u_{L}=w_{\Pi L-1}$, otherwise set up the right-hand side for level $i+1$,

$$\begin{aligned} r_{i+1}\in {\widetilde{W}}_{\Pi i}^{\prime },\quad \left\langle r_{i+1},z_{i+1}\right\rangle =\left\langle r_{Bi},E_{i}z_{i+1}\right\rangle ,\quad \forall z_{i+1}\in {\widetilde{W}}_{\Pi i}=U_{i+1}, \end{aligned}$$

(21)

end.

for $i=L-1,\ldots ,1$

Average the approximate corrections on substructure interfaces on level $i$,

$$\begin{aligned} u_{Bi}=E_{i}\left( w_{\Delta i}+u_{i+1}\right). \end{aligned}$$

(22)

Compute the interior post-correction on level $i$,

$$\begin{aligned} v_{Ii}\in U_{Ii}:a\left( v_{Ii},z_{Ii}\right) =a\left( u_{Bi},z_{Ii}\right) ,\quad \forall z_{Ii}\in U_{Ii}. \end{aligned}$$

(23)

Apply the combined corrections,

$$\begin{aligned} u_{i}=u_{Ii}+u_{Bi}-v_{Ii}. \end{aligned}$$

(24)

end.

The condition number bound for Multilevel BDDC is given as follows.

Lemma 1

[26, Lemma 20] The condition number $\kappa$ of Multilevel BDDC from Algorithm 1 satisfies

$$\begin{aligned} \kappa \le \omega \equiv \Pi _{i=1}^{L-1}\omega _{i}\,\,,\quad \end{aligned}$$

(25)

where

$$\begin{aligned} \omega _{i}=\sup _{w \in {\widetilde{W}}_{i}}\frac{{\left\Vert\left(I-P_{i}\right) E_{i}{w}\right\Vert}_{a}^{2}}{{\left\Vert{w}\right\Vert}_{a}^{2}}. \end{aligned}$$

(26)

For the purpose of the adaptive selection of constraints, we use the bound based on jump at the interface defined on the subspace of discrete harmonic functions from $\widetilde{W}_{i}$. More precisely, we modify (26) using the identity

$$\begin{aligned} (I-P_{i})E_{i}(I-P_{i}) = (I-P_{i})E_{i} \end{aligned}$$

(27)

and the fact that $P_{i}$ is an $a$-orthogonal projection, as

$$\begin{aligned} \begin{aligned} \omega _{i}&=\sup _{w\in {\widetilde{W}}_{i}}\frac{{\Bigg \Vert \left(I-P_{i}\right) E_{i}w\Bigg \Vert } _{a}^{2}}{ {\Bigg \Vert w\Bigg \Vert }_{a}^{2}} =\sup _{w\in {\widetilde{W}}_{i}}\frac{ {\Bigg \Vert \left(I-P_{i}\right) E_{i}\left(I-P_{i}\right)w\Bigg \Vert } _{a}^{2}}{{\Bigg \Vert w\Bigg \Vert }_{a}^{2}}\\&=\sup _{w\in {\widetilde{W}}_{i}}\frac{ {\Bigg \Vert \left(I-P_{i}\right) E_{i}\left(I-P_{i}\right)w\Bigg \Vert }_{a}^{2} }{{\Bigg \Vert P_{i}w\Bigg \Vert }_{a}^{2} + {\Bigg \Vert \left(I-P_{i}\right)w\Bigg \Vert }_{a}^{2}} =\sup _{w\in {\widetilde{W}}_{i}}\frac{ {\Bigg \Vert \left(I-P_{i}\right) E_{i}\left(I-P_{i}\right)w\Bigg \Vert }_{a}^{2}}{{\Bigg \Vert \left(I-P_{i}\right)w\Bigg \Vert }_{a}^{2}} \\&=\sup _{w\in \left(I-P_{i}\right){\widetilde{W}}_{i}}\frac{ {\Bigg \Vert \left(I-P_{i}\right) E_{i}w\Bigg \Vert } _{a}^{2}}{ {\Bigg \Vert w\Bigg \Vert }_{a}^{2}} =\sup _{w\in \left(I-P_{i}\right){\widetilde{W}}_{i}}\frac{ {\Bigg \Vert \left(I - \left(I-P_{i}\right) E_{i}\right)w\Bigg \Vert }_{a}^{2}}{{\Bigg \Vert w\Bigg \Vert }_{a}^{2}}. \qquad \quad \end{aligned} \end{aligned}$$

(28)

The last equality in (28) holds because $\left(I-P_{i}\right)E_{i}$ is a projection and the norm of a nontrivial projection in an inner product space depends only on the angle between its range and its nullspace [10].

4 Adaptive coarse degrees of freedom

To simplify notation, we formulate the algorithm for the adaptive selection of the coarse degrees of freedom for one level at a time and drop the subscript $i$. The basic idea of the method is still the same as in [23, 27, 35]. However, the current formulation in terms of the BDDC method, though equivalent and written similarly as in [27], is different enough to allow for an explicit treatment of the coarse space correction. Therefore, it is suitable for multilevel extension which will be introduced later in Sect. 6.

As mentioned before, the space $\widetilde{W}$ is constructed using coarse degrees of freedom. These can be, e.g., values at corners, and averages over edges or faces. The space $\widetilde{W}$ is then given by the requirement that the coarse degrees of freedom on adjacent substructures coincide; for this reason, the terms coarse degrees of freedom and constraints are used interchangeably. The edge (or face) averages are necessary in 3D problems to obtain scalability with subdomain size. Ideally, one can prove the polylogarithmic condition number bound

$$\begin{aligned} \kappa \le const\left( 1+\log \frac{H}{h}\right) ^{2}, \end{aligned}$$

(29)

where $H$ is the subdomain size and $h$ is the finite element size.

Remark 1

The initial selection of constraints in the proposed adaptive approach will be done in a way such that (29) is satisfied for problems with sufficiently regular structure. See, e.g., [15] for a theoretical justification.

To choose the space $\widetilde{W}$, cf. [23, Section 2.3] , suppose we are given a space $X$ and a linear operator $C:W\rightarrow X$ and define,

$$\begin{aligned} {\widetilde{W}}=\left\{ w\in W:C\left( I-E\right) w=0\right\} . \end{aligned}$$

(30)

The values $Cw$ will be called local coarse degrees of freedom, and the space $~\widetilde{W}$ consists of all functions $w$ whose local coarse degrees of freedom on adjacent substructures have zero jumps. To represent their common values, i.e., the global coarse degrees of freedom of vectors $u\in \widetilde{W}$, we use a space $U_{c}$ and a one-to-one linear operator $R_{c}:U_{c}\rightarrow X$ such that

$$\begin{aligned} {\widetilde{W}}=\left\{ w\in W:\exists u_{c}\in U_{c}:Cw=R_{c}u_{c}\right\} . \end{aligned}$$

Observe that $\left( I-E\right) Pv=0$ for all $v\in W$, so we can define the space $\widetilde{W}$ in (30) using discrete harmonic functions $w\in W_{\Gamma } = \left( I-P\right) W$, for which

$$\begin{aligned} \left( I-\left( I-P\right) E\right) w=\left( I-P\right) \left( I-E\right) w. \end{aligned}$$

(31)

Let us denote ${\widetilde{W}}_{\Gamma } = (I-P){\widetilde{W}} = \widetilde{W} \cap W_{\Gamma }$. Then the bound (26) in the form of the last term in Eq. (28) can be found, for a fixed level $i$, as a maximum eigenvalue of an associated eigenvalue problem, which can be using (31) written as

$$\begin{aligned} a\left( \left( I-P\right) \left( I-E\right) w,\left( I-P\right) \left( I-E\right) z\right)=\lambda a\left( w,z\right) \quad \forall z\in \widetilde{W}_{\Gamma }. \end{aligned}$$

(32)

We can then control the condition number bound by adding constraints adaptively by taking advantage of the Courant–Fisher–Weyl minimax principle, cf., e.g., [6, Theorem 5.2], in the same way as in [23, 27, 35].

Corollary 1

[27] The generalized eigenvalue problem (32) has eigenvalues $\lambda _{1}\ge \lambda _{2}\ge \cdots \ge \lambda _{n}\ge 0$. Denote the corresponding eigenvectors by $w_{\ell }$. Then, for any $k=1,\ldots ,n-1$, and any linear functionals $L_{\ell },\,\ell =1,\ldots ,k$,

$$\begin{aligned} \max \left\{ \frac{{\Bigg \Vert \left( I-P \right) \left( I-E \right) w\Bigg \Vert }_{a}^{2}}{{\Bigg \Vert w \Bigg \Vert }_{a}^{2}}:w\in {\widetilde{W}}_{\Gamma },L_{\ell }\left( w\right) =0\quad \forall \ell =1,\ldots ,k\right\} \ge \lambda _{k+1}, \end{aligned}$$

with equality if

$$\begin{aligned} L_{\ell }\left( w\right) =a\left( \left( I-P\right) \left( I-E\right) w_{\ell },\left( I-P\right) \left( I-E\right) w\right). \end{aligned}$$

(33)

Therefore, because $\left( I-E\right)$ is a projection, the optimal decrease of the condition number bound (26) can be achieved by adding to the constraint matrix $C$ in the definition of $\widetilde{W}$ the rows $c_{\ell }$ defined by $c_{\ell }^{T}w=L_{\ell }\left( w\right)$.

Solving the global eigenvalue problem (32) is expensive, and the vectors $c_{\ell }$ are not of the form required for substructuring, i.e., each $c_{\ell }$ with nonzero entries corresponding to only one corner, an edge or a face at a time. For these reasons, we replace (32) by a collection of local problems, each defined by considering only two adjacent subdomains $\Omega ^{s}$ and $\Omega ^{t}$. Subdomains are called adjacent if they share a face. All quantities associated with such pairs will be denoted by a superscript $st$. In particular, we define

$$\begin{aligned} W^{st} = W^{s} \times W^{t}, \quad W^{st}_{\Gamma } = (I-P^{st})W^{st}, \end{aligned}$$

(34)

where $(I-P^{st})$ realizes the discrete harmonic extension from the local interfaces $\Gamma ^{s}$ and $\Gamma ^{t}$ to interiors. Thus, functions from $W^{st}_{\Gamma }$ are fully determined by their values at the local interfaces $\Gamma ^{s}$ and $\Gamma ^{t}$, and they may be discontinuous at the common part $\Gamma ^{st} = \Gamma ^{s} \cap \Gamma ^{t}$.

The bilinear form $a^{st}(\cdot ,\cdot )$ is associated on the space $W^{st}_{\Gamma }$ with the operator $S^{st}$ of Schur complement with respect to the local interfaces, defined by

$$\begin{aligned} S^{st}:W^{st}_{\Gamma }\mapsto {W^{st}_{\Gamma }}^{\prime }, \quad a^{st}(u,v)=\langle S^{st}u,v\rangle , \quad \forall u,v \in W^{st}_{\Gamma }. \end{aligned}$$

(35)

Operator $S^{st}$ is represented by a block-diagonal matrix composed of symmetric positive semi-definite matrices $S^{s}$ and $S^{t}$ of individual Schur complements of the subdomain matrices with respect to local interfaces $\Gamma ^{s}$ and $\Gamma ^{t}$, resp.,

$$\begin{aligned} \quad S^{st}=\left[ \begin{array}{cc} S^{s}&\\&S^{t} \end{array} \right]. \end{aligned}$$

(36)

The action of the local projection operator $E^{st}$ is realized as a (weighted) average at $\Gamma ^{st}$ and as an identity operator at $(\Gamma ^{s} \cup \Gamma ^{t})\backslash \Gamma ^{st}$.

Let $C^{st}$ be the operator defining the initial coarse degrees of freedom that are common to both subdomains of the pair. We define the local space of functions with the shared coarse degrees of freedom continuous as

$$\begin{aligned} {\widetilde{W}}^{st} = \left\{ w\in W^{st}: \ \ C^{st}(I-E^{st})w = 0 \right\} . \end{aligned}$$

(37)

Finally, we introduce the space $\widetilde{W}^{st}_{\Gamma } = \widetilde{W}^{st} \cap W^{st}_{\Gamma }$.

Now the generalized eigenvalue problem (32) becomes a localized problem to find $w\in \widetilde{W}_{\Gamma }^{st}$ such that

$$\begin{aligned} a^{st}\left( \left( I-P^{st}\right) \left( I-E^{st}\right) w,\left( I-P^{st}\right) \left( I-E^{st}\right) z\right) =\lambda \,a^{st}\left( w,z\right) \quad \forall z\in \widetilde{W}_{\Gamma }^{st}. \nonumber \\ \end{aligned}$$

(38)

Assumption 1

The corner constraints are already sufficient to prevent relative rigid body motions of any pair of adjacent substructures, so

$$\begin{aligned} \forall w\in {\widetilde{W}}^{st}:a^{st}(w,w)=0\Rightarrow \left( I-{E} ^{st}\right) w=0, \end{aligned}$$

i.e., the corner degrees of freedom are sufficient to constrain the rigid body modes of the two substructures into a single set of rigid body modes, which are continuous across the interface $\Gamma ^{st}$.

The maximal eigenvalue $\omega ^{st}$ of (38) is finite due to Assumption 1, and we define the heuristic condition number indicator

$$\begin{aligned} {\widetilde{\omega }}=\max \left\{ \omega ^{st}:\Omega ^{s} \text{ and} \Omega ^{t} \text{ are} \text{ adjacent}\right\} . \end{aligned}$$

(39)

Considering two adjacent subdomains $\Omega ^{s}$ and $\Omega ^{t}$ only, we get the added constraints $L_{\ell }\left( w\right) =0$ from (33) as

$$\begin{aligned} a^{st}\left( \left( I-P^{st}\right) \left( I-E^{st}\right) w_{\ell },\left( I-P^{st}\right) \left( I-E^{st}\right) w\right) =0\quad \forall \ell =1,\ldots ,k, \qquad \end{aligned}$$

(40)

where $w_{\ell }$ are the eigenvectors corresponding to the $k$ largest eigenvalues from (38).

Let us denote $D$ the matrix corresponding to $C^{st}(I-E^{st})$. We define the orthogonal projection onto $\text{ null}\,D$ by

$$\begin{aligned} \Pi =I-D^{T}\left( DD^{T}\right) ^{-1}D. \end{aligned}$$

The generalized eigenvalue problem (32) now becomes

$$\begin{aligned} \Pi \left( I-P^{st}\right) ^{T}\left( I-E^{st}\right) ^{T}S^{st}\left( I-E^{st}\right) \left( I-P^{st}\right) \Pi w=\lambda \Pi S^{st}\Pi w. \end{aligned}$$

(41)

Since

$$\begin{aligned} \text{ null}\Pi S^{st}\Pi \subset \text{ null}\Pi \left( I-P^{st}\right) ^{T}\left( I-E^{st}\right) ^{T}S^{st}\left( I-E^{st}\right) \left( I-P^{st}\right) \Pi , \end{aligned}$$

(42)

the eigenvalue problem (41) reduces in the factorspace modulo $\text{ null}\Pi S^{st}\Pi$ to a problem with the operator on the right-hand side positive definite. In our computations, we have used the subspace iteration method LOBPCG [16] to find the dominant eigenvalues and their eigenvectors. The LOBPCG iterations then simply run in the factorspace.

From (41), the constraints to be added are

$$\begin{aligned} L_{\ell }\left( w\right) =w_{\ell }^{T}\Pi \left( I-P^{st}\right) ^{T}\left( I-E^{st}\right) ^{T}S^{st}\left( I-E^{st}\right) \left( I-P^{st}\right) \Pi w=0. \end{aligned}$$

That is, we wish to add to the constraint matrix $C$ the rows

$$\begin{aligned} c^{st}_{\ell }=w_{\ell }^{T}\Pi \left( I-P^{st}\right) ^{T}\left( I-E^{st}\right) ^{T}S^{st}\left( I-E^{st}\right) \left( I-P^{st}\right) \Pi . \end{aligned}$$

(43)

Proposition 1

[27] The vectors $c^{st}_{\ell }$, constructed for a domain consisting of only two substructures $\Omega ^{s}$ and $\Omega ^{t}$, have matching entries on the interface between the two substructures, with opposite signs.

That is, each row $c^{st}_{\ell }$ can be split into two blocks and written as

$$\begin{aligned} c^{st}_{\ell }=\left[ \begin{array}{cc} c_{\ell }^{s}&-c_{\ell }^{s} \end{array} \right]. \end{aligned}$$

Either half of each row from the block $c^{st}_\ell$ is then added into the matrices $C^{s}$ and $C^{t}$ corresponding to the subdomains $\Omega ^{s}$ and $\Omega ^{t}$. Unfortunately, the added rows will generally have nonzero entries over the whole $\Gamma ^{s}$ and $\Gamma ^{t}$, including the edges in 3D where $\Omega ^{s}$ and $\Omega ^{t}$ intersect other substructures. Consequently, the added rows are not of the form required for substructuring, i.e., each row with nonzeros in one edge or face only. In the computations reported in Sect. 8, we drop the adaptively generated edge constraints in 3D. Then it is no longer guaranteed that the condition number indicator $\widetilde{\omega }\le \tau$. However, the method is still observed to perform well.

The proposed adaptive algorithm follows.

Algorithm 2

(Adaptive BDDC [23]) Find the smallest $k$ for every two adjacent substructures $\Omega ^{s}$ and $\Omega ^{t}$ to guarantee that $\lambda ^{st}_{k+1}\le \tau$, where $\tau$ is a given tolerance, and add the constraints (40) to the definition of $\widetilde{W}$.

5 Preconditioned LOBPCG

As pointed out already for adaptive 2-level BDDC method in [27], an important step for a parallel implementation of the adaptive selection of constraints is an efficient solution of the generalized eigenvalue problem (41) for each pair of adjacent subdomains.

There are several aspects of the method immediately making such implementation challenging: (i) parallel layout of pairs of subdomains does not follow the natural layout of a domain decomposition computation with distribution of data based on subdomains, (ii) the multiplication by $S^{st}$ on both sides of Eq. (41) is done only implicitly, since action of $S^s$ and $S^t$ is available only through solution of local discrete Dirichlet problems on subdomains $\Omega ^s_i$ and $\Omega ^t_i$, (iii) the process responsible for solving an $st$-eigenproblem typically does not have data for subdomains $\Omega ^s_i$ and $\Omega ^t_i$, and thus it has to communicate the vector for multiplication to processors able to compute the actions of $S^s$ and $S^t$.

With respect to these issues, it is necessary to use an inverse-free method for the solution of each of these problems. In our case, the LOBPCG method [16] is applied to find several largest eigenvalues $\lambda _\ell$ and corresponding eigenvectors $w_\ell$ solving the homogeneous problem

$$\begin{aligned} \mathcal{M }(\mathcal{A } - \lambda _\ell \mathcal{B })w_\ell = 0, \end{aligned}$$

(44)

with

$$\begin{aligned} \mathcal{A } = \Pi \left( I-P^{st}\right) ^{T}\left( I-E^{st}\right) ^{T}S^{st}\left( I-E^{st}\right) \left( I-P^{st}\right) \Pi ,\quad \mathcal{B } = \Pi S^{st}\Pi , \end{aligned}$$

and $\mathcal{M }$ a suitable preconditioner. The LOBPCG method requires only multiplications by matrices $\mathcal{M },\,\mathcal{A }$, and $\mathcal{B }$, and it can run in the factorspace with $\mathcal{B }$ only positive semi-definite. This is important for our situation – although each pair of subdomains has enough initial constraints by corners and edge averages to avoid mechanisms between the two substructures (enforced by the projection $\Pi$), no essential boundary conditions are applied to the pair as a whole, and matrix $\mathcal{B }$ of such ‘floating’ pair typically has a nontrivial nullspace (e.g. rigid body modes for elasticity problems).

Initial experiments in [27, 35, 36] revealed that while the unpreconditioned LOBPCG ($\mathcal{M } = I$) works reasonably well for simple problems, it requires prohibitively many iterations for problems with very irregular substructures and/or high jumps in coefficients. Since each iteration requires communicating the vector for multiplication, reducing the iteration counts of LOBPCG by preconditioning is a very sensible way of accelerating the adaptive BDDC method.

Recall, that the BDDC method provides a preconditioner for the interface problem of the Schur complement by the exact solution of the problem at the larger space $\widetilde{W}$. As such, components of a BDDC implementation, the coarse solver and subdomain corrections, can be used to determine the approximate action of the Moore–Penrose pseudoinverse of the matrix $\mathcal{B }$, denoted as $M^{loc}_{BDDC}\approx (\Pi S^{st}\Pi )^{+}$. This operator can be used as the preconditioner $\mathcal{M }$ for problem (44), effectively converting the generalized eigenvalue problem to an ordinary eigenproblem inside the iterations. Using notation from (36), the preconditioner is formally written as

$$\begin{aligned} M^{loc}_{BDDC} = \Pi \left( \left[ \begin{matrix} I&0 \end{matrix} \right] \left[ \begin{matrix} S^{st}&C^T \\ C&0 \end{matrix} \right]^{-1} \left[ \begin{matrix} I \\ 0 \end{matrix} \right] + \Psi ( \Psi ^T S^{st} \Psi )^{+} \Psi ^T \right) \Pi , \end{aligned}$$

(45)

where in addition $C = \left[ \begin{matrix} C^s&\\&C^t \end{matrix}\right]$ is the matrix of initial constraints (continuity at corners and arithmetic averages on edges), and $\Psi = \left[ \begin{matrix} \Psi ^s R^s_c \\ \Psi ^t R^t_c \end{matrix}\right]$ denotes the matrix of coarse basis functions for the two subdomains. Here $R^i_c,\ i = s,t$, is the zero-one matrix of restriction of the vector of global coarse degrees of freedom of the pair to subdomain coarse degrees of freedom. Since some coarse degrees of freedom are shared by the two subdomains, corresponding columns in $\Psi$ are nonzero in both parts, while columns of coarse degrees of freedom not common to the two subdomains are only nonzero in either $\Psi ^s R^s_c$ or $\Psi ^t R^t_c$. Let us recall that in BDDC, the local coarse basis functions are computed as the solution to the problem with multiple right hand sides

$$\begin{aligned} \left[ \begin{aligned} S^s&\,&C^{sT}&\\ &S^t&\,&C^{tT} \\ C^s&\,&\\ &C^t&\,&\end{aligned} \right] \left[ \begin{aligned} \Psi ^s&\\&\Psi ^t \\ \mu ^s&\\&\mu ^t \end{aligned} \right] = \left[ \begin{aligned}&\\&\\ I^s&\\&I^t \end{aligned} \right], \end{aligned}$$

(46)

which represents an independent saddle-point problem with invertible matrix for each subdomain, and factorization of which is later reused in applications of the preconditioner (45). We also note that the coarse matrix is in the implementation explicitly computed using the second part of the solution of (46) as

$$\begin{aligned} \Psi ^T S^{st} \Psi = - R^{sT}_c \mu ^s R^{s}_c - R^{tT}_c \mu ^t R^{t}_c. \end{aligned}$$

(47)

The coarse matrix of the $st$-pair $\Psi ^T S^{st} \Psi$ has dimension of the union of the coarse degrees of freedom of the subdomains of the pair, and it is typically only positive semi-definite for a floating pair. Due to its small dimension, we compute its pseudoinverse by means of dense eigenvalue decomposition performed by the LAPACK library,

$$\begin{aligned} \Psi ^T S^{st} \Psi = V \Lambda V^T, \quad (\Psi ^T S^{st} \Psi )^{+} \approx V \Lambda ^{\prime -1} V^T, \end{aligned}$$

(48)

where diagonal matrix $\Lambda ^{\prime }$ arises from $\Lambda$ by dropping eigenvalues lower than a prescribed tolerance.

Unlike the standard BDDC preconditioner, no interface averaging is applied to the function before and after the action of $M^{loc}_{BDDC}$, because problem (41) is defined in the space $\widetilde{W}^{st}_{\Gamma }$. Correspondingly, the only approximation is due to using $\Lambda ^{\prime }$ instead of $\Lambda$.

6 Adaptive-Multilevel BDDC

We build on Sects. 3 and 4 to propose a new variant of the Multilevel BDDC with adaptive selection of constraints on each level.

The development of adaptive selection of constraints in Multilevel BDDC now proceeds similarly as in Sect. 4. We formulate (26) as a set of eigenvalue problems for each decomposition level. On each level we solve for every two adjacent substructures a generalized eigenvalue problem and we add the constraints to the definitions of $\widetilde{W}_{i}$.

The heuristic condition number indicator is defined as

$$\begin{aligned} {\widetilde{\omega }}=\Pi _{i=1}^{L-1} {\widetilde{\omega }}_{i},\quad {\widetilde{\omega }}_{i} = \max \left\{ \omega _{i}^{st}:\Omega _{i}^{s} \text{ and} \Omega _{i}^{t} \text{ are} \text{ adjacent}\right\} . \end{aligned}$$

(49)

We now describe the Adaptive-Multilevel BDDC in more detail. The algorithm consists of two main steps: (i) set-up (including adaptive selection of constraints), and (ii) loop of the preconditioned conjugate gradients (PCG) with the Multilevel BDDC from Algorithm 1 as a preconditioner. The set-up can be summarized as follows (cf. [36, Algorithm 4 ] for the 2D case):

Algorithm 3

(Set-up of Adaptive-Multilevel BDDC) Adding of coarse degrees of freedom to guarantee that the condition number indicator $\widetilde{\omega }\le \tau ^{L-1}$, for a given target value$~\tau$:

for levels $i=1:L-1 \mathbf ,$

• Create substructures with roughly the same numbers of degrees of freedom.

• Find a set of initial constraints (in particular sufficient number of corners), and set up the BDDC structures for the adaptive algorithm (the next loop over faces).

for all faces $\mathcal F _{i}$ on level $i\mathbf ,$

Compute the largest local eigenvalues and corresponding eigenvectors, until the first $m^{st}$ is found such that $\lambda _{m^{st}}^{st}\le \tau$.

Compute the constraint weights and add these rows to the subdomain matrices of constraints $C^s$ and $C^t$.

end.

Set-up the BDDC structures for level $i$. If the prescribed number of levels is reached, solve the problem directly.

end.

7 Implementation remarks

Serial implementation has been developed in Matlab in the thesis [36]. Parallel results use the open-source package BDDCML¹ (version 2.0). This solver is written in Fortran 95 programming language and parallelized using MPI library. Apart of symmetric positive definite problems studied in this paper, the solver also supports symmetric indefinite and general non-symmetric linear systems arising from discretizations of PDEs.

The matrices of the averaging operator $E$ were constructed with entries proportional to the diagonal entries of the substructure matrices before elimination of interiors, which is also known as the stiffness scaling [13].

7.1 Initial constraints

Following Remark 1, in order to satisfy the polylogarithmic condition number bounds, we have used corners and arithmetic averages over edges as initial constraints. It is essential (Assumption 1) to generate a sufficient number of initial constraints to prevent rigid body motions between any pair of adjacent substructures. The selection of corners in our parallel implementation follows the recent face-based algorithm from [33].

7.2 Adaptive constraints

The adaptive algorithm uses matrices and operators that are readily available in an implementation of the BDDC method with an explicit coarse space, with one exception: in order to satisfy the local partition of unity, cf. [24, eq. (9)],

$$\begin{aligned} E_{i}^{st}R_{i}^{st}=I, \end{aligned}$$

we need to generate locally the weight matrices $E_{i}^{st}$ to act as an identity operator at $(\Gamma ^{s} \cup \Gamma ^{t})\backslash \Gamma ^{st}$ (cf. Sect. 4).

In the computations reported in Sect. 8, we drop the adaptively generated edge constraints in 3D. Then, it is no longer guaranteed that the condition number indicator $\widetilde{\omega }\le \tau ^{L-1}$. However, the method is still observed to perform well. Since the constraint weights are thus supported only on faces, and the entries corresponding to edges are set to be zero, we orthogonalize and normalize the vectors of constraint weights (by reduced QR decomposition from LAPACK) to preserve numerical stability.

In our experience, preconditioning of the LOBPCG method as described in Sect. 5 led to a considerable reduction of the number of LOBPCG iterations. Or in other words, since we usually put a limit of maximum 15 iterations for an eigenproblem, the resulting eigenvectors are much better converged than without preconditioning. In the parallel implementation of the adaptive selection of constraints, pairs are assigned to processors independently of assignment of subdomains. The BDDCML package uses the open-source implementation of LOBPCG method [16] available in the BLOPEX package.² Details of the parallel implementation of adaptive selection of constrains were described for two-level BDDC method in detail in [31].

7.3 Multilevel implementation

The BDDCML library allows assignment of multiple subdomains at each process. At each level, subdomains are assigned to available processors, always starting from root. Distribution of subdomains on the first level is either provided by user’s application, or created by the solver using ParMETIS library (version 3.2). On higher levels, where the mesh is considerably smaller, METIS (version 4.0) [11] is internally used by BDDCML to create mesh partitions. This means, that on higher levels, where number of subdomains is lower than number of processors, cores with higher ranks are left idle by the preconditioner.

For solving local discrete Dirichlet and Neumann problems on each subdomain, BDDCML relies on a sequential instance of direct solver MUMPS [1]. A parallel instance of MUMPS is also invoked for factorization and repeated solution of the final coarse problem at the top level. More details on implementation of the (non-adaptive) multilevel approach in BDDCML can be found in [32].

8 Numerical examples

To study the properties of the Adaptive-Multilevel BDDC method numerically, we have selected four problems of structural analysis—two artificial benchmark problems and two realistic engineering problems. Some of the results were obtained by our serial implementation written in Matlab and reported in thesis [36]. This implementation is mainly used to study convergence behaviour with respect to prescribed tolerance on the condition number indicator $\tau$. The other set of results is obtained using our newly developed parallel implementation within the BDDCML library. Parallel results were obtained on Cray XE6 supercomputer Hector at the Edinburgh Parallel Computing Centre. In the computations, one step of the Adaptive-Multilevel BDDC method is used as the preconditioner in the preconditioned conjugate gradient (PCG) method, which is run until the (relative) norm of residual decreases below $10^{-8}$ (in Matlab tests) or $10^{-6}$ (in BDDCML runs).

8.1 Elasticity in a cube without and with jump in material coefficients

As the first problem, we use the standard benchmark problem of a unit cube. In our setting, we solve the elastic response of the cube under loading by its own weight, when it is fixed at one vertical edge. There are nine bars cutting horizontally through the cube. We test the case when the bars are of the same material as the rest of the cube (homogeneous material) and the case when Young’s modulus of the outer material $E_1$ is $10^6$ times smaller than that of the bars $E_2$, creating contrast in coefficients $E_2/E_1 = 10^6$. In Fig. 1 (right), the (magnified) deformed shape of the cube is shown for this jump in Young’s modulus. We have recently presented a detailed study of behaviour of the standard (2-level) BDDC method and its adaptive extension with respect to contrast on the same problem in [31]. It was shown in that reference, that while convergence of BDDC with the standard choice of arithmetic averages on faces quickly deteriorates with increasing contrast, adaptive version of the algorithm is capable of maintaining good convergence also for large values of contrast, at the cost of quite expensive set-up phase.

Fig. 1

Example of a division of the cube into 64 subdomains (left) and (magnified) deformed shape for contrast $E_2/E_1 = 10^6$ coloured by vertical displacement (right)

The multilevel approach (without adaptivity), although it may lead to faster solution, suffers from exponentially growing condition number and related number of iterations, as reported in [26], or recently in [32]. Here, we investigate the effect of constraints adaptively generated at higher levels in the multilevel algorithm. We also study the parallel performance of our solver on this test problem.

The cube is discretized using uniform mesh of tri-linear finite elements and divided into an increasing number of subdomains. On the first level, subdomains are cubic with constant $H/h = 16$ ratio (see Fig. 1 left for an example of a division into 64 subdomains). On higher levels, divisions into subdomains are created automatically inside BDDCML by the METIS package, in general not preserving cubic shape of subdomains.

In Tables 1 and 2, we present results of a weak scaling test for the case of the homogeneous cube, i.e. $E_2/E_1 = 1$. This problem is very well suited for the BDDC method, and the performance is generally very good. The growing problem is solved on 8 to 32,768 processors (with each core handling one subdomain of the first level). In these tables, $N$ denotes the number of subdomains (and computer cores), $n$ denotes global problem size, $n_{\Gamma }$ represents the size of the reduced problem defined at the interface $\Gamma ,\,n_f$ is the number of faces in divisions on the levels (corresponding to number of generalized eigenproblems solved in the adaptive approach), ‘its.’ is the number of iterations needed by the PCG method, and ‘cond.’ is the estimated condition number obtained from the tridiagonal matrix generated in PCG. We report times needed by the set-up phase (‘set-up’), by PCG iterations (‘PCG’) and their sum (‘solve’).

Table 1 Weak scaling for the cube problem with homogeneous material, non-adaptive multilevel BDDC

Table 2 Weak scaling for the cube problem with homogeneous material, adaptive multilevel BDDC

In Table 1, no adaptivity is used, and only the number of levels is varying. We can see, that for the standard (2-level) BDDC, we obtain the well-known independence of number of iterations on problem size. We can also see, how condition number (and number of PCG iterations) grows when using more levels. Although this can lead to savings in time in certain circumstances (due-to cheaper set-up), no such benefits are seen here and these are more common in tests of strong scaling with fixed problem size [32].

The independence on problem size is slightly biased on higher levels, probably due to the irregular subdomains. Computational times slightly grow with problem size, suggesting sub-optimal scaling of BDDCML, especially when going from 512 to 4,096 computing cores. For the largest problem of $32\times 32\times 32$ subdomains with 405 million degrees of freedom solved on 32,768 cores, all times grow considerably. This is most likely due to the higher cost of global communication functions at this core count, and these results will serve for future performance analysis and optimization of the BDDCML solver. Note, that in the case of two levels, parallel direct solver MUMPS failed to solve the resulting coarse problem at this level of parallelism, which is marked by ‘n/a’ in the tables.

We are now interested in the effect of adaptively generated constraints on convergence of the multilevel BDDC method. Based on recommendations from [31], we limit number of LOBPCG iterations to 15 and maximal number of computed eigenvectors to 10 to maintain the cost of LOBPCG solution low. The target condition number limit is set low, $\tau = 1.5$, which leads to using most of the adaptively generated constraints in actual computation. Results are reported in Table 2. We can see, that the adaptive approach is capable of keeping the iteration counts lower, and although the independence of the number of levels is not achieved, the growth is slower than for the non-adaptive approach. While the scalability of the solver is similar to the non-adaptive case, it is not surprising that the computational time is now dominated by the solution of the generalized eigenvalue problems. This fact makes the adaptive method unsuitable for simple problems like this one, in agreement with conclusions for the 2-level BDDC in [31].

The situation changes however, when some numerical difficulties appear in the problem of interest. One source of such difficulties may be presented by jumps in material coefficients. To model this effect, we increased the jump between Young’s moduli of the stiff rods and soft outer material to $E_2/E_1 = 10^6$, and these results are reported in Tables 3 and 4. For the non-adaptive method (Table 3) we can see growth of number of iterations and condition number not only with adding levels, but also for growing problem size. This growth is translated to large time spent in PCG iterations, which now dominate the whole solution.

Table 3 Weak scaling for the cube problem with jump in coefficients $E_2/E_1 = 10^6$, non-adaptive multilevel BDDC

Table 4 Weak scaling for the cube problem with jump in coefficients $E_2/E_1 = 10^6$, adaptive multilevel BDDC

Results are very different for the adaptive approach in Table 4, for which the main cost is still presented by the solution of the related eigenproblems (included into time of ‘set-up’). Since we keep the number of computed eigenvectors constant (ten) for each pair of subdomains, the method is not able to maintain a low condition number after all these eigenvectors are used for generating constraints. However, number of iterations is always significantly lower than in the non-adaptive approach, and the method typically requires about one half of the computational time. While this is an important saving of computational time, it is also shown in [31], that the adaptive approach can solve even problems with contrasts such high, that they are not solvable by the non-adaptive approach with arithmetic averages on all faces and edges.

Finally, we compare properties of the coarse basis functions on the first and the second level on this problem. We consider homogeneous material of the cube which is divided into regular cubic subdomains both on the first and the second (unlike in the previous test) level. Namely, the cube is divided into $4\times 4\times 4=64$ subdomains on the second level. Each of these subdomains is composed again of $4\times 4\times 4=64$ subdomains of the first level, which gives 4,096 subdomains. Each of these first-level subdomains is composed of $4\times 4\times 4=64$ tri-linear finite elements. The problem has in total 262,144 elements and 823,872 unknowns. Table 5 summarizes results of the adaptive 3-level BDDC method for different values of prescribed tolerance $\tau$. For comparison, the non-adaptive 3-level BDDC method with three arithmetic averages on each face requires 19 PCG iterations and the resulting estimated condition number is 6.88.

Table 5 Comparison of adaptively selected constraints for different target condition number $\tau ^2$, adaptive 3-level BDDC

We can see, that significantly (roughly five times) more constraints are selected on the second level than on the first one, which suggests that the discrete harmonic basis functions of the first level lead to worse conditioned coarse problem on the second level. Thus, it underlines the importance of adaptive selection of constraints on higher levels. For $\tau ^2 = 2.25$, the maximal number of adaptive constraints (ten) is used on each pair, and the algorithm is ‘saturated’. Consequently, more constraints would be necessary on each pair to satisfy the condition $\widetilde{\omega }\le \tau ^2$ from Algorithm 3.

8.2 Elasticity in a cube with variable size of regions of jumps in coefficients

The performance of the Adaptive-Multilevel BDDC method in the presence of jumps in material coefficients has been tested on a cube designed similarly as the problem above, with material properties $E_1=10^{6},\,\nu _1=0.45$, and $E_2=2.1\times 10^{11},\,\nu _2= 0.3$. However, the stiff bars now vary in size, and while the thin bars create numerical difficulties on the first level, the large bar creates a jump in the decomposition on the second level, see Fig. 2. The computational mesh consists of 823k degrees of freedom and it is distributed into 512 substructures with 1,344 faces on the first decomposition level, and into 4 substructures with 4 faces on the second decomposition level (see Fig. 2).

Fig. 2

Cube with variable size of regions of jumps in coefficients: distribution of material with stiff bars ($E_2=2.1\times 10^{11},\,\nu _2= 0.3$), and soft outer material ($E_1=10^{6},\,\nu _1=0.45$) (left), mesh consisting of 823k degrees of freedom distributed into 512 substructures with 1,344 faces on the first decomposition level (centre), and 4 substructures with 4 faces on the second decomposition level (right). Reproduced from [36]

First, we present results by our serial implementation in Matlab, published initially in the thesis [36]. We include them here along the parallel results to make this study of Adaptive-Multilevel BDDC more self-contained. Comparing the results in Tables 6 and 7 we see that a relatively small number of (additional) constraints leads to a considerable decrease in number of iterations of the 2-level method. In these tables, $Nc$ denotes number of constraints, ‘c’,‘c+e’, ‘c+e+f’ denote combinations of constraints at corners, and arithmetic averages at edges and faces, ‘3eigv’ corresponds to using three adaptive constraints on faces instead of the three arithmetic averages, $\tau$ denotes the target condition number from Algorithm 3, $\widetilde{\omega }$ is the indicator of the condition number from (49), ‘cond.’ denotes estimated condition number, and ‘its.’ the number of PCG iterations.

Table 6 Results for the cube with variable size of regions of jumps in coefficients (Fig. 2) obtained using the non-adaptive 2-level BDDC method

Table 7 Results for the cube with variable size of regions of jumps in coefficients (Fig. 2) obtained using the adaptive 2-level BDDC method

When the non-adaptive 2-level is replaced by the 3-level method (Tables 8 and 9), the condition number estimate as well as the number of iterations grow, in agreement with the estimate (25). However, with the adaptive 3-level approach (Table 9) we were able to achieve nearly the same convergence properties for small $\tau$ as in the adaptive 2-level method (Table 7).

Table 8 Results for the cube with variable size of regions of jumps in coefficients (Fig. 2) obtained using the non-adaptive 3-level BDDC method

Table 9 Results for the cube with variable size of regions of jumps in coefficients (Fig. 2) obtained using the adaptive 3-level BDDC method

Next, we use this test problem to perform a strong scaling test of our parallel implementation of adaptive multilevel BDDC method. Since BDDCML supports assigning several subdomains to each processor, the division is kept constant with 512 subdomains on the basic level, and 4 subdomains on the second level (as in Fig. 2), and number of cores is varied.

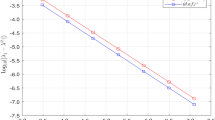
Figure 3 presents parallel computational time and speed-up when this problem is solved by the parallel 2-level BDDC method, comparing efficiency of the non-adaptive and adaptive solver. We report times and speed-ups independently for the set-up phase (including solution of eigenproblems for adaptive method), the phase of PCG iterations, and their sum (‘solve’). Figure 4 then presents parallel computational time and speed-up for 3-level BDDC method.

Fig. 3

Strong scaling test for the cube with variable size of regions of jumps in coefficients (Fig. 2) containing 823k degrees of freedom, on the first level divided into 512 subdomains with 1,344 faces with arithmetic/adaptive constraints. Computational time (left) and speed-up (right) separately for set-up and PCG phases, and their sum (‘solve’), comparison of non-adaptive (680 its.) and adaptive (85 its.) parallel 2-level BDDC

Fig. 4

Strong scaling test for the cube with variable size of regions of jumps in coefficients (Fig. 2) containing 823k degrees of freedom, on the first level divided into 512 subdomains with 1,344 faces with arithmetic/adaptive constraints, and on the second level into 4 subdomains with 4 faces. Computational time (left) and speed-up (right) separately for set-up and PCG phases, and their sum (‘solve’), comparison of non-adaptive (894 its.) and adaptive (150 its.) parallel 3-level BDDC

We can see, that both phases of the solution are reasonably scalable. For large core counts, scalability worsens, as each core has only little work with subdomain problems and (the less scalable) solution of the coarse problem dominates the computation. It is worth noting, that the overall fastest solution was delivered by the adaptive 2-level BDDC method on 512 cores, while both other extensions of BDDC—non-adaptive 3-level BDDC and adaptive 3-level BDDC—were also considerably faster than the standard (non-adaptive 2-level) BDDC method on large number of cores.

8.3 Linear elasticity analysis of a mining reel

The performance of the Adaptive-Multilevel BDDC has been tested on an engineering problem of linear elasticity analysis of a mining reel. The problem was provided for testing by Jan Leština and Jaroslav Novotný. The computational mesh consists of 141k quadratic finite elements, 579k nodes, and approximately 1.7M degrees of freedom. It was divided into 1,024 subdomains with 3,893 faces (see Fig. 5).

Fig. 5

Finite element discretization and substructuring of the mining reel problem, consisting of 1.7M degrees of freedom, divided into 1,024 subdomains with 3,893 faces. Data by courtesy of Jan Leština and Jaroslav Novotný. Reproduced from [36]

The problem presents a very challenging application for iterative solvers due to its very complicated geometry. It contains a steel rope, which is not modelled as a contact problem but just by a complicated mesh with elements connected through edges of three-dimensional elements (Fig. 6). Its automatic partitioning by METIS creates further problems such as thin elongated subdomains, disconnected subdomains, or subdomains with insufficiently coupled elements leading to ‘spurious mechanisms’ inside subdomains. See Fig. 6 for examples.

Fig. 6

Examples of difficulties with computational mesh and its partitioning for the mining reel problem: (i) rope modelled as axisymmetric rings connected at edges of three-dimensional elements (top left), (ii) disconnected subdomains (top right), (iii) elongated substructures (bottom left), (iv) spurious mechanisms within subdomains, such as elements connected to rest of the subdomain only at single node (bottom right). Reproduced from [36]

We first perform a series of computations by our serial implementation in Matlab to study the effect of prescribed target condition number $\tau$ on convergence. Comparing results by non-adaptive 2-level BDDC (Table 10) with adaptive 2-level BDDC (Table 11), we see that the adaptive approach allows for a significant improvement in the number of iterations.

Table 10 Convergence of the non-adaptive 2-level BDDC method with different constraints, mining reel problem

Table 11 Convergence of the adaptive 2-level BDDC method with variable target condition number parameter $\tau$, mining reel problem

We can also see, that convergence of the adaptive two- and three-level method (Tables 11, 12) is nearly identical. For the three-level method, automatic division into 32 subdomains was used on the second level.

Table 12 Convergence of the adaptive 3-level BDDC method with variable target condition number parameter $\tau$, mining reel problem

We note that the observed approximate condition number computed from the Lanczos sequence in PCG (‘cond.’) is larger than the target condition number $\tau$ for this problem. In [23, 36], it was shown that these two numbers match remarkably well for simpler problems, especially in 2D. Despite this difference, the algorithm still performs very well.

Next, we solved this problem with the parallel implementation of the algorithm. In Fig. 7, we present results of a strong scaling test.

Fig. 7

Strong scaling test for the mining reel problem containing 1.7M degrees of freedom and on the first level divided into 1,024 subdomains with 3,893 faces with arithmetic/adaptive constraints, computational time (left) and speed-up (right) separately for set-up and PCG phases, and their sum (‘solve’), comparison of non-adaptive (610 its.) and adaptive (200 its.) parallel 2-level BDDC

The non-adaptive 2-level BDDC method requires 610 PCG iterations, while the adaptive 2-level BDDC needs only 200 PCG iterations. Nevertheless, this difference is only able to compensate the cost of solving the eigenproblems, and the adaptive method is advantageous with respect to computing time only for 1,024 cores.

We can see, that the scaling is nearly optimal, with the deviation caused probably again by the small size of the problem compared to the core counts used in this experiment. In the parallel case, the 3-level approach did not work well neither with nor without adaptive selection of constraints, requiring more than 5,000 PCG iterations in both cases. The slow convergence of the adaptive 3-level method is probably caused by the limit of ten adaptive constraints per face, which seems to be insufficient for this difficult problem—in Matlab experiments, as many as 8,681 adaptive constraints were generated among 32 subdomains on the second level in order to satisfy $\widetilde{\omega } \le \tau ^2 = 5$ (Table 12).

8.4 Linear elasticity analysis of a geocomposite sample

Finally, the algorithm is applied to a problem of elasticity analysis of a cubic geocomposite sample. The sample was analyzed in [2] and provided by the authors for testing of our implementation. The length of the edge of the cube is 75 mm, and the cube is composed of five distinct materials identified by means of computer tomography.

Different material properties cause anisotropic response of the cube even for simple axial stretching in z-direction (Fig. 8 right). The problem is discretized using unstructured grid of about 12 million linear tetrahedral elements, resulting in approximately 6 million degrees of freedom. The mesh was divided into 1,024 subdomains on the first and into 32 subdomains on the second level, resulting in 5,635 and 100 faces, respectively.

Fig. 8

Elasticity in a geocomposite sample; Young’s modulus due to different materials (left), magnitude of displacement on slices (right). Mesh contains 12 million linear tetrahedral elements and approx. 6 million degrees of freedom. Data by courtesy of Radim Blaheta and Jiří Starý

Table 13 summarizes the number of iterations and estimated condition number of the preconditioned operator for the combinations of 2- and 3-level BDDC with non-adaptive and adaptive selection of constraints. For this problem, number of iterations was reduced to approximately one half by using adaptivity. We can also see, that number of iterations grows considerably when going from 2 to 3 levels for this problem.

Table 13 Number of iterations and condition number estimate for the geocomposite problem, 6 million degrees of freedom

In Figs. 9 and 10, we report strong scaling of the parallel implementation on this problem for 2-level and 3-level BDDC, respectively. The strong scaling is again nearly optimal.

Fig. 9

Strong scaling test for the geocomposite problem (Fig. 8) containing approx. 6 million degrees of freedom, on the first level divided into 1,024 subdomains with 5,635 faces with arithmetic/adaptive constraints. Computational time (left) and speed-up (right) separately for set-up and PCG phases, and their sum (‘solve’), comparison of non-adaptive (65 its.) and adaptive (36 its.) parallel 2-level BDDC

Fig. 10

Strong scaling test for the geocomposite problem (Fig. 8) containing approx. 6 million degrees of freedom, on the first level divided into 1,024 subdomains with 5,635 faces with arithmetic/adaptive constraints, and on the second level into 32 subdomains with 100 faces. Computational time (left) and speed-up (right) separately for set-up and PCG phases, and their sum (‘solve’), comparison of non-adaptive (214 its.) and adaptive (113 its.) parallel 3-level BDDC

We can again see that while for the non-adaptive approach, most time is spent in the PCG iterations, for the adaptive approach, the curve for the set-up phase is almost indistinguishable from the one for total solution time, and the set-up clearly dominates the solution. For the two-level method, MUMPS was not able to solve the coarse problem on 1,024 cores and so this value is omitted in Fig. 9.

9 Conclusion

We have presented the algorithm of Adaptive-Multilevel BDDC method for three-dimensional problems, and its parallel implementation. The algorithm represents the concluding step of combining ideas developed separately for adaptive selection of constraints in BDDC  [23, 27, 31, 35], and for the multilevel extension of the BDDC method [25, 26, 32]. The algorithm and its serial implementation was studied in the thesis [36], and the serial algorithm for two dimensional problems also in [39].

The Adaptive BDDC method aims at numerically difficult problems, like those containing severe jumps in material coefficients within the computational domain. It recognizes troublesome parts of the interface by solving a generalized eigenvalue problem for each pair of adjacent subdomains which share a face. By dominant eigenvalues the method detects where constraints need to be concentrated in order to improve the coarse space, thus reducing number of iterations. On the other hand, the Multilevel BDDC aims at improving scalability of the BDDC method for very large numbers of subdomains, for which the coarse problem gets too large and/or fragmented to be solved by a parallel direct solver. However, as theory suggests and experiments confirm, Multilevel BDDC leads to an exponential growth of the condition number and the number of iterations.

The Adaptive-Multilevel BDDC method provides a kind of synergy of the adaptive and the multilevel approaches. Our results confirm, that adaptively generated constraints are capable of reducing the rate of growth of the condition number with levels. At the same time, the extension to three levels improved scalability of the adaptive 2-level approach, and for large problems and core counts, we have been able to obtain results we could not get by the 2-level method.

A convenient way of preconditioning the LOBPCG method based on components of BDDC was presented, effectively converting the generalized eigenvalue problems to ordinary eigenproblems. In our computations, this preconditioning led to large savings of number of LOBPCG iterations and corresponding computing time. However, to reduce the time necessary for solving the eigenproblems further, we have restricted the maximal number of adaptively generated constraints per face to ten in our parallel computations. For this reason, the resulting performance of the adaptive method was not as optimal as the serial tests (with arbitrary number of constraints per face) suggested.

We have described a parallel implementation of the algorithm available in our open-source library BDDCML. The solver has been successfully applied to systems of equations with over 400 million unknowns solved on 32 thousand cores. Presented results confirm, that both adaptive and non-adaptive implementations are reasonably scalable. However, presented computations have also revealed sub-optimal scaling especially on large numbers of cores, and these results will provide a basis for further optimization of the solver.

We have presented results of two benchmark and two engineering problems of structural analysis. On all problems, the adaptive selection of constraints led to reduced number of PCG iterations. However, for most problems, this fact did not lead to savings in computational time, and the cost of generating adaptive constraints was not compensated by saved iterations.

It can be concluded that the adaptive method is not suitable for simple problems, where also non-adaptive (even multilevel) method would converge reasonably fast. For problems with difficulties, the non-adaptive BDDC method leads to large cost of PCG iterations, especially for using several levels. On the contrary, the set-up phase with solution of local eigenproblems mostly dominates the overall solution time for the Adaptive-Multilevel BDDC method. Which approach is finally advantageous depends on a particular problem. Apart of the aspect of computational time, we have already encountered several problems for which the non-adaptive BDDC method failed, and which have been successfully solved by adaptive BDDC.