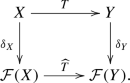Lipschitz p-compact mappings

Abstract

We introduce the notion of Lipschitz p-compact operators. We show that they can be seen as a natural extension of the linear p-compact operators of Sinha and Karn and we transfer some properties of the linear case into the Lipschitz setting. Also, we introduce the notions of Lipschitz-free p-compact operators and Lipschitz locally p-compact operators. We compare all these three notions and show different properties. Finally, we exhibit examples to show that these three notions are different.

1 Introduction

Since the work of Farmer and Johnson [8], where the notion of p-summing Lipschitz functions was introduced, there was an increasing interest in the study of different classes of Lipschitz functions between (pointed) metric spaces and Banach spaces. Most of them, can be seen as a generalization of different linear operators ideals between Banach spaces. Recently, the first author, Rueda et al. [1] and, independently, Cabrera–Padilla et al. [4] introduced the notion of Lipschitz operator ideals in the same spirit of linear operator ideals. It turns out that almost all of the new classes of Lipschitz mappings studied fit in the framework of Lipschitz operator ideals.

On the other hand, in the theory of linear operator ideals, some classes are characterized by the nature of their image on some neighborhoods of the origin of a Banach space. For example the classes of compact and weakly compact linear operators. In 2002, Sinha and Karn [21] introduced the p-compact sets in Banach spaces, which can be seen as a refinement of the notion of compact sets. Associated with the concept of p-compact sets, they define and begin the study of p-compact linear operators. A linear operator between Banach spaces is p-compact if maps a neighborhood of the origin into a relatively p-compact set. The p-compact sets and operators deserved the attention of many authors in the last years, not only in the linear case but also in the non-linear case.

The aim of this work is to study Lipschitz operators between pointed metric spaces and Banach spaces which are determined by p-compact sets. For this, we introduce three different notions of Lipschitz operators related with p-compact sets: the Lipschitz p-compact operators, the Lipschitz free-p-compact operators, and the locally p-compact Lipschitz operators.

The article is organized as follows. After fixing some notation and establishing the basics of the theory of Lipschitz operators and p-compact sets that we will use throughout the manuscript, in Sect. 3 we focus in the study of Lipschitz p-compact operators. We show that this type of operators fits in the theory of composition Banach Lipschitz operator ideal. This allows us to extend to the Lipschitz mappings setting the majority of the results obtained in the linear case. For instance, we show that the Lipschitz p-compact operators are a regular, but not an injective Banach Lipschitz operator ideal. Also, from the factorization of linear p-compact operators, we get a suitable factorization of the Lipschitz p-compact operators. Section 4 is devoted to the Lipschitz free-p-compact operators and the locally p-compact Lipschitz operators. We compare all these three notions which are, in particular, different.

2 Notation and preliminaries

As usual, X and Y will be pointed metric spaces with a base point denoted by 0 and metric will be denoted by d. For $x_0 \in X$ and $\varepsilon >0$, we denote by $B_{\varepsilon }(x_0)$ the open ball centered at $x_0$ with radius $\varepsilon$, meanwhile $B_{X}$ denotes the closure of the ball centered at 0 with radius 1. Also, E and F will stand for Banach spaces over the same field ${\mathbb {K}}$ (either ${\mathbb {R}}$ or ${\mathbb {C}}$) with dual spaces $E^*$ and $F^*$. A Banach space E will be considered as pointed metric spaces with distinguished point 0 and distance $d(x,x')=\Vert x-x'\Vert$. With $Lip_{0}(X;Y)$ we denote the set of all Lipschitz mappings from X to Y such that maps 0 to 0. In particular, $Lip_{0}(X,E)$ is the Banach space of all Lipschitz mappings T from X to E that vanish at 0, under the Lipschitz norm

$$\begin{aligned} Lip\left( T\right) =\inf \{C>0:\left\| T(x)-T(x^{\prime })\right\| \le Cd(x,x^{\prime }); \ \forall x,x^{\prime }\in X \}. \end{aligned}$$

When $E={\mathbb {K}}$, $Lip_{0}(X,{\mathbb {K}})$ is denoted by $X^{\#}$ and it is called the Lipschitz dual of X. The space of all linear operators from E to F is denoted by ${\mathcal {L}}(E,F)$ and it is a Banach space with the usual supremum norm. It is clear that ${\mathcal {L}}(E,F)$ is a subspace of $Lip_0(E,F)$ and, in particular, $E^*$ is a subspace of $E^{\#}$. One of the main tools that we will use is the Lipschitz-free Banach space of a metric space X, ${\mathcal {F}}(X)$ (also known as the Arens–Ells space). For $x\in X$, denote by $\delta _x$ the function $\delta _{x}:X^{\#}\longrightarrow {\mathbb {K}}$ defined as

$$\begin{aligned} \delta _{x}(f)=f(x),\text { }f\in X^{\#}. \end{aligned}$$

Then ${\mathcal {F}}(X)$ is the closed linear span of $\left\{ \delta _{x},x\in X\right\}$ in $\left( X^{\#}\right) ^{*}$. The Dirac map $\delta _X:X\rightarrow {\mathcal {F}}(X)$ is defined as $\delta _X(x)(f)=\delta _x(f)$ for all $x \in X$ and $f \in X^{\#}$. In [10] or [11], it is proved that ${\mathcal {F}}({\mathbb {R}})$ is isometric to $L_{1}({\mathbb {R}})$. We summarize some basic properties concerning Lipschitz-free Banach spaces in the following lemma. This can be found for instance in [14]. Will use it without further mentioning.

Lemma 2.1

Let X,  Y be pointed metric spaces and E be a Banach space.

• (1) The dual space of ${\mathcal {F}}(X)$ is isometrically isomorphic to $X^{\#}$ through the mapping $Q_{X}:X^{\#}\rightarrow {\mathcal {F}}(X)^{*}$ given by

  $$\begin{aligned} Q_{X}(f)(\gamma )=\gamma (f),\text { }f\in X^{\#},\gamma \in {\mathcal {F}}(X).\end{aligned}$$

• (2) For any Lipschitz mapping $T\in Lip_{0}(X,Y)$ there exists a unique linear map ${\widehat{T}}:{\mathcal {F}}(X)\rightarrow {\mathcal {F}}(Y)$ such that ${\widehat{T}}\circ \delta _{X}=\delta _{Y}\circ T$. That is, the following diagram commutes

  

  Moreover, $\Vert {{\widehat{T}}}\Vert =Lip(T)$.

• (3) There exists a quotient map $\beta _E:{\mathcal {F}}(E)\rightarrow E$ such that $\beta _E \circ \delta _E=Id_E$.

• (4) For any Lipschitz operator $T\in Lip_{0}(X,E)$ there exists a unique linear map $T_{L}:{\mathcal {F}}(X)\longrightarrow E$ such that $T=T_{L}\circ \delta _{X}$.That is, the following diagram commutes

  

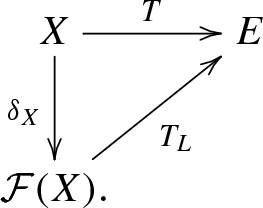
  Moreover, $\Vert T_L\Vert =Lip(T)$.

In particular, from (2) and (3) we can deduce (4) with $T_L=\beta _E{\widehat{T}}$. The map $\beta _E:{\mathcal {F}}(E)\rightarrow E$ is called the barycenter map. For $T\in Lip_{0}(X,E)$, we will consider the Lipschitz adjoint (or dual) of T, defined by Sawashima [20]. That is, $T^{\#}\in {\mathcal {L}}(E^{\#},X^{\#})$ is the linear operator given by $T^{\#}(g)=g\circ T$ for all $g\in E^{\#}$. The restriction of $T^{\#}$ to $E^{*}$ is called the Lipschitz transpose map of T and is denoted here by $T^{t}$. Is clear that $Q_X\circ T^{t}=T_L^{*}$, where $T_L^{*}$ denotes the transpose map of the linearization of T and also that ${\widehat{T}}^{*} \circ Q_Y=Q_X\circ T^{\#}$.

For $p\ge 1,$ and $p^{*}$ the conjugate index of p (i.e. $1/p+1/p^{*}=1$ with the convention $1/\infty =0$), a sequence $(x_i)_{i=1}^{\infty }$ in E is p-summable if

$$\begin{aligned}\left\| \left( x_{i}\right) _{i=1}^{\infty }\right\| _{p} =\left( \sum \limits _{i=1}^{\infty }\left\| x_{i}\right\| ^{p}\right) ^{\frac{1}{p}}<\infty . \end{aligned}$$

We denote by $\ell _p(E)$ the space of all p-summable sequences in E. This space is a Banach space if we endow it with the norm $\left\| \cdot \right\| _{p}$. Also, $c_0(E)$ and $\ell _\infty (E)$ are the spaces of null sequences and bounded sequences of E. Both spaces, endowed with the supremum norm are Banach spaces.

For $1\le p<\infty$, p-compact sets and linear operators were introduced by Sinha and Karn [21] and deeply studied in [2, 6, 9, 15, 18] among others. Recall that the p-convex hull of a sequence $\left( x_{i}\right) _{_{i=1} }^{\infty }\in \ell _{p}\left( E\right)$ is defined by

$$\begin{aligned} {{ p}{\mathrm{-conv}}}\left\{ \left( x_{i}\right) _{i=1}^{\infty }\right\} :=\left\{ \sum \limits _{i=1}^{\infty }a_{i}x_{i}:\left( a_{i}\right) _{i=1}^{\infty }\in B_{\ell _{p^{*}}}\right\} \subset E, \end{aligned}$$

where $\ell _{p^*}=c_0$ if $p=1$. Note that $\infty \text {-conv} \{\left( x_{i}\right) _{_{i=1} }^{\infty }\}={\overline{\Gamma }}(\{\left( x_{i}\right) _{_{i=1} }^{\infty }\})$, the closed absolutely convex hull of $\{\left( x_{i}\right) _{_{i=1} }^{\infty }\}.$ A set $K\subset E$ is said to be relatively p-compact if there exists a sequence $\left( x_{i}\right) _{_{i=1}}^{\infty }\in \ell _{p}(E)$ such that $K\subset {{ p}{\mathrm{-conv}}}\{\left( x_{i}\right) _{_{i=1}}^{\infty }\}$. Such a sequence is not unique, so Lassalle and the third author in [15] defined the measure of the size of the p-compact set K as

$$\begin{aligned} m_{p}(K,E)=\inf \left\{ \left\| (x_{i})_{i=1}^{\infty }\right\| _{p}:K\subset p\text {-conv}\left\{ (x_{i})_{i=1}^{\infty }\right\} \right\} \end{aligned}$$

and $m_{p}(K,E)=\infty$ if K is not p-compact. When the context $K\subset E$ is understood, we simply write $m_{p}(K)$ instead of $m_{p}(K,E)$. From Grothendieck’s classical characterization of compact sets (see [12, Chapter I, p. 112]), we have that a set $K\subset E$ is relatively compact if and only if there exists a sequence $\left( x_{i}\right) _{i=1}^{\infty }\in c_{0}(E)$ such that $K\subset \infty \text {-conv}\left\{ \left( x_{i}\right) _{i=1}^{\infty }\right\}$ and also $m_{\infty }(K,E)=\sup _{x\in K}\Vert x\Vert$.

A linear operator $T \in {\mathcal {L}}(E,F)$ is said to be p-compact if $T(B_E)$ is a relatively p-compact set. The space of all p-compact linear operators from E to F is denoted by ${\mathcal {K}}_p(E,F)$ and it becomes a Banach space if we endow it with the norm

$$\begin{aligned}k_p (T)=m_p(T(B_E)).\end{aligned}$$

We refer to the reader to Weaver’s book [22] for the basics of Lipschitz operators and to the book of Pietsch [16] for linear operator ideals.

3 The composition ideal of Lipschitz p-compact operators

We start with the Lipschitz p-compact operators which, as in the linear case, can be seen as a refinement of Lipschitz compact operators. Recall that, for a pointed metric space X, a Banach space E and $T\in Lip_0(X,E)$, Jiménez–Vargas, Sepulcre and Villegas–Vallecillos defined in [13] the Lipschitz image of T as

$$\begin{aligned} Im_{Lip}(T)=\left\{ \frac{T(x)-T(y)}{d(x,y)}:x,y\in X,x\ne y\right\} . \end{aligned}$$

Definition 3.1

Let X be a pointed metric space, E a Banach space and let $p\ge 1$. A Lipschitz operator $T\in Lip_{0}(X,E)$ is Lipschitz p-compact if its Lipschitz image is relatively p-compact. We denote by ${\mathcal {K}}_{p}^{L}(X,E)$ the set of all Lipschitz p-compact mappings from X to E. Moreover, if $T\in {\mathcal {K}}_{p}^{L}(X,E)$, then we set

$$\begin{aligned} k_{p}^{L}(T)=m_p(Im_{Lip}(T)). \end{aligned}$$

If $p=\infty$, then ${\mathcal {K}}_{\infty }^{L}(X,E)=Lip_{0K}(X,E)$, the space of Lipschitz compact operators defined and studied in [13].

The Lipschitz p-compact operators can be seen as an extension of the linear p-compact operators. Indeed, for E and F Banach spaces, for any linear operator $T:E\rightarrow F$ we have that the absolutely convex hull of $Im_{Lip}(T)$ coincides with $T(B_E)$. Then, since a set is p-compact if and only if its absolutely convex hull is also p-compact with the same measure (see the bottom of [15, p. 1205]), we have the following result.

Proposition 3.2

Let E and F be Banach spaces. Then a linear operator $T\in {\mathcal {L}}(E,F)$ is p-compact if and only if it is Lipschitz p-compact. Moreover, we have

$$\begin{aligned} k_{p}^{L}(T)=k_p(T). \end{aligned}$$

It is well-known that, if $1\le p\le q\le \infty$, then every relatively p-compact set is relatively q-compact. Therefore, we immediately get the following inclusion results.

Proposition 3.3

Let $1\le p\le q\le \infty$, X be a pointed metric and E be a Banach space. Then the Lipschitz p-compact operators are q -compact, and $k_{q}^{L}(T)\le k_{p}^{L}(T)$ for any $T\in {\mathcal {K}} _{p}^{L}(X,E)$. In particular, the Lipschitz p-compact operators are Lipschitz compact.

Mimicking the proof of [13, Proposition 2.1], we have the following result.

Theorem 3.4

Let X be a pointed metric space, E a Banach space and let $p\ge 1$. An operator $T\in Lip_{0}(X,E)$ is Lipschitz p-compact if and only if its linearization $T_{L}:{\mathcal {F}} (X)\rightarrow E$ is linear p-compact. Moreover, we have

$$\begin{aligned} k_{p}^{L}(T)=k_{p}(T_{L}). \end{aligned}$$

(1)

Proof

In the proof of [13, Proposition 2.1] it is shown that, for $T \in Lip_0(X,E)$,

$$\begin{aligned} Im_{Lip}(T)\subset T_{L}(B_{{\mathcal {F}}(X)})\subset \overline{\Gamma }\left( Im_{Lip}(T)\right) . \end{aligned}$$

(2)

Then, by [15, p. 1205], we get that

$$\begin{aligned} m_p(Im_{Lip}(T))=m_p(T_{L}(B_{{\mathcal {F}}(X)}))=m_p(\overline{\Gamma }\left( Im_{Lip}(T)\right) ), \end{aligned}$$

and the result follows. $\square$

Recently, the notion of Banach Lipschitz operator ideal was introduced by the first author, Rueda et al. [1] and, independently, Cabrera–Padilla et al. [4] (this last under the name of generic Banach Lipschitz operator ideal). This can be seen as an extension of the linear Banach operator ideal. A Lipschitz operator ideal ${\mathcal {I}}_{{L}ip}$ is a subclass of $Lip_{0}$ such that for every pointed metric space X and every Banach space E the components

$$\begin{aligned} {\mathcal {I}}_{{L}ip}(X,E):=Lip_{0}(X,E)\cap {\mathcal {I}}_{{L}ip} \end{aligned}$$

satisfy

• (i) ${\mathcal {I}}_{{L}ip}(X,E)$ is a linear subspace of $Lip_{0}(X,E)$.

• (ii) $vg\in {\mathcal {I}}_{{L}ip}(X,E)$ for $v\in E$ and $g\in X^{\#}$.

• (iii) The ideal property: if $S\in Lip_{0}(Y,X)$, $T\in {\mathcal {I}}_{{L}ip}(X,E)$ and $w\in {\mathcal {L}}(E,F)$, then the composition wTS is in ${\mathcal {I}}_{{L}ip}(Y,F)$.

A Lipschitz operator ideal ${\mathcal {I}}_{{L}ip}$ is a normed (Banach) Lipschitz operator ideal if there is $\left\| .\right\| _{{\mathcal {I}}_{{L}ip}}:{\mathcal {I}}_{{L} ip}\longrightarrow [ 0,+\infty [$ that satisfies

• (i’) For every pointed metric space X and every Banach space E, the pair $({\mathcal {I}}_{{L}ip}(X,E),\left\| .\right\| _{{\mathcal {I}}_{{L}ip}})$ is a normed (Banach) space and $Lip(T)\le \Vert T\Vert _{{\mathcal {I}}_{{L}ip}}$ for all $T\in {\mathcal {I}}_{{L}ip}(X,E)$.

• (ii’) $\left\| Id_{{\mathbb {K}}}:{\mathbb {K}} \longrightarrow {\mathbb {K}},Id_{{\mathbb {K}}}(\lambda )=\lambda \right\| _{{\mathcal {I}}_{{L}ip}}=1$.

• (iii’) If $S\in Lip_{0}(Y,X)$, $T\in {\mathcal {I}}_{{L}ip}(X,E)$ and $w\in {\mathcal {L}}(E,F),$ then $\left\| wTS\right\| _{{\mathcal {I}}_{{L}ip}}\le Lip(S)\left\| T\right\| _{{\mathcal {I}}_{{L}ip}}\left\| w\right\|$.

Following [1, Definition 3.1], there is a way to construct a (Banach) Lipschitz operator ideal from a (Banach) linear operator ideal, called composition method. Let ${\mathcal {A}}$ be a (Banach) linear operator ideal. A Lipschitz mapping $T\in Lip_{0}(X,E)$ belongs to the composition Lipschitz ideal${\mathcal {A}}\circ Lip_{0}$ if there exists a Banach space F,  a Lipschitz operator$S\in Lip_{0} (X,F)$ and a linear operator $u\in {\mathcal {A}}(F,E)$ such that $T=u\circ S$. If $({\mathcal {A}},\left\| .\right\| _{{\mathcal {A}}})$ is a Banach operator ideal we write

$$\begin{aligned} \left\| T\right\| _{ {{\mathcal {A}}\circ } Lip_{0}}=\inf \left\| u\right\| _{{\mathcal {A}}}Lip(S), \end{aligned}$$

where the infimum is taken over all u and S as above.

In [1], the authors establish a criterion to decide whenever a Lipschitz operator ideal is of composition or not.

Proposition 3.5

[1, Proposition 3.2] Let X be a pointed metric space, E a Banach space and ${{\mathcal {A}}}$ an operator ideal. A Lipschitz operator $T\in Lip_{0}(X,E)$ belongs to ${\mathcal {A}} \circ Lip_0(X,E)$ if and only if its linearization $T_{L}$ belongs to ${\mathcal {A}}({\mathcal {F}}(X),E).$

Furthermore, if $( {{\mathcal {A}}} ,\left\| \cdot \right\| _{ {{\mathcal {A}}} })$ is a Banach operator ideal then $( {{\mathcal {A}}\circ } Lip_{0},\left\| \cdot \right\| _{ {{\mathcal {A}}\circ } Lip_{0}})$ is Banach Lipschitz operator ideal with

$$\begin{aligned} \left\| T\right\| _{ {{\mathcal {A}}\circ } Lip_{0}}=\left\| T_{L}\right\| _{ {{\mathcal {A}}} }. \end{aligned}$$

By Theorem 3.4 and the above criterion, we have the following.

Proposition 3.6

The class ${\mathcal {K}}_{p}^{L}$ is the Banach Lipschitz operator ideal generated by the composition method from the Banach operator ideal ${\mathcal {K}}_{p}$. In other words

$$\begin{aligned} {\mathcal {K}}_{p}^{L}(X,E)={\mathcal {K}}_{p}\circ Lip_{0}(X,E) \quad isometrically \end{aligned}$$

for every pointed metric space X and every Banach space E.

At the light of Propositions 3.2 and 3.6, the ideal of Lipschitz p-compact operators can be seen as an extension of the ideal of p-compact linear operators. Moreover, the nature of this extension allow us to transfer some properties of the ideal of p-compact linear operators to the Lipschitz case, such as the regularity and the injectivity. Recall that, for normed Lipschitz operator ideal ${\mathcal {I}}_{Lip}$ it is said to be injective if for every linear isometric embedding $I:E\hookrightarrow F$ and every $T\in Lip_{0}(X,E)$ it follows from $I\circ T\in {\mathcal {I}}_{Lip}(X,F)$ that $T\in {\mathcal {I}}_{Lip}(X,E)$ and $\left\| T\right\| _{{\mathcal {I}}_{Lip}}=\left\| I_E\circ T\right\| _{{\mathcal {I}}_{Lip}}$ where $I_E:E\hookrightarrow \ell _{\infty }(B_{E^*})$ is the natural inclusion (see [1]). On the other hand, ${\mathcal {I}}_{Lip}$ is said to be regular if for every $T\in Lip_{0}(X,E)$ we have $T\in {\mathcal {I}}_{Lip}(X,E)$ if and only if $J_{E}\circ T\in {\mathcal {I}} _{Lip}(X,E^{**})$ and $\left\| T\right\| _{{\mathcal {I}}_{Lip}}=\left\| J_{E}\circ T\right\| _{{\mathcal {I}}_{Lip}}$, where $J_{E}:E\hookrightarrow E^{**}$ is the canonical embedding (see [4]). The next proposition follows directly from the definitions and we omit the proof.

Proposition 3.7

The operator ideal ${\mathcal {I}}$ is injective or regular if and only if the corresponding composition Lipschitz ideals ${\mathcal {I}}\circ Lip_{0}$ is.

As a consequence of the above and the regularity of the ideal of p-compact linear operators [9, Theorem 2.5] or [18, Theorem 5] and the non injectivity of it [9, Proposition 3.4], we obtain the following.

Proposition 3.8

Let $1\le p < \infty$. The Banach Lipschitz operator ideal of p-compact operators is regular but not injective.

The characterization of Lipschitz p-compact operators obtained in Theorem 3.4 allow us to translate some known properties of the Banach operator ideal ${\mathcal {K}}_p$ to the Banach Lipschitz operator ideal ${\mathcal {K}}^{L}_p$.

From the factorization of p-compact operators obtained in [9, Proposition 2.9], we get a factorization of the p-compact Lipschitz operators through a p-compact linear operator from a quotient of $\ell _{p*}$ to a separable space.

Proposition 3.9

Let X be a pointed metric space and E a Banach space. For $1\le p < \infty$, a mapping $T\in Lip_0(X,E)$ is Lipschitz p-compact if and only if there exist a closed subspace $M\subset \ell _{p^*}$, a separable Banach space Z, a linear p-compact operator $u\in {\mathcal {K}}_p(\ell _{p^*}/M,Z)$, a Lipschitz compact mapping $S\in Lip_{0 {\mathcal {K}}}(X,\ell _{p^*}/M)$ and a linear compact operator $w\in {\mathcal {K}}(Z,E)$ such that $T=w\circ u\circ S$.

Moreover, $k^L_p(T)=\inf \{Lip(S) k_p(u) \Vert w\Vert \}$, where the infimum is taken over all factorizations as above.

Proof

If a Lipschitz operator $T \in {\mathcal {K}}_p^{L}(X,E)$ has such factorization, by Proposition 3.6, the mapping $u\circ S$ is Lipschitz p-compact. Consequently, $T=w\circ u\circ S$ is also Lipschitz p-compact by the ideal property. For the converse, suppose that $T \in {\mathcal {K}}_p^{L}(X,E)$. By Theorem 3.4, its linearization $T_L$ belongs to ${\mathcal {K}}_p({\mathcal {F}}(X),E)$ with $k_p^{L}(T)=k_p(T_L)$. Applying [9, Proposition 2.9] to the operator $T_L$, for $\varepsilon >0$, we may find a closed subspace $M\subset \ell _{p*}$, a separable Banach space Z, linear operators $u\in {\mathcal {K}}_p(\ell _{p^*}/M,Z)$, $w\in {\mathcal {K}}(Z,E)$ and ${\widetilde{w}} \in {\mathcal {K}}({\mathcal {F}}(X),\ell _{p^*}/M)$ such that $T_L=w \circ t \circ {\widetilde{w}}$, and $\Vert w\Vert k_p(u) \Vert \widetilde{w}\Vert \le k_p(T_L)+\varepsilon$. Denoting $S={\widetilde{w}} \circ \delta _X$, we get that $S\in Lip_{0 {\mathcal {K}}}(X, \ell _{p^*}/M)$ with $Lip_{0 {\mathcal {K}}}(S)\le \Vert {\widetilde{w}}\Vert$ and the result follows. $\square$

Cabrera-Padilla et al. introduce the maximal hull of a Lipschitz Banach operator ideal by extending that of the linear case (see [7, Definition 17.2] for the definition). Roughly speaking, for a Lipschitz Banach operator ideal ${\mathcal {I}}_{Lip}$, its maximal hull ${\mathcal {I}} _{Lip}^{max}$ is the biggest Banach Lipschitz operator ideal that satisfies ${\mathcal {I}}_{Lip}(X_0;N)={\mathcal {I}}_{Lip}^{max}(X_0;N)$ isometrically, for every finite metric space $X_0$ and any finite dimensional space N (see [4, Definition 2.5]). To characterize the maximal hull of ${\mathcal {K}}_{p}^{L}$, we appeal to the Banach Lipschitz operator ideal ${\mathcal {D}}_{st,p}^{L}$ of strongly Lipschitz p-summing mappings, introduced by the first author, Yahi et al. in [23]. By [1, Example 3.4] we have ${\mathcal {D}}_{st,p}^{L}={\mathcal {D}} _{p}\circ Lip_{0}$, where ${\mathcal {D}}_{p}$ stands for the Banach operator ideal of strongly p-summing operators introduced by Cohen in [5]. The p-compact and strongly p-summing operators ideals are related as ${\mathcal {K}}_{p}^{max}={\mathcal {D}}_{p}$ (see [9, Corollary 3.6] or [18, Theorem 12]). The same relation can be extended to the Lipschitz case and it is a consequence of the following theorem.

Theorem 3.10

Let ${\mathcal {A}}$ and ${\mathcal {B}}$ Banach operator ideals such that ${\mathcal {A}}^{max}={\mathcal {B}}$. Then $({\mathcal {A}}\circ Lip_0)^{max}={\mathcal {B}} \circ Lip_0$ isometrically.

Proof

Since ${\mathcal {B}}$ is a maximal Banach operator ideal, using the Representation Theorem for maximal operators ideals [7, Sect. 17.5], combining [19, Corollary 3.3] and [4, Corollary 5.2], we get that ${\mathcal {B}} \circ Lip_0$ is a maximal Lipschitz Banach operator ideal. To conclude the proof, as a consequence of [4, Lemma 2.4], it is enough to see that for every finite pointed metric space $X_0$ and every finite-dimensional space $E_0$, ${\mathcal {A}} \circ Lip_o(X_{0},E_{0})={\mathcal {B}} \circ Lip_0(X_{0},E_{0})$ isometrically. Now, if $X_0$ is a finite pointed metric space, then ${\mathcal {F}}(X_0)$ is a finite dimensional space. If $E_0$ is a finite dimensional space, then

$$\begin{aligned} {\mathcal {A}}({\mathcal {F}}(X_0),E_0)={\mathcal {B}}({\mathcal {F}}(X_0),E_0) \end{aligned}$$

isometrically. Thus, by Theorem 3.4 and [23, Proposition 3.2], for $T \in Lip_0(X_0,E_0)$ we have the equalities

$$\begin{aligned} \Vert T \Vert _{{\mathcal {A}} \circ Lip_ 0}=\Vert T_{L}\Vert _{\mathcal A}=\Vert T_{L}\Vert _{{\mathcal {B}}}=\Vert T\Vert _{{\mathcal {B}} \circ Lip_0}, \end{aligned}$$

and the proof conclude. $\square$

Theorem 3.11

For $1\le p <\infty$, $({\mathcal {K}}_p^{L})^{max}= {\mathcal {D}}_{st,p}^{L}$ isometrically.

To finish this section, we give a characterization of the Lipschitz p-compact operators in terms of its transpose. For this, we appeal again to some results obtained in the linear case. Before proceeding, recall that following [17], an operator $u\in {\mathcal {L}}(E,F)$ is quasi p-nuclear if and only if there is a sequence $(x_{i}^{*})_{i=1}^{ \infty }\in \ell _{p^{*}}(E^{*})$ such that

$$\begin{aligned} \left\| u(x)\right\| \le \left( \sum \limits _{i=1}^{\infty }\left| \left\langle x,x_{i}^{*}\right\rangle \right| ^{p}\right) ^{\frac{1}{p}}, \end{aligned}$$

(3)

for all $x\in X.$ The Banach ideal of such operators is denoted by ${\mathcal {Q}}{\mathcal {N}}_{p}$ with the ideal norm

$$\begin{aligned} \nu _{p}^{Q}(u)=\inf \left\{ \left\| (x_{i}^{*})_{i=1}^{\infty }\right\| _{p}:(x_{i}^{*})_{i=1}^{\infty }\text { satisfying} (3) \right\} . \end{aligned}$$

Delgado et al. showed in [6, Proposition 3.8] that a linear operator is p-compact if and only if its adjoint is quasi p-nuclear. The isometry was obtained in [9, Corollary 2.7] and in [18, Theorem 6] independently. The next proposition extend these results for the Lipschitz case.

Proposition 3.12

Let X be a pointed metric space, E a Banach space. For $1\le p<\infty$, a mapping $T\in Lip_{0}(X,E)$ is Lipschitz p-compact if and only if its Lipschitz transpose $T^{t}:E^{*}\longrightarrow X^{\#}$ is a quasi p-nuclear operator. Moreover, in this case, $\kappa _p^L(T)=\nu _{p}^Q(T^{t})$.

Proof

By Theorem 3.4 we know that T belongs to ${\mathcal {K}} _{p}^{L}(X,E)$ if and only if its linearization $T_{L}:{\mathcal {F}} (X)\longrightarrow E$ is linear p-compact with $k_p(T_L)=k_p^{L}(T)$. By [6, Proposition 3.8], the operator $T_{L}^{*}:E^{*}\rightarrow {\mathcal {F}}(X)^{*}$ is quasi p-nuclear operator and, by [9, Corollary 2.7] or [18, Theorem 6], $\nu _p^Q(T_{L}^{*})=k_p(T_L)$. On the other hand, as it was noticed after Lemma 2.1 we have the equality $T_{L}^{*}=Q_{X}\circ T^{t}$ where $Q_{X}:X^{\#}\longrightarrow {\mathcal {F}}(X)^{*}$ is the canonical isometric isomorphism. It follows that $T_{L}^{*}$ is quasi p-nuclear if and only if $T^{t}=Q_{X}^{-1}\circ T_{L}^{*} \in {\mathcal {Q}}{\mathcal {N}} _{p}(E^{*},X^{\#})$ with $\nu _{p}^{Q}(T^{t})=\nu _{p}^{Q}(T_{L}^{*})$. The result follows. $\square$

Proposition 3.13

Let X and Z be pointed metric spaces and E a Banach space. Let $T\in Lip_{0}(X,E)$ and $S\in Lip_{0}(Z,E^{*}).$ For $1\le p <\infty$, if $T_{L}$ is p-summing and S is Lipschitz compact; then $T^{t}\circ S$ is Lipschitz p-compact with

$$\begin{aligned} k_{p}^{L}(T^{t}\circ S)\le \pi _{p}(T_{L})Lip_{0}(S) \end{aligned}$$

Proof

Take $T\in Lip_{0}(X,E)$ such that $T_L$ is a p-summing operator and $S\in Lip_{0}(Z,E^{*})$ a Lipschitz compact operator. By [13, Proposition 2.1], the linearization of S, $S_{L}$, is a compact linear operator. Consequently, by [6, Proposition 3.13] the linear mapping $T_{L}^{*}\circ S_{L}=Q_{X}\circ T^{t}\circ S_{L}$ is linear p-compact with $k_{p}\left( T_{L}^{*}\circ S_{L}\right) \le \pi _{p}(T_{L})\left\| S_{L}\right\|$. Then $T^{t}\circ S_{L}$ is linear p-compact which, by Proposition 3.2 is Lipschitz p-compact with $k_{p}^{L}(T^{t}\circ S)=k_{p}(T^{t}\circ S)$. Furthermore,

$$\begin{aligned} k_{p}^{L}(T^{t}\circ S)=k_{p}(Q_{X}^{-1}\circ T_{L}^{*}\circ S_{L})\le \pi _{p}(T_{L})\left\| S_{L}\right\| =\pi _{p}(T_{L})Lip_{0}(S), \end{aligned}$$

concluding the proof. $\square$

4 Lipschitz-free and locally p-compact mappings

This section is devoted to another two classes of Lipschitz mappings related with p-compact sets. The first class we discuss is motivated by notion of Lipschitz-free compact operators, recently introduced by Cabrera–Padilla and Jiménez–Vargas in [3]. Note that, in particular, this class can be defined for Lipschitz operators between metric spaces.

Definition 4.1

Let X and Y be pointed metric spaces and $p\ge 1$. A Lipschitz operator $T\in Lip_{0}(X,Y)$ is called Lipschitz-free p-compact if the mapping $\delta _{Y}\circ T:X\rightarrow {\mathcal {F}}(Y)$ is a Lipschitz p-compact operator. The set of all Lipschitz-free p-compact operators between X and Y will be denoted by $\mathcal {FK}_{p}^{L}(X,Y)$.

Note that the Lipschitz-free $\infty$-compact mappings coincide with the Lipschitz-free compact operators of Cabrera–Padilla and Jiménez–Vargas. The first result that we present of the Lipschitz-free p-compact operators can be seen as an extension of [3, Theorem 2.3]. We sketch the proof.

Theorem 4.2

Let X and Y be pointed metric spaces and $T\in Lip_0(X,Y)$. For $p\ge 1$, the following are equivalent

• (1) T is Lipschitz-free p-compact.

• (2) The operator ${\widehat{T}}:{\mathcal {F}}(X)\rightarrow {\mathcal {F}}(Y)$ is p-compact.

• (3) The operator $T^{\#}:Y^{\#}\rightarrow X^{\#}$ is quasi p-nuclear.

Proof

Applying Theorem 3.4, we get that T is Lipschitz-free p-compact if and only if $(\delta _Y \circ T)_L:{\mathcal {F}}(X)\rightarrow {\mathcal {F}}(Y)$ is a p-compact operator. Then, the equivalence between (1) and (2) follows by noticing that the operator $(\delta _Y \circ T)_L$ coincides with the operator ${\widehat{T}}$. That (2) is equivalent to (3) follows since a linear operator is p-compact if and only if its transpose is quasi p-nuclear [6, Proposition 3.8] and from the equality ${\widehat{T}}^{*}=Q_{X}\circ T^{\#}\circ (Q_{Y})^{-1}$ (for this last equality, see the remarks after Lemma 2.1). $\square$

The other class that we will deal in this section is the class of Lipschitz locally p-compact operators, whose definition arise in a natural way.

Definition 4.3

Let X be a pointed metric space, E a Banach space and let $p\ge 1$. A Lipschitz operator $T\in Lip_{0}(X,E)$ is called Lipschitz locally p-compact at $x_{0}\in X$ if there exists $\varepsilon >0$ such that $T(B_{\varepsilon }(x_{0}))$ is a relatively p-compact set in E. The operator T is said to be Lipschitz locally p-compact if it is locally p-compact at $x_0$ for every $x_0\in X$. We denote by ${\mathcal {K}}_p^{Loc}(X,E)$ the set of all locally Lipschitz p-compact operators.

Remark 4.4

Note that a linear operator between Banach spaces is p-compact if and only if maps bounded sets into relatively p-compact sets. Then, every linear operator is p-compact if and only if is Lipschitz locally p-compact.

Remark 4.5

Since every relatively p-compact set is q-compact whenever $1\le p\le q\le \infty$, we have that $\mathcal {FK}_{p}^{L}\subset \mathcal {FK}_{q}^{L}$ and ${\mathcal {K}}_{p}^{Loc}\subset {\mathcal {K}}_{q}^{Loc}$.

The next result describes the relationship between the three classes of Lipschitz operators that we introduced.

Proposition 4.6

Let $p\ge 1$. Then $\mathcal {FK}_{p}^{L}\subset {\mathcal {K}}_{p}^{L}\subset {\mathcal {K}}_{p}^{Loc}$ and these inclusions are strict.

Proof

Fix a pointed metric space X and a Banach space E and take $T\in \mathcal {FK}_{p}^{L}(X;E)$. Then $\delta _E\circ T$ is a Lipschitz p-compact operator. That is, the Lipschitz image of $\delta _E\circ T$ is a relatively p-compact set in ${\mathcal {F}}(E)$. As in the proof of [3, Proposition 2.2], we have the equality $Im_{Lip}(T)=\beta _E(Im_{Lip}(\delta _E\circ T))$, where $\beta _E$ is the barycenter map. Thus $Im_{Lip}(T)$ is a relatively p-compact set in E and, in particular, T is a Lipschitz p-compact operator. Then, we showed that $\mathcal {FK}_{p}^{L}\subset {\mathcal {K}}_{p}^{L}$. To see that this inclusion is strict, by Proposition 3.6 the Lipschitz p-compact operators are a Lipschitz Banach ideal. In particular, the identity map of ${\mathbb {R}}$, $Id_{{\mathbb {R}}}$, is a Lipschitz p-compact operator. However, if $Id_{{\mathbb {R}}}$ were Lipschitz-free p-compact, by Theorem 4.2, $\widehat{Id_{\mathbb R}} \in {\mathcal {K}}_p({\mathcal {F}}({\mathbb {R}}),{\mathcal {F}}({\mathbb {R}}))$. Since, by [10] or [11], ${\mathcal {F}}(\mathbb R)=L_1$ and $\widehat{Id_{{\mathbb {R}}}}=Id_{L_1({\mathbb {R}})}$, we get that the identity map of an infinite dimensional space is a compact operator, which can not occur.

For the other inclusion, if $S\in {\mathcal {K}}_p^{L}(X;E)$, then its linearization is a p-compact operator. Then, for any $x \in X$ and any $\epsilon >0$, we have $T(B_{\epsilon }(x))=T_{L}(\delta _X(B_{\epsilon }(x)))$. Since $\delta _X(B_{\epsilon }(x))$ is a bounded set of ${\mathcal {F}}(X)$, we conclude that $T(B_{\epsilon }(x))$ is a p-compact set. Thus ${\mathcal {K}}_{p}^{L}\subset {\mathcal {K}}_{p}^{Loc}$. The next example show that this inclusion is strict. $\square$

Example 4.7

There exists $f\in Lip_{0}({\mathbb {R}},\ell _{1})$ which is Lipschitz locally 1-compact which is not Lipschitz compact. As a consequence, f is Lipschitz locally p-compact but not Lipschitz p-compact for all $1\le p<\infty$.

Proof

Consider the function $f:{\mathbb {R}}\rightarrow \ell _{1}$

$$\begin{aligned} f(t)=\left\{ \begin{array}{l@{\quad }l@{\quad }l} 0 &{} \hbox {if} &{} t\le 0 \\ \sin (t)e_{n} &{} \hbox {if} &{} t\in [2(n-1)\pi ,(2n-1)\pi [\ \hbox {for some}\ n\in {\mathbb {N}}^{*} \\ 0 &{} \hbox {if} &{} t\in [(2n-1)\pi ,2n\pi [\ \hbox {for some}\ n\in {\mathbb {N}}^{*} \end{array} \right. \end{aligned}$$

where $(e_n)_{n=1}^\infty$ stands for unit vector basis of $\ell _1$. First we check that $f\in Lip_{0}({\mathbb {R}},\ell _{1})$ with $Lip(f)\le 2/\pi$. Clearly $f(0)=0$. Now, take $t_{0}$ and $t_{1}$ in ${\mathbb {R}}$ with $t_{0}\ne t_{1}$.

If $t_{0}\le 0$ or $t_{0}\in [(2n-1)\pi ,2n\pi ]$ for some $n\in {\mathbb {N}}^{*}$ and $t_{1}\le 0$ or $t_{1}\in [(2m-1)\pi ,2m\pi ]$ for some $m\in {\mathbb {N}}^{*}$, then

$$\begin{aligned} \displaystyle \frac{\Vert f(t_{0})-f(t_{1})\Vert }{|t_{0}-t_{1}|}=0. \end{aligned}$$

Now suppose that $t_{0}\in [2(n-1)\pi ,(2n-1)\pi ]$ for some $m\in {\mathbb {N}}^{*}$ and $t_{1}\in [2(m-1)\pi ,(2m-1)\pi ]$ for some $m\in {\mathbb {N}}^{*}$.

If $n=m$, then

$$\begin{aligned} \frac{\Vert f(t_{0})-f(t_{1})\Vert }{|t_{0}-t_{1}|}=\frac{\Vert (\sin (t_{0})-\sin (t_{1}))e_{n}\Vert }{|t_{0}-t_{1}|}=\frac{|\sin (t_{0})-\sin (t_{1})|}{|t_{0}-t_{1}|}\le 1. \end{aligned}$$

If $n\ne m$, note that $\pi \le |t_0-t_1|$. Thus,

$$\begin{aligned} \frac{\Vert f(t_{0})-f(t_{1})\Vert }{|t_{0}-t_{1}|}=\frac{\Vert \sin (t_{0})e_{n}-\sin (t_{1})e_{m}\Vert }{|t_{0}-t_{1}|}\le \frac{2}{ |t_{0}-t_{1}|}\le \frac{2}{\pi }. \end{aligned}$$

Finally, if $t_{0}\in [2(n-1)\pi ,(2n-1)\pi ]$ for some $n\in {\mathbb {N}}^{*}$ and $t_{1}\in [(2m-1)\pi ,2m\pi ]$ for some $m\in {\mathbb {N}}$. There exists $0\le \mu _{0}\le \pi$ such that $t_{0}=2(n-1)\pi +\mu _{0}$. If $\mu _{0}=\pi$, then $|f(t_{0})|=0$. If not, since $|t_{0}-t_{1}|\ge \mu _{0}>0$, we have

$$\begin{aligned} \frac{\Vert f(t_{0})-f(t_{1})\Vert }{|t_{0}-t_{1}|}\le \frac{\Vert f(t_{0})\Vert }{\mu _{0}}=\frac{|\sin (t_{0})|}{\mu _{0}}=\frac{|\sin (2(n-1)\pi +\mu _{0})|}{\mu _{0}}\le 1. \end{aligned}$$

With this, we get that $f\in Lip_0({\mathbb {R}},\ell _1)$. To see that f is locally 1-compact, take $t_{0}\in {\mathbb {R}}$. Then, easy to see that for any $t\in [t_{0}-\pi /4,t_{0}+\pi /4]$ there exist some $n\in {\mathbb {N}}$ such that $f(t_{0})=\lambda e_{n}$ with $-1\le \lambda \le 1$. Thus $f([t_{0}-\pi /4,t_{0}+\pi /4])\subset 1$-conv$\left\{ (e_{n})_{n}\right\}$, implying that f is Lipschitz locally 1-compact. Finally, to show that f is not Lipschitz compact, we show that the Lipschitz image of f is not a relatively compact set. For any $n\in {\mathbb {N}}$ we have $f(2(n-1)\pi +\pi /2)=e_{n}$ and $f(2(n-1)\pi )=0$. Thus

$$\begin{aligned} \frac{e_{n}}{2\pi }=\frac{f(2(n-1)\pi +\pi /2)-f(2(n-1)\pi ) }{2\pi }. \end{aligned}$$

Then, the sequence $\displaystyle (\frac{1}{2\pi }e_{n})_{n} \subset Im_{Lip}(f)$ and the result follows. $\square$

Is not difficult to see that the Lipschitz locally p-compact operators are a Lipschitz ideal, and in particular, satisfy the ideal property. This also happens with the Banach ideal of Lipschitz p-compact operators. However, the class of Lipschitz-free p-compact operators is not an ideal since, as we see in the proof of Proposition 4.6, the identity of ${\mathbb {R}}$ is not Lipschitz-free p-compact. Despite this, we have the following result.

Theorem 4.8

(The strong ideal property) Let $p\ge 1$. For all pointed metric spaces X, Y, Z, W,  if $R\in Lip_{0}(X,Y),$$T\in \mathcal {FK}_{p}^{L}(Y,Z)$ and $S\in Lip_{0}(Z,W)$ then $S\circ T\circ R\in \mathcal {FK}_{p}^{L}(X,W)$.

Proof

We have to prove that $\widehat{S\circ T\circ R}:\mathcal F(X)\rightarrow {\mathcal {F}}(W)$ is a p-compact operator. It is straightforward to check that $\widehat{S\circ T\circ R}={\widehat{S}}\circ {\widehat{T}}\circ {\widehat{R}}$. The result follows since ${\widehat{T}}:{\mathcal {F}}(Y)\rightarrow \mathcal F(Z)$ is a p-compact linear operator. $\square$

Before finishing, we give a brief discussion of the Lipschitz images of the Lipschitz locally p-compact operators. For this, given $x_{0}\in X$ and $0<\eta <\varepsilon \le \infty$ we define

$$\begin{aligned} Im_{Lip}(T)(x_{0};\eta ,\varepsilon )=\left\{ \frac{T(x)-T(x_{0})}{d(x,x_{0})} :\eta<d(x,x_{0})<\varepsilon \right\} . \end{aligned}$$

Note that $Im_{Lip}(T)=\bigcup _{x_{0}\in X}Im_{Lip}(T)(x_{0};0,\infty )$.

Proposition 4.9

Let$\ p\ge 1,$$T\in Lip_{0}(X,E)$ and fix $x_{0}\in X$. Then

• (1) If T is Lipschitz locally p-compact at $x_{0}$, then there exists $\varepsilon >0$ such that, for all $0<\eta <\varepsilon$ the set $Im_{Lip}(T)(x_{0};\eta ,\varepsilon )$ is relatively p-compact. Moreover, there exists $C>0$ such that

  $$\begin{aligned} m_{p}(Im_{Lip}(T)(x_{0};\eta ,\varepsilon ))\le \frac{C}{\eta }. \end{aligned}$$

• (2) If there exists $\varepsilon >0$ such that $Im_{Lip}(T)(x_{0};0,\varepsilon )$ is a relatively p-compact set in E, then T is Lipschitz locally p -compact at $x_{0}$. Moreover, there exists $C>0$ such that

  $$\begin{aligned} m_{p}(T(B_{\varepsilon }(x_{0}))-T(x_{0}))\le C \varepsilon . \end{aligned}$$

Proof

Suppose that T is Lipschitz locally p-compact at $x_{0}$, there exists $\varepsilon >0$ such that $T(B_{\varepsilon }(x_{0}))$ is relatively p -compact. Then, for every $\eta >0$, the set $\{T(x)-T(x_{0}):\eta<d(x,x_{0})<\varepsilon \}$ is relatively p-compact. If we show that

$$\begin{aligned} Im_{Lip}(T)(x_{0};\eta ,\varepsilon )\subset \frac{1}{\eta }\Gamma \{T(x)-T(x_{0}):\eta<d(x,x_{0})<\varepsilon \} \end{aligned}$$

then (1) follows. Indeed, if $z\in Im_{Lip}(T)(x_{0};\eta ,\varepsilon )$, then there exists $x\in X$ with $\eta<d(x,x_{0})<\varepsilon$ such that $z= \frac{T(x)-T(x_{0})}{d(x,x_{0})}$. As $z=\frac{\eta }{d(x,x_{0})}\frac{1}{ \eta }(T(x)-T(x_{0}))$ and $\frac{\eta }{d(x,x_{0})}<1$, the claim follows.

The proof of (2) follows if we show that for any $\varepsilon >0$, the inclusion

$$\begin{aligned} \frac{1}{\varepsilon }\left\{ T(x)-T(x_{0}):d(x,x_{0})<\varepsilon \right\} \subset \Gamma (Im_{Lip}(T)(x_{0};0,\varepsilon )). \end{aligned}$$

holds. Take $x\in X$ such that $0<d(x,x_{0})<\varepsilon$. As

$$\begin{aligned} \frac{1}{\varepsilon }(T(x)-T(x_{0}))=\frac{d(x,x_{0})}{\varepsilon \ d(x,x_{0})}\big (T(x)-T(x_{0})\big )=\frac{d(x,x_{0})}{\varepsilon }\left( \frac{T(x)-T(x_{0})}{d(x,x_{0})}\right) , \end{aligned}$$

since $\left( \frac{T(x)-T(x_{0})}{d(x,x_{0})}\right) \in Im_{Lip}(T)(x_{0};0,\varepsilon )$ and $\frac{d(x,x_{0})}{\varepsilon }<1$, then the claim is proved. $\square$

Proposition 4.10

Let X be a compact pointed metric space and E a Banach space. Let $\ p\ge 1$ and $T\in Lip_{0}(X,E)$. If T is Lipschitz locally p-compact, then for every $0<\eta <\sup _{x,y \in X}d(x,y)$, the set $\bigcup _{x_{0}\in X}Im_{Lip}(T)(x_{0};\eta ,\infty )$ is relatively p-compact. Moreover, there exists $C>0$ such that

$$\begin{aligned} m_{p}\left( \bigcup _{x_{0}\in X}Im_{Lip}(T)(x_{0};\eta ,\infty )\right) \le \frac{C}{\eta }. \end{aligned}$$

Proof

Note that since f is Lipschitz locally p-compact and X is compact, T(X) is a p-compact set. Fix $\eta >0$ and we will show that $\bigcup _{x_{0}\in X}Im_{Lip}(T)(x_{0};\eta ,\infty )\subset \frac{2}{\eta }\Gamma (T(X))$. With this, the result follows. If $z\in \bigcup _{x_{0}\in X}Im_{Lip}(T)(x_{0};\eta ,\infty )$, then there exist $x,y\in X$, with $\eta <d(x,y)$ such that $z=\frac{1}{d(x,y)} (T(x)-T(y))$. Then $z=\frac{1}{\eta }\frac{\eta }{d(x,y)}(T(x)-T(y))$ and, since $\frac{\eta }{d(x,y)}<1$, then we have the inclusion that we needed. $\square$