1 Introduction

Joints exist widely in rock masses, and the propagation of stress waves is always related to the characteristics of the wave source and the physical properties of the joint (Zhao et al. 2008a, b; Perino et al. 2010; Ma et al. 2011; Li et al. 2015a; Zou et al. 2017; Chai et al. 2019; Fan et al. 2020a). For stress waves propagate in a rock mass with different wave impedance on either side of the joint, the propagation of stress waves is also related to the wave impedance ratio of the rock on either side of the joint. If the characteristics of the wave source, the physical properties of the joint and the wave impedance ratio are considered, particle vibration may be non-attenuated under certain conditions (Fan et al. 2018a, 2020b). Thus, it is of significance to study the non-attenuation phenomenon of stress waves.

In a general case, when a stress wave propagates across an interface between two different media, both transmission and reflection take place (Kolsky 1963; Wang 2005). The particle velocity and stress at the interface are continuous. When the stress wave propagates from a medium with a small wave impedance to a medium with a large wave impedance, the particle velocity amplitude of the transmitted wave is smaller than that of the incident wave. When the stress wave propagates from a medium with a large wave impedance to a medium with a small wave impedance, the particle velocity amplitude of the transmitted wave is larger than that of the incident wave. For the special case of stress waves propagating across an interface between media with the same wave impedances, no reflection takes place at the interface, and a stress wave can be totally transmitted (Wang 2005). Therefore, the non-attenuation propagation of stress waves can occur when the stress waves propagate from a medium with a large wave impedance to a medium with a small wave impedance or the stress waves propagate across an interface between media with the same wave impedances.

However, joints are different from connected interfaces, and a stress wave is always attenuated by a joint (Zhao et al. 2008a, b; Zhu et al. 2011; Wu et al. 2013; Huang et al. 2014a, b; Li et al. 2015b; Niu et al. 2018). Generally, discontinuous structural planes which are large in extent and thin in thickness relative to the wavelength can be physically viewed as joints in theoretical research (Zhao et al. 2008a; b). When a stress wave was incident on a linear joint, the joint can be modeled via a displacement discontinuity boundary condition between two elastic half-spaces. The amplitude of the transmitted wave can be controlled by the joint stiffness, and the transmission coefficients were always smaller than 1.0 (Pyrak-Nolte et al. 1990a, b; Gu et al. 1996; Pyrak-Nolte 1996; Zhao et al. 2006). When a stress wave propagates across a single joint with nonlinearly normal deformational behavior, the transmission coefficient increases as the nonlinear coefficient increases. Although a nonlinearly deformable joint can transmit more energy than a linearly deformable joint, the transmission coefficient was still smaller than 1.0 (Zhao and Cai 2001; Li 2013; Chai et al. 2019). For a filled joint, the effect of joint thickness on wave propagation can be taken into consideration by a thin-layer interface model. The filling material was equivalent to an elastic and continuum medium. The transmission coefficient decreases as the joint thickness increases. When the joint thickness approached zero, the transmission coefficient approached 1.0 (Li et al. 2013). If the joint was filled with saturated sand or clay, the filling materials exhibited viscoelastic behavior, the transmission coefficient across a viscoelastic joint was smaller than that across an elastic joint, and the transmission coefficient decreased with increasing viscosity, which indicated that the more viscous the filled medium is, the less wave energy transmitted (Zhu et al. 2012; Fan et al. 2018b). Therefore, the transmission coefficient is usually smaller than 1.0 when a stress wave propagates in a rock mass with the same wave impedance on both sides of the joint, and the transmission coefficient will approach 1.0 under only certain conditions.

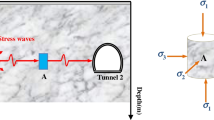
Joints often exist between different rocks, and the propagation of stress waves is affected by the wave impedance ratio, as shown in Fig. 1a. For a stress wave propagating across a joint in a rock mass with different wave impedances on two sides of the joint, particle vibration may be non-attenuated under certain conditions (Fan et al. 2018b, 2020b). The critical condition and the mechanism of the non-attenuation propagation of stress waves need to be studied for such a case.

Fig. 1
figure 1

Stress wave propagation. a Complex formation; b “hard” rock to “soft” rock

Full size image

This paper considers the case in which a stress wave propagates from rock with a large wave impedance to rock with a small wave impedance, as shown in Fig. 1b. Combined with the displacement discontinuity model and the characteristic method, the particle velocity transmission coefficient of a stress wave passing through a joint was derived. The relationships between the particle velocity transmission coefficient and frequency of the incident wave, joint stiffness and wave impedance ratio were studied, and the non-attenuation propagation of the stress wave was observed. Parametric studies with respect to frequency, joint stiffness and wave impedance ratio on threshold frequency, threshold joint stiffness and threshold wave impedance ratio were carried out. Furthermore, a threshold surface for the non-attenuation propagation of stress waves was identified in FKN space.

2 Theory

Across a joint, the stress is continuous, but the displacement is discontinuous (Schoenberg and Muir 1989; Pyrak-Nolte and Nolte 1992; Gu et al. 1996; Pyrak-Nolte 1996). In most seismic investigations of jointed rock masses, the wave amplitudes are relatively small and insufficient to excite joint nonlinearity. Therefore, the linear displacement discontinuity method is valid and adopted in this paper (Pyrak-Nolte et al. 1990a; Zhao et al. 2006; Li and Ma 2010). To focus purely on the effects of incident wave characteristics, joint characteristics and material characteristics on stress wave propagation and the essential reasons for non-attenuation propagation of stress wave, the case of normal incidence of waves was studied.

In the present study, rock with a large wave impedance is referred to as “hard” rock, and rock with a small wave impedance is referred to as “soft” rock. Since the wave impedance represents the physical parameters of rock, the “hard” and “soft” here are used to represent the physical properties of rock (Wang 2005).

A stress wave in the x-direction is normally incident on the rock mass. The stress wave propagates from the rock with a large wave impedance to rock with a small wave impedance. When the stress wave propagates across the joint located at x = x1, reflected and transmitted waves appear, as shown in Fig. 2. According to the linear displacement discontinuity method, when waves propagate across a joint, the stress is continuous, but the displacement is discontinuous due to the joint deformation, the normal stress σ and normal displacement u in “hard” rock and “soft” rock at x1 are

$$\sigma_{{\text{H}}} \left( {x_{1} ,t} \right) = \sigma_{{\text{S}}} \left( {x_{1} ,t} \right) = \sigma \left( {x_{1} ,t} \right),$$
(1)
$$u_{{\text{H}}} \left( {x_{1} ,t} \right) - u_{{\text{S}}} \left( {x_{1} ,t} \right) = \frac{{\sigma \left( {x_{1} ,t} \right)}}{{k_{{\text{n}}} }},$$
(2)

where kn is the normal joint stiffness, σH (x1, t) and σS (x1, t) are the normal stresses in the “hard” rock and “soft” rock, respectively, and uH (x1, t) and uS (x1, t) are the normal displacements in the “hard” rock and “soft” rock, respectively.

Combined with the displacement discontinuity method, the characteristic method is often used to study stress wave propagation in jointed rock masses. In the conventional displacement discontinuity method, the wave impendences on two sides of the joint are assumed to be the same. When the stress wave propagates from the rock with a large wave impedance to rock with a small wave impedance, the conventional characteristic method is not applicable. Therefore, we improved the method, as shown in Fig. 2. The slopes of the characteristic lines on the two sides of the joint are not equal. In Fig. 2, lines ab and bc represent the left-running and right-running characteristic lines in “hard” rock. Line cd represents the left-running characteristic line in “soft” rock. The absolute value of the slope of the characteristic line is equal to the reciprocal of the wave propagation velocity in intact rock (Cai and Zhao 2000).

Fig. 2
figure 2

Characteristic method

Full size image

Along the left-running and right-running characteristic lines in “hard” rock

$$z_{{\text{H}}} v_{{\text{H}}} \pm \sigma_{H} = {\text{constant}},$$
(3)

where zH is the wave impedance of the “hard” rock and vH and σH are the particle velocity and normal stress of the “hard” rock, respectively.

Along the left-running and right-running characteristic lines in “soft” rock

$$z_{{\text{S}}} v_{{\text{S}}} \pm \sigma_{{\text{S}}} = {\text{constant,}}$$
(4)

where zS is the wave impedance of the “soft” rock and vS and σS are the particle velocity and normal stress of the “soft” rock, respectively.

For a rock mass undisturbed at t = 0, the particle velocity and normal stress at each point on the x-axis are equal to zero. The left-running characteristic line ab and right-running characteristic line bc intersect the t-axis at point (0, t − x1/CH). Therefore, based on Eq. (3), along the characteristic line ab, the relation between the particle velocity and normal stress at points b and a is

$$z_{{\text{H}}} v_{{\text{I}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) - \sigma_{{\text{H}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) = 0.$$
(5)

Along characteristic line bc, the relation between the particle velocity and normal stress at points b and c is

$$z_{{\text{H}}} v_{{\text{I}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) + \sigma_{{\text{H}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) = z_{{\text{H}}} v_{{\text{H}}} \left( {x_{1} ,t} \right) + \sigma_{{\text{H}}} \left( {x_{1} ,t} \right).$$
(6)

Along characteristic line cd, the relation between the particle velocity and normal stress at points c and d is

$$z_{{\text{S}}} v_{{\text{S}}} \left( {x_{1} ,t} \right) - \sigma_{{\text{S}}} \left( {x_{1} ,t} \right) = 0.$$
(7)

Based on Eqs. (5), (6) and (7), the derivative of Eq. (2) becomes

$$\frac{{\partial v_{{\text{S}}} \left( {x_{1} ,t} \right)}}{\partial t} = \frac{{2k_{{\text{n}}} }}{{z_{{\text{S}}} }}v_{{\text{I}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) - k_{{\text{n}}} \left( {1/z_{{\text{S}}} + 1/z_{{\text{H}}} } \right)v_{{\text{S}}} \left( {x_{1} ,t} \right).$$
(8)

The derivative \(\frac{{\partial v_{{\text{S}}} \left( {x_{1} ,t} \right)}}{\partial t}\) can be replaced by \(\frac{{v_{{\text{S}}} \left( {x_{1} ,t_{j + 1} } \right) - v_{{\text{S}}} \left( {x_{1} ,t_{j} } \right)}}{\Delta t}\) if Δt is sufficiently small. Therefore, Eq. (8) can be rewritten as

$$v_{{\text{S}}} \left( {x_{1} ,t_{j + 1} } \right) = \frac{{2k_{{\text{n}}} \Delta t}}{{z_{{\text{S}}} }}v_{{\text{I}}} \left( {0,t - x_{1} /C_{{\text{H}}} } \right) + \left[ {1 - k_{{\text{n}}} \Delta t\left( {1/z_{{\text{H}}} + 1/z_{{\text{S}}} } \right)} \right]v_{{\text{S}}} \left( {x_{1} ,t_{j} } \right).$$
(9)

With known incident wave and parameter values, the particle velocity in the “soft” rock (transmitted wave) after a stress wave crosses the joint can be calculated based on Eq. (9).

The particle velocity transmission coefficient is defined as the peak particle velocity in the “soft” rock divided by the peak particle velocity of the incident wave

$$T_{{\text{v}}} = \frac{{\max \left( {v_{{\text{S}}} } \right)}}{{\max \left( {v_{{\text{I}}} } \right)}}.$$
(10)

When the joint stiffness approaches infinite, the stress wave propagates at the interface of different materials, and the transmission coefficient is equal to that of the wave propagation at the interface of different materials (Wang 2005). When the wave impedances on both sides of the joint are the same, the stress wave propagates in jointed rock mass. Therefore, Eq. (9) can be verified through these two cases.

3 Transmitted Waves When Stress Waves Propagate from “Hard” Rock to “Soft” Rock

For the deformation of the joint is linear in this paper, the incident wave is assumed to be a half-sinusoidal wave with an amplitude of A0 = 0.02 m/s. The density of the “hard rock” in front of the joint is ρH = 2650 kg/m3, the wave velocity is CH = 5830 m/s (Zhao et al. 2006), the wave impedance is zH = ρH CH, and the wave impedance of the “soft rock” behind the joint is determined by the wave impedance ratio n (zS = zH/n).

Figure 3 shows the incident waves and the corresponding transmitted waves under different conditions. In Fig. 3a, the joint stiffness is kn = 1.00 GPa/m, and the wave impedance ratio of the rock mass is n = 3.00. When the frequency of the incident wave is f0 = 80 Hz, the transmitted wave is attenuated, and the particle velocity amplitude is smaller than that of the incident wave. However, when the frequency of the incident wave is f0 = 20 Hz, the transmitted wave is enlarged, and the particle velocity amplitude is larger than that of the incident wave. Therefore, with the change in frequency of the incident wave, a threshold frequency is reached. At this threshold, the amplitude of the transmitted wave is exactly equal to that of the incident wave, and non-attenuation propagation of the stress wave occurs. Through calculations, the threshold frequency is approximately f0 = 57 Hz. In Fig. 3b, the frequency of the incident wave is f0 = 50 Hz, and the wave impedance ratio of the rock mass is n = 3.00. When the joint stiffness is kn = 0.50 GPa/m, the transmitted wave is attenuated, and the amplitude of the particle velocity is smaller than that of the incident wave. However, when the joint stiffness is kn = 2.50 GPa/m, the transmitted wave is enlarged, and the amplitude of the particle velocity is larger than that of the incident wave. Similar to the results in Fig. 3a, as the joint stiffness changes, a threshold joint stiffness is reached, and the non-attenuation propagation of stress waves is observed beyond this value. The calculated threshold joint stiffness is approximately kn = 0.88 GPa/m. In Fig. 3c, the frequency of the incident wave is f0 = 50 Hz, and the joint stiffness is kn = 1.00 GPa/m. When the wave impedance ratio is n = 2.00, the transmitted wave is attenuated, and the particle velocity amplitude is smaller than that of the incident wave. However, when the wave impedance ratio is n = 5.00, the transmitted wave is enlarged, and the particle velocity amplitude is larger than that of the incident wave. The threshold wave impedance ratio corresponding to the non-attenuation propagation of stress waves is approximately n = 2.72.

Fig. 3
figure 3

Incident wave and corresponding transmitted waves under different conditions. a kn = 1.00 GPa/m and n = 3.00; b f0 = 50 Hz and n = 3.00; c f0 = 50 Hz and kn = 1.00 GPa/m

Full size image

For a given joint stiffness and wave impedance ratio, the amplitude of the transmitted wave increases with decreasing frequency, so the non-attenuation propagation of stress waves is most likely to occur when the frequency is relatively low. Due to the existence of joints in the crust, the high-frequency components are usually quickly lost in the process of stress wave propagation, and the low-frequency components slowly attenuate; therefore, the main stress wave that reaches the ground is a low-frequency wave. When stress waves propagate from deep rocks with a large wave impedance to weak rocks and soils with a small wave impedance, the amplitude of the particle velocity may increase, which will cause serious damage to the buildings above these areas. For a given frequency and wave impedance ratio, the amplitude of the transmitted wave increases as the joint stiffness increases, so the non-attenuation propagation of stress waves is most likely to occur when the joint stiffness is relatively large. When the joint stiffness approaches zero, the joint becomes weak, and the particle velocity transmission coefficient decreases to a minimum value. If the joint stiffness approaches infinity, the joint acts as an interface, the particle velocity transmission coefficient increases to a maximum value, and the non-attenuation property of the stress wave is the strongest. For a given frequency and joint stiffness, the amplitude of the transmitted wave increases with the wave impedance ratio. In fact, the wave impedance ratios in Fig. 3a–c are always larger than 1.00, which indicates that the non-attenuation phenomenon of the particle velocity only occurs when the stress wave propagates from the rock with a large wave impedance to rock with a small wave impedance.

Therefore, the threshold frequency ft, the threshold joint stiffness kt and the threshold wave impedance ratio nt are defined as the frequency, joint stiffness and wave impedance ratio for the case of a wave transmission coefficient equals 1.0

$$\left\{ \begin{gathered} f_{{\text{t}}} = \left( {f_{0} } \right)_{{T_{{\text{v}}} = 1}} \hfill \\ k_{{\text{t}}} = \left( {k_{n} } \right)_{{T_{{\text{v}}} = 1}} \hfill \\ n_{{\text{t}}} = \left( n \right)_{{T_{{\text{v}}} = 1}} \hfill \\ \end{gathered} \right..$$
(11)

Therefore, the threshold frequency, threshold joint stiffness and threshold wave impedance ratio can be used to evaluate the non-attenuation propagation of stress waves in rock masses.

4 Discussion

4.1 Variation in Threshold Frequency

Figure 4 shows the variation in the threshold frequency with respect to joint stiffness with wave impedance ratios of n = 1.50, 1.75, 2.00, 2.25 and 2.50, respectively. For a fixed wave impedance ratio and joint stiffness, the threshold frequency can be obtained by Eqs. (9) and (10). It is seen that the threshold frequency increases linearly with increasing joint stiffness. When the joint stiffness is small, non-attenuation propagation of stress waves can occur when the frequency is low. When the joint stiffness is large, non-attenuation propagation of stress waves can occur when the frequency is high. It can also be seen that the threshold frequency increases with increasing wave impedance ratio for a fixed joint stiffness. When the wave impedance ratio is small, the threshold frequency increases slowly with the joint stiffness. As the wave impedance ratio increases, the threshold frequency increases rapidly with increasing joint stiffness.

Fig. 4
figure 4

Effect of joint stiffness on threshold frequency

Full size image

Figure 5 shows the variation in the threshold frequency with respect to the wave impedance ratio with joint stiffnesses of kn = 1.5, 2.0, 2.5, 3.0 and 3.5 GPa/m, respectively. The threshold frequency increases linearly with increasing wave impedance ratio. For a fixed wave impedance ratio, the threshold frequency of the non-attenuation propagation of the stress wave increases as the joint stiffness increases, which is consistent with the result shown in Fig. 4. Figure 5 also shows that the threshold frequency increases slowly with increasing wave impedance ratio when the joint stiffness is small, while the threshold frequency increases rapidly with increasing wave impedance ratio when the joint stiffness is large.

Fig. 5
figure 5

Effect of wave impedance ratio on threshold frequency

Full size image

4.2 Variation in Threshold Joint Stiffness

Figure 6 shows the variation in the joint stiffness with respect to frequency with wave impedance ratios of n = 1.50, 1.75, 2.00, 2.25 and 2.50, respectively. It is seen that the threshold joint stiffness increases linearly with increasing frequency. When a stress wave with a low frequency propagates in the jointed rock mass, non-attenuation propagation of the stress wave can occur when the joint stiffness is small. With the increase of frequency, the non-attenuation propagation of stress waves occurs with an increasing joint stiffness. For a fixed frequency, the threshold joint stiffness increases with decreasing wave impedance ratio, and the threshold joint stiffness increases rapidly when the wave impedance ratio is large.

Fig. 6
figure 6

Effect of frequency on threshold joint stiffness

Full size image

Figure 7 shows the variation in the threshold joint stiffness with respect to wave impedance ratios with frequencies of f0 = 50, 100, 150, 200 and 250 Hz, respectively. It is seen that the threshold joint stiffness decreases with increasing wave impedance ratio. When the wave impedance ratio is small, the threshold joint stiffness decreases rapidly. Subsequently, the threshold joint stiffness decreases slowly and tends to become stable as the wave impedance ratio further increases. In addition, the threshold joint stiffness increases with increasing frequency for a given wave impedance ratio, and these results are in accordance with those shown in Fig. 6.

Fig. 7
figure 7

Effect of wave impedance ratio on threshold joint stiffness

Full size image

4.3 Variation in Threshold Wave Impedance Ratio

Figure 8 shows the variation in the threshold wave impedance ratio with respect to frequency with joint stiffnesses of kn = 1.5, 2.0, 2.5, 3.0 and 3.5 GPa/m, respectively. The threshold wave impedance ratio increases linearly with increasing frequency. When the stress wave with a low frequency propagates in the jointed rock mass, non-attenuation propagation of the stress wave can occur when the wave impedance ratio of the rock mass is small. With increasing frequency, the wave impedance ratio of the non-attenuation propagation of stress waves increases. It can also be seen that the threshold wave impedance ratio increases with decreasing joint stiffness for a fixed frequency and that the threshold wave impedance ratio increases rapidly when the joint stiffness is small.

Fig. 8
figure 8

Effect of frequency on threshold wave impedance ratio

Full size image

The variation in the threshold wave impedance ratio with respect to joint stiffness with frequencies of f0 = 50, 100, 150, 200 and 250 Hz is shown in Fig. 9. It can be observed that the threshold wave impedance ratio decreases with increasing joint stiffness. When the joint stiffness is relatively small, the threshold wave impedance ratio decreases rapidly as the joint stiffness increases. Subsequently, the threshold wave impedance ratio decreases slowly and finally tends to be stable as the joint stiffness further increases. In general, the joint is weak when the joint stiffness is small, so the attenuation of the stress wave is strong. To achieve the non-attenuation propagation of stress waves, the wave impedance ratio must be increased. When the joint stiffness approaches infinity, the attenuation of the stress wave by the joint can be ignored. The non-attenuation propagation of stress waves can occur when the wave impedance is equal to 1.0. In addition, the threshold wave impedance ratio increases with increasing frequency for a given joint stiffness, which is in accordance with the results shown in Fig. 8.

Fig. 9
figure 9

Effect of joint stiffness on threshold wave impedance ratio

Full size image

5 A Threshold Surface in FKN Space

Figure 10 shows a threshold surface in FKN space (F refers to the frequency of the incident wave, K refers to the joint stiffness, and N refers to the wave impedance ratio). Arbitrary points on the threshold surface can keep the stress wave from attenuation, and the amplitude of the transmitted wave is exactly equal to that of the incident wave. Figure 10 shows that the region of attenuated stress wave propagation exists above the threshold surface. The region corresponding to the non-attenuation propagation of stress waves exists below the threshold surface. The region of non-attenuation exists under the conditions of a low incident wave frequency, large joint stiffness or large wave impedance ratio. The amplification of stress wave has an important impact on the stability of underground engineering. The threshold surface can be used as a criterion for the attenuation or amplification behavior of wave propagation in jointed rock.

Fig. 10
figure 10

Threshold surface in FKN space

Full size image

When a stress wave propagates in an isotropic and homogeneous rock mass with the same wave impedances on two sides of the joint, the energy can be transferred completely if the joint stiffness approaches infinity. When a stress wave propagates from rock with a large wave impedance to rock with a small wave impedance, the relation between the wave impedances inevitably leads to the particle velocity in the “soft” rock being faster than that in the “hard” rock. Additionally, the phenomenon of the non-attenuation propagation of stress waves occurs. However, the rock joint slows the propagation of a stress wave, which is why the particle velocity of the transmitted wave is not always faster than that of the incident wave when the stress wave propagates from rock with a large wave impedance to rock with a small wave impedance. When the amplification effect caused by the wave impedance ratio is stronger than the attenuation effect caused by the joint, the non-attenuation propagation of stress waves occurs.

6 Conclusions

When a stress wave propagates from rock with a large wave impedance to rock with a small wave impedance, the non-attenuation propagation of stress waves may occur under certain conditions, and this process is related to the wave source, the properties of the joint and the wave impedance of the propagation medium.

The threshold frequency, threshold joint stiffness and threshold wave impedance ratio can be used to evaluate the non-attenuation propagation of stress waves in rock masses. The threshold frequency increases linearly with increasing joint stiffness and wave impedance ratio. The threshold joint stiffness increases linearly with increasing frequency and decreases with increasing wave impedance ratio. The threshold wave impedance ratio increases linearly with increasing frequency and decreases with increasing joint stiffness.

When the amplification effect caused by the wave impedance ratio is stronger than the attenuation effect caused by the joint, the non-attenuation propagation of stress waves occurs. Similarly, when the amplification effect caused by the wave impedance ratio is weaker than the attenuation effect caused by the joint, the stress wave is attenuated.

In FKN space, the threshold surface divides the space into a region of attenuation and a region of non-attenuation. Below the threshold surface, the stress wave’s propagation displays obvious non-attenuation at low incident wave frequencies, large joint stiffnesses and large wave impedance ratios.

Usually, deep rocks in the Earth’s crust are “hard” rock, and shallow rocks are “soft” rock. Therefore, the non-attenuation propagation of stress waves may occur, and particle motion is strengthened when the ground surface is reached, especially in areas of soft rock, soil and buildings.