Coupled Thermo-Hydro-Mechanical Numerical Modeling of Evolving Fractures in Rocks

Abstract

We present a numerical technique capable of handling evolving fractures in rocks triggered by coupled thermo-hydro-mechanical (THM) phenomena. The approach is formulated in the context of the finite-element method (FEM) and consists in introducing especial (high-aspect ratio) finite elements in-between the regular (bulk) finite elements. We called this method the mesh fragmentation technique (MFT). The MFT has been successfully used to model mechanical and hydro-mechanical problems related to drying cracks in soils, fractures in concrete, and hydraulic fractures in rocks. In this paper, we extend the MFT for tackling non-isothermal problems in porous media. We present the main components of the mathematical formulation together with its implementation in a fully coupled THM computer code. The proposed method is verified and validated using available analytical, experimental, and numerical results. A very satisfactory performance of the proposed method is observed in all the analyzed cases. These results are encouraging and show the potential of the MFT to tackle THM applications involving fractured rocks. A clear advantage of the proposed framework is that it can be easily implemented in existing numerical FEM codes for continuous porous media to upgrade them to tackle THM engineering problems with evolving discontinuities.

1 Introduction

The formation and propagation of discontinuities in porous media have been a subject of increasing interest lately. The presence of fractures and cracks has a significant impact on the performance of geo-engineering problems involving soils and rocks (e.g., embankments, tunnels, gas and oil reservoirs, nuclear waste disposal, and geothermal systems, amongst others). The widespread use of hydraulic fracturing as a well stimulation techniques to produce oil and gas from unconventional and conventional reservoirs has allowed to substantially improve the understanding of the main hydro-mechanical phenomena behind the formation of fractures when a fluid is injected at high pressure in a rock mass. In some engineering applications it is also critical to incorporate the effect of the temperature in the analysis, as, e.g., high-level nuclear waste disposal, hydraulic fracturing in conventional oil reservoirs (e.g., Siddhamshetty et al. 2018), and Enhanced Geothermal Systems (EGS, e.g., Parker 1999; Nadimi et al. 2020). Particularly, analysis related to EGS has promoted the study of the thermo-hydraulic fracturing process.

Enhanced Geothermal System enables producing geothermal energy from Hot Dry Rock (HDR) reservoirs, which are deficient in water and permeability, the two basic components necessary to exploit their geothermal potential (e.g., Parker 1999; Genter et al. 2010). EGS implementation requires the drilling of injection and production wells. Through the first one, a cold fluid is injected, whereas hot water and/or steam is recovered from the production well. A key feature of this methodology is the network of fractures that connect these two wells. The discontinuities can be either (naturally) pre-existing fractures, or (artificially) triggered fractures by the thermal shock induced by the contact between the cool injection fluid and the hot natural rock. Water and liquid nitrogen (at around − 196 °C) are contemplated as potential injection fluids. This type of project envisages reservoirs at depth with temperature above 180 °C. Several field tests in different countries have been conducted to evaluate the feasibility of EGS (e.g., Parker 1999; Genter et al. 2010; Elders et al. 2014; Kaieda 2015; Frioleifsson et al. 2014, 2017; Kingdon et al. 2019a, b; Kneafsey et al. 2018, 2019; Boon et al. 2019), including the ongoing Utha-FORGE project in the USA (e.g., Nadimi et al. 2020).

Laboratory tests have assisted to gain a better understanding of fractures formation under non-isothermal conditions. For example, King (1983) studied the use of liquid nitrogen as an alternative approach to conventional fracturing fluids (e.g., water or oil). Cha et al. (2014) investigated the feasibility of using cryogenic fluids (e.g., liquid nitrogen) for fracture stimulation. Frash et al. (2014) replicated the formation of hydraulically fractures in HDR. Zhao et al. (2015) investigated the instability and failure of boreholes in granite specimens at high temperature and high pressure. Cha et al. (2018) assessed the performance of cryogenic fracturing to assist energy recovery. Zhou et al. (2018) studied the hydraulic fracturing process at different temperatures.

Several numerical techniques have been adopted to model thermo-hydraulic fractures in rocks. Kohl et al. (1995) simulated the long-term behavior of a two-dimensional (2D) HDR reservoir with a single fracture assuming a joint closure law with a linear stress–temperature and stress–pressure relationship. Ghassemi and Zhou (2011) adopted a hybrid approach to model the cold fluid injection in a three-dimensional (3D) EGS which is based on the discretization of the fracture using the finite element method (FEM). Tarasovs and Ghassemi (2011) used a boundary element model to investigate the influence of secondary fractures under thermal stress. Secondary fractures were also studied by Tran et al. (2012). Guo et al. (2016) investigated the impact of the heterogeneity of fracture aperture on the energy production. Hadgu et al. (2016) studied the influence of fracture orientation on energy production. Wu et al. (2016) proposed a model to optimize the temperature production based on the number of fractures, its distribution, fracture spacing, and well depth. Pandey et al. (2017) developed a control volume finite-element program to study the fracture aperture evolution throughout the reservoir lifespan. Song et al. (2018) compared the performance of multilateral production wells (in terms of heat extraction and production temperature) against a single production well. Guo et al. (2019) analyzed the performance of EGS with different fracture networks and working fluids (water and CO₂) through a 3D THM FE model. Multifractured models have also been used to THM phenomena in fractured rocks (Asai et al. 2019; Slatlem Vik et al. 2018). The papers cited above account for the presence of fractures in the rock mass, but the modeling of the THM processes leading to the crack formation is not considered. Enayatpour et al. (2018) analyzed the enhancement in hydraulic fracturing because of thermally induced fractures using the Cohesive Zone Method.

In this paper, we propose the Mesh Fragmentation Technique (MFT) to model evolving THM fractures in rocks. The MFT is a new methodology that allows upgrading FEs standard codes by incorporating High Aspect Ratio (HAR) elements (Manzoli et al. 2012) in-between the standard FE of the mesh. This technique has been applied with success to model the propagation of desiccation cracks in soils (Sanchez et al. 2014; Manzoli et al. 2017; Maedo et al. 2020); the development of mechanically induced discontinuities in concrete (Manzoli et al. 2016, Rodrigues et al. 2018); and the formation of hydraulically induced fractures in rocks (Manzoli et al. 2019; Cleto et al. 2020). These previous applications of the MFT involved isothermal conditions. In this work, this method is extended to incorporate thermal effects in the analyses. Typical continuous constitutive models for rocks are adopted to represent the behavior of the standard FEs. The HAR interface elements are also equipped with continuous constitutive models, for the thermal, hydraulic, and mechanical problems which are formulated to properly account for the energy dissipation associated with the fracturing process, as well as for the dependence of hydraulic permeability and thermal conductivity on fracture aperture. Therefore, the proposed MFT make use of a fully coupled continuous THM formulation to tackle non-isothermal, hydro-mechanical problems in geological media with evolving discontinuities.

In the following sections, we present first the main components of the MFT, then the adopted mathematical formulation, together with its FE discretization; afterward, we discuss the application cases, and finally, we close the paper with the main conclusion of this work.

2 Mesh Fragmentation Technique

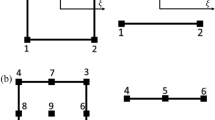
The MFT allows extending FE programs to deal with discontinuities in 2D and 3D problems. To explain the main steps involved in this process, the model of a cubic rock mass will be used as an example. The first step is to develop the standard FE mesh associated with the problem at stake, including all the materials and components related to the case (Fig. 1a). Then, the bulk (standard) FEs are slightly reduced homothetically. This process leads to the formation of small gaps between adjacent elements (Fig. 1b). Finally, the gaps between the elements are filled with HAR finite elements (Fig. 1c). The number of nodes and elements of the fragmented mesh are higher than the ones in the original mesh, because of the additional nodes and elements added during this process. The size of the gaps is very small (typically around 0.1% of the size of the smallest bulk element); therefore, the interface elements added between them have a high-aspect ratio (Manzoli et al. 2012). The fragmentation process could involve the whole mesh, or can be limited to a region around the anticipated damaged zone (Fig. 1d).

Fig. 1

Main stages associated with the mesh fragmentation technique: a materials and finite-element mesh; b size reduction of the bulk elements with the development of the associated gaps between them; c pair of HAR finite elements filling the gaps; and d cross sections showing the damaged area

Standard triangular and tetrahedron finite elements are adopted as HAR interface elements (Fig. 2) when dealing with 2D and 3D problems, respectively. The discontinuities are tackled in an entirely continuous approach. It is assumed that the bulk elements (representing the rock) behave elastically and all the material inelastic response is associated with the HAR elements, which behavior is represented by a damage model that incorporates a characteristic length in the softening law to regularize the numerical solution and avoid mesh dependency issues (as explained in Sect. 3.1). Different constitutive models can be adopted for the HAR elements to represent different types of interfaces. For example, looking at Fig. 1a, different models may be selected to represent the rock–rock, and rock–borehole interfaces. Suitable laws for different type of interfaces have been described elsewhere (e.g., Manzoli et al. 2012, 2019; Sánchez et al. 2014; Maedo et al. 2020).

Fig. 2

High aspect ratio interface elements: a three-node triangular element; b four-node tetrahedral element

The strain tensor of the HAR element can be written as (Manzoli et al. 2012):

$$\varepsilon = \tilde{\varepsilon } + \frac{1}{h}\left( {{\mathbf{n}} \otimes \left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]} \right)^{S} ,$$

(1)

where the first term of the right-hand side ($\tilde{\varepsilon }$) involves the strain components that do not depend on h; the second term contains the other strain components that express the discontinuity behavior across the fracture; $\left( \cdot \right)^{S}$ is the symmetric part of $\left( \cdot \right)$; ${\mathbf{n}}$ is the unit vector normal to the base of the finite element; $\otimes$ is the dyadic product; and $\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]$ is the vector containing the components of the relative displacement between node 1 and its projection at the element base (1′). When $h \to 0$, the term that depends on $h$ is no longer bounded and the element strains are almost exclusively defined by the relative displacement $\left[\kern-0.15em\left[ {\mathbf{u}} \right]\kern-0.15em\right]$, and therefore, this term becomes a measure of strong discontinuity (Manzoli et al. 2016).

The volumetric strain in this case can be written as follows (Manzoli et al. 2019):

$$\nabla \cdot {\mathbf{u}} = \nabla \cdot {\tilde{\mathbf{u}}} + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} }}{h},$$

(2)

in which ${\mathbf{u}}$ denotes the displacement field, ${\tilde{\mathbf{u}}}$ is the continuous part of ${\mathbf{u}}$ and $\left[\kern-0.15em\left[ {u } \right]\kern-0.15em\right]_{n}$ is the discontinuity in the $n$-direction.

It was also shown that the gradient of liquid pressure $\left( {\nabla p_{{\text{l}}} } \right)$ can be expressed as (Manzoli et al. 2019):

$$\nabla p_{{\text{l}}} = \nabla \tilde{p}_{{\text{l}}} + \frac{1}{h}\left[\kern-0.15em\left[ {p_{{\text{l}}} } \right]\kern-0.15em\right]{\mathbf{n}},$$

(3)

where $\left[\kern-0.15em\left[ { p_{{\text{l}}} } \right]\kern-0.15em\right]$ is the discontinuity in the pressure field, and $\nabla \tilde{p}_{{\text{l}}}$ corresponds to the continuous parts of $\nabla p_{{\text{l}}}$.

Following a similar procedure, the temperature gradient $\left( {\nabla T} \right)$ is given by:

$$\nabla T = \nabla \tilde{T} + \frac{1}{h}\left[\kern-0.15em\left[ T \right]\kern-0.15em\right]{\mathbf{n}},$$

(4)

where $\left[\kern-0.15em\left[ {T } \right]\kern-0.15em\right]$ is the discontinuity in the temperature field, and $\nabla \tilde{T}$ corresponds to the continuous parts of $\nabla T$.

Figure 3 illustrates a region of the domain where Ω_h corresponds to a narrow discontinuity of width h delimited by the material surfaces S⁺ and S⁻. The coordinate systems (ξ, η) and (s, n) correspond to the curvilinear (i.e., along the fracture) and the local reference systems, respectively. This figure also shows schematically the variation of the displacement, fluid pressure, and temperature fields in a region containing a fracture.

Fig. 3

Fracture behavior in terms of displacement, temperature, and liquid pressure fields

In typical applications, the fracture permeability is high, which leads to an almost constant fluid pressure across the fracture. As for the temperature, two main processes associated with heat transfer in fractures should be considered: conduction and advection. A jump of temperatures across the fracture can be anticipated in problems where the heat conduction process prevails, because the thermal conductivity of the fracture is much smaller than the thermal conductivity of the intact rock. However, if heat advection is the dominant heat transfer phenomenon in the discontinuity, a rather uniform temperature across the fracture is expected.

The fracturing process starts when the component of effective stress normal to be base of the HAR element reaches the rock tensile strength (as explained in detail in the next section). Thus, the damage of the HAR elements initiates and evolves naturally through the domain, controlled by the local stress and material properties. The users can decide (beforehand) whether the whole mesh or only some zone(s) of it are enhanced with HAR elements. Alternatively, adaptive algorithms (as the ones used in mesh refinement techniques, e.g., Favino et al. 2020) can be adopted to gradually insert HAR elements during the numerical simulation in those zones where the stress level (or other indicators) suggests that fractures are prone to form. In this work, we have inserted HAR elements in-between all the bulk elements, so the fractures can form in any point and propagate though the domain. In previous works, we have proved that the MFT numerical solutions do not depend on the mesh size (e.g., Sanchez et al. 2014; Manzoli et al. 2019). In those works, we have also discussed the main advantages and shortcomings of the MFT with respect to other numerical techniques typically used to handle discontinuities in porous media.

In summary, the formation and subsequent propagation of fractures depend on local stresses and local materials properties only; there is no need to define tracking algorithms to establish the direction and orientation in which the fractures propagate; and there is no need to define special interpolation functions or integration rules for the finite elements representing the fractures, as it is necessary in other approaches typically used to handle discontinuities (e.g., Caballero et al. 2008; Segura and Carol 2010; Gordeliy and Peirce 2013; Wang 2015; Meschke and Leonhart 2015).

3 Governing Equations

The set of governing equations that mathematically describes the physical problem under consideration in a fully saturated porous medium encompasses: balance equations, constitutive relationships, and equilibrium restrictions. The main components of these equations, together with the initial and boundary conditions are explained next.

3.1 Mechanical

Neglecting the inertial term, the porous medium momentum balance equation is given by:

$$\nabla \cdot {\varvec{\sigma}} + {\mathbf{b}} = 0,$$

(5)

where ${\mathbf{b}}$ is the vector of body forces, and ${\varvec{\sigma}}$ is the total stress tensor expressed in terms of effective stress ${\varvec{\sigma}}^{\prime}$ and liquid pressure $\left( {p_{{\text{l}}} } \right)$:

$${\varvec{\sigma^{\prime}}} = {\varvec{\sigma}} + {\mathbf{I}}bp_{l} ,$$

(6)

where ${\mathbf{I}}$ is the identity tensor and $b$ is the Biot's coefficient defined as:

$$b = 1 - \frac{K}{{K_{{\text{s}}} }},$$

(7)

with $K$ and $K_{{\text{s}}}$ denoting the bulk moduli of the porous medium and the solid phase, respectively.

We assumed an elastic behavior of the rock. If necessary, more advanced models can be adopted to describe the behavior of the bulk elements. Under this assumption, the effective stress can be expressed in terms of the changes in both strain tensor $\varepsilon$, and temperature, as follows:

$${\varvec{\dot{\sigma }^{\prime}}} = {\mathbb{C}}:\left( {\dot{\varepsilon } - \dot{\varepsilon }^{o} } \right) = {\mathbb{C}}:\left( {\dot{\varepsilon } - {\mathbf{I}}\alpha_{{\text{T}}} \dot{T}} \right),$$

(8)

where ${\mathbb{C}}$ is the fourth-order elastic tensor; and $\alpha_{{\text{T}}}$ is the thermal expansion coefficient.

The HAR finite elements are equipped with a temperature-dependent scalar tension damage model able to deal with the formation of fractures, as follows:

$${\varvec{\sigma ^{\prime}}} = \left( {1 - d} \right){\mathbb{\varvec {\mathbf{C}}}}:\varvec\varepsilon = \left( {1 - d} \right){\bar{\varvec{\mathbf{\sigma}}}}^{\prime},$$

(9)

where $d \in \left[ {0,1} \right]$ is the damage variable ($d = 0$ corresponds to the case of the intact/undamaged material, and $d = 1$ to the case of a fully damaged material), $\varepsilon$ is the strain tensor, and $\overline{\mathbf{\sigma }} ^{\prime }$ is the elastic stress tensor.

The damage criterion can be written in terms of effective stresses as follows:

$$f = \sigma_{{{\text{nn}}}}^{^{\prime}} - q\left( r \right) \le 0,$$

(10)

where $\sigma_{{{\text{nn}}}}^{^{\prime}}$ is the component of the effective stress tensor normal to the base of the HAR element, $q$ is an internal variable of the model that controls the size of the elastic domain in the space of the effective stresses, and $r$ is another internal variable of the model. If we divide Eq. (10) by (1 − d), the damage criterion can be expressed in terms of the elastic stresses, as follows:

$$\overline{f} = \overline{\sigma }_{{{\text{nn}}}}^{^{\prime}} - r \le 0,$$

(11)

where r is a measure of the size of the elastic domain in the space of elastic effective stresses. Since the elastic normal stress $\overline{\sigma }$ is obtained directly after multiplying the strains by the elastic constants (i.e., Eq. 9), r also defines (indirectly) the elastic domain of the model in the strain space (Eq. 11). The units of the internal variables q and r are stresses, and they are generally identified as the stress-like and strain-like internal variables, respectively (Oliver et al. 2008). Considering $r = q/\left( {1 - d} \right)$, we can write the following damage evolution law in terms of the internal variable r:

$$d\left( r \right) = 1 - \frac{q\left( r \right)}{r}.$$

(12)

Another key element of the formulation is the Kuhn–Tucker relationship:

$$\overline{f} \le 0, \,\, \dot{r} \ge 0, \,\,\dot{r} \overline{f} = 0.$$

(13)

The last ingredient of the damage model is the consistency condition:

$$\dot{r} \dot{\overline{f}} = 0 \quad {\text{if}}\quad \overline{f} = 0.$$

(14)

The evolution law of the strain-like internal variable can be obtained by combining Eqs. (12) and (17), as follows:

$$r_{t} = \mathop {\max }\limits_{{s \in \left[ {0,t} \right]}} \left[ {\sigma_{{\text{u}}} ,\overline{\sigma }_{{{\text{nn}}\left( {\text{s}} \right)}}^{^{\prime}} } \right],$$

(15)

where t is the pseudo-time (i.e., related to the loading process), and $\sigma_{{\text{u}}}$ is the rock tensile strength. The stress-like variable evolves according to the following exponential law:

$$q\left( r \right) = \sigma_{{\text{u}}} \exp \left[ {\frac{{\sigma_{{\text{u}}}^{2} }}{{E G_{{\text{f}}} }} h\left( {1 - \frac{r}{{\sigma_{{\text{u}}} }}} \right)} \right],$$

(16)

where, $E$ is the young modulus and $G_{{\text{f}}}$ is the fracture energy of the rock.

Experimental evidences show that the elastic modulus and tensile strength of rocks depend on temperature. For example, it has been reported that elastic properties of rocks tend to decrease with the increase of temperature (Ding et al. 2016; Wu et al. 2013, Araújo et al. 1997; Sirdesai et al. 2017). These works also show that the elastic properties do not present an abrupt variation in the range of temperatures between 20 and 200 °C, therefore we assumed a linear decrease of E with the increase of T (Fig. 4a) as follows:

$$E = E_{20} - \alpha_{1} \left( {T - 20} \right),$$

(17)

where E₂₀ is the reference Young’s modulus at 20 °C, $\alpha_{1}$ is a model parameter that is calibrated from experiments, and T is the current temperature in [°C].

It has also been reported that the tensile strength decreases with the increase of temperature (Rao et al. 2007; Lu et al. 2017; Sirdesai et al. 2017). Based on these experimental evidences, we assumed an exponential decay of $\sigma_{u}$ with temperature (Fig. 4b), as follows:

$$\sigma_{{\text{u}}} = \sigma_{{{\text{u}}20}} e^{{\left[ { - \alpha_{2} \left( {T - 20} \right)} \right]}} ,$$

(18)

where $\sigma_{{{\text{u}}20}}$ is the reference tensile strength at 20 °C, $\alpha_{2}$ is a model parameter that is calibrated from experiments, and T is the current temperature in [°C].

It is important to point out that Eqs. 17 and 18 are general evolution laws that we adopted to represent typical trends of the mechanical properties based on evidences reported in the literature. The proposed MFT formulation is general and any other evolution law suitable to model the geomaterial behavior can be implemented.

We implemented the constitutive model explained in this section in CODE_BRIGHT using the IMPL-EX stress integration scheme proposed by Oliver et al. (2008). The algorithm we adopted for the implementation of the damage model is described elsewhere (Manzoli et al. 2016, 2019).

3.2 Hydraulic

The water mass balance equation for a porous medium can be written as (Olivella et al. 1994):

$$\phi \frac{{{\text{D}}\rho_{{\text{l}}} }}{{{\text{D}}t}} + \left[ {\frac{{\left( {1 - \phi } \right)}}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right]\rho_{{\text{l}}} + \nabla \cdot \left( {\rho_{{\text{l}}} \user2{ }{\mathbf{q}}_{{\text{l}}} } \right) = 0,$$

(19)

where $\phi$ is the porosity, $\rho_{{\text{l}}}$ is the liquid density, $\rho_{{\text{s}}}$ is the solid density, ${\dot{\mathbf{u}}}$ is the velocity vector, and ${\mathbf{q}}_{{\text{l}}}$ is the fluid Darcy's velocity vector expressed as:

$${\mathbf{q}}_{{\text{l}}} = - \frac{{\mathbf{k}}}{{\mu_{{\text{l}}} }}\left[ {\nabla p_{{\text{l}}} - \rho_{{\text{l}}} \user2{ }{\mathbf{g}}} \right],$$

(20)

where ${\mathbf{k}}$ is the intrinsic permeability tensor of the porous medium and $\mu_{{\text{l}}}$ is the liquid dynamic viscosity. Darcy’s law rules the liquid flow in both, the bulk and interface elements. In the fracture domain ${\Omega }^{{\text{h}}}$, Eq. (20) can be written as (Manzoli et al. 2019):

$$\left( {{\mathbf{q}}_{{\text{l}}} } \right)_{{{\Omega }^{{\text{h}}} }} = - \frac{{{\mathbf{k}}_{{{\Omega }^{{\text{h}}} }} }}{{\mu_{{\text{l}}} }}\nabla p_{{\text{l}}} = - \frac{1}{{\mu_{{\text{l}}} }}\left[ {{\mathbf{k}} + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n}^{3} }}{R 12 h}{\mathbf{s}} \otimes {\mathbf{s}}} \right]\nabla p_{{\text{l}}} ,$$

(21)

where the first term on the right-hand side corresponds to the continuous part of the liquid flux and the second term is the discontinuous counterpart associated with the fluid flow in the s-direction of the fracture (see Fig. 3), which is modeled by means of the well-known cubic law (Snow 1965). $R \ge 1$ is the parameter that accounts for deviations from the ideal parallel surface conditions (Witherspoon et al. 1980). In this work, we assumed $R = 1$ in all the analyses.

The porosity is also affected by the fracture opening as follows (Manzoli et al. 2019):

$$\phi_{{{\Omega }^{{\text{h}}} }} = \phi + \frac{{ \left[\kern-0.15em\left[ {u } \right]\kern-0.15em\right]_{n} }}{h},$$

(22)

where the second term on the right-hand side represents the porosity enhancement associated with the fracturing process. Before the hydraulic process starts (i.e., $d = 0$), the second term is zero, because there is not a displacement jump. Once the fracturing process initiates (i.e., $d > 0$), both terms (i.e., matrix material porosity and fracture) contribute to the total porosity; however, the second term becomes dominant, so the rock porosity can be disregarded (i.e., $\phi_{{{\Omega }^{{\text{h}}} }} \sim \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} /h)$.

Finally, the solid density is updated as follows:

$$\rho_{{\text{s}}} = \rho_{{{\text{s}}_{o} }} \exp \left[ {\frac{{\left( {b - \phi } \right)}}{{K_{{\text{s}}} }}\left( {p_{{\text{l}}} - p_{{{\text{l}}_{{\text{o}}} }} } \right) - \left( {b - \phi } \right)\alpha_{{\text{T}}} \left( {T - T_{{\text{o}}} } \right) - \left( {1 - b} \right)\varepsilon_{{\text{v}}} } \right],$$

(23)

where $\varepsilon_{{\text{v}}}$ is the volumetric deformation, and p_l0 and T₀ are the reference pressure and temperature, respectively.

3.3 Thermal

The balance of the internal energy equation for a porous medium is given by:

$$\begin{aligned} & \phi \frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right) + \left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right)\left[ {\frac{{\left( {1 - \phi } \right)}}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right] \\ & \quad + \left( {1 - \phi } \right)\rho_{{\text{s}}} \frac{{{\text{D}}e_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot \left( {{\mathbf{i}}_{{\text{c}}} + e_{{\text{l}}} \rho_{{\text{l}}} {\mathbf{q}}_{{\text{l}}} } \right) = f_{{\text{E}}} , \\ \end{aligned}$$

(24)

where $e_{{\text{s}}}$ and $e_{{\text{l}}}$ are the specific internal energies of solid and liquid phases, respectively (computed as explained in Olivella et al. (1996)), and ${\mathbf{i}}_{{\text{c}}}$ is the thermal conductivity flux. The following thermal conductivity law is adopted:

$${\mathbf{i}}_{{\text{c}}} = {\mathbf{I}} \lambda \nabla T = {\mathbf{I}} \left[ {\lambda_{{\text{s}}} \left( {1 - \phi } \right) + \lambda_{{\text{l}}} \phi } \right]\user2{ }\nabla T,$$

(25)

where $\lambda_{{}}$ is global (average) thermal conductivity of the rock, $\lambda_{{\text{s}}}$ and $\lambda_{{\text{l}}}$ represent the thermal conductivity of the solid and liquid phases, respectively. Once the damage process is initiated, the thermal conductivity in the ${\Omega }^{h}$ domain is given by Eq. (25), with the corresponding impact of the fracture on the thermal conductivity through the enhanced porosity described by Eq. (20). Alternative thermal conductivity laws are available (CODE_BRIGHT 2020).

4 Finite-Element Formulation

The weak form equations associated with the mathematical formulation described above for both, rock matrix and fractures, are presented next based on continuous mechanics concepts.

4.1 Governing Equations: Weak Form

The weak forms of the mechanical, hydraulic, and thermal governing equations are obtained after multiplying (both sides) of Eqs. (5), (19), and (24), respectively, by the corresponding weight functions and integrating them in the domain, as follows:

$$\mathop \int \limits_{\Omega } \delta {\mathbf{u}}:\left[ {\Sigma_{*} \left( \varepsilon \right) + {\mathbf{m}} b p_{{\text{l}}} } \right]{\text{d}}\Omega = \mathop \int \limits_{{\Gamma_{\sigma } }} \delta {\mathbf{u}} \cdot {\overline{\mathbf{t}}}{\text{d}}\Gamma + \mathop \int \limits_{\Omega } \delta {\mathbf{u}} \cdot {\mathbf{b}}{\text{d}}\Omega \quad \forall {\updelta }{\mathbf{u}} \in {\mathbf{U}}_{{\text{o}}} ,$$

(26)

$$\begin{array}{*{20}c} {\mathop \int \limits_{\Omega } \delta p_{{\text{l}}} \cdot \left( {\phi_{*} \frac{{{\text{D}}p_{l} }}{{{\text{D}}t}}} \right){\text{d}}\Omega + \mathop \int \limits_{\Omega } \delta p_{{\text{l}}} \cdot \left[ {\frac{{\left( {1 - \phi } \right)_{*} }}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right]\rho_{{\text{l}}} {\text{d}}\Omega } \\ {\quad + \mathop \int \limits_{\Omega } \nabla \delta p_{{\text{l}}} \cdot \left[ {\rho_{{\text{l}}} \left( {{\mathbf{q}}_{{\text{l}}} } \right)_{*} } \right] {\text{d}}\Omega = \mathop \int \limits_{{\Gamma_{{\text{q}}} }} \delta p_{{\text{l}}} \rho_{{\text{l}}} \overline{q}_{{\text{l}}} {\text{d}}\Gamma } \\ \end{array} \quad \forall \delta p_{{\text{l}}} \in {\mathbf{P}}_{{\text{o}}} ,$$

(27)

$$\begin{array}{*{20}c} {\mathop \int \limits_{\Omega } \delta T\left[ {\phi_{*} \frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right) + \left( {1 - \phi } \right)_{*} \rho_{{\text{s}}} \frac{{{\text{D}}e_{{\text{s}}} }}{{{\text{D}}t}}} \right]{\text{d}}\Omega } \\ { + \mathop \int \limits_{\Omega } \delta T e_{{\text{l}}} \rho_{{\text{l}}} \left[ {\frac{{\left( {1 - \phi } \right)_{*} }}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right]{\text{d}}\Omega } \\ { + \mathop \int \limits_{\Omega } \nabla \delta T \cdot \left( {{\mathbf{i}}_{{\text{c}}} } \right)_{*} {\text{d}}\Omega + \mathop \int \limits_{\Omega } \nabla \delta T \cdot \left[ {e_{{\text{l}}} \rho_{{\text{l}}} \left( {{\mathbf{q}}_{{\text{l}}} } \right)_{*} } \right] {\text{d}}\Omega } \\ { = \mathop \int \limits_{{\Gamma_{{{\text{j}}_{{\text{E}}} }} }} \delta T \overline{j}_{{\text{E}}}^{^{\prime}} {\text{d}}\Gamma ,} \\ \end{array} \quad \forall {\updelta }T \in {\mathbf{T}}_{{\text{o}}}$$

(28)

where ${\mathbf{U}}_{{\text{o}}}$, ${\mathbf{P}}_{{\text{o}}}$, and ${\mathbf{T}}_{{\text{o}}}$ are the admissible displacement, pressure, and temperature fields, respectively. The set of material parameters can be defined as follows:

$$\left[ {{{\varvec{\Sigma}}}_{\user2{*}} \left( \cdot \right),{\mathbf{k}}_{*} ,\phi_{*} ,\left( {1 - \phi } \right)_{*} ,\lambda_{*} } \right] = \left\{ {\begin{array}{*{20}c} {\left[ {{{\varvec{\Sigma}}}_{{{\Omega }^{h} }} \left( \cdot \right),{\mathbf{k}}_{{{\Omega }^{h} }} ,\phi_{{{\Omega }^{h} }} ,0,\lambda_{{{\Omega }^{h} }} } \right] {\text{in}}\, \Omega^{h} } \\ {} \\ {\left[ {{{\varvec{\Sigma}}}\left( \cdot \right),{\mathbf{k}},\phi ,\left( {1 - \phi } \right),\lambda } \right] {\text{in}}\, \Omega \backslash \Omega^{h} } \\ \end{array} } \right..$$

(29)

The subscript ‘$*$’ corresponds to the domains and properties that need to be used depending on whether the bulk or the HAR elements are considered. In the following sub-sections, the fluid-mass and internal energy balance equations for the fractures are described in more detail. The equations related to the mechanical problem are presented in Manzoli et al. (2016, 2019).

4.2 Fracture Water Mass Balance Equation: Weak from

The weak form of the fluid-mass balance equation in the fracture is given by:

$$\begin{aligned} & \mathop \int \limits_{{\Omega^{{\text{h}}} }} \delta p_{{\text{l}}} \cdot \left( {\phi_{{\Omega^{{\text{h}}} }} \frac{{{\text{D}}p_{{\text{l}}} }}{{{\text{D}}t}}} \right){\text{d}}\Omega + \mathop \int \limits_{{\Omega^{{\text{h}}} }} \delta p_{{\text{l}}} \cdot \left[ {\frac{{\left( {1 - \phi } \right)_{{\Omega^{{\text{h}}} }} }}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right]\rho_{{\text{l}}} {\text{d}}\Omega \\ & \quad + \mathop \int \limits_{{\Omega^{{\text{h}}} }} \nabla \delta p_{{\text{l}}} \cdot \left[ {\rho_{{\text{l}}} \left( {{\mathbf{q}}_{{\text{l}}} } \right)_{{\Omega^{{\text{h}}} }} } \right] {\text{d}}\Omega \\ & \quad = - \left[ {\mathop \int \limits_{S} \delta p_{{\text{l}}} \rho_{{\text{l}}} q_{{{\text{l}}_{{S^{ + } }} }} {\text{d}}S - \mathop \int \limits_{S} \delta p_{{\text{l}}} \rho_{{\text{l}}} q_{{{\text{l}}_{{S^{ - } }} }} {\text{d}}S} \right], \\ \end{aligned}$$

(30)

where $q_{{{\text{l}}_{{S^{ + } }} }} = {\mathbf{q}}_{{{\text{l}}_{{S^{ + } }} }} \cdot {\mathbf{n}}$ and $q_{{{\text{l}}_{{S^{ - } }} }} = {\mathbf{q}}_{{{\text{l}}_{{S^{ - } }} }} \cdot \left( { - {\mathbf{n}}} \right)$ correspond to fluid exchange between the subdomain ${\Omega }^{h}$ and the surrounding medium (S⁺ and S⁻, Fig. 3). Substituting Eqs. (2), (21), and (22) into (30), the weak form can be rewritten as:

$$\begin{aligned} & \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \delta p_{{\text{l}}} \left[ {\left( {\phi + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} }}{h}} \right)\frac{{{\text{D}}p_{{\text{l}}} }}{{{\text{D}}t}}} \right]{\text{d}}\eta {\text{ d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \delta p_{{\text{l}}} \left( {\nabla \cdot {\mathbf{\dot{\tilde{u}}}} + \frac{{ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n} }}{h}} \right)\rho_{{\text{l}}} {\text{d}}\eta {\text{ d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \nabla \delta p_{{\text{l}}} \cdot \left[ {\frac{{\rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\left( {{\mathbf{k}} + \frac{{ \ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n}^{3} }}{R 12 h}{\mathbf{t}} \otimes {\mathbf{t}}} \right)\left( {\nabla p_{{\text{l}}} - \rho_{{\text{l}}} {\mathbf{g}}} \right)} \right]{\text{d}}\eta {\text{ d}}\xi \\ & \quad = - \left[ {\mathop \int \limits_{S} \delta p_{{\text{l}}} \rho_{{\text{l}}} q_{{{\text{l}}_{{S^{ + } }} }} {\text{d}}S - \mathop \int \limits_{S} \delta p_{{\text{l}}} \rho_{{\text{l}}} q_{{{\text{l}}_{{S^{ - } }} }} {\text{d}}S} \right]. \\ \end{aligned}$$

(31)

The final form is obtained by integrating the previous equation over the width $h$ and taking the limit as $h \to 0$:

$$\begin{aligned} & \mathop \int \limits_{S} \delta p_{{\text{l}}} \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} \frac{{{\text{D}}p_{{\text{l}}} }}{{{\text{D}}t}}{\text{d}}\xi + \mathop \int \limits_{S} \delta p_{{\text{l}}} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n} \rho_{{\text{l}}} {\text{d}}\xi \\ & \quad + \mathop \int \limits_{S} \frac{{\partial \delta p_{{\text{l}}} }}{\partial \xi }\frac{{\rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n}^{3} }}{R 12}\left( {\frac{{\partial p_{{\text{l}}} }}{\partial \xi } - \rho_{{\text{l}}} g} \right){\text{d}}\xi = - \mathop \int \limits_{S} \delta p_{{\text{l}}} \rho_{{\text{l}}} \left[\kern-0.15em\left[ {q_{{\text{l}}} } \right]\kern-0.15em\right] {\text{d}}S, \\ \end{aligned}$$

(32)

where $\left[\kern-0.15em\left[ {q_{{\text{l}}} } \right]\kern-0.15em\right]$ is the jump in the water flow caused by the discontinuity.

The previous expression is the weak form of the following differential equation:

$$\left[\kern-0.15em\left[ { u} \right]\kern-0.15em\right] _{n} \frac{{{\text{D}}p_{{\text{l}}} }}{{{\text{D}}t}} + \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n} \rho_{{\text{l}}} + \frac{\partial }{\partial \xi }\left[ {\frac{{\rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n}^{3} }}{R 12}\left( {\frac{{\partial p_{{\text{l}}} }}{\partial \xi } - \rho_{{\text{l}}} g} \right)} \right] + \rho_{{\text{l}}} \left[\kern-0.15em\left[ {q_{{\text{l}}} } \right]\kern-0.15em\right] = 0,$$

(33)

which correspond to the strong form of the fluid-mass balance equation in the discontinuity.

4.3 Fracture Internal Energy Balance Equation: Weak form

Similarly, the internal energy balance equation in the fracture is expressed as:

$$\begin{aligned} & \mathop \int \limits_{{{\Omega }^{{\text{h}}} }} \delta T\left[ {\phi_{{{\Omega }^{{\text{h}}} }} \frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right) + \left( {1 - \phi } \right)_{{{\Omega }^{{\text{h}}} }} \rho_{{\text{s}}} \frac{{{\text{D}}e_{{\text{s}}} }}{{{\text{D}}t}}} \right]{\text{d}}\Omega \\ & \quad \quad + \mathop \int \limits_{{{\Omega }^{{\text{h}}} }} \delta T e_{{\text{l}}} \rho_{{\text{l}}} \left[ {\frac{{\left( {1 - \phi } \right)_{{{\Omega }^{{\text{h}}} }} }}{{\rho_{{\text{s}}} }}\frac{{{\text{D}}\rho_{{\text{s}}} }}{{{\text{D}}t}} + \nabla \cdot {\dot{\mathbf{u}}}} \right]{\text{d}}\Omega \\ & \quad \quad + \mathop \int \limits_{{{\Omega }^{{\text{h}}} }} \nabla \delta T \cdot \left( {{\mathbf{i}}_{{\text{c}}} } \right)_{{{\Omega }^{{\text{h}}} }} {\text{d}}\Omega + \mathop \int \limits_{{{\Omega }^{{\text{h}}} }} \nabla \delta T \cdot \left[ {e_{{\text{l}}} \rho_{{\text{l}}} \left( {{\mathbf{q}}_{{\text{l}}} } \right)_{{{\Omega }^{{\text{h}}} }} } \right] {\text{d}}\Omega \\ & \quad = - \left[ {\mathop \int \limits_{{\Gamma_{S} }} \delta T j_{{{\text{E}}_{{S^{ + } }} }}^{^{\prime}} {\text{d}}S - \mathop \int \limits_{{\Gamma_{S} }} \delta T j_{{{\text{E}}_{{S^{ - } }} }}^{^{\prime}} {\text{d}}S} \right], \\ \end{aligned}$$

(34)

where $j_{{{\text{E}}_{{S^{ + } }} }}^{^{\prime}} = {\mathbf{j}}_{{{\text{E}}_{{S^{ + } }} }}^{^{\prime}} \cdot {\mathbf{n}}$ and $j_{{{\text{E}}_{{S^{ - } }} }}^{^{\prime}} = {\mathbf{j}}_{{{\text{E}}_{{S^{ - } }} }}^{^{\prime}} \cdot \left( { - {\mathbf{n}}} \right)$ are related to the heat exchange between the discontinuity and the surrounding medium.

Inserting Eqs. (2), (21), (22), and (25) into (34) gives:

$$\begin{aligned} & \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \delta T\left[ {\left( {\phi + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{{\text{n}}} }}{h}} \right)\frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right)} \right]{\text{d}}\eta {\text{ d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \delta T e_{{\text{l}}} \rho_{{\text{l}}} \left( {\nabla \cdot {\mathbf{\dot{\tilde{u}}}} + \frac{{ \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n} }}{h}} \right){\text{d}}\eta {\text{ d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \nabla \delta T \cdot \left[ {\lambda_{{\text{l}}} {\mathbf{I}}\left( {\phi + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} }}{h}} \right)} \right] \cdot \nabla T{\text{d}}\eta {\text{ d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \mathop \int \limits_{{ - \frac{h}{2}}}^{\frac{h}{2}} \nabla \delta T \cdot \left[ {\frac{{e_{{\text{l}}} \rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\left( {{\mathbf{k}} + \frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n}^{3} }}{R 12 h}{\mathbf{t}} \otimes {\mathbf{t}}} \right)\left( {\nabla p_{{\text{l}}} - \rho_{{\text{l}}} {\mathbf{g}}} \right)} \right]{\text{d}}\eta {\text{ d}}\xi \\ & \quad = - \left[ {\mathop \int \limits_{{\Gamma_{S} }} \delta T j_{{{\text{E}}_{{S^{ + } }} }}^{^{\prime}} {\text{d}}S - \mathop \int \limits_{{\Gamma_{S} }} \delta T j_{{{\text{E}}_{{S^{ - } }} }}^{^{\prime}} {\text{d}}S} \right]. \\ \end{aligned}$$

(35)

Integrating the above equation over $\left[ { - h/2,h/2, } \right]$ (Fig. 3) and taking the limit as $h \to 0$:

$$\begin{aligned} & \mathop \int \limits_{S} \delta T \left[\kern-0.15em\left[ { u} \right]\kern-0.15em\right] _{n} \frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right){\text{ d}}\xi + \mathop \int \limits_{S} \delta T e_{{\text{l}}} \rho_{{\text{l}}} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{n} {\text{d}}\xi \\ & \quad \quad + \mathop \int \limits_{S} \frac{\partial T}{{\partial \xi }}\left( {\lambda_{{\text{l}}} \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n} } \right)\frac{\partial T}{{\partial \xi }}{\text{d}}\xi + \mathop \int \limits_{S} \frac{\partial \delta T}{{\partial \xi }}\left[ {\frac{{e_{{\text{l}}} \rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{n}^{3} }}{R 12}} \right]\left( {\frac{{\partial p_{{\text{l}}} }}{\partial \xi } - \rho_{{\text{l}}} g} \right){\text{d}}\xi \\ & \quad = \mathop \int \limits_{{\Gamma_{S} }} \delta T \left[\kern-0.15em\left[ {j_{{\text{E}}}^{^{\prime}} } \right]\kern-0.15em\right]{\text{d}}S. \\ \end{aligned}$$

(36)

Fig. 4

a Influence of temperature (T) on Young modulus (E); b adopted relationship between tensile strength (σ_u) and temperature

Equation (36) is the weak form of the internal energy balance equation in the fracture:

$$\left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{{\text{n}}} \frac{{\text{D}}}{{{\text{D}}t}}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right){ } + e_{{\text{l}}} \rho_{{\text{l}}} \left[\kern-0.15em\left[ {\dot{u}} \right]\kern-0.15em\right] _{{\text{n}}} + \left( {\lambda_{{\text{l}}} \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{{\text{n}}} \frac{\partial T}{{\partial \xi }}} \right) + \left[ {\frac{{e_{{\text{l}}} \rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\frac{{ \left[\kern-0.15em\left[ u \right]\kern-0.15em\right] _{{\text{n}}}^{3} }}{R 12}\left( {\frac{{\partial p_{{\text{l}}} }}{\partial \xi } - \rho_{{\text{l}}} g} \right)} \right] = \left[\kern-0.15em\left[ {j_{{\text{E}}}^{^{\prime}} } \right]\kern-0.15em\right].$$

(37)

4.4 FEM Approximation

The finite element approximation of the displacement, liquid pressure, and temperature fields are:

$${\mathbf{u}}\left( {{\mathbf{X}},t} \right) \approx {\mathbf{N}}_{{\text{u}}} \left( {\mathbf{X}} \right) {\mathbf{U}}\left( t \right),$$

(38)

$$p_{{\text{l}}} \left( {{\mathbf{X}},t} \right) \approx {\mathbf{N}}_{{\text{p}}} \left( {\mathbf{X}} \right) {\mathbf{P}}_{{\text{l}}} \left( t \right),$$

(39)

$$T\left( {{\mathbf{X}},t} \right) \approx {\mathbf{N}}_{{\text{p}}} \left( {\mathbf{X}} \right) {\mathbf{T}}\left( t \right),$$

(40)

where ${\mathbf{N}}_{{\text{u}}}$ and ${\mathbf{N}}_{{\text{p}}}$ are the standard FEs shape functions matrices for the vector and scalar fields problems, respectively; ${\mathbf{U}}$, ${\mathbf{P}}_{{\text{l}}}$, and ${\mathbf{T}}$ are the nodal displacement, nodal liquid pressure, and nodal temperature vectors, respectively. The strains, liquid pressure, and temperature gradients are obtained evaluating the derivatives of the shape functions:

$$\varepsilon \left( {{\mathbf{X}},t} \right) \approx {\mathbf{B}}\left( {\mathbf{X}} \right) {\mathbf{U}}\left( t \right),$$

(41)

$$\nabla p_{{\text{l}}} \left( {{\mathbf{X}},t} \right) \approx \nabla {\mathbf{N}}_{{\text{p}}} \left( {\mathbf{X}} \right) {\mathbf{P}}_{{\text{l}}} \left( t \right),$$

(42)

$$\nabla T\left( {{\mathbf{X}},t} \right) \approx \nabla {\mathbf{N}}_{{\text{p}}} \left( {\mathbf{X}} \right) {\mathbf{T}}\left( t \right),$$

(43)

in which ${\mathbf{B}}$ and ${\mathbf{N}}_{{\text{p}}}$ are the shape function derivative matrices.

The discrete Galerkin approximations of the governing equations [Eqs. (26), (27), and (28)] are expressed as:

$$\begin{aligned} & \mathop \int \limits_{{\Omega }} \left( {\mathbf{B}} \right)^{{\text{T}}} {{\varvec{\Sigma}}}_{*} \left( \varepsilon \right){\text{d}}\Omega + {\mathbf{Q}}_{{\left( {{\text{u}} {\text{p}}_{{\text{l}}} } \right)}} {\dot{\mathbf{P}}}_{{\text{l}}} + {\mathbf{Q}}_{{\left( {\text{u T}} \right)}} {\dot{\mathbf{T}}} + {\dot{\mathbf{F}}}_{{\left( {\text{u}} \right)}} = {\mathbf{R}}_{{\left( {\text{u}} \right)}} \approx 0 \\ \user2{ } & \quad {\mathbf{C}}_{{\left( {{\text{p}}_{{\text{l}}} {\text{ u}}} \right)}} {\dot{\mathbf{U}}} + {\dot{\mathbf{S}}}_{{\left( {{\text{p}}_{{\text{l}}} } \right)}} + {\mathbf{A}}_{{\left( {{\text{p}}_{{\text{l}}} {\text{ p}}_{{\text{l}}} } \right)}} {\mathbf{P}}_{{\text{l}}} + {\mathbf{F}}_{{\left( {{\text{p}}_{{\text{l}}} } \right)}} = {\mathbf{R}}_{{\left( {{\text{p}}_{{\text{l}}} } \right)}} \approx 0 \\ & \quad \user2{ }{\mathbf{C}}_{{\left( {\text{T u}} \right)}} {\dot{\mathbf{U}}} + {\dot{\mathbf{S}}}_{{\left( {\text{T}} \right)}} + {\mathbf{A}}_{{\left( {{\text{T p}}_{{\text{l}}} } \right)}} {\mathbf{P}}_{{\text{l}}} + {\mathbf{A}}_{{\left( {\text{T T}} \right)}} {\mathbf{T}} + {\mathbf{F}}_{{\left( {\text{T}} \right)}} = {\mathbf{R}}_{{\left( {\text{T}} \right)}} \approx 0, \\ \end{aligned}$$

(44)

where the mechanical, hydraulic, and thermal matrices are:

$${\mathbf{Q}}_{{\left( {{\text{u p}}_{{\text{l}}} } \right)}} = \mathop \int \limits_{\Omega } \left( {\mathbf{B}} \right)^{{\text{T}}} b {\mathbf{m}} {\mathbf{N}}_{{\text{p}}} {\text{d}}\Omega ,$$

$${\mathbf{Q}}_{{\left( {\text{u T}} \right)}} = \mathop \int \limits_{\Omega } \left( {\mathbf{B}} \right)^{{\text{T}}} {\mathbb{C}} \alpha_{{\text{T}}} {\mathbf{m}} {\mathbf{N}}_{{\text{p}}} {\text{d}}\Omega ,$$

$${\dot{\mathbf{F}}}_{{\text{u}}} = \mathop \int \limits_{{\Gamma_{\sigma } }} \left( {{\mathbf{N}}_{{\text{u}}} } \right)^{{\text{T}}} {\overline{\mathbf{t}}}{\text{d}}\Gamma + \mathop \int \limits_{\Omega } \left( {{\mathbf{N}}_{{\text{u}}} } \right)^{{\text{T}}} {\mathbf{b}}{\text{d}}\Omega ,$$

$${\mathbf{C}}_{{\left( {{\text{p}}_{{\text{l}}} {\text{ u}}} \right)}} = \rho_{{\text{l}}} \mathop \int \limits_{\Omega } \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{m}} {\mathbf{B}}{\text{d}}\Omega ,$$

$${\mathbf{C}}_{{\left( {\text{T u}} \right)}} = e_{{\text{l}}} \user2{ }\rho_{{\text{l}}} \mathop \int \limits_{\Omega } \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{m}} {\mathbf{B}}{\text{d}}\Omega ,$$

$${\dot{\mathbf{S}}}_{{\left( {{\text{p}}_{{\text{l}}} {\text{ p}}_{{\text{l}}} } \right)}} = \left[ {\phi_{*} \frac{{\partial \rho_{{\text{l}}} }}{\partial t} + \frac{{\left( {1 - \phi } \right)_{*} }}{{\rho_{{\text{s}}} }}\frac{{\partial \rho_{{\text{s}}} }}{\partial t}\rho_{l} } \right]\mathop \int \limits_{\Omega } \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\text{d}}\Omega ,$$

$${\dot{\mathbf{S}}}_{{\left( {T T} \right)}} = \left[ {\phi_{*} \frac{\partial }{\partial t}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right) + \frac{{\left( {1 - \phi } \right)_{*} }}{{\rho_{{\text{s}}} }}\frac{{\partial \rho_{{\text{s}}} }}{\partial t}\left( {e_{{\text{l}}} \rho_{{\text{l}}} } \right) + \left( {1 - \phi } \right)_{*} \rho_{{\text{s}}} \frac{{\partial e_{{\text{s}}} }}{\partial t}} \right]\mathop \int \limits_{\Omega } \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\text{d}}\Omega ,$$

$${\mathbf{A}}_{{\left( {{\text{p}}_{{\text{l}}} {\text{ p}}_{{\text{l}}} } \right)}} = \frac{{\rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\mathop \int \limits_{\Omega } \left( {\nabla {\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{k}}_{*} \nabla {\mathbf{N}}_{{\text{p}}} {\text{d}}\Omega ,$$

$${\mathbf{A}}_{{\left( {\text{T T}} \right)}} = \mathop \int \limits_{\Omega } \left( {\nabla {\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {{\varvec{\uplambda}}}_{*} \nabla {\mathbf{N}}_{{\text{p}}} {\text{d}}\Omega ,$$

$${\mathbf{A}}_{{\left( {{\text{T p}}_{{\text{l}}} } \right)}} = \frac{{e_{{\text{l}}} \rho_{{\text{l}}} }}{{\mu_{{\text{l}}} }}\mathop \int \limits_{\Omega } \left( {\nabla {\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{k}}_{*} \nabla {\mathbf{N}}_{{\text{p}}} {\text{d}}\Omega ,$$

$${\mathbf{F}}_{{\left( {{\text{p}}_{{\text{l}}} } \right)}} = \mathop \int \limits_{{\Gamma_{{{\text{q}}_{{\text{l}}} }} }} \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} \rho_{{\text{l}}} \overline{q}_{{\text{l}}} {\text{d}}\Gamma + \frac{{\rho_{{\text{l}}}^{2} }}{{\mu_{{\text{l}}} }}\mathop \int \limits_{\Omega } \left( {\nabla {\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{k}}_{*} {\mathbf{g}}{\text{d}}\Omega ,$$

$${\mathbf{F}}_{{\left( {\text{T}} \right)}} = \mathop \int \limits_{{\Gamma_{{j_{{\text{E}}}^{^{\prime}} }} }} \left( {{\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} \overline{j}_{{\text{E}}}^{^{\prime}} {\text{d}}\Gamma + e_{{\text{l}}} \frac{{\rho_{{\text{l}}}^{2} }}{{\mu_{{\text{l}}} }}\mathop \int \limits_{\Omega } \left( {\nabla {\mathbf{N}}_{{\text{p}}} } \right)^{{\text{T}}} {\mathbf{k}}_{*} {\mathbf{g}}{\text{d}}\Omega .$$

We adopted the methodology proposed in Olivella et al. (1996) for the numerical discretization of the governing equations. The finite difference method is used for the time discretization with a variable time-stepping algorithm. The Newton–Raphson method is used to solve in a fully coupled and monolithic manner the non-linear system of equations.

5 Model Applications

We selected three application cases to verify and validate the approach discussed above. The first analysis is related to the formation of hydraulic fractures. The main objective is to verify the implementation of the proposed framework into CODE_BRIGHT using published analytic solutions for the hydro-mechanical behavior. The approach is also validated against a published FE solution obtained using zero-thickness elements. The second case involves the study of the breakdown pressure in a reservoir under different thermal and stresses state conditions. In the third case, we applied the MFT to study laboratory tests involving the formation of fracture developed in a solid during the injection of a cryogenic fluid under different conditions.

5.1 Hydraulic Fracturing: H–M Verification

Two dissipative processes govern the formation and propagation of hydraulic fractures, namely: flow of a viscous fluid within the fracture, and creation of new fracture surfaces. Also, the water storage can be either, in the fracture or in the surrounding rock (i.e., leak-off). The combination of these factors results in four main fracture propagation regimens (Carrier and Granet 2012): storage-toughness; storage-viscosity; leak-off-toughness; and leak-off-viscosity. In this section, we analyze the two first regimens (i.e., storage-toughness and storage-viscosity) using the MFT.

The formation and propagation of fractures in a rock is induced by the injection of an incompressible Newtonian viscous fluid at a constant rate $\overline{q}_{{\text{l}}} = 0.5$ kg/s. The initial liquid pressure of the entire porous medium was set to zero. A 45 m × 60 m domain is considered, in which the in-situ vertical stress $\sigma_{{\text{o}}}$ = 3.7 MPa, and the initial liquid pressure $p_{{{\text{l}}_{0} }} = 0$. Figure 5 presents the main component of the problem under study, including: geometry, boundary conditions, and FE mesh (which contains 4666 nodes and 9264 elements). As in Carrier and Granet (2012), the interface elements were introduced at the center of the domain in the horizontal direction. Also, as in Carrier and Granet (2012), a couple of broken elements (i.e., elements of high permeability and low stiffness) near the injection point were considered to obtain the initial configuration of the KGD fracture problem. The storage-toughness and storage-viscosity regimes are given by the near-K and M solutions, respectively (Bao et al. 2015).

Fig. 5

adapted from Carrier and Granet 2012)

Mesh, geometry, and boundary conditions of the hydraulic fracturing (

To model different fracture regimes, the dynamic viscosity and intrinsic permeability are adjusted accordingly. Table 1 lists the material properties adopted in this work.

Table 1 Parameters adopted for the H–M verification (Sect. 5.1)

The parameters considered in the analytical solutions are:

$$E^{\prime} = \frac{E}{{1 - \nu^{2} }}, \quad \nu^{\prime} = 12\nu ,\quad K^{\prime} = 4K_{{{\text{Ic}}}} \sqrt {\frac{2}{\pi }} , \quad C^{\prime} = 2C_{{\text{L}}} ,$$

(45)

in which $\nu$ is the Poisson’s ratio, $C_{{\text{L}}}$ is the leak-off parameter, and $K_{{{\text{Ic}}}}$ is the fracture toughness in mode-I, defined as:

$$K_{{{\text{Ic}}}} = \sqrt {G_{{\text{f}}} \frac{E}{{1 - \nu^{2} }}} ,$$

(46)

5.1.1 Storage-Toughness Dominated Regime

Numerical simulations were conducted to study the effect of permeability on fracture aperture, length, and pressure considering two intrinsic permeability values with a difference of one order of magnitude between them (i.e., $k = 1.0 \times 10^{ - 16}$ m² and $k = 1.0 \times 10^{ - 15}$ m²). The leak-off coefficients related to $k = 1.0 \times 10^{ - 16}$ m² and $k = 1.0 \times 10^{ - 15}$ m² are $1.47 \times 10^{ - 5}$ ms^−1/2 and $6.28 \times 10^{ - 5}$ ms^−1/2, respectively. We assumed a fracture propagation in the storage-toughness dominated regime by considering $\mu = 1.0 \times 10^{ - 10}$ MPa s, and by adopting the Near-K solutions proposed by Bunger et al. (2005) in terms of the injection pressure, fracture aperture, and length, as follows:

$$p_{{\text{l}}} = \varepsilon E^{\prime}\left( {2^{ - 5/2} \gamma^{ - 1/2} } \right),\,\,\,\,w = \varepsilon L \sqrt {\gamma \frac{{1 - \xi^{2} }}{2}} ,\,\,\,\,l = \gamma L,$$

(47)

where:

$$\tau = \frac{t}{{t_{*} }},\quad \xi = \frac{x}{l\left( t \right)},\quad \gamma = \tau^{2/3} \mathop \sum \limits_{i = 0}^{n} \gamma_{{k_{i} }} \tau^{i/6} ,$$

(48)

where the parameter $\varepsilon$, the length-scale $L$, and the timescale $t_{*}$ for the KGD model are expressed as:

$$\varepsilon = \frac{{C^{^{\prime}2} }}{{\overline{q}_{{\text{l}}} }},\quad L = \left( {\frac{{K^{\prime}\overline{q}_{{\text{l}}} }}{{E^{\prime}C^{{\prime}{2}} }}} \right)^{2} ,\quad t_{*} = \frac{{K^{^{\prime}4} \overline{q}_{{\text{l}}}^{2} }}{{E^{^{\prime}4} C^{^{\prime}6} }},$$

(49)

and $\gamma_{{k_{i} }}$ (Eq. (47)) are factors determined by Bunger et al. (2005). They are listed in Table 2.

Table 2 Terms used in the analytical solution according to Bunger et al. 2005 (Sect. 5.1.1)

Figure 6a, b presents the comparison between the numerical results obtained in this work using the MFT and the ones reported by Carrier and Granet (2012) (represented by filled and empty squares, respectively), together with the analytical solution (solid line) in terms of both fracture aperture and length, for the two permeabilities under consideration. As expected, the fracture aperture of the medium with lower permeability leads to a wider fracture mouth and a larger aperture, since the fluid is forced to propagate in the fracture, because of the lower permeability reduces the ability of the fluid to permeate in the surrounding medium. The numerical results (i.e., both Carrier and Granet 2012 and this solution) match very satisfactorily with the analytic solution.

Fig. 6

HAR finite-element solution related to the storage-toughness dominated regime together with published numerical results (Carrier and Granet 2012) and the analytical near-K solutions (Bunger et al. 2005) in terms of fracture time evolution: a aperture, b length, c injection pressure. ($k=1\times {10}^{-16}$ m²), d fracture profile at $t=10$ s

Figure 6c shows that the numerical solutions (both) tend to slightly overpredict the fluid injection pressure (i.e., $p_{{\text{l}}} + \sigma_{{\text{o}}}$; $k = 1 \times 10^{ - 16}$ m²) when compared against the analytic solution. This type of issue was already reported (Kovalyshen 2010; Vandamme and Roegiers 1990) and it is associated with the so-called ‘back-stress effect’, which is related to the large fluid pressure required at the beginning of the process to break the rock and initiate the fracture propagation. Then, the injection pressure exhibits an asymptotic decay, because the pressure needed to maintain the fracture propagation is smaller than the one to open it. A good match between numerical and analytic results is observed for others fracture variables (like aperture and length), as shown in Fig. 6d, for the fracture lip profiles (at $t = 10s$), where a very satisfactory agreement is observed between the different solutions for both permeabilities.

5.1.2 Storage-Viscosity Dominated Regime

The storage-viscosity dominated regime is associated with a highly viscous fluid. In this study, we assumed that $k = 1 \times 10^{ - 16}$ m² and $\mu = 1 \times 10^{ - 7}$ MPa s. The M-analytical solution developed by Adachi and Detournay (2002) describes the fracture aperture, injection pressure, and fracture length for the storage-viscosity dominated regime, as follows:

$$w = 1126 \varepsilon_{{\text{m}}} L_{{\text{m}}} ,\quad p_{{\text{l}}} = 0.54495 \varepsilon_{{\text{m}}} E^{\prime}, \quad l = 0.61524 L_{{\text{m}}} ,$$

(50)

where:

$$\varepsilon_{{\text{m}}} = \left( {\frac{\mu }{{E^{\prime} t}}} \right)^{1/3} ,\quad L_{{\text{m}}} = \left( {\frac{{E^{\prime} \overline{q}_{{\text{l}}}^{3} t^{4} }}{{\mu^{\prime}}}} \right)^{1/6} .$$

(51)

The time evolution of the fracture aperture, fracture length, and injection pressure are shown in Fig. 7a–c, respectively. Also in this case, the results from MFT, Carrier and Granet (2012), and analytic solution agree very well.  However, for the injection pressure, a slight overprediction of the FE solutions with respect to the analytic one is observed. As in the previous case, the back-stress effect can be the responsible of this difference.

Fig. 7

Numerical and analytical results for the storage-viscosity dominated regime: a fracture aperture; b fracture length; c injection pressure

5.2 Single Well Simulation

In this section, we model a single well test based on the geometry and conditions shown in Fig. 8. The wellbore is positioned at the center of a homogeneous reservoir subjected to a constant flow rate. The MFT model predictions in terms of the breakdown pressure associated with this well are compared for different cases, combining different initial reservoir temperatures (T_R), well temperatures (T_W), and anisotropic confinement conditions.

Fig. 8

Geometry and boundary conditions adopted for the single well analysis

The pore-pressure built-ups during the fluid injection, inducing a progressive reduction of the rock (compressive) effective stress. Eventually, in a point of the domain, the damage criterion is met and the damage process of the rock starts, with the corresponding fracture initiation. The peak of the fluid pressure occurs just before the fracture process starts. This pressure is the well-known breakdown pressure (p_b). Just after the fracture forms, the pore-pressure decreases until archiving a value that is rather constant during fracture propagation. This pressure is known as the propagation pressure (p_e).

The damage criterion of the adopted model (i.e., Eqs. 10 and 11) depends (amongst others) on the rock tensile strength, which in turn depends on temperature (i.e., Eq. 13 and Fig. 4b). To investigate the effect of temperature on the breakdown pressure, we consider three reservoirs temperatures, T_R = 20 °C; T_R = 70 °C; T_R = 150 °C. We also assume that the fluid is injected at the reservoir temperature (i.e., T_R = T_W) in the three cases, which is related to the hypothetical scenario where the fluid achieves thermal equilibrium with the reservoir while descending through the bore well. The adopted initial stress state depends on the depth, according to the values reported for the Utah FORGE test site, USA (McLennan 2017). For a depth of 2.1 km and the stress gradients for the minor and major principal horizontal stress of − 14.251 MPa/km and − 16.287 MPa/km, respectively (McLennan 2017), the initial stress state is given by σ_h = − 31.35 MPa, σ_H = − 35.83 MPa, and p_l = 21.58 MPa; where σ_h is the minor compressive stress (i.e., the major principal stress, because tensile stresses are considered positive); and σ_H is the major compressive stress (i.e., minor principal stress). At T_R = T_W = 70 °C, we performed two additional analyses, one of them assuming an anisotropic stress field that is rotated 90° respect to the previous cases (i.e., σ_h = − 35.83 MPa and σ_H = − 31.35 MPa), and a case at a depth of 1.1 km with lower confinement, σ_h = − 15.68 MPa, σ_H = − 17.92 MPa, and p_l = 10.79 MPa.

We adopted unstructured mesh consisting of 31,570 regular elements, and 23,399 nodes. We assumed that a Newtonian fluid was injected at a constant rate (Q₀ = 6.0 × 10⁻⁴ kg/s) at the center of the wellbore. Table 3 lists the main rock and fluid properties considered in the modeling. We considered that the liquid density depends on both pressure and temperature through the following law (CODE_BRIGHT 2020):

$$\rho_{{\text{l}}} = \rho_{{{\text{l}}_{{\text{o}}} }} \exp \left[ {\beta \left( {p_{{\text{l}}} - p_{{{\text{l}}_{{\text{o}}} }} } \right) + \alpha \left( {T - T_{{\text{o}}} } \right)} \right],$$

(52)

Table 3 Parameters adopted for modeling the single well test stimulation (Sect. 5.2)

where ρ_l0 is the reference liquid density at the reference pressure (p_l0); α is the volumetric thermal expansion coefficient for the water (we assumed α = − 3.4 × 10^–4 °C⁻¹); and β is the water compressibility coefficient (we assumed β = 4.5 × 10⁻⁴ MPa⁻¹). The viscosity of the liquid phase (μ_ℓ) varies with temperature T [°C] (i.e., Olivella 1995):

$$\mu_{{\text{l}}} = 2.1 \times 10^{ - 6} \exp \left( {\frac{1808.5}{{273.15 + T}}} \right).$$

(53)

Figure 9 presents the results related to the three reservoir temperatures. As expected, an increase in the reservoir temperature is associated with a decrease of the breakdown pressure. It is also observed that the decrease of liquid viscosity and density with the increase of temperature prolong the pressurization time necessary to achieve the breakdown pressure.

Fig. 9

Breakdown (p_b) and propagation pressures (p_e) associated with the single well analyses at different temperatures

In the same figure, we included the breakdown pressure obtained from the analytical solution suggested by Hubbert and Willis (1957) for the case T = 20°, as follows:

$$p_{{\text{b}}} = - 3\sigma_{{\text{h}}} + \sigma_{{\text{H}}} - p_{{\text{l}}} + \sigma_{{\text{u}}} .$$

(54)

The agreement between model and analytical solution is very satisfactory. The model slightly underpredicts the p_b provided by the analytical solution. This figure also includes the propagation pressure, which can be roughly estimated based on the following equation (Koning 1988):

$$p_{{\text{e}}} \sim - \sigma_{{\text{h}}} + \sigma_{{\text{u}}} .$$

(55)

The model prediction is satisfactory in this case, as well. The reservoir temperature has almost no impact on the propagation pressure. Figure 10 is related to the effect of the in-situ stress on the breakdown and propagation pressures for a reservoir at T_R = 70 °C. The study involves reservoirs at two different depths, ‘deep’ (with principal stresses − 35.83 MPa and − 31.35 MPa) and ‘shallow’ (with principal stresses − 17.92 MPa and − 15.68 MPa). As for the deep reservoir, we considered two orientations of the principal stresses (rotated 90° apart). It is observed that the orientation of the principal stresses does not affect the breakdown and propagation pressures. As expected, the level of confinement does affect the breakdown and propagation pressures. It is worth highlighting that Eqs. (54) and (55) correspond to rough estimations of p_b and p_e.

Fig. 10

Breakdown (p_b) and propagation pressures (p_e) associated with the single well analyses considering different orientations of the in-situ stresses and different reservoir depths, deep and shallow

5.3 Hydro-Thermal Fracking in a Transparent Sample

The laboratory tests conducted by Cha et al. (2016) involving the formation of fractures triggered by a thermal shock are simulated to validate the full THM formulation based on the MFT. The tests were based on cylindrical specimens (10 cm diameter and 23 cm height) made of acrylic with a hole (1.3 cm diameter and 18 cm deep) drilled at the center of the sample. A steel tube was introduced and attached with epoxy to the borehole wall. The initial temperature was around 20 °C (uniform in the whole domain). Then, liquid nitrogen (LN₂) at − 196 °C was injected through the well, the fractures developed triggered by the applied thermal gradient, and (because of the transparent nature of the acrylic samples) the full crack network was observed and tracked.

To investigate the effect of the position of the injection point on the crack pattern, Cha et al. (2016) carried out experiments with two different well configurations identified as Specimens 1 and 2, which are described and analyzed in Sects. 5.3.1 and 5.3.2, respectively. To reduce the computational effort, axisymmetric conditions were assumed to model these cases. Table 4 lists the mechanical and thermal parameters adopted for modeling Specimens 1 and 2. Acrylic and steel are simulated as very low porosity materials (ϕ₀ = 0.01). The hole is simulated as a ‘void material’ with very high porosity, permeability, and compressibility.

Table 4 Mechanical properties adopted for the THM numerical analyses (Sect. 5.3)

5.3.1 Modeling Specimen 1

This case considers the steel tube (simulating the well) inserted 12 cm down in the sample and attached with epoxy to the borehole walls in the first 6 cm only (which is identified as the ‘SS casing’ depth). Figure 11a shows the main test components and 11b presents the adopted mesh (composed of 35,604 elements and 17,964 nodes) together with different materials (i.e., acrylic, steel, void, and epoxy) and boundary conditions. Figure 11b also presents the points selected to track the evolution of temperatures during the experiment, identified as ‘1’ (wall-hole), ‘2’ (base), and ‘3’ (perimeter).

Fig. 11

Acrylic Specimen 1: a experimental sample (Cha et al. 2016); b mesh, geometry, and boundary conditions

We adopted the material properties, and initial and boundary conditions based on the reported experimental information with the aim of properly capturing the conditions prevailing during the tests. For example, Fig. 12 shows the excellent agreement achieved between the experimental (symbols) and modeling (lines) results in terms of the time evolution of temperatures at different positions as follows: wall-hole (1), specimen-base (2), and lateral perimeter of sample (3), as indicated in Fig. 11b.

Fig. 12

Temperature evolution at the selected points as indicated in Fig. 11 [i.e., ‘1 (square)’; ‘2 (circle)’; and ‘3 (triangle)’], experimental and numerical results

The evolution of fractures observed in the experiment at different steps is shown in Fig. 13a–d. The initial crack pattern (Fig. 13a) is characterized by the formation of three (sub) horizontal radial cracks that start to propagate from the borehole radially outwards as soon as the LN₂ is injected into the borehole. Then, an additional crack at the top of the sample (i.e., where epoxy was used to fix the steel tube to the acrylic) started to develop (Fig. 13b). Afterward (Fig. 13c, d), these family of fractures continued propagating until reaching the external face of the sample. Figure 13e–f presents the corresponding cracks patterns predicted by the MFT. The model is able to replicate satisfactorily the main trends observed in the experiments, but the upper fracture. A possible reason for this problem is that the model assumes a very low thermal conductivity for the epoxy (i.e., Spurgeon 2018), preventing the development of high thermal gradients in this zone. In the following section, an alternative scenario to explain this behavior is analyzed.

Fig. 13

Specimen 1 results at different steps of the experiment: a–d images (test, Cha et al. 2016); e–h crack patterns (model); and i–l contours of temperature (model)

The thermal fracturing process is explained with the aid of Figs. 13i to 13l. As reported in Cha et al. (2016), the highest thermal gradient is at the end of the steel tube and just after injecting LN₂ (Fig. 13i). This high thermal change induced the contraction of the bulk elements, with the corresponding increase of the tensile stress in the HAR elements located in the vicinity of the borehole wall. Fractures started to develop once the damage criterion was met in this region. Then, the low temperatures propagated radially, as well as, down and up (Figs. 13j, 13k) inducing the propagation of the already formed fractures at the center of the sample, and also the formation of a new set of fractures at the bottom of the borehole. The low thermal conductivity of the epoxy considered in this simulation in the upper portion of the specimen prevented the development of high thermal gradients in that zone. Therefore, the model was not able to predict the formation of the fractures observed in the top of the specimen. Afterward, the ambient heat started to cool down the specimen (Fig. 13l) and the fractures remained stable.

5.3.2 Modeling Specimen 2

In this case, both steel tube and epoxy are 3.8 cm deep. Figure 14a corresponds to a photo of the acrylic specimen detailing the tube configuration. Figure 14b presents the mesh, materials, and boundary conditions considered in the numerical analysis. The mesh consists of 20,190 nodes, 3095 bulk, and 8599 HAR elements. As in the previous case, the initial temperature of the domain was set to 20 °C and the same protocol was applied to inject the LN₂.

Fig. 14

Acrylic Specimen 2: a experimental sample (Cha et al. 2016); b mesh, geometry, and boundary conditions

One sub-horizontal fracture formed first around the injection point (Fig. 14a) and then, with the concurrent propagation of this initial fracture, another crack developed in the upper part of the specimen (Figs. 15b to 15d). The model predicts well the formation of the initial fracture (Fig. 15e) and its subsequent propagation (Figs. 15f to 15h), but (as in the previous case) it was not able to simulate the formation of the upper crack. Figure 15i shows that the very high thermal gradient developed at the bottom of the metallic tube triggered the facture initially, and assisted to propagate the fractures afterward (Figs. 15j to 15l). The fractures observed at the bottom of Specimen 1 did not develop in this case. The thermal gradient at the bottom of the sample was not high enough to develop a fracture in this case. Note that in Specimen 2, the distance between the bottom of the sample and the injection, point is larger than in Specimen 1. The predicted thermal gradient above the injection point was not large enough either (i.e., because of the low thermal conductivity of the epoxy, which acted as an insulator in this case) to develop the fracture observed in the upper part of the sample.

Fig. 15

Specimen 2 results at different steps of the experiment: a–d images (test, Cha et al. 2016); e–h crack patterns (model); and i–l contours of temperature (model)

In both Specimens, the model was not able to replicate the formation of the fractures in the upper part of the borehole. To investigate this difference between the models and the experiments, an additional simulation was conducted based on Specimen 2, considering that the epoxy can detach from the acrylic allowing the LN₂ to penetrate in that space jeopardizing in this way the insulating effect of the epoxy. This possible separation between the acrylic and the metallic tube can be triggered by the combined effect of the high temperature changes and the different thermal expansion coefficients between steel, acrylic, and epoxy. Figure 16 presents the crack pattern predicted under this scenario, showing the two set of fractures developed under this assumption, i.e., one at the end of the metallic tube and another one above it, resembling the behavior observed in the experiments.

Fig. 16

Numerical analysis related to Specimen 2 assuming leakage of LN₂ in the upper part: a–d crack patterns of the; and e–h contour of temperatures

Figure 17 shows a satisfactory agreement between the observed and simulated crack patterns. It is worth highlighting that the fracture morphology observed in these experiments is close to 2D axisymmetric (particularly for the case of Specimen 2). Therefore, it can be considered that the numerical analyses based on the 2D axisymmetric models have validated qualitatively the proposed approach, and showed that the MFT was able to predict the overall fracture patterns, including number of fractures, fractures positions, and their evolution in time.

Fig. 17

Experimental envelopes and numerical predictions of crack patterns: a specimen 1; b specimen 2; c specimen 2 with leakage of LN₂

6 Summary and Conclusions

We presented a comprehensive mathematical framework based on the mesh fragmentation technique capable of modeling evolving fractures triggered by thermo-hydro-mechanical phenomena. The high-aspect ratio elements (used to model the fracture formation and propagation) are equipped with appropriate constitutive models to describe the mechanical, hydraulic, and thermal behaviors of discontinuities. We applied the proposed numerical technique to study different problems involving the formation and propagation of fractures considering hydro-mechanical, thermo-hydraulic, and thermo-hydro-mechanical coupled processes. In those applications, the MFT results were compared against experimental results, and analytic and numerical solutions of problems involving the presence of evolving discontinuities. In all the cases the results obtained with the proposed approach were very satisfactory, showing the capability of the MFT to deal with different scenarios and conditions related to the formation of fractures.

The main findings of this work can be summarized as follows:

• The MFT simulates evolving fractures in rocks using continuous mechanics concepts and standard finite-element methodology.

• The MFT incorporates THM constitutive models capable of dealing with the dissipation of energy associated with the formation of fractures, and with the fluid flow and heat transfer through fractured rocks.

• Fractures evolve naturally by contouring the boundaries of the bulk elements.

• The formation and propagation of fractures depend on the local THM conditions and material properties only. There is no need to incorporate special tracking algorithms or remeshing techniques.

• A clear advantage of the MFT is that it can be easily implemented in existing THM finite-element codes for continuous porous media, enabling their upgrade to deal with engineering applications involving discontinuities.