1 Introduction

Subject to external loads, the defects and microcracks pre-existing inside the rock are activated and propagated, generating new cracks in both micro- and macro-scale, and the resulting damage eventually leads to failure, even catastrophic hazards (Hoek and Martin 2014). Therefore, understanding the spatial distribution of different cracks inside the rock mass is not only a fundamental study of rock failure, but also a promotion way to evaluate the geotechnical disasters.

In previous studies, the patterns of crack formation and distribution were deeply investigated by scholars from the failure type of crack characteristics, and attributed the characteristic parameters to different crack types, such as uniaxial compression test (Dong et al. 2018), Brazilian splitting test (Zhang et al. 2020), and three-point-bend fracture test (Granger et al. 2007). However, only one macrocrack was usually obtained in these experimental results. These researchers did not consider the multi-cracked failure of on-site stress environments. In practice, the cracks formed in rock engineering are discretely distributed on the microscopically and mixedly distributed on the macroscopically, from the near-surface to the interior (Baud et al. 2017; Liu et al. 2015; Wang et al. 2019a). However, these loading tests usually form one major macrocrack after rock failure, which limits the consideration of the independent of different macrocracks. In contrast, the true triaxial loading simulates the occurrence of real rock hazard through different stress loading paths, and evaluates the damage results in different areas of the loading surface, which is more consistent with the on-site failure (He et al. 2012; Li et al. 2015). Studies of multi-cracked failure have substantially aided in elucidating detailed rock damage and mechanical behavior in the complex stress environment (Liu et al. 2015; Nasseri et al. 2014; Ning et al. 2018). To investigate the propagation and formation of multiple cracks that appeared on the surface, a three-point bending test was carried out on a concrete beam with a length of 9 m and a height of 1.5 m, it was found that only one-third new cracks were created by the preexisting cracks, and microcracks disappeared from Fracture 1 when Fracture 2 formed (Katsaga et al. 2007). These studies have deepened the understanding of the complex fracture of rocks. Therefore, studying the selected crack of multi-cracked failure is of great significance for further understanding of rock engineering hazards.

As we know, after the defects are activated, the energy generated by the microcracks is released in the form of elastic waves and propagates in rock materials, causing acoustic emission (AE) (Michlmayr et al. 2012). As the distribution of AE source localization has been thoroughly verified by various technologies, such as computed tomography scanning (Benson et al. 2007), fluorescent liquid (Naoi et al. 2018), and optical crack inspection (Zang et al. 2000), the spatiotemporal evolution of AE events reflects internal fractures during rock failure, and the digital data from AE monitoring provide a basis for analyzing the macrocracks (Creager 2019; Grosse et al. 2004; Perol et al. 2018; Rouet-Leduc et al. 2018). The majority of realized cracks or fractures that follow the microcrack distribution has been assessed by AE or seismic monitoring (Bunger et al. 2015; Feng et al. 2015; Moradian et al. 2016; Ruck et al. 2017). In the field microseismic research, microcrack monitoring results for up to 3 months showed that the high-density areas of microcracks appeared clustered in both front view and side view (Yabe et al. 2015; Zhao et al. 2018). Besides, a hydraulic fracturing test was carried out in a laboratory at 414 m depth underground, the microcrack locations were analyzed by a Kernel density estimator, which exhibited a potential elliptical distribution on two-dimensional sections (López-Comino et al. 2017). Moreover, a 3D Kernel function was also adopted to estimate AE location data through time (4D data) that were collected from a granite boulder for more than 3 years; it visualizes the spatiotemporal change of a macroscopic crack (Hohl et al. 2018). The results of the three-dimensional spatial distribution of microcracks corresponding to multiple macrocracks show a very promising potential for optimization studies on cracks. However, further theoretical explanations and applications are needed for the research on crack recognition of multi-cracked failure.

The spatial distribution of the mixed fractures or cracks is difficult to distinguish and characterize. Because, even in the case where only several macrocracks are found after rock failure, thousands of ubiquitous AE event coordinates will be collected by the monitoring system (Bunger et al. 2015; Feng et al. 2015; Katsaga et al. 2007; Li et al. 2018; Liu et al. 2015; Nasseri et al. 2014; Zhang et al. 2018). Besides, the coordinate dataset finally obtained is relatively incomplete. Not only because there are cracks that weaken and block the propagation of the signal wave (Moradian et al. 2016), but also some microcrack signals are artificially excluded when the threshold was set to reduce the effects of the ambient noise (Wang 2018; Wang et al. 2019b). It is likely that some very small signals representing microcracks go unrecorded and unidentified herein (Baud et al. 2017; Faillettaz et al. 2016; Meier et al. 2019; Rouet-Leduc et al. 2017). Therefore, the chaotic and incomplete dataset results in an obstacle to the analysis of crack distribution by traditional methods.

Facing the problem, machine learning algorithm exhibits the potential to extract knowledge from big data (Collobert et al. 2011; Hinton et al. 2012; Krizhevsky et al. 2017; Shin et al. 2016), and has already shown promise in performing a wide range of geotechnical tasks (Creager 2019; Rouet-Leduc et al. 2018), including signal detection (Bi et al. 2019; Hibert et al. 2017; Meier et al. 2019; Meyer et al. 2019; Rouet-Leduc et al. 2019), hypocentre and AE source location (Hensman et al. 2010; Perol et al. 2018). However, few studies have documented or attempted to analyse the spatial distribution of multiple macrocracks, especially in the case of staggered cracks (Lei et al. 2000; Manthei 2019; Ruck et al. 2017; Yabe et al. 2015). Therefore, for the problem the multi-macrocrack recognition task faces, machine learning algorithms have great potential to recognize cracks that appear to be ubiquitously distributed.

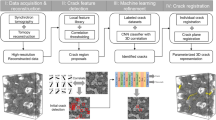
In this study, the true triaxial loading test was performed to simulate the complex failure of rocks in the real environment. AE data were obtained during the formation of multiple cracks in granite specimens. Based on the results of previous studies, the three-dimensional spatial distribution hypothesis of microcrack was proposed, and the single macrocrack model and the three-dimensional crack recognition model (3-DCRM) of AE were given. An unsupervised machine learning algorithm was adopted to realize the cracks recognition utilizing the microcrack coordinate datasets. The results showed that the recognized three-dimensional cracks were consistent with the real crack distribution of multi-cracked failure results. These results reveal the 3D distribution pattern of cracks, and provide a reference for AE/microseismic monitoring in rock engineering hazard.

2 Materials and Methods

2.1 Experiment and Materials

In this experiment, a computer-controlled electro-hydraulic servo rock triaxial testing machine (Chaoyang Test Instruments Co., Changchun, China) and an AE testing system (PCI-2, Physical Acoustics Company Co., New Jersey, USA) were adopted to implement the function of stress loading and AE signal collection, respectively. Loading time, stress, and strain data can be precisely and automatically obtained by the rock triaxial testing machine. The AE testing system consists of AE sensors, preamplifiers, cables, the host computer, and AEwin software. AE signals could be collected by the AE testing system in real time via its 6 channels and 18-bit analogue-to-digital converter.

In this experiment, five granite specimens were adopted for rock fracture testing under tunnel excavation conditions. The specimens were taken from the same granite sample, which has a dense texture with white veins. The sensors close to the specimen will be affected if the larger size specimen fails under higher stress and throws out rock debris. The smaller the specimen size, the lower the relative accuracy of the signal. Therefore, the specimen was processed into a cube with side lengths of 200 mm for more effective signals. After grinding, the flatness of each section was less than 0.02 mm, and the axial deviation did not exceed 0.25°. The rock triaxial testing machine and the AE testing system were synchronously operated to record the mechanical parameters and AE signals in real time. The loading path was designed to have three stages, following previous research (He et al. 2012; Li et al. 2015). The loading path is shown in Fig. 1. In stage I, a set of pressure thresholds was set to simulate the original stress where the specimens were located. We simplified the stress state by setting σ1 to 15 MPa, and σ2 and σ3 to 10 MPa, according to the field stress test. The loading speeds of σ1, σ2, and σ3 were set to 0.03 MPa/s, 0.02 MPa/s, and 0.02 MPa/s, respectively. In stage II, the stress was maintained in all three directions for 5 min. Then σ3 was suddenly released. In stage III, the maintained stress σ2 was constant. Displacement control was adopted to keep the specimen stable for unidirectional loading in the σ3 direction. The loading speed of σ1 was set to 0.2 MPa/s until the specimen was destroyed.

Fig. 1
figure 1

The loading path

Full size image

This cube is a schematic diagram of the granite specimen. Three differently coloured arrows pointing to the surfaces represent three different loading directions. The black arrow represents the vertical stress \({\sigma }_{1}\), and the red and blue arrows represent horizontal stress \({\sigma }_{2}\) and stress \({\sigma }_{3}\), respectively. The background noise was recorded after the test, and the acquisition threshold was 40 dB to eliminate the interference of external noises during the experiments; the sampling frequency of the sensor was set to 1 MHz, and the amplification was set to 40 dB. Six sensors were used to monitor and collect AE signals in this experiment. The sensors and the gaskets were smeared with Vaseline and the sensors were sealed with plasticine. Figure 2 shows the layout of the sensors. In addition, a lead-off test was performed to confirm that all six channels could steadily receive the AE signal before the experiment.

Fig. 2
figure 2

AE sensor layout (unit mm)

Full size image

It is the schematic diagram of AE sensor layout on a granite specimen that corresponds to the cube of Fig. 1. The specimen is a cube with a side length of 200 mm. The red dots on the specimen surfaces represent the AE sensors. The surface facing us is the unloading surface, and an AE sensor was placed on its opposite surface, which was subjected to horizontal loading, stress \({\sigma }_{3}\). The surface on which four sensors are arranged and its opposite surface were subjected to vertical loading, stress \({\sigma }_{1}\). The remaining two surfaces were subjected to horizontal loading, stress \({\sigma }_{2}\).

2.2 Theoretical Basis

A microscopic crack is usually projected as an ellipse for theoretical analysis in a two-dimensional plane (Balland et al. 2018; Zhu 2009). For three-dimensional space, the microscopic crack can be assumed as an ellipsoid. To further understand the macrocrack, many studies have investigated rock fractures from microcracks and obtained their spatial distribution with AE events (Chang and Lee 2004; Hou et al. 2018; Li et al. 2018; Naoi et al. 2018; Nasseri et al. 2014; Zhao et al. 2018). It was found that the microcracks corresponding to a macrocrack were densely distributed in the middle and sparsely distributed at both ends (Li et al. 2018; Ruck et al. 2017; Zhang et al. 2018), which conform to the shape of an ellipsoid in three-dimensional space too. Therefore, it is to be assumed that the spatial distribution of microcracks generated by a macrocrack is an ellipsoid in this research. In addition, the shape of the probability density function of the single Gaussian distribution in three dimensions conforms to the spatial characteristics of the ellipsoid, which can be represented as a single macrocrack. Therefore, the single Gaussian distribution model is adopted to analyse the microcracks of a single macrocrack in this study.

For the three-dimensional coordinate vector x, the distribution of the single macrocrack is represented by a multivariate Gaussian distribution model. Therefore, the single macrocrack model takes the form

$$\begin{array}{c}p\left({\varvec{x}}\right)=\frac{1}{\sqrt{{\left(2\pi \right)}^{3}\left|{\varvec{\Sigma}}\right|}}\mathrm{exp}\left[-\frac{1}{2}{\left({\varvec{x}}-{\varvec{\mu}}\right)}^{T}{{\varvec{\Sigma}}}^{-1}\left({\varvec{x}}-{\varvec{\mu}}\right)\right],\end{array}$$
(1)

where the vector x is the microcrack coordinates expressed in matrix form. Note that \(p\left({\varvec{x}}\right)\) obeys \(N\left({\varvec{x}}|{\varvec{\mu}},{\varvec{\Sigma}}\right)\). The vector \({\varvec{\mu}}={\left({{\varvec{\mu}}}_{1},{{\varvec{\mu}}}_{2},\ldots ,{{\varvec{\mu}}}_{{\varvec{d}}}\right)}^{T}\) is a mean vector that is equal to the expectation of x, denoted as \(E\left({\varvec{x}}\right)\), and where \(E\left({\varvec{x}}\right)={\left(E\left({{\varvec{x}}}_{1}\right),E\left({{\varvec{x}}}_{2}\right),\ldots ,E\left({{\varvec{x}}}_{d}\right)\right)}^{T}\). \({\varvec{\Sigma}}\) is a covariance matrix, which is equal to the covariance of vector x, denoted as \(Cov\left({\varvec{x}}\right)\). \(Cov\left({\varvec{x}}\right)\) is expressed as

$$\begin{array}{c}Cov\left({\varvec{x}}\right)=E\left[\left({\varvec{x}}-E\left({\varvec{x}}\right)\right){\left({\varvec{x}}-E\left({\varvec{x}}\right)\right)}^{T}\right]=\left(\begin{array}{cc}\begin{array}{cc}Var\left({{\varvec{x}}}_{1}\right)& Cov\left({{\varvec{x}}}_{1},{{\varvec{x}}}_{2}\right)\\ Cov\left({{\varvec{x}}}_{2},{{\varvec{x}}}_{1}\right)& Var\left({{\varvec{x}}}_{2}\right)\end{array}& \begin{array}{cc}\cdots & Cov\left({{\varvec{x}}}_{1},{{\varvec{x}}}_{d}\right)\\ \cdots & Cov\left({{\varvec{x}}}_{2},{{\varvec{x}}}_{d}\right)\end{array}\\ \begin{array}{cc}\vdots & \vdots \\ Cov\left({{\varvec{x}}}_{d},{{\varvec{x}}}_{1}\right)& Cov\left({{\varvec{x}}}_{d},{{\varvec{x}}}_{2}\right)\end{array}& \begin{array}{cc}\ddots & \vdots \\ \cdots & Var\left({{\varvec{x}}}_{d}\right)\end{array}\end{array}\right)\end{array}$$
(2)

where \(Var\left({\varvec{x}}\right)=Cov\left({\varvec{x}},{\varvec{x}}\right)\).

As mentioned above, more than one crack was found in each damaged rock specimen. The monitored AE signals were generated by multiple macrocracks rather than one. Therefore, when dealing with complex failure, these microcracks were considered to obey a combined distribution in three dimensions. In this study, the combined distribution was assumed to be a linear superposition of multiple single macrocrack models, and they could be written as the Gaussian mixture model (Celik and Tjahjadi 2012) in the form

$$\begin{array}{c}P\left({\varvec{x}}\right)=\sum\limits_{j=1}^{m}{\alpha }_{j}{N}_{j}\left({\varvec{x}}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right),\end{array}$$
(3)

where m is the number of single macrocrack models, \({N}_{j}\left({\varvec{x}}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right)\) is the jth single macrocrack model, and \({\alpha }_{j}\) is the combined coefficient of the jth single macrocrack model, where \({\sum }_{j=1}^{m}{\alpha }_{j}=1\) and \(0\le {\alpha }_{j}\le 1\).

Substituting the three-dimensional single macrocrack model into the combined macrocrack model, the 3-DCRM was obtained as

$$\begin{array}{c}P\left({\varvec{x}}\right)=\sum\limits_{j=1}^{m}{\alpha }_{j}\left\{\frac{1}{\sqrt{{\left(2\pi \right)}^{3}\left|{{\varvec{\Sigma}}}_{j}\right|}}\mathrm{exp}\left[-\frac{1}{2}{\left({\varvec{x}}-{{\varvec{\mu}}}_{j}\right)}^{T}{{\Sigma }_{j}}^{-1}\left({\varvec{x}}-{{\varvec{\mu}}}_{j}\right)\right]\right\}.\end{array}$$
(4)

The expectation–maximization algorithm (Dempster et al. 1977) was adopted to estimate the parameters in the 3-DCRM. From Eq. (3), the log of the likelihood function is given by

$$\begin{array}{c}L\left(\theta \right)=\sum\limits_{i=1}^{n}\mathrm{log}\left({\sum }_{j=1}^{m}{\alpha }_{j}{N}_{j}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right)\right).\end{array}$$
(5)

E step. According to Bayesian theory, for \({{\varvec{x}}}_{i}\), the probability that it belongs to the jth single Gaussian model can be expressed by the posterior probability of \({\alpha }_{j}\) as

$$\begin{array}{c}\gamma \left(i,j\right)=\frac{{\alpha }_{j}{N}_{j}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right)}{{\sum }_{k=1}^{m}{\alpha }_{k}{N}_{k}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{k},{{\varvec{\Sigma}}}_{k}\right)}.\end{array}$$
(6)

M step. Setting the derivatives of Eq. (5) with respect to \({{\varvec{\mu}}}_{j}\) to zero, Eq. (7) was obtained as

$$\begin{array}{c}0=-\sum\limits_{i=1}^{n}\frac{{\alpha }_{j}{N}_{j}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right)}{\sum_{k=1}^{m}{\alpha }_{k}{N}_{k}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{k},{{\varvec{\Sigma}}}_{k}\right)}{\sum }_{j}\left({{\varvec{x}}}_{i}-{{\varvec{\mu}}}_{j}\right).\end{array}$$
(7)

Equation (8) was rearranged from Eq. (7):

$$\begin{array}{c}{{\varvec{\mu}}}_{j}=\frac{1}{{N}_{j}}\sum\limits _{i=1}^{n}\gamma \left(i,j\right){{\varvec{x}}}_{i}.\end{array}$$
(8)

where \({N}_{j}={\sum }_{i=1}^{n}\gamma \left(i,j\right).\)

Setting the derivative of Eq. (5) with respect to \({{\varvec{\Sigma}}}_{j}\) to zero, we can deduce Eq. (9) as follows:

$$\begin{array}{c}{{\varvec{\Sigma}}}_{j}=\frac{1}{{N}_{j}}\sum\limits_{i=1}^{n}\gamma \left(i,j\right)\left({{\varvec{x}}}_{i}-{{\varvec{\mu}}}_{j}\right){\left({{\varvec{x}}}_{i}-{{\varvec{\mu}}}_{j}\right)}^{T}.\end{array}$$
(9)

Consider \({\sum }_{j=1}^{m}{\alpha }_{j}=1\) in Eq. (3), using a Lagrange multiplier and maximizing Eq. (10):

$$\begin{array}{c}L\left(\theta \right)+\lambda \left(\sum\limits_{j=1}^{m}{\alpha }_{j}-1\right),\end{array}$$
(10)

which gives

$$\begin{array}{c}0=\sum\limits_{i=1}^{n}\frac{{N}_{j}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{j},{{\varvec{\Sigma}}}_{j}\right)}{\sum_{k=1}^{m}{\alpha }_{k}{N}_{k}\left({{\varvec{x}}}_{i}|{{\varvec{\mu}}}_{k},{{\varvec{\Sigma}}}_{k}\right)}+\lambda .\end{array}$$
(11)

Equation (12) was rearranged from Eq. (11),

$$\begin{array}{c}{\alpha }_{j}=\frac{{N}_{j}}{N}.\end{array}$$
(12)

The macrocrack model parameters corresponding to the microcracks can be obtained in the iterative calculation, such as \({\alpha }_{j}\), \({{\varvec{\mu}}}_{j}\), and \({{\varvec{\Sigma}}}_{j}\). These parameters are used to confirm the attribution of microcracks, which together form different macrocracks. When the log-likelihood function of the combined model converges, the optimal parameters are obtained. The convergence condition is shown in Eq. (13), and \(\varepsilon =1\times 1{0}^{-5}\) in this article.

$$\begin{array}{c}\left|L\left(\theta \right)-L{\left(\theta \right)}^{^{\prime}}\right|<\varepsilon .\end{array}$$
(13)

3 Results

The real cracks and the monitored microcracks are shown in Part A and Part B of Fig. 3, respectively. The macrocracks were recognized (Part C of Fig. 3) by the expectation–maximization algorithm that calculates the coordinates of microcracks based on the distribution pattern of AE events.

Fig. 3
figure 3

Microcrack distribution of fractured specimens and crack recognition results

Full size image

Figure 3a–e represents the labels of the granite specimens, from specimen B1 to specimen B5. Part A shows the fractured specimens after triaxial compression. One of the surfaces is under unloading conditions, and there are more small cracks in the vicinity of that surface. Different angles were selected for five specimens to show the cracks that formed. Part B shows the 3D distribution of the microcracks monitored by AE technology, and each red sphere represents a microcrack. The X–Z plane at Y = 0 is the unloading surface. Part C refers to crack recognition results. Microcracks belonging to different macrocracks are distinguished by different colours. Each recognized macrocrack is represented by an ellipsoidal contour of the same colour as the microcracks. These recognized macrocracks are marked in Part A with the same colour.

In Fig. 3a, the upper-right corner of the specimen experienced a fracture during triaxial compression (Part A) and microcracks were detected at the same location, resulting in 1022 microcrack coordinates (Part B). It is impractical to calculate either the number of macrocracks or to deduce the mechanism that formed those cracks via conventional methods. However, through crack recognition, each macrocrack that formed was marked in different colours and is shown in Part C. Among the four recognized macrocracks, the blue ellipsoid that is almost vertically inclined and the red ellipsoid that is slightly skewed to the left are the main fractures and further cause the failure of specimen B1 in Fig. 3a. The recognized purple ellipsoid in the upper part of specimen B1 is oriented approximately horizontally. The number of microcracks attributed to the green ellipsoid is less than 10% of all the microcracks, and there is no obvious observation of a corresponding macrocrack in the specimen.

For specimen B2 (Fig. 3b), a number of macrocracks can be identified visually, some of which are approximately vertically oriented near the unloading surface. The location of the microcracks in part B shows that the microcracks are mainly clustered in the middle and left side of specimen B2. Part C shows that four macrocracks were identified in crack recognition. The blue ellipsoid (attributed to 27.6% of the number of microcracks) represents the vertically oriented macrocracks on the left side of specimen B2 adjacent to the unload surface. The red ellipsoid (13%) extends from the top right to the middle bottom through specimen B2, corresponding to the macrocrack on the right side of specimen B2. A black macrocrack (45.8%) was recognized to the upper left of the center of the specimen. In fact, the white background behind specimen B2 can be seen through the black ellipsoid. This illustrates that the material on the upper left side of the back has fallen off, corresponding to the green ellipsoid that is approximately axially oriented and located at the backside of specimen B2.

As shown in Fig. 3c, d, 299 (part C in Fig. 3c) and 162 (part C in Fig. 3d) microcracks were detected in specimens B3 (Fig. 3c) and B4 (Fig. 3d), respectively. The number of microcrack coordinates is relatively small compared that of other specimens. As shown in Fig. 3c, the specimen was highly damaged, and there were more cracks near the unloading surface. In part C of specimen B3, the black macrocrack representing the large crack at the edge of the fracture that penetrates the whole specimen can be attributed to most of the microcrack coordinates. In addition, a red ellipsoid located at the intersection of three cracks was recognized in the upper part of the specimen. Figure 3d shows two recognized macrocracks of specimen B4. The three-dimensional crack recognition algorithm generated a red ellipsoid (part C) with 15 microcrack coordinates, which corresponds to several vertically oriented small cracks near the unloading surface. Other coordinates were recognized that formed one crack at the intersection of the white joint and the crack on the right side, which was horizontally oriented and vertically penetrated the specimen.

In Fig. 3e, a large number of microcracks (5871) clustered in the very left of the specimen (part B). Their spatial distributions fit well with the actual fractures that formed in specimen B5 (part A). Part C is the result of crack recognition, and the locations of the microcracks were removed to improve the visualization. According to Part A of Fig. 3e, two macrocracks, denoted in red and black ellipsoids, are the main macrocracks (48.4%) that form the fracture; the red ellipsoid (22.3%) is located in the centre of the specimen, while the black ellipsoid (26.1%) dip 45° and cuts through the whole specimen. The blue ellipsoid is located in the upper left part of the specimen, and the green ellipsoid (35.4%) is located in the left front part of the specimen but extends backward. Therefore, two cracks intersect at the upper left corner to form a fracture zone on the left side of the specimen. A relatively small purple ellipsoid (12%) is recognized in the lower back part of the specimen.

4 Discussion

4.1 Connections Between Microscopic and Macroscopic Crack Patterns

The majority of previous studies on cracks have focused on the characteristics of all the microcracks (Bunger et al. 2015; Feng et al. 2015; Moradian et al. 2016). Additionally, tens and thousands of microcracks often constitute more than one macrocrack (Baud et al. 2017; Liu et al. 2015; Wang et al. 2019a), and each macrocrack contributes differently to the failure or fracture of a rock (Li et al. 2018; Nasseri et al. 2014). Therefore, explaining rock failure is limited by the analysis of either the overall microcracks or an individual microcrack (Baud et al. 2017; Feng et al. 2015). As shown in Fig. 3, the proposed 3-DCRM overcomes this problem by considering a number of microcracks as several macrocracks in a distribution pattern. In this way, the microscopic and macroscopic fracture patterns are closely linked. The macrocrack distribution (random and intersecting) was realized by the presented crack recognition method using microcracks. The characteristics of macrocracks under complex fracturing failure were obtained, such as the crack quantity, locations, directions, sizes, and proportions. From the perspective of the accurate and refined study of rock failure, this research provides a new approach to further understand the propagation of a crack and the development of rock fracturing, such as crack size analysis of the fracture zone (Granger et al. 2007) and the mechanical behavior of a single macrocrack (Katsaga et al. 2007) in rock mechanics, and the stability of potential cracks regions and rockburst prediction in rock engineering (Wang 2018). Complying with the conventional consideration of visual observation and understanding the distribution of cracks, the relationship between macrocracks is assumed to be a linear combination in this study.

The spatial coordinates from acoustic emission events provided the basic data for the 3D crack recognition, and only such data were utilized. The parameters such as the energy and amplitude of the acoustic emission events should also be considered in the recognition of cracks in future research. For example, the types of cracks can be classified with the rise time, amplitude, and average frequency. Microcracks with high energy may result in larger cracks (Moradian et al. 2016). High-energy microcracks can lead to greater deformation due to their energy level and thus generate even larger macrocracks. Adding different AE parameters, the distribution of crack at higher dimensional promotes the understanding of crack classification and accuracy. But these factors have not been considered in spatial distribution. To explore the existence of non-linear combination relationships, adding more AE parameters in the 3D crack model is suggested for further investigation in high dimensions.

4.2 Advantages of 3-DCRM Adaptability

The recognition results in Fig. 3 demonstrate the advantages of the 3-DCRM in terms of the adaptability of the number of samples, data volume range, the analysis of random microcrack distributions, and the display of random multiple macrocracks. It is a tool for analysing the formation of rock failure and fracture with macrocracks because the monitored microcrack data is normally produced in a large quantity and at a high resolution.

The adopted crack recognition algorithm is an unsupervised machine learning algorithm. It does not require samples to train and learn the characteristics like a supervised machine learning algorithm. Therefore, there is no direct relationship between the accuracy of the unsupervised learning results and the number and size of samples. They are directly related to hypothetical relationships. There is a comparison of ten commonly used unsupervised algorithms by Scikit-learn (Scikit-Learn Developers 2020), namely K-Means, Affinity propagation, Mean-shift, Spectral clustering, Ward hierarchical clustering, Agglomerative clustering, Density-Based Spatial Clustering of Applications with Noise (DBSCAN), Ordering Points To Identify the Clustering Structure, Gaussian mixtures, and Birch. In the results: (1) when there is a significant distance between clusters, all the ten algorithms accurately recognize the targets. (2) When the clusters are close to each other, only DBSCAN and Gaussian mixtures give the correct results. (3) When there is a crossover between clusters, Gaussian mixture model is more accurate than the DBSCAN model. Comparable results may be obtained in other models through parameter adjustment. (4) When it comes to a group of chaotic points, there are some algorithms that give different results; however, only Gaussian mixture model shows the core of multivariate Gaussian distribution, which presents an ellipsoid in 3D. This key point is highly consistent with the proposed hypothesis.

Usually, the shape and size of the recognized results are based on the hypothetical theory and the distribution range of samples. The hypothesis in this paper determines that the shape of the crack is an ellipsoid. Compared with the non-fixed shape hypothesis, the proposed hypothesis has better regularity. To consider morphological variation, 3-DCRM shows good adaptability to the spatial distribution of data. First, the shape of the macrocrack is determined as an ellipsoid by the hypothetical theory. What’s more, by adjusting the parameters, ellipsoids with different sizes and shapes can be obtained, ranging from approximately thin cylinders to spheres to discs. Therefore, good adaptability in the variation in spatial distribution was found in the ellipsoid, which gives it advantages in representing the macrocrack compared to the representation provided by a sphere or cube. Most of the macrocracks were recognized successfully in this research. However, it is worth mentioning that in some cases, the profiles of cracks are complex (Feng et al. 2015), such as a fault surface with subparallel cracks (Nasseri et al. 2014), or irregular or discontinuous fracture surface with several branching fracture surfaces (Katsaga et al. 2007). This method would recognize such features as one macrocrack (e.g., part C in specimen B2) or a combination of several macrocracks. Besides, several abnormal microcracks may be collected far away from the cluster area. Therefore, to improve the accuracy of shape and size, it is suggested to further optimize the recognized cracks from the perspective of space and shape.

After comparing the amount of microcrack data monitored in the five specimens, the recognition task will face the challenges and the requirements of dealing with changes in the amount of coordinate data. According to the relevant literature, there are approximately hundreds of microcracks in a cubic rock specimen with a side length of 300 mm (Li et al. 2018), while more than ten thousand microcracks can be found in a standard cylindrical specimen (Φ50 mm × 100 mm) (Zhang et al. 2018). In this research, under the same experimental conditions and instrumental settings, 5871 coordinates were obtained in specimen B5 while only 299 and 162 coordinates were obtained in specimens B3 and B4, respectively. This result is discussed and explained in the following paragraphs. In the case of relatively large quantities of microcracks, the proposed method successfully recognized five cracks with different distributions, and these cracks coincided well with the experimental observations of the macrocracks. With regard to the relatively small quantities of coordinates, the present crack recognition method still generated trustworthy results for the crack distribution of specimens B3 and B4. The recognition results indicate that the proposed method has an advantage in terms of the data volume requirements, ranging from 162 to 5,874 microcrack coordinates.

4.3 Incomplete Dataset of Microcrack Coordinates

Theoretically, microcracks expand during a loading procedure and a number of them ultimately merge to form one or multiple observable macrocracks (Katsaga et al. 2007; Ruck et al. 2017). However, sometimes the expansion or quantity of the coalesced microcracks is insufficient to form a macrocrack during artificial loading. It is different from the ideal situation where all microcracks are collected. Taking specimen B1 as an example (Fig. 3a), the crack denoted in the green ellipsoid is treated as a potential macrocrack. The green and purple ellipsoids linked on the left side of the specimen to form a fracture at the upper surface of the specimen. In contrast, the penetration of cracks especially macrocracks will affect the propagation of AE signals, which causes fewer microcrack coordinates to be collected in the dataset (Li et al. 2018; Moradian et al. 2016; Zhang et al. 2018), such as in part C in specimen B3, as shown in Fig. 3c. As for specimen B4 in Fig. 3d, it is considered to be the results of the actions of the crack initiation position, direction, and speed. Only a group of horizontally distributed microcracks was monitored in the middle of the corresponding macrocrack on the right side. The crack initiation position is in the middle of the macrocrack, but the crack fracture speed along the cracking direction is very fast. The large macrocrack formed instantaneously hinder the propagation of other signals, so the microcracks cannot be located. Although macrocracks have been recognized in this article, such influences must be considered to improve the accuracy of the results. It is a part of the reason why the artificial number setting is adopted in this research. As shown in Fig. 3c, the result of two cracks set for specimen B3 shows a good explanation for rock failure, even though the results of three cracks have better visual results. In future research, it is recommended to adopt the most recent technology of microcrack localization to improve the detection accuracy and acquire a more complete microcrack dataset.

Moreover, some microcrack signals may be artificially excluded in AE experiments, when the threshold is set to filter out a specific range of signals for reducing the effect of ambient noise, such as voices and machine noise (Wang 2018; Wang et al. 2019b). It is likely that some small signals representing microcracks go unrecorded and are thus unidentified herein (Baud et al. 2017; Faillettaz et al. 2016; Meier et al. 2019; Rouet-Leduc et al. 2017).

4.4 Crack Number and Threshold

Unsupervised algorithms are usually subjected to several parameters; the most common parameters are the threshold and the number of targets. The settings of the number of cracks and the threshold are required before crack recognition. It is worth mentioning that in computing, the calculation of each additional crack and the increase in accuracy will greatly increase the computational workload and calculation time. However, in this exploratory study of crack distribution patterns in rock mechanics and engineering, based on the discussion in the previous sections, the pursuit of accuracy is more of mathematically significant. Therefore, it is appropriate to select a moderate accuracy that will not cause deviations to the main area of the recognized crack, but shows potentially fault tolerance of the cracks space. In the end, the convergence threshold in this research is selected. The main area of the macrocrack remains stable and the accuracy can be guaranteed at this level.

Moreover, the background work we have conducted shows that small cracks (less than 10%) would overlap if the number of macrocracks are large. They will not only interfere with the results, but also result in poor visualization for crack recognition. For specimen B5 (Fig. 3e), 5781 microcrack coordinates were obtained and the number of cracks was required as input. On the one hand, potentially recognizable macrocracks would be ignored if this number is set too small. In this study, the crack number setting tests indicated that if the number of macrocracks is set to less than four, the smaller crack in the upper left corner will not be recognized. On the other hand, if the number of cracks is set to more than five, the workload increases exponentially for each additional crack and more macrocraks will be distributed across corresponding to the original macrocrack position. With some cracks overlapping, it is computationally inappropriate to recognize the cracks in a fixed size area. Therefore, five cracks were considered for B5. Due to the small volume of data, specimen B4 (Fig. 3d) displayed a good recognition result with a crack number of two. If the crack number of B4 was set to four, the black ellipsoid would decompose into three smaller parallel macrocracks very close to each other. Therefore, they were considered to be one crack in the result. For the same reason, two macrocracks were generated for specimen B3 (Fig. 3c). On the one hand, if the number of cracks was set to four or more, the generated cracks would overlap, and show less efficiency than the results of setting two cracks. On the other hand, if the number of cracks is less than four, for specimen B2 (Fig. 3b), a large crack will not be recognized. The explanation of the detailed cracks is limited, and the effectiveness of the proposed method cannot be demonstrated. Following the implementation of such tests with different numbers of crack, it was suggested to choose five or less as the number of cracks for crack recognition under similar conditions.

The currently employed crack recognition algorithm requires human analysis to define the number of cracks. Such interference can be critical to the results because people may have different opinions on the mechanism of crack generation. However, manual analysis is also an important basis for judging the recognition results. Thus, considering the correspondence between the number of target macrocracks and real macrocracks, a function to automatically define the number of target macrocracks should be further investigated on the approximate inference algorithm.

5 Conclusion

In conclusion, we present a crack recognition model for rocks based on the spatial distribution of microcracks that formed primarily along the throughgoing fracture under triaxial compression conditions. In doing so, we reconcile rock fracture observations and rock mechanics analysis results with an unsupervised machine learning algorithm for the complex 3D spatial distribution characterization of microcracks, as it has critical implications for crack recognition, rock fracture analysis, and seismic hazard. The results are as follows:

  1. 1.

    Using the proposed crack distribution hypothesis, the crack recognition results were obtained under the triaxial compression. They coincide well with the experimental observations of random macrocracks. The differences between the recognition results and experiments were explained. The proposed hypothesis can be used to recognize and analyse multiple macrocracks based on microcracks.

  2. 2.

    Ten unsupervised machine learning algorithms were used for comparison. As a result, only the proposed method explains the crack distribution hypothesis well. Therefore, it is considered to be the most suitable method for the theoretical hypothesis.

  3. 3.

    The crack recognition method shows no requirements on the number of samples, and it has good adaptability to the data volume, the microcrack data sets range from 162 to 5874.

  4. 4.

    These research results connect the microcracks and the macrocracks and deepen the understanding of rock failure at multiple macrocracks. This research provides a meaningful method to explore the formation of multiple macrocracks at once. The detailed formation can be widely adopted by rock mechanics and engineering, such as mechanical behavior interpretation and rockburst prediction.