Modeling of Simultaneous Propagation of Multiple Blade-Like Hydraulic Fractures from a Horizontal Well

Abstract

We explore different aspects of the multi-stage fracturing process such as stress interaction between growing hydraulic fractures, perforation friction, as well as the wellbore flow dynamics using a specifically developed numerical solver. In particular, great care is taken to appropriately solve for the fluid partition between the different growing fractures at any given time. We restrict the hydraulic fractures to be fully contained in the reservoir (fractures of constant height) thus reducing the problem to two dimensions. After discussions of the numerical algorithm, a number of verification tests are presented. We then define via scaling arguments the key dimensionless parameters controlling the growth of multiple hydraulic fractures during a single pumping stage. We perform a series of numerical simulations spanning the practical range of parameters to quantify which conditions promote uniform versus non-uniform growth. Our results notably show that, although large perforations friction helps to equalize the fluid partitioning between fractures, the pressure drop in the well along the length of the stage has a pronounced adverse effect on fluid partitioning as a result on the uniformity of growth of the different hydraulic fractures.

1 Introduction

Multi-stage fracturing is the completion of choice of horizontal wells in unconventional reservoirs. It consists in the stimulation of the horizontal portion of the well from its end (i.e., the well toe) in sequences referred to as stages. Each stage typically has several (typically from three to six or more) clusters of perforations, and is hydraulically isolated from the previous stages by a bridge plug. The design of a stage aims at propagating multiple hydraulic fractures during a single injection often performed at a constant rate. The number of perforation clusters controls the maximum number of hydraulic fractures that can initiate and simultaneously propagate during a stage.

Fig. 1

A schematic view of multiple blade-like hydraulic fractures growing simultaneously from a horizontal well. Scales in meters

A number of contributions in the past years have investigated simultaneous propagation of several hydraulic fractures during a pumping stage (see, e.g., Bunger and Lecampion (2017) for a review). These contributions have notably highlighted the importance of the horizontal in-situ stress contrast (Kresse et al. 2013b), stress interaction between the fractures (i.e., stress shadow) (Roussel and Sharma 2011; Xu and Wong 2013; Wu and Olson 2015b), hydraulic fracture propagation regimes (Bunger 2013; Kresse et al. 2013a; Bunger et al. 2014), as well as the importance of the well perforation friction and near-wellbore friction (Desroches et al. 2014; Lecampion and Desroches 2015c, 2018). The key to ensure simultaneous growth of all the fractures within one stage is to achieve equal fluid partitioning. In other words, the rates entering all the hydraulic fractures should be equal throughout the injection duration. From the previously mentioned contributions, it notably appears that the coupling between wellbore hydraulic and hydraulic fracture mechanics is extremely important. Moreover, the local pressure drop at the hydraulic fracture entrance—denoted as entry friction—is in most cases critical for stability of the fluid partitioning. Notably, for the simple case of strictly axisymmetric hydraulic fractures, it appears that large entry friction—as typically used in practice—is often sufficient to counteract the stress interaction between growing fractures, thus promoting simultaneous growth (Lecampion and Desroches 2015b, c).

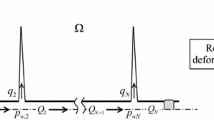
In this contribution, we focus on the case of multiple blade-like hydraulic fractures (constant height fractures) that may curve due to their stress interactions (Fig. 1). Such a geometry—like the case of solely axisymmetric fractures (Lecampion and Desroches 2015c)—is an end member. Whereas the hypothesis of axisymmetric fractures is relevant at early time or within a reservoir of infinitely homogeneous properties, a blade-like geometry will be encountered in a reservoir of finite height bounded by layers with significantly larger in-situ confining stress that restrict fracture growth to occur solely in the reservoir layer. As a result, fluid flow is uni-dimensional inside the fractures with a strictly horizontal velocity. Such a model assuming constant height is not geared to explore the early time of growth from a horizontal wellbore where the fractures typically have a axisymmetric shape. It starts to be valid when the length of the fracture has reached the height of the reservoir.

We explore different aspects of the multi-stage stimulation problem for blade-like fractures using a specifically developed numerical model that solves, in a fully coupled implicit manner, the propagation of multiple blade-like hydraulic fractures (and their stress interactions), the fluid flow in the wellbore, and the fractures as well as the fluid partitioning between fractures.

Although, in this model, the fractures are assumed to be of constant height, the fractures are allowed to curve due to stress interactions or in-situ stress heterogeneities. We restrict our discussion here to the zero leak-off case for simplicity—which corresponds to tight rocks for which the diffusion time-scale is smaller than the injection duration. The wellbore-fracture entry connection is modeled using engineering perforation friction and near-wellbore tortuosity terms which impose a non-linear relationship between the flux entering the fracture and the fluid pressure difference between the well and the fracture entry (Lagrone and Rasmussen 1963; Economides and Nolte 2000).

After presenting several verifications of the numerical model, we explore the parameters controlling the stability of simultaneous propagation of hydraulic fractures from a horizontal well drilled in the direction of the minimum horizontal in-situ stress. In particular, we investigate through combined numerical simulations and scaling arguments what controls the uniform growth of all fractures compared to the growth of only a subset of the desired fractures. We quantify the impact of the different competing physical processes: stress shadow/interactions between fractures, perforation friction, as well as pressure drop in the wellbore along the stage length. We also highlight the numerical difficulties associated with the coupling of the wellbore flow with the simultaneous propagation of multiple hydraulic fractures—a problem that we may refer to as the fluid partitioning problem.

2 Problem Formulation

Under the assumption of blade-like geometries of the different hydraulic fractures, we account for the mechanical deformation of the rock, its coupling with fluid flow in the different fractures, fracture propagation, as well as fluid flow in the wellbore and its partitioning between the different propagating fractures. We assume the rock to be linearly elastic with uniform properties and restrict ourselves to the impermeable case (i.e., a rock hydraulic diffusion time-scale smaller than the injection duration) for clarity.

2.1 Solid Deformation

Restricting to an isotropic elastic homogeneous material, the quasi-static balance of momentum allow for an integral representation. The normal $\sigma ^{in}$ and shear $\tau ^{in}$ tractions induced at a point $\mathbf {x}$ (on the fracture surface with known orientation) by displacement discontinuities (DD) distributed over the fracture surface S are given by the following (Crouch and Starfield 1983):

$$\begin{aligned} \sigma ^{in}(\mathbf {x})= & {} \int _{\varSigma }\left( K^{nn}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{n}(\mathbf {x}')\right. \nonumber \\&\left. +K^{ns}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{s}(\mathbf {x}')\right) \text {d}\mathbf {x}'\nonumber \\ \tau ^{in}(\mathbf {x})= & {} \int _{\varSigma }\left( K^{sn}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{n}(\mathbf {x}')\right. \nonumber \\&\left. +K^{ss}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{s}(\mathbf {x}')\right) \text {d}\mathbf {x}', \end{aligned}$$

(1)

where $\delta ^{n}$ is the normal DD (fracture opening) and $\delta ^{s}$ is the shear DD (shear slip). Note that Eq. (1) directly extends to the case of multiple fractures (in that case, $\varSigma$ denotes the union of the $N_{\text {frac}}$ fracture surfaces). It gives the interaction stress induced by multiple fractures at a point $\mathbf {x}$ located on the crack surface (provided that the normal and shear components of tractions and DD are defined in the appropriate local normal and tangent system of coordinates).

The elastic kernel $K^{kl}(\mathbf {x}-\mathbf {x}',\,H),\,k,l=n,s$ used here corresponds to a simplified 2D approximation obtained from the full three-dimensional kernel for a rectangular DD with appropriate corrections factors to account for a given fracture height as suggested by Wu and Olson (2015a). It is chosen here as a computationally effective alternative to the direct integration of the full 3D kernel over the height of the fracture(s). Normal and shear displacement discontinuities $\delta ^{n}$, $\delta ^{s}$, and the corresponding tractions are taken in the horizontal mid-plane of the blade-like fractures. The displacement discontinuity are thus uniform over the fracture height. It is, however, important to keep in mind that such an approximate kernel leads to erroneous stress predictions (about 10–15% difference compared to a full 3D solution) when the spacing between fractures are lower than 0.25 the fracture height according to Wu and Olson (2015a). We believe that it is a proper approximation only for fracture spacing larger than half the fracture height. We will thus not report simulations for lower spacing-to-height ratio in the following. Another possible choice for blade-like fractures (constant height) is to assume an elliptical variation of DD in the vertical direction, therefore, allowing to also reduce the problem from 3D to 2D—see Adachi and Peirce (2008) and Protasov et al. (2018) for details. We solely report here results using the approximated kernel described in Wu and Olson (2015a).

Superposing the interaction stress with the in-situ stress field $\sigma ^{o}(\mathbf {x}),\,\tau ^{o}(\mathbf {x})$ and taking into account the balance of normal traction with the net fluid pressure $p(\mathbf {x})-\sigma ^{o}(\mathbf {x})$, we obtain the following set of boundary integral equations on all fracture surface:

$$\begin{aligned} p(\mathbf {x})-\sigma ^{o}(\mathbf {x})= & {} \int _{\varSigma }\left( K^{nn}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{n}(\mathbf {x}')\right. \nonumber \\&\left. +K^{ns}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{s}(\mathbf {x}')\right) \text {d}\mathbf {x}'\nonumber \\ -\tau ^{o}(\mathbf {x})= & {} \int _{\varSigma }\left( K^{sn}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{n}(\mathbf {x}')\right. \nonumber \\&\left. +K^{ss}(\mathbf {x}-\mathbf {x}',\,H)\delta ^{s}(\mathbf {x}')\right) \text {d}\mathbf {x}', \end{aligned}$$

(2)

where p denotes the fluid pressure.

2.2 Fluid Flow in the Fractures

The mass conservation per unit of fracture height H averaged over the width of fracture I ($I=1,\ldots ,N$) in the absence of leak-off reduces to the following one-dimensional equation along the curvilinear coordinate system defined by the local tangent to the fracture, we denote s the corresponding curvilinear coordinate:

$$\begin{aligned} \frac{\partial w}{\partial t}+c_{f}w\frac{\partial p}{\partial t}+\frac{\partial q}{\partial s}=\widetilde{Q}_{I}(t)\delta (s-s_{I}), \end{aligned}$$

(3)

where $c_{f}$ denotes the fluid compressibility, p is the fluid pressure, $w=w_{o}+\delta ^{n}$ is the total hydraulic width of the fracture, where $w_o$ is a small constant initial aperture only active in the initial flaw, $\widetilde{Q}_{I}=\frac{Q_{I}}{H}$ is the entry volume rate per unit fracture height H, $s_{I}$ denotes the coordinates of the intersection of the well with fracture I, and $\delta (s)$ is the Kronecker delta.

Assuming laminar flow inside the fracture, the width averaged fluid balance of momentum reduce to Poiseuille’s law. The local fluid flux q(s) is given as:

$$\begin{aligned} q(s)=-\frac{w^{3}}{12\mu }\frac{\partial p}{\partial s}, \end{aligned}$$

(4)

where $\mu$ is the fracturing fluid viscosity.

2.2.1 Fluid Flow in the Wellbore

To solve for the simultaneous propagation of several hydraulic fractures from a horizontal well, fluid flow inside the wellbore must be solved for. The aim is to properly solve for the partitioning of the fluid injected from the well head into the different fractures. Neglecting fluid flow inertial effects that may be associated with short transient pressure changes (water hammer etc.), the mass and momentum balance in the wellbore after integration over the wellbore cross-section reduce in the curvilinear coordinate s along the well trajectory to:

$$\begin{aligned}&A \, c_{f}\frac{\partial p}{\partial t}+\frac{\partial A\,V}{\partial s}+A\, V \,c_{f}\frac{\partial p}{\partial s}=Q_{o}(t)\delta (s)\nonumber \\&\quad -\sum _{I=1}^{N}Q_{I}(t)\delta (s-s_{I}), \end{aligned}$$

(5)

$$\begin{aligned}&\frac{\partial p}{\partial s}=-\frac{2\pi a}{A}\times \frac{f(Re,\epsilon )}{4}\times \frac{\rho V|V|}{2}+\rho g\sin \theta (s), \end{aligned}$$

(6)

where a is the wellbore radius and A is the well pipe cross-section area ($A=\pi a^{2}$). $\rho$ denotes the fracturing fluid density and V is the average fluid velocity. $Q_{o}(t)$ is the volumetric pump rate imposed at the well head (i.e., at $s=0$), whereas $Q_{I}(t)$ is the flow rate entering the Ith fracture. $f(Re,\epsilon )$ is the Darcy friction factor which is function of the Reynolds number $Re=\frac{2\rho a|V|}{\mu }$ and pipe relative surface roughness $\epsilon$. We use the Churchill (1977) approximation [fitting the experimental data of Nikuradse (1950)] to estimate the friction factor $f(Re,\epsilon )$. Churchill approximation has the advantage of being explicit (thus does not require the solution of a non-linear equation) at the expense of slight inaccuracies in the laminar–turbulent transition region. Other models are possible (see, e.g., (Lecampion and Desroches 2015c; Zia and Lecampion 2017) for discussion)—the results being qualitatively similar.

2.3 Fracture Entry Friction: Coupling Between Wellbore and Fracture Flow

We account for a local pressure drop due to entry friction between the wellbore and the fracture. Such a local pressure drop is related to the fluid going through the perforations connecting the cased and cemented wellbore with the fracture. An additional pressure drop is also usually related to the tortuosity of the fracture geometry near the wellbore—see Bunger and Lecampion (2017) for discussions. We use here an accepted relation for such entry friction (Lagrone and Rasmussen 1963; Economides and Nolte 2000). It relates the pressure drop between the wellbore and the fracture I to the fluid flux entering the fracture I as follows:

$$\begin{aligned} p_{w,I}-p_{{\text {in}},I}=f_{\text {p}}\times Q_I^{2}+f_{t}\times Q_I^{\beta }, \end{aligned}$$

(7)

where $p_{w,I}=p(s_I)$ is the fluid pressure inside the wellbore at the location of the perforation clusters in front of fracture I and $p_{{\text {in}}, I}$ is the fluid pressure at the inlet of fracture I (just inside the fracture). $Q_I$ is the total fluid flux entering fracture I which is an unknown function of time resulting from the fluid partitioning between the different propagating hydraulic fractures. The first quadratic term in Eq. (7) corresponds to a classic turbulent pressure drop associated with the perforations connecting the fracture to the well. The coefficient $f_{\text {p}}$ is function of the fluid density $\rho$, diameter $D_{\text {p}}$, and number $n_{\text {p}}$ of the perforations. It can be estimated using an empirical formula $f_{\text {p}}=0.807249\dfrac{\rho }{n_{\text {p}}^{2}D_{\text {p}}^{4}C^{2}}$ (in SI units) (see, e.g., Crump and Conway (1988); Economides and Nolte (2000) for details) where the dimensionless discharge coefficient C is typically between 0.5 and 0.9. Typical number of perforations and diameters used provide values of $f_{\text {p}}$ in the range $[10^6$–$10^{10}]$ Pa/(m$^3$/s)$^2$. The second term in Eq. (7) is added to account for additional pressure drop associated with near-wellbore-fracture tortuosity (see Bunger and Lecampion (2017) and Lecampion and Desroches (2015c) for more details). The coefficient $f_{t}$ and $\beta$ can be estimated from step-down tests in-situ (Economides and Nolte 2000; Lecampion et al. 2015; Desroches et al. 2014).

2.4 Fracture Propagation Criteria/Tip Asymptotic

Under the hypothesis of linear elastic fracture mechanics (lefm), the quasi-static fracture propagation condition reduces for pure mode I fracture to:

$$\begin{aligned} v_{\text {tip}} \times (K_I-K_{\text {Ic}}) =0,\quad v_c \ge 0, \end{aligned}$$

(8)

where $K_I$ is the mode I stress intensity factor and $K_{\text {Ic}}$ is the rock fracture toughness. $v_{\text {tip}}$ denotes the local crack tip velocity. We account for the possibility of fracture curving under mixed mode (I and II) loading. Mode II emerges from stress interactions between fractures. We use here a maximum tensile stress direction criteria to solve for the propagation direction. A maximum tensile stress criterion is known to give similar predictions than the principle of local symmetry (minimum $K_{II}$)—see, e.g., Pham et al. (2017).

Locally at the fracture tip, we thus assume condition of pure mode I, such that the fracture width of a propagating fracture results in the well-known lefm asymptote (Rice 1968):

$$\begin{aligned} w = \sqrt{32/\pi } \frac{K_{\text {Ic}}}{E^\prime } \sqrt{\ell -x} \quad \ell -x\ll \ell . \end{aligned}$$

(9)

This near-tip behavior may be visible only over a very small characteristic length near the tip for a propagating hydraulic fracture where an outer viscous asymptote may dominates (Desroches et al. 1994; Garagash et al. 2011). This renders the use of a sole linear elastic fracture mechanics criteria extremely demanding computationally as the mesh size must then resolve the small lengthscale where the lefm asymptote is valid (see Lecampion et al. 2013; Detournay and Peirce 2014; Lecampion et al. 2018 for discussion). For this reason, we use the complete multi-scale solution for a steadily propagating plane-strain hydraulic fracture as an “universal” tip asymptote (Garagash et al. 2011; Dontsov and Peirce 2015) covering toughness-, viscosity-, and leak-off-dominated regimes near the fracture tip. The use of such complete asymptotic solution is similar to the previous contribution e.g. (Lecampion and Desroches 2015c; Peirce and Detournay 2008; Peirce 2015; Dontsov and Peirce 2017). Further details on the fracture propagation scheme are provided in Sect. 3.1.1.

2.5 Initial/Boundary Conditions

Prior to the start of the injection, at time $t = 0$, the well is under hydrostatic pressure: $p(s, t = 0) = \rho \,g\,z(s)$ and $V(s, t = 0) = 0$. At the scale of this 2D model which assumes a constant fracture height, the details of fracture initiation from the perforations are obviously not properly captured. We thus assume a small pre-existing fracture transverse to the well axis at the location of each perforation clusters. In other words, each fracture is pre-initiated with an initial length ($\ell _I(t = 0) = L_o$) and assumed initially closed at $t = 0$. The fluid flux at the end of stage (at the location of the bridge plug) is assumed to be zero at all times $V(s = S_{\text {plug}}, t) = 0$, while we assume that the surface pump rate is prescribed $Q(s = 0, t)$. We notably restrict here our discussion to the case of a constant pump rate.

3 Numerical Scheme Description

The numerical solution of the previously described model must couple the solution of the propagation of multiple hydraulic fractures with the wellbore fluid flow to notably solve for the rates $Q_I(t)$ entering the different fractures at any given time. We have developed an implicit time discretization scheme. From a known solution at time $t^{k-1}$, we solve at time $t^{k}=t^{k-1}+\varDelta t$ for the increment of displacement discontinuities, fluid pressure, and increment of length of all the fractures tips as well as fluid pressure increment and flow rates entering each fracture during the time-step. For one time-step, we solve such a highly non-linear problem iteratively using three nested loops. The most outer loop solves iteratively for the fluid partitioning between fractures, i.e., for the flow rates $Q_I$ entering the different fractures by minimizing the residuals of Eq. (7) describing the relation of rates and the well-fracture entry pressure drop. For a given set of rates $Q_I$, the wellbore flow and multiple hydraulic fracture increment problems can be solved separately. The solution of the propagation of the multiple hydraulic fractures is achieved via two nested loops: the outer loop iterates on the fracture length increment, while the inner loop solves (for a given new trial position of the fractures tip) the elasto-hydrodynamics system.

We describe below the numerical discretization of the different equations and the steps of the different parts of the algorithm over one time-step.

3.1 Elasto-Hydrodynamics Flow Inside the Fractures

For each time-step, elasto-hydrodynamics equations are solved iteratively assuming known the new fracture tip locations (these are iterated for in an external loop, see 3.1.1). In other words, while iterating for $\delta ^{n}(x)$, $\delta ^{s}(x)$, and p(x) within a time-step, the fracture length is fixed. Yet, the opening $\delta ^{n}$ in the tip region may be imposed to enforce mass conservation in line with the near-tip hydraulic fracture solution, see 3.1.1.

After discretization using piece-wise constant displacement discontinuity elements (Crouch and Starfield 1983; Wu and Olson 2015a), the elasticity equations reduce to the following linear system:

$$\begin{aligned} p_{i}-\sigma _{i}^{o}&=\sum _{j}A_{ij}^{nn}\delta _{j}^{n}+A_{ij}^{ns}\delta _{j}^{s}\nonumber \\ -\tau _{i}^{o}&=\sum _{j}A_{ij}^{sn}\delta _{j}^{n}+A_{ij}^{ss}\delta _{j}^{s}, \end{aligned}$$

(10)

where $\delta _{j}^{n}=-d_{j}^{n}$ is the fracture width in the middle of element j taken positive in opening, and $\delta _{j}^{s}=-d_{j}^{s}$ is the shear slip (+ minus −). $\sigma _{i}^{o}$ is the normal component of the in-situ traction on the element i and $\tau _{i}^{o}$ the shear component along the tangential direction s (with the convention of in-situ stress positive in compression). The coefficients $A_{ij}^{kl},\,k,l=n,s$ are integrals of $K^{kl}(z-z',\,H)$ over the element j—see Wu and Olson (2015a) for the simplified 3D kernels for constant fracture height used here.

The lubrication Eq. (3) is integrated over an element (cell), thus resulting in a finite volume discretization. Restricting to the case of zero leak-off case for simplicity, one obtains:

$$\begin{aligned} h_{i}c_{f}\delta _{i}^{n}\frac{\varDelta p_{i}}{\varDelta t}+h_{i}\frac{\varDelta \delta _{i}^{n}}{\varDelta t}+q_{i+\nicefrac {1}{2}}-q_{i-\nicefrac {1}{2}}=\widetilde{Q}_{I}(t)\delta _{iw_{I}}, \end{aligned}$$

(11)

where $h_{i}$ is the size of the ith element and $w_{I}$ is the index of the element of the Ith fracture where the well is located. We discretize the fluid fluxes through the left and right boundaries of the cell (element) via centered finite difference:

$$\begin{aligned} q_{i+\nicefrac {1}{2}}=-C_{i+\nicefrac {1}{2}}\frac{p_{i+1}-p_{i}}{(h_{i}+h_{i+1})/2}, \end{aligned}$$

(12)

where for the “right” edge conductivity $C_{i+1/2}$ (function of the edge width obtained by harmonic mean), we have:

$$\begin{aligned} C_{i+\nicefrac {1}{2}}=\frac{1}{12\mu }\times 2\frac{w_{i}^{3}w_{i+1}^{3}}{w_{i}^{3}+w_{i+1}^{3}}\quad w_{i}=\delta _{i}^{n}+w_{o}. \end{aligned}$$

(13)

Similarly, for the “left” edge:

$$\begin{aligned} q_{i-\nicefrac {1}{2}}=-C_{i-\nicefrac {1}{2}}\frac{p_{i}-p_{i-1}}{(h_{i}+h_{i-1})/2}. \end{aligned}$$

(14)

Finally, the discretized lubrication equation becomes:

$$\begin{aligned}&h_{i}c_{f}\delta _{i}^{n}\frac{\varDelta p_{i}}{\varDelta t}+h_{i}\frac{\varDelta \delta _{i}^{n}}{\varDelta t} -\frac{C_{i-\nicefrac {1}{2}}}{(h_{i}+h_{i-1})/2}p_{i-1}\nonumber \\&\qquad +\left( \frac{C_{i+\nicefrac {1}{2}}}{(h_{i}+h_{i+1})/2}+\frac{C_{i-\nicefrac {1}{2}}}{(h_{i}+h_{i-1})/2}\right) p_{i}\nonumber \\&\qquad -\frac{C_{i+\nicefrac {1}{2}}}{(h_{i}+h_{i+1})/2}p_{i+1}\nonumber \\&\quad =\widetilde{Q}_{I}(t)\delta _{iw_{I}}, \end{aligned}$$

(15)

for all elements i except for tip ones where $q_{i+\nicefrac {1}{2}}=0$ (or $q_{i-\nicefrac {1}{2}}=0$ depending on the tip orientation). For a tip element, e.g., the “right” one, we have:

$$\begin{aligned} h_{i}c_{f}\delta _{i}^{n}\frac{\varDelta p_{i}}{\varDelta t}+h_{i}\frac{\varDelta \delta _{i}^{n}}{\varDelta t}+\frac{C_{i-\nicefrac {1}{2}}}{(h_{i}+h_{i-1})/2}p_{i}-\frac{C_{i-\nicefrac {1}{2}}}{(h_{i}+h_{i-1})/2}p_{i-1}=0. \end{aligned}$$

(16)

Finally, we can re-write the coupled elasto-hydrodynamics system in matrix-vector format, using the increment of vector displacement discontinuities $\varDelta {\varvec{\delta }{}^{(k)}}=\left( {\varvec{\delta }{}^{(k)}-\varvec{\delta }{}^{(k-1)}}\right)$ and fluid pressures $\varDelta \mathbf {p}_{}^{{ (k) }} =({\mathbf {p}_{}^{{ (k) }}-\mathbf {p}_{}^{{ (k-1) }}})$ over the time-step $t^k=t^{k-1}+\varDelta t$ as the primary unknowns:

$$\begin{aligned}&\mathbb {A}\cdot \varDelta {\varvec{\delta }{}^{(k)}} -\mathbb {I}_{\text {p}}\cdot \varDelta {\mathbf {p}^{{ (k) }}} =-\mathbf {T}_{{o}} -\mathbb {A}\cdot {\varvec{\delta }^{(k-1)}}\nonumber \\&\mathbb {I}_{{s}}\cdot \varDelta {\varvec{\delta }^{(k)}} +\left( \varDelta t\mathbb {L}({\varvec{\delta }^{(k)}})+c_{f}\mathbb {I}_{c}\right) \cdot \varDelta {\mathbf {p}_{}^{{ (k) }}} =\varDelta t \mathbf {Q} -{{\Delta } t }\mathbb {L}\cdot \mathbf {p}^{{ (k-1) }}, \end{aligned}$$

(17)

with the following matrices:

• elastic DDM influence matrix

  $$\begin{aligned} \mathbb {A}=\left[ \begin{array}{ccccccccc} A_{11}^{ss} &{} A_{11}^{sn} &{} A_{12}^{ss} &{} A_{12}^{sn} &{} &{} \ldots &{} &{} A_{1N}^{ss} &{} A_{1N}^{sn}\\ A_{11}^{ns} &{} A_{11}^{nn} &{} A_{12}^{ns} &{} A_{12}^{nn} &{} &{} \ldots &{} &{} A_{1N}^{ns} &{} A_{1N}^{nn}\\ A_{21}^{ss} &{} A_{21}^{sn} &{} A_{22}^{ss} &{} A_{22}^{sn}\\ A_{21}^{ns} &{} A_{21}^{nn} &{} A_{22}^{ns} &{} A_{22}^{nn}\\ &{} &{} &{} &{} &{} &{} &{} \vdots &{} \vdots \\ \vdots &{} \vdots &{} &{} &{} &{} \ddots \\ \\ A_{N1}^{ss} &{} A_{N1}^{sn} &{} &{} &{} \ldots &{} &{} &{} A_{NN}^{ss} &{} A_{NN}^{sn}\\ A_{N1}^{ns} &{} A_{N1}^{nn} &{} &{} &{} \ldots &{} &{} &{} A_{NN}^{ns} &{} A_{NN}^{nn} \end{array}\right] ; \end{aligned}$$

• fluid pressure increment on elasticity

  $$\begin{aligned} \mathbb {I}_{\text {p}}=\left[ \begin{array}{ccccccc} 0 &{} 0 &{} 0 &{} &{} \ldots \\ 1 &{} 0 &{} 0 &{} &{} \ldots \\ 0 &{} 0 &{} 0 &{} &{} \ldots \\ 0 &{} 1 &{} 0 &{} &{} \ldots \\ 0 &{} 0 &{} 0 &{} &{} \ldots \\ &{} \vdots &{} &{} \ddots &{} &{} \vdots \\ &{} &{} \ldots &{} &{} 0 &{} 0\\ &{} &{} \ldots &{} &{} 0 &{} 1 \end{array}\right] . \end{aligned}$$

• initial tractions vector

  $$\begin{aligned} \mathbf {T}_{o}=\left[ \begin{array}{ccccccc} \tau _{1}^{o}&\sigma _{1}^{o}&\tau _{2}^{o}&\sigma _{2}^{o}&\ldots&\sigma _{N}^{o} \end{array}\right] ^{\text {T}}. \end{aligned}$$

• Lubrication finite-difference matrix (non-linearly dependent on the current opening displacement discontinuities)

  $$\begin{aligned} \mathbb {L}({\varvec{\delta }{}^{(k)}})=\left[ \begin{array}{ccccc} \ddots &{} &{} &{} &{} 0\\ &{} \ddots \\ 0 &{} -\frac{C_{i-1/2}}{h_{i-\nicefrac {1}{2}}} &{} \left( \frac{C_{i+1/2}}{h_{i+\nicefrac {1}{2}}} +\frac{C_{i-1/2}}{h_{i-\nicefrac {1}{2}}}\right) &{} -\frac{C_{i+1/2}}{h_{i+\nicefrac {1}{2}}} &{} 0\\ &{} &{} &{} \ddots \\ 0 &{} &{} 0 &{} -\frac{C_{N-1/2}}{h_{N-\nicefrac {1}{2}}} &{} \frac{C_{N-1/2}}{h_{N-\nicefrac {1}{2}}} \end{array}\right] , \end{aligned}$$

  where $h_{i\pm \nicefrac {1}{2}}=\frac{h_{i}+h_{i\pm 1}}{2}$ is the neighboring element centroid distance.

• local volume increment

  $$\begin{aligned} \mathbb {I}_{s}=\left[ \begin{array}{ccccccccc} 0 &{} h_{1} &{} 0 &{} 0 &{} 0 &{} &{} \ldots \\ 0 &{} 0 &{} 0 &{} h_{2} &{} 0 &{} &{} \ldots \\ 0 &{} 0 &{} &{} &{} \ddots &{} &{} &{} 0\\ &{} \vdots &{} &{} &{} 0 &{} h_{i} &{} 0 &{} &{} \vdots \\ &{} \vdots &{} &{} &{} &{} &{} \ddots &{} &{} \vdots \\ &{} \ldots &{} &{} &{} &{} &{} 0 &{} 0 &{} h_{N} \end{array}\right] ; \end{aligned}$$

• the fracture local volume matrix

  $$\begin{aligned} \mathbb {I}_{c}=\left[ \begin{array}{cccccc} h_{1}\delta _{1}^{n} &{} 0 &{} 0 &{} \ldots \\ 0 &{} h_{2}\delta _{2}^{n} &{} 0 &{} \ldots \\ \vdots &{} &{} \ddots &{} \vdots \\ \ldots &{} &{} 0 &{} h_{N}\delta _{N}^{n} \end{array}\right] ; \end{aligned}$$

• and the inlet flow rate vector (entering the different fractures)

  $$\begin{aligned} \mathbf {Q}=\left[ \begin{array}{ccccccccccccccc} 0&\ldots&0&\widetilde{Q}_{1}&0&\ldots&0&\widetilde{Q}_{2}&0&\ldots&0&\widetilde{Q}_{N_{\text {frac}}}&0&\ldots&0 \end{array}\right] ^{\text {T}} \end{aligned}$$

  where $Q_{w_{I}}=\widetilde{Q}_{I}=\nicefrac {Q_{I}}{H}, \quad I=1,\ldots ,N_{\text {frac}}.$

The superscripts (k) and $(k-1)$ correspond to the current and the previous time-steps. At each time-step, the mixed system is solved iteratively using fixed-point iterations, with back-substitution of the new estimate of $\delta _{i}^{n}$ into the matrices $\mathbb {I}_{c}$ and $\mathbb {L}$ via the conductivity coefficients $C_{i+1/2}$ and $C_{i-1/2}$. The matrices $\mathbb {A}$, $\mathbb {I}_{\text {p}}$, and $\mathbb {I}_{s}$ do not change for a fixed fractures’ geometry. Convergence is achieved when the relative difference of the solution for the increment of DDs and fluid pressure between two subsequent iterations is below $10^{-5}$–$10^{-6}$. Convergence of such non-linear system typically takes between five and ten fixed-point iterations.

3.1.1 Fracture Propagation

Once a fracture is initiated, we assume quasi-static equilibrium $K_{I}=K_{\text {Ic}}$ (yet, $K_{I}$ can be less than $K_{\text {Ic}}$ for an arrested fracture). To solve for the advancement of each hydraulic fracture tips, we use an approach combining an explicit scheme for the propagation direction (updated at the end of every time-step) and an implicit algorithm to obtain the increment of fracture length during the time-step.

We determine at the end of the time-step (i.e., when the solution has converged) the new propagation direction for each fracture tip using the maximum tensile stress direction. To do so, we minimize the dot product of the proposed direction of propagation and the first principal stress direction at a finite distance from the tip node (1.5 element size). This minimization is performed iteratively using a classical quasi-Newton method with bracketing. Once determined, the propagation direction (for all the different fracture tips) for the next time-step is fixed.

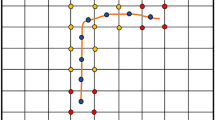
Over one time-step (with a given propagation direction for each tip), the increment of fracture length is obtained implicitly using an one-dimensional approach similar to the implicit level set algorithm (ILSA) originally developed in Peirce and Detournay (2008). Such an implicit scheme relies on the use of a survey element located just behind the tip element (see Fig. 2). Knowing the width of this survey element, we invert the hydraulic fracture tip asymptotic solution to estimate the new distance from this survey element to the fracture tip. The width in the tip element is then imposed according to the near-tip asymptote, and the elasto-hydrodynamic system is resolved with this new trial position of the fracture tips. This is repeated until convergence of the new position of the fracture tips in relative term between two subsequent iterations. A tolerance of $10^{-3}$ is used.

The determination of the new distance between the survey point (where width is known) and the fracture tip relies on the inversion of the near-tip asymptote (which provide width as function of distance to the fracture tip). Since the near-tip behavior of a hydraulic fracture is intrinsically multi-scale (Garagash et al. 2011); using the classical linear elastic fracture mechanics (lefm) square root asymptote may lead to over-estimation of the distance from the ribbon element to the tip and, subsequently, to non-physical oscillations in the solution (Lecampion et al. 2013). To avoid these numerical effects, the fracture mesh should be sufficiently fine to capture the region of validity of lefm asymptote (at least the cell size should be less than the characteristic lefm-viscous transition scale $\ell _{mk}\propto \dfrac{K_{\text {Ic}}^{6}}{E'^{4}\mu ^{2} v_{\text {tip}}^{2}}$). This can considerably raise computational costs (Lecampion et al. 2013, 2018). The use of the complete tip asymptote (Garagash et al. 2011; Dontsov and Peirce 2015, 2017), which covers the different asymptotic regions (toughness-, viscosity-, and leak-off-dominated regimes) as well as the transition between them, helps to relieve requirements on the mesh. Since this tip asymptotic solution is given as an implicit function of the current fracture velocity, its inversion (i.e., knowing the opening and inverting for the corresponding distance to the tip) is performed via a root-finding scheme. We use here a Brent root-finding method (see, e.g., Quarteroni et al. 2000). More details on the inversion of such tip asymptotic solution can be found in Peirce and Detournay (2008), Peirce (2015), and Lecampion and Desroches (2015c) notably.

Fig. 2

Schematic of the fracture mesh: tip region and ribbon element and evolution of the fracture tip position over a time-step. The ribbon element allows to couple the tip region [where the solution follows the near-tip hydraulic fracture asymptotes (Garagash et al. 2011)] with the rest of the fracture (e.g., channel region). The number of elements in the tip region can increase during a propagation step

3.2 Wellbore Flow and Fracture Entry Flow Coupling

3.2.1 Wellbore Flow Solver

The wellbore fluid flow mass balance equation (5) is discretized using a classical finite volume approach with piece-wise approximation of fluid pressure similar to the one described above for the lubrication in the fracture(s). One difference is that the radius and the cross-section of the well are assumed to not change due to the well pressurization, and thus, no hydro-mechanical coupling is needed. Another difference is the use of Darcy friction factor approach to determine the cross-sectional conductivities $C_{i\pm \nicefrac {1}{2}}$ for laminar, turbulent, or transient flow regime (indeed, Poiseuille model corresponds to laminar regime with $f=\dfrac{64}{Re}$). We obtain for element i along the curvilinear 1D mesh of the well:

$$\begin{aligned}&\varDelta s_{i}A_{i}c_{f}\times \frac{p_{i}^{(k)}-p_{i}^{(k-1)}}{\varDelta t}+q_{i+\nicefrac {1}{2}}-q_{i-\nicefrac {1}{2}}\nonumber \\&\quad =Q_{o}\delta (s_{i})-\sum _{I=1}^{N}Q_{I}\delta (s_{i}-s_{I}), \end{aligned}$$

(18)

where

$$\begin{aligned} q_{i\pm \nicefrac {1}{2}}= \,& {} A_{i\pm \nicefrac {1}{2}}V_{i\pm \nicefrac {1}{2}} \end{aligned}$$

(19)

$$\begin{aligned} V_{i+\nicefrac {1}{2}}= & {} -\frac{4a_{i+\nicefrac {1}{2}}}{\rho f(Re,\epsilon )|V_{i+\nicefrac {1}{2}}|}\times \frac{\widetilde{p}_{i+1}^{(k)}-\widetilde{p}_{i}^{(k)}}{(\varDelta s_{i}+\varDelta s_{i+1})/2}; \end{aligned}$$

(20)

$\varDelta s_{i}$ is the length of the i-th element and $\widetilde{p}$ denotes the fluid pressure in excess over the hydrostatic pressure: $\widetilde{p}=p-p_{H}$. The superscripts (k) and $(k-1)$ correspond to the current and the previous time-steps. At each time step, Eq.  (18) is solved by fixed-point iterations, while back-substituting the average velocity V re-calculated via Eq. (20) into (19). The friction factor f is also updated, since it depends on the Reynolds number. At each iteration, one has to solve a linear system with a three-band matrix constructed similarly to the lubrication matrix $\mathbb {L}$ (see above) with the well over-pressure increment $\varDelta {\tilde{\mathbf {p}}_{ w }^{{ (k) }}}= \ {\tilde{\mathbf {p}} _{ w }^{{ (k) }}}- {\tilde{\mathbf {p}} _{ w }^{{ (k-1) }}}$ as the primary unknowns:

$$\begin{aligned} \left( c_{f}\mathbb {I}_{cw}+\varDelta t\mathbb {L_{ w }}\right) \cdot \varDelta {\tilde{\mathbf {p}} _{ w }^{{ (k) }}}=\varDelta t\mathbf {Q}-{\Delta t }\mathbb {L_{ w }}\cdot {\tilde{\mathbf {p}}_{ w }^{{ (k-1) }}}, \end{aligned}$$

(21)

with

$$\begin{aligned} \mathbb {I}_{cw}= \,& {} \left[ \begin{array}{ccccc} \varDelta s_{1}A_{1} &{} 0 &{} \ldots \\ 0 &{} \ddots &{} 0\\ \vdots &{} 0 &{} \varDelta s_{1}A_{i} &{} 0 &{} \vdots \\ &{} &{} 0 &{} \ddots &{} 0\\ &{} &{} \ldots &{} 0 &{} \varDelta s_{1}A_{N_{w}} \end{array}\right] ,\\ A_{i}= \,& {} \frac{A_{i+\nicefrac {1}{2}}+A_{i-\nicefrac {1}{2}}}{2}\\ \mathbb {L}_{ w }= \,& {} \left[ \begin{array}{ccccc} \ddots &{} &{} &{} &{} 0\\ &{} \ddots \\ 0 &{} -\frac{C^w_{i-\nicefrac {1}{2}}}{\widetilde{h}_{i-\nicefrac {1}{2}}} &{} \left( \frac{C^w_{i+\nicefrac {1}{2}}}{\widetilde{h}_{i+\nicefrac {1}{2}}}+\frac{C^w_{i-\nicefrac {1}{2}}}{\widetilde{h}_{i-\nicefrac {1}{2}}}\right) &{} -\frac{C^w_{i+\nicefrac {1}{2}}}{\widetilde{h}_{i+\nicefrac {1}{2}}} &{} 0\\ &{} &{} &{} \ddots \\ 0 &{} &{} 0 &{} -\frac{C^w_{N_{w}-\nicefrac {1}{2}}}{\widetilde{h}_{N_{w}-\nicefrac {1}{2}}} &{} \frac{C^w_{N_{w}-\nicefrac {1}{2}}}{\widetilde{h}_{N_{w}-\nicefrac {1}{2}}} \end{array}\right] , \end{aligned}$$

where

$$\begin{aligned} \widetilde{h}_{i\pm \nicefrac {1}{2}}= \,& {} \frac{\varDelta s_{i}+\varDelta s_{i\pm 1}}{2},\quad C^w_{i\pm 1/2}=-\frac{4a_{i\pm \nicefrac {1}{2}}A_{i\pm \nicefrac {1}{2}}}{\rho f(Re_{i\pm \nicefrac {1}{2}},\epsilon )|V_{i\pm \nicefrac {1}{2}}|}, \\ Re_{i\pm \nicefrac {1}{2}}= \,& {} \frac{2\rho a_{i\pm \nicefrac {1}{2}}|V_{i\pm \nicefrac {1}{2}}|}{\mu }. \end{aligned}$$

We have used here Churchill (1977) approximation which provides an explicit equation for the friction factor $f(Re,\epsilon )$.

3.2.2 Wellbore Fractures Entry

In Eqs. (15) and (18), the volume rates $Q_{i}$ entering each fracture are assumed to be known at each time step. In case of injection into multiple fractures via the well, to close the system of equations, one needs to relate these volume rates to the entry pressures in each fracture, which are parts of the solution of the results of the mixed elasto-hydrodynamics system, and the pressure in the corresponding well locations. It is performed via introducing the pressure drop associated with perforations and near-wellbore tortuosity of the fractures (entry friction):

$$\begin{aligned} \varDelta p_{I}(Q_{I})&=p_{w,I}(Q_{I})-p_{f,I}(Q_{i})=f_{p,I}Q_{I}^{2}+f_{t,i}Q_{I}^{\beta _{I}},\nonumber \\ I&=1,\ldots ,N_{\text {frac}}, \end{aligned}$$

(22)

where $f_{p,I}$ and $f_{t,i}$ can vary from perforation clusters to clusters. In all the examples presented further, we assume zero near-wellbore tortuosity, i.e., $f_{t,i}=0$.

The solutions of the elasto-hydrodynamics equations in the different fractures of the fluid flow in the wellbore and the coupling via fracture entry friction can be represented schematically as the following system of residuals:

$$\begin{aligned} {\mathscr{R}}_{f}({\mathbf{Q}})={\mathbf {p}}_{ f },\quad {\mathscr{R}}_{w}({\mathbf{Q}})={\mathbf{p}}_{w} ,\quad {\mathscr{C}}({\mathbf{p}}_{w}, {\mathbf{p}}_{ f })={\mathbf{Q}}. \end{aligned}$$

(23)

This system of non-linear equations that solves for pressure (and DDs) in the fracture, in the well, as well as the flow rate entering the different fractures is actually extremely stiff. Practically, fixed-point iterations on these equations do not converge. We, therefore, use a quasi-Newton scheme, which involves finite-difference estimation of the Jacobian matrix. To reduce the time needed for re-calculation of the Jacobian matrix (at the price of some reduction of convergence rate), the latter is re-used in several (in our implementation, up to 4) iteration steps.

4 Verifications

4.1 Toughness- and Viscosity-Dominated Plane-Strain Benchmark (KGD Geometry)

First, two verification tests of spanning toughness and viscosity-dominated propagation have been performed with two fractures of sufficiently large height (100 m) located far enough from each other (1000 m) to ensure (1) that any stress interaction between them is negligible and (2) that the fracture geometry can be assumed to be in state of plane strain. The flow rates entering both fractures were forced to be equal (i.e., wellbore flow was not considered). We compare our results to the known semi-analytical solutions for a plane-strain hydraulic fracture propagating in both the viscosity (Garagash and Detournay 2005) and toughness-dominated regimes (Garagash 2006).

The parameters for the toughness-dominated case were as follows: $E^\prime =10\,\text {GPa}$, $\mu =0.01\,\text {Pa s}$, $K_{\text {Ic}}=2\,\text {MPa}\,\text {m}^{1/2}$ , $Q_{o}\,\text {(per unit height)}=0.0001\,\text {m}^{2}/\text {s}$ (which corresponds to a dimensionless viscosity $\mathscr {M}=12\mu Q_{o}E'^{3}/K'^{4}=0.0072$—see Detournay (2004) for definition). As can be seen in Figs. 3 and 4, the accuracy of the scheme is excellent with at most 5% error compared to the analytical solution.

Fig. 3

Toughness-dominated fracture propagation of two far-apart hydraulic fractures (constant equal rate): fracture length vs. time (for the four different tips); numerical vs. analytical solution. Relative error in inset

Fig. 4

Toughness-dominated fracture propagation of two far-apart hydraulic fractures (constant equal rate): a inlet pressure vs. time; b inlet width vs time; numerical vs. analytical solution. Relative error in insets

For the viscosity-dominated example, the parameters were set as follows: $E^\prime =10\,\text {GPa}$, $\mu =0.1\,\text {Pa s}$, $K_{\text {Ic}}=0.5\,\text {MPa m}^{1/2}$, $Q_{o}=0.0001\,\text {m}^{2}/\text {s}$ ($\mathscr {M}=18.5$). Except for an early transient associated with the initial conditions set in the scheme, the agreement between the numerical results and the semi-analytical solution is always below 4% of relative error, both on inlet pressure, width and fracture length as can be seen in Figs. 5 and 6.

Fig. 5

Viscosity-dominated fracture propagation of two far-apart hydraulic fractures (constant equal rate): fracture length vs. time; numerical vs. analytical solution. Relative error in inset

Fig. 6

Viscosity-dominated fracture propagation of two far-apart hydraulic fractures (constant equal rate): a inlet pressure vs. time; b inlet width vs time; numerical vs. analytical solution. Relative error

4.2 Viscosity-Dominated KGD-to-PKN Transition

This test was performed for a single fracture of constant height $H=10\,m$ and initial length $L_{0}=1\,m$, ensuring that the injection time is long enough for the fracture to evolve to a final length much larger than its height. The aim is here to observe the transition from an initially plane-strain (KGD) geometry where the fracture height is much larger than its length to a blade-like (PKN) geometry at large time/for large length compared to height. The other parameters were set as follows: rock properties $E=25\,\text {GPa}$, $\nu =\,0.3$, $K_{\text {Ic}}=\,1\,\text {MPa m}^{1/2}$, zero leak-off, confining stress $\sigma _{h}=\,10\,\text {MPa}$, $\sigma _{H}=\,12\,\text {MPa}$, injection fluid viscosity $\mu =0.01\,\text {Pa s}$, and entry rate $Q=\,0.05\,\text {m}^3/\text {s}$ ($\sim 20\,\text {BPM}$). It is interesting to note that for such a choice of parameters, the propagation of the hydraulic fracture is viscosity dominated for the plane-strain geometry. We compare here the numerical results, therefore, to the viscosity-dominated KGD solution and the classical PKN/blade-like solution which does not account for toughness (and is, thus, restricted to the viscosity-dominated regime).

As can be seen in Fig. 7, the scheme properly captures the transition between the KGD geometry solution (where the height of the fracture is much larger than its length) and the PKN solution (solution for a constant height fracture).

Fig. 7

KGD-to-PKN transition (viscosity-dominated regime), numerical vs. analytical solutions: a fracture length vs. time; b fracture inlet opening vs. time

5 Competition Between Stage Length, Entry Friction, and Stress Interaction

We now turn to study the competing effects of the length of the stage, stress interaction between fractures (stress shadowing), and entry friction on the uniform versus non-uniform growth of multiple fractures during a stages. We focus our numerical investigation to the case of three fractures and a wellbore aligned with the minimum principal horizontal stress for the sake of simplicity. We first discuss via scaling arguments the controlling dimensionless parameters governing the simultaneous growth of multiple hydraulic fractures.

5.1 Scaling Arguments

One can argue that, in case of a homogeneous medium and small/negligible leak-off, 11 parameters define the problem:

$$\begin{aligned} E^\prime ,\nu ,\,\,K_{\text {Ic}},\,\mu ,\,f_{\text {p}},\,S,\,H,\,N_{\text {frac}},\,\sigma _{H}-\sigma _{h},\,Q_{o},\,t, \end{aligned}$$

(24)

where S denotes the spacing between fractures along the wellbore, and $\sigma _{\text {H}}$ and $\sigma _{\text {h}}$ are the maximum and minimum principal horizontal stress magnitude.

From the Buckingham-Pi theorem, we thus see that at most 7 dimensionless parameters control the problem. Moreover, focusing on viscosity-dominated regime, only six dimensionless parameters define the parametric space. In other words, the dimensionless solution of the problem (represented as $\varPhi$) depends on the following dimensionless parameters:

$$\begin{aligned}&\varPhi =\varPhi \Big (\nu ,\; N_{\text {frac}},\;\frac{S}{h},\;\mathscr {K}^{KGD} = \frac{K'}{(E'^3\,Q_o\,\mu )^{1/4}}, \nonumber \\&\frac{\sigma _{H}-\sigma _{h}}{K_{\text {Ic}}}\sqrt{S},\; \varGamma =\frac{\sigma _{\text {int}}}{f_{\text {p}}(Q_{o}/N_{\text {frac}})^{2}} ,\nonumber \\&\varPi =\frac{\varDelta P_{\text {well}}}{f_{\text {p}}(Q_{o}/N_{\text {frac}})^{2}} \Big ). \end{aligned}$$

(25)

The $\varGamma$ parameter expresses the ratio of characteristic interaction stress $\sigma _{\text {int}}$ to the pressure drop due to perforation friction (at the well—fracture connection) at the time when the length of the fracture(s) L is of the same order as spacing S:

$$\begin{aligned} \varGamma=\, & {} \frac{\sigma _{\text {int}}}{f_{\text {p}} Q_n^2} = \frac{E'<w>L\,H}{4 \pi \,S^3\,f_{\text {p}}\,Q_n^2} = \frac{E'\,Q_n\,t}{4 \pi \,S^3\,f_{\text {p}}\,Q_n^2};\nonumber \\ Q_n= & {} \frac{Q_o}{N_{\text {frac}}}. \end{aligned}$$

(26)

The time t when the length of the fracture(s) L is of the same order as spacing S can be estimated by order of magnitude from the system parameters using the estimate of L for a specific geometry and regime of propagation (Detournay 2004; Garagash and Detournay 2005; Garagash 2006). Thus, for a KGD fracture geometry ($L \ll H$) propagating in the toughness-dominated regime, we obtain the following estimate for $\varGamma$ that we denote $\varGamma _k^{(KGD)}$:

$$\begin{aligned} L \sim \left( \frac{E'(Q_n/H)}{K'}\right) ^{2/3}t^{2/3}; \quad \varGamma _k^{(KGD)} = \frac{K' H}{4 \pi \,f_{\text {p}}\,Q_n^2\,S^{3/2}}. \end{aligned}$$

(27)

For viscosity-dominated regime in KGD geometry ($L \ll H$), we obtain the following estimate for $\varGamma$ that we denote $\varGamma _{m}^{(KGD)}$:

$$\begin{aligned} L \sim \left( \frac{E'(Q_n/H)^3}{12 \mu }\right) ^{1/6}t^{2/3}; \quad \varGamma _{m}^{(KGD)} = \frac{\left( 3 E'^3\,\mu \,H^3\right) ^{1/4}}{2 \sqrt{2} \,\pi \,f_{\text {p}}\,Q_n^{7/4}\,S^{3/2}}. \end{aligned}$$

(28)

For a PKN geometry ($L \gg H$) (see, e.g., Kemp (1990); Economides and Nolte (2000)), we have the following estimate for $\varGamma$ that we denote $\varGamma _{m}^{(PKN)}$:

$$\begin{aligned} L \sim \left( \frac{E'\,Q_n^3}{4 \pi ^3\,\mu \,H^4}\right) ^{1/5}t^{4/5}; \quad \varGamma _{m}^{(PKN)} = \frac{E'^{3/4}\,\mu ^{1/4}\,H}{2 \sqrt{2} \,\pi ^{1/4}\,f_{\text {p}}\,Q_n^{7/4}\,S^{7/4}}. \end{aligned}$$

(29)

Note that in Eqs. (28) and (29), all power exponents are the same except those of S and H. In the following, we use the PKN estimate dropping the factor ${2 \sqrt{2} \,\pi ^{1/4} }$ (which is of order 1) to quantify such competition between stress interactions and perforation friction, and thus choose:

$$\begin{aligned} \varGamma _{m}^{(PKN)} =\varGamma _{m} = \frac{E'^{3/4}\,\mu ^{1/4}\,H}{f_{\text {p}}\,Q_n^{7/4}\,S^{7/4}}. \end{aligned}$$

(30)

The $\varPi$ parameter expresses the ratio of the pressure drop between clusters in the well to the pressure drop due to perforation friction. The order of magnitude of the pressure drop along the well (in steady-state conditions) can be estimated as $\varDelta P^{(well)} \sim \rho Q_o^2 S Re^{-\beta }/D^5$ where $\beta$ depends on the flow regime in the well (turbulent vs laminar). The friction factor scales as $f\propto Re^{-\beta }$. The pressure drop across the perforation scales as $\varDelta P^{(perf)} \sim f_{\text {p}} (Q_o/N_{\text {frac}})^2$. We can thus estimate $\varPi$ as:

$$\begin{aligned} \varPi _{\beta }= \,& {} \frac{\varDelta P^{(\text {well})}}{\varDelta P^{(\text {perf})}} = \frac{\rho \,S\,Q_o^2\,Re^{-\beta }/D^5}{f_{\text {p}} (Q_n)^2}\nonumber \\= \,& {} \frac{\rho \,S\,N_{\text {frac}}^2\,Re^{-\beta }}{D^5\,f_{\text {p}}}; \quad Re=\frac{\rho Q_o}{\mu D}. \end{aligned}$$

(31)

In the following, we use $\beta = 1/4$ corresponding to the fully turbulent scaling of Blasius (1913), valid for turbulent flow in a smooth pipe. This assumption is realistic for industrial hydraulic fracturing conditions.

5.2 Numerical Simulations

In these simulations, we considered three fractures initiated from the horizontal part of the well at a depth of $1\,km$; the height of the fractures was taken to $H=20\,m$ and the initial half-length of the fractures as $L_{0}=2.5\,\text {m}$. The following rock properties were assumed: $E=25\,\text {GPa}$, $\nu =0.2$, $K_{\text {Ic}}=1\,\text {Mpa m}^{1/2}$, negligible leak-off. The other parameters are as follows: in-situ minimum and maximum compressive stresses $\sigma _{h}=10\,\text {MPa}$, and $\sigma _{H}=10.1$–$\,12\,\text {MPa}$, injection fluid viscosity $\mu =0.01\,\text {Pa s}$, and pump rate $Q=0.15\,\text {m}^3/\text {s}\;(0.05\,\text {m}^3/\text {s}\text { per fracture})$. The entry friction $f_{\text {p}}$ was the same for all clusters. We varied its value between $10^{2}$ and $10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$ (from small to large friction). The injection time was limited to 5 min for all cases. To account for pressure drop between the clusters numerically, the mesh density for the well flow solver was chosen to provide about ten cells between the clusters in all the considered cases of cluster spacing. The geometry of the well and location of the clusters are sketched in Fig. 1.

Here, we provide detailed results on fracture growth and fluid partitioning for some extreme cases: close ($S=10\,\text {m}$) and far ($S=40\,\text {m}$) cluster spacing, low ($f_{\text {p}}=10^{2}\,{\text {Pa}}\,({\text {s/m}}^{3})^{2}$), and high ($f_{\text {p}}=10^{9}\,{\text {Pa}}\,({\text {s/m}}^{3})^{2}$) perforation friction, low ($\sigma _{H}/\sigma _{h}=1.01$) and high ($\sigma _{H} / \sigma _{h}=1.2$) in-situ stress contrast). Figures 8, 9, 10, 11 illustrate the case of initial fracture spacing of 10 m ($S/H = 0.5$). Figure 12 illustrate the case of initial fracture spacing of 40 m ($S/H = 2$).

Fig. 8

Top view of fractures after 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=10.1$ MPa, fracture height $H=20$ m, and initial fracture spacing $S=10$ m; perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$ , b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$. Scales in meters

Fig. 9

Fracture volume rate evolution during 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=10.1$ MPa, fracture height $H=20$ m, and initial fracture spacing $S=10$ m; perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$ , b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$

Fig. 10

Top view of fractures after 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=12$ MPa, fracture height $H=20$ m, initial fracture spacing $S=10$ m, and perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$; b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$. Scales in meters

Fig. 11

Fracture volume rates evolution during 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=12$ MPa, fracture height $H=20$ m, initial fracture spacing $S=10$ m, and perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$; b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$

As seen in these figures, in general, high perforation friction promotes even fluid partitioning and high in-situ stress contrast suppresses fracture curving due to stress interaction. Note the change in localization pattern as the in-situ stress contrast grows.

With increasing cluster spacing/stage length, the moderating effect of perforation friction starts to concede to the effect of pressure gradient in the well (Figs. 13, 14, 15).

Fig. 12

Top view of fractures after 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=10.1$ MPa, fracture height $H=20$ m, initial fracture spacing $S=40$ m, and perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$; b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$. Scales in meters

Fig. 13

Fracture volume rate evolution during 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=10.1$ MPa, fracture height $H=20$ m, initial fracture spacing $S=40$ m, and perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$; b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$

Fig. 14

Top view of fractures after 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=12$ MPa, fracture height $H=20$ m, initial fracture spacing $S=40$ m, perforation friction a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$ , b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$. Scales in meters

Fig. 15

Fracture volume rates during 5 min of injection; confining stress $\sigma _{h}=10$ MPa, $\sigma _{H}=12$ MPa, fracture height $H=20$ m, initial fracture spacing $S=40$ m, and perforation friction: a$f_{\text {p}}=10^{2}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$; b$f_{\text {p}}=10^{9}\,\text {Pa}\,(\text {s}/\text {m}^3)^{2}$

5.3 Short Summary

To summarize these results, let us study the effect of the most important dimensionless parameters ($\varGamma _{m}$ and $\varPi _{\beta }$) on variation (relative standard deviation) of fractures’ length and injected volumes after given time of injection.

Fig. 16

Effect of parameter $\varGamma _{m}$ on localization of fracture growth (relative standard deviation of length after 5 min of injection)

Fig. 17

Effect of parameter $\varGamma _{m}$ on fluid partitioning (relative standard deviation of injected volume after 5 min of injection)

As one can see from Figs. 16 and 17, in general, at values of $\varGamma _{m} \ll 1$, fracture growth/fluid partitioning is equalized; localized growth/fluid partitioning occurs at values of $\varGamma _{m}>1$; for larger $\varGamma _{m}$, the values of $\delta L/<L>$ and $\delta Q/<Q>$ stay around 25–30% showing some noticeable but minor effect of cluster spacing and in-situ stress contrast. Yet, the parameter $\varGamma _{m}$ does not fully account for the effect of cluster spacing/stage length (and the corresponding pressure gradient in the well) on fracture localization. For larger spacing, localization occurs at smaller values of $\varGamma _{m}$.

Figures 18, 19 show the variation of L and Q against the parameter $\varPi _{\beta }$ (scaled pressure drop between the clusters).

Fig. 18

Effect of parameter $\varPi _{\beta }$ on localization of fracture growth (relative standard deviation of length after 5 min of injection)

Fig. 19

Effect of parameter $\varPi _{\beta }$ on fluid partitioning (relative standard deviation of injected volume after 5 min of injection)

5.4 Neglecting Stage Length-Related Effects

This configuration corresponds to the case of a relatively short stage length, such that the pressure gradient along the well can be neglected. To do so, we coarsen the 1D wellbore mesh to fit all clusters in one element, so the pressure in all cluster entries (on the well side) is equal, since a piece-wise approximation is used for pressure in the well.

The results on variation of injected volume between the clusters with and without the effect of pressure gradient along the well are displayed in Fig. 20.

Fig. 20

Effect of parameter $\varGamma _{m}$ on fluid partitioning (relative standard deviation of injected volume after 5 min of injection) with pressure gradient in the well-neglected (dashed lines) and accounted for (solid lines)

It is clear from these results that when the pressure gradient along the well is neglected, the variation of injected volume between fractures is under-predicted even in case of relatively close cluster spacing. The larger the cluster spacing, the larger the discrepancy.

Here, we should recall that in case of too small a ratio of fracture spacing to fracture height (less than 0.25), the chosen elastic kernel fails to produce trustworthy results for elasticity (see Wu and Olson 2015a) making it hard to explore the cases with shorter stage length. Yet, the above considered range of ratios of cluster spacing and fracture/reservoir height were chosen to reflect typical values for industry applications, thus, the given example is a good demonstration of importance of the wellbore- and stage length-related effects on fluid partitioning and localization of the fracture growth.

6 Conclusions

We have developed a fully coupled numerical solver for the simultaneous propagation of multiple blade-like hydraulic fractures due to fluid injection in a horizontal well. The proposed scheme properly solves the fluid partitioning problem at any given time by coupling wellbore flow and hydraulic fracture propagation.

Our results are in line with the previous studies restricted to the growth of simultaneous radial hydraulic fractures (see Lecampion and Desroches 2015c, b) that were intrinsically confined to the early stage of growth (axisymmetric fractures).

Low entry friction [large $\varGamma _{m}$ dimensionless parameter defined in Eq. (30)] promotes uneven fluid partitioning and fracture growth localization; generally, for $\varGamma _{m} \ll 1$, fluid partitioning and fracture growth are even, yet the boundary between uniform and non-uniform growth depends on the stage length [the $\varPi _\beta$ dimensionless parameter defined in Eq. (31)]. On the other hand, the effect of parameter $\varPi _{\beta }$ on fluid partitioning and fracture length shows little-to-no dependence on $\varGamma _{m}$. For low in-situ stress differential ($\sigma _{\text {H}} \sim \sigma _{\text {h}}$), fracture curving helps balancing the flow rate between the fractures, as stress interactions between the growing fractures decrease as they move away from one another. Yet, the effect of in-situ stress/fracture curving on variation of fluid entry rates and fractures length is minor compared to the first two. However, as expected, the pattern of fracture growth is highly sensitive to the in-situ stress contrast and entry friction. Notably, large entry friction appears to always counteract the adverse effect of stress interaction between the fractures, yet the pressure drop along the stage (i.e., the length of the stage) can have a more pronounced negative effect than the stress interaction on fluid partitioning. As a result, one cannot disregard it to obtain a proper picture of fluid partitioning and growth of multiple fractures during a pumping stage.

In this contribution, we restricted our numerical investigations to the case of even (spatially homogeneous) entry friction. However, the fluid partitioning and the consequent fractures’ propagation rates will most likely be highly sensitive to spatial variations of the entry friction, especially the term associated with near-wellbore-fracture tortuosity. Such variations are likely to happen and hard to control (see the examples reported in Desroches et al. (2014); Lecampion and Desroches (2015a)). Investigation of the effect of heterogeneous entry friction should be investigated further.

We should also highlight the importance of accurate coupling of the fractures propagation with the wellbore fluid flow: being a non-linear process that directly controls the fluid partitioning, it is particularly hard to handle numerically: precision is crucial to handle such a stiff non-linearity. On one hand, simple fixed-point iteration schemes for such non-linear coupling are typically unstable. On the other hand, evaluation of the partial derivatives of pressure vs. entry rates (to implement a quasi-Newton or higher order iteration scheme) is necessarily numerical (and, therefore, costly) due to the non-local nature of the fracture propagation process. We believe that more work is required to speed up the solution of such highly non-linear problems (e.g., a typical simulation reported in Sect. 5.2 run for about 5 h on a 10 cores desktop) while keeping the robustness of the solver presented here.