Rock Cutting Experiments with an Actuated Disc

Abstract

This paper reports the results of actuated disc cutting (ADC) experiments, conducted with an instrumented tabletop ADC rig on a soft limestone. The experiments were designed to assess the predictions of an ADC model (Dehkhoda and Detournay in Rock Mech Rock Eng 50(2):465–483, 2016) and the validity of the assumptions on which the model is constructed, in particular the invariance of the specific energy on actuation. All the experiments were conducted at the same depth of cut, which was selected to ensure a brittle mode of failure, characterized by the formation of chips. By changing the disc size and actuation amplitude, as well as the actuation frequency and the cartridge velocity, the experiments covered a large enough range of the two numbers controlling the cutting response, to rigorously test the theoretical model and its assumptions. Analyses of the experimental data show in general good agreement with the theoretical predictions, in particular the decrease of the thrust force with increased actuation and the partitioning of the external power between actuation of the disc and translation of the cartridge. The experimental results do not show any significant dependence of the specific energy on actuation.

1 Introduction

Mechanization of hard rock excavation in mining and civil engineering projects has to address the twofold challenge of large thrust forces and rapid wear of the cutters. These two issues impose restrictions to the application of conventional cutting tools—either rolling disc cutters that are pressed against the rock, or picks that are dragged along the rock surface—to hard rock excavation. Indeed, the susceptibility of picks to wear and failure restrict their use to low-to-medium strength and non-abrasive rocks, while the very high thrust forces required for roller disc cutter limit their use to civil projects, where large and heavy machines can be deployed.

The undercutting concept that uses a rolling disc as a drag tool and its extension to actuated disc cutting have been proposed as alternative methods for the mechanized excavation of hard rocks. In actuated disc cutting, an additional mechanism forces an off-centric revolution of the disc cutter around a secondary axis, as it is linearly dragged on the rock surface. These alternative methods combine the advantages of roller cutters (low wear rate) and drag picks (low cutting forces). Particular realizations of the actuated undercutting concept exist in large scale laboratory equipment and field prototypes (Hood et al 2005; Karekal 2013; Pickering and Ebner 2002) based on the original concept of Sugden (2005), as well as in industrial equipments (Pickering et al 2006; Sandvik-Mining 2012; de Andrade et al 2011; Anonymous 2014).

Interest in the concept of actuated disc cutting stems from experimental results showing strong evidence of a reduction of the thrust force when the cutter is actuated (Hood et al 2005; Hood and Alehossein 2000). The root cause of this reduction is, however, still under debate. On the one hand, it has been speculated that this force reduction reflects a decrease of the energy required to fragment the rock due fatigue cracking caused by cyclic loading (Hood and Alehossein 2000). On the other hand, kinematical models, based on simple cutter/rock interface laws and on the critical assumption that the specific energy is not affected by actuation, also predicts a decrease of thrust force with increasing actuation. This result also reflects an increase of the power to actuate the disc, which is not required in drag cutter (Kovalyshen 2015; Dehkhoda and Detournay 2016). Although analysis of existing laboratory data showed that the reduction of the thrust force with actuation was consistent with the prediction of a kinematical model (Dehkhoda and Detournay 2016), it was not possible to assess the assumption regarding the independence of the specific energy on actuation, due to the unavailability of critical data.

This paper summarizes an experimental study specifically designed to assess the prediction of the ADC model proposed by Dehkhoda and Detournay (2016) and the validity of the assumptions on which the model is constructed, in particular the invariance of the specific energy on actuation. The experiments were conducted using a custom-designed ADC rig, dubbed as Wobble. This rig makes it possible to sweep the parametric space of two dimensionless parameters, a geometry number and an actuation number, that are controlling the cutting response according to the theoretical model.

The paper is organized as follows: First, we give a brief overview of the ADC model and of the main theoretical results. Next, we describe the laboratory set-up and the design of the experimental campaign. A sample of results on the force history and on the variation of the force with the actuation angle is then presented, followed by an analysis of the data in light of the theoretical model.

Fig. 1

Definition of actuated disc cutting

2 Model of an Actuated Disc Cutter

2.1 Kinematic Model

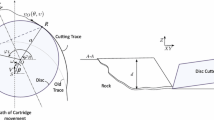
The simplified ADC system considered in this study is sketched in Fig. 1. It consists of a cartridge on which the disc cutter is mounted, together with the actuation mechanism. The cartridge is moving parallel to the free face of the rock at an assumed constant velocity V, with the disc removing rock over a constant depth of cut d. The disc is slightly tilted on the free surface, but this tilt is neglected here. A fixed cartesian coordinates system (X, Y, Z) is oriented in such a way that the Z-axis corresponds to the external normal to the free surface and that the Y-axis is pointing in the direction of V.

The disc cutter is free to rotate around its axis O, here assumed to be parallel to the Z-axis. An actuation mechanism revolves the disc axis O at a constant angular velocity $\omega$ around a secondary axis S fixed to the cartridge. The link SO is the actuation amplitude e and the disc radius is a. The inclination $\theta$ of the link SO on the X-axis is the angular position of axis O on the cartridge.

The motion of the disc cutter, a combination of translation of the cartridge and actuation of the disc relative to the cartridge, leaves a cut in the rock that nominally has a constant depth d and a width approximately equal to 2a if the relative actuation amplitude e/a is small. The motion of the disc cutter and the nominal geometry of the cut are entirely defined by the parameters V, $\omega$, a, e, d, and angular position $\theta$.

2.2 Basic Hypotheses

The model is kinematic in nature as it is based on the assumptions that the disc motion is prescribed and that there is always perfect conformance between the disc cutter and the rock. The evolution of the cut geometry and of the disc/rock contact surface is thus completely defined by the kinematics of the disc. In combination with elementary cutter/rock interaction law based on single cutter experiments, knowledge about the evolution of the contact surface can be translated into forces acting on the disc. Besides the above kinematic assumptions, the critical hypotheses on which the ADC model is constructed can be formulated as follows:

• 1. The excavation rate is completely determined by the disc kinematics.

• 2. The magnitude of the cutting force is proportional to the arc length of the contact between the disc and the rock.

• 3. The orientation of the cutting force in the plane of actuation is given by the normal to the chord subtending the contact arc.

• 4. At a given depth of cut, the specific energy—the energy required to break a unit volume of rock—is a constant, independent of actuation, penetration per cycle, and disc size.

2.3 Key Parameters

The design and control of the ADC is completely embodied in two numbers $\epsilon$ and $\upsilon$ defined as follows:

$$\begin{aligned} \epsilon =\frac{e}{a},\qquad \upsilon =\frac{V}{\omega e}. \end{aligned}$$

(1)

Number $\epsilon$ is a scaled actuation amplitude, while $2\pi \upsilon$ represents the average penetration per revolution scaled by e. Drag cutting corresponds, therefore, to the simultaneous limits $\epsilon \rightarrow 0$ and $\upsilon \rightarrow \infty$. Calculation of the cutting force acting on the actuated disc relies on determining two angles $\gamma (\theta ;\,\epsilon ,\upsilon )$ and $\psi (\theta ;\,\epsilon ,\upsilon )$ shown in Fig. 1. Angle $\gamma (\theta )$ is the inclination of the normal to the chord subtending the nominal contact arc between the disc and the rock while $\psi (\theta )$ is half the contact angle. According to the model assumptions, $\gamma$ gives the orientation of the cutting force while $\psi$ controls the force magnitude. Both functions have to be computed numerically.

The scaled solution depends only on angular position $\theta$ and on numbers $\epsilon$ and $\upsilon$ for quantities varying during a cycle (such as the excavation rate), and evidently only on $\epsilon$ and $\upsilon$ for quantities that are either averaged over a cycle (such as the average power) or that are only defined over a cycle (such as the volume of rock excavated). There are four variables of primary interest, namely: excavation rate Q, volume of rock excavated over a cycle A, cutting force ${\varvec{F}}$, and power expended P. All these variables can be scaled by characteristic quantities that are defined within the context of drag cutting. These scales, denoted by an asterisk, are

$$\begin{aligned} Q_{*}=2adV,\; A_{*}=\frac{2\pi }{\omega }Q_{*},\;F_{*}=2ad\varXi ,\; P_{*}=F_{*}V, \end{aligned}$$

(2)

where $\varXi$ denotes the specific energy, a parameter related to the strength properties of the rock. Depending on the mode of failure induced by the cutter, $\varXi$ is either constant (ductile mode) or a decreasing function of the depth of cut (brittle mode). In the above, scale $A_{*}$ represents the volume of rock excavated by an equivalent drag disc-cutter over a time equal to the duration of an actuation cycle. The scaled variables ${\mathcal {Q}}(\theta ;\,\epsilon ,\,\upsilon )$, ${\mathcal {A}}(\epsilon ,\upsilon )$, $\varvec{{\mathcal {F}}}(\theta ;\,\epsilon ,\upsilon )$, and ${\mathcal {P}}(\theta ;\,\epsilon ,\upsilon )$ are thus naturally defined as

$$\begin{aligned} {\mathcal {Q}}=\frac{Q}{Q_{*}},\qquad {\mathcal {A}}=\frac{A}{A_{*}},\qquad \varvec{{\mathcal {F}}}=\frac{{\varvec{F}}}{F_{*}},\qquad {\mathcal {P}}=\frac{P}{P_{*}}. \end{aligned}$$

(3)

In view of the definition of the scales, ${\mathcal {Q}},{\mathcal {A}},{\mathcal {F}},{\mathcal {P}}\rightarrow 1$ when simultaneously $\epsilon \rightarrow 0$ and $\upsilon \rightarrow \infty$. All these variables have to be evaluated numerically, in view of their dependence on contact angle $\psi$ and inclination angle $\gamma$.

2.4 Main Results

The volume of rock excavated during an actuation cycle, ${\mathcal {A}}$, is calculated by integrating excavation rate ${\mathcal {Q}}(\theta )$ over a cycle

$$\begin{aligned} {\mathcal {A}}=\frac{1}{2\pi }\int _{-\pi }^{\pi }{\mathcal {Q}}(\theta )\,\mathrm {d}\theta , \end{aligned}$$

(4)

where

$$\begin{aligned} {\mathcal {Q}}=\sin \psi \left[ \frac{1}{\upsilon }\sin (\gamma -\theta )+\sin \gamma \right] . \end{aligned}$$

(5)

Volume ${\mathcal {A}}$ can simply be interpreted as the ratio of the average width of the cut over the diameter of the disc. Figure 2, illustrating the variation of ${\mathcal {A}}$ with $\epsilon$ and $2\pi \upsilon$, shows that ${\mathcal {A}}$ increases with actuation amplitude $\epsilon$ and actuation frequency $1/\upsilon$ (decreasing $\upsilon$). The graph confirms that $\lim _{\upsilon \rightarrow 0}{\mathcal {A}}=1+\epsilon$ and that $\lim _{\upsilon \rightarrow \infty }{\mathcal {A}}=1$. The small $\upsilon$ limit corresponds to the case where the width of the cut is maximum.

Fig. 2

Plot of excavation volume per actuation cycle ${\mathcal {A}}$ versus $\epsilon$ and $2\pi \upsilon$

The scaled cutting force $\varvec{{\mathcal {F}}}(\theta )$ in the plane of actuation is given by

$$\begin{aligned} \varvec{{\mathcal {F}}}=\sin \psi {\varvec{n}}(\gamma ), \end{aligned}$$

(6)

where ${\varvec{n}}(\gamma )$ is the unit vector (in the X–Y plane) inclined by an angle $\gamma$ on the X-axis. The average thrust force $\bar{{\mathcal {F}}}_{y}$ in the direction of the cartridge movement, and the force component $\bar{{\mathcal {F}}}_{x}$ orthogonal to V can thus be expressed as

$$\begin{aligned} \begin{aligned}&\bar{{\mathcal {F}}}_{x}=\frac{1}{2\pi }\int _{-\pi }^{\pi }\sin \psi \cos \gamma \,\mathrm {d}\theta \\&\bar{{\mathcal {F}}}_{y}=\frac{1}{2\pi }\int _{-\pi }^{\pi }\sin \psi \sin \gamma \mathrm {d}\theta . \end{aligned} \end{aligned}$$

(7)

The thrust force $\bar{{\mathcal {F}}}_{y}$ can actually be written as

$$\begin{aligned} \bar{{\mathcal {F}}}_{y}={\mathcal {A}}(1-\eta ), \end{aligned}$$

(8)

where actuation efficiency $\eta \left( \epsilon ,\upsilon \right)$ is defined as

$$\begin{aligned} \eta \left( \epsilon ,\upsilon \right) =1-\frac{1}{2\pi {\mathcal {A}}}\int _{-\pi }^{\pi }\sin \psi \sin \gamma \,\mathrm {d}\theta , \end{aligned}$$

(9)

noting that $0\le \eta \le 1$. Figure 3 depicts the variation of $\eta$ with $\epsilon$ and $2\pi \upsilon$. This plot indicates that $\eta$ decreases with $\upsilon$ and that there is only a weak dependence of $\eta$ on $\epsilon$. The thrust force on an actuated cutter is thus smaller than on a drag disc of same diameter, for the same depth of cut. With increasing $\upsilon$, the average thrust force tends to the force on a drag cutter ($\bar{{\mathcal {F}}}_{y}\simeq 1$ for $\upsilon \gg 1$). Despite its strong assumptions, this kinematic model is expected to yield adequate estimate of the cutting force when averaged over many cycles of actuation.

Fig. 3

Plot of actuation efficiency $\eta$ versus $\epsilon$ and $2\pi \upsilon$

The average power $\bar{{\mathcal {P}}}$ expended by the actuated disc cutter is partitioned into $\bar{{\mathcal {P}}}_{{\text {a}}}$ to actuate the disc and $\bar{{\mathcal {P}}}_{{\text {t}}}$ to translate the cartridge. By definition,

$$\begin{aligned} \begin{aligned}&\bar{{\mathcal {P}}}_{a}=\frac{1}{2\pi \upsilon }\int _{-\pi }^{\pi }{\mathcal {F}}\,\sin \left( \gamma -\theta \right) \mathrm {d}\theta \\&\bar{{\mathcal {P}}}_{t}=\frac{1}{2\pi }\int _{-\pi }^{\pi }{\mathcal {F}}\,\sin \gamma \,\mathrm {d}\theta , \end{aligned} \end{aligned}$$

(10)

which can be rewritten as

$$\begin{aligned} {\bar{\mathcal {P}}}_{a}=\eta {\mathcal {A}},\qquad \bar{{\mathcal {P}}}_{t}=(1-\eta ){\mathcal {A}}. \end{aligned}$$

(11)

Power partitioning between actuation of the disc and translation of the cartridge is thus also quantified by $\eta (\epsilon ,\upsilon )$, which represents the fraction of the total power required to actuate the disc cutter. The equality $\bar{{\mathcal {P}}}={\mathcal {A}}$ is an obvious consequence of assuming that specific energy $\varXi$ is not affected by the actuation.

3 Description of Laboratory Set-up and Experiments

3.1 Wobble: The Rock Cutting Test-Unit

The cutting experiments are conducted using CSIRO’s unique custom-made actuated disc cutting test-unit, dubbed as Wobble (Fig. 4). Wobble is a small-scale rig capable of performing cutting tests under kinematic control. It actuates the cutter at various amplitudes and frequencies on the surface parallel to the cutting direction, where the cutter is free to rotate around its axis. The speed of the linear cutting can also be varied. The control system allows prescribing accurate motions to the disc axis. The response of the rock is captured through measurements of the reaction forces.

Wobble is instrumented with displacement, force, and torque sensors to accurately record the response of the rock to the cutting process. The forces are measured using strain gauge based sensors in directions parallel and normal to the cutting direction. The depth of cut, linear cutting speed, and angular velocity of the disc cutter are also monitored using displacement sensors. Table 1 lists the general specifications of Wobble and the mounted measurement instruments. The accuracy of the force measurements in lateral direction and torque around the shaft are the lowest of the system with $\pm \;0.1\;\hbox {kN}$ and $\pm \;0.5\;\hbox {Nm}$ precision, respectively.

Fig. 4

Overview of actuated disc cutting test-unit, Wobble

Table 1 Specifications of Wobble and its instrumentation

The accuracy of the torque measurements is evaluated by comparing the direct torque measured on the shaft with torque values indirectly calculated using the cutting force $F_{{\text {h}}}$ in the plane of actuation:

$$\begin{aligned} T=eF_{{\text {h}}}\sin \left( \gamma -\theta \right) . \end{aligned}$$

(12)

A close match between direct measurements of the torque and values estimated on the basis of (12) was consistently observed, whenever the actual torque was well above the accuracy and resolution of the torque sensor. However, where the torque values were close to the resolution of the sensor ($\le \;\pm \;0.5$ Nm), the discrepancy between the two torque measurements reached 50%. In view of the limitation of direct torque data and for the sake of consistency, the indirectly computed torque data are used for calculation of the energy in the following sections.

One of the design criteria of Wobble was the requirement of a stiff frame to minimize variations of the assigned depth of cut caused by the deformation of the frame. Achieving this goal was proven difficult, however, due to the two bearings required for the actuation of the shaft and for the free rotation of the disc. In a compliant system, the elastic energy is accumulated during loading and is released abruptly following the removal of a chip. Figure 5 illustrates the variation in the set depth of cut with normal force, with the non-linearity reflecting the response of the bearings. To eliminate potential errors caused by the frame compliance in the analysis of data, in particular the specific energy, the actual depth of cut was directly measured during the experiments.

Fig. 5

Change in depth of cut as a function of normal force ($2\pi \upsilon =3$, $\epsilon =0.2$, $f=5\hbox { Hz}$, $p=15\hbox { mm/rev}$, $V=75\hbox { mm/s}$)

3.2 Rock

A limestone, Savonniere, has been selected for the cutting experiments due to its uniform and homogeneous structure. The physical and mechanical properties of this rock are: unit density, $\rho =1771\hbox { kg}/\hbox {m}^{3}$; compressive strength, $\sigma _{{\text {c}}}=16.5\hbox { MPa}$; Young modulus, $E=12.2\hbox { GPa}$; tensile strength, $\sigma _{{\text {t}}}=1.77\hbox { MPa}$; fracture toughness, $K_{{\text {Ic}}}=0.45 \hbox { MPa}\surd \hbox {m}$.

The rock samples were prepared in slab shape with length and width of 250 mm and thickness of 40 mm. Each slab was then used for four cutting experiments, two on each side with no more than 5 mm depth of cut. Cutting paths were also spaced from the side of the slab and from each other at twice the diameter of the disc cutter to avoid boundary influence.

The intrinsic length scale of Savonniere is estimated to be $\ell \simeq 0.7$ mm, where $\ell =(K_{{\text {Ic}}}/\sigma _{{\text {c}}})^{2}$. This length scale marks the transition between ductile and brittle failure with respect to the depth of cut (Huang and Detournay 2008).

3.3 Description of Cutting Tests

The main control variables in the experiments are advance velocity V, actuation amplitude e and angular velocity $\omega$ or frequency f, cutter size a, and depth of cut d. These variables are reduced to the two numbers $\upsilon ={V}/{e\omega }$ and $\epsilon ={e}/{a}$, as well as the penetration per cycle ${2\pi V}/{\omega }$, which have all been varied in about 50 experiments that have been conducted, see Table 2 and Fig. 6. Although the scaled forces in the ADC model only depend on the two numbers, $\epsilon$ and $\upsilon$, on account that the specific energy is assumed to be constant (at a given depth of cut), the penetration per cycle was purposely changed to ascertain a possible dependence of the specific energy on p due to the existence of intrinsic length scale $\ell$.

A constant depth of cut d of 4 mm, well above the intrinsic length, was chosen for all the experiments to enforce a brittle failure mode (associated with chip production), similar to what would be observed in excavating hard rock in the field.

Table 2 Test parameters of the conducted experiments

Fig. 6

Contour plots depicting $2\pi \upsilon$ (left) and $\epsilon$ (right) variation with p, e and a; red circles indicate tested conditions. (Color figure online)

In each experiment, the response of the rock to the cutting process was captured using force and torque sensors. The forces are measured in directions parallel and normal to the cutting direction and torque is measured on the main shaft. The variation of the depth of cut is also recorded during a test alongside the free rotation of the disc around its axis. After each cutting test, the fragments were collected for further evaluation of the excavation volume.

4 Experimental Results

4.1 Cutter Trajectory

Figure 7 compares the predicted trajectories of the ADC with the geometry of the groove traced by the ADC. The good match between theory and experiments demonstrates the validity of the kinematic model in defining the geometry of the cut.

Fig. 7

Trajectory of ADC for selected values, model vs experiments

4.2 Force Versus Time

Examples of force signals measured during cutting are shown in Figs. 8 and 9 for experiments TN11 and TN48. Thrust $F_{{\text {c}}}$, lateral $F_{{\text {l}}}$, and normal $F_{{\text {n}}}$ in these figures refer to the Y-, X-, and Z-component of the cutting force acting on the disc. The cyclic nature of the cutting process can be clearly observed within the waveform pattern with a reproducible period.

Fig. 8

Force signal (TN11: $2\pi \upsilon =4.9,\,\epsilon =0.12,\,p=15$ mm/rev)

Fig. 9

Force signal (TN48: $2\pi \upsilon =0.3,\,\epsilon =0.25,\,p=1$ mm/rev)

The frequency content of the signals are shown in Figs. 10 and 11. With a 2400 Hz sampling frequency, the Nyquist frequency is 1200 Hz. As can be observed, the five discrete peaks in the power spectrum correspond to the 5 Hz actuation frequency and its harmonics. A high-frequency noise can be detected in the signal; analysis of the signal indicates a Gaussian distribution. The background noise and vibrations in the system can explain the random noise. The frequency analyses do not suggest any significant event above 200 Hz.

Fig. 10

Frequency analyses of the force data (TN11: $2\pi \upsilon =4.9,\,\epsilon =0.12,\,p=15\;\hbox {mm/rev}$)

Fig. 11

Frequency analyses of the force data (TN48: $2\pi \upsilon =0.3,\,\epsilon =0.25,\,p=1\;\hbox {mm/rev}$)

4.3 Average Force vs Rotation Angle

Because of the nature of the proposed model, the experimental force data have to be averaged over several cycles, to enable a meaningful comparison with theoretical results. Figures 12 and 13 show the variation of the mean force (thrust, lateral, and normal) and torque with angle $\theta$, averaged over the cycles of actuation for the two tests, reported in Figs. 8 and 9. The $\mu \pm \sigma$ profiles in these two figures depict the dispersion of the reaction force due to dynamics of the cutting process, where $\mu$ is the mean and $\sigma$ is the standard deviation, both a function of $\theta$.

Fig. 12

Averaged and standard deviation of force profile over one actuation with $\theta$; TN11: $2\pi \upsilon =4.9,\,\epsilon =0.12,\,p=15$ mm/rev

Fig. 13

Averaged and standard deviation of force profile over one actuation with $\theta$; TN48: $2\pi \upsilon =0.3,\,\epsilon =0.25,\,p=1$ mm/rev

As can be observed in Figs. 12 and 13, the mean profiles for TN48 contain less “noise” than TN11. This is simply explained by the order of magnitude less cycles in TN11 over which to average, compared to TN48, due to the much larger penetration per revolution (1 mm/rev in TN48 and 15 mm/rev in TN11). This limitation was imposed by the constant length of cut (sample length of 250 mm). Only the mean response is compared to the theoretical predictions, as it contains enough failure events to suppress the stochastic nature of the rock fragmentation process.

4.4 Resultant Force

The magnitude of the in-plane resultant force $F_{{\text {h}}}$ and its inclination $\gamma$ on X-axis are calculated using the thrust and lateral forces averaged over the actuation cycles

$$\begin{aligned} F_{{\text {h}}}=\sqrt{F_{{\text {l}}}^{2}+F_{{\text {c}}}^{2}},\qquad \gamma =\arctan \left( \frac{F_{{\text {c}}}}{F_{{\text {l}}}}\right) . \end{aligned}$$

(13)

Figure 14a shows the variation of the resultant horizontal force withe $\theta$ for four experiments. It can be observed that increasing $\epsilon$ and $\upsilon$, in general, leads to larger cutting forces. Besides, the duration of cutting (nonzero force) is longer when $\upsilon$ is large. The ratio between resultant force in the plane of actuation and its normal $F_{{\text {n}}}$ does not show any significant variation between different tests (Fig. 14b). The data points are, however, more widely dispersed for higher values of $F_{{\text {n}}}$ and $F_{{\text {h}}}$.

Fig. 14

Variation of resultant force with disc angular position $\theta$ and inclination of resultant force on horizontal plane

5 Analysis

In this section, we aim to assess the validity of the ADC model (Dehkhoda and Detournay 2016) by examining the legitimacy of the key model assumption, namely the independence of the specific energy on actuation, and by comparing experimental results with model predictions in regard to (i) the volume of rock excavated per actuation cycle, (ii) the variation of the magnitude and orientation of the cutting force with the rotation of the disc center during a cycle, and (iii) the dependence of actuation efficiency $\eta$ on $\epsilon$ and $\upsilon$.

5.1 Volume of Excavated Rock

Figure 15 compares the theoretical (scaled) volume of rock excavated per cycle ${\mathcal {A}}(\epsilon ,\upsilon )$ with the experimental values ${\mathcal {A}}$ measured for the various pairs $(\epsilon ,\upsilon )$ selected for this experimental campaign. The experimental ${\mathcal {A}}$ was calculated as

$$\begin{aligned} {\mathcal {A}}=V_{{\text {rock}}}/A_{*}n, \end{aligned}$$

where n is the number of actuation cycles and $V_{{\text {rock}}}$ is the total excavation volume, determined from the measured weight of the collected fragments and the measured rock density. The figure indicates that the measured volume ${\mathcal {A}}$ is typically larger than its theoretical counterpart ${\mathcal {A}}$, likely due to side chipping of the groove (see photos of the groove in Fig. 7). The measured ${\mathcal {A}}$ were used to determine the specific energy for each experiment.

Fig. 15

Volume of excavated rock (measured vs model)

5.2 Specific Energy

The theoretical model is based on the assumption that the specific energy $\varXi$ does not depend on the actuation ($\upsilon$ and $\epsilon$) and on the penetration per revolution (p) at a given depth of cut d. Here we assess this critical hypothesis by calculating the average $\varXi$ for each experiment and testing for a possible dependence with respect to $\epsilon$, $\upsilon$, and p. The specific energy for each test was evaluated on the basis of the equality $\bar{{\mathcal {P}}}={\mathcal {A}}$, see (11). After writing $\bar{{\mathcal {P}}}$ as the ratio of the average external power ${\bar{P}}$ over the scale $P_{*}=2adV\varXi$, we deduce from $\bar{{\mathcal {P}}}={\mathcal {A}}$ an expression for $\varXi$, which relies solely on indirectly $({\bar{P}}$, ${\mathcal {A}}$) and directly (d, V) measured quantities and known parameters (a, $\omega$):

$$\begin{aligned} \varXi =\frac{{\bar{P}}}{2adV{\mathcal {A}}}. \end{aligned}$$

(14)

The average power expended by the actuated disc ${\bar{P}}={\bar{P}}_{{\text {a}}}+{\bar{P}}_{{\text {t}}}$ is computed by numerically evaluating the two integrals involving the measured forces for $\theta \in [-\pi ,\pi ]$:

$$\begin{aligned} \begin{aligned}&{\bar{P}}_{{\text {t}}}=\frac{V}{2\pi }\int _{-\pi }^{\pi }F_{{\text {h}}}(\theta )\sin \gamma \,\mathrm {d}\theta \qquad \\&{\bar{P}}_{{\text {a}}}=\frac{\omega e}{2\pi }\int _{-\pi }^{\pi }F_{{\text {h}}}(\theta )\sin (\gamma -\theta )\mathrm {d}\theta , \end{aligned} \end{aligned}$$

(15)

where $F_{{\text {h}}}$ and its orientation $\gamma$ are calculated using (13) for every force data for the duration of the experiment. The first term represents the power associated with the translation of the cart and the second with the actuation mechanism. In evaluating the actuation component of ${\bar{P}}$, it is assumed that $\theta =0$ at $t=0$.

Figure 16 shows plots of $\varXi$ versus $2\pi \upsilon$ (left) and $\varXi$ versus $\epsilon$ (right), with the size of the markers being indicative of p. Variation of $\varXi$ with respect to p is also depicted in Fig. 17. These plots do not betray any obvious underlying dependence of $\varXi$ on $\upsilon$. The data, however, suggest a slight increase of $\varXi$ with $\epsilon$ and p. This observation is consistent with examination of the sizes of the generated fragments. Coarseness index, which represents the production of larger chips in relation to fines, decreases with $\epsilon$ and $\upsilon$. A multi-variable regression analysis has been conducted on the data to access the relationship between the independent variables $\upsilon$, $\epsilon$ and p and the dependent variable $\varXi$.

Fig. 16

Variation of specific energy with $2\pi \upsilon$ and $\epsilon$, marker size reflects p

Fig. 17

Variation of specific energy with p, marker size reflects $2\pi \upsilon$

Evaluation of a three-variable ($\epsilon$, $\upsilon$, and p) linear model, with and without interaction terms, suggests that the effect of $\upsilon$ on $\varXi$ is not significant at the 5% significance level (p-value of the F-statistic greater than 0.05). Combination of two-variable analyses led to 3 models with acceptable p-values with terms $\upsilon$ and $\epsilon$, and $\epsilon$, p and their interaction. Figure 18 compares the developed models with respect to the observed data. The equally spread residuals (difference between predicted values and observations) in this figure is also a good indication of the absence of missed non-linear relationships. The highest R-squared value ($R^{2}$ = 0.452) belongs to the model with $\epsilon$, p and their interaction as independent variables. In other words, the model with the selected predictors can explain about $45\%$ of the variability in the response variable $\varXi$. Low p-value ($\sim e^{-4}$) for the F-test conducted on this model confirms a relationship between the response variable $\varXi$ and the predictor variables: $\epsilon$, p and interaction at the 5% significance level. There might be, however, other predictor variables that are not included in the current model.

Fig. 18

Regression models vs data

Figure 17 also shows that variability in $\varXi$ reduces with p. Low p and $\upsilon$ correspond to cases where the cutter briefly breaks off engagement with the rock in its backward movement within the actuation cycle, until it establishes contact again in a forward movement. During this backward movement, the base of the cutter grinds the uneven surface of the rock, creating fines. Also at the start of the cutting process, the depth of cut is not immediately at its set value, but rather increases from zero to the maximum with a rate that is controlled by the angle of the tapered edge of the cutter and speed of cutting $v_{{\text {o}}}$. The grinding process and the varying depth cut strengthen the hypothesis of continuous transitioning between ductile and brittle failures at small p and $\upsilon$, which can also explain the wide variation interval for $\varXi$ when $\upsilon <1$. Nonetheless, taking into account variability in rock strength, the experimental results does not suggest any significant departure from the original assumption of invariance of $\varXi$ on $\epsilon$, $\upsilon$, and p.

Invariance of the specific energy can also be assessed globally by testing the equality ${\bar{\mathcal {P}}}={\mathcal {A}}$ using only experimental data. Figure 19 shows the variation of the scaled total power for each experiment with the total volume of cut. Recall that such an equality simply expresses that the energy requirement to excavate a given volume of rock remains unchanged when the disc is actuated. The best fit line (passing through the origin) corresponds to ${\bar{\varXi }}\simeq 6.4\hbox { J}/\hbox {cm}^{3}$ (or equivalently MPa). The relatively small dispersion of the experimental points around the best fit line confirms that the assumption of a constant intrinsic specific energy (at a given depth of cut) is valid to first order.

Fig. 19

Variation of total power with $\epsilon$ and $\upsilon$; marker size reflects $2\pi \upsilon$

5.3 Ductile Versus Brittle Failure

All the experiments reported in this paper were conducted at the depth of cut $d=4$ mm. As noted earlier, the depth of cut was chosen to enforce a brittle failure mode and chip production similar to what is observed in excavating hard rock in the field. Hence, we expect that specific energy $\varXi =\beta K_{{\text {Ic}}}/\sqrt{d}$, with $\beta =O(0.1\sim 1)$ (Huang and Detournay 2008; Dehkhoda and Detournay 2016). With an average specific energy ${\bar{\varXi }}\simeq 6.02\pm 0.97$ MPa deduced from the experimental data, $\beta$ is in the interval [0.6, 1.2] with an average ${\bar{\beta }}\simeq 0.9$, which is consistent with the expected magnitude for $\beta$. Furthermore, an interpretation based on the ductile regime, which implies that $\varXi =\alpha \sigma _{{\text {c}}}$ with $\sigma _{{\text {c}}}$ denoting the unconfined compressive strength of the rock, would lead to $\alpha \in [0.25,0.55]$, which is smaller by a factor of 2 to 3 to the narrow range of empirical value of $\alpha$ obtained in linear cutting tests (Richard et al 2012). These remarks as well as the large number chips produced in the experiments (Fig. 20), support the claim that cutting takes place in the brittle regime.

Fig. 20

Overview of cutting fragments with the Wobble

5.4 Force Variation During an Actuation Cycle

The theoretical force predicted by the ADC model can be interpreted as the mean of the expected values. The adequacy of the model can then be tested by comparing the variation of the averaged thrust ($F_{y})$ and lateral ($F_{x})$ forces with the angular position $\theta$ in experiments with the model predictions. This is done in Fig. 21 for experiments T1 and T2 (refer to Table 2). The scale $F_{*}$ used to translate the theoretical dimensionless forces ${\mathcal {F}}_{x}(\theta )$ and ${\mathcal {F}}_{y}(\theta )$ into physical quantities was calculated with specific energy $\varXi$ estimated for each experiment ($\varXi =7.11\hbox {MPa}$ for both T1 and T2). The force variation is well predicted by the theoretical model as demonstrated in Fig. 21. Comparison between prediction and experimental data for the variation with $\theta$ of the force orientation in the horizontal plane, $\gamma$, also shows an excellent match. This comparison strongly supports the validity of the model assumptions regarding the magnitude and the orientation of the cutting force.

Fig. 21

Comparison of experiment with model

5.5 Actuation Efficiency $\eta$

According to its theoretical expression, (9), actuation efficiency $\eta$ only depends on the actuation number $\upsilon$ and on the geometry number $\epsilon$. Since $\eta$ represents the fraction of the total power required to actuate the disc, it can be estimated from the experimental data as

$$\begin{aligned} \eta =\frac{{\bar{P}}_{{\text {a}}}}{{\bar{P}}_{{\text {a}}}+{\bar{P}}_{{\text {t}}}}, \end{aligned}$$

where actuation power ${\bar{P}}_{{\text {a}}}$ and translation power ${\bar{P}}_{{\text {t}}}$ are calculated from the force measurements according to (15). Figure 22 compares the theoretical $\eta$ ($1-\eta$) with the experimental ${\bar{P}}_{a}/{\bar{P}}$ (${\bar{P}}_{t}/{\bar{P}}$) as a function of $2\pi \upsilon$. The theoretical curves are plotted for $\epsilon =0.05$ and $\epsilon =0.5$, noting that the geometry number $\epsilon$ varies between 0.04 and 0.5 in the experiments. These plots show an excellent match between the model predictions and the experimental data and confirm the weak dependence of $\eta$ on $\epsilon$ that is predicted by the model.

Fig. 22

Scaled power vs $2\pi \upsilon$; comparison between model and experiment

6 Conclusions

In this paper, we have presented and analyzed the results of actuated cutting experiments carried out with a table-top ADC test unit on a soft limestone. All the experiments were conducted at the same depth of cut, which was selected to ensure a brittle mode of failure characterized by the formation of chips. By changing the disc size and actuation amplitude, as well as the actuation frequency and the cartridge velocity, the experiments covered a realistic region of the parametric space ($2\pi \upsilon \,,\,\epsilon$) and over a large enough range of these two numbers to rigorously test the theoretical model and its assumptions.

The main conclusions which can be drawn from this preliminary study can be summarized as follows:

• 1. The specific energy $\varXi$ is, to first order, independent of the actuation, a critical assumption of the model. Although $\varXi$ fluctuates between approximately 4 and 8 MPa, no systematic trend with the actuation number $\upsilon$ can be detected. However, the data suggest a slight increase of $\varXi$ with $\epsilon$.

• 2. Partitioning of the power between actuation of the disc and translation of the cartridge is consistent with the theoretical prediction. Similarly, the variation of the average thrust force with $\upsilon$ follows the predicted variation.

• 3. Variation of the magnitude and orientation of the cycle-averaged cutting force with the actuation angle follows the theoretical variation for many tests. This result came as a surprise as the model is based on the simple assumptions of a conforming contact between the disc and the rock and on a uniform contact pressure. Interestingly, these assumptions are met on average and thus the theoretical force model can be interpreted as a prediction of the expected force magnitude and inclination.

Further testing with another rock is needed to confirm the above conclusions. Also, experiments with varying depth of cut d are required to assess the dependence of the specific energy on d. The analytical studies are also being furthered to incorporate the cutter tilt angle in deriving cutter/rock interface laws (Dehkhoda and Hill 2019). This improvement extends the proposed kinematic and geometry based model to take into account the variable depth of cut in estimating the forces associated with cutting in one actuation cycle.