1 Introduction

The common presence of salt in sedimentary basins around the world and its physical properties such as an almost vanishing permeability make rock salt involved in many geomechanical applications. These include the storage of nuclear waste (Westbrook 2016), oil and gas (Preece 1987), CO2 (da Costa et al. 2011), compressed air (Djizanne et al. 2014) and hydrogen (Lord et al. 2011). Another group of applications is related with drilling (Kim 1988; Barker et al. 1994; Dusseault et al. 2004; Poiate et al. 2006) and the abandonment of caverns and wells (van Heekeren et al. 2009; Hou et al. 2012; Bérest and Brouard 2014; Orlic and Buijze 2014). Cavities located in salt tend to close with time due to the creeping properties of rock salt, which can lead to fluid overpressure, loss of storage volume or stuck pipe incidents during drilling. A proper planning strategy relying on a good understanding of hole closure in rock salt is the key to insure the success of these applications.

Laboratory experiments show that under conditions encountered in the underground rock salt may exhibit the behavior of a viscoelastic fluid at engineering timescales (Cristescu and Hunsche 1997; Munson 1997; Fossum and Fredrich 2002). The long-term fluid-like behavior of salt may originate from microscopic deformation mechanisms such as dislocation and pressure solution creep. The apparent viscosity due to the movement of dislocations is best described using a power law stress dependence model. The power law viscosity model has often been applied to fit laboratory data obtained for various rock salt types (Carter and Hansen 1983; Wawersik and Zeuch 1986; Berest and Brouard 1998), giving the stress exponent in the range between 3 and 6. Dislocation creep is dominant at high deformation rates and, in addition to its strong dependence on stress, it is also dependent on temperature. Pressure solution, on the other hand, is a water-activated solution-precipitation process dominant at low rates of deformation in fine-grained salts (Rutter 1983; Spiers et al. 1990; Ter Heege et al. 2005a; Urai and Spiers 2007; Brouard et al. 2009), during which salt dissolves at grain contacts and diffuses through wet grain boundaries. At the macroscopic scale, pressure solution results in a linear viscosity, which is strongly grain size dependent. Although there is no single threshold grain size under which pressure solution is always dominant, deformation in a salt with 1 mm grain size is almost always driven by pressure solution (Urai and Spiers 2007; Cornet et al. 2018). Deformation in the range of typical halokinetic rates (10−16 to −9 s−1) and temperatures (20–140 °C) falls in the transition between dislocation and solution-precipitation creep (van Keken et al. 1993; Spiers and Carter 1996; Urai and Spiers 2007; Li and Urai 2016), indicating that both mechanisms need to be taken into account when modeling rock salt deformation. The wide grain size distribution in natural salts, going from a fraction of mm to several cm (Ter Heege et al. 2005a; Ter Heege et al. 2005b), also suggest that both mechanisms may occur concurrently.

The time evolution of pressure-driven hole closure in salt has been studied both numerically and during in situ experiments. Experimentally, hole closure is recorded at different times and an empirical description of it is given for any specific scenario (Preece 1987; Kim 1988; Senseny 1990). Numerical studies, on the other hand, investigate systematically the influence of the input parameters on the closure using complex rheological models for salt (Munson 1997; Hunsche and Hampel 1999; Heusermann et al. 2003; Mackay et al. 2008; van Heekeren et al. 2009; Hou et al. 2012; Xie and Tao 2013; Orlic and Buijze 2014; Günther et al. 2015). Although both approaches prove to be efficient at describing closure, they lack the full insight into the process provided by analytical solutions based on simpler models. However, analytical solutions for viscoelastic media are limited as soon as the constitutive law is nonlinear. In linear viscoelasticity, the correspondence principle applies and solutions can be derived (Gnirk and Johnson 1964). In nonlinear viscoelasticity, solutions are available for the steady-state closure velocity (Liu et al. 2011; Wang et al. 2015; Cornet et al. 2017). Analytical solutions also exist for the initial closure velocity in the case of a viscoelastic Maxwell model with power law viscosity (Karimi-Jafari et al. 2006; Wang et al. 2015), but a detailed description of the time-dependent behavior is missing.

We study the pressure-driven closure of a cylindrical circular cavity in rock salt using numerical and analytical modeling. The pressure in the hole is kept constant such that this study can be directly applied to oil or liquefied petroleum gas storage. The constitutive law for salt is an incompressible viscoelastic Maxwell model with a nonlinear viscosity. The deformation mechanisms associated with the viscous behavior are dislocation creep and pressure solution. We use an Ellis model (Bird et al. 1960; van Keken et al. 1993), which takes into account the concurrent occurrence of the two end-member creep processes in the parallel series connection, to take both deformation mechanisms into account. We quantify the time evolution of hole closure which includes the initial, transient and long-term responses. We also investigate how closure speed evolves with depth and time under typical conditions. The magnitude and time dependence of the closure velocities of wells and shafts are preferably given in the form of figures from which the interested reader can directly estimate the closure velocity in any problem he faces. Our approach will hopefully increase the rate of success of drilling and mining operations thanks to the more realistic modeling of salt flow implemented here compared to the one currently used in the industry.

2 Model

2.1 Constitutive Model

The viscoelastic fluid-like behavior of salt can be described using an isotropic Maxwell model, in which the total deformation rate is given by a sum of its elastic and viscous contributions:

$${{\mathbf{D}}_{ij}}={\mathbf{D}}_{{ij}}^{{{\text{el}}}}+{\mathbf{D}}_{{ij}}^{{{\text{vis}}}},$$
(1)

where i, j are indices going from 1 to 3, D is the total rate of deformation tensor, and the superscripts el and vis refer to the elastic and viscous contributions, respectively. Assuming that there is no volumetric creep, we rewrite Eq. (1) in terms of pressure and deviatoric stress as:

$${{\mathbf{D}}_{ij}}= - \frac{{\dot{p}}}{K}{\delta _{ij}}+\frac{{{{{\dot{\boldsymbol{\tau }}}}_{ij}}}}{{2G}}+\frac{{{{\boldsymbol{\tau }}_{ij}}}}{{2{\mu _{{\text{app}}}}}},$$
(2)

where p is the pressure (taken positive in compression), K is the bulk modulus, δ is the Kronecker delta, τ is the deviatoric stress tensor, G is the elastic shear modulus and µapp is the apparent viscosity. The overdot is used to denote differentiation with respect to time. Since we assume small deformations, the time derivative is just a partial derivative and the material derivatives are dismissed (Wang et al. 2015).

The elastic shear modulus of salt is well constrained and a representative value is G = 12.4 GPa (Fredrich et al. 2007). The elastic moduli of rock salt are nearly independent of their origin (Senseny et al. 1992) because many salts are primarily (more than 95%) composed of pure halite. Homogeneous rock salts are usually near-isotropic, but the addition of argillaceous elements can change the elastic properties of the salt and introduce some degree of anisotropy (Zong et al. 2016).

Rock salt creep is compressible below the compressibility/dilatancy boundary and dilatant above (Cristescu 1993; Hunsche and Hampel 1999; Schulze et al. 2001). Dilatancy corresponds to an increase in volume during deformation due to microcracking. It is a process that increases damage and it has a dramatic impact on the permeability which, in turn, promotes fluid flow and pressure solution. Viscous compressibility, on the other hand, is a healing process associated with a volume decrease caused by the closure of microcracks. Since this volumetric creep cannot occur indefinitely, salt can be considered incompressible in the long term. Above a mean stress of 5–10 MPa, salt has been reported to flow with a constant volume (Fossum and Fredrich 2002). These confining pressures are reached in the subsurface at depths greater than 250–500 m.

In the following, we also neglect elastic effects related to compressibility and assume incompressibility (Dii = 0). The constitutive law Eq. (2) becomes:

$${{\mathbf{D}}_{ij}}=\frac{{{{{\dot{\boldsymbol{\tau }}}}_{ij}}}}{{2G}}+\frac{{{{\boldsymbol{\tau }}_{ij}}}}{{2{\mu _{{\text{app}}}}}}.$$
(3)

The viscosity of salt can vary greatly depending on the salt type and local conditions. The viscous model considered for rock salt in this study is an incompressible Ellis model which combines linear viscous pressure solution and nonlinear dislocation creep:

$${{\mathbf{D}}^{{\text{vis}}}}={{\mathbf{D}}^{{\text{PS}}}}+{{\mathbf{D}}^{\text{D}}},$$
(4)

where DPS and DD are, respectively, the deviatoric rate of deformation due to pressure solution and dislocation creep. Both creep processes are assumed to operate independently. The constitutive relationship for diffusion creep is:

$${{\boldsymbol{\tau }}_{ij}}=2\mu _{0}^{{{\text{PS}}}}{\mathbf{D}}_{{ij}}^{{{\text{PS}}}}.$$
(5)

\(\mu _{0}^{{{\text{PS}}}}\) is a Newtonian viscosity (Spiers et al. 1990; Turcotte and Schubert 2014):

$$\mu _{0}^{{{\text{PS}}}}=\frac{1}{3}\frac{{T{d^3}}}{{{B_{\text{P}}}}}\exp \left({\frac{{{Q_{\text{P}}}}}{{{R_{\text{u}}}T}}} \right),$$
(6)

where BP is a prefactor for pressure solution in K mm3 MPa−1 s−1, QP is the apparent activation energy in J mol−1, d is the grain size in mm, T is the temperature in Kelvin and Ru = 8.31 J mol−1 K−1 is the universal gas constant. In the following, we use the parameters established by Spiers et al. (1990): BP = 4.7 × 10−4 K mm3 MPa−1 s−1 and QP = 24.5 × 103 J mol−1. The grain size is 7.5 mm for our reference salt presented in Table 1 (Carter et al. 1993).

Table 1 Power law flow law properties of three different natural salts
Full size table

Dislocation creep is modeled using a power law relationship between the components of deviatoric stress and rate of deformation tensors (Carter and Hansen 1983; Ranalli 1995):

$${{\boldsymbol{\tau }}_{ij}}=2{\mu ^{\text{D}}}{\mathbf{D}}_{{ij}}^{{\text{D}}}.$$
(7)

The viscosity µD is:

$${\mu ^{\text{D}}}=\frac{{{A_{\text{D}}}}}{2}\tau _{{{\text{II}}}}^{{1 - n}},$$
(8)

where AD is a material parameter, τII is the second invariant of the deviatoric stress tensor \({\tau _{{\text{II}}}}=\sqrt{{{\left({\tau _{{11}}^{2}+\tau _{{22}}^{2}+\tau _{{33}}^{2}} \right)} \mathord{\left/{\vphantom{{\left({\tau _{{11}}^{2}+\tau _{{22}}^{2}+\tau _{{33}}^{2}} \right)} 2}} \right. \kern-0pt} 2}+\tau _{{12}}^{2}+\tau _{{13}}^{2}+\tau _{{23}}^{2}}\) and n is the stress exponent (n > 1 for shear thinning media such as rocks). The prefactor AD is given by:

$${A_{\text{D}}}=\frac{2}{{{{\sqrt 3 }^{n+1}}}}\frac{{\exp \left({\frac{{{Q_{\text{D}}}}}{{{R_{\text{u}}}T}}} \right)}}{{{B_{\text{D}}}}}.$$
(9)

Compilations of experimentally determined values for BD, QD and n have been reported for both natural and synthetic salts (Wawersik and Zeuch 1986; Kirby and Kronenberg 1987; Carter et al. 1993; Berest and Brouard 1998; Hunsche and Hampel 1999). We focus on three different salt kinds whose material properties are presented in Table 1 and which are representative of the variety of salts found in nature. Salt A represents a weak salt from Avery Island, USA (Berest and Brouard 1998), Salt B values are based on several Avery Island salts (Carter et al. 1993) and Salt C refers to a competent salt from the Asse mine in Germany (Berest and Brouard 1998). Salt B is the reference salt.

The apparent viscosity µapp for an Ellis model is derived from Eq. (4):

$${\mu _{{\text{app}}}}=\frac{1}{2}{\left({\frac{1}{{{A_{{\text{PS}}}}}}+\frac{{\tau _{{{\text{II}}}}^{{n - 1}}}}{{{A_{\text{D}}}}}} \right)^{ - 1}},$$
(10)

where \({A_{{\text{PS}}}}=2\mu _{0}^{{{\text{PS}}}}\). For low deviatoric stresses, the Ellis model reproduces a linear viscosity, while for high deviatoric stresses, power law viscosities are recovered (Fig. 1). The transition from one behavior to the other occurs when DPS = DD, so:

Fig. 1
figure 1

Normalized viscosity as a function of the second deviatoric stress invariant for pressure solution, dislocation creep and the Ellis model for Salt B

Full size image
$$\tau _{{{\text{II}}}}^{*}={\left({\frac{{{A_{\text{D}}}}}{{{A_{{\text{PS}}}}}}} \right)^{\frac{1}{{n - 1}}}}=\frac{{{A_{{\text{PS}}}}}}{2}D_{{{\text{II}}}}^{*},$$
(11)

where \(\tau _{{{\text{II}}}}^{*}\) is the transition stress and \(D_{{{\text{II}}}}^{*}\) is the transition deformation rate.

2.2 Setup

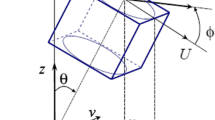
We study the closure velocity at the rim of a cylindrical hole with radius R embedded in rock salt and subjected to internal and far-field pressure loads. We consider a highly elongated cylinder as representative of boreholes and caverns, and we use a plane strain condition in the plane perpendicular to the hole axis. We assume that the host rock is homogeneous and isotropic.

At the hole rim, we apply normal tractions corresponding to the well pressure − pw and at the exterior far-field boundaries, we consider an ambient pressure \(- \;\overline{p}\) (Fig. 2). Pressures are taken positive in compression while stresses are positive in extension. The pressure difference \(\Delta p={p_{\text{w}}} - \bar{p}\) is taken to be always negative leading to borehole closure. In the following, r and θ are used to denote polar coordinates. Due to the rotational symmetry of the setup around the z-axis, the problem reduces to one dimension along the radial coordinate (Fig. 2). In the following, the radial component of the stress or rate of deformation tensor is implied when no subscripts and no tilde are used. The pressures of reference used hereafter correspond to the conditions encountered at 2000 m depth. \(\overline{p} =45\) MPa and pw = 40 MPa results in a negative pressure difference of 5 MPa.

Fig. 2
figure 2

Sketches of the two- and one-dimensional geometries of the problem with boundary conditions. The nodes in the numerical models are distributed according to a geometric sequence, giving a much finer mesh close to the hole. The domain size is much larger in the actual simulations

Full size image

A purely mechanical approach is adopted in this study and we neglect porous fluid flow, thermal diffusion and chemical interactions. The mechanical parameters are dependent on temperatures, however, and we define 60 °C as a temperature of reference at 2000 m depth.

2.3 Numerical Modelling

General analytical solutions are not readily available in the case of pressure-driven hole closure in a material obeying a nonlinear viscoelastic rheological behavior, and we need to resort to numerical approaches. In polar coordinates, the non-vanishing components of the rate of deformation tensor for the setup considered here are:

$${{\mathbf{D}}_{{\text{rr}}}}=\frac{{{\text{d}}{v_{\text{r}}}}}{{{\text{d}}r}};\quad{{\mathbf{D}}_{\theta \theta }}=\frac{{{v_{\text{r}}}}}{r},$$
(12)

where vr is the only non-zero radial component of the velocity vector. Applying the incompressibility condition gives:

$$\frac{{{\text{d}}{v_{\text{r}}}}}{{{\text{d}}r}}+\frac{{{v_{\text{r}}}}}{r}=0,$$
(13)

which after integration leads to:

$${v_{\text{r}}}={v_{\text{R}}}\frac{R}{r},$$
(14)

where vR is the closure velocity at the rim. Assuming there is no body force, the force balance is:

$$\frac{{\partial \sigma }}{{\partial r}}+2\frac{\tau }{r}=0,$$
(15)

where σ is the radial component of the total stress tensor defined as \(\sigma = - p+\tau\).We use two independent numerical codes based on the above equations to validate each other in the general case for which no analytical solutions are available. The first numerical code is based on the finite-element method (FEM) (Zienkiewicz et al. 2005) and uses a mixed formulation to deal with incompressibility. A three-node truss element is used to interpolate the velocity field and the pressure is discretized only at the exterior element nodes to ensure that the resulting mixed system of equations is solvable. We use an implicit scheme to discretize the constitutive law from Eq. (2) in time and we assume to be in the limit of small deformations such that:

$${D^{k+1}}=\frac{{{\tau ^{k+1}} -{\tau ^k}}}{{2G\Delta t}}+\frac{{{\tau ^{k+1}}}}{{2\mu _{{{\text{app}}}}^{{k+1}}}},$$
(16)

where k is the time index and ∆t is the time increment. Finally, we have:

$${\tau ^{k+1}}=2\mu _{{{\text{eff}}}}^{{k+1}}{D^{k+1}}+\eta _{{{\text{eff}}}}^{{k+1}}{\tau ^k},$$
(17)

where

$$\mu _{{{\text{eff}}}}^{{k+1}}={\left({\frac{1}{{G\Delta t}}+\frac{1}{{\mu _{{{\text{app}}}}^{{k+1}}}}} \right)^{ - 1}},$$
(18)
$$\eta _{{{\text{eff}}}}^{{k+1}}=\frac{{\mu _{{{\text{eff}}}}^{{k+1}}}}{{G\Delta t}}.$$
(19)

Equation (17) is used in the discretization of the force balance Eq. (15), expressed at the time step k + 1, in which \({\mu _{{\text{app}}}}\) is treated as a function of the unknown deviatoric stress \({\tau ^{k+1}}\). The approach to solve the nonlinear set of equations is based on using a combination of Picard iterations as done in FOLDER (Adamuszek et al. 2016) and incomplete stress updates. The initial guess for µapp is its value at the previous time step, except for the first time step, where µapp is evaluated for n = 1. In each Picard iteration, the nonlinear viscosity µapp is taken from the previous iteration, the resulting linear system is solved for the velocity, the new deviatoric rate of deformation and stress distributions are then computed and µapp is updated. During the Picard iterations, the stress in Eq. (17) is:

$${\tau ^{k+1}}({\text{iter}}+1)=2\mu _{{{\text{eff}}}}^{{k+1}}({\text{iter}}){D^{k+1}}({\text{iter}}+1)+\eta _{{{\text{eff}}}}^{{k+1}}({\text{iter}}){\tau ^k},$$
(20)

where iter is the Picard iteration number. The deviatoric stress at the first time step is the one obtained by solving the linear elastic problem.

The second numerical approach is based on an integral rather than differential formulation, which explicitly incorporates the incompressibility limit. The force balance from Eq. (15) can be integrated from r = R to ∞:

$$\int\limits_{R}^{\infty }{\frac{{{\text{d}}\sigma }}{{{\text{d}}r}}{\text{d}}r} +2\int\limits_{R}^{\infty }{\frac{\tau }{r}{\text{d}}r} =0.$$
(21)

Differentiating the first term in Eq. (21) with respect to time in the limit of small deformations (R is considered constant) gives:

$$\frac{{\text{d}}}{{{\text{d}}t}}\left({\int\limits_{R}^{\infty }{\frac{{{\text{d}}\sigma }}{{{\text{d}}r}}{\text{d}}r} } \right)=\frac{{\text{d}}}{{{\text{d}}t}}\Delta p=0.$$
(22)

Thus, we obtain:

$$\int\limits_{R}^{\infty }{\frac{{\dot{\tau }}}{r}{\text{d}}r} =0.$$
(23)

Dividing the constitutive law for a Maxwell body Eq. (3) by r and integrating from r = R to ∞:

$$2G\int\limits_{R}^{\infty }{\frac{D}{r}{\text{d}}r} =\int\limits_{R}^{\infty }{\frac{{\dot{\tau }}}{r}{\text{d}}r} +\int\limits_{R}^{\infty }{\frac{G}{{{\mu _{{\text{app}}}}}}\frac{\tau }{r}{\text{d}}r} .$$
(24)

Using the result obtained in Eq. (23) gives:

$$2\int\limits_{R}^{\infty }{\frac{D}{r}{\text{d}}r} =\int\limits_{R}^{\infty } {\frac{\tau }{{{\mu _{{\text{app}}}}r}}{\text{d}}r} .$$
(25)

With \(D= - \;{v_R}{R \mathord{\left/ {\vphantom {R {{r^2}}}} \right. \kern-0pt} {{r^2}}}\) in the incompressible limit from Eq. (14):

$$\frac{{{v_R}}}{R}= - \int\limits_{R}^{\infty } {\frac{1}{{{\mu _{{\text{app}}}}}}\frac{\tau }{r}{\text{d}}r} .$$
(26)

The closure velocity is evaluated numerically at every time step using the above expression. After evaluating the rate of deformation using vR, the stress at the next step is then computed using the implicit scheme from Eq. (20). Several Picard iterations are performed at every time step to ensure that a converged solution is reached. This approach is much faster than the FEM one because no system of equations needs to be solved.

As both numerical models are incompressible, a strong boundary effect may be observed due to the finite size of the numerical domain. This effect is stronger the more nonlinear the problem is and we minimize it by putting the exterior boundary far enough to approach the infinite body condition. This is important to reproduce some of the analytical solutions and to validate the numerical codes. In our simulations, the boundary is set at most at a distance of one hundred thousand times the borehole radius.

3 Analytical Solutions for End-Member Constitutive Laws

3.1 Elastic and Linear Viscoelastic Hole Closure

The response to instantaneous loads in a viscoelastic body is dictated by elasticity. In our case, elasticity is linear and the material is isotropic and incompressible, the displacement and stress fields for pressure-driven hole closure are (Jaeger et al. 2007):

$${u_{\text{r}}}=\frac{{\Delta p}}{{2G}}\frac{{{R^2}}}{r},$$
(27)
$${\sigma _{{\text{rr}}}}= - \overline {p} - \Delta p{\left( {\frac{R}{r}} \right)^2},$$
(28)
$${\sigma _{\theta \theta }}= - \overline {p} +\Delta p{\left( {\frac{R}{r}} \right)^2},$$
(29)
$$p=\overline {p} ,$$
(30)

where ur is the radial displacement. We note from the last expression that pressure remains constant throughout the body. The linear viscoelastic solution is now readily derived from these expressions using the correspondence principle. The behavior of a viscoelastic fluid can be described by a linear Maxwell model with relaxation function \({G_t}(t)=G{e^{{{ - t} \mathord{\left/ {\vphantom {{ - t} {{T_{\text{M}}}}}} \right. \kern-0pt} {{T_{\text{M}}}}}}},\) where \({T_{\text{M}}}={\mu \mathord{\left/ {\vphantom {\mu G}} \right. \kern-0pt} G}\) is the intrinsic material relaxation time and µ is the linear viscosity of this material. Other models than Maxwell can be considered to treat linear viscoelastic bodies and a review of closure displacements governed by these models is given by Gnirk and Johnson (1964). The expressions for total stress components Eqs. (28) and (29) obtained for elastic bodies are independent of material parameters, and they remain valid for the viscoelastic case. The closure displacement and velocity, on the other hand, in the case of a linear Maxwell model, become:

$${u_{\text{r}}}(r,t)=\frac{{\Delta p}}{{2G}}\left( {H(t)+\frac{t}{{{T_{\text{M}}}}}} \right)\frac{{{R^2}}}{r},$$
(31)
$${v_{\text{r}}}(r,t)=\frac{{\Delta p}}{{2G}}\frac{{{R^2}}}{r}\delta (t)+\frac{{\Delta p}}{{2\mu }}\frac{{{R^2}}}{r}H(t),$$
(32)

for \(t \geq 0\).

These expressions are valid in the limit of small deformations, where the borehole radius is considered constant. The closure velocity solution is used to benchmark the time dependence of the numerical codes in the linear limit.

In the compressible case, the closure velocity in a linear viscoelastic Maxwell body due to the creation of a hole in a preexisting pressure field \(- \;\bar {p}\) is:

$${v_{\text{r}}}(r,t)=\frac{{\Delta p}}{{2G}}\frac{{{R^2}}}{r}\delta (t)+\frac{{\Delta p}}{{2\mu }}\frac{{{R^2}}}{r}H(t),$$
(33)

which confirms that only the pressure difference \(\Delta p\) matters for closure. The elastic volumetric deformation is, therefore, not involved in the closure of linear viscoelastic bodies and it does not play a role in closure at all.

3.2 Nonlinear Viscous Hole Closure

The steady-state behavior of a viscoelastic fluid is governed by its viscous component, which we base on an incompressible Ellis model. The deviatoric stress at the rim in an Ellis viscous fluid is computed by solving (see “Steady-State Closure Velocity for an Incompressible Ellis Fluid” for derivation):

$$\left| {\tau \left( R \right)} \right|\left( {n - \frac{{\tau _{{{\text{II}}}}^{*}}}{{\left| {\tau \left( R \right)} \right|}}B\left( {{{\left( {1+{{\left( {\frac{{\tau _{{{\text{II}}}}^{*}}}{{\left| {\tau \left( R \right)} \right|}}} \right)}^{n - 1}}} \right)}^{ - 1}};\quad \frac{1}{{n - 1}},\frac{{n - 2}}{{n - 1}}} \right)} \right)=\left| {\Delta p} \right|,$$
(34)

where B is the incomplete beta function. The rate of deformation at the rim is then estimated:

$$D(R)=\frac{{\tau (R)}}{{{A_{{\text{PS}}}}}}+\operatorname{sgn} (\tau )\frac{{{{\left| {\tau (R)} \right|}^n}}}{{{A_D}}},$$
(35)

and the steady-state velocity at the rim is obtained from \(D(R)= - \;{{v_{{\text{R}}}^{{{\text{Ell}}}}(\infty )} \mathord{\left/ {\vphantom {{v_{{\text{R}}}^{{{\text{Ell}}}}(\infty )} R}} \right. \kern-0pt} R}\). The steady-state quantities for time-dependent variables are denoted with the infinite symbol ∞.

When \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) tends to infinity, the power law limit is approached (Wang et al. 2015; Cornet et al. 2016), and the velocity at the rim is:

$$v_{{\text{R}}}^{{{\text{pl}}}}(\infty )=\operatorname{sgn} \left( {\Delta p} \right)R\frac{{{{\left( {\left| {\Delta p} \right|/n} \right)}^n}}}{{{A_D}}}.$$
(36)

In Fig. 3, the closure velocity at the rim vR is plotted as a function of the load \(\Delta p\) for an Ellis viscous fluid. This plot is a graphical representation of the general analytical solution presented above. The load level \({{\Delta p} \mathord{\left/ {\vphantom {{\Delta p} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) provides a good estimation of the dominant deformation mechanism. When \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}<1\), there is a linear increase of the velocity with the load indicating that the linear deformation mechanism, i.e., pressure solution, is dominant. When \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}>1\), the velocity increase due to an increase in the load is nonlinear and depends on the stress exponent n, and when \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}} \gg 1\), vR is governed by \(\Delta {p^n}\). The dominant deformation mechanism in this limit is dislocation creep. This figure is very similar to the one obtained by Cornet et al. (2017) for a Carreau viscous fluid, which is expected as Ellis and Carreau fluids are largely similar.

Fig. 3
figure 3

Normalized steady-state closure velocity at the rim as a function of the load level \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) for an Ellis viscous fluid for the three salts from Table 1

Full size image

Looking at the stress distributions for different load ratios \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) (Fig. 4) confirms that when \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}<1\) the material behaves linearly everywhere and for \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}>1\) a zone dominated by nonlinear behavior is present adjacent to the hole. This zone is characterized by a less pronounced decrease of stress with distance and with a different stress split: the pressure is no longer constant and it supports an increasingly bigger portion of the total stress for higher stress exponents n.

Fig. 4
figure 4

Normalized stress distributions as a function of the distance to the hole for different values of the load level \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) for n = 4.5. The analytical solutions are plotted using lines while the numerical results from the first and second approaches are represented by markers

Full size image

The analytical solution presented above is used to benchmark our numerical approaches. Both numerical codes reproduce correctly the analytical solution as seen from Fig. 4. In the following, we use the second approach, which does not rely on FEM, to model the time-dependent closure of salt cavities.

4 Hole Closure for a Power Law Viscoelastic Rock Salt

4.1 Initial Closure Velocity

We first use a simple power law relationship for the viscous component of an incompressible Maxwell model. Upon an abrupt load, the initial response of the system is purely elastic and the stresses are given by:

$$\tau = - \Delta p\frac{{{R^2}}}{{{r^2}}}.$$
(37)

Wang et al. (2015) established that the initial closure velocity at the rim is (see “Initial Closure Velocity for an Incompressible Nonlinearly Viscoelastic Material Having a Power Law Viscosity Model” for derivation):

$$v_{{\text{R}}}^{{{\text{pl}}}}(t=0+)=\operatorname{sgn} (\Delta p)R\frac{{{{\left| {\Delta p} \right|}^n}}}{{n{A_{\text{D}}}}}={n^{n - 1}}v_{{\text{R}}}^{{{\text{pl}}}}(t=\infty ).$$
(38)

This expression is independent of the elastic modulus, as indicated by Eq. (26). The derivation of this result relies on the fact that \(\int_{R}^{\infty } {{{{D^{{\text{el}}}}} \mathord{\left/ {\vphantom {{{D^{{\text{el}}}}} r}} \right. \kern-0pt} r}{\text{d}}r=0}\) (from Eq. (23)), which does not mean that the elastic rate of deformation is initially zero everywhere, as was assumed by Barker et al. (1994). Their expression for the initial closure velocity at the rim is:

$$v_{{\text{R}}}^{{{\text{Barker}}}}(t=0+)=\operatorname{sgn} (\Delta p)R\frac{{{3^{{{\left( {n - 1} \right)} \mathord{\left/ {\vphantom {{\left( {n - 1} \right)} 2}} \right. \kern-0pt} 2}}}}}{{2n - 1}}\frac{{{{\left| {\Delta p} \right|}^n}}}{{{A_{\text{D}}}}},$$
(39)

which is similar to the one above and has been used in the oil industry (Liu et al. 2011), although it is internally inconsistent (Cornet et al. 2016). Their prefactor is as much as five times larger than the correct one when n = 5.

From the initial closure velocity, the total rate of deformation is computed: \(D= - \;v_{{\text{R}}}^{{{\text{pl}}}}{R \mathord{\left/ {\vphantom {R {{r^2}}}} \right. \kern-0pt} {{r^2}}}\). The initial viscous rate of deformation is derived from the stress distribution Eq. (37):

$${D^{{\text{vis}}}}= - \;\operatorname{sgn} \left( {\Delta p} \right)\frac{{{{\left| {\Delta p} \right|}^n}}}{{{A_{\text{D}}}}}\frac{{{R^{2n}}}}{{{r^{2n}}}},$$
(40)

and the elastic rate of deformation is then computed from \({D^{{\text{el}}}}=D - {D^{{\text{vis}}}}\). The initial rate of deformation and stress distribution are, therefore, fully characterized. In Fig. 5, we plot the rates of deformation for the reference case. The elastic rate of deformation is negative at the rim but quickly changes sign away from it to become equal to the total rate of deformation in the far field. Initially, the viscous rate of deformation at the rim is always n times larger than the total one while the magnitude of the negative elastic rate of deformation is n − 1 times larger.

Fig. 5
figure 5

Initial normalized rates of deformation distributions when n = 3. The circles denote negative values of the elastic rate of deformation

Full size image

The entire domain can be divided into a zone dominated by elastic deformation and another one dominated by viscous deformation. The size of the proximal, viscously dominated zone Rvis, i.e., the zone where the magnitude of the viscous rate of deformation is larger than the elastic one, is initially equal to:

$$\frac{{{R_{{\text{vis}}}}(t=0)}}{R}={\left( {2n} \right)^{\frac{1}{{2n - 2}}}},$$
(41)

which shows that a viscous-dominated zone is always present around the rim, no matter the type of salt.

4.2 Time-Dependent Hole Closure

In this section, we focus on the complete evolution of hole closure with time. Wang et al. (2015) defined a characteristic relaxation time \(\Theta\) as the ratio of the initial closure velocity to the rate of closure velocity (see “Initial Closure Acceleration for an Incompressible Nonlinearly Viscoelastic Material Having a Power Law Viscosity Model” for derivation) at the rim. We propose a slightly modified expression for the characteristic relaxation time denoted:

$$\theta = - \frac{{{v_{\text{R}}}(t=0+) - {v_{\text{R}}}(\infty )}}{{{{\dot {v}}_{\text{R}}}(t=0+)}}.$$
(42)

Since \(v_{{\text{R}}}^{{{\text{pl}}}}(\infty )={n^{1 - n}}v_{{\text{R}}}^{{{\text{pl}}}}(t=0+)\):

$$\theta =\frac{{2n - 1}}{{{{\left( {n - 1} \right)}^2}}}\frac{{{A_{\text{D}}}}}{{2G}}{\left| {\Delta p} \right|^{1 - n}}\left( {1 - {n^{1 - n}}} \right)=\Theta \cdot \left( {1 - {n^{1 - n}}} \right).$$
(43)

The correction factor \(1 - {n^{1 - n}}\) is equal to 0.89 for n = 3 and 0.99 for n = 4.5, so the difference between the characteristic relaxation time of Wang et al. (2015) and ours is hardly noticeable for closure in a power law-based Maxwell body.

In Fig. 6, θ is plotted as a function of pressure load for the three different salts from Table 1 and at different temperatures. A shear modulus G of 12.4 GPa is used in the computations. θ spans several orders of magnitude and is strongly influenced by the load, salt type and temperature. θ is a strongly decreasing function of \(\Delta p\).

Fig. 6
figure 6

θ as a function of the pressure difference for the three salts from Table 1 at 60 °C (left) and different temperatures for Salt B (right)

Full size image

In Fig. 7, the closure velocity drop from initial to steady state is investigated for the three salts from Table 1. The plots confirm the validity of the solutions for the instantaneous and long-term velocities and the relevance of the characteristic time since at t = θ the velocity drop is close to 50% irrespective of the salt type and load. If we define steady state as the moment when over 97% of the drop occurred, then steady state is reached after about t = 620θ The ratio between the initial and the steady-state velocity is nn−1 which is equal to 9 when n = 3 and 625 when n = 5. The magnitude of the velocity drop is, therefore, appreciably different for the three types of salts, even though the decay proceeds with the same normalized time. The right plot of Fig. 7 shows that the normalized velocity drop does not depend on the load \(\left| {\Delta p} \right|\). This implies that the closure velocity depends at all time on the load as \({\left| {\Delta p} \right|^n}\). It also suggests that the velocity drop for all salts can be described by a master curve for which we propose an empirical expression:

Fig. 7
figure 7

Normalized closure velocity at the rim as a function of time for power law viscoelastic salts. Left: closure velocity for three different salts, under reference conditions (semi-log scale). Right: closure velocity for different loads, for Salt B (loglog scale)

Full size image
$$v_{{\text{R}}}^{{{\text{pl}}}}(t)=v_{{\text{R}}}^{{{\text{pl}}}}(t=\infty )+\left( {v_{{\text{R}}}^{{{\text{pl}}}}(t=0+) - v_{{\text{R}}}^{{{\text{pl}}}}(t=\infty )} \right){\left( {1+{{\left( {2.55\frac{t}{\theta }} \right)}^{1.08}}} \right)^{ - {{0.48} \mathord{\left/ {\vphantom {{0.48} {1.08}}} \right. \kern-0pt} {1.08}}}}.$$
(44)

This proxy for the closure velocity has less than 3% error when \(t<3\theta\) independently of the salt, load and temperature considered. At larger times, the decay is dependent on the stress exponent n and the − 0.48 power we propose approximates the decays for n = 3.14 and n = 4.5 but not the one for n = 6.25. This proxy should, therefore, not be used at large times for large stress exponents.

The transition from the initial to the long-term behavior can also be seen in the time evolution of the stress distribution (left column of Fig. 8). The distribution of is initially governed everywhere by the linear elastic behavior of the material and becomes progressively governed by its nonlinear behavior in the neighborhood of the hole. In the elastic-dominated zone, the deviatoric stress is distributed as r−2 while in the viscous-dominated zone the spatial dependency is as r−2/n. The stress split between pressure and deviatoric stress evolves with time, with pressure supporting an increasingly bigger proportion of the total stress in the viscous zone. The right column of Fig. 8 shows the total, elastic and viscous rates of deformation. Due to incompressibility, the total rate of deformation scales as r−2 at all times. The elastic rate of deformation Del is always negative close to the rim and becomes positive and equal to the total rate of deformation at distances greater than Rvis. Finally, the viscous rate of deformation Dvis progressively evolves from a dependency in r−2n initially to a dependency in r−2 at steady state. In the transition from initial to steady state, Dvis has one branch in r−2 close to the rim and one in r−2n in the far field.

Fig. 8
figure 8

Normalized stress (left) and rate of deformation (right) distributions at different times. \(t=1e - 1*\theta\), \(t=1e1*\theta\) and \(t=1e3*\theta\) for Salt B under reference conditions. The circles in the strain rate plots show the magnitude of the elastic strain rate when it is negative

Full size image

Finally, Fig. 9 investigates the evolution of the radius of the viscous-dominated zone Rvis with time for the three salts from Table 1. Initially, Rvis is given by Eq. (41) and is only governed by the stress exponent n. Figure 9 shows how the growth of the viscous-dominated zone changes with time until it reaches its late-stage evolution.

Fig. 9
figure 9

Evolution of the size of the viscous-dominated zone with time for three different salts under reference conditions

Full size image

5 Hole Closure for an Ellis Viscoelastic Rock Salt

5.1 Initial Closure Velocity

In this section, we use an Ellis model for viscosity in the viscoelastic Maxwell constitutive law and we investigate how it affects the closure velocity. The initial stress is again purely elastic Eq. (37) and an expression for the initial closure velocity at the rim is (see “Initial Closure Velocity for an Incompressible Nonlinearly Viscoelastic Material Having an Ellis Viscosity Model” for derivation):

$$\frac{{v_{{\text{R}}}^{{{\text{Ell}}}}(t=0+)}}{R}=\frac{{\Delta p}}{{{A_{{\text{PS}}}}}}\left( {1+\frac{1}{n}{{\left( {\frac{{\left| {\Delta p} \right|}}{{\tau _{{{\text{II}}}}^{*}}}} \right)}^{n - 1}}} \right)=\frac{{\Delta p}}{{{A_{{\text{PS}}}}}}+v_{{\text{R}}}^{{{\text{pl}}}}(t=0+).$$
(45)

As for the power law viscoelastic material, the total, viscous and elastic rates of deformation can be derived so the instantaneous closure in an Ellis viscoelastic material is also fully characterized analytically for any load ratio \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) (Fig. 10).

Fig. 10
figure 10

Distributions of the normalized initial rates of deformation for different loads \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\) for Salt B. The circles denote negative values of the elastic rate of deformation

Full size image

The size of the initial viscously dominated zone is then estimated:

$$\frac{{{R_{{\text{vis}}}}(t=0)}}{R}={\left( {\frac{1}{{2n}} - \frac{1}{2}{{\left( {\frac{{\tau _{{{\text{II}}}}^{*}}}{{\left| {\Delta p} \right|}}} \right)}^{n - 1}}} \right)^{\frac{{ - 1}}{{2n - 2}}}}.$$
(46)

When \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}} \gg 1\), i.e., when dislocation creep is the dominant viscous deformation mechanism, Eq. (41) and Fig. 5 are recovered. The case \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}={n^{{1 \mathord{\left/ {\vphantom {1 {n - 1}}} \right. \kern-0pt} {n - 1}}}}\) corresponds to an infinitely large \({R_{{\text{vis}}}}(t=0)\) meaning that the viscous deformation is dominant everywhere. We use this criterion to define a pseudo-steady state which is reached instantaneously in an Ellis-based Maxwell material for all loads \(\left| {\Delta p} \right|\) smaller than \({n^{{1 \mathord{\left/ {\vphantom {1 {n - 1}}} \right. \kern-0pt} {n - 1}}}}\tau _{{{\text{II}}}}^{*}\) (Fig. 10).

In Fig. 11 the ratios of the initial to the steady-state closure velocities are plotted as a function of the load ratio \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\). For \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}<1\), pressure solution is the dominant viscous deformation mechanism and the initial and steady-state closure velocities are equal. For \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}>1\), dislocation creep is the dominant viscous deformation mechanism and for \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}} \gg 1\) the initial closure velocity is nn−1 larger than the steady-state one (Eq. (38)).

Fig. 11
figure 11

Ratios of the instantaneous to the steady-state closure velocities using an Ellis viscoelastic constitutive law for the three salts from Table 1 as a function of the load ratio \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}\)

Full size image

5.2 Transient Hole Closure

We use the characteristic relaxation time θ defined by Eq. (42) to evaluate the time at which the transition in closure velocity from initial to final occurs. θ can be computed analytically for an Ellis-based Maxwell material (see “Initial closure acceleration for an incompressible nonlinearly viscoelastic material having an Ellis viscosity model” for the derivation of the initial closure velocity rate at the rim). The expression for \(\Theta\) that was originally proposed by Wang et al. (2015) overestimates the time at which the drop from initial to steady-state closure occurs when pressure solution is important. For example, when \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}=1\), the characteristic time is overestimated by a factor 12.5 for Salt B if the unmodified version of θ is used.

In Fig. 12, the initial to steady-state closure velocity drop is plotted for different salts and loads. The time is normalized by the version of θ proposed in Eq. (42). The figure confirms the validity of using this characteristic time as it captures the moment at which the closure velocity has dropped by approximately half its net change no matter the salt or load. The curves for \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}=0.1\) and 1 show the same pattern as the ones for loads larger than \({n^{{1 \mathord{\left/ {\vphantom {1 {n - 1}}} \right. \kern-0pt} {n - 1}}}}\tau _{{{\text{II}}}}^{*}\). When \(\left| {\Delta p} \right|<{n^{{1 \mathord{\left/ {\vphantom {1 {n - 1}}} \right. \kern-0pt} {n - 1}}}}\tau _{{{\text{II}}}}^{*}\), the magnitude of the velocity drop (Fig. 11) is so small that steady state can be approximated even though true steady state is never reached instantaneously in an Ellis-based Maxwell material. When \(\left| {\Delta p} \right| \gg \tau _{{{\text{II}}}}^{*}\), dislocation creep is the dominant viscous deformation mechanism and the time evolution of the velocity drop for a power law-based Maxwell body is retrieved.

Fig. 12
figure 12

Normalized closure velocities at the rim as a function of time for Ellis-based Maxwell salts. Left: closure velocities for three different salts, when \({{\left| {\Delta p} \right|} \mathord{\left/ {\vphantom {{\left| {\Delta p} \right|} {\tau _{{{\text{II}}}}^{*}}}} \right. \kern-0pt} {\tau _{{{\text{II}}}}^{*}}}=5\). Right: closure velocities for different loads, for Salt B. The proxy for the closure velocity in a power law-based Maxwell Eq. (44) is also shown in both plots for comparison

Full size image

5.3 Depth Dependence

In the subsurface, both the temperature and the pressure difference ∆p increase with depth, and we investigate how hole closure speed varies with depth and time in a typical application. The salt considered here is Salt B from Table 1. It is incompressible and its constitutive law is viscoelastic with nonlinear viscosity. The viscosity is based on an Ellis model with a depth-independent grain size of 7.5 mm. Figure 13 presents the depth distribution of the temperature and differential pressure load ∆p used in this application. At shallow depths where temperatures and loads are low, pressure solution is the dominant viscous deformation mechanism while at great depths dislocation creep dominates.

Fig. 13
figure 13

Evolution of the temperature, load and characteristic times θ, \(\Theta\) and γ with depth

Full size image

The third column of Fig. 13 shows the evolution with depth of three characteristic times: θ, \(\Theta\) and γ. γ is the pseudo-steady-state time, i.e., the time necessary for the viscous rate of deformation to be dominant over the elastic one everywhere: \({R_{{\text{vis}}}}=\infty\). The depth distributions of θ and \(\Theta\) are very similar with differences appearing only at shallow depths, where pressure solution is the dominant viscous deformation mechanism. This figure illustrates the magnitude of the overestimation done if \(\Theta\) is used to evaluate the relaxation time. Comparing the curves for θ and γ shows that their behavior is opposite: θ decreases with depth while γ increases. From 1100 to 1300 m depth, γ is not represented because the closure velocity at these depths reaches pseudo-steady state instantaneously. This interpretation of cavity closure is very different from the one that would be done based on θ alone and illustrates the usefulness of using both characteristic times θ and γ in combination when interpreting hole closure data.

In Fig. 14, closure velocity profiles are displayed at different times to show their evolution for the Ellis and the power law-based viscoelastic models. Initially at t = 10−3 year, the velocity profiles of the two approaches are only different in the upper 200 m from 1100 to 1300 m. At these depths, the salt is already behaving almost completely viscously for the Ellis model. With time, the overlap of the two curves at the deeper depths disappears and the closure velocities are higher for the Ellis model. The increase in closure velocities is larger, the more dominant pressure solution is as a deformation mechanism. Finally, the complete velocity profile for the Ellis model does not change a lot after 1 year which confirms the use of the time γ to evaluate when steady state is approached.

Fig. 14
figure 14

Profiles for the velocity at the rim as a function of time for the Ellis and power law-based viscoelastic models

Full size image

6 Discussion

6.1 Plasticity

This study focuses on the viscoelastic behavior of salt and dismisses plasticity. This assumption has been made due to the observation that above 5–10 MPa confining pressure, salt is incompressible (Fossum and Fredrich 2002). As already pointed out, these confining pressures are reached below 250–500 m and the no-plasticity assumption is, therefore, valid for most applications. Only shallow applications like mines and certain caverns need to take plastic behavior into account. The cavity-induced stress concentration close to the rim can, however, lead to a deeper extension of the zone influenced by plasticity. At the depths where dilatancy is important, an increase in permeability is observed (Hunsche and Hampel 1999; Alkan 2009). If brine is present in the cavity, increased pressure solution can occur when the brine permeates through the damaged zone. If natural gas or air is present, on the other hand, pressure solution is prevented (Peach et al. 2001). As pointed out above, the stress in the salt body is initially linear elastic and the deviatoric stresses close to the rim are high. As it is high, a dominantly nonlinear viscous zone appears in the neighborhood of the hole and starts to grow. In this viscously dominated zone, the deviatoric stresses decrease with time and an analysis of the factor of safety shows that plasticity is most important for short timescales (Wang et al. 2015). For long timescales, the stresses close to the hole converge to the viscous steady-state solution and only changes in cavern pressure are problematic. In the case of storage facilities, the pressure drops due to production have to be controlled to prevent catastrophic failure. As pointed out by Wang et al. (2011), hole pressure changes larger than ∆p/n lead to failure and should, therefore, be avoided. More than the instantaneous plastic behavior of the salt, it is the reactivation of cavity closure through pressure changes after a long idle time which should be planned with great care.

6.2 Viscosity

This study describes the viscous component of the viscoelastic law by its steady-state behavior. The transient rheological creep behavior has been dismissed because the relaxation time associated with transient geometrical creep closure is much longer (Karimi-Jafari et al. 2006; Wang et al. 2015). The transient rheological behavior of salt is due to the microstructure of salt rearranging to adapt to the newly applied stress and it leads to strain hardening during creep tests. Geometrical creep, on the other hand, comes from the slow redistribution of stresses following a change in hole pressure and makes hole closure time dependent, even though the constitutive law does not take into account transient creep. As pointed out by Karimi-Jafari et al. (2006), rheological transient creep vanishes rapidly and it, therefore, does not have a large impact for long-term applications. In the short term, following a change in cavern pressure, rheological transient creep leads to faster closure rates and hole relaxation has two different relaxation times: one due to transient rheological creep and the other one due to transient geometrical creep closure. The salt in the subsurface is pre-stressed so the microstructure of the salt does not have to rearrange extensively and strain hardening is limited. In this light, the magnitude of the closure velocity drop due to transient rheological creep might be much smaller than the other one.

Fluid-assisted grain boundary migration is a strain-activated process which happens in relation with dislocation creep. During dislocation creep, dislocations accumulate in grains to form subgrains. The progressive accumulation of dislocations at subgrain boundaries leads to the rotation of the subgrains until they are detached and form new small grains (Drury and Urai 1990). Grain boundary migration, on the other hand, leads to increased grain sizes. The difference in strain energy between neighboring grains promotes the growth of the small undeformed grains at the expense of the old deformed ones. From this perspective, grain size is best described by a distribution (Ter Heege et al. 2005b) and a single value like mean or median does not capture the competition between the grain size increase and reduction processes (Ter Heege 2002). As pointed out by Cornet et al. (2018), the viscosity of salt is highly sensitive to grain size and a more elaborated model taking into account grain size distributions should be considered. In this study, a constant grain size has been used for the salt body because there is a lack of data regarding grain size distributions in Avery Island salts. On the other hand, the dislocation creep parameters used in this study have been established under steady-state conditions, when grain boundary migration was active, implying that the softening associated with this recrystallization process is already included in the parameters used above.

6.3 Practical Implications

Engineers like to have ready-to-use tools and formulas which evaluate the importance of various input parameters to determine their significance. One of these formulas is the one giving the initial closure velocity presented by Barker et al. (1994) which relies on a power law-based viscoelastic model. Although it is widely used in the field to assess hole closure, it is inconsistent and breaks its own assumptions (Cornet et al. 2016). Furthermore, it dismisses the contribution of pressure solution and only considers dislocation creep. Pressure solution is often dismissed or referred to as an undefined mechanism (Munson 1997) and considered not relevant when it comes to cavity closure in rock salt. This is due to the fact that dislocation creep is the deformation mechanism investigated in the high-load creep tests usually implemented in the laboratory. Under low loads, however, Bérest et al. (2015) showed that pressure solution is governing deformation. In this study, we have come up with new analytical solutions giving the closure velocity at the rim which are both consistent and considering the additional contribution from pressure solution. We have shown that it is of high importance to take pressure solution into account close to the surface or at large timescales. If this is not done, the closure velocity might be underestimated by several orders of magnitude. Using our analytical solutions, better estimates of the closure rate will be done resulting on a better forecast of cavity closure.

7 Conclusion

Pressure difference-driven closure of infinitely long cylindrical holes is investigated numerically and analytically in Maxwell type nonlinear viscoelastic salts. Two models are considered for the viscosity: the power law and the Ellis model which assumes that pressure solution and dislocation creep operate independently. The latter prevents viscosities to reach infinite values and is more general by including both the first model and a grain size-dependent linear viscous regime. Plasticity is not considered in this study due to the high confining pressures encountered at depths larger than 500 m and transient viscosity is also dismissed. A constant mean grain size is assumed in the salt body but the parameters for dislocation creep include the softening effect due to water-assisted grain boundary migration.

First, hole closure in power law-based viscoelastic models is considered and fully characterized initially. The transient evolution of hole closure is complex but its time dependency is well captured by the characteristic time θ, which is a modified version of the one proposed by Wang et al. (2015). This characteristic time describes the moment when half the drop from initial to steady-state closure velocity has occurred. A proxy for the closure velocity at the rim is proposed which has less than 3% inaccuracy for times smaller than 3θ, irrespective of the load or salt type. The time evolution of the stress and rate of deformation distributions are also investigated and show the growth of a nonlinear viscously dominated zone in the neighborhood of the hole.

Hole closure in Ellis-based Maxwell salts is also investigated and analytical solutions are provided for the instantaneous and steady-state cases. A load threshold is defined analytically to determine whether steady state is already approached initially in these salts. The time evolution of closure is analyzed and the characteristic time θ is shown to be also relevant to describe the viscoelastic relaxation occurring for this constitutive law. Finally, the evolution with depth and time of closure in an underground application is considered. The closure velocity at shallow depths is shown to reach steady state almost instantaneously due to pressure solution. This underlines the necessity of considering pressure solution as a deformation mechanism in rock salt. The characteristic times and load thresholds described in this study are efficient tools to better understand how closure occurs in salt cavities at depth and will hopefully bring some answers to engineers working in this field.