1 Introduction

Fractures commonly exist in geotechnical media, such as rock joints, faults, and ground fractures. These fractures make geotechnical media discontinuous and have significant effects on wave propagation (Hudson et al. 1996; Gu et al. 1996a). Transmission and reflection appear at the fracture interface, whose boundary is not uniform and homogeneous (Miller 1978; Schoenberg 1983). The displacement discontinuity model (DDM) treats the stress at the front and rear interfaces as continuous but not the displacement. It is suitable for studying wave propagation through unfilled fractures, while fracture thickness is sufficiently smaller than the wavelength. Meanwhile, linear elastic, nonlinear elastic, viscoelastic, and coulomb-slip behaviors have been applied to describe the deformation behavior of fractures (Pyrak-Nolte et al. 1990a, b; Gu et al. 1996b; Zhao and Cai 2001; Zhao et al. 2006a, b; Li 2013). Many methods have been established regarding the frequency or time domains in investigations of stress wave propagation through unfilled fractures (Miller 1977; Schoenberg 1980; Cai and Zhao 2000; Li and Ma 2010; Zhu et al. 2011b; Zhao et al. 2012).

Compared with unfilled fractures, filled fractures are more common in nature. Considering the mass of filled medium, the DDM is no longer appropriate for describing the dynamic behavior of filled fractures (Zhu et al. 2011a). Results of dynamic tests using a split Hopkinson pressure bar have indicated that the displacement and stress discontinuity model (DSDM) is more suitable than DDM in describing filled joint effects on wave propagation when up to 10 mm in thickness (Wu et al. 2013). The physical properties and the mass of filled medium both influence wave propagation across filled fractures (Li and Ma 2009; Zhu et al. 2011a, 2012). Li and Ma (2009) have studied nonlinear elastic behaviors of filled rock joints using a modified split Hopkinson pressure bar apparatus and established a nonlinear elastic model different from the Bandis–Barton (B–B) model. Fan and Wong (2013) have investigated the influence of differences between loading and unloading behaviors on wave propagation across filled joints using the B–B model. Also, Wu et al. (2014), using the method of characteristics (MC), have investigated the effects of filling material on P-waves propagating normally through fractures. Taking the thickness of fracture into account, Li et al. (2013, 2014, 2015) have proposed a thin-layer interface model (TLIM) and studied wave propagation obliquely through filled joints and shear wave propagation across filled joints with interfacial shear strength.

In addition to nonlinear elastic behavior, viscoelastic behavior of filled joints is also of great significance. Dynamic behavior of filled joints is mostly controlled by the filled medium (Li and Ma 2009; Zhu et al. 2012; Wu et al. 2012, 2013). Natural joints are often filled with weathered rock, saturated sand, or clay, which behave as viscoelastic deformation behavior under dynamic loads (Zhu et al. 2011a, 2012; Wu et al. 2013; Huang et al. 2015b). Additionally, liquid might also introduce viscous coupling between the two fracture surfaces (Pyrak-Nolte et al. 1990a). Myer et al. (1990) and Pyrak-Nolte et al. (1990a) have provided closed-form solutions of wave propagation, in the frequency domain, across fractures with viscoelastic behavior. Considering filled medium mass, Zhu et al. (2011a) have extended these closed-form solutions to filled joints with viscoelastic deformational behavior. Zhu et al. (2012) and Wu et al. (2012) have studied normal wave propagation through parallel rock joints filled with viscoelastic medium, adopting the DSDM and modified recursive method (MRM) in the frequency domain. The propagator matrix method (PMM) has also been used to study stress wave propagation through a set of viscoelastic joints (Huang et al. 2015a).

A time-domain recursive method (TDRM) has been proposed based on the conservation of momentum at wave fronts, which predicts the time-history curves of transmitted and reflected waves in obliquely incident conditions (Li and Ma 2010; Li et al. 2012; Chai et al. 2016). Coulomb-slip and nonlinear elastic behaviors of joints have been studied in TDRM with DDM (Li et al. 2011; Li 2013). However, there has been to date no investigations regarding TDRM that takes the mass or viscoelastic behavior of the filled medium into account.

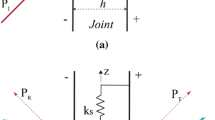
In the present study, the standard linear solid (SLS) model (i.e., an auxiliary spring in series with a Kelvin model, as shown in Fig. 1, where k represents the elastic stiffness of the spring and η represents the viscous stiffness of the dashpot) was adopted to derive modified time-domain recursive method. It can be degenerated into a typical viscoelastic model, such as the Kelvin or Maxwell models used by Zhu et al. (2011a). The DDM was then extended to the DSDM in TDRM, and the differential constitutive relationship of the SLS model was adopted to introduce the filled medium mass and viscoelastic behavior. Then, verification by comparison of this new method with the results of closed-form solutions calculated by the frequency-domain method (FDM) was conducted. Finally, the effects of the frequency, incident waveform, and type of viscoelastic model on wave propagation across filled joints were discussed as well as the efficiency and adaptability of this method.

Fig. 1
figure 1

Standard linear solid (SLS) model

Full size image

2 Theoretical Analysis

2.1 Viscoelastic Model

Filled medium might display viscoelastic properties when seismic waves propagate across filled fractures (Pyrak-Nolte et al. 1990a; Zhu et al. 2011a). The Kelvin model approximately describes creep behaviors of filled material but is not suitable for describing stress relaxation behaviors. The Maxwell model approximately describes stress relaxation behaviors and just describes Newton’s viscous flow but cannot describe complex creep behaviors. In comparison, the SLS model with three parameters can describe creep and stress relaxation behaviors and can degrade into the viscoelastic model with two parameters, i.e., the Kelvin and Maxwell models. To obtain a more general solution, the SLS deformation model was selected for theoretical derivation. Mechanical properties of the viscoelastic model were described in the frequency and time domains. As the ratio of stress to strain, the complex modulus used in the frequency domain was a constant form with different parameters for different models. In the time domain, stress and strain were related by linear differential equations that involve stress, strain, and their derivatives with respect to time.

The differential constitutive relationship of the SLS model can be expressed as:

$$p_{0} \sigma + p_{1} \frac{\partial \sigma }{\partial t} = q_{0} \varepsilon + q_{1} \frac{\partial \varepsilon }{\partial t}$$
(1)

where σ is the stress, ε the strain, p 0 = k 1 + k 2, p 1 = η, q 0 = k 1·k 2, and q 1 = η·k 2.

When an alternate strain was input (i.e., \(\varepsilon \left( t \right) = \varepsilon_{0} \left[ {\cos \left( {\omega t} \right) - i\sin \left( {\omega t} \right)} \right] = \varepsilon_{0} e^{ - i\omega t}\)), the complex modulus of the SLS model can be written as:

$$k\left( {i\omega } \right) = \frac{{q_{0} - i\omega q_{1} }}{{p_{0} - i\omega p_{1} }}$$
(2)

where k(iω) denotes the complex modulus of the SLS model, i the complex unit, and ω the angular frequency. For the Kelvin model, p 0 = 1, p 1 = 0, q 0 = k 1, and q 1 = η; for Maxwell model, p 0 = k 2, p 1 = η, q 0 = 0, and q 1 = η·k 2.

2.2 Method Introduction

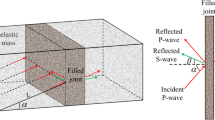
The theoretical basis of TDRM was the conservation of momentum at wave fronts. As a function of particle velocity, wave stress was obtained through the conservation of momentum at wave fronts, i.e., σ = zv, where z is the wave impedance of medium and v the particle velocity. Combined with Snell’s law, the stress and particle velocity at the front and rear interfaces was established (Li and Ma 2010). Then, expressions of transmitted and reflected waves were deduced by substituting the stress and particle velocities at the two sides of the interface considering the boundary condition. The propagation of a stress wave through a fracture is shown in Fig. 2, where α and β are the angles of the P- and SV-waves, respectively.

Fig. 2
figure 2

Transmission and reflection of obliquely incident of P- and SV-wave across a fracture

Full size image

2.3 Wave Propagation Equation

According to consideration of filled medium mass in the frequency domain (Zhu et al. 2011a), stresses at the fracture interface in the time domain satisfied the relation as follows:

$$\left. \begin{aligned} \sigma^{ - } - \sigma^{ + } = m_{n} a_{n}^{2} \hfill \\ \tau^{ - } - \tau^{ + } = m_{\tau } a_{\tau }^{2} \hfill \\ \end{aligned} \right\}$$
(3)

where \(\sigma\) and \(\tau\) are the normal and tangential wave stresses, respectively, acceleration the first derivative of particle velocity with the respect to time, i.e., \(a_{i} = \frac{{v_{i} - v_{i - 1} }}{\Delta t}\). \(\Delta t\) is a small time interval between \(v_{i - 1}\) and \(v_{i}\), and superscripts − and + refer to interfaces of the incidence and transmission half-space, respectively. The subscripts n and \(\tau\) refer to the normal and tangential directions, respectively. The m is the mass, where \(m_{n} = \rho_{0} h\), \(m_{\tau } = \left[ {1 - \left( {{{C_{\text{plate}} } \mathord{\left/ {\vphantom {{C_{\text{plate}} } C}} \right. \kern-0pt} C}} \right)^{2} \sin^{2} \chi } \right]m_{n}\), \(\rho_{0}\) is the filled medium density, h the fracture thickness, and C and χ the wave velocity and incident angle of the incident wave, respectively. C plate is the plate velocity of the filled medium, i.e.,\(C_{\text{plate}} = \sqrt {{{E_{0} } \mathord{\left/ {\vphantom {{E_{0} } {\left[ {\rho_{0} \left( {1 - \upsilon_{0}^{2} } \right)} \right]}}} \right. \kern-0pt} {\left[ {\rho_{0} \left( {1 - \upsilon_{0}^{2} } \right)} \right]}}}\), where \(E_{0}\) and \(\upsilon_{0}\) are the Young’s modulus and Poisson’s ratio of the filled medium, respectively (Zhu et al. 2011a; Rokhlin and Wang 1991).

The DDM was an equivalent velocity discontinuity model. For the differential constitutive relationship of a viscoelastic model, velocity was determined as the derivative of displacement with respect to time as follows:

$$q_{0} \frac{{\partial \left( {u^{ - } - u^{ + } } \right)}}{\partial t} + q_{1} \frac{{\partial \left( {v^{ - } - v^{ + } } \right)}}{\partial t} = p_{0} \frac{{\partial \sigma^{ + } }}{\partial t} + p_{1} \frac{{\partial^{2} \sigma^{ + } }}{{\partial t^{2} }}$$
(4)

where

$$v = \frac{\partial u}{\partial t}$$
(5)

The discontinuity assumption regarding displacement is illustrated below by velocity and its derivative with respect to time:

$$\left. \begin{aligned} q_{n0} \left( {v_{n\left( i \right)}^{ - } - v_{n\left( i \right)}^{ + } } \right) = p_{n0} \frac{{\partial \sigma_{\left( i \right)}^{ + } }}{\partial t} + p_{n1} \frac{{\partial^{2} \sigma_{\left( i \right)}^{ + } }}{{\partial t^{2} }} - q_{n1} \frac{{\partial \left( {v_{n\left( i \right)}^{ - } - v_{n\left( i \right)}^{ + } } \right)}}{\partial t} \hfill \\ q_{t0} \left( {v_{t\left( i \right)}^{ - } - v_{t\left( i \right)}^{ + } } \right) = p_{t0} \frac{{\partial \tau_{\left( i \right)}^{ + } }}{\partial t} + p_{t1} \frac{{\partial^{2} \tau_{\left( i \right)}^{ + } }}{{\partial t^{2} }} - q_{t1} \frac{{\partial \left( {v_{t\left( i \right)}^{ - } - v_{t\left( i \right)}^{ + } } \right)}}{\partial t} \hfill \\ \end{aligned} \right\}$$
(6)

where

$$\frac{{\partial \sigma_{\left( i \right)}^{ + } }}{\partial t} = \frac{{\sigma_{{\left( {i + 1} \right)}}^{ + } - \sigma_{\left( i \right)}^{ + } }}{\Delta t}$$
(7)
$$\frac{{\partial^{2} \sigma_{\left( i \right)}^{ + } }}{{\partial t^{2} }} = \frac{{\sigma_{{\left( {i + 1} \right)}}^{ + } - 2\sigma_{\left( i \right)}^{ + } + \sigma_{{\left( {i - 1} \right)}}^{ + } }}{{\Delta t^{2} }}$$
(8)
$$\frac{{\partial v_{n\left( i \right)}^{ - } }}{\partial t} = \frac{{v_{{n\left( {i + 1} \right)}}^{ - } - v_{n\left( i \right)}^{ - } }}{\Delta t}$$
(9)

For an incident P-wave, recursive formulas were obtained by substituting the stress and particle velocities at each side (Li and Ma 2010) into Eqs. (3) and (6), which are expressed in matrix form as follows:

$$Av_{I(i)} + B\left[ {\begin{array}{*{20}l} {v_{{R_{P} (i)}} } \\ {v_{{R_{S} (i)}} } \\ \end{array} } \right] + C\left[ {\begin{array}{*{20}l} {v_{{T_{P} (i)}} } \\ {v_{{T_{S} (i)}} } \\ \end{array} } \right] = D\left[ {\begin{array}{*{20}l} {v_{{T_{P} (i - 1)}} } \\ {v_{{T_{S} (i - 1)}} } \\ \end{array} } \right]$$
(10)
$$Ev_{I(i + 1)} + F\left[ {\begin{array}{*{20}l} {v_{{R_{P} (i + 1)}} } \\ {v_{{R_{S} (i + 1)}} } \\ \end{array} } \right] + G\left[ {\begin{array}{*{20}l} {v_{{T_{P} (i + 1)}} } \\ {v_{{T_{S} (i + 1)}} } \\ \end{array} } \right] = Hv_{I(i)} + I\left[ {\begin{array}{*{20}l} {v_{{R_{P} (i)}} } \\ {v_{{R_{S} (i)}} } \\ \end{array} } \right] + J\left[ {\begin{array}{*{20}l} {v_{{T_{P} (i)}} } \\ {v_{{T_{S} (i)}} } \\ \end{array} } \right] + K\left[ {\begin{array}{*{20}l} {v_{{T_{P} (i - 1)}} } \\ {v_{{T_{S} (i - 1)}} } \\ \end{array} } \right]$$
(11)

where

$$A = \left[ {\begin{array}{*{20}l} {z_{p} \cos 2\beta } \\ {z_{p} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha } \\ \end{array} } \right]$$
(12)
$$B = \left[ {\begin{array}{*{20}l} {z_{p} \cos 2\beta } & { - z_{s} \sin 2\beta } \\ { - z_{p} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha } & { - z_{s} \cos 2\beta } \\ \end{array} } \right]$$
(13)
$$C = \left[ {\begin{array}{*{20}l} { - z_{p} \cos 2\beta - \frac{{m_{n} \cos \alpha }}{\Delta t}} & { - z_{s} \sin 2\beta - \frac{{m_{n} \sin \beta }}{\Delta t}} \\ { - z_{p} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha - \frac{{m_{\tau } \sin \alpha }}{\Delta t}} & {z_{s} \cos 2\beta + \frac{{m_{\tau } \cos \beta }}{\Delta t}} \\ \end{array} } \right]$$
(14)
$$D = \frac{1}{\Delta t}\left[ {\begin{array}{*{20}l} { - m_{n} \cos \alpha } & { - m_{n} \sin \beta } \\ { - m_{\tau } \sin \alpha } & {m_{\tau } \cos \beta } \\ \end{array} } \right]$$
(15)
$$E = \left[ {\begin{array}{*{20}l} {q_{n1} \cos \alpha } \\ {q_{\tau 1} \sin \alpha } \\ \end{array} } \right]$$
(16)
$$F = \left[ {\begin{array}{*{20}l} { - q_{n1} \cos \alpha } & {q_{n1} \sin \beta } \\ {q_{\tau 1} \sin \alpha } & {q_{\tau 1} \cos \beta } \\ \end{array} } \right]$$
(17)
$$G = \left[ {\begin{array}{*{20}l} { - q_{n1} \cos \alpha - z_{p} \cos 2\beta \left( {p_{n0} + \frac{{p_{n1} }}{\Delta t}} \right)} & { - q_{n1} \sin \beta - z_{s} \sin 2\beta \left( {p_{n0} + \frac{{p_{n1} }}{\Delta t}} \right)} \\ { - q_{\tau 1} \sin \alpha - z_{p} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha \left( {p_{\tau 0} + \frac{{p_{\tau 1} }}{\Delta t}} \right)} & {q_{\tau 1} \cos \beta + z_{s} \cos 2\beta \left( {p_{\tau 0} + \frac{{p_{\tau 1} }}{\Delta t}} \right)} \\ \end{array} } \right]$$
(18)
$$H = \left[ {\begin{array}{*{20}l} {\left( {q_{n1} - q_{n0} \Delta t} \right)\cos \alpha } \\ {\left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\sin \alpha } \\ \end{array} } \right]$$
(19)
$$I = \left[ {\begin{array}{*{20}l} { - \left( {q_{n1} - q_{n0} \Delta t} \right)\cos \alpha } & {\left( {q_{n1} - q_{n0} \Delta t} \right)\sin \beta } \\ {\left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\sin \alpha } & {\left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\cos \beta } \\ \end{array} } \right]$$
(20)
$$J = \left[ {\begin{array}{*{20}l} { - \left( {q_{n1} - q_{n0} \Delta t} \right)\cos - z_{p} \cos 2\beta \left( {p_{n0} + \frac{{2p_{n1} }}{\Delta t}} \right)} & { - \left( {q_{n1} - q_{n0} \Delta t} \right)\sin \beta - z_{s} \sin 2\beta \left( {p_{n0} + \frac{{2p_{n1} }}{\Delta t}} \right)} \\ { - \left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\sin \alpha - z_{p} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha \left( {p_{\tau 0} + \frac{{2p_{\tau 1} }}{\Delta t}} \right)} & {\left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\cos \beta + z_{s} \cos 2\beta \left( {p_{\tau 0} + \frac{{2p_{\tau 1} }}{\Delta t}} \right)} \\ \end{array} } \right]$$
(21)
$$K = \frac{1}{\Delta t}\left[ {\begin{array}{*{20}l} {p_{n1} z_{p} \cos 2\beta } & {p_{n1} z_{s} \sin 2\beta } \\ {p_{\tau 1} \sin 2\beta {\text{tg}}\beta {\text{ctg}}\alpha } & { - p_{\tau 1} z_{s} \cos 2\beta } \\ \end{array} } \right]$$
(22)

where v is the components of particle velocity, z p the P-wave impedance of the rock solid, i.e., z p  = ρc p , where ρ and c p denote the density and P-wave velocity of the rock solid, respectively. I, T, and R mean incident, transmitted, and reflected, and P and S refer to as P- and SV-waves, respectively.

The recursive formulas for SV-wave incidence were similar to P-wave incidence, with only the coefficient matrices of the incident wave, i.e., A, E, and H, changed as follows:

$$A = \left[ {\begin{array}{*{20}l} {z_{s} \sin 2\beta } \\ { - z_{s} \cos 2\beta } \\ \end{array} } \right]$$
(23)
$$E = \left[ {\begin{array}{*{20}l} {q_{n1} \sin \beta } \\ {q_{\tau 1} \cos \beta } \\ \end{array} } \right]$$
(24)
$$H = \left[ {\begin{array}{*{20}l} {\left( {q_{n1} - q_{n0} \Delta t} \right)\sin \beta } \\ {\left( {q_{\tau 1} - q_{\tau 0} \Delta t} \right)\cos \beta } \\ \end{array} } \right]$$
(25)

where z s  = ρc s , z s and c s are the SV-wave impedance and the SV-wave velocity of the rock solid, respectively.

The transmission and reflection coefficients, i.e., T fr and R fr, for an incident P- or SV-wave are determined as the amplitude ratios of transmitted and reflected waves to the incident wave. Where T and R refer to transmission and reflection, respectively, the first subscript f refers to the incident wave (f = p or s), the second subscript r the transmitted or reflected wave (r = p or s). In the initial calculation, the initial value of the transmitted wave was assumed to be zero (Li and Ma 2010).

3 Verification

Closed-form solutions for wave propagation across fractures have been proposed in the frequency domain by Pyrak-Nolte et al. (1990b) and Gu et al. (1996a). In the present study, wave propagation was expressed by trend changes of the transmission and reflection coefficients as a function of the relative parameter. To verify the method proposed in this paper, a comparison was performed between the transmission and reflection coefficients from the present method and closed-form solutions. The parameters of a rock solid applied in this paper were the same as those used in Zhu et al. (2011a). The joint elastic stiffness K, defined as K = k/(z s ω), and viscous stiffness H defined as H = η/z s were adopted. It was also assumed that α = 30°, β = 20°, and ω = 100 rad/s, i.e., (100/2π)Hz, and K n1, K n2, H n and K τ1, K τ2, H τ taken as 1.0. The filled medium mass was taken into account by assuming d = ωm n /z s in the closed-form solutions. This parameter was adopted here, i.e., m n  = dz s /ω, and the value of d assumed to be 0.0001.

The transmission and reflection coefficients of seismic wave propagation through a filled viscoelastic joint with the Maxwell and Kelvin models were studied in the frequency domain (Zhu et al. 2011a). Substituting the complex modulus of the SLS model into the matrix for a filled viscoelastic joint, the closed-form solutions of the SLS model were obtained (Zhu and Zhao. 2013). Here, cycle sinusoidal waves were imported into the modified TDRM. As a function of incident angle and incident wave frequency, the transmission and reflection coefficients are shown in Figs. 3 and 4.

Fig. 3
figure 3

Reflection–transmission coefficients of wave propagation across a filled joint with viscoelastic behavior of the Kelvin model. Incident P-wave (a, b) and incident SV-wave (c, d)

Full size image
Fig. 4
figure 4

Reflection–transmission coefficients of P-wave propagation across a filled joint with viscoelastic behavior. Maxwell model (a, b) and SLS model (c, d)

Full size image

It can be seen that calculations from the present method agree very well with the FDM solutions and the variation tendencies of the transmission and reflection coefficients that varied with incident angle were similar to those of an unfilled joint with linear elastic behavior (Li and Ma 2010).

4 Parametric Studies and Discussion

The influences of frequency and waveforms of incident waves and the viscoelastic model on wave propagation across a filled joint were investigated in this section. In addition, the efficiency and adaptability of the present method were compared and discussed with the FDM.

4.1 Frequency of Incident Wave

The transmission and reflection coefficients of P- and SV-wave propagation through a filled joint with viscoelastic behavior versus the frequency are shown in Figs. 3 and 4. With frequency increasing, T pp and T ss decreased and then gradually stabilized. As frequency rose from 0 Hz, there were small initial increases in both T ps and T sp, which then decreased slowly. For the Kelvin model, the range in which T pp decreased was smaller and value decreases less than those of the Maxwell and SLS models. Reflection coefficients, i.e., R pp, R ps, R ss, and R sp, increased with increased frequency and then gradually stabilized. When the frequency was close to 0 Hz, the coefficient of a transmitted P- or SV-wave (with P- and SV-wave incidence, respectively) for the Kelvin and SLS models approached 1 and the coefficients of other waves approached 0. In the Maxwell model, no coefficient approached 1 or 0 when the frequency approached 0 Hz. The filled fracture described by viscoelastic model was observed to have a similar effect of low-pass filtering with an unfilled joint with linear elastic behavior. For an elastic fracture, the cutoff frequency was determined by the ratio of specific joint stiffness to the rock solid’s wave impedance. However, for a fracture with viscoelastic behavior, the effect of low-pass filtering still existed, but the cutoff frequency became frequency independent when the specific viscosity term dominated the solution (Pyrak-Nolte et al. 1990b; Li and Ma 2010).

4.2 Incident Waveforms

The time-history curves of transmitted and reflected waves were calculated directly in the time domain. The effects of waveform on wave propagation were estimated using two different waveforms, half-cycle sinusoidal and rectangular, with the same peak value.

Figure 5 illustrates the transmitted and reflected waves with a half-cycle sinusoidal incident wave for these three viscoelastic models. Wave propagation through these three models was found to be similar to each other. Nevertheless, different from the Kelvin and SLS models, the value of each wave in the Maxwell model did not go to zero gradually at the end of loading and the difference between the SLS and Kelvin models was that the transmitted wave phase delay in the SLS model was longer than that for the Kelvin model.

Fig. 5
figure 5

Transmitted and reflected waves with half-cycle sinusoidal incident P-wave. Kelvin (a), Maxwell (b), and SLS (c) models

Full size image

Figure 6 illustrates the results of wave propagation with a rectangular incident wave. As with the half-cycle sinusoidal incident wave, wave propagations in the Kelvin and SLS models with a rectangular wave were similar to each other. The amplitude of the transmitted P-wave gradually approached that of the rectangular incident wave amplitude. However, other waves basically have zero amplitude. In the Maxwell model, transmitted and reflected wave values did not change in the process of loading with a rectangular wave.

Fig. 6
figure 6

Transmitted and reflected waves with rectangular incident P-wave. Kelvin (a), Maxwell (b), and SLS (c) models

Full size image

4.3 Type of Viscoelastic Model

As can be seen in Figs. 3, 4, 5, and 6, wave propagations for the Kelvin and SLS models were similar to each other in most cases and the variation tendencies of transmission and reflection coefficients versus the incident angle were similar to those of an unfilled joint with elastic behavior (Li and Ma 2010). The mass and coupling of viscosity of filled medium did not fundamentally change the wave propagation of the solid model. With a rectangular wave incident in a solid model, the value of the transmitted P-wave gradually became equal to the incident wave amplitude. This was in good agreement with transmission and reflection coefficient values when the frequency approached 0 Hz (Figs. 3, 4). For the Maxwell model, values of each wave remained the same in the process of loading with a rectangular wave and did not fit with transmission and reflection coefficient values when the frequency approached 0 Hz. The Kelvin and SLS models are viscoelastic solid models. The Maxwell model is a fluid model without the term of ε in the differential constitutive relationship. Thus, the mechanical behavior of the Maxwell model just depends on the derivative of strain with respect to time. For a filled joint with viscoelastic behavior described by the Maxwell model, which can be thought as the fracture viscosity, depends on the relative particle velocity change between the front and rear sides of the fracture. Once the relative particle velocity was constant, the stress wave did not transmit through the fracture anymore, as shown in Figs. 5b and 6b. Selection of a model for filled fractures depends on the character of filled medium. For viscoelastic behavior, the Kelvin model is the most commonly used (Huang et al. 2015a).

4.4 Comparison Between the FDM and the Time-Domain Method in Detail

Transmission and reflection coefficients are often used to verify the accuracy of a time-domain method by comparing them with those of the FDM. However, the phases and time courses of transmitted and reflected waves calculated by these two methods have never been compared. The efficiency and adaptability of these two methods were estimated and compared using transmitted waves in the time domain with P-wave incidence through a filled joint. Sinusoidal and practical seismic waves were selected as the incident waves, with the sinusoidal wave frequency at 1 Hz and the seismic wave from the first 10 s of the El-Centro wave record. The Kelvin model was selected to describe the viscoelastic properties of the filled medium, with the model parameters taken as K n1 = K τ1 = 1, H n  = H τ  = 0.01 and ω = 1 rad/s. A transmitted wave calculated by FDM was obtained by fast Fourier transform (FFT) and inverse fast Fourier transform (IFFT). Although the transmitted waveforms calculated by these two methods were very similar (Fig. 7), there were still differences in the initial stages of the process.

Fig. 7
figure 7

Transmitted waves for Kelvin model. Sinusoidal wave incidence (a) and seismic wave incidence (b)

Full size image

According to some existing literature, setting the value of transmitted wave as 0 in the beginning was most reasonable (Li and Ma 2009, 2010; Fan and Wong 2013; Cui et al. 2016). The FDM, however, did not identify the beginning of the time course. Phase and amplitude of the transmitted wave was only decided by solutions of frequency-domain equations. To eliminate the aliasing effect in processing of FFT, Huang et al. (2015a) have suggested that the start time should has some delay rather than from 0 s, such that the unstable stage was blocked out (Fig. 8).

Fig. 8
figure 8

Transmitted waves for the Kelvin model of seismic wave incidence with a time delay

Full size image

Avoiding the FFT and the delay of time, the time-domain method was more convenient and efficient than the FDM. In addition, the FDM could only be used to study conventional deformation behaviors that were described in the frequency domain. However, the time-domain method was also suitable for describing nonlinear deformation behaviors of joints (Li 2013).

5 Conclusions

The propagation of a stress wave across a single filled joint was studied using a modified TDRM proposed in this study. In the modified method, the DDM was extended to the DSDM and the differential constitutive relationship of a viscoelastic model was adopted to consider the mass and viscoelastic behavior of filled medium. The expression of the transmitted and reflected waves can be easily deduced, and the transmission and reflection coefficients can be directly calculated in the time domain by using this method. Compared with the FDM, the present method was concluded to be more efficient to study wave propagation across a filled rock joint. As a function of incident wave angle, the change tendencies of the transmission and reflection coefficients for viscoelastic models addressed here were similar to each other. Wave propagations through the Kelvin and SLS models were similar to those of an unfilled joint with linear elastic behavior. The mass and viscosity coupling of filled medium did not fundamentally change wave propagation in a solid model. The fracture viscosity was dependent on the particle velocity change between the front and rear sides of a fracture for the Maxwell model. The stress wave from a rectangular incident wave did not transmit through a filled joint described by the Maxwell model.