1 Introduction

Blasting is generally inevitable for rock excavation in mining, quarrying and civil engineering. Except for its high efficiency and convenience in fragmenting and displacing rocks, blasting may cause many adverse effects, for example ground vibration, air blasts, fly rocks and noise (Hagan 1979). Among such effects, ground vibration is a major concern to engineering design and environment. Vibration not only reduces the safety and stability of the excavated area, but also leads to problems in adjacent buildings. (Dowding et al. 1981; Fomel and Landa 2014; Lu et al. 2001, 2012; Singh and Roy 2010). Three factors of ground vibration used to assess the associated damage on adjacent rock mass and structures are amplitude (peak particle velocity), dominant frequency and vibration duration (Aldas 2010; Aldas and Ecevitoglu 2008; Singh and Roy 2010). A deep insight into characteristics of these factors should be obtained to understand the influences of vibration during the seismic wave propagation.

PPV has been considered as a crucial index in many safety criteria for evaluating blast vibration intensity and assessing blast-induced damage for many years, and comprehensive investigations on PPV have been conducted by many researchers (Ak et al. 2009; Liang et al. 2011; Sambuelli 2009). However, in many cases, the monitored vibration velocity is much higher than the critical PPV, while structures remain intact. On the contrary, blasts with vibration velocity that are much lower than the allowed PPV may cause severe damage. (Lu et al. 2012). In addition to PPV, vibration frequency also has significant effects on the structural response to the blast vibration. Dowding (1985) underlined the importance of frequency because the structural response depended on the frequency of ground vibration. A critical PPV corresponding to a specific frequency band was proposed by Dowding (1996) as the evaluation criterion. Nowadays, frequency-based control has been adopted by the US Office of Surface Mining and many members of the European Common Market. With developments in blasting safety control, many studies demonstrate that the vibration frequency is an important index to improve the accuracy of assessing blast-induced damage (Khandelwal and Singh 2006; Monjezi et al. 2011). As mentioned above, it is necessary to identify the characteristics of frequency-dependent attenuation of blast-induced ground vibration.

Recently, some empirical or semiempirical formulas were obtained. For example, according to the theory of surface wave propagation in viscoelastic material, Foti et al. (2010) deduced a vibration PPV attenuation equation (Eq. 1).

$${\text{PPV}} = K\frac{\sqrt Q }{{\sqrt {r^{3} } }}\left( {\frac{2edf}{{\rho C_{\text{R}} }}} \right)^{1/2}$$
(1)

where e is the explosive specific energy, d is the borehole diameter, ρ is the rock density, and C R is the Rayleigh wave velocity.

Equation 1 aimed to solve ground vibration problems induced by a concentrated charge. It revealed that the frequency has an influence on the attenuation of PPV and indicated that the dominant frequency decayed versus distance smoothly without any rapid drop. However, an inherent defect existed deriving Eq. 1: the concepts of blast seismic wave energy flux density and total energy were confused.

Amplitude spectrum analysis based on Fourier transform is utilized to reveal and verify the frequency-dependent attenuation mechanism of blast-induced vibration. The dominant frequency applied in this paper is obtained from the frequency spectrum shown in Fig. 1. The present paper is divided into four sections: firstly, theoretical analysis was proposed for the frequency-dependent attenuation of ground vibration induced by a spherical charge propagating in a viscoelastic medium; secondly, the cylindrical charge which is a more complicated condition was investigated by numerical simulation; thirdly, analytical and numerical results are validated by field experiments; and finally, an optimized piecewise assessment associated with the drop point is proposed.

Fig. 1
figure 1

Schematic plot of dominant frequencies. a Velocity time history. b Vibration spectrum

Full size image

2 Spherical Charge

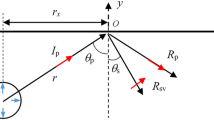
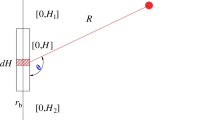
Dauetas et al. (1993) derived the frequency spectrum of seismic vibrations due to blasting of a spherical charge. In Dauetas’ research, it was assumed that the blast source and irreversible deformation zones are a spherical cavity, and blasting loads directly act on the inside boundary of this zone which in other words is the elastic boundary. This concept, which is referred to as the equivalent radius of the source, is widely accepted.

Let a source of blasting vibrations with equivalent radius r e propagate in an absolute elastic isotropic medium, characterized by density ρ and elastic Lame constants λ and μ, and assume that λ = μ. The time-dependent stress σ(τ) is applied on the equivalent elastic boundary of the source. The problem of the velocity spectrum of a seismic wave was considered in the following formulation.

The field of disturbances u arising from the source has a spherical symmetry and satisfies Eq. (2)

$$\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{2}{r}\frac{\partial u}{\partial r} - \frac{2u}{{r^{2} }} = \frac{1}{{V_{p}^{2} }}\frac{{\partial^{2} u}}{{\partial t^{2} }}$$
(2)

where \(V_{\text{p}} = \sqrt {\frac{\lambda + 2\mu }{\rho }}\). The solution to Eq. (2) is:

$$u = \frac{\partial f(\tau /r)}{\partial r} = - \frac{f(\tau /r)}{{r^{2} }} - \frac{1}{{rV_{\text{p}} }}\frac{\partial f(\tau /r)}{\partial \tau }$$
(3)

where \(\tau = t - \frac{{r - r_{e} }}{{V_{\text{p}} }}\) and f(τ/r) is a function that can be established from boundary conditions:

$$\left[ {(\lambda + 2\mu )\frac{\partial u}{\partial r} + 2\lambda \frac{u}{r}} \right]_{{r = r_{\text{e}} }} = - \sigma (t).$$
(4)

From Eq. (3), we get \(\frac{\partial u}{\partial r}\), and submitting in Eqs. (4), (5) will be obtained.

$$\sigma (t) = - \frac{\lambda + 2\mu }{{rV_{\text{p}}^{2} }} + f^{{\prime \prime }} (\tau /r) - \frac{4\mu }{{r^{2} V_{\text{p}} }}f^{{\prime }} (\tau /r) - \frac{4\mu }{{r^{3} }}f(\tau /r)$$
(5)

Multiplying the right-hand and left-hand sides of Eq. (5) by e−jωt, we get:

$$S_{\sigma } (j\omega ) = - \frac{\lambda + 2\mu }{{r_{\text{e}} V_{\text{p}}^{2} }}(j\omega )^{2} S_{\text{f}} (j\omega ) - \frac{4\mu }{{r_{\text{e}}^{2} V_{\text{p}} }}j\omega S_{\text{f}} (j\omega ) - \frac{4\mu }{{r_{\text{e}}^{3} }}S_{\text{f}} (j\omega ) = - S_{\text{f}} (j\omega )\left( {\frac{4\mu }{{r_{\text{e}}^{3} }} + \frac{4\mu }{{r_{\text{e}}^{2} V_{\text{p}} }}j\omega - \frac{\lambda + 2\mu }{{r_{\text{e}} V_{\text{p}}^{2} }}\omega^{2} } \right)$$
(6)

where S σ (jω)is the complex spectrum of function σ(τ) and S f(jω) is the complex spectrum of function f(τ/r).

For the complex spectrum of displacement S u(jω), make Fourier transformation of Eq. (3)

$$S_{\text{u}} (j\omega ) = - S_{\text{f}} (j\omega )/r^{2} - j\omega S_{\text{f}} (j\omega )/(rV_{\text{p}} ) = - S_{\text{f}} (j\omega )\left[ {1/r^{2} + j\omega /(rV_{\text{p}} )} \right]$$
(7)

Substituting Eq. (6) in Eq. (7)

$$S_{\text{u}} (j\omega ) = S_{\sigma } (j\omega )M(j\omega )$$
(8)
$$M(j\omega ) = \frac{{r_{\text{e}} \left[ {1/r^{2} + j\omega /(rV_{\text{p}} )} \right]}}{{4\mu /r_{\text{e}}^{2} - (\lambda + 2\mu )\omega^{2} /V_{\text{p}}^{2} + 4\mu j\omega /(r_{\text{e}} V_{\text{p}} )}}$$
(9)

where M(jω) is the transfer function considered as a complex frequency spectrum of a spherical emitter of longitudinal waves with distance r > r e.

From Eq. (8), the amplitude spectrum of vibration F (ω) is obtained as in Eq. (10).

$$F(\omega ) = \left| {j\omega S_{\text{u}} (j\omega )} \right| = \frac{{\left| {S_{\sigma } (j\omega )} \right|r_{\text{e}} V_{\text{p}} \omega \sqrt {V_{\text{p}}^{2} + r^{2} \omega^{2} } }}{{4\mu r^{2} \sqrt {(V_{\text{p}} /r_{\text{e}} )^{4} + \left[ {1 - {{(\lambda + 2\mu )} \mathord{\left/ {\vphantom {{(\lambda + 2\mu )} {(2\mu )}}} \right. \kern-0pt} {(2\mu )}}} \right](V_{\text{p}} /r_{\text{e}} )^{2} \omega^{2} + \left[ {{{(\lambda + 2\mu )} \mathord{\left/ {\vphantom {{(\lambda + 2\mu )} {(4\mu )}}} \right. \kern-0pt} {(4\mu )}}} \right]^{2} \omega^{4} } }}$$
(10)

For the simulation of wave propagation in solids, particularly for applications in geophysics, it is commonly admitted that taking into account the attenuation effects induced by the viscoelastic nature of the medium is important (Singh et al. 2015). In view of the model first introduced by Ricker (1977) to compute the absorptive properties (attenuation), Eq. (10) is modified by a material damping term, Q r (Aldas 2010) as shown in Eq. (11) to model the frequency-dependent attenuation of blasting vibration.

$${\text{Fn}}(\omega ) = \frac{{{{\exp \left( { - \frac{\omega r}{{2Q_{\text{r}} V_{\text{p}} }}} \right)\left| {S_{\sigma } (j\omega )} \right|r_{\text{e}} V_{\text{p}} \omega \sqrt {V_{\text{p}}^{2} + r^{2} \omega^{2} } } \mathord{\left/ {\vphantom {{\exp \left( { - \frac{\omega r}{{2Q_{\text{r}} V_{\text{p}} }}} \right)\left| {S_{\sigma } (j\omega )} \right|r_{\text{e}} V_{\text{p}} \omega \sqrt {V_{\text{p}}^{2} + r^{2} \omega^{2} } } {4\mu r^{2} }}} \right. \kern-0pt} {4\mu r^{2} }}}}{{\sqrt {(V_{\text{p}} /r_{\text{e}} )^{4} + \left[ {1 - (\lambda + 2\mu )/(2\mu )} \right](V_{\text{p}} /r_{\text{e}} )^{2} \omega^{2} + \left[ {(\lambda + 2\mu )/(4\mu )} \right]^{2} \omega^{4} } }}$$
(11)

where F n (ω) is the frequency spectrum of vibration in viscoelastic media. The bigger the Q r , the less internal energy loss during vibration propagation. With the material damping term, the media have internal energy losses during seismic wave propagation which lead to frequency-dependent attenuation of vibration.

The blasting loads acting on the equivalent elastic boundary are simplified as Eq. (12). After Fourier transformation, the blasting load history turns to the Fourier amplitude–frequency spectrum as in Eq. (13).

$$\sigma (t) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & t < - \tau_{1}; \hfill \\ {\sigma_{\hbox{max} } (1 + t/\tau_{1} ),} \hfill & { - \tau_{1} \le t \le 0;} \hfill \\ {\sigma_{\hbox{max} } (1 - t/\tau_{2} ),} \hfill & {0 \le t \le \tau_{2} ;} \hfill \\ {0,} \hfill & {t > \tau_{2} ;} \hfill \\ \end{array} } \right.$$
(12)
$$\left| {S_{\sigma } (\omega )} \right| = \frac{{\sigma_{\hbox{max} } }}{{a_{\text{e}} b_{\text{e}} \tau \omega^{2} }}\left[ {1 + a_{\text{e}}^{2} + b_{\text{e}}^{2} + 2a_{\text{e}} b_{\text{e}} \cos \omega \tau - 2(a_{\text{e}} \cos b_{\text{e}} \omega \tau + b_{\text{e}} \cos a_{\text{e}} \omega \tau )} \right]^{1/2}$$
(13)

where σ max is the peak value of the blasting load, τ is the duration of the blasting load, τ 1 is the load rising time, and τ 2 is the load decreasing time, a e = τ 1/τ and b e = τ 2/τ.

In the present analysis, parameters were assumed as follows: σ max = 50 MPa, V P = 3400 m/s, ρ = 2600 kg/m3, r e = 2.0 m, a e = 0.25, b e = 0.75, τ = 10 ms, and ν = 0.25. The rock herein was supposed to be intact. According to Barton et al. (1974), Q r was selected as 12.

Figure 2 shows that f d is decreasing with the increase in distances from blast source gradually, but a rapid drop occurs at r = 50 m. Figure 3 presents frequency spectra of measuring points at different distance away from the explosive charge. To emphasize the change in frequency, the ratios between current values of amplitude of frequency spectra to its maximum value are plotted on the vertical axis.

Fig. 2
figure 2

Dominant frequency-dependent attenuation versus r of blasting vibration induced by spherical charge

Full size image
Fig. 3
figure 3

Velocity spectra of normalized amplitude under different r of spherical charge

Full size image

Energy corresponding to high frequency attenuates quickly when the ground motion propagates in the rock mass. (Wu and Hao 2005). As shown in Fig. 3, three frequency bands are considered: 0–150, 150–250 and 250–400 Hz. At first, the dominant frequency lies in the frequency band 150–250 Hz. The vibration frequency spectrum is three-peak structural with f d as its symmetric axis. With the increase in r, high-frequency components of vibration decay more quickly than low-frequency components. Frequency components of vibration ranging from 150 to 250 Hz translate into 0–150 Hz band, and vibration in 0–150 Hz band attenuates slower. As a result, the value of second-peak amplitude in frequency band 0–150 Hz is equal to that corresponding to the dominant frequency in high-frequency band. Then, a rapid drop of frequency-dependent attenuation occurs during the propagation of blasting vibration. And the dominant frequency shifts to half the original value after the drop. With the increase in r, vibration frequency spectra transform from three-peak structures to single-peak structures located in a lower-frequency band. No other rapid drop occurs after the spectrum structure transformation end.

3 Cylindrical Charge

Commonly used blasting sources in engineering are cylindrical charges, usually with free surfaces. As discussed above, we find that frequency-dependent attenuation of blasting vibration induced by spherical charge exhibits a rapid drop at certain distance. Whether the frequency-dependent attenuation of blasting vibration induced by cylindrical charge is similar to that of spherical charge or not will be discussed in this section.

The cylindrical charge is equivalent to the superposition of several spherical charge elements (Fig. 4); therefore, a more complicated frequency-dependent attenuation phenomenon is expected. The theoretical analysis on the spherical charge condition is insufficient to represent the frequency-dependent attenuation mechanism of cylindrical charge, (1) because only P-waves are considered in the spherical charge condition, whereas P-waves, S-waves and surface waves are all included in the cylindrical condition and (2) because of the nonlinear superposition in time region (Blair 2008).

Fig. 4
figure 4

Diagram of cylindrical charge equivalent to spherical charges

Full size image

Ground vibration induced by a cylindrical charge, which propagates in a half space, is analyzed through numerical simulation by the well-developed system LS-DYNA. The numerical simulation method used for modeling blasting has been verified by site experiments implemented by Wang (2014).

As shown in Fig. 5a, the model is a rectangular block. The length, width and height of the block are 132.5, 80 and 14 m, respectively. The depth of borehole is 8 m. In the borehole, the upper 1.7 m is stemming. The diameter of the borehole is 90 mm. The radial decouple coefficient of charge structure (i.e., the ratio between the borehole diameter and the charge diameter) is 1.125. Except for the charge, the rest of space in the borehole is filled with air. The burden is 2.5 m. Transmitting boundary is applied on all the other faces except the ground surface. Imaginary test points are placed on the ground surface of the model. The numerical simulation model and the layout of test points are similar to those shown in Fig. 5.

Fig. 5
figure 5

Numerical simulation model of cylindrical charge. a Rock model. b Profile of explosion and test points distribution

Full size image

Table 1 lists parameters of MAT_HIGH_EXPLOSIVE_ BURN material to describe explosive charge. The EOS of JWL (Eq. 14) is applied to evaluate the relation between pressure and volume in the explosion process.

$$P = A\left( {1 - \frac{\omega }{{R_{1} V}}} \right){\text{e}}^{{ - R_{1} V}} + B\left( {1 - \frac{\omega }{{R_{2} V}}} \right){\text{e}}^{{ - R_{2} V}} + \frac{{\omega E_{0} }}{V}$$
(14)

where P is the pressure of detonation product calculated by EOS of JWL, V is the relative volume, E 0 is the internal energy density per unit initial volume, and A, B, R 1, R 2 and ω are independent indicators used in JWL.

Table 1 Parameters of charge in numerical simulation
Full size table

The MAT_NULL material is applied to describe gas pressure in the borehole, and Eq. (15) is a multivariate linear formula to evaluate the effect of air.

$$P = C_{0} + C_{1} \mu + C_{2} \mu^{2} + C_{3} \mu^{3} + (C_{4} + C_{5} \mu + C_{6} \mu^{2} )E_{0}$$
(15)

where C 0 = C 1 = C 2 = C 3 = C 6 = 0, C 4 = C 5 = 0.4, μ = ρ/ρ 0, ρ and ρ 0 are the initial and present material density, respectively.

Taking the damage assessment of rock mass into consideration, a tension–compression damage rock model is adopted in the numerical simulation and parameters are presented in Table 2.

Table 2 Parameters of rock in numerical simulation
Full size table

The vertical component of ground vibration is selected as an example in this paper, and its amplitude spectrum is computed by Fourier transformation. Figure 6 shows that the dominant frequency decreases with the increase in distance in overall trend. Compared to the whole attenuation trend, a relative rapid dominant frequency drop occurs within 20 m and a frequency fluctuation occurs around 40 m. In order to reveal the frequency-dependent attenuation mechanism, Fig. 7 presents blast vibration spectra at different test points. Vertical axis in Fig. 7 is normalized in the same way as in Fig. 3.

Fig. 6
figure 6

Dominant frequency-dependent attenuation versus r of blasting vibration induced by cylindrical charge

Full size image
Fig. 7
figure 7

Velocity spectra of normalized amplitude under different r of cylindrical charge

Full size image

As shown in Fig. 7, the dominant frequency is located in high-frequency band within 10 m. Vibration corresponding to high frequency attenuates more quickly than that of low-frequency components. As a result, the dominant frequency corresponding to peak value amplitude shifts from a higher-frequency band to a lower-frequency band. Therefore, a relative rapid frequency drop occurs within 20 m away from the blast source. This drop is similar to the spherical charge condition. Additionally, a slight fluctuation occurs at r = 40 m. In the range of 30–50 m, because of the decay rate difference, the structure of amplitude spectrum in the transformation process is unstable. Thus, dominant frequencies fluctuate slightly in the frequency zone. After that, in the range of 60–100 m, vibration spectra change from multimodal structure to single-peak structure in a low-frequency band and f d decreases slowly.

4 Field Experiments

If the rapid drop or fluctuation of frequency-dependent attenuation phenomenon revealed by the above analysis exists in engineering, field experiments were conducted to verify the frequency-dependent attenuation.

4.1 Fengning Pumped Storage Power Station Experiment

The construction of Fengning pumped storage power station in China provided a good opportunity to conduct field experiments to study the frequency-dependent attenuation of blast-induced vibration. The installed capacity of the station plans to be 3600 MW, and the whole construction will be completed in two phases. Construction of the second phase will have an inevitable effect on the constructions of first phase; it is thus important to ensure safety and rationality of the underground power house excavation in the second phase. Therefore, single-hole blasting experiments were conducted in the test tunnel, which was connected to underground powerhouses of the second phase. The topography indicates that the construction site can be considered flat. Rocks in the experiment area are intact granite with high mechanical intensity.

The site experiment included six vertical boreholes initiated by half second delay detonators in a sequence. No. 2 rock emulsion explosive was adopted in the blasting experiment. The blasting design is shown in Fig. 8. In this paper, two boreholes coding Nos. 4 and 6, which are bottom initiated, are selected to study the frequency-dependent attenuation of blasting vibration. Table 3 lists parameters of the two boreholes.

Fig. 8
figure 8

Design of the cutting blasting experiment in Fengning pumped storage power station. a The plan layout of boreholes and monitoring points. b Charge structure of the two boreholes

Full size image
Table 3 Parameters of the two boreholes in the blast experiment
Full size table

There were 10 monitoring points on the ground surface along the test line at successive distances from the blasting source. The monitoring system was composed of a three-axis velocity transducer (Fig. 9a), a blasting vibration intelligent monitor (TC-4850 (Fig. 9b) or Mini Pro4). IBM portable computers with BM View analysis software were used to withdraw field test data. In order to eliminate the influence of vibration monitor types, measured data of six monitoring points recorded by TC-4850 were analyzed in this paper. The monitoring amplitude range and frequency range of TC-4850 are 0.001–35.4 cm/s and 1–500 Hz, respectively. As frequency bands of blasting vibrations far from resonance frequencies of the vibration monitor, no substantial amount of information loss around the resonance frequency occurs (Aldas 2010).

Fig. 9
figure 9

Instruments for blast experiments. a Three-axis velocity transducer. b TC-4850

Full size image

Due to space limitation, vertical components of vibrations acquired from 6 test points ranging from 10 to 150 m are selected for analysis. Data of the two vertical borehole blasting experiments are summarized in Table 4.

Table 4 Summary of experiment data in the two boreholes blasting experiments
Full size table

As shown in Fig. 10, dominant frequency-dependent attenuations are not smooth and steady in the two borehole blasting experiments. Even though the experiment site and monitoring points were chosen carefully, slight deviation of measuring data exists due to the geology difference at each monitoring point. It should be pointed out that since the rock intensity at the first monitoring point may not be as good as the other points, PPV at the first monitoring point is slightly higher and the dominant frequency is slight lower. Nevertheless, field data of the two borehole blasting experiments reveal the unsmooth frequency-dependent attenuation phenomenon. There is an obvious fluctuation during the frequency attenuation versus distance in Fig. 10a. In Fig. 10b, the dominant frequency decays rapidly within 23 m. After that, a frequency fluctuation occurs around 50 m. Then, the frequency decays slowly and steadily.

Fig. 10
figure 10

Frequency-dependent attenuation of blasting vibrations in the field experiment. a No. 4 blasting borehole with 6 m in depth. b No. 6 blasting borehole with 4.5 m in depth

Full size image

4.2 Changba–Lijiagou Lead–Zinc Mine Experiment

The field experiments conducted by Zhong (2006) in a heading tunnel of Changba–Lijiagou lead–zinc mine provided abundant data of blast-induced vibrations. The blasting design was introduced by Zhong et al. (2009) in detail. The tunnel had a horseshoe-shaped cross section with total area of 18.436 m2. Rocks surrounding the heading tunnel composed of quartzite, biotite–quartz schist and marble, their hardness coefficient ranged from 8 to 10, and the lithology was consistent. Therefore, effects of geology at different monitoring point were neglected when analyzing the attenuation mechanism of blasting vibration waves.

The blast of the heading tunnel was divided into eight delays, and non-electric millisecond delayed detonators were adopted. The topography of the test site was considered flat. Six measuring points were arranged aligned with the blast source on the ground rock surface to measure blast-induced vibration per delay. In the survey, IDTS3850 vibration monitor was applied to record data of blast-induced ground vibration. The monitoring amplitude range and frequency range of IDTS3850 were 0.001–66 cm/s and 1–40,000 Hz, respectively.

Zhong et al. (2009) used the field experiment data to investigate the influence of explosive parameters on energy distribution of blasting vibration signal. In this paper, we used the same field experiment data to analyze the dominant frequency-dependent attenuation. Blast-induced vibrations of the first two delays were selected. Vertical components of the selected vibrations are summarized in Table 5, and the dominant frequency-dependent attenuations are shown in Fig. 11.

Table 5 Summary of blasting vibrations of the first two delays obtained by Zhong (2006)
Full size table
Fig. 11
figure 11

Frequency-dependent attenuation of blasting vibrations in the field experiment. a Blast-induced vibration of the first delay. b Blast-induced vibration of the second delay

Full size image

The dominant frequencies decay rapidly within 37 m, and frequency drops occur during the frequency attenuation versus r in both Fig. 11a, b. The dominant frequencies decrease approximately to half the original values when rapid drops occur. After that, the dominant frequencies in Fig. 11a, b decay slower compared to those of the near field. Slight frequency fluctuations occur around 65 m.

According to the above analysis, we conclude that the particular frequency drop and fluctuation phenomenon do exist in field experiments. The frequency-dependent attenuation mechanism is verified by field experiments.

5 Discussion

To sum up, dominant frequency-dependent attenuation, different from PPV attenuation, is not smooth attenuation versus distance; it exhibits rapid frequency drop or fluctuation at certain distance. This phenomenon can be explained by two main factors: (1) Vibrations corresponding to various frequency components attenuate with different decay rates, and (2) amplitude spectra are multi-structural. As shown in Figs. 3 and 7, dominant frequencies shift from a higher-frequency band to a lower one; it leads to a rapid drop during the frequency-dependent attenuation of blasting vibration. Figures 2, 6 and 11 indicate that dominant frequencies almost decrease to half the original value when drops occur. In this section, the meaning of research on frequency-dependent attenuation will be discussed.

PPV cannot solely explain the damage from blast-induced vibrations in settlement areas (Aldas 2010). In China, a new safety PPV standard for blasting vibration has been proposed in GB6722-2014 shown in Table 6. The safety standard provides different critical PPV levels according to dominant frequency. The bold line in Table 6 is the critical PPV level applied in the following analysis. The way to select the right critical PPV associated with proper frequency will be optimized using the present research.

Table 6 Safety PPV for blasting vibration (GB6722-2014, China)
Full size table

According to frequency-based vibration standard, we usually select the critical PPV from one frequency band and the critical frequency band is generally judged by experience. For example, as shown in Fig. 12a, X and Y are two brick houses adjacent to a mining excavation. There are two monitoring points marked by A and B corresponding to X and Y, respectively. After getting the PPV attenuation formulae, we assess the structure safety based on the safety PPV for blasting vibration (GB6722-2014, China in Table 6 the bold line). In the past assessment, critical PPV is supposed to select from one frequency band. If the conventional assessment is used here, dominant frequencies of A and B are in the same anticipatory frequency band. And in the selected frequency band, peak particle velocities of A and B are lower than in the critical PPV as shown in Fig. 12b. They are supposed to be safe. However, a rapid frequency drop occurs between A and B (Fig. 12c). The dominant frequency of B deceases to a lower-frequency band. As shown in Fig. 12d, the PPV standard at B should be changed then and the PPV at B exceeds the critical PPV. As a result, the blast excavation may cause damage at Y house. Additionally, as the vibration dominant frequency drops, it becomes closer to the nature frequency of B. Structures are sensitive to low vibration frequencies so that it may cause vibration amplification. Therefore, all reasons mentioned above increase the damage possibility of Y house.

Fig. 12
figure 12

Influence of frequency fluctuation on structure safety assessment according to GB6722-2014 of China. a The sketch of two brick houses under mining excavation without frequency drop. b Safety assessment without frequency drop. c The sketch of two brick houses under mining excavation with frequency drop. d Safety assessment with frequency drop

Full size image

Based on the above discussion, a new piecewise assessment method to assess the blast vibration safety is proposed. Take the safety PPV of brick house as an example. As shown in Fig. 12d, the critical PPV is selected from two frequency bands according to the drop. To set the drop point as the breakpoint, the assessment is divided into two independent sections along vibration propagating path. Criteria in a higher-frequency band are adopted at monitoring points closer to the blast source than the drop; criteria in lower-frequency band are adopted at monitoring points farther to the blast source than the drop. Thus, blast vibration safety standard could be selected more precisely, and the assessment of blast safety will be more accurate.

6 Conclusions

Within the framework of this research, the following conclusions can be drawn. We find that the dominant frequency-dependent attenuation is a more complicated process compared to the PPV attenuation. The absorptive property of the medium results in the frequency attenuation versus distance, whereas a rapid frequency drop or fluctuation occurs during the attenuation. Vibration energy with high frequency attenuates more quickly when the ground vibration propagates in a viscoelastic rock. Moreover, the vibration amplitude spectra are multimodal structure and the transformation processes of spectra are unstable. Both of the above two factors contribute to the unsmooth attenuation of the dominant frequency of blasting vibrations.

Mechanism of frequency-dependent attenuation has great significance in the structure safety assessment. The present research points out that it is imprecise to select critical safety standard from one frequency band. Piecewise assessment with the frequency drop point as a breakpoint is more accurate. Moreover, structures on the ground are sensitive to ground vibration with low frequencies which are close to their nature frequencies. The dynamic response of structures that are located around the frequency drop point should be considered with more attention.

With high concern to the drop or fluctuation during the frequency-dependent attenuation, a method to determine the drop or fluctuation specific location needs further discussion. An optimized blasting safety assessment will be proposed in further studies.