1 Introduction

Rock fracture toughness represents the capability of rocks containing initial cracks to resist further fracturing, which is considered to be an immanent property of rocks. It has acquired extensive engineering and geophysical applications involving rock classification, rock bursts control and prevention, rock crushing and cutting, hydro-fracturing etc. (Singh and Sun 1990). Depending on the exerted stresses, the cracks may propagate with the combination of three basic fracture modes: mode I (tension/opening mode), mode II (in-plane shear/sliding mode), and mode III (out-of-plane shear/tearing mode) (Irwin 1957). Since the opening mode is the predominant failure mode generally encountered in practical situations, a wide variety of methods and specimen configurations have been developed for measuring the mode I fracture toughness of rocks, as usually characterized by the critical value of stress intensity factor (SIF) in the vicinity of a prefabricated crack tip. For standardization, the International Society for Rock Mechanics (ISRM) has recommended four suggested methods, namely, the chevron bend (CB) and the short rod (SR) (Ouchterlony 1988), the cracked chevron notched Brazilian disc (CCNBD) (Fowell 1995) and the semi-circular bend (SCB) (Kuruppu et al. 2014). Among these methods, the CCNBD method has been broadly used due to its distinct advantages of simple sample preparation and installation, much higher failure loads, and a wide range of specimen geometries that can be tested (Fowell 1995; Nasseri et al. 2006).

A certain consistency of fracture toughness values has been achieved via these suggested methods, while some discrepancies still exist (Dwivedi et al. 2000; Cui et al. 2010; Chang et al. 2002; Tutluoglu and Keles 2011). In particular, the fracture toughness values obtained by the CCNBD method are generally found to be higher than those obtained on the straight through notched specimens for the same type of rock. When compared with the SCB method, the fracture toughness values obtained via the CCNBD method turn out to be 66 % higher for Keochang Granite, 20 % higher for Yeosan Marble, 54 % higher for Ankara Andesite, and 75 % higher for Afyon Marble, respectively (Chang et al. 2002; Tutluoglu and Keles 2011). The apparent discrepancy can possibly result from the critical dimensionless stress intensity factor (SIF) value used in the calculating formula, size effect, anisotropy and heterogeneity of rocks etc. Among these, the critical dimensionless SIF value is considered to be the essential factor since it is closely related to the critical state of the crack propagation within the CCNBD specimen (Iqbal and Mohanty 2007). In this regard, previous contributions on enhancing the reliability of the CCNBD method have been dedicated to calibrating the critical dimensionless SIF values (Chen 1990; Xu and Fowell 1994; Wang et al. 2003, 2013).

Recently, several numerical investigations (Dai et al. 2015a, b; Wei et al. 2015a; Xu et al. 2016) have demonstrated that the critical crack front during the progressive fracture of typical chevron-notched specimens, including CCNBD, is far from straight but rather curved. This observation violates the straight-through crack assumption adopted prevailingly in the calibration of the critical dimensionless SIF. In addition, some analytic studies (Kourkoulis and Markides 2014; Markides and Kourkoulis 2016) have revealed that the actual shape of the crack, i.e., the width of the initial crack and the slight curvature of its corners, affects the local stress amplification, and also on the stress concentration around the crown of the crack. Ideally, the realistic crack front shall be incorporated into the calibration of the critical dimensionless SIF. However, practically, the SIF determination taking into account the realistic crack front is challenging. Additional factors could also play a role in the correct determination of the SIF according to the ISRM standard and therefore, the respective procedure should be reconsidered.

As developed by Irwin (1957), the SIF is related to the strain energy release rate G (Griffith 1920), which describes a measure of the energy available for an increment of crack extension. Thus, the critical SIF, i.e., fracture toughness, can also be determined from the critical energy release rate. Based on the energy criterion, a new method termed G-method is proposed in this study to determine the fracture toughness of rock mass. In contrast to the experimental measurement that is hard to capture the released strain energy, the numerical approach such as the discrete element method (DEM) can efficiently analyze the energy partitions (Cundall and Strack 1979; Potyondy and Cundall 2004), and thus, it can be used to study the G-method. The feasibility of DEM in analyzing rock fracturing has been validated in numerous investigations (Hazzard and Young 2000; Hazzard et al. 2000; Yoon et al. 2012; Khazaei et al. 2015).

In this study, both experimental and numerical studies have been conducted on the ISRM-suggested CCNBD tests, and the mode I fracture toughness is obtained via the proposed G-method. The paper is organized as follows: Sect. 2 reports the fracture experiments using the ISRM-suggested CCNBD method. Section 3 proposes the G-method for mode I fracture toughness determination. In Sect. 4, the CCNBD tests are numerically analyzed and the determination of mode I fracture toughness via the G-method is demonstrated. Section 5 discusses the comparison between the G-method and some conventional methods, with regard to the fracture toughness. Section 6 gives out the concluding points of this research.

2 The CCNBD Fracture Experiments

2.1 The ISRM Suggested CCNBD Method

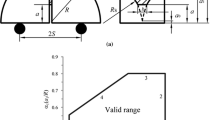
Figure 1 shows the schematic of the CCNBD specimen, which is generally sampled from rock cores and loaded diametrically. As shown in Fig. 1, R is the radius of the rock disc and B is the thickness; the disc is chevron notched by two symmetric cuts with a saw radius of R s. a 0 is the initial chevron notched crack length, a 1 is the final chevron notched crack length, and a is the propagating crack length.

Fig. 1
figure 1

Schematic of the ISRM suggested method to determine mode I fracture toughness using the CCNBD specimen

Full size image

As suggested by ISRM, the mode I fracture toughness K IC, i.e., critical mode I SIF, shall be calculated using the peak load P max for convenient data acquisition. It is noted that the measuring principle presumes that cracks emerge at the chevron notch tips due to stress concentration, and then extend symmetrically and stably toward the loading ends. Shortly afterward, the stable propagation turns into the unstable fracturing somewhere between the initial and final crack length, a 0 and a 1, of the disc, while the loading force reaches its peak value. The critical SIF of the CCNBD specimen correlates with the stable-unstable transition of the crack propagation and can be calculated as:

$$K_{\text{IC}} = \frac{{P_{\hbox{max} } }}{B \cdot \sqrt D } \cdot Y_{\hbox{min} }^{*}$$
(1)

where Y *min is the minimum dimensionless SIF for the CCNBD specimen, which depends only on the geometric dimensions of rock specimen. Suggested values are provided by ISRM (Fowell 1995), and more accurate Y *min values of the CCNBD specimens with a wide range of geometries are calibrated and updated by Wang et al. (2013). Note that in all these previous contributions reported in the literature, the straight through crack assumption (STCA) is adopted in the calibration of Y *min .

2.2 Laboratory Experiments

The MTS815 Flex Test GT rock mechanics testing system is employed to conduct the fracture experiments, in which a group of four CCNBD specimens of Dazhou sandstone (Fig. 2) are tested. All tests are controlled by a constant axial displacement loading rate of 0.02 mm/min, so that each CCNBD specimen is ensured to be split completely within 10 min as suggested by ISRM (Fowell 1995). Table 1 exhibits the geometry of the tested CCNBD specimens as well as the corresponding fracture toughness values obtained by the original formula of ISRM using the relevant Y *min values by ISRM (Fowell 1995) and Wang et al. (2013), respectively. The mean values are 0.62 and 0.72 MPa m0.5, with minor standard deviations of 0.013 and 0.017, respectively.

Fig. 2
figure 2

Virgin CCNBD samples of Dazhou sandstone

Full size image
Table 1 Geometry and fracture testing results of the CCNBD specimens
Full size table

3 The G-Method for Fracture Toughness Determination

According to the Griffith energy criterion (Griffith 1920), the strain energy release rate G can be defined as follows.

$$G = \frac{\partial U}{\partial A}$$
(2)

where ∂A denotes the differential increment of the fracture area, and ∂U refers to the relevant differential decrement of the strain energy stored in the rock mass. Given the evolution of the strain energy and the fracture area, the fracture energy G at any time instant can be obtained. Subsequently, the critical SIF can be derived via Eq. 3, as long as the critical fracture energy G c is determined (Irwin 1957).

$$K_{\text{IC}} = \left\{ \begin{aligned} \sqrt {G_{\text{c}} E} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({\text{plane}}\;{\text{stress}}\;{\text{condition}}) \hfill \\ \sqrt {G_{\text{c}} E / (1 - \nu^{2} )} \;\;\;\;\;\;\;\;\;\;({\text{plane}}\;{\text{strain}}\;{\text{condition}}) \hfill \\ \end{aligned} \right.$$
(3)

where K IC is the fracture toughness; E is the Young’s modulus, and ν is the Possion’s ratio.

The two parameters in Eq. 3, U and A, however, can hardly be attained in the laboratory tests because of the limited experimental techniques. In contrast, with all the energy components traced in the DEM model, the total energy input in generating new fracture surfaces can be obtained. The energy partitions of interest in this study are, in order, boundary energy, potential energy, frictional energy, and kinetic energy, for which the algorithms are depicted in Eqs. 4–7:

$$E_{\text{w}} = \sum\limits_{{N_{\text{t}} }} {\left( {\sum\limits_{{N_{\text{w}} }} {(F_{i} \cdot {\text{d}}U_{i} + M_{i} \cdot {\text{d}}\theta_{i} )} } \right)}$$
(4)

where E w is the boundary energy which is calculated incrementally, denoting the accumulated work done by both walls on the particle assembly; N t and N w denote the number of total steps and broken bonds, respectively; F i and M i are the resultant force and moment acting on the wall at the start of the current timestep, respectively; dU i and dθ i are the incremental translational and rotational components of the applied displacement during the current timestep, respectively.

$$E_{\text{p}} = E_{\text{c}} + E_{\text{b}}$$
(5)
$$E_{\text{c}} = \frac{1}{2}\sum\limits_{{N_{\text{c}} }} {\left( {\left( {F_{i}^{\text{n}} } \right)^{2} /k_{i}^{\text{n}} + \left( {F_{i}^{\text{s}} } \right)^{2} /k_{i}^{\text{s}} } \right)}$$
(5-1)
$$E_{\text{b}} = \frac{1}{2}\sum\limits_{{N_{\text{b}} }} {\left( {(F_{bi}^{\text{n}} )^{2} /k_{bi}^{\text{n}} + (F_{bi}^{\text{s}} )^{2} /k_{bi}^{\text{s}} + (M_{bi} )^{2} /(I_{bi} k_{bi}^{\text{n}} )} \right)}$$
(5-2)

where E p is the total potential energy; E c and E b are the potential energy stored in all contacts and bonds, respectively; N c denotes the number of contacts. For each contact individual i, F n i and F s i are normal force and shear force, respectively; k n i and k s i are the mean values of the normal and shear stiffness of the two particle constituents; N b denotes the number of bonds, and for individual bond i, M bi is the applied moment; F n bi and F s bi are the normal force and shear forces, respectively; k n bi and k s bi are the normal and shear stiffness, and I bi is the moment of inertia.

$$E_{\text{f}} = \sum\limits_{{N_{\text{t}} }} {\left( {\sum\limits_{{N_{\text{broken}} }} {F_{\text{s}} \cdot {\text{d}}s} } \right)}$$
(6)

where E f denotes the accumulated energy dissipated by friction; N t and N broken denote the number of total steps and broken bonds up to current step, respectively; F s is the average shear force and ds is the increment of the relative displacement.

$$E_{\text{k}} = \frac{1}{2}\sum\limits_{{N_{\text{p}} }} {(m_{i} v_{i}^{2} } + I_{i} \omega_{i}^{2} )$$
(7)

where E k denotes the kinetic energy, and N p denotes the number of the particles; m i , I i , v i and ω i are mass, moment of inertial, translational and rotational velocities of particle i, respectively.

Based on the first law of thermodynamics, the accumulated fracture energy E s at current iteration step can be calculated as:

$$E_{\text{s}} = E_{\text{w}} - (E_{\text{p}} + E_{\text{k}} + E_{\text{f}} ).$$
(8)

It is noted that the propagating fracture can be traced by real-time monitoring of the AE distribution in DEM simulations. In practice, the point set of the monitored AE sources is projected onto the diametrical plane through the notched tip, since the fracture profile of the CCNBD specimen recovered from experiments can be approximated as a smooth surface. Thus, the finite domain occupied by the point set is taken as the fracture surface. However, existing methods to characterize the particular domain of a point set, such as the widely used Delaunay triangulation algorithm, Voronoi diagrams or alpha shapes (Amenta et al. 1998; Edelsbrunner and Mücke 1994), are not applicable in this case because, the propagating crack front of the CCNBD specimen is a concave curve. As a result, the Delaunay triangulation algorithm and other methods would generally result in a convex hull, which will overestimate the realistic fracture area.

Given that the primary fracture of the CCNBD specimen evolves in a unidirectional manner, an outline detecting algorithm based on MATLAB programming is proposed herein to determine the fracture surface profile and subsequently, the fracture area. In the program, when an AE event occurs somewhere inside the specimen, its position quantified by the three Cartesian coordinates can be precisely recorded. Then, the upper and lower boundary-points of the fracture profile are determined according to the coordinate components of AE along the cracking direction. Finally, the corresponding fracture area can be calculated as the area of a polygon, given the coordinates of the boundary vertices.

4 Numerical Simulations

4.1 Model Setup

The numerical model of the CCNBD specimen is created by the DEM open source code ESyS-Particle herein (Abe et al. 2004; Utili et al. 2014; Zhao et al. 2015). In the model, the dispersed particles are bonded together to model the brittle rock, and the bonds break once they are loaded beyond their strength capacity. Rigid walls are used as loading platens which move at a constant and rather low velocity about 5 × 10−9 m per iteration step to guarantee the quasi-static loading state. The geometric dimensions of the DEM model are set the same as real rock specimens.

Before the CCNBD fracture modeling, it is necessary to tune the microscopic parameters of the DEM model, so that the response of a DEM rock sample can match the macroscopic properties of a real rock mass. As an example, the experimental and numerical force–displacement curves of specimen C-8 are illustrated in Fig. 3. It can be observed that before reaching the peak value, the curve of experimental results rises slowly at the initial compression stage. The nonlinearity of the curve indicates the closure of microvoids and fissures inside the rock sample. Then, the curve increases linearly with slight fluctuation, showing a typical linear normal deformation of rock sample. However, the numerical model presents a linear deformation in the pre-peak region, which fails to reproduce the initial nonlinearity. Since the linear part of the force–displacement curve is associated with the predominant characteristics of rock cracking, the numerical force–displacement curve is offset to match the pre-peak linear portion of the experimental results. As shown in Fig. 3, the slope of the force–displacement curve obtained numerically is almost identical to that obtained experimentally, i.e., k E ≈ k N. When reaching the peak value, the numerical result can match the experimental one. Subsequently, in the post-peak region, both the loading forces of the experiment and the simulation decrease sharply as the cracks propagate in an unstable manner. In general, the mechanical responses (e.g. the deformability and the failure resistance) of the numerical CCNBD model can be consistent with the rock specimen used in laboratory experiments.

Fig. 3
figure 3

Calibration for the force–displacement curves of the CCNBD model

Full size image

As with the above discussed model calibration procedure, the input parameters of the numerical CCNBD models for the four specimens can be obtained, as shown in Table 2. In addition, one cylindrical sample with the calibrated microscopic parameters is tested on a uniaxial compression test, and the Young’s modulus and Poisson’s ratio are determined as 3.66 and 0.28 GPa, respectively.

Table 2 Calibrated microscopic parameters of the numerical CCNBD model
Full size table

4.2 Progressive Fracture of CCNBD Specimen

The numerical modeling on specimen C-8 is also used to demonstrate the whole measuring process by the G-method. The energy partitions mentioned in Sect. 3 (i.e. the boundary energy, the frictional energy, the kinetic energy and the potential energy), and the AE events and their positions are recorded during the tests. Figure 4 depicts the evolution of these energy partitions along with the AE rate (herein defined as the number of AE events per measured displacement increment) and the loading force. The boundary energy increases with the axial displacement of the specimen under the constant displacement loading, serving as the total input energy. The potential energy stored in the specimen increases in accordance with the boundary energy. Due to rock damage denoted by the AE events, the increasing rate of the potential energy slows down as the force approaches the peak force. The frictional energy increases slowly as a result of the relative displacements between the touching rough interfaces including the specimen-loading device interfaces and the rough fracture surfaces. The tiny kinetic energy originated from the movement of the two split-up halves of the disc in the quasi-static test is also incorporated in the energy analyses for an accurate measurement of the accumulated fracture energy. The evolution of the AE rate in Fig. 4 shows that AE occurs sporadically in the early loading stage, and then, it accumulates, and increases sharply as the load approaches its peak. Finally, it drops sharply as the loading force decreases. This corresponds to the processes of crack initiation, coalescence to macro fractures, stable propagation of fractures, and subsequently the propagation of unstable fractures.

Fig. 4
figure 4

Evolution of energy partitions, AE events and loading force of the simulated CCNBD test

Full size image

Figure 5 illustrates the spatial distribution of AE, covering six representative stages, i.e., (a) 60 % peak force, (b) 75 % peak force, (c) 90 % peak force, (d) 95 % peak force, (e) 100 % peak force, and (f) post 95 % peak force, in two perspectives [perpendicular to the disc surface (left) and to the plane through the notch tip (right)]. It can be seen from the diametrically cut view figures that at stage (a), a few microcracks initiate around the notch tip due to stress concentration, but they remain rather inactive during the period from stage (a) to stage (b), i.e., above the medium level of the loading force. From stage (c), i.e., a short time before the peak force, fractures initiated from the notch tip coalesce and propagate toward both loading ends. Meanwhile, new cracks appear on the chevron edges, forming a couple of asymmetrical fracture profiles with curved cracking front. At stage (e), i.e., the peak force moment, fractures approach the base of the chevron notch. Note that at this critical state, the fracture fronts in both sides with trivial jags are rather curved, which violates the assumption adopted in the measuring principle of the CCNBD method suggested by ISRM (Fowell 1995). The above simulations validate what has been reported in Dai et al. (2015a). Subsequently, the loading force decreases as cracks continue to propagate diametrically toward both loading ends in an unstable manner. It can also be observed in Fig. 5 that the propagating fracture is nearly confined in the notch ligament (see left-hand figure series of Fig. 5), during the whole cracking process of the CCNBD specimen.

Fig. 5
figure 5

Progressive fracture process of a CCNBD specimen: AE distribution in the view of the direction perpendicular to the disc surface and to the diametrically cut plane through the notch tip

Full size image

4.3 K IC Determined by the G-Method

Figure 6 exhibits the outlines of the fracture surfaces in the view perpendicular to the sample surface at the six typical stages. It can be seen that the projected fracture surfaces keep consistent with those characterized by the AE distribution in Fig. 5. Meanwhile, the energy partitions and the accumulated fracture energy can be calculated by Eqs. 4–8. Accordingly, the relationship between the accumulated fracture energy and the fracture area during the progressive fracture of the specimen can be established, as shown in Fig. 7. Since all points at the fracture front should possess an identical SIF value during fracture propagation, it is reasonable to quantify the SIF around the cracking tip of a certain thickness using a unique SIF value. By combining Eqs. 2 and 3, the SIF value is determined by the derivative of the accumulated fracture energy with respect to the fracture area, namely, the slope of the energy–area curve in Fig. 7 (denoted as the dashed line). The overlapping of the energy–area curve and its linear regression indicates that the accumulated fracture energy and the fracture area are linearly correlated, and thus, the SIF around the propagating crack tip can be regarded as constant throughout the tests.

Fig. 6
figure 6

The fracture profiles of a CCNBD specimen at six typical progressive fracture stages

Full size image
Fig. 7
figure 7

Variation of the accumulated fracture energy versus the fracture surface area

Full size image

Similar linear regression analyses have been conducted on several groups of the energy–area data chosen symmetrically on both sides of the peak force. The statistical results of the regression are depicted in Table 3, including an estimate of the monomial coefficient (i.e., the slope G of the regression line), the relevant determination of coefficient R 2, the F statistic and its p value, and an estimate of the error variance. Note that the R 2 values and the p values nearly approach 1.0 and 0.0, respectively, indicating that the accumulated fracture energy and the fracture surface area data in the neighbor of the peak force are linearly correlated. Thus, the group of G values are reasonable to represent the energy release rate of the specimen around the peak force. Substituting the G values into Eq. 3, the K IC of specimen C-8 is determined as 0.61 MPa m0.5. Similarly, the G-method is applied to the other three specimens (C-1, C-12, and C-35), yielding fracture toughness of 0.63, 0.63, and 0.65 MPa m0.5, respectively.

Table 3 Simple linear regression of data around the peak force
Full size table

5 Discussions

To assess the merit of the G-method, results are compared with those obtained from experiments (Table 1). In addition, compared to the specimen with chevron notches, the fracture mechanism of the straight through cracked specimen is unambiguous, since it is generally believed that as the crack initiates, the load reaches its maximum. Therefore, results of the SCB fracture tests of Dazhou sandstone (Wei et al. 2015b) can be referred herein, of which the average K IC value is 0.56 MPa m0.5. Figure 8 displays the fracture toughness values of the four CCNBD specimens obtained via the above mentioned methods, as well as their mean values with the standard deviations shown in parentheses on the graph. It can be seen that the data in each group are very close because, the tested sandstone is rather isotropic. Coincidentally, the average K IC value obtained by the G-method (0.63 MPa m0.5) approaches what is derived from the peak force using the Y *min value as suggested by ISRM (Fowell 1995) (0.62 MPa m0.5). Note that the mean (0.72 MPa m0.5) using the Y *min value updated by Wang et al. (2013) is 16 % higher than that by ISRM (Fowell 1995). Most importantly, compared with the average K IC value (0.56 MPa m0.5) of the SCB specimens, those derived from the CCNBD specimens using the G-method, and the Y *min values calibrated by Wang et al. (2013) are 13 and 29 % higher, respectively.

Fig. 8
figure 8

Comparison of the mode I fracture toughness measurements

Full size image

It is noted that, employing the straight through crack assumption (Fowell 1995), the Y *min value calibrated by Wang et al. (2013) is more accurate than what has been documented in the ISRM suggested method (Fowell 1995), which has also been numerically confirmed by Dai et al. (2010). Thus, in the framework of linear elastic fracture mechanics, given the ISRM suggested calculating equation (Fowell 1995), the mode I fracture toughness determination using the CCNBD specimens should adopt Y *min values updated in Wang et al. (2013) for a better measurement of K IC values. Our studies demonstrate that the G-method incorporating the realistic fracture profiles contributes to reducing the discrepancy of the fracture toughness measurements between the CCNBD and the SCB method from 29 to 13 % (Fig. 8). This difference can be partially explained by graphs plotted on Fig. 9, in which the red curves describe approximately the simulated critical crack front (consistent with Fig. 5e), while the black dashed lines locate the critical cracking front of the standard CCNBD specimen as documented by ISRM (Fowell 1995), with a m denoting the documented critical crack length by ISRM. Apparently, the simulated critical crack length is longer than that determined by ISRM, and the similar phenomena have been validated in recent researches (Dai et al. 2015a, b). When the loading force reaches its peak value, the realistic fracture area corresponding to the critical fracture profile is larger than that assumed by ISRM (see Fig. 9b, c), and the resulting fracture toughness value calculated by Eq. 2 is lower.

Fig. 9
figure 9

Schematics of the critical fracture profiles in various methods: a critical fracture fronts, b critical fracture surface obtained in the simulation, and c critical fracture surface assumed by ISRM

Full size image

Notwithstanding the current improvement of the fracture toughness determination of the CCNBD method, the measuring discrepancies among the CCNBD and other methods have not been fully understood. Actually, the DEM-based G-method assumes that the numerically obtained AE distribution reproduces the realistic fracture profile, and that the propagating fracture surface can be approximated by a 2D polygon that is dictated by the AE sources. In addition, this method is more appropriate for relatively homogeneous rocks in which the AE events would gather intensively to identify the main fracture surface. More accurate approaches for identifying fracture profiles from the AE events are expected in the future to improve the G-method.

6 Conclusion

The ISRM suggested CCNBD method has been widely used in laboratory tests to measure the mode I fracture toughness of rock mass. Nevertheless, a certain discrepancy has been observed among results derived from methods using straight through cracked specimens, which might be partially ascribed to the fact that the fracture profile disagrees with the assumed straight through crack front. To assess the influence of realistic cracking profiles on the mode I fracture toughness measurements, DEM has been employed in this study to investigate the progressive fracturing of the CCNBD specimen and to determine the corresponding fracture toughness via an energy approach.

The numerical investigation on the progressive failure of the CCNBD specimen shows that cracks initiate from the notch tip as well as the saw-cut edge of the chevron ligament, representing the curved fracture fronts throughout the fracture process. Taking the realistic fracture profiles into consideration, our proposed G-method (derived from Griffith’s energy release rate criterion) can determine the mode I fracture toughness of the CCNBD specimen, in which the evolution of the realistic fracture profile is obtained by DEM simulations, and the accumulated fracture energy can be derived according to the first law of thermodynamics. A comparison with experimental results of both the CCNBD and the SCB specimens verifies that the G-method incorporating the realistic fracture profiles contributes to narrowing the discrepancy between the fracture toughness values measured via the CCNBD and the SCB method from 29 to 13 %. The remaining difference might be reduced by more accurate characterization of fracture profiles from the AE events, considering additional factors (e.g., the actual geometry of the initial crack) that can influence the value of SIF.