1 Introduction

Creep behavior is significant for judging the long-term stability of rocks (Miura et al. 2003; Damjanac and Fairhurst 2010; Chandler 2013; Lacroix and Amitrano 2013). The stress path strongly influences creep behavior. Based on the experimental results of creep under step loading for axial stress, the effects of confining pressure on axial, lateral, and volumetric strain; strain rate; and porosity of rock were studied (Singh 1975; Boukharov et al. 1995; Baud and Meredith 1997; Yang and Daemen 1997; Fabre and Pellet 2006; Ma and Daemen 2006; Heap et al. 2009, 2011; Zhang et al. 2012). Numerous viscoplastic creep models were presented by a phenomenological approach. The parameters in the proposed equations can be obtained from a series of basic experiments. Creep failure behaviors of rock under different constant loads (Munson 1997; Bellenger and Bussy 2001; Challamel et al. 2005), step loading of axial stress (Jin et al. 2003; Aydan et al. 2014; Yang et al. 2014), and step unloading of confining pressure (Xia et al. 2009) were predicted. These creep properties were studied through the aforementioned phenomenological method.

The transient creep law was derived from mechanisms of time-dependent cracking in non-homogeneous brittle materials. The stress dependence of creep was also predicted by using this theoretical model (Scholz 1968). Based on Scholz’s theory and Charles’ law, the effects of micromechanical parameters on creep behavior were studied in brittle rocks subjected to uniaxial compressive loading (Cruden 1970). Based on the mechanism of subcritical crack growth under stress corrosion, a micromechanics-based method for predicting the creep failure was presented. The creep failure of rock was also predicted under different stress states, temperatures, and contents of water (Miura et al. 2003; Nara et al. 2010, 2013). Furthermore, based on the acoustic emission from microcrack growth during creep under step loading for axial stress, the correlation between the cumulative number of emission events and inelastic creep strain was examined (Lockner and Byerlee 1977; Ohnaka 1983; Grgic and Amitrano 2009; Eslami et al. 2012). The rock creep failure process under the step unloading of confining pressure was studied by the acoustic emission monitoring technique. The frequency–amplitude relationships of acoustic emission signals during different stress paths were investigated (He et al. 2010). The microcrack growth during creep was studied using a scanning electron microscope. The interaction between cracks increases with the increase in the number of individual cracks over time, and the coalescence of cracks plays an important role in tertiary creep (Kranz 1979).

Previous studies have hardly focused on the micromechanical and theoretical background of the effects of stress paths on creep properties in brittle rock. A major challenge of this area is linking the microcrack growth behavior with the macroscopic mechanical behavior. Employing the energy method, some researchers have studied the correlation between macroscopic strain and microcrack growth (Kostrov 1974; Rice 1975; Costin 1985; Johnson and Sammis 2001; Deshpande and Evans 2008; Bhat et al. 2011; Brantut et al. 2012). In the present study, we aim to establish the relationship between microcrack length and macroscopic strain based on the definition of damage between micromechanical and macroscopic scales. Furthermore, Ashby’s microcrack model, Charles’ law, and the stress path function are used to propose a new micromechanics-based model for studying the macroscopic creep mechanical behaviors caused by microcrack growth under step loading and unloading. The theoretical expression of stress–strain relationships is derived. The theoretical results are validated by the experimental data of Jinping marble. The effects of model parameters on creep behavior are also discussed.

2 Description of the Theoretical Model

2.1 Relationship Between Stress and Crack Growth in Compression

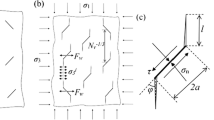
The micromechanical model with initial microcracks of brittle rock is shown in Fig. 1 (Ashby and Sammis 1990). This classical model is widely applied to study the micromechanical properties of brittle material (Deshpande and Evans 2008; Bhat et al. 2011; Brantut et al. 2012; Mallet et al. 2015). The rock is assumed to be an isotropic elastic body that contains initial penny-shaped microcracks with radius a, and the angle between each initial microcrack and maximum principal stress σ 1 is assumed to be φ. As a result of the initial crack growth of brittle rock in compression, the wing crack (with length denoted by l) occurs at both initial crack ends. Compressive stress is denoted in theory as negative for calculation and positive in plotting for observation.

Fig. 1
figure 1

a Model of microcracks growth under triaxial pressure. b Mechanical behavior of a single microcrack

Full size image

For the conventional triaxial test, σ 1 is the axial stress, and confining pressure σ 3 is equal to σ 2. The crack density was defined by Bristow (1960), and its generalization was provided by Walsh (1965a, b). The initial crack density was concluded to possess great significance for the mechanical behaviors of rocks. Furthermore, the size and density of the initial crack were characterized by an initial damage defined as \(D_{\text{o}} = 4\pi N_{\text{V}} \left( {\alpha a} \right)^{ 3} / 3\) (Ashby and Sammis 1990), where N V is the number of initial microcracks per unit volume and \(\alpha = { \cos }\varphi\).

The stress intensity factor of mode I cracks could be expressed as follows (Ashby and Sammis 1990):

$$K_{\text{I}} = \frac{{F_{\text{w}} }}{{[\pi (l + \beta a)]^{{\frac{3}{2}}} }} + \frac{2}{\pi }(\sigma_{3} + \sigma^{i}_{3} )\sqrt {\pi l}$$
(1)

where:

$$\sigma_{3}^{i} = \frac{{F_{\text{w}} }}{{\pi^{ 1/ 3} \left[ {{ 3\mathord{\left/ {\vphantom { 3{\left( { 4N_{\text{V}} } \right)}}} \right. \kern-0pt} {\left( { 4N_{\text{V}} } \right)}}} \right]^{ 2/ 3} - \pi (l + \alpha a)^{2} }}$$
(2)
$$F_{\text{w}} = (\tau + \mu \sigma_{\text{n}} )\pi a^{2} \sin \varphi = - (A_{1} \sigma_{1} - A_{2} \sigma_{3} )a^{2}$$
(3)
$$A_{ 1} = \pi \sqrt {{\beta \mathord{\left/ {\vphantom {\beta 3}} \right. \kern-0pt} 3}} \left[ {\sqrt {1 + \mu^{2} } - \mu } \right]$$
(4)
$$A_{2} \, =\, A_{ 1} {{\left( {\sqrt {1 + \mu^{2} } + \mu } \right)} \mathord{\left/ {\vphantom {{\left( {\sqrt {1 + \mu^{2} } + \mu } \right)} {\left( {\sqrt {1 + \mu^{2} } - \mu } \right)}}} \right. \kern-0pt} {\left( {\sqrt {1 + \mu^{2} } - \mu } \right)}}$$
(5)

where μ is the friction coefficient on the initial microcrack interface and β is a constant. The function of parameter β is to prevent the value of stress intensity factor K I from reaching an infinite value in the case of l = 0. The wedging force F w is balanced by internal stress \(\sigma_{3}^{i}\) between two wing crack tips (Fig. 1a).

Simplifying Eq. (1), we can rewrite the stress intensity factor as:

$$K_{\text{I}} = \sqrt {\pi a} \left[ {\sigma_{3} c_{3} - (A_{1} \sigma_{1} - A_{2} \sigma_{3} )(c_{1} + c_{2} )} \right]$$
(6)

where:

$$c_{1} = \pi^{ - 2} ({l \mathord{\left/ {\vphantom {l a}} \right. \kern-0pt} a} + \beta )^{{ - {3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0pt} 2}}}$$
(7)
$$c_{2} = {{2(\pi \alpha )^{ - 2} \sqrt {{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0pt} a}} } \mathord{\left/ {\vphantom {{2(\pi \alpha )^{ - 2} \sqrt {{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0pt} a}} } {\left[ {D_{\text{o}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} - \left( {1 + \frac{l}{\alpha a}} \right)^{2} } \right]}}} \right. \kern-0pt} {\left[ {D_{\text{o}}^{{ - {2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}} - \left( {1 + \frac{l}{\alpha a}} \right)^{2} } \right]}}$$
(8)
$$c_{3} = 2\pi^{ - 1} \sqrt {{l \mathord{\left/ {\vphantom {l a}} \right. \kern-0pt} a}}$$
(9)

The theory of mechanics of fracture posits that cracks can grow when the stress intensity factor at the tips of wing cracks K I reaches the critical value K IC in brittle rocks. However, the crack experiences slow and steady crack growth before the stress intensity factor at the tips of wing cracks K I reaches the critical value K IC, which is called subcritical crack growth (Charles 1958; Atkinson 1984). If the subcritical crack growth is neglected, the crack starts to grow when the stress intensity factor K I reaches the critical value K IC. According to Eq. (6), the relation between the wing crack length l and stress state (σ 1, σ 3) can be expressed as:

$$\sigma_{1} (l) = \frac{{\sigma_{3} [c_{3} (l) + A_{2} (c_{1} (l) + c_{2} (l))] - {{K_{{\text{IC}}} } \mathord{\left/ {\vphantom {{K_{{\text{IC}}} } {\sqrt {\pi a} }}} \right. \kern-0pt} {\sqrt {\pi a} }}}}{{A_{1} [c_{1} (l) + c_{2} (l)]}}$$
(10)

The function σ 1(l) exhibits a maximum σ 1peak corresponding to the short-term strength in brittle rocks (Ashby and Sammis 1990; Brantut et al. 2012), which shows that the relationship between axial stress and crack length is similar to a stress–strain relationship.

At the low-stress level, the initial cracks do not slide and the rock behaves elastically at |τ| ≤ μ|σ n |. When axial stress σ 1 reaches the critical stress σ 1c, wing cracks start to form from the initial crack tips. This critical stress can be achieved as in (Ashby and Hallam 1986):

$$\sigma_{{1\text{c}}} = \frac{{\sqrt {1 + \mu^{2} } + \mu }}{{\sqrt {1 + \mu^{2} } - \mu }}\sigma_{3} - \frac{\sqrt 3 }{{\sqrt {1 + \mu^{2} } - \mu }}\frac{{K_{{\text{IC}}} }}{{\sqrt {\pi a} }}$$
(11)

The parameters a and μ can be obtained by comparing the linear empirical relationship between confining pressure σ 3 and axial stress σ 1c at the onset of cracking from triaxial compressive experiments with the theoretical relationship from Eq. (11). The parameter β is assumed to be a variable that relates to the friction coefficient μ (Brantut et al. 2012). In this study, we obtained a constant value of parameter β (i.e., β = 0.32) by comparing Eqs. (11) and (10) at σ 1c = σ 1 (l = 0). This value is also found in the results reported by Bhat et al. (2011).

2.2 Crack Growth Law

Given the effects of subcritical crack growth, cracks in brittle rocks start to grow when K I < K IC. For a mode I crack, the crack growth rate can be expressed as (Charles 1958; Atkinson 1984):

$$\frac{{{\text{d}}l}}{{{\text{d}}t}} \,=\, v\left( {\frac{{K_{\text{I}} }}{{K_{{\text{IC}}} }}} \right)^{n}$$
(12)

where exponent n is the stress corrosion index and v is the characteristic crack velocity. Both constants can be achieved via a subcritical crack growth test (Evans 1972; Atkinson 1979; Nara et al. 2010, 2013).

Substituting Eqs. (6) into (12), we can obtain a differential equation of wing crack length over time as:

$$\frac{{{\text{d}}l}}{{{\text{d}}t}} = v(\pi a)^{n/2} \left[ {\frac{{(A_{2} \sigma_{3} - A_{1} \sigma_{1} )(c_{1} + c_{2} ) + \sigma_{3} c_{3} }}{{K_{{\text{IC}}} }}} \right]^{n}$$
(13)

Crack growth under constant stress state (σ 1, σ 3) can be obtained from Eq. (13). However, the stress state applied to rocks changes upon excavation of underground engineering and the evolution of the earth’s crust (Lockner and Byerlee 1977; Ohnaka 1983; Fabre and Pellet 2006; Ma and Daemen 2006; Grgic and Amitrano 2009; Heap et al. 2009, 2011; He et al. 2010; Eslami et al. 2012). The stress path has significance for rock deformation. The stress path is defined by a stress–time function. Coupling this stress–time function and Eq. (13), a new expression of the effect of the stress path on crack growth can be written as:

$$\frac{{{\text{d}}l}}{{{\text{d}}t}} = v(\pi a)^{n/2} \left\{ {\frac{{\left[ {A_{2} \sigma_{3} (t) - A_{1} \sigma_{1} (t)} \right](c_{1} + c_{2} ) + \sigma_{3} (t)c_{3} }}{{K_{{\text{IC}}} }}} \right\}^{n}$$
(14)

When the axial stress σ 1(l) is less than the short-term strength and larger than the crack initiation stress, the equilibrium crack length l o can be achieved by Eq. (10) at applied constant axial stress. This value of equilibrium crack length can be taken as the initial wing crack length for the numerical integration of Eq. (14). The numerical solution for the evolution of wing crack length can be obtained by substituting the equilibrium crack length l o into Eq. (14).

2.3 Relationship Between Microcrack Growth and Macroscopic Strain

Damage is a degradation factor that affects the mechanical property of the material caused by the change of microdefects. The continuous damage theory developed by Lemaitre and Plumtree (1979) was used by other researchers to quantify damage (Krajcinovic 1983; Kachanov 1986; Ashby and Sammis 1990; Wang and Lou 1990). The damage could be defined by many different variables (e.g., microcrack size, strain, and others).

Numerous microcracks exist in brittle rock and the distribution of microcracks is random. Based on the Weibull (1951) probability distribution, the damage was expressed as (Chen et al. 1997):

$$D = 1 - \exp \left[ { - \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\varepsilon_{\text{o}} }}} \right. \kern-0pt} {\varepsilon_{\text{o}} }}} \right)^{m} } \right]$$
(15)

where m and ε o are the material constants, and ε is the axial strain. Substituting initial damage D o into Eq. (15), we can derive the elastic strain before cracking as ε e = ε o[−ln(1 − D o)]1/m.

According to the density and size of the microcracks, the damage can be defined as (Ashby and Sammis 1990):

$$D = \frac{4}{3}\pi N_{\text{V}} (l + \alpha a)^{3}$$
(16)

For the single rock sample, the same damage value between micromechanical and macroscopic scales can be obtained. Comparing Eq. (15) with Eq. (16), we can derive the correlation of the macroscopic strain and microcrack growth as:

$$\varepsilon = \varepsilon_{\text{o}} \left( { - \text{ln}\left[ {1 - {{(l + a\alpha )^{3} D_{\text{o}} } \mathord{\left/ {\vphantom {{(l + a\alpha )^{3} D_{\text{o}} } {(a\alpha )^{3} }}} \right. \kern-0pt} {(a\alpha )^{3} }}} \right]} \right)^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}}}$$
(17)
$$l = a\alpha \left[ {D_{\text{o}}^{{^{ - 1/3} }} \left( {1 - \exp \left[ { - \left( {{\varepsilon \mathord{\left/ {\vphantom {\varepsilon {\varepsilon_{\text{o}} }}} \right. \kern-0pt} {\varepsilon_{\text{o}} }}} \right)^{m} } \right]} \right)^{1/3} - 1} \right]$$
(18)

2.4 Stress–Strain Relationship During Progressive Failure

Substituting Eq. (18) into Eq. (10), we can express the stress–strain relationship as:

$$\sigma_{1} (\varepsilon ) = \frac{{\sigma_{3} [J_{3} + A_{2} (J_{1} + J_{2} )] - {{K_{{\text{IC}}} } \mathord{\left/ {\vphantom {{K_{{\text{IC}}} } {\sqrt {\pi a} }}} \right. \kern-0pt} {\sqrt {\pi a} }}}}{{A_{1} (J_{1} + J_{2} )}}$$
(19)

where:

$$J_{1} = \pi^{ - 2} \left( {\alpha J_{4} + \beta } \right)^{ - 3/2}$$
(20)
$$J_{2} = {{2\pi^{ - 2} \alpha^{ - 3/2} J_{4}^{1/2} } \mathord{\left/ {\vphantom {{2\pi^{ - 2} \alpha^{ - 3/2} J_{4}^{1/2} } {\left[ {D_{\text{o}}^{ - 2/3} - \left( {J_{4} + 1} \right)^{2} } \right]}}} \right. \kern-0pt} {\left[ {D_{\text{o}}^{ - 2/3} - \left( {J_{4} + 1} \right)^{2} } \right]}}$$
(21)
$$J_{3} = {{2\left( {\alpha J_{4} } \right)^{1/2} } \mathord{\left/ {\vphantom {{2\left( {\alpha J_{4} } \right)^{1/2} } \pi }} \right. \kern-0pt} \pi }$$
(22)

where:

$$J_{4} = D_{\text{o}}^{ - 1/3} \left[ {1 - \exp \left[ { - (\varepsilon /\varepsilon_{\text{o}} )^{m} } \right]} \right]^{1/3} - 1$$
(23)

2.5 Relationship Between Strain and Time During Creep Failure

The time-dependent wing crack length (i.e., l(t)) can be calculated by the numerical integration of Eq. (14). Substituting the solution of evolution for wing crack length into Eq. (17), we can achieve the relation between time and strain as:

$$\varepsilon (t) = \varepsilon_{\text{o}} \left( { - \text{ln}\left[ {1 - {{(l(t) + a\alpha )^{3} D_{\text{o}} } \mathord{\left/ {\vphantom {{(l(t) + a\alpha )^{3} D_{\text{o}} } {(a\alpha )^{3} }}} \right. \kern-0pt} {(a\alpha )^{3} }}} \right]} \right)^{{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-0pt} m}}}$$
(24)

Due to these contributions of modes II and III, stress intensity factors that act along the edges of the initial cracks during sliding are much less significant than the contribution of K I with the wing cracking. These contributions are negligible in consideration of the axial strain (Kachanov 1982; Bhat et al. 2011).

3 Results

In the following analysis, all parameters are taken from the experimental results of Jinping marble in China. The value of model parameters measured by the experiment commonly has certain errors. However, to determine the experimental parameters used in the theoretical model, the macroscopic theoretical results (i.e., the axial stress–axial strain curve and evolution of the creep curve) after each trial are used to calibrate the parameters by comparing the macroscopic experiment results of Jinping marble in China (Wang et al. 2008; Xia et al. 2009; She and Cui 2010). This process is repeated until the theoretical results achieve sufficient consistency with the experimental results. The specific parameters of the micromechanics-based model for Jinping marble specimens are listed in Table 1.

Table 1 Parameters of Jinping marble specimens in this study
Full size table

The critical stress intensity factor, index of stress corrosion, and characteristic crack velocity in Table 1 were obtained via the subcritical crack growth test (Atkinson 1979; Wan et al. 2010). Initial damage was measured by a scanning electron microscope test. Material constants m and ε o were selected based on the studies by Chen et al. (1997) and Zhang et al. (2005). Based on the triaxial test results, an empirical relationship of crack initiation stress states in granite was suggested as σ 1c = 2.67σ 3 + 46 MPa (Wang et al. 2008). The friction coefficient and initial crack size was obtained by comparison with the empirical relationship and Eq. (11). To maximize the effect of the microcrack angle, the crack angle was often assumed to be φ = 45° (Ashby and Sammis 1990; Bhat et al. 2011; Brantut et al. 2012). The error of parameters for the experiment is also provided. The sensitivity of parameters is discussed in detail in the following section.

3.1 Progressive Failure

During progressive failure in brittle rocks, microcrack growth is closely associated with applied stress. This phenomenon has been widely studied by integrating the use of strain gauge measurements and acoustic emission monitoring. Microcrack growth can be characterized by several distinct phases: crack closure (which corresponds to stress σ cc), crack initiation (σ ci), and crack damage (σ cd) (Martin and Chandler 1994). Thus, the study of crack growth plays an important role in evaluating the micromechanical properties of brittle rocks in progressive failure.

As shown in Fig. 2, the relationships between axial stress σ 1 and the crack length at different confining pressures were obtained by Eq. (10). Figure 2 shows that the axial stress increases and reaches peak stress before decreasing with increments of crack length. The increments of crack length correspond to the process of crack initiation, propagation, and coalescence in the brittle rocks.

Fig. 2
figure 2

Relationships between axial stress and crack length under different confining pressures

Full size image

Figure 3 shows that the numerical stress–strain relationships at different confining pressures are presented by Eq. (19). Axial stress increased and achieved peak stress before arriving at failure with increments of axial strain. The peak stress and axial strain in peak stress both increased with the increment of confining pressure. Figure 4 shows that the crack initiation stress and peak stress both increased with increments of confining pressure. Furthermore, the difference between crack initiation stress and peak stress also increased with the increment of confining pressure. These theoretical results are highly consistent with the experimental results of Jinping marble (Wang et al. 2008). Only when the applied axial stress is in the range between crack initiation stress and peak stress can the initial equilibrium crack length l o be solved by Eq. (10) and the evolution of crack length and strain under creep be obtained by Eqs. (14) and (24). The rock deformation is elastic when the applied axial stress is smaller than the crack initiation stress. Thus, the range between crack initiation stress and peak stress at different confining pressures in Fig. 4 assists in selecting the initial value of axial stress in the experiment of creep under step loading. Much time is saved by selecting the appropriate axial stress at a given confining pressure.

Fig. 3
figure 3

Theoretical and experimental (Wang et al. 2008) stress–strain curves under different confining pressures

Full size image
Fig. 4
figure 4

Relationships between crack initiation stress, peak stress, and confining pressures in experimental (Wang et al. 2008) and theoretical results

Full size image

3.2 Stress-Stepping Creep Failure

The function of step loading is defined as σ 1(t) = σ 1i + Δσ[t/T] (σ 1i , Δσ are both positive), where T is the cycle time and [t/T] denotes that t/T is integerized (e.g., if t/T = 0.4, [t/T] = 0, and if t/T = 1.9, [t/T] = 1). The function of step unloading is defined as σ 3(t) = σ 3i  − Δσ[t/T] (σ 3i , Δσ are both positive), and the minimum of confining pressure σ 3 equals 0.

3.2.1 Creep Failure Under Step Axial Loading

The function of step loading of axial stress was selected as σ 1 = 60 MPa + 10 MPa [t/T] at σ 3 = 2 MPa and σ 1 = 90 MPa + 4 MPa [t/T] at σ 3 = 11 MPa, respectively. T = 100,000 s ≈ 27.78 h. The initial value of step loading for axial stress was 60 MPa for σ 3 = 2 MPa and 90 MP for σ 3 = 11 MPa. Certainly, initial axial stresses were selected in the range between crack initiation stress and peak stress in Fig. 4.

The evolutions of crack length were obtained by substituting the functions of step loading (i.e., σ 1 = 60 MPa + 10 MPa [t/100,000 s] for σ 3 = 2 MPa and σ 1 = 90 MPa + 4 MPa [t/100,000 s] for σ 3 = 11 MPa) into Eq. (14). Figure 5 shows that the crack length experienced transient and steady-state growth at low axial stress. Accelerated growth appeared at the last step when the axial stress reached 110 MPa (for σ 3 = 2 MPa) and 174 MPa (for σ 3 = 11 MPa).

Fig. 5
figure 5

Evolutions of crack length under step axial loading

Full size image

Evolutions of axial strain under step loading of axial stress were obtained by Eq. (24). Figure 6 shows that the axial strain has two creep stages at low axial stress: transient and steady-state creep. The accelerated creep appeared at the last step when the axial stress reached 110 MPa (σ 3 = 2 MPa) and 174 MPa (σ 3 = 11 MPa). Figure 6 shows that the rock failed when the axial stress reached 110 MPa (σ 3 = 2 MPa) and 174 MPa (σ 3 = 11 MPa). The figure also shows that the increment of axial strain for each step increased with incremental steps. This phenomenon corresponds to the variation of the steady-state creep strain rate. The axial creep strain rate for each step increased incrementally.

Fig. 6
figure 6

Evolutions of axial strain and strain rate under step axial loading. a σ 3 = 2 MPa, b σ 3 = 11 MPa

Full size image

3.2.2 Creep Failure Under Step Unloading of Confining Pressure

The function of the step unloading of confining pressure was selected as σ 3 = 20 MPa–6 MPa [t/100 h]. The initial values of step unloading for confining pressure were both 20 MPa for σ 1 = 110 MPa and 130 MPa.

The evolutions of crack length under step unloading of confining pressure were identified as σ 1 = 110 MPa and 130 MPa by substituting the function of step unloading (i.e., σ 3 = 20 MPa–6 MPa [t/100 h]) into Eq. (14). Figure 7 shows that the creep failure time at σ 1 = 110 MPa was smaller than the creep failure time at σ 1 = 130 MPa. The crack length experienced a transient and steady-state growth at high confining pressure. The accelerated growth appeared at the last step when the confining pressure reached 2 MPa (for σ 1 = 130 MPa) and 0 MPa (for σ 1 = 110 MPa).

Fig. 7
figure 7

Evolutions of crack length under step unloading of confining pressure

Full size image

The evolution of the axial strain under step unloading of confining pressure was identified as σ 1 = 110 MPa and 130 MPa in Fig. 8. The axial strain showed two creep stages at high confining pressure: transient and steady-state creep. The accelerated creep appeared at the last step when the confining pressure reached 2 MPa (for σ 1 = 130 MPa) and 174 MPa (for σ 3 = 11 MPa). Furthermore, the increment of strain for each step increased incrementally. This result corresponds to the variation of the steady-state creep rate. The steady-state creep strain rate increased incrementally.

Fig. 8
figure 8

Evolutions of axial strain and strain rate under step unloading of confining pressure. a σ 1 = 110 MPa, b σ 1 = 130 MPa

Full size image

4 Discussions

4.1 Validation of the Theoretical Model

To verify the rationality of the theoretical model, the theoretical results are compared with the published experimental results of Jinping marble in China (Xia et al. 2009; She and Cui 2010). This stress-stepping test approach has been widely used and is reliable (Fabre and Pellet 2006; Ma and Daemen 2006; Zhang et al. 2012; Yang et al. 2014). The experimental and theoretical results of axial creep strain under different loading conditions are shown in Fig. 9. The figure shows that the theoretical results are consistent with the experimental results (She and Cui 2010).

Fig. 9
figure 9

Theoretical and experimental (She and Cui 2010) results of axial creep strain under loading of axial stress

Full size image

The numerical results are not exactly the same as the experimental results. For the experimental results, the stress gradually increased after stabilization of the axial deformation. This deformation was considered to be stabilized when the strain rate became lower than a smaller value. Therefore, the step value Δσ is different at each step in the stress-stepping creep test. However, because the stress path controlled by the strain rate can hardly be implemented in the analytical method, the step value Δσ for the stress path is assumed to be constant. Thus, the numerical axial stress value could not accurately equal the experimental axial stress value in Fig. 9. The percentage of difference of axial stress for each step ranged from 0.7 to 13.4 %. However, it worked well, and the experimental results would be well recovered. Furthermore, the experimental axial stress value at each step was larger than the numerical stress, and the strain corresponding to the axial stress at each step in the experimental results was also larger than those in the numerical results. The larger axial stress corresponds to the larger strain. This phenomenon is known, and it shows that the difference between numerical and experimental results is acceptable.

Figure 4 shows that crack initiation stresses are 153 MPa for σ 3 = 40 MPa and 126 MPa for σ 3 = 30 MPa. Thus, the deformation behaved elastically when the applied axial stress was smaller than the crack initiation stress at a given confining pressure. As shown in Fig. 10, the deformation of rock (e.g., for σ 3 = 40 MPa and 30 MPa at σ 1 = 110 MPa, and σ 3 = 40 at σ 1 = 130 MPa) behaved elastically in the experimental results. However, the theoretical curves in Fig. 10 were only obtained from the stage of inelastic deformation.

Fig. 10
figure 10

Theoretical and experimental (Xia et al. 2009) results of creep strain under step unloading of confining pressure

Full size image

During the stress-stepping test, the rock was observed to fail abruptly after the last decrement of the confining pressure and before the beginning of the accelerated creep phase (Fig. 10). This indicates that the applied axial stress was close to the rock compressive strength at this confining pressure. Furthermore, owing to the extremely short time of the rock failure stage under the unloading of confining pressure, the creep curves under the last step were difficult to obtain from the experiment in Fig. 10. The theoretical results show that the time was very short in the last step. Neglecting these effect factors and the diffidence of confining pressure between the theoretical and experimental value, the theoretical results are similar to the experimental results at the stage of inelastic deformation (Xia et al. 2009). This step provides theoretical assistance in studying the creep behavior under step unloading of confining pressure.

In the present study, the rationality of the theoretical creep results is only verified for brittle rocks. Actually, compressive creep behavior has also been widely studied for other brittle materials, such as glass and concrete (Liu et al. 2002; Ranaivomanana et al. 2013; Mallet et al. 2014). Mechanisms such as the microcrack growth of brittle rocks were also observed. Thus, the theoretical model may also be applied to these brittle materials.

4.2 Sensitivity of Model Parameters

The effect of initial crack size on creep behavior under step loading of axial stress is shown in Fig. 11. Due to the initial damage \(D_{\text{o}} = 4\pi N_{\text{V}} \left( {\alpha a} \right)^{ 3} / 3\), the initial crack size is closely related to the initial damage. It other words, the initial crack size corresponds to the initial damage under the given initial microcrack number N V.

Fig. 11
figure 11

Effect of initial crack size on creep behavior under step loading of axial stress

Full size image

The creep failure time increased with decrements of initial crack size (i.e., initial damage). The creep failure time was 3676 s, and the creep failure appeared at the second step loading of axial stress when the initial crack size a =1.4 mm. The creep failure time was 21,945 s, and the creep failure appeared at the seventh step loading of axial stress when the initial crack size a = 1.3 mm. This means that the number of steps during the creep failure also increases with decrements of initial crack size. The initial strain also increases with increments of initial crack size (i.e., initial damage). These results show that the larger the initial damage, the larger the initial strain.

The effects of friction coefficient, stress corrosion index, and fracture toughness on creep behavior under step loading of axial stress are shown in Figs. 12, 13, and 14, respectively. The creep failure time increased with increments of friction coefficients, stress corrosion index, or fracture toughness.

Fig. 12
figure 12

Effect of friction coefficient on creep behavior under step loading of axial stress

Full size image
Fig. 13
figure 13

Effect of stress corrosion index on creep behavior under step loading of axial stress

Full size image
Fig. 14
figure 14

Effect of fracture toughness on creep behavior under step loading of axial stress

Full size image

4.3 Effects of the Unloading Rate of Confining Pressure

The effects of the unloading rate of confining pressure on the strain and strain rate were obtained based on creep in Fig. 15. The constant axial stress σ 1 = 110 MPa and the initial confining pressure σ 3 = 5 MPa. As shown in Fig. 15a, the creep failure time was 1.3 × 1012 s (i.e., 4122 years) when the confining pressure σ 3 = 5 MPa.

Fig. 15
figure 15

Effects of the unloading rate of confining pressure on axial strain and strain rate during creep

Full size image

As shown in Fig. 15b–d, the creep failure process was given when the unloading rate of confining pressure V unloading = 0.1, 0.01, and 0.01 MPa/s, respectively. The creep failure process had two stages: the evolutions of axial strain at σ 3 = 5 MPa − (V unloading)t and σ 3 = 0 MPa, respectively. Due to the break of the strain rate, an inflection point of axial strain appeared when the confining pressure decreased to 0 MPa. The time of the inflection point of axial strain was 50, 500, and 5000 s. The strain value of the inflection point was 4.0 × 10−3, 4.6 × 10−3, and 5.8 × 10−3. The creep failure time was 650, 1050, and 5250 s or so throughout the process. The time was 570, 550, and 240 s or so at σ 3 = 0 MP. Furthermore, due to small variations of the strain rate at t = 5000 s in Fig. 15d, the inflection point of axial strain was not apparent when the confining pressure decreases to 0 MPa.

A comparison of Fig. 15a–d shows that the creep failure time decreases with increments of unloading rate of confining pressure throughout the process. However, the time during σ 3 = 0 MPa increased with increments of unloading rate. A smaller unloading rate led to longer unloading time and then led to larger strain during the unloading stage and a shorter time at σ 3 = 0 MPa. Furthermore, the creep failure time at the unloading of confining pressure was significantly less than the creep failure time at constant confining pressure. This result shows that the unloading of confining pressure strongly influences the creep failure time.

4.4 Coupling Effect of Step Axial Stress and Confining Pressure

In the previous sections, the stress path was only focused on studying either axial stress or confining pressure. However, in reality, the coupling of stress paths in step axial stress and confining pressure has more significance for the application of underground engineering. In this section, the coupling effect of step axial stress and confining pressure on creep failure is examined, thereby providing theoretical assistance to studies on rock mechanical behavior under loading and unloading during the underground excavation. The initial axial stress σ 1i  = 210 MPa, initial confining pressure σ 3i  = 40 MPa, and the step value Δσ = 5 MPa and below.

As shown in Fig. 16, the function of the stress path was σ 1 = 210 MPa + 5 MPa [t/3600 s] for σ 3 = 40 MPa under step loading of axial stress. The accelerated creep failure stage appeared at σ 1 = 390 MPa. The creep failure time was 130,312 s. The function of stress path was σ 3 = 40 MPa − 5 MPa [t/3600 s] for σ 1 = 210 MPa under step unloading of confining pressure. The accelerated creep failure stage appeared at σ 3 = 10 MPa. The creep failure time was 21,601 s. The creep failure time for unloading of confining pressure was smaller than the loading of axial stress under the same step value and the initial stress state. These results show that the dependence of confining pressure on creep failure is larger than the dependence of axial stress on creep failure.

Fig. 16
figure 16

Comparison of evolutions of axial strain under step loading of axial stress and step unloading of confining pressure

Full size image

As shown in Fig. 17, the function of the stress path was σ 1 = 210 MPa + 5 MPa [t/3600 s] and σ 3 = 40 MPa − 5 MPa [t/3600 s]. The accelerated creep failure stage appeared at σ 1 = 235 MPa and σ 3 = 15 MPa. The creep failure time was 18,001 s. The creep failure time in Fig. 17 was smaller than the creep failure time in Fig. 16, which shows that the coupling effect of step confining pressure and axial stress was larger than the single effect of axial stress or confining pressure on creep failure.

Fig. 17
figure 17

Evolutions of axial strain and strain rate under step loading of axial stress and unloading of confining pressure

Full size image

As shown in Fig. 18, the function of step loading for the axial stress path was σ 1 = 210 MPa + 5 MPa [t/3600 s]. The confining pressure was applied by the loading and unloading of the cycle step (i.e., σ 3 = 40 MPa and 35 MPa). The accelerated creep failure stage appeared at σ 1 = 355 MPa and σ 3 = 35 MPa. The failure time was 105,093 s, which is smaller than the failure time at step loading of axial stress in Fig. 16. These results show that the cycle loading and unloading of confining pressure weakens the mechanical property, increases the damage, and accelerates the failure rate of rock. The strain rate at σ 3 = 40 MPa was significantly smaller than σ 3 = 35 MPa. Thus, the strain rate at σ 3 = 40 MPa approximately equals a constant value as shown in Fig. 18. Furthermore, the minimum strain rate at σ 3 = 35 MPa increases incrementally.

Fig. 18
figure 18

Evolutions of axial strain and strain rate under step loading of axial stress and cycle step loading and unloading of confining pressure

Full size image

The theoretical results are similar to triaxial unloading experiment results of studies in which the delayed rockburst of surrounding rock was studied during underground quarrying (He et al. 2010, 2012). The findings assist in understanding deformation behavior and time-delayed rockburst mechanism for surrounding rock during underground excavations.

5 Conclusions

A micromechanics-based model is presented to study the effects of the stress path on macroscopic creep failure. Ashby’s microcrack model, Charles’ law, the micro–macro relation, and the stress path function are employed in this model. This micro–macro relation is proposed by using the correlation between the definition of damage from micromechanical and macroscopic scales. The stress path function is applied by the relationship between stress and time. Using the parameters taken from Jinping marble, the stress–strain relationship and creep behavior are investigated in detail. The rationality of this proposed theoretical model is verified by the experimental results. The effects of model parameters on creep behavior are also discussed. The following conclusions are drawn from this study:

  1. 1.

    Effects of confining pressure on relationships between crack length, strain, and axial stress are studied. Relationships between crack initiation stress, peak stress, and confining pressure during progressive failure are obtained. Crack initiation and peak stress both approximately linearly increase with increments of confining pressure. This phenomenon provides important information in selecting objects for the study of applied stress under creep.

  2. 2.

    The crack growth, strain, and strain rate are investigated under step loading for axial stress at constant confining pressure or step unloading for confining pressure at constant axial stress. The two applied stress paths both accelerate the crack growth and shorten creep failure time.

  3. 3.

    Effects of initial crack size, friction coefficient, stress corrosion index, and fracture toughness on stress-stepping creep behavior are studied. The increments of friction coefficient, stress corrosion index, and fracture toughness or decrements of initial crack size accelerate the stress-stepping creep failure.

  4. 4.

    Effects of the unloading rate of confining pressure on axial strain and strain rate are studied during creep. Creep failure time decreases with increment of the unloading rate of confining pressure during the entire creep process. Coupling effects of step loading of axial stress and step unloading of confining pressure or step loading of axial stress and cycle loading and unloading of confining pressure on creep failure are also predicted. The coupling stress path weakens the mechanical property, increases the damage, and accelerates the failure of rock compared to the single stress path. This result provides information on understanding the deformation behavior and time-delayed rockburst mechanism for surrounding rock during the excavation of deep underground space.