Evidence for a Long-Term Strength Threshold in Crystalline Rock

Abstract

The mechanical response of brittle rock to long-duration compression loading is of particular concern in underground disposal of nuclear waste, where radionuclides must be isolated from the biosphere for periods of the order of a million years. Does the strength decrease without limit over such time, or is there, for some rock types, a lower “threshold” strength below which the rock will cease to deform? This paper examines the possibility of such a threshold in silicate crystalline rocks from several perspectives, including: (1) interpretation of the results of short-term creep tests on rock; (2) numerical analysis of the effect of decrease in fracture toughness due to stress corrosion on the strength of a crystalline rock; and (3) evidence from plate tectonics, and observations of in situ rock stress in granite quarries. The study concludes that there is clear evidence of threshold strength. The threshold is of the order of 40% of the unconfined compressive strength or higher for laboratory specimens under unconfined compressive loading, and increases rapidly in absolute value with confinement. Field evidence also leads to the conclusion that the long-term strength of crystalline rock in situ is of comparable magnitude to the laboratory value.

1 Introduction

Determination of the mechanical response of rock in situ to applied loads is a central challenge of rock mechanics. This response is controlled predominantly by two scale factors: size and time. The effect of time on rock deformability and strength is a topic of considerable interest in rock mechanics (Einstein and Meyer 1999). It is of special importance to the geological isolation of highly radioactive nuclear waste, as it is necessary to establish that the rock can isolate the waste from the biosphere for the order of a million years. This, in turn, implies an understanding of how rock deformability and strength will change over such a period. All materials will creep when subjected to the appropriate long-term loading conditions. At a nuclear waste repository in Precambrian crystalline rock at depths of 400–700 m, loading conditions will be compressive and temperatures less than 100°C. Hence, an important question related to repository design is “Will the strength decline essentially to zero after such extended periods or does the rock have a non-zero ultimate strength or ‘threshold’ that can be considered time-independent, for the time-scale of interest?”

Weak rocks such as evaporites, although responding as brittle materials in the short term (Wang 2004), creep, and they are unable to sustain any deviatoric stress over geological times. As a result, the measured in situ state of stress in evaporite formations is typically isotropic even at shallow depths (Wawersik and Stone 1989). Crystalline rocks behave very differently, supporting substantial deviatoric stresses more or less indefinitely, even at shallow depths, as shown by Hoek and Brown (1982) and Martin et al. (1990). Hence, for crystalline rock, the creep processes are either extremely slow or do not occur at the deviatoric stress magnitude created by geological processes at shallow depths.

A fundamental difference between evaporite and granite is the atomic structure of the minerals making up those rocks. Evaporites are composed of minerals that yield by dislocation slip when subjected to deviatoric stress, even at low temperatures (Senseny et al. 1992). Granites, however, are composed of a heterogeneous assembly of polycrystalline minerals. Dislocation slip of such minerals is inhibited greatly, especially at the low ambient temperatures of typical waste repositories, and yield takes place by tensile rupture.

Permanent deformations in crystalline rocks initiate by the development of tensile microcracks that propagate parallel to the direction of maximum compression, eventually interacting with each other to result in localization, instability and collapse (Hallbauer et al. 1973; Germanovich et al. 1994). Confining pressure, acting normal to the extending cracks, is very effective in suppressing the tensions induced at the crack tips, so that crack growth is inhibited, and the rock strength increases rapidly with confinement as the zone of tension is suppressed. The initial crack extension results in an associated volume increase of the rock (Scholz 1968; Kranz and Scholz 1977). This fact is supported by the work of Matsushima (1960), who observed that, in creep tests on granite loaded in axial compression, creep strain lateral to the direction of compression was larger than creep strain in the longitudinal direction. He concluded, as noted above, that the high lateral strain was caused by extension of the microcracks aligned with the direction of loading. Lajtai and Bielus (1968) came to similar conclusions from uniaxial compression tests on Lac du Bonnet granite. Hence, if tensile-induced microcracking causes creep in crystalline rocks loaded in compression, there may be a minimum compressive boundary stress required to develop these internal micro-tensile cracks.

Crack extension in siliceous rocks under constant tensile stress is attributed to the chemical process of “stress corrosion” (Charles 1959), whereby the “fracture toughness” (i.e., the energy required to create new fracture surface) of the crack tip is reduced over time. In rock, the overall stress is typically compressive, and the tensile stresses are localized to the grain scale due to the application of deviatoric compressive stress. In this paper, we explore the notion that a limiting deviatoric compressive stress—i.e., a “stress threshold”—is required to produce these micro-tensions in heterogeneous crystalline rock. If the deviatoric stress is below this threshold, creep in crystalline rocks will be of no practical consequence to the disposal of nuclear waste.

Much of the understanding of creep of rocks is based on laboratory tests on small specimens. This has provided considerable insight into creep behavior, but the practical inability to carry out laboratory tests for more than the order of a few months or less limits the ability to predict creep behavior over much longer times. This is especially the case when information on creep extending to a million or more years is required, as it is for waste isolation. This paper attempts to overcome this obstacle by two series of enquiries:

• 1. review of the mechanics of creep by stress corrosion in crystalline rock; and

• 2. assessment of insights on long-term creep based on tectonic loading in stable plates, and field observations of in situ stresses.

2 Deformation of Rock Specimens Under Compression Loading

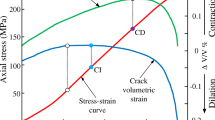
Deformation of rock specimens under compression loading is illustrated in Fig. 1, which shows the typical deformation response of a rock specimen when subjected to a progressively increasing uniaxial compressive load. Initially, the specimen may contract as flaws, if present in the specimen, tend to close; the net volume of the specimen decreases—i.e., the volumetric strain ΔV/V is negative¹ (lower curve in Fig. 1).

Fig. 1

Stages of brittle rock fracture in Lac du Bonnet granite (after Martin 1997). (“Crack Initiation”—σ _ci and “Crack Damage”—σ _cd stress levels are indicated.)

As the load increases, microcracks begin to develop, essentially parallel to the direction of applied load, opening as they extend. The volumetric decrease starts to change progressively to a volumetric increase or “dilation” of the specimen. Monitoring of microseismic activity or “acoustic emissions” (AE in Fig. 1) in the specimen identifies this dilation with opening of microcracks, generating internal voids. This “crack initiation” activity appears to develop at a load (defined as the “Crack Initiation Stress”, σ _ci) of about 0.4 σ _f , where σ _f is the maximum (or peak) load that is reached before the specimen collapses. The cracks lengthen in stable fashion (i.e., extending only with increase of load) parallel to the direction of loading. At a load of the order of 0.8 σ _f or so (higher or lower depending on the homogeneity of the rock), the lengthening cracks start to interact either with each other or with the sides of the specimen. This interaction leads to a mechanism for macro-scale shear deformation, and to instability. This onset of instability is associated with a rapid increase in dilation. These characteristic stress states (i.e., peak strength, σ _f , crack initiation stress, σ _ci, and crack damage stress, σ _cd, measured on Lac du Bonnet granite for different levels of confinement) are shown in σ ₁–σ ₃ space in Fig. 2, together with different fits (e.g., Hoek–Brown failure envelope for peak strength and σ _cd).

Fig. 2

Hoek-Brown failure envelope for Lac du Bonnet granite based on laboratory peak strength (Lab Peak), crack damage stress (Lab σ _cd) and crack initiation stress (Lab σ _ci) (from microseismic monitoring) (Martin 1997)

The mechanics of crack growth, dilation and development of instability such as illustrated in Fig. 1, are discussed in detail by Germanovich et al. (1994). The authors pay particular attention to the differences between these processes as they develop in the three- (3D) and two-dimensional (2D) representations often used in analysis. In general, in the 3D case, the early stages of crack growth are more restricted, but volumetric dilation is larger for the 3D case. Additional Mode III cracking develops around the edge of the initial crack as the load increases. Similar results have been discussed by Palaniswamy and Knauss (1978). Energy consumed in generating these secondary cracks tends to (1) limit extension of the primary crack; (2) increase the volumetric dilation; and (3) increase the strength—of a 3D specimen compared to its 2D counterpart.

In both 2D and 3D cases, the same phases of deformation defined in Fig. 1 are observed. Thus, deformation and instability/collapse in compression of brittle rocks is a process involving (a) micro-scale initiation and extension—parallel to the direction of maximum compression—of numerous independent microcracks; (b) preferential growth of the longer cracks; and (c) interaction of the longer cracks, leading to macro-scale shear slip, instability, and final collapse of the specimen.

Wong and Einstein (2009) have carried out a detailed study of crack coalescence between a pair of pre-existing cracks in specimens of Carrara marble and molded gypsum, both at the macroscopic and microscopic levels. Tensile cracking was the dominant mechanism of coalescence in the marble whereas shear played a more prominent role in the molded gypsum. This illustrates that, although the macroscopic response may be similar to that shown in Fig. 1, interplay between tensile and shear mechanisms may differ at the microscopic level.

For the brittle Lac du Bonnet granites, and crystalline rocks more generally, tensile cracking tends to dominate with “shear-type” deformation tending to develop during crack interaction.

3 Creep of Brittle Rock

Creep is the general term often used to describe any time-dependent deformation of materials. Much of the early interest in creep phenomena was focused on the behavior of metals, with representation of the creep regimes often characterized in terms of rheological or mechanical models of varying degrees of complexity. It should be noted that the atomic structure of most metals is such that deformations occur by dislocation slip caused by the application of deviatoric stress. Hence, the yield in metals often is described adequately by a Tresca yield function of the form: σ ₁–σ ₃ = q, where q is a constant.

Figure 3a illustrates three regimes that often are defined: (I) Primary–Transient Creep; (II) Secondary–Viscous, Steady-State Creep; and (III) Tertiary–Accelerating Creep, together with a corresponding mechanical model—attributed to Burgers (see Jaeger and Cook 1969). The tertiary regime leads to collapse of the test specimen if the load is not removed. Unloading during the primary or secondary phases leads to an immediate elastic recovery followed by a time-dependent response. The Burgers model, illustrated in Fig. 3b, often is used to represent loading and unloading response (AB, BCD; and AE, EFG) during Phases I and II; the Burgers model does not consider Tertiary creep.

Fig. 3

a Phases of time-dependent deformation; b Burgers mechanical model of creep

Many rock creep experiments are recorded in terms of the parameters of the three-stage creep model of Fig. 3, although, as noted earlier, the deformation mechanisms may be very different from the model, especially in the case of brittle rocks. Cruden (1970) statistically re-analyzed an extensive body of published data on rock creep, and asserts that deformation-time curves of the form shown in Fig. 4 describe observed behavior at least as well as those of Fig. 3a. The curves of Fig. 4 do not include a steady-state phase. (Elastic deformation is not shown in Fig. 4.) At high applied loads, an initial phase in which the creep rate is declining, eventually changes to a phase in which the creep rate increases, leading inevitably to collapse. At still higher loads, the changes occur more rapidly, and collapse ensues earlier. In both cases, according to Griggs (1939), the transition to tertiary creep in rock occurs when a critical strain, ε _1, is reached.

Fig. 4

Onset of accelerating creep after a critical strain (ε ₁)—no steady-state creep phase (Cruden 1971)

Griggs noted, however, a difficulty in estimating the onset of the stage of Steady State Creep. Referring to his longest creep test, on Solenhofen limestone at a load of 53% of its short-term strength, he indicated that he could identify “no pseudo-viscous flow.”

This observation led Cruden (1971) to carry out a comprehensive statistical analysis of a large sample of published creep test data. He concluded that there was indeed “no evidence for steady state creep in any of these experiments” and that “all could be adequately described by a creep law of the form”

$$ \dot{\varepsilon } = b_{1} \,t^{{b_{2} }} $$

(1)

where $\dot{\varepsilon }$ is the strain rate at time t; b ₁ is the strain rate at unit time; and b ₂ is a strain-hardening parameter usually with a value about −1. When b ₂ is equal to −1, integration of Eq. 1 gives Griggs’ familiar logarithmic creep law as a special case of this equation.

The onset of tertiary creep occurs when a critical strain, ε ₁, is reached. If accelerating creep begins at time t _A under a stress σ _A, then the critical creep strain can be estimated by integrating Eq. 1 from the start of creep in the experiment to t _A.

If another similar specimen under a stress σ _B begins accelerating creep after a time t _B, then Cruden (1974) showed that

$$ \log (\sigma_{\rm A} /\sigma_{\rm B} ) = (b_{2} + 1/P)\log (t_{\rm B} /t_{\rm A} ) $$

(2)

where P is the exponent of the power-law dependence of the strain rate on stress in creep.

From his theory of brittle creep, Cruden (1970) showed that

$$ (b_{2} + 1/P) = 1/n $$

(3)

Thus,

$$ n\log (\sigma_{\rm A} /\sigma_{\rm B} ) = \log (t_{\rm B} /t_{\rm A} ) $$

(4)

The parameter n is the exponent of the rate of corrosion on the stress at a crack tip within the creeping material. He tested the validity of this “Static Fatigue Law”, Eq. 4, on several series of published creep results, and suggested that “values of n around 5 might describe the behavior of wet evaporates: values around 15 will describe the behavior of strong, drier sedimentary rocks.”

Applying Eq. 4 to the Lac du Bonnet unconfined test results shown in Fig. 5, we see that a value of n = 20 fits the data, indicating a strength of about 60% of the short-term strength after about 10 days of loading; a value of about 30% after 20,000 years, and 25% after 2 million years. Thus, if we assume a short-term strength of 240 MPa for Lac du Bonnet granite, the effective threshold strength is predicted to be about 0.25 × 240 MPa, or 60 MPa.

Fig. 5

Creep test data for Lac du Bonnet granite showing (a) linear and (b) exponential extrapolation of data (Potyondy 2007). LdB1 data are from tests of Schmidtke and Lajtai (1985) on 2:1 aspect-ratio, right-circular cylinders of 31.7-mm diameter. LdB2 data are from tests of Lau et al. (2000) on 2.5:1 aspect-ratio, right-circular cylinders of 61-mm diameter

3.1 Terminating Creep

One of the assumptions underlying the derivation of the static fatigue law, Eq. 4, is that the strain-hardening parameter, b ₂, in Eq. 1 does not depend on stress (over the range of stresses covered by the law).

Cruden (1974) asserts, however, that creep in some rocks shows strain-hardening parameters that decrease at lower stresses. The strain-hardening parameters in Griggs’ alabaster experiments showed such a tendency, and his experiments on Carrara marble showed a decrease in b ₂ from about −1 for creep loads above 70% of the short-term strength, to −2 at 53% (Cruden 1974, Table 1). At very long times, the creep strain in such experiments tends to a limit of [−b ₁/(b ₂ + 1)], and creep is “terminating” (Cruden 1983), i.e., the critical creep strain is not reached—the curve “Creep at σ ₃” in Fig. 4 becomes asymptotic to a finite creep strain value below ε ₁. The stress level at which the strain becomes asymptotic to the strain value ε ₁ is the Threshold Stress for that rock. Cruden (1983) suggests that Lac du Bonnet granite specimens tested at a driving stress ratio of 0.49 and 0.64 showed terminating creep.

The greatest load that results in terminating creep represents a “threshold stress”. Cruden’s analysis is attractive in that it reflects the essentially “geometrical” nature of the strength of brittle rock, whereby small, initially independent tension-induced microcracks, lengthen and interact progressively until localization ensues and macro-scale shear collapse occurs.

4 Time-Dependent Weakening of Crystalline Rock

Specimens of crystalline rock subject to creep tests—i.e., sustained constant loading that is below the instantaneous compressive strength—are found to collapse after a period of time. Figure 5 illustrates a typical series of results, obtained, in this case, on cylindrical specimens of Lac du Bonnet (Canada) granite loaded in compression at different constant loads, expressed as a proportion of the “instantaneous” strength. Potyondy (2007) refers to this proportion as the “driving stress ratio”.² The majority of the tests were for unconfined loading, but some confined loading results are included.

It is seen in Fig. 5 that the individual tests all were carried out at driving stress ratios greater than 0.6 and for periods of less than 2 weeks. Clearly, time constraints do not allow laboratory tests to be carried out to obtain data for low stress ratios, so most estimates of the rock strength for loading times of the order of one million years are obtained by extrapolation from the short-term data. Two such extrapolations are shown:

• 1. a linear extrapolation, which predicts that the rock eventually will reach zero strength, or collapse “under its own weight” in about one million years; and

• 2. a non-linear extrapolation, indicating that the rock has a finite threshold strength that can be sustained for an indefinite period.

The exponential fits suggest that Lac du Bonnet granite has a long-term strength that is of the order of 45–53% of the UCS for this rock—i.e., the granite is predicted to be able to sustain, indefinitely, a deviatoric stress of ~100 MPa under unconfined loading. The linear extrapolation indicates that the rock essentially will “collapse under its own weight” (i.e., the strength declines to zero) after approximately one million years. Although the data for 10 and 20-MPa confinement in Fig. 5 are quite limited, they appear to exhibit a more rapid rise in “time to failure” than the unconfined data, which supports the possibility of an even higher long-term strength under confinement. This seems logical, as confinement acts to inhibit axial crack propagation, the process by which the rock weakens. Clearly, the difference between the linear and exponential extrapolations leaves a much too large uncertainty in long-term strength prediction. Additional evidence of the long-term strength of rocks is required.

Scholz (1972) carried out uniaxial compression experiments on single crystals of quartz and observed time-dependent weakening. His results are shown in Fig. 6 (redrawn to a format comparable to that of Fig. 5). Again, the Driving Stress Ratios (expressed here as the percentage C/C ₀, where C = creep strength; C ₀ = instantaneous compressive strength) of the tests are all above 60%, and individual test durations are all less than 2 weeks.

Fig. 6

Creep tests on single crystals of quartz

These results are of particular interest because quartz is a major constituent of granite. The single crystals exhibit behavior similar to that observed in the Lac Du Bonnet granite, although the UCS of the single crystals (2450 MPa) is an order of magnitude higher than that of the Lac du Bonnet specimens (240 MPa). This illustrates the important effects on overall strength of the relative homogeneity and small size of the quartz single crystals compared to the granite specimens.

In describing the time-dependent strength behavior, Scholz (1972) notes “It is tempting to ascribe these effects to some unknown viscoelastic or plastic deformation in rock. However, no evidence for inelastic intra crystalline deformation has as yet been identified in silicate rocks deformed at the low temperatures and pressures of the brittle fracture regime.”

5 Stress Corrosion

The generally accepted mechanism for time-dependent weakening of crystalline silicate rocks such as granites currently is referred to as “stress corrosion.”

Early studies of the phenomenon focused on the strength of silicate glass loaded in tension (e.g., Griffith 1921). It was suggested (Orowan 1949, Sect. 16, p. 199) that time-dependent weakening (“delayed fracture”) “occurs because the surface energy of a surface crack is lowered by atmospheric adsorption, and thus the crack propagating stress is reduced if the propagation is slow enough for the adsorbed material to diffuse to the tip of the crack during its propagation (Orowan 1944). The adsorption may be a physical or a chemical one;…” Charles (1959) explained the chemical reaction between silica and water, and suggested that a similar effect could occur between silicates and water, leading to the strength reduction or “static fatigue” in these materials, and possibly in rocks containing silicate minerals. It should be noted that all of these conclusions were developed for cracks subjected to boundary tensile stresses, often using beam-bending tests.

Potyondy (2007) provides a comprehensive review of stress corrosion research in various brittle materials. He concludes that, while the stress corrosion (chemical) process, which is operative in glass and perhaps silicate minerals, may not be the only operative time-dependent mechanism, they all tend to have a similar effect to stress corrosion.³ He notes also that “a stress-corrosion threshold, below which no crack growth is observed… has been observed in soda-lime silicate and borosilicate glasses, but it is not yet clear whether all materials behave in this way (Freiman 1984)” He asserts, however, that the path of crack propagation in rock is predominantly along grain boundaries, and “will be controlled by the details of grain boundary surface chemistry and the reaction of grain boundaries and matrix materials with the stress–corrosion agent…. Little relevant data are available. Stress corrosion is considered to be the primary mechanism producing time-dependent behavior of rock in the brittle regime.”

In summary, crystalline rocks respond to loading by the generation of internal microcracks. When the load is sustained, chemical environmental effects, now referred to generally as “stress corrosion”, act on the surfaces of the induced cracks, progressively reducing their surface energy. This allows the crack tip to lengthen over time until crack interaction results in instability and collapse.

6 Numerical Analysis of Crack Propagation by Stress Corrosion

The following numerical analysis is designed to examine the consequences of stress corrosion. It examines the relation between reduction of the rock strength and crack growth, including the case where the energy for crack growth (i.e., the fracture toughness) is reduced to zero. Although it is a 2D representation of a 3D fracture process, we believe, as outlined earlier, that the analysis is qualitatively correct and allows valid conclusions to be drawn concerning the effect of crack-fracture toughness reduction on rock deformation. The 2D Voronoi scheme in this analysis has been found to serve as a good representation of a cemented, granular, brittle material such as rock. The particle angularity that results automatically from the Voronoi approach provides a good representation of brittle rock.

Eberhardt et al. (1999) have studied crack propagation in specimens of Lac du Bonnet granite during compression loading. They observe that, initially, most cracks follow grain boundaries. At higher loads, intra-granular cracks may develop, primarily through quartz grains. Although the Voronoi interfaces in the model discussed below may be described as “grain boundaries”, they also can be considered more generally as “planes of weakness” within the rock.

6.1 Wing-Crack Analysis of Crack Propagation in a Compression Test

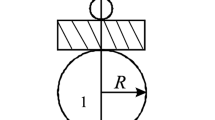
It was shown previously that the failure process in brittle rock is initiated and dominated by micro-scale tensile cracks. The heterogeneities in the rock are considered the most likely source for these tensile stresses. The so-called “wing-crack” model (see Fig. 7a) has been used widely in the analysis of tensile crack growth in brittle materials under compressive loads. It is derived from the original analysis by Griffith (1924), which, in turn, was inspired by Inglis’ (1913) analytical solution for the stress distribution around an elliptical crack.⁴ Fairhurst and Cook (1966) used the inclined (micro) crack of the wing-crack model as a mechanism to generate local tensile forces normal to the direction of compressive loading in rock (see Figs. 7a and 15), and to explain the observed development of cracks parallel to the applied load. Hoek and Bieniawski (1966) demonstrated experimentally the propagation of wing cracks from an inclined crack, and the major effect of confining pressure on reducing the development of wing cracks. The applied compressive load σ will produce a tension stress normal to σ, which will tend to generate a crack (the length of the initial inclined crack in Fig. 7a is 2a) extending parallel to the direction of σ. However, as noted by Germanovich et al. (1997), the length, l, of the crack produced by the inclined line crack is proportional to the second power of the applied stress—i.e., l ∝ σ ².

Fig. 7

Axial cracks developed from (a) an inclined crack, (b) a pore space in a brittle material, and (c) localized lateral tension and compression forces in a specimen loaded vertically in compression (schematic)

The heterogeneous nature of most rocks provides several such mechanisms for development of tension. Figure 7b, for example, shows a two-dimensional pore (radius a) in a rock. The pore will develop a tension normal to the applied stress, which can result in an axial crack that propagates vertically from the top and bottom of the pore. In this case, however, the length of the crack, l, is proportional to σ ^2/5—i.e., l ∝ σ ^2/5, which is a much shorter range effect. In reality, the pore is three-dimensional and will have an even shorter range effect. “Hard” grains can induce similar tension cracks, also of similarly short range. The heterogeneous nature of crystalline also will result in local zones of tension (and compression) along the primary loading axis in an unconfined test (Fig. 7c). These tension zones will accentuate the tensions developed locally by “flaws” such as in Fig. 7a and b. Addition of a confining stress (σ ₃) will be very effective in suppressing such cracks, as the confining pressure will be exerted directly across the crack length, tending to eliminate the crack-tip tension. The major (σ ₁) stress must then be increased to reestablish crack-tip tension if crack propagation is to continue.

We use the wing-crack model in the following analysis both to examine crack tip propagation and to allow comparison of the numerical results with published analytical results. Different conditions of confinement and their effect on the strength of brittle rock has been investigated numerically and analytically. An approximate analytical model by Germanovich and Dyskin (2000) has been used primarily to validate the numerical model. For the sake of simplicity, the analyses are two-dimensional, but the conclusions based on their results are general. The reason that this problem is investigated is that failure of a brittle rock occurs when pre-existing cracks propagate sufficiently to interact and connect with each other. Initially, a model with a single crack is analyzed. The model size represents typical crack spacing.

A series of uniaxial and biaxial stress tests on rectangular samples (width, w, and height, h) with geometry as illustrated in Fig. 8 were simulated numerically. The vertical stress, σ ₁, was increased gradually (in a quasi-static manner) during the simulations, while confining stress, σ ₃, if applied, was kept constant. Most of the analyses were carried out on a sample with a pre-existing crack of length 2a, and at an angle, α, in the middle of the sample.

Fig. 8

Geometry and boundary conditions of the analyzed problem (d/w ~ 0.02)

A micro-mechanical model was used to represent the brittle rock. In this approach, the domain is discretized into a large number of relatively small blocks—i.e., d/2a ≪ 1, where d is the block characteristic dimension (Fig. 8). (Ratio d/w is approximately 1:50 in the results discussed below.) The blocks, which are polygonal in shape (created by Voronoi tessellation in 2D), are assumed to be elastic in these simulations. Inelastic deformation and damage occur along the interfaces or joints between the blocks. Initially, the joints are bonded together, and assigned a specific tensile and shear strength. In this model, the bond shear strength is assumed to obey the Coulomb slip law. Breaking of bonds between the blocks is equivalent to creation of tensile or shear microcracks. This model is considered to be a realistic representation of rocks that possess a granular internal structure (e.g., granite), in which the grains are much stronger than the bonded joints between the grains. In such materials, fractures propagate mainly between the grains.

Microcracking of the tested samples at two different loading stages is shown in Fig. 9 (an intact unconfined sample), Fig. 10 (an unconfined sample with a pre-existing crack) and Fig. 11 (sample with a pre-existing crack and 0.5-MPa confinement). The black lines in the figures represent the microcracks. When the microcracks coalesce into a macrocrack and the resulting opening is sufficiently large, it appears as a gap (i.e., a thick white line or surface) in the plots.

Fig. 9

Model configuration and fracturing at two stages during a test: Intact, unconfined sample

Fig. 10

Model configuration and fracturing at two stages during a test: Unconfined sample with pre-existing crack

Fig. 11

Model configuration and fracturing at two stages during a test: Sample with pre-existing crack and 0.5 MPa confinement

Because the model represents a relatively brittle and homogeneously granular material, the damage in the initially intact sample is distributed uniformly throughout the sample, even for stress levels close to the peak strength. For example, at a load of 88% of the peak strength (Fig. 9a), there is no indication of localization or formation of microcracks. Such behavior is manifested by a relatively linear pre-peak stress–strain curve, as shown in Fig. 12 for the intact sample. The sample fails as the microcracks coalesce to form the axial microcracks, Fig. 9b), some of which interact with the free surface of the sample to produce “spalling” of the material and, eventually, instability. The state shown in Fig. 9b corresponds to the last point on the stress–strain curve for the intact sample shown in Fig. 12. Relatively small confinement is sufficient to suppress this observed surface instability, and results in an increase in strength of the sample.

Fig. 12

Stress-strain curves for unconfined compressive test

Introduction of a pre-existing crack in the sample (as shown in Fig. 10) reduces the uniaxial strength of the sample as illustrated in Fig. 12, which shows the stress–strain curves for the intact and cracked samples. As the load increases, the pre-existing crack propagates by re-orienting itself in the direction of the major compressive stress, σ ₁. Initially, most of the microcracking in the sample is associated with propagation of the wing crack. Only when the load approaches levels close to the short-term strength does the damage spread throughout the sample, as shown in Fig. 10a. Eventually, the wing crack reaches the model boundary, splitting the sample axially into at least two pieces (Fig. 10b).

Confining the sample with a stress that is small compared to the uniaxial compressive strength (e.g., 0.1 or 0.5 MPa), not only increases the sample strength, as shown in Fig. 13, but also changes the mode of failure (Fig. 11). The wing crack initially propagates as the load is increased, as in the unconfined case, but at a slower rate. However, failure does not occur by axial splitting of the sample when the wing crack reaches the sample boundaries. Instead, there is a change in failure mechanism just before the peak strength is reached. Localized fracturing along the wing crack changes to diffuse fracturing throughout the matrix, which eventually localizes into what appears, on a macro-scale, to be a shear fracture (Fig. 11b). Closer examination of the apparent shear macrocrack reveals that it is composed of a myriad of tensile microcracks.

Fig. 13

Effect of confinement on stress–strain curves for the sample with an initial crack

Figure 14 shows the length of the wing crack as a function of axial load for all three of the above-mentioned tests (i.e., unconfined, 0.1- and 0.5-MPa confinement). The crack length is scaled to the vertical projection, l _i = 2a sin α, of the original crack l = 2a (Fig. 8), and the stress is scaled to the short-term (or instantaneous) rock strength, σ _u (i.e., the stress at which the sample fails). In all three cases, the crack extends to the boundary when the peak strength is reached. (In this problem, h/l _i = 8.) However, as the peak strength is approached in the confined cases, the wing-crack tip becomes obscured by diffuse damage and fracturing of the surrounding intact rock, which eventually connects the wing crack to the model boundary. Thus, the final increment of wing-crack length for the confined cases, indicated in Fig. 14, is a result of change in the failure mechanism due to the proximity of the sample boundary—not due to actual propagation of the wing crack. Clearly, increase in confinement reduces the length of the wing crack. In this case, confinement of the order of 2% of the strength (i.e., 0.5 MPa) reduces the wing crack length by approximately 50%—for load levels less than 0.8σ _u.

Fig. 14

Wing-crack length as a function of load and confinement

6.2 Comparison of Numerical and Analytical Solutions for Wing-Crack Length

A model for the effect of wing cracks on the compressive strength of brittle rocks was proposed by Fairhurst and Cook (1966). The model is illustrated in Fig. 15. Germanovich and Dyskin (2000) have used this model to investigate the relation between axial load, confinement and crack length in compressive loading of brittle rock.

Fig. 15

Wing-crack growth under compression, Fairhurst and Cook (1966) model

Using this model, the stress intensity factor, K _I, at the wing-crack tip can be approximated as

$$ K_{\rm I} = {\frac{F}{{\sqrt {\pi l} }}} - q\sqrt {\pi l} $$

(5)

where q = σ ₃, F = 2akσ ₁, k = sin² α(cos α-sin α tan ϕ), and ϕ is the friction angle along the initial crack. The equation is transformed to provide a relation between the dimensionless crack length, n = l/a; a dimensionless confinement, m = σ ₃/σ ₁; and a dimensionless rock toughness, ${\rm K} = K_{\rm Ic} /\left( {\sigma_{1} \sqrt a } \right){:}$

$$ {\frac{2k}{{\sqrt {\pi n} }}} = {\text{K}} + m\sqrt {\pi n} $$

(6)

The solid line in Fig. 16 shows the crack length, scaled to the vertical projection of the initial wing crack length, l _i = 2a sin α, as a function of the applied load for an unconfined sample [i.e., m = 0], as calculated using Eq. 6. When there is no confinement, the dimensionless length of the wing crack, l/l _i = n/(2 sin α), is defined by the ratio of fracture toughness to the applied load multiplied by the square root of the initial crack half-length, K = K _Ic/(σ ₁ a ^1/2). The open diamonds in Fig. 16 are the corresponding results obtained from the numerical results.

Fig. 16

Suppression of crack growth by fracture toughness: Semi-analytical (line) and numerical model (open diamond points) results

Figure 17 shows the relation between confinement, m, and crack length, n, for two values of a constant non-zero confining pressure, σ ₃. For these conditions, Eq. 6 can be written in the form

Fig. 17

Suppression of crack growth by confining pressure: Semi-analytical (lines) and numerical (dots) models

$$ {\frac{2k}{{\sqrt {\pi n} }}} = m\left( {{\frac{{K_{\rm Ic} }}{{\sigma_{3} \sqrt a }}} + \sqrt {\pi n} } \right) $$

(7)

The relation, Eq. 7, results in different n-versus-m curves for different, non-zero values of σ ₃. The curves for σ ₃ = 0.1 MPa and 0.5 MPa are plotted as continuous and dashed lines, respectively. The discrete points are calculated from the numerical results.

The numerical results shown in Figs. 16 and 17 were obtained using a fracture toughness of 2.4 MPa m^1/2. However, the value of the fracture toughness calculated based on a direct tension (numerical) test on the specimen with a pre-existing crack was found to be approximately 3.1 MPa m^1/2. The discrepancy between these two values of fracture toughness is due to the approximate nature of Eq. 5, which determines the stress intensity factors for a fracture in an infinite medium, whereas the numerical model is for a fracture in a specimen of finite size. The numerical results are generally in good agreement with the predictions of the simple analytical model. The disagreements arise when (1) the crack is short—i.e., l/l _i ≈ 1, in which case, the simple analytical model of Eq. 5 is not applicable; and (2) the wing-crack in the numerical model approaches the model boundary, and sample failure occurs as a result of a change in the failure mode.

In the case of a material with no fracture toughness, Eq. 6 simplifies to

$$ m = {\frac{2k}{n\pi }} $$

(8)

and the n-versus-m curve, as shown in Fig. 18, becomes independent of confinement. This curve illustrates the importance of confinement on the suppression of crack growth. This case (i.e., for a crack of zero fracture toughness) is of particular interest with respect to the effect of confining stress on long-term rock strength, as it represents the limiting state of time-dependent strength decay of a tensile crack.

Fig. 18

Suppression of crack growth by confining pressure in a material with no fracture toughness

6.3 Effect of Rock Strength Reduction on Wing-Crack Propagation

The effect of time-dependent strength degradation on the length of a wing crack, and ultimately the strength of rock, can be represented effectively by reduction of the fracture toughness in Eq. 6. The strength of the rock is reached when the wing cracks become sufficiently long to interact with each other. Thus, it is not only a function of load and rock toughness, but also a function of the spacing of pre-existing cracks or the level of damage (at the state) when the time-dependent strength degradation is activated.

The analysis presented here considers the effect of toughness reduction on rock strength without direct reference to time. Thus, the time effect is implicit, through its effect on rock toughness (or micro strength).

It is assumed that stress corrosion is the mechanism of strength degradation. Two necessary conditions for stress corrosion to be active are (1) the existence of cracks, and (2) tension at the crack tip. In fact, the tensile stress at the crack tip has to be greater than a threshold stress that is proportional to the activation energy (Scholz 1972). If the activation energy is neglected, or assumed to be negligible, the fracture toughness will decrease to zero with time and, according to Eqs. 6 and 7, the length of the wing crack in the unconfined sample [i.e., m = 0 in Eq. 7], will approach infinity, indicating rock failure. Under those conditions, based on the simple analytical model of Germanovich and Dyskin (2000), the long-term strength of unconfined rock is zero. As will be shown below, a more realistic model, which considers a finite-size sample with discrete rock structure, yields a different result.

The numerical model investigated the effect of toughness (or micro-strength) reduction due to stress corrosion on (a) the wing-crack length and (2) the rock strength. The samples with the wing crack were loaded to a number of different levels, represented as increasing fractions of the short-term strength of the cracked samples. The top boundary condition was velocity-controlled (i.e., infinitely stiff) during the short-term strength testing. Once the required load level was reached, the top boundary condition was changed to load-controlled (i.e., infinitely soft) and held constant at this level. The effect of time-dependent toughness reduction caused by stress corrosion was represented in the analysis by a reduction of both tensile strength and cohesion in the joints between the grains ahead of those existing crack tips which were open (i.e., loaded in tension). In other words, the strength was not reduced everywhere throughout the sample, because stress corrosion is considered to take place at the open crack tips only. The micro-strength reduction is implemented in finite increments of 10% of the short-term strength.

Thus, if the sample is loaded at a stress level σ ₁, then the driving stress ratio (i.e., as defined in Fig. 5 with respect to creep tests) will be σ ₁/σ _u, where σ _u is the instantaneous strength of the sample. The critical strength-reduction ratio, r _c, or fraction of strength reduction required to fail the sample, (i.e., the number of 10% strength decrements—i.e., reduction in crack tensile strength and cohesion or, effectively, reduction in fracture toughness—required before the sample will fail) is defined by

$$ r_{\rm c} = 1 - {\frac{{\sigma_{1} }}{{\sigma_{\rm u} }}} $$

(9)

The results from the simulations of an unconfined test for a specific axial load σ ₁ of 0.16 σ _u are shown in Fig. 19. Two states are shown: (a) the initial state, before the strength is reduced; and (b) the final state, after an incremental strength reduction to zero.

Fig. 19

Model configuration and fracturing at two stages during test: Strength reduction at the tip of an unconfined sample with a single crack loaded to 0.16 σ _u

There are two interesting observations from this numerical experiment. Based on Eq. 9, the sample should have failed for r = r _c = 0.84 Since the creep load is reduced in 10% increments in the simulations, this indicates that the sample would not fail at 0.8 reduction, but would fail when the strength was reduced by a further 10% increment, at a stress reduction ratio equal to 0.9—i.e., r ≥ r _c). The results of the simulation indicate that the model did not fail—i.e., it reached a stable configuration (Fig. 19b) even when the strength was reduced to zero.⁵ Also, although Eq. 6 and Fig. 16 indicate that the crack length should be infinite, the wing crack is arrested at a finite length.

The reason for this apparent anomaly is that the numerical model includes a representation of the internal structure of the rock, where the small elastic blocks behave as grains with much greater strength than the bond strength of the contacts between the grains. When the crack becomes sufficiently long, the finite-sized grains effectively blunt the crack tip. Details of the geometry around the arrested crack tip (the upper tip in Fig. 19b), including grain geometry, and stress state are shown in Fig. 20. Although there is a tensile stress state ahead of the tip perpendicular to the general crack direction, both crack branches, initiated around a grain ahead of the tip, are arrested, because of compressive stresses perpendicular to the direction of these branches.

Fig. 20

Stress state ahead of the arrested crack

This example demonstrates that the long-term strength of real rocks under unconfined conditions is finite, even when the activation energy is neglected.

The importance of confinement on suppression of crack growth is illustrated clearly in Fig. 17. The numerical experiment of strength reduction in the confined sample shown in Fig. 21, demonstrates this effect even more dramatically. The sample, confined at m = 0.008 and loaded at 0.43σ _u, where σ _u is the short-term strength, is subjected to a gradual stress- corrosion-related strength reduction. The critical strength reduction ratio, r _c, is 0.57. The sample does not fail even for a strength reduction ratio of 1.0. Again, if the strength is reduced uniformly, irrespective of cracking or stresses, the sample fails for the strength reduction ratio of 0.6—i.e., just greater than r _c = 0.57, considering the strength reduction increment of 0.1.

Fig. 21

Model configuration and fracturing at two stages during test: Strength reduction at the tip of a sample with a single crack confinement m = 0.008, load 0.43 σ _u

In reality, rock contains a multiplicity of cracks, and interaction between those cracks affects the rock strength. To assess these situations both the evolution of damage and the effect of strength degradation in a specimen with a regular pattern of pre-existing cracks was studied on the basis of a numerical model of a granular rock. The sample was tested under both unconfined and confined loading conditions. In both cases, the specimen was loaded to a fraction of its short-term strength, after which the strength was degraded progressively to simulate the stress-corrosion process. The results of two simulations, one for unconfined loading, the other confined, are shown in Figs. 22 and 23.

Fig. 22

Model configuration and fracturing at two stages during a test: Strength reduction at the tip of unconfined sample with a crack pattern loaded to 0.59 σ _u

Fig. 23

Model configuration and fracturing at two stages during a test: Strength reduction at the tip of a sample with a single crack confined at m = 0.019, loaded to 0.56 σ _u

The specimen with multiple initial cracks under unconfined conditions fails at a much smaller strength-reduction ratio than the case with a single crack in the middle of the specimen. The state of failure of the specimen, shown in Fig. 22b, is for a strength reduction ratio of 0.5. Although the critical strength-reduction ratio, r _c, is 0.41, the chip of loose rock (in the upper-right corner) formed at a strength reduction ratio of 0.3, which is less than r _c. (The strength reduction decrement was 0.1.) Analyses also were made for different crack patterns; the results are qualitatively similar to those presented here. Clearly, in the case of multiple cracks, interaction between the cracks and the free-surface boundary becomes an important factor leading to surface instability in a manner similar to spalling. However, it is somewhat surprising that the rock fails at a strength reduction ratio smaller than the critical strength-reduction ratio. In other words, the rock loaded to 0.59 UCS fails (or chips form on its surface) when its strength is reduced to 0.7 UCS. The reason for this apparent anomaly is a change that occurs in the boundary condition on top of the sample. During uniaxial or biaxial loading tests, a velocity boundary condition, equivalent to an infinitely stiff testing machine, is applied at the top boundary. A numerical servo-mechanism is implemented to control the velocity by requiring that the stresses calculated from the reaction forces at the top and bottom boundaries, and the average value of the stresses across the (horizontal) mid-plane are within a prescribed tolerance (less than 5% of the ultimate strength). This algorithm allows the model to follow even very brittle sample response (as illustrated in Fig. 12) without general instability and inertial effects. During the strength-reduction part of the numerical experiment, the top boundary condition was changed to stress-controlled, or infinitely soft. The constant, uniform stress, which remains unchanged, independent of the sample deformation, is applied on the model top boundary. Such a boundary condition promotes local instability associated with cracks close to the boundary. This change in boundary condition does not affect cracks that do not interact with the boundary (e.g., as in the case of a single crack).

The results of the simulation shown in Fig. 23, for a relatively small confinement, again illustrate the effect of confinement on stabilization of the cracks. The applied confinement was sufficient to maintain stability of the sample loaded to 0.56 σ _u, even when the strength was reduced to zero, using the stress-corrosion strength reduction procedure described above.

7 Tectonic Evidence of a Stress Threshold in Crystalline Rock

The difficulty in extrapolating the results of creep tests conducted over days to times of the order of a million years suggests the possibility of examining evidence that may be available from plate tectonics. In this context, a time of the order of one million years can be relatively small, but it appears that some useful insights can be gained with respect to the possibility of a threshold stress in crystalline rock.

There are several compilations of global data on the state of stress, as determined by various techniques used in a variety of rock types around the world (Hoek and Brown 1982; Wesseloo and Stacey 2006, Heidbach et al. 2008 ⁶). A general review of these data indicates that a deviatoric stress is always observed in crystalline rocks. As noted in the Introduction, this deformation behavior is in marked contrast to various sedimentary rocks and evaporites, where it is not unusual to observe isotropic in situ stresses, indicating the absence of a long-term threshold stress for these materials (see Wileveau et al. 2007; Senseny et al. 1992).

However, the global data are compiled from active as well as stable tectonic regions, so the fact that a deviatoric stress state exists today cannot be considered as definite proof of the existence of a stress threshold in crystalline rock. Examination of a few situations in stable plate regions provides more convincing evidence.

7.1 Canadian Shield Region

Gordon (2000) has attempted to establish values for the strain rates of tectonic plates across the earth. He interprets plate deformation behavior in terms of a simple Kelvin visco-elastic rheological model (Fig. 24).

Fig. 24

Kelvin rheological model

For the Kelvin model, the applied stress, σ, is given by

$$ \sigma = \eta_{1} \dot{\varepsilon } + k_{1} \varepsilon $$

(10)

or, equivalently,

$$ \sigma = \dot{\varepsilon }(\eta_{1} + k_{1} t) $$

(11)

where t is the time that the constant strain rate, $\dot{\varepsilon }$, has been active, k ₁ is the stiffness, and η ₁ is the viscosity.

The strain rate is a “vertically averaged” value over the (200 km or more⁷) thickness of the lithospheric plate. Rock close to the surface will be relatively strong and brittle, becoming progressively weaker and visco-plastic as the temperature increases with depth. Gordon notes:

“The estimation of strain rates in stable plate interiors is problematic for two reasons: First, the strain rates are so low that they are beneath the threshold of detection by direct measurements. Second, the straining that does occur is concentrated in zones of weakness, leaving unresolved the even lower strain rates outside these zones of weakness. Thus, the following discussion can only be a rough guide to the actual rates of strain. The rare occurrence of earthquake in stable plate interiors indicates that deformation rates are not zero”

These considerations suggest that the rock within say the top kilometer or so of a stable plate interior is “essentially elastic” with the viscous component of the Kelvin model in Fig. 24, being associated mainly with slip (or time-dependent stress release mechanisms) at local “weaknesses”, e.g. fractures, within the plate.

Recognizing these limitations, it seems reasonable to use these values to provide a general indication of the rate of change of stress in a near-surface rock due to plate motion.

The Lac du Bonnet batholith, part of the Canadian Shield, is approximately 2.6 billion years old and was uplifted, to essentially its present position, about 2.1 billion years ago. [The near-surface thrust faulting in the region is considered to have formed about 2.3 billion years ago while the magma temperature was still elevated (Everitt and Brown 1992).]

The samples of Lac du Bonnet granite used in the tests shown in Fig. 5 were obtained from the 420-m level of the Underground Research Laboratory (URL) at Pinawa, Canada. Except for microcracks found in core, this rock shows no evidence of fracturing. The minimum principal stress (sub-vertical) at 450 m is of the order of 14 MPa; the maximum horizontal (i.e., tectonic) stress is approximately 60 MPa, with trend of 145° and plunge of 11°–14° (Martin 1997). At confining pressure of 14 MPa, Lac du Bonnet granite has a compressive strength of the order of 400 MPa, so the current maximum tectonic stress is 15% of the confined strength. (Periodic, relatively short episodes of glacial loading, of up to 3 km of ice, would increase the confining stress by 30 MPa, further increasing the strength of the rock.)

For “stable interior plates”, such as is the case for the Canadian Shield region (of which the Lac du Bonnet granite is a part) of the North American plate, Gordon estimates the following values⁸:

$$ \begin{aligned} & {\text{Strain}}\,{\text{rate}}\quad \dot{\varepsilon } = 10^{ - 9.5} \,{\text{to}}\,10^{ - 12} 1/{\text{y}} \\ & {\text{Effective}}\,{\text{viscosity}}\quad \eta_{1} = 10^{25} \,{\text{to}}\,10^{27} \,{\text{Pa}} \times {\text{s}}\,\sim \,(10^{11} \,{\text{to}}\,10^{13} ){\text{MPa}} \times {\text{y}} \\ \end{aligned} $$

If we assume that the tectonic strain rate has remained essentially constant in direction for the order of ten or more million years,⁹ then the lack of fracturing in the rock suggests that the stress has increased monotonically to its present magnitude from a lower initial value at the start of this period—i.e., the stress increase over this period cannot be higher than the current value of 60 MPa.

Assuming a value for k ₁ of 50 GPa, slightly lower than measured for samples of Lac du Bonnet granite, and a time t of 10⁷ years, and substituting in Eq. 11, possible evolutions of tectonic stress are estimated for the suggested range of viscosity (and including the extreme case of no viscosity); these are shown in Fig. 25.

Fig. 25

Possible evolutions of horizontal tectonic stress at URL at Pinawa, Canada for the last 10 million years for different viscosities, estimated using the Kelvin creep model

Figure 25 illustrates that the tectonic stress will increase by no more than 0.1–1.0 MPa per million years. Thus, it seems reasonable to assert that the current tectonic stress of 60 MPa has been “essentially constant” for a very long period (i.e., several million years). This appears to be quite inconsistent with the linear extrapolation of Fig. 5a which suggests that the granite would tend to weaken considerably over such a period.

The granite at Lac du Bonnet would appear to have exhibited no evidence of time-dependent deformation (which would tend to reduce the 60 MPa stress), under a deviatoric stress (σ _max − σ _min) = (60 − 14) = 46 MPa, at 14 MPa confining pressure. The “instantaneous” compressive strength of Lac du Bonnet granite under a confining stress of 14 MPa is approximately 400 MPa (Fig. 2).

Thus, tectonic evidence supports the view that a threshold stress exists for Lac du Bonnet granite under confined loading. As other granites have essentially similar crystalline structures, it is reasonable to infer that other granites also will have a high threshold stress.

7.2 Field Observations of Long Duration in Situ Stresses in Granite Quarries

Quarries for dimension stone are selected and developed because the granite is essentially unfractured over a considerable area. The rock is, therefore, of high strength, capable of supporting high stresses. Review of a few examples, in the North American Plate, where stresses have been determined or estimated in granite quarries indicates the existence of a stress threshold. In these cases, the rock is at the surface and essentially unconfined.

7.2.1 Granite Quarry, Manitoba, Canada

Martin et al. (2003) report the results of a series of stress determinations in a granite quarry in southeastern Manitoba, where rock slabs “popped up” from the quarry floor due to the high horizontal stresses in the rock at the site and the quarry-induced stresses. The tendency for the rock to fracture horizontally and to buckle or “pop-up” tends to be exacerbated during hot summer days, when thermal stresses can increase the in situ stress¹⁰ significantly at and close to the surface. Overcoring measurements made at various depths from the surface to approximately 18 m show no such temperature-induced variations. The maximum value is approximately 20 MPa. This stress, which must have been maintained for the order of millions of years, indicates that granite is capable of sustaining a deviatoric stress indefinitely—i.e., that granite exhibits a non-zero threshold stress, even though unconfined (i.e., at the surface).

7.2.2 Cold Spring Granite, St. Cloud, MN, USA

A program of in situ overcoring measurements at the surface of quarries in the Charcoal Gray granite, near St. Cloud, MN (Crouch 1967) has established a biaxial state of stress of σ _max ∼ 28 MPa; σ _int ∼ 15 MPa; σ _min ∼ 0 MPa (surface) and an azimuth of N14°E. Although this Cold Spring granite is somewhat younger than the Lac du Bonnet granite, it is part of the same stable interior plate and subjected to similar strain rates. The granite in the quarry has horizontal “seams” (essentially long, through-going fractures) that are used to define the depth or thickness of “lifts” of granite in some of the quarries. It is possible that these seams are attributable to the same general surface-instability problem described by Martel (2006) discussed below, and that this has served to limit the maximum horizontal compression to its current value of ~28 MPa.

7.2.3 Exfoliation Jointing in Surface Exposures of Granite in North America

Martel (2006) has conducted an extensive field investigation of the phenomenon of “exfoliation” or “sheeting joints” (i.e., long fractures parallel to the surface) often observed in hard, massive rock formations exposed at the surface. The rock surface tends to be slightly undulating, usually a consequence of glaciation. He notes that horizontal stresses applied to a slightly convex surface will generate tensile stresses normal to the surface, which may result in fracturing parallel to the surface. He presents the results of in situ stress determinations from several quarries in the USA, primarily in granite, where sheet jointing is observed. The values all lie within a range of ~10 MPa to 27 MPa. The stress and radius of surface curvature values correlate well, with increased stress in regions of increased convex radius of surface curvature. This indicates that the upper limit of in situ horizontal stress observed in surface quarries is determined by the development of a tension stress normal to the surface and consequent buckling of the rock.¹¹ The stress state under these conditions is comparable to the region of negative confining stress, σ ₃, in Fig. 2, where the compressive strength decreases rapidly as σ ₃ becomes tensile. Thus, it appears that the granite in surface quarries would be able to sustain a higher long-term horizontal stress in the absence of the surface, which introduces a stress-limiting instability mechanism. Even so, the quarry observations are further evidence that crystalline rock can support a significant long-term threshold stress under unconfined conditions and represent a lower-bound value, limited by development of a triaxial condition, consisting of biaxial horizontal compression and tension in the normal direction.

8 Discussion and Summary

The predominant approach used currently to assess the long-term response of rock is to extrapolate the results of laboratory creep tests, which typically involve loading test specimens over a period of several days, to the much longer times of interest. One of the principal concerns in this extrapolation is to establish whether the rock strength will decline progressively without limit and fail for any non-zero deviatoric stress, or whether it will approach a finite lower limit, or “threshold” stress. This paper has examined evidence for the existence of a threshold stress in crystalline rock, with reference to laboratory creep tests, tectonic data, analytical predictions and a numerical model of rock weakening by “stress corrosion” that takes into account the discrete particulate structure of crystalline.

It is not possible to extrapolate reliably from short-term creep tests on rock to predict the long-term compressive behavior. Linear extrapolation in a semi-log plot of short-term creep data on crystalline rock suggests that the rock would, in effect, collapse completely within the order of a million years. This is clearly not consistent with the evidence of extremely old (millions to billions of years or more) crystalline rock that has maintained a highly coherent crystalline structure to the present time. Stress determinations in surface granite quarries indicate significant horizontal stresses (approximately 10–20% of the short-term compressive strength of granite). Because these quarries are within the interior of very stable tectonic plates, where the rates of stress increase are extremely low (1 MPa per million years, or less), clearly indicates a stress threshold for unconfined loading conditions. It seems that curvature of the surface serves to limit the magnitude of the observed values for horizontal stresses, and that higher stresses could be sustained if the surface instability of sheet jointing caused by this curvature did not develop.

It is now recognized that rock subjective to deviatoric compressive stress fails by the growth of tension-induced microcracks and their coalescence. A semi-analytical model of tensile crack propagation indicates that, although the rate of crack growth may decline to a low level with decrease in toughness, it will not cease to propagate. This is clearly a consequence of failing to consider the effect of rock structure and confining stress on crack propagation. The model also neglects that tensile stresses in heterogeneous rock are localized by this heterogeneity. Consequently, the size of the tensile crack is a function of the size of the tensile region (see Diederichs 2007).

Stress corrosion often is proposed as the most likely mechanism for time-dependent strength degradation of crystalline rocks. There are two necessary conditions for activation of stress corrosion: (1) the existence of fractures, and (2) tension at the fracture tips greater than the limit imposed by the stress-corrosion activation energy. Consequently, the long-term strength threshold of intact rock with no pre-existing fractures should be equal to or greater than the crack initiation stress, σ _ci, which is in the range of 40–60% of the short-term strength.

A two-dimensional numerical modeling study was used to examine how tension cracks induced by an inclined pre-existing fracture will propagate as the fracture toughness is reduced progressively to zero. The model uses a wing-crack model embedded in a Voronoi tessellation procedure to allow the effect of a discrete granular micro-structure to be simulated. It is found that the existence of grain boundaries is sufficient to arrest crack growth even when the toughness at the crack tip is eliminated. This clearly supports the existence of a stress threshold in crystalline rock. This is an important finding, as it indicates that rock with a discrete heterogeneous granular structure, such as examined in this study, never will become cohesionless, even if the fracture toughness of the rock could reduce to zero over time. Because the rock will be frictional, this means, for example, that an unsupported underground tunnel or borehole will stabilize, even if unsupported. This is confirmed by mining observations that overstressed openings stabilize without support by simply changing shape (Ortlepp 1997).

The objective of the analysis was to determine whether there is a lower bound to the long-term strength of rocks. The analysis has demonstrated that there is always a stress threshold for confined conditions, because confinement acts to suppress the tension stresses associated with crack growth. Furthermore, even under unconfined conditions, the internal structure and heterogeneity of the rock, with grains several orders of magnitude tougher than the interface, results in blunting of the fracture tip and arrest of the fracture, even when the fracture toughness is reduced to zero (i.e., assuming that the stress-corrosion activation energy is zero). The actual magnitude of the lower bound to the long-term strength, when the stress-corrosion activation energy is assumed to be zero, will depend on a number of parameters, including pre-existing fracture size, their spacing, grain size and magnitude of confining stress.

In summary, the following overwhelming evidence is provided.

• 1. A “stress threshold”—i.e., a deviatoric stress that can be sustained indefinitely—exists for crystalline rocks. This threshold is likely to be a significant proportion of the crack initiation stress (i.e., 40–60% of the compressive strength.)

• 2. Thus, exponential extrapolation of short term creep tests, as shown in Fig. 5b of this paper, leading to a time-independent strength of the order of 45% of the instantaneous compressive strength is more realistic. Linear extrapolation to an ultimate strength of zero is completely unwarranted.