Displacement Forecasting Method in Brittle Crack Surrounding Rock Under Excavation Unloading Incorporating Opening Deformation

Abstract

Splitting failure, which is recognized as a special engineering geology phenomenon, occurs continually in the brittle rock mass of caverns during underground excavation. In this paper, a splitting model of linear slippage crack groups is built with fracture mechanics, energy analysis, and crack extension theories. Considering intrinsic cracks in rock mass and change of outer stress, intrinsic cracks propagate into macroscopical splitting cracks that are approximately parallel to the side wall of caverns. The splitting criterion of cavern rock mass and the method for predicting displacement in view of splitting opening displacement are proposed. In the end, the forecasting method is applied to the Jinping-I Hydropower Station, underground caverns engineering in China, the splitting failure zone and forecasting displacement are accordant with the monitoring data. The new forecasting displacement method is proven to contribute to the construction of similar underground caverns.

1 Introduction

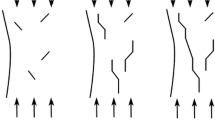
In southwest China, the engineering of large-scale hydropower projects in underground cavities is done predominantly in high mountain and canyon environments. In such environments, the cavity locations are characterized by a high initial in situ stress field. As a consequence, brittle fracturing and deformation of the surrounding rock can occur during cavity construction. Oblique splitting and the development of large fissures in the high side walls of large-scale cavities can influence severely the stability of the surrounding rock mass. Power stations such as Yu Zixi, Ming tombs, Er’tan, as well as those recently built, such as Laxiwa, Waterfall Channel, Jinping-I, have large fractures and nearly vertical fracture areas in their cavity side walls. The underground cavities of Jinping-I Hydropower Station are accompanied with fracture of surrounding rock and spray-up. Many researchers have conducted analyses of this engineering phenomenon via numerical simulation and experimental evaluation. For example, the volumetric deformation state and its consequences were exhibited in maximum supporting pressure zone including the analysis of stress state, deformation, and failure of rock mass around tunnels at different stages (Wang et al. 2006). A novel intelligent optimization method was developed for optimization of excavation sequence and support parameters for large underground caverns under condition of high geostress (Su et al. 2007). Li (2007) used a typical hydropower station as an example to study the cause of fracturing and to assess solutions to the problem using a 3D finite element method. Jiang et al. (2009) performed experiments utilizing a base friction test apparatus to verify their numerical model (EDEM), which was used to simulate crack generation and propagation resulting from shear and tension failures in the matrix rocks. The phenomenon of splitting in underground cavern walls and stability analysis of the surrounding rock mass has been investigated by others using different simulation methods, including FEM (Yoshida and Horii 2004; Dhawan et al. 2004; Maghousa et al. 2008; Barla et al. 2008), DEM (Dasgupta et al. 1995; Fan et al. 2004; Wang et al. 2005), and DDA (Wu et al. 2006). During construction of Er’tan Hydropower Station, the release and redistribution of high horizontal stress resulted in the formation of a series of cracks in the side walls of the main power house, some of which were more than 20 m deep (Fig. 1).

Fig. 1

Sketch of splitting cracks in Er’tan project

Exadaktylos and Tsouterlis (1995) proposed an analytical approximate elastic model of the pillar failure mechanism for the case of multiple underground openings in brittle rocks by parallel equidistant vertical splitting to form slabs. Bauch and Lempp (2004) simulated the rock failure process using rock mechanics experiments. Their experiments were performed under extensional conditions in triaxial tests using three different boundary conditions and modifying pore pressure conditions as well as strain and stress rates.

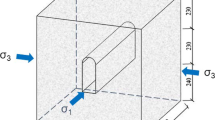
Zhu et al. (2011) employed a true triaxial loading and unloading device to conduct experiments on an analogue material to simulate the stress variation state, crack formation processes, and the stress condition of the surrounding rock in excavated underground caverns. After numerous comparisons of analogue materials, a mortar composed of river sand and cement with certain particle size (120 × 120 × 240 mm) distribution was selected as the analogue material. The test device and experiment result are shown in Figs. 2 and 3 (Zhu et al. 2011), respectively.

Fig. 2

True triaxial loading–unloading device

Fig. 3

Splitting failure of samples in loading–unloading tests

The Central Electric Power Research Institute in Japan made statistical analysis of monitoring data from 16 large-scale underground power houses. Their analysis suggests that one-quarter to two-thirds of the displacement of powerhouse side walls is caused by fracturing, and in some projects this can amount to 7/10 or 4/5. Hibino and Motojma (1995) utilized a borehole TV multipoint-displacement meter to make statistical analysis of 16 cavities from the electric power system of Japan. From comparison of the displacement from two cavities, Hibino and Motojma (1995) also demonstrated that displacement due to fractures also exists in deeply buried cavities (Table 1). These monitoring results illustrate that fracture deformation constitutes a relatively large portion of total deformation.

Table 1 Displacement analysis surveyed by Hibino in Japan (note: ratio η is opening displacement/the whole displacement)

Most underground hydropower stations in southwest China are built in mountains with hard brittle country rock. Currently, methods such as FEM and FDM are unable to predict additional opening displacement. However, the extent of displacement of the surrounding rock is important for verifying the stability of surrounding rock and whether the reinforcement scheme employed will be effective. It is clear from the results of previous studies that investigation of the failure mechanism and displacement forecasting for the surrounding rock during cavity excavation is of great theoretical and practical significance. By so doing, it will put forward foundation and afford reasonable method for engineering optimization design and optimization excavation.

2 Mechanism of Tension Crack Formation

During underground excavation, the removal of rock causes stress redistribution and concentration. When a brittle rock mass with a pre-existing fracture is in a high-stress condition, the compression state of rock mass is altered to a biaxial or even uniaxial condition from a triaxial condition due to the excavation. Elastic strain energy is dissipated by crack initiation, propagation, and coalescence, which finally leads to tensional failure as illustrated in Fig. 4.

Fig. 4

Sketch of splitting failure mode around openings

The state of both stress and strain during this process is complicated, and, consequently, it is not appropriate to analyze and evaluate the process in terms of solely stress or strain. In this contribution, we analyze and explore tensional failure and deformation of rock from the viewpoint of crack propagation and energy principle.

2.1 Splitting Model

Figure 5a is a sketch of a linear sliding crack model. This model is utilized to study the effect of dilatancy on rock (Kemeny 1991). The crack body is made up of an initial crack and wing crack. The wing crack is induced by the relative slippage of initial crack surface under compressive stress in far field.

Fig. 5

Simplified model of splitting

In Fig. 5b, the linear tensile crack, which is under a small lateral stress ($\sigma_{3}$), expands parallel to the direction of the maximum compressive stress ($u = u_{e} + u_{c}$) and interacts with neighboring propagating cracks leading to coalescence and ultimately to failure. For the sake of convenience, we assume that initial cracks are distributed with an even density and that crack propagation is synchronous during loading. This simplified model is regarded as the research object of fracture mechanism (Martin and Chandler 1994). The lengths of the initial crack and wing crack are 2c and 2l ₀. The distance between neighboring cracks is 2w, the angle between the initial crack surface and the horizontal is θ, and the coefficient of friction of the sliding surface is μ. When l ₀ is equal to w, splitting crack is coined and its length is defined as L.

When the initial crack expands into a macroscopic tensional crack, the model is simplified into the crack configuration shown in Fig. 5c.

2.2 Splitting Criterion

The effective shear stress, $\tau^{*}$, generated through $\sigma_{1}$ and $\sigma_{3}$ in a single linear sliding crack can be expressed as:

$$\tau^{ * } = \tau - \mu \sigma_{n}$$

(1)

Note: $\sigma_{n} = \frac{{\sigma_{1} + \sigma_{3} }}{2} - \frac{{\sigma_{1} - \sigma_{3} }}{2}\cos 2\theta$; $\tau = \frac{{\sigma_{1} - \sigma_{3} }}{2}\sin 2\theta$

Then the stress intensity factor of linear sliding crack is:

$$K_{\text{I}} = \frac{{2c\tau^{*} \cos \theta }}{{\sqrt {\pi l} }} - \sigma_{3} \sqrt {\pi l}$$

(2)

Note: c is half of the length of initial crack; $l = l_{0} + c$.

For a single crack, the tensile force of a wing crack can be defined as a horizontal projection of the effective shear stress.

$$\frac{\partial U}{\partial P} = \Delta$$

(3)

The resultant tensile force (F) across the whole crack surface is equivalent to: (Miao and An 1999)

$$F = \int\limits_{A}^{{}} {f{\text{d}}A}$$

(4)

where A is the surface area of the tensional crack. Therefore, from Eqs. (1), (3), and (4), the resultant tensile force is:

$$F = \int\limits_{A}^{{}} {f{\text{d}}A} = \tau^{*} \cos \theta L = L\cos \theta \cdot\left[ {\left( {\sigma_{1} - \sigma_{3} } \right)\sin \theta \cos \theta - \mu \left( {\sigma_{1} \sin^{2} \theta + \sigma_{3} \cos^{2} \theta } \right)} \right]$$

(5)

Crack coalescence is influenced by the stress intensity factor of the crack tip ($K_{\text{I}}$). Thus, $K_{\text{I}}$ which results in the formation of a tensional crack can be expressed as:

$$K_{\text{I}} = \frac{F}{{\sqrt {\pi L} }} - \sigma_{3} \sqrt {\pi L}$$

(6)

Since crack friction is not taken into account, the stress concentration caused by II-type crack can be ignored. So with inequality $K_{\text{I}} \ge K_{\text{IC}}$, the inequality between $\sigma_{1}$ and $\sigma_{3}$ can be obtained.

$$\frac{F}{{\sqrt {\pi L} }} - \sigma_{3} \sqrt {\pi L} \ge K_{\text{IC}}$$

(7)

Finally, stress inequality is produced after tensional failure occurs:

$$\sigma_{1} \ge \frac{{K_{\text{IC}} \sqrt {\pi L} }}{{L\left( {\sin \theta \cos^{2} \theta - \mu \sin^{2} \theta \cos \theta } \right)}} + \sigma_{3} \frac{{\pi + \left( {\sin \theta \cos^{2} \theta + \mu \cos^{3} \theta } \right)}}{{\left( {\sin \theta \cos^{2} \theta - \mu \sin^{2} \theta \cos \theta } \right)}}$$

(8)

Inequality (8) can function as a fracture criterion for the surrounding rock. Where $\mu$ is friction coefficient of crack while L is average length of ultimately formed splitting crack. θ is the angle between initial crack and horizontal principal stress.

3 Tensional Deformation Mechanism

In the overall pre-peak deformation process of brittle rock, the total deformation comprises both elastic deformation and deformation generated by the opening of fractures.

The displacement of the surrounding rock is normally acquired by the method of continuum mechanics by selecting an appropriate elastic constant and intensity parameter. However, this method cannot describe the mechanics of the brittle failure of rock when tensional fracturing occurs. Hence, in this section the deformation caused by fracture opening is modeled using the method of energy analysis in order to better describe the real deformation mechanism of brittle rock. An approach of displacement prediction for the surrounding rock is proposed herein that can take brittle tensional failure and deformation into account.

After the excavation unloading of rock surrounding a cavern, tensional failure results primarily through release of horizontal stress. Thus, vertical deformation is not analyzed.

3.1 Fundamental

For a simplified splitting model, the lateral deformation of a brittle rock mass is $\varepsilon_{\text{l}}$, and includes two components. Firstly, there is $\varepsilon_{\text{le}}$, the lateral elastic strain, which is not caused by crack body as a function of external far-field force. Secondly, $\varepsilon_{\text{lc}}$ is the lateral opening deformation resulting from microcrack propagation within the model. Consequently, $\varepsilon_{\text{l}}$ = $\varepsilon_{\text{le}}$ + $\varepsilon_{\text{lc}}$. The model does not take crack closure and plastic deformation into account. The density function of splitting opening deformation can be defined as $\Gamma = \varepsilon_{\text{lc}} /\varepsilon_{\text{le}}$ and lateral elastic deformation is defined as: $\varepsilon_{\text{le}} = \frac{{\left( {\sigma_{3} - \upsilon \sigma_{1} } \right)}}{{E_{0} }}$.

The dilation of a crack is based upon Castigliano’s first theorem ($\frac{\partial U}{\partial P} = \Delta$), in which $U$ represents the complementary energy of system, P is the generalized force, and Δ is the generalized displacement. This theorem is applied to both linear and nonlinear elastic deformation.

The model presented in this paper describes a nonlinear elastomer with fractures and consequently the complementary energy of the system can be symbolized as the energy causing crack propagation. Therefore, it is feasible to adopt Castigliano’s first theorem to describe fracture deformation. According to Li and Lajtai (1998), horizontal deformation, $\varepsilon_{\text{lc}}$, resulting from fracturing, is obtained by an analytical method that combines the energy principle and fracture mechanics (Dyskin and Germanovich 1993).

$$\varepsilon_{i} = \frac{{\partial \Delta U_{\text{e}} }}{{\partial \sigma_{i} \Delta V_{i} }}$$

(9)

where $\Delta U_{\text{e}}$ is the strain energy of the element and $\sigma_{i}$ and $\Delta V_{i}$ are the horizontal stress and the volume of the element, respectively. From Eqs. (8) and (9), it can be seen that the fracture toughness of rock mass, the angle between initial crack and horizontal plane, the length of splitting crack, Poisson’s ratio, the stress state of element and so on are taken into account.

3.2 Strain Energy of Splitting Model

One description of the strain energy is defined by the stress intensity factor of the crack tip, which was expressed by Li and Lajtai (1998) as:

$$\Delta U_{\text{e}} = \frac{2}{E}\int\limits_{c}^{{l_{0} + c}} {K_{\text{I}}^{2} } {\text{d}}l$$

(10)

where the domain of integration is over the length of single wing fracture. In this $c$ denotes half of the length of the initial fracture and l ₀ is the length of wing fracture.

From Eqs. (2) and (10):

$$\Delta U_{\text{e}} = \frac{{8c^{2} \cos^{2} \theta }}{E\pi }\ln \left( {\frac{{l_{0} + c}}{c}} \right)\tau^{*2} + \frac{\pi }{E}\left( {\left( {l_{0} + c} \right)^{2} - c^{2} } \right)\sigma_{3}^{2} - \frac{{8cl_{0} \cos \theta }}{E}\tau^{*} \sigma_{3}$$

(11)

3.3 Splitting Opening Deformation

After obtaining the strain energy from Eq. (11), Eq. (9) can be used to obtain the horizontal deformation generated by fracturing:

$$\varepsilon_{\text{lc}}^{{}} = \frac{{\partial \Delta U_{\text{e}} }}{{\partial \sigma_{3} }}\cdot\frac{N}{V} = \frac{ - N}{2V}\beta \cdot\left[ {\frac{{8c^{2} \cos^{2} \theta }}{E\pi }\ln \left( {\frac{{l_{0} + c}}{c}} \right)\cdot2\tau^{*} - \frac{{8cl_{0} \cos \theta }}{E}\cdot\sigma_{3} } \right] - \frac{{8Ncl_{0} \cos \theta }}{EV}\cdot\tau^{*} + \frac{2N\pi }{EV}\left( {\left( {l_{0} + c} \right)^{2} - c^{2} } \right)\sigma_{3}$$

(12)

To simplify the calculation, we assume: $\alpha = { \sin }2\theta - \mu (1 - { \cos }2\theta )$; $\beta = { \sin }2\theta + \mu \left( {1 + { \cos }2\theta } \right)$. The density of fracturing is $\chi = \frac{{Nc^{2} }}{V}$ where N is the number of fractures and V is the volume of the element.

Combining $\sigma_{n}$ and $\tau$, with equation $\tau^{*} = \tau - \mu \sigma_{n}$ we derive:

$$\tau^{*} = \frac{{\sigma_{1} - \sigma_{3} }}{2}\sin 2\theta - \mu \left( {\frac{{\sigma_{1} + \sigma_{3} }}{2} - \frac{{\sigma_{1} - \sigma_{3} }}{2}\cos 2\theta } \right) = \frac{1}{2}\left( {\alpha \sigma_{1} - \beta \sigma_{3} } \right)$$

(13)

And so when $\tau^{*}$ is substituted into Eq. (12) the horizontal deformation is defined as a function of $u = u_{e} + u_{c}$ and $\sigma_{3}$:

$$\varepsilon_{\text{lc}}^{{}} = \Phi (\chi ,\theta ,c,l_{0} ,E)\cdot\sigma_{1} + \Psi \left( {\chi ,\theta ,c,l_{0} ,E} \right)\cdot\sigma_{3}$$

(14)

Among them,

$$\Phi (\chi ,\theta ,c,l_{0} ,E) = - \frac{4\alpha \cos \theta }{\pi }\left( {\beta \cos \theta \ln \left( {\frac{{l_{0} + c}}{c}} \right) + \frac{{\pi l_{0} }}{c}} \right)\cdot\frac{\chi }{E}$$

(15)

$$\Psi \left( {\chi ,\theta ,c,l_{0} ,E} \right) = \left[ {2\pi \cdot\left( {\frac{{l_{0}^{2} + 2l_{0} \cdot c}}{{c^{2} }}} \right) + \frac{{4\beta \cdot\cos^{2} \theta }}{\pi }\cdot\ln \left( {\frac{{l_{0} + c}}{c}} \right) + 8\beta \cdot\cos \theta \cdot\frac{{l_{0} }}{c}} \right]\cdot\frac{\chi }{E}$$

(16)

where $\chi ,\theta ,c,l_{0} ,E$ are constants related to rock mass.

3.4 Density Function of Fracture Deformation

The function describing fracture density is:

$$\Gamma = {{\varepsilon_{\text{lc}} } \mathord{\left/ {\vphantom {{\varepsilon_{\text{lc}} } {\varepsilon_{\text{le}} }}} \right. \kern-0pt} {\varepsilon_{\text{le}} }} = \frac{{\Phi (\chi ,\theta ,c,l_{0} ,E)\cdot\sigma_{1} + \Psi \left( {\chi ,\theta ,c,l_{0} ,E} \right)\cdot\sigma_{3} }}{{\frac{{\left( {\sigma_{3} - \upsilon \sigma_{1} } \right)}}{{E_{0} }}}}$$

(17)

This function of fracture density reflects not only the mechanical properties of the rock mass, but also the fracture layout state and stress state of rock mass. By way of function 17, it is not complicated to tackle the issue of opening discontinuous deformation, which is not available by continuous analytical software in engineering project.

4 Forecasting Fracture Displacement in a Construction Site

4.1 Implementation of Forecasting Method

Flac-3D (2009) is employed to simulate excavation unloading of underground groups of cavities to determine the stress and displacement of surrounding rock. Using the criterion defined by Eq. (8), the stress inequality about $\sigma_{1}$ and $\sigma_{3}$ is obtained. Using the inequality and procedure defined above, the stress arising from excavation in surrounding caverns is determined, and so the fracture failure region and the corresponding elastic displacement are also determined. Γ is obtained based on the loading and unloading direction in the fracture failure zone. Using Flac-3D and taking the strain increment, ($\varepsilon_{\text{lc}}^{{}} = \Phi (\chi ,\theta ,c,l_{0} ,E)\cdot\sigma_{1} + \Psi \left( {\chi ,\theta ,c,l_{0} ,E} \right)\cdot\sigma_{3}$), into account $u_{\text{c}}$is determined. After obtaining both the elastic and splitting opening displacement, the overall horizontal displacement of the surrounding rock is determined by $u = u_{\text{e}} + u_{\text{c}}$. This methodology is illustrated in Fig. 6.

Fig. 6

Flow chart of forecasting method

4.2 Application of Forecasting Method

The object of this study is hard brittle rock mass. The presence of large-scale weak planar heterogeneities such as faults, fracture zones, or compositional changes is not considered in this model.

When the surrounding rock is in a condition of relatively high horizontal in situ stress, then more excavation results in more fracturing. In the fracture criterion formula (Eq. 8), the angle between the initial fracture and the horizontal principal stress will be large. Fractures at a small angle to the horizontal principal stress are not considered in this model.

The length of the fracture in the splitting margin can only be treated with homogenization according to the field-monitoring situation. So in the fracture criterion, the fracture length of all fractures is uniform. Thus, the fracture failure region defined by the model criterion is a qualitative description, which represents the potential zones in which fractures can develop in rock surrounding an underground excavation.

5 Engineering Verification of the Forecasting Method

Because of the extensive size of excavation at the Jinping-I Hydropower Station, the geostress is relatively high because tectonic stress and gravitational stress both contribute. During the excavation process, the brittle rock surrounding the caverns such as the power house displays strong fracturing and spalling phenomena. It is widespread that there are core discing in the prospecting process, slabbing and buckling in the exploiting tunnels earlier in prospecting period, which greatly jeopardize engineering stability (Dyskin and Germanovich 1993).

5.1 Calculation Scope

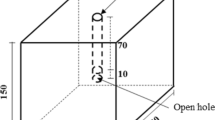
The underground cavities at the Jinping-I Hydropower Station are of an enormous scale, and consist of diversion tunnels, the main power house, the busbar tunnel, and the main transformer chamber among others. The excavated height of the main power house is 69.30 m and the excavated height of the main transformer chamber is 32.70 m. The layout of the excavations is based on the report of Chen et al. (2009).

The underground caverns in assembly of number 3 are taken as the research target since the splitting phenomenon of this region is most obvious and representative. In terms of the model, quasi-three-dimensional calculation is performed with a unit thickness of 5 m. The model has a horizontal length of 540 m; the power house and the main transform chamber are located in the central zone of the model. The vertical scope of the model ranges from the ground surface to a depth of 200 m below the main power house. The overall model comprises 44,425 elements and 17,699 nodes.

5.2 Parameter Selection

5.2.1 Deformation Modulus During Loading and Unloading

When taking the variation of deformation modulus into account during loading and unloading, it is presumed that the cell deforms elastically during loading and brittle failure occurs once exceeding the cell strength. Based on previous work (Zheng et al. 2012), the stress–strain curve for the elastic-brittle model considering energy dissipation is shown in Fig. 7. It is assumed that the total elemental energy of deformation of a rock mass element is S _AOC during loading to point A and the recovered energy is S _ABC when the rock mass is unloaded and deformation returned to point B. During this process, the dissipated energy is S _AOB. It follows that:

Fig. 7

Stress–strain curve of the elastic-brittle model considering energy dissipation

$$\overline{E} = \frac{{S_{\text{AOC}} }}{{S_{\text{ABC}} }}E = \left( {1 + \frac{{S_{\text{AOB}} }}{{S_{\text{AOC}} - S_{\text{AOB}} }}} \right)E.$$

(18)

Let $1 + \frac{{S_{\text{AOB}} }}{{S_{\text{AOC}} - S_{\text{AOB}} }} = T$, then $\overline{E} = tE$.

Therefore, when the energy dissipation is considered,

$${\text{Deformation modulus}} = \left\{ {\begin{array}{*{20}l} {E,} & {\text{loading}} \\ {\overline{E} = tE,} & {\text{unloading}} \\ \end{array} } \right.$$

(19)

Based on the above theory, the key feature of the constitutive model for the rock mass considering energy dissipation is the different deformation modulus, namely $E$ and $\overline{E}$ during loading and unloading process, respectively. Specifically, the modulus during unloading is an equivalent deformation modulus $\overline{E}$.

5.2.2 Criterion for Judging Loading and Unloading

The hydrostatic (bulk) stress and octahedral shear stress expressed by the yield invariant surface are adopted to evaluate the criterion of judging loading and unloading. The loading is defined by the increase of the first and second invariants of the stress tensor I ₁ and J ₂ and the unloading is defined by the decrease of I ₁ and J ₂ (Zheng et al. 2002). As is well known, the Mohr–Coulomb criterion is expressed as follows:

$$F = \alpha I_{1} + \sqrt {J_{2} } - K = 0.$$

(20)

In which, $\alpha = \frac{\sin \varphi }{{\sqrt 3 \left( {\sqrt 3 \cos \theta_{\sigma } - \sin \theta_{\sigma } \sin \varphi } \right)}}$, $K = \frac{\sqrt 3 c\cos \varphi }{{\sqrt 3 \cos \;\theta_{\sigma } \; - \sin \;\theta_{\sigma } \;\sin \;\varphi }}$, $\theta_{\sigma } = \arctan \left( {\frac{{2\sigma_{2} - \sigma_{1} - \sigma_{3} }}{{\sqrt 3 (\sigma_{1} - \sigma_{3} )}}} \right)$ where $\varphi$ denotes the internal friction angle and $\sigma_{1}$, $\sigma_{2}$, $\sigma_{3}$ principal stress, respectively.

Therefore, the criterion for differentiating loading and unloading is:

$$\left\{ {\begin{array}{*{20}c} F & {{\text{increases}} \to {\text{loading}}} \\ F & {{\text{decreases}} \to {\text{unloading}}} \\ \end{array} } \right.$$

This criterion may better reflect the effects of the three principal stresses and can be applied to describe the loading history of the rock mass.

According to the above theory, the constitutive model in Flac-3D is accordingly modified. For finding the solution within an element, the loading and unloading criterion is used to interpret the stress state: if it is in the loading stage, the deformation modulus is defined as the original modulus; if it is in the unloading stage, the deformation modulus is defined as the equivalent modulus. Next, the equivalent deformation modulus involving consideration of energy dissipation is calculated according to the stress–strain state of the element and the relevant parameters. Then, the user-defined constitutive equation is integrated into the Flac-3D program. Finally, the solution can be found by Flac-3D through a number of iterative computation cycles.

5.2.3 Input Value of Mechanical Property

The value of the in situ stress is based upon the measured geostress. The cavern is excavated within metamorphic rocks comprising marbles and sediments metamorphosed at greenschist facies. The deformation modulus of the unexcavated rock is 20 GPa, while the deformation modulus of the excavated rock is approximately 10 Gpa. The value of $\nu$is 0.25 and fracture toughness is 0.91 MPa$\sqrt m$. As shown in Fig. 8, the constructional drawing of the numerical model and in Table 2 are the mechanical parameters of surrounding rock. In addition, the rock is classified by the criterion of “Standard Classification Grade of Underground Surrounding Rock of China Water Conservancy and Hydropower Engineering” and the excavation sequence is depicted in Fig. 9.

Fig. 8

Constructional drawing of numerical model

Table 2 Mechanical parameters of surrounding rock

Fig. 9

Excavation sequence of cavern groups

The initial boundary condition for the model is that lateral geostress is imposed on the two sides of the excavation with the bottom of the excavation representing a geometric constraint on the lateral stress. The lateral stress is obtained by data inversion of the measured geostress.

Based on the geological description of the rock’s mechanical properties combined with the analysis of micro cracks in a rock-like material from Lajtai et al. (1991), some assumptions related to fracture parameters in the fracture criterion are made in Table 3. We deduce that the splitting criterion and density function (note: the unit of stress is MPa) related to this project based on the parameters provided above are:

Table 3 Micro-crack parameters for marble in Jinping-I

$${\text{Fracture criterion:}}\, \sigma_{1} \ge 4.09 + 20.40\sigma_{3}$$

(21)

$${\text{Density function:}}\;\Gamma = \frac{{2.66\sigma_{3} - 0.16\sigma_{1} }}{{\sigma_{3} - 0.25\sigma_{1} }}$$

(22)

Equation (21) is obtained from Eq. (8) while Eq. (22) is obtained from Eqs. (15), (16), and (17) in view of the associated parameters regarding the research project.

5.3 Numerical Simulation and Engineering Validation

5.3.1 Stress State

Figures 10 and 11 result from our numerical calculation of elastic stress and demonstrate that the horizontal stress of the caverns after excavation is substantially reduced. The stress in the side wall approaches zero even with tensile stress. Conversely, the vertical stress of the surrounding rock is increased markedly. The stress in the side wall reaches more than twice the level before excavation. This results in a change of the compression state, which leads to fracture generation. This effect is gradually reduced with increasing distance of the surrounding rock from the excavated cavity and recovers to the initial stress state at a distance from the cavity. The predicted variation of stress state is in close agreement with the distribution of the fracture failure zone, which was obtained through numerical calculation. In Fig. 12, the maximum depth of fracturing in the upstream side wall of the main power house is 11.1 m and in the splitting depth of corresponding part of downstream side wall the depth is 14.2 m.

Fig. 10

Schematic of vertical stress of caverns

Fig. 11

Schematic of horizontal stress of caverns

Fig. 12

Splitting failure zone of caverns after excavation

5.3.2 Displacement Field Distribution

As shown in Fig. 13, after excavation the horizontal displacement occurs within the cavern walls towards to interior of the cavern. The maximum horizontal displacement of the upstream and downstream side walls is calculated to be only 1.03 and 4.22 cm, respectively, which does not coincide with multipoint extensometer measurements (Fig. 14).

Fig. 13

Schematic of horizontal displacement of caverns

Fig. 14

Multipoint extensometer data in the middle of main house sidewall of Jinping-I Hydropower Station (note: an abscissa symbolizes the distance between side wall and multipoint extensometer unit: m b Ordinate symbolizes monitoring displacement unit: cm)

However, in Tables 4 and 5, it can be seen that the point displacement obtained by our prediction method is close to field monitoring data.

Table 4 Comparison between forecasting and monitor displacement of downstream main power house sidewall

Table 5 Comparison between forecasting and monitor displacement of upstream main power house sidewall

Taking downstream main house sidewall monitoring points as examples, the elastic horizontal displacement is 4.22 cm, the density of splitting opening displacement resulting from the stress state created by excavation, Γ_downstream0, is 0.64, the forecast displacement is 6.92 cm, and the rate of splitting deformation to the overall displacement η is 39 %. The error compared with actual monitoring data is merely 4.62 %. The displacement error for remaining key points is minimal, which is consistent with monitoring data (Figs. 15, 16).

Fig. 15

Diagram of different displacements for downstream sidewall monitoring points of main power house

Fig. 16

Diagram of different displacements for upstream sidewall monitoring points of main power house

By increasing the depth into the surrounding rock away from the excavation wall (Tables 4, 5), the density of splitting opening displacement at the key points declines accordingly. At a depth of 15 m away from the excavation wall, Γ_downstream20 is 0.08, which approaches nearly zero. This agrees with the margin of splitting failure zone and splitting opening deformation of key points outside the fracture failure zone is zero. The monitoring points in the upstream sidewall of the main power house have the same characteristic and show an equally good fit of forecasting result compared with observation.

On the basis of predicted and measured stress, characteristics of displacement variation and a comparison of predictions with field monitoring data, it is apparent that our proposed modeling approach is feasible and is able successfully to predict fracture opening displacement of rock surrounding large excavated cavities.

6 Discussion

The splitting failure phenomenon in rock surrounding excavated cavities with associated high stress resulting from excavation is of importance because the fracture and relaxation region imposes three detrimental effects on the sidewall which influence engineering stability: (a) the upper section of fracture region impacts the stability and carrying capacity of the crane beam, since the crane beam is likely to be located in a zone of strong relaxation, which disturbs its foundation. (b) The development of the fractured region will provide an open pathway to supply air which erodes both anchor cables and bolts until failure. (c) The power house is infused with water seepage. Due to the stochastic nature of fracture distribution in the surrounding rock, it is almost impossible to investigate the layout or pattern of the fractures in detail. However, some analysis can be performed to establish the overall regularity of fracture distribution. From this standpoint, the fracture failure model has practical importance. Only anatomizing geological investigation report and selecting model parameters reasonably can we apply achievement to direct engineering construction.

In reality, the excavation unloading effect parallel to the axial direction is relatively insignificant and the mechanical characteristics in this direction are not considered in the model. In the forthcoming research, 3D splitting failure strain energy will be taken into account and fracture propagation and the distribution of splitting failure will be investigated in a 3D compression state.

In terms of application of our forecasting method, the more apparent the excavation effect, the greater the apparent fracture splitting that results (Li et al. 2008a, b, 2009; Zhu et al. 2010). For analysis of similar engineering projects, the angle between maximum principal stress and axial direction of the cavern as well as the lateral pressure coefficient’s influence for fracture failure used to be studied. Generally speaking, the larger the angle and lateral pressure coefficient, the larger the possibility of fracture failure and consequently the initial stress should be analyzed in numerical simulation to better inform the practical engineering of excavated cavities.

7 Conclusions

During engineering construction of large cavities, excavation results in stress release, which induces deformation in the rock surrounding the cavern. This deformation is divided into two types. The discontinuous deformation caused by fracture propagation accounts for the greatest proportion of the total deformation. This paper links theoretical analysis of the problem to numerical simulation, investigating the deformation mechanism of splitting fractures and methods for predicting their formation.

When a brittle rock mass is under a high stress state, due to excavation unloading, the compression state of the rock surrounding the excavation transfers from three-way to two-way or one-way. Thus, elastic strain energy stored in the rock mass dissipates by means of crack initiation, propagation, and coalescence. We deduce that fracture failure of the rock is an engineering phenomenon generated by energy dissipation.

A fracture model that predicts the development of a linear sliding fracture group is proposed. The model considers that the initial fracture exists in the surrounding rock and that the initial fracture transfers into a secondary fracture with a change of stress state, which produces a high-angle splitting fracture array approximately parallel to the cavity side wall. The fracture failure criterion of the surrounding rock of the cavern is obtained from the basic principles of fracture mechanics and crack propagation. This criterion reflects not only the mechanical properties of the brittle rock mass but also the distribution pattern and parameters of cracks included within it. The criterion can be used to discriminate zones of potential fracture damage based on the stress distribution in surrounding rock after excavation unloading.

Combined with the energy principle and the Castigliano theorem, the splitting opening deformation mechanism and computational formula are discussed a splitting model under external loading is deduced. The density function, Γ, of the fracture opening deformation is proposed and the deformation modulus, crack distribution, crack density, and the stress state per unit of rock mass are considered within this function. As such, the properties of the deformation can be comprehensively represented in the model.

Based on the splitting criterion and the density function of fracture deformation, a new method of displacement prediction in rock surrounding excavated cavities is proposed. This method tackles the problem that continuous analysis methods such as FEM or FDM cannot predict discontinuous deformation caused by crack propagation. Our method not only predicts potential fracture damage zones generated by excavation unloading but also determines the deformation of rock surrounding cavities due to splitting opening deformation. The practical application of this method to underground group cavities in the Jinping-I Hydropower Station, results in the forecasting of potential fracture damage zones and total displacements, which are in close agreement with the results of field monitoring data. The Jinping-I simulation results verify the feasibility and applicability of our proposed forecasting method.