Anisotropic Deformation of a Circular Tunnel Excavated in a Rock Mass Containing Sets of Ubiquitous Joints: Theory Analysis and Numerical Modeling

Abstract

Determining anisotropic deformation surrounding underground excavations for tunnels is an intuitional task that involves many difficulties due to the inherent anisotropies in the strength and deformability of natural rocks. This study investigates joint-induced anisotropic deformation surrounding a tunnel via a numerical simulation that accounts for the mechanical behavior of intact rock, the orientations of joint sets, and the mechanical behavior of joint planes; this numerical simulation can model the complete stress–strain relationship with anisotropic rock mass characteristics. Simulation results demonstrate that the well-known excavation-induced stress variation–decrease in the radial component and increase in the tangential component–decrease shear strength and increase shear stress for the joint plane tangential to the tunnel wall, resulting in joint sliding failure and considerable shear deformation. This joint sliding failure and significant shear deformation account for the joint-induced anisotropic deformation surrounding a tunnel. When a rock mass has two joint sets with unfavorable joint orientations, the area with joint sliding failure can deteriorate mutually, resulting in large anisotropic deformation. Additionally, for a rock mass containing three joint sets with well-distributed orientations, joint sliding in various joint sets and associated stress variations can counter balance each other, resulting in less anisotropic deformation than those of rock masses containing one or two joint sets.

1 Introduction

Anisotropic deformation, commonly for tunnels excavated from rock masses, reduces the stability of the usual bilaterally symmetrical supporting system (Hoek and Brown 1980; Bhasin et al. 1995; Hefny and Lo 1999; Tonon and Amadei 2003; Fortsakis et al. 2012; Vu et al. 2012). The inherent anisotropies in both strength and deformability for natural rocks generate difficulties when simulating the mechanical behaviors of rock masses, including pre- and post-peak anisotropic deformation (Amadei et al. 1987; Amadei and Savage 1991; Amadei and Pan 1992; Pine et al. 2006; Wang et al. 2009). As such, for tunnel designs, the determination of anisotropic deformation surrounding underground excavations in rocks is a seemingly intuitional task that involves many complexities and compromises (Pariseau 1999; Prudencio and Prudencio and Van Sint 2007; Wang and Huang 2011; Zhou et al. 2012).

The anisotropy of a rock mass resulting from foliation or lamination of intact rocks, such as schistosity in schists or bedding in sandstones, can be taken into account by a transversely isotropic constitutive model that is integrated with directional failure-related criteria (Chen et al. 1998; Singh et al. 2002; Singh and Rao 2005; Weng et al. 2008; Kolymbas et al. 2012). Anisotropic deformation caused by underground excavation can be determined via an associated numerical implementation with little difficulty, and usually has a ratio of maximum to minimum deformation of <1.5 (Kulatilake et al. 2001; Weng et al. 2010). However, anisotropy due to rock formations cut by one or several regularly spaced ubiquitous joint sets is far more complex, as the rock has significant differences in strength and deformability of the joint plane and arbitrary orientations of joint sets, resulting in various failure modes and various complete stress–strain relationships of rock masses (Singh et al. 2002; Wang 2003; Wang and Huang 2006). Underground excavation in such a rock mass can induce highly anisotropic deformation with the ratio of the maximum to minimum deformation exceeding three, jeopardizing tunnel stability (Wang 2003; Singh and Singh 2008; Maghous et al. 2008).

Focusing on joint-induced anisotropic deformation, this study investigates how joint sets deform and fail under stress variation caused by tunnel excavation, which induces an additional failure mode and asymmetrical deformation components from those of intact rocks as well leading to diverse deformational behaviors of rock masses surrounding a tunnel. The non-linear constitutive model and associated numerical implementation proposed by the authors are adopted (Wang and Huang 2009). The characteristics of the adopted methodology are introduced via simulations of a series of uniaxial compressive loading tests on rock masses containing one joint set with distinct dip angles. Circular tunnels excavated in rock masses containing various joint sets are then simulated to characterize the influence of excavation induced stress variation on joint deformation and related failure. The interaction between different joint sets is also examined. Finally, factors affecting joint-induced anisotropic deformation surrounding a tunnel, such as the joint orientation, joint strength, and in situ stress conditions, are discussed.

2 Methodology

Wang and Huang (2009) developed a three-dimensional non-linear constitutive model and an associated two-dimensional numerical implementation for a rock mass with regularly distributed ubiquitous joint sets. The model combines the mechanical behavior of intact rock, the spatial configuration of joint sets, and mechanical behavior of the joint plane into the rock mass using representative volume elements. Thus, this model can characterize joint-induced anisotropy in terms of strength and deformation of a rock mass.

2.1 Constitutive Model and Associated Numerical Implementation

2.1.1 Deformation Behavior for Intact Rock and Joints

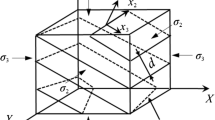
A rock mass with a unit volume consisting of $M$ sets of ubiquitous joints, as shown in Fig. 1, under a uniform stress state ${\varvec{\sigma}}$ is considered. When subjected to a small increment of stress ${\mathbf{d\sigma }}$, the corresponding incremental strain of the rock mass is ${\mathbf{d\varepsilon }}$. The incremental strains typically consist two components–one from the intact rock deformation ${\mathbf{d\varepsilon }}^{I}$, and the other by deformations of $M$ sets of joints, ${\mathbf{d\varepsilon }}^{J}$. Thus,

Fig. 1

Configuration of multi-sets of ubiquitous joints in a rock mass. a Three parameters, strike $\beta$, dip $\gamma$ and spacing $S$, allocate the spatial configuration of each joint set. b Configuration of a 3-D rock mass with unit length in all sides and containing the $\alpha$th joint set for a particular set of joints considered. A local coordinate for each joint set is defined. c Deformation in the XZ-plane associated with deformation of the $\alpha$th joint set (Wang and Huang 2009) (color figure online)

$${\mathbf{d\varepsilon }} = {\mathbf{d\varepsilon }}^{I} + {\mathbf{d\varepsilon }}^{J} $$

(1)

Before the applied load reaches peak-strength, ${\mathbf{d\varepsilon }}^{I}$ can be expressed in terms of the compliance matrix of intact rock ${\mathbf{C}}^{I}$, as.

$${\mathbf{d\varepsilon }}^{I} = {\mathbf{C}}^{I} {\mathbf{d\sigma }} $$

(2)

To derive ${\mathbf{d\varepsilon }}^{J}$, an individual joint plane, the α-th set among $M$ sets of joints, is considered first. Corresponding to this particular set of joints, the three axes of local coordinates (n, s, and t), as shown in Fig. 1b, are set to be (1) the unit inward normal vector, n, (2) the orientation of strike, s, and (3) the third direction, t, which is determined by the right-hand rule.

Local deformation on joint plane ${\mathbf{d\delta }}^{\alpha }$ caused by incremental stress ${\mathbf{d\sigma }}$ is related to the constitutive relation ${\mathbf{D}}^{\alpha }$ as.

$${\mathbf{d\delta }}^{\alpha } = {\mathbf{D}}^{\alpha } {\mathbf{L}}^{\alpha } {\mathbf{B}}^{\alpha } {\mathbf{d\sigma }} $$

(3)

where ${\mathbf{D}}^{\alpha } = \left[ {{\mathbf{D}}_{ij} } \right]$, D _ij (i,j = n,s,t) is the element of the compliance matrix associated with the α-th joint plane. The transformation matrix, ${\mathbf{L}}^{\alpha }$, is composed of directional cosines between local coordinates (n ^α, s ^α, and t ^α) and global coordinates (X, Y, and Z). The ${\mathbf{B}}^{\alpha }$ is a matrix representing the area projection of the α-th joint plane onto the Y–Z plane, Z-X plane, and X–Y plane. The local deformation on joint plane ${\mathbf{d\delta }}^{\alpha }$ can also be expressed in terms of deformation in the global coordinate, ${\mathbf{du}}^{\alpha }$, through a further transformation as.

$${\mathbf{du}}^{\alpha } = {\mathbf{L}}^{\alpha T} {\mathbf{D}}^{\alpha } {\mathbf{L}}^{\alpha } {\mathbf{B}}^{\alpha } {\mathbf{d\sigma }} $$

(4)

Equation (4) describes global deformation associated with a single joint plane α with an inward unit normal n ^α = $(n_{x}^{\alpha } ,n_{y}^{\alpha } ,n_{z}^{\alpha } )$ caused by the small increment of stress ${\mathbf{d\sigma }}$, where $n_{x}^{\alpha }$, $n_{y}^{\alpha }$ and $n_{z}^{\alpha }$ represent the area projection of the α-th joint plane onto the Y–Z plane, Z-X plane, and X–Y plane, respectively.

If the considered joint set has a spacing of $S^{\alpha }$, the apparent frequency in a unit length in the X-axis direction should be $n_{x}^{\alpha } (1)/S^{\alpha }$ (Fig. 1c). Consequently, for a unit volume of the rock mass subjected to incremental stress, deformation of the total $M$ sets of joints ${\mathbf{d\varepsilon }}^{J}$ can be derived as.

$${\mathbf{d\varepsilon }}^{J} = \sum\limits_{\alpha = 1}^{M} {\frac{1}{{S^{\alpha } }}{\mathbf{T}}^{\alpha T} {\mathbf{D}}^{\alpha } {\mathbf{T}}^{\alpha } } {\mathbf{d\sigma }} $$

(5)

Equation (5) can be rewritten as ${\mathbf{d\varepsilon }}^{J} = {\mathbf{C}}^{J} {\mathbf{d\sigma }}$, where ${\mathbf{C}}^{J} = \sum\limits_{\alpha = 1}^{M} {\frac{1}{{S^{\alpha } }}{\mathbf{T}}^{\alpha T} {\mathbf{D}}^{\alpha } {\mathbf{T}}^{\alpha } }$ represents the compliance matrix of all joint sets, and ${\mathbf{T = LB}}$.

The overall average strain of a rock mass can be calculated by Eqs. (1), (2) and (5). When this representative volume of a rock mass is infinitively small, the joints become ubiquitous. Notably, the jointed rock is regarded as a homogenized medium in the macroscopic scale, and interactions between joints are currently neglected (Wang 2003; Wang and Huang 2009). Nevertheless, deformation preserves the anisotropic nature induced by the existence of joints in a rock mass, as in Eq. (5).

2.1.2 Failure modes and strength criteria

For a specific representative volume element, three failure modes are considered and incorporated into the adopted model (Wang 2003; Wang and Huang 2009); these three failure modes are (1) tensile failure of intact rock, (2) shear failure of intact rock and (3) joint sliding.

The conventional Mohr–Coulomb failure criterion with peak friction angle, $\phi_{p}$, peak cohesion, $c_{p}$ and tensile strength, ${\varvec{\sigma}}_{t}$, of intact rock is adopted as the failure criterion for intact rock. Barton’s empirical formula (Barton et al. 1985) is used to estimate the shear strength of joint plane and as the failure criterion of joint sliding through three parameters–joint roughness coefficient, JRC, uni-axial compressive strength of a joint wall, JCS, and its basic friction angle, $\phi_{b}$.

The applied stress state dominates the failure mode of a rock mass. Prior to failure, existing stress ${\varvec{\sigma}}$ is updated by adding $\bf d\sigma$ computed from the previous loading step. The updated stress state is checked to determine whether it reaches the failure criteria in turn. Additionally, tensile normal stress leads to joint opening, which cannot sustain tension, and the local stress will be redistributed to the surrounding rock mass.

Following the above-mentioned processes, either intact rock failure or joint sliding failure along any joint set can be identified, and, accordingly, the strength of the rock mass can then be determined. Once failure mode is determined the corresponding post-peak deformation can be determined, as in the following section.

2.1.3 Deformation of Intact Rock and the Joint System

The stress–strain relationship of intact rock before and after failure can be respectively described by Eq. (2) and plasticity theories. If strain softening or hardening occur, the plasticity normality rule can be used to describe the development of the yield/failure surface. These methods are adopted in the model used.

For each set of joints, three independent elements (D _ss , D _ns and D _nn ) of the compliance matrix are considered. Four terms, D _st , D _ts , D _sn , and D _tn , represent deformation in one direction induced by stress acting in another direction and are ignored. Roughness in the s -direction and t-direction are assumed the same, i.e. D _ss  = D _tt and D _ns  = D _nt .

Element D _nn represents normal deformation induced by normal stress and equals the reciprocal of normal stiffness $k_{nn}$. The empirical relation, which utilizes initial normal stiffness $k_{ni}$ and maximum closure $u_{n}^{m}$, proposed by Bandis et al. (1983) are utilized to determine D _nn under various stress state. Element D _ss represents shear deformation induced by shear stress and equals the reciprocal of shear stiffness $k_{ss}$. The mobilization of the JRC during shearing, proposed by Barton et al. (1985), is used to determine D _ss corresponding to various shearing levels. For sake of simplicity, the adopted variation of the JRC can be mobilized as soon as shear displacement occurs (Wang and Huang 2009). Additionally, we assume shear stiffness during the unloading and reloading stages is twice that in the initial condition. Element D _ns represents normal deformation induced by shear stress; thus, shear dilatancy reported by Barton et al. (1985) is adopted.

Remarkably, only element D _ss involves post-peak deformation. Furthermore, deformation behaviors adopted in the model are mainly based on published results and commonly used in engineering practice. The model combines these behaviors, such that a sophisticated deformation model capable of describing anisotropic pre- and post-peak deformation and strain softening/hardening is accordingly adopted to investigate anisotropic deformation of a circular tunnel that is excavated in a rock mass containing sets of ubiquitous joints.

2.1.4 Numerical Implementation

Wang and Huang (2009) incorporated the above-mentioned constitutive model for a two-dimensional rock mass into a subroutine for the explicit finite difference software program, FLAC. Through the numerical implementation, the adopted constituted model can be utilized to simulate a practical engineering task in a rock mass containing sets of ubiquitous joints with the following features.

• (1) The failure modes corresponding to stress conditions, which inherently determine anisotropic strength, can be selected automatically.

• (2) The major properties of joints, such as closure, shear and the associated dilatancy of joints, can be considered in the stress–strain relationship.

• (3) The progressive failure, which results in strain softening of a rock mass, can be described in post-peak deformation.

The numerical implementation for the adopted constitutive model has been verified through a series of comparisons between its predictions to the results of existing models and laboratory experiments via one single element (Yang et al. 1998). To further validate its applications to rock engineering and to illustrate the features of the adopted methodology, failure mode and anisotropy of mechanical behavior of jointed rock–based on the laboratory physical test by Yang et al. (1998), which in fact represented a two-dimensional jointed rock mass with one or two non-orthogonal joint sets–are simulated and discussed in the following section.

2.2 Characteristics of Used Methodology

Table 1 summarizes the mechanical parameters of the intact rock and joints that comprise the jointed rock. Input parameters of these artificial intact rocks are reduced due to scale effects (Wang 2003; Wang and Huang 2009; Yang et al. 1998). Numerical simulation adopts 10 × 24 (horizontal by vertical) elements to simulate physical model tests. The numerical model is fixed vertically in its lower boundary and horizontally in its central bottom, and is loaded from its top boundary by constant vertical downward displacement.

Table 1 Mechanical parameters obtained by Yang et al. (1998) and associated input parameters used for characterizing features of the adopted methodology

Figure 2a shows the variation in strength, expressed in terms of $\sigma_{{1{\text{f}}}}$, corresponding to different dip angles obtained by the adopted model and experimentally. Numerical simulation results show that the strength of rock mass varies significantly with joint dip and exhibits anisotropy. The predicted strengths are consistent with physical model test results, and differences between test and simulation results are less significant than test variations.

Fig. 2

Comparison of shear strength a and failure modes b between model tests (Yang et al. 1998) and prediction results. Results of physical model tests, indicated by hollow symbols in a, show that failure modes and corresponding shear strength of rock mass vary markedly with joint dip and, thus, exhibit anisotropy. The prediction results, marked by solid symbols in a and with distinct colors in b, are consistent with tendencies obtained experimentally (color figure online)

Figure 2b shows failure modes for rock masses with various joint dips subjected to uni-axial compressive loading. Failure modes are illustrated when each rock mass surpasses its peak-strength. Furthermore, the failure modes should be interpreted in a lump specimen instead of any particular element, since the numerical model contains 240 elements. The intact rock failure mode is observed for rock masses containing joint dips of 0°, 15°, 30° and 90°, and joint sliding failure mode is observed for rock masses with joint dips of 45°, 60° and 75°, which are consistent with physical model test results.

The deformation of rock masses is also anisotropic and varies with joint dip. Figure 3a compares the pre-peak tangential deformation modulus at half peak strength, E ₅₀, determined from physical model tests and numerical simulations. Simulation results are consistent with experimental results. Figure 3b shows the deformed shapes of the rock mass with various joint dips. These deformed shapes are illustrated when each rock mass reaches its approximate peak strength. Joint-induced anisotropic deformations, even under intact rock failure conditions, are observed, except for rock masses with a joint plane perpendicular to or parallel to the loading direction, i.e. dip angle of 0° or 90° for the vertically loaded case. Furthermore, since the shear strength of joint is far less than that of the intact rock, joint sliding occurs rapidly when angles between joint dips and the applied load are small. As a result, deformations of the rock masses with joint sliding failure mode at peak strength are smaller than those under intact rock failure modes.

Fig. 3

Comparison of pre-peak deformation from model test (Yang et al. 1998) and prediction results. a The pre-peak tangential deformation modulus at half peak strength of a rock mass from physical model tests, marked by hollow symbols, varies markedly with joint dip and exhibits anisotropy. The prediction results, marked by solid symbols, are consistent with the tendency obtained experimentally. b The deformed shapes for the rock mass with various joint dips while each reaches its peak strength approximately (color figure online)

Figure 4 shows the complete stress–strain behavior the rock mass predicted by the adopted methodology. The changes to failure modes during the post-peak stage are also given. The stress–strain curves are concave when the stress level is low, which is a direct result of joint closure. As loading stress approaches peak strength, these curves display interesting phenomena.

Fig. 4

Comparison of complete stress–strain behavior from model test (Yang et al. 1998) and prediction results. a Complete stress–strain curve. b, c and d are failure modes and associated variation in the post-peak stage ($\varepsilon_{1}$= 1.0$\varepsilon_{{1{\text{f}}}}$,1.5$\varepsilon_{{1{\text{f}}}}$, and 2.0$\varepsilon_{{1{\text{f}}}}$) for rock masses containing joint set with dips of 0°, 30° and 60° (color figure online)

For example, in the case of a rock mass with a joint dip of 0°, intact rock failure occurs and intact rock stiffness controls corresponding stress–strain curve after joint closure. When peak strength is exceeded, a significant decline in strength occurs due to loss of intact rock strength resulting from strain softening behavior. At peak strength, with vertical strain defined as $\varepsilon_{{1{\text{f}}}}$, failure mode of elements in the rock mass indicate that intact rock failure is generally distributed randomly throughout the specimen (Fig. 4b). When the rock mass is continuously loaded by vertical downward displacement to an axial strain of approximately 1.5$\varepsilon_{{1{\text{f}}}}$, intact rock failure spreads all over the specimen. Furthermore, the elements indicating intact rock failure with just plastic flow occurring aggregate into a cross band in the central part of the specimen. Thus, the specimen bulges. The cross band composed of elements indicating intact rock failure with plastic flowing then gradually change into an inclined band as loading is applied continuously, resulting in asymmetrical lateral deformation of the specimen when axial strain is approximately 2.0$\varepsilon_{{1{\text{f}}}}$.

In the case of a rock mass with a joint dip of 60°, joint sliding failure mode controls strength and, thus, deformation behavior of the joint controls global deformation, in which stiffness decrease progressively before peaking. At peak strength, joint sliding failure mode occurs in most elements (Fig. 4d). The failure mode does not change until axial strain reaches approximately 2.0$\varepsilon_{{1{\text{f}}}}$. Nevertheless, specimen anisotropic deformation increase as continuous loading increases.

In the case of a rock mass with a joint dip of 30°, intact rock failure occurs at peak strength (Fig. 4c). Intact rock stiffness controls the stress–strain curve after the closure of joints; strain softening behavior of intact rock then dominates the stress–strain curves in the early post-peak stage. However, as applied loading continues in the post-peak stage, stress-redistribution due to intact rock plasticity changes the failure mode, i.e. failure mode gradually transforms from intact rock failure into joint sliding failure. With axial strain of approximately 2.0$\varepsilon_{{1{\text{f}}}}$, an inclined band with elements indicating joint sliding forms, instead of those indicating intact rock failure for the rock mass with a joint dip of 0°. Obviously, the deformation characteristics of a rock mass containing ubiquitous joint sets are strongly influenced by the corresponding failure modes and the mechanical behaviors of rock mass components.

3 Numerical Modeling

To investigate joint-induced anisotropic deformation of rock surrounding a tunnel, numerical simulations using the above constitutive model and associated numerical implementation are conducted to model a tunnel excavated from rock masses containing non-ubiquitous joint set, and one, two, and three ubiquitous joint sets.

3.1 Model Setting up

A circular tunnel with a radius of 5.0 m is considered. The numerical model adopts a mesh sized 160 × 160 m with roller boundaries to minimize the influence of the boundary effect. The element size near the tunnel is 0.8 × 0.8 m. The rock mass has a unit weight of 25 kN/m³. We assume overburden is 400 m and the stress state is hydrostatic, i.e. both horizontal stresses, $\sigma_{xx}$ and $\sigma_{zz}$, equal vertical stress,$\sigma_{yy}$.

Rock masses composed of medium-strength intact rock and various ubiquitous joint sets are considered. Table 2 summaries the mechanical parameters for intact rock and the joint plane as well as attitudes and geometrical properties of the various joint sets. For sake of simplification, the mechanical behaviors of the joint plane are set the same for all conditions. Full face excavation of the tunnel is simulated. The tunnel is supported by 0.1-m-thick shotcrete as soon as surrounding rock deformation reaches 0.05 m. Table 2c lists the mechanical parameters of the tunnel support.

Table 2 Input parameters for the investigation of joint-induced anisotropic deformation surrounding a tunnel

3.2 Simulation Results

Figure 5 shows the failure zones surrounding a tunnel in rock masses containing various sets of ubiquitous joints. For a rock mass containing no joint set, only intact rock failure can occur. The failure zones size approximate 0.8–1.2 m surround the tunnel symmetrically, expect have rectangular mesh-induced edges and corners (Fig. 5a). For a rock mass containing one joint set, the failure zone is about 0.8 m larger in upper right and lower left area than that with no joint set (Fig. 5b). Moreover, the failure mode in these areas, the upper right and lower left area, is mainly joint sliding, not intact rock failure mode that occurred in another areas as the same as that with no joint set. For the well-known stress variation caused by tunnel excavation, stress decreasing in the radial component and increasing in the tangential component, decrease the shear strength of joint planes with a dip of 30°, leading to joint sliding in the aforementioned areas, since normal stress for these joints is reduced, and the shear stress acting on these joints is increased. The adopted methodology determines the failure modes of a rock mass automatically and describes their distribution surrounding a tunnel with significant physical meaning.

Fig. 5

Excavation-induced failure zones surrounding a tunnel for rock masses containing various sets of ubiquitous joints. a For a rock mass containing no joint set, the zone of intact rock failure surrounding a tunnel is symmetrical with thicknesses of 0.8–1.2 m. b For a rock mass containing one joint set with a dip of 30°, joint sliding induces further failure in the upper right and lower left areas surrounding the tunnel in addition to another intact rock failure zone, generating an anisotropic failure zone. c For a rock mass containing two joint sets with dips of 30° and −30°, joint sliding induced failure influences reciprocally and results in a large anisotropic failure zone. d For a rock mass containing three joint sets with dips of 30°, 0° and −30°, the failure zone tends to be well-distributed as strength and deformation anisotropy is reduced significantly (color figure online)

For a rock mass containing two joint sets, stress variations corresponding to joint sliding for these two joint sets deteriorate each other, resulting in very large failure zones in the area of the joint planes parallel to tunnel walls (Fig. 5c). For a rock mass containing three joint sets, the anisotropies of strength and deformation are markedly reduced; the failure zones tend to be well-distributed than those of a rock mass containing two joint sets (Fig. 5d).

Figure 6 compares the rock deformations surrounding a tunnel. For comparisons, normalized radial strain is utilized and defined as radial displacement divided by distance to the tunnel center from each point. For a rock mass containing no joint set, normalized radial strain is uniformly and circularly distributed with a maximum magnitude of approximately 0.012 along the tunnel wall (Fig. 6a). For a rock mass containing one joint set, the normalized radial strain exhibits anisotropy and is obviously increased in the upper right and lower left areas, i.e. the areas where joint sliding occurs, with a maximum of approximately 0.018 (Fig. 6b). The normalized radial strain in the upper left and lower right areas is very close to that of a rock mass containing no joint set.

Fig. 6

Excavation-induced normalized radial strain surrounding a tunnel for rock masses containing various sets of ubiquitous joints. a For a rock mass containing no joint set, strain is distributed uniformly and circularly with a maximum magnitude of about 0.012. b For a rock mass containing one joint set, strain exhibits anisotropy and is increased in the upper right and lower left areas with a maximum of 0.018. c For a rock mass containing two joint sets, strain exhibits high anisotropy with a maximum exceeding 0.028 in the top left and right down areas. d For a rock mass containing three joint sets, the anisotropy of strain decreases markedly and maximum strain along the tunnel wall is 0.020 (color figure online)

For a rock mass containing two joint sets, normalized radial strain has a highly anisotropic distribution with a maximum exceeding 0.028 along the tunnel wall in the top left and right down directions (Fig. 6c). The mutual influence of the two joint sets with joint sliding failure mode accounts for this significant convergence. For a rock mass containing three joint sets, anisotropy of deformation decreases obviously (Fig. 6d). However, normalized radial strain increases with a peak of 0.020 along the tunnel wall. Compared with that of a rock mass containing no joint set, joint closure, shear displacement, and dilatancy clearly contribute to the increases in deformation. Notably, maximum normalized radial strain is less than that of a rock mass containing two joint sets, but the area with a normalized radial strain exceeding 0.005 is increased. The three well-distributed joint sets existing in the rock mass provide more flexibility, accommodating the excavation-induced stress–strain redistribution and reducing deformational anisotropy, with a tradeoff instead of increasing the size of the influenced area.

Figure 7 shows the displacement of surrounding rock along a tunnel wall. The abscissa $\theta$ is measured clockwise from the tunnel vault. Figure 7a shows the defined displacement vector ${\mathbf{u}}$ and the magnitudes of its radial component, $u_{r}$, and tangential component, $u_{\theta }$. For a rock mass containing no joint set, both $u_{r}$ and $u_{\theta }$ are distributed uniformly, except for minor variations caused by the rectangular mesh; thus, rock deformation surrounding a tunnel is isotropic. For a rock mass containing one joint set, $u_{r}$ has two peaks at $\theta$ of 30° and 210°, where the joint plane is just parallel to tunnel periphery tangents. Joint sliding induces additional 30-mm displacements than that at other locations without sliding failure, resulting in obvious anisotropic deformation of the tunnel wall. The peaks of $u_{\theta }$ occur when $\theta$ is approximately 0° and 180°, which are roughly 30° away from the $u_{r}$ peaks. The asymmetrical shear deformation caused by joint sliding neighboring to the locations with peak $u_{r}$, i.e. $\theta$ is 30° or 210°, accounts for these gaps.

Fig. 7

Displacement of surrounding rock along a tunnel wall for rock masses containing various sets of ubiquitous joints. a The definition of $\theta$. b Magnitude of the radial component of the displacement vector. c Magnitude of the tangential component of the displacement vector (color figure online)

For a rock mass containing two joint sets, four locations exist where joint planes are parallel to tunnel periphery tangents, i.e. $\theta$ is 30° and 210° for the first joint, and 150° and 330° for the second joint set. However, both the $u_{r}$ and $u_{\theta }$ peaks appear at locations where $\theta$ is 120° and 300° due to the synergistic effect associated with shear deformation caused by the sliding of the two joint sets. For a rock mass containing three joint sets, the locations of $u_{r}$ and $u_{\theta }$ peaks appear are similar to those of a rock mass containing two joint sets; however, both $u_{r}$ and $u_{\theta }$ peaks are much less in magnitude. Again, the flexibility provided by additional joint sets accommodating the stress–strain redistribution accounts for this phenomenon.

The existence of joints induces anisotropic deformation of rock surrounding a tunnel, and changes the ambient stress distribution. Figure 8 shows variations in the radial stress component and tangential stress component with distance to the tunnel center r, where $\theta$ is 0° and the additional deformation caused by joint sliding is moderate. The typical stress redistributions induced by excavating a tunnel in a rock mass containing various joint set(s), i.e. decreasing radial stress and increasing tangential stress, are similar as those of a rock mass containing no joint set. In the region r >7.5 m, where the rock masses remain elastic for all conditions, the radial stress distribution of rock masses containing three joint sets resembles that of the condition with no joint set, which is generally isotropic. However, the radial stress distribution for rock masses containing one or two joint sets strays from the isotropic condition, and have greater (negative) magnitudes as excavation-induced stress variation tends to increase normal stress and decrease shear stress on nearby joint planes, which mobilizes the JRC and shear strength; increasing shear strength of the joint while the stress–strain redistribution is complete. As the locations of rock masses approach the boundaries of the elastic and plastic regions, the radial stress component tends to be less different than each other because the stress state for all cases must match one of the two failure criteria, i.e. the Mohr–Coulomb criterion for intact rock failure or the modified Barton’s empirical formula for joint sliding. In the failure zone neighboring the tunnel wall, both radial and tangential stresses differ significantly. This results in various support stresses at particular positions along a tunnel wall.

Fig. 8

Variation in the radial stress component a and tangential stress component b with the distance to the tunnel center at $\theta$ is 0° (color figure online)

Figure 9 shows variations in the radial stress component and tangential stress component with distance to the tunnel center, where $\theta$ is 120° and there is generally additional deformation caused by joint sliding. In the elastic region roughly 12 m from the tunnel center, tangential stresses in all cases are generally similar, but radial stress of rock masses containing one or two joint sets deviates from the isotropic condition, and have small magnitudes as the adopted Barton’s empirical formula for joint sliding tends to have less shear strength than peak strength. In the plastic region neighboring the tunnel wall, radial stress is typically close to each supporting stress, and the difference in radial stress for all case is getting small. The radial stresses are greater (negative) than those when $\theta$ is 0° (Fig. 8a). Moreover, the distribution of tangential stresses differs from that conditions with $\theta$ of 0° owing to various thicknesses of plastic regions and largely joint-sliding-induced anisotropic deformation (Fig. 8b).

Fig. 9

Variation in the radial stress component a and tangential stress component b with the distance to the tunnel center at $\theta$ is 120° (color figure online)

4 Discussion

This study now discusses the main factors, including joint orientation, joint strength, tunnel overburden, and the ratio of horizontal to vertical components of in situ stress, affecting joint-induced anisotropic deformation of rock surrounding a tunnel.

4.1 Influence of Joint Orientation

To investigate the influence of joint orientation on surrounding deformation, this study simulates a tunnel excavated in rock masses containing two joint sets with dip angles of 15°/−15°, 30°/−30°, and 45°/−45°. The adopted mechanical parameters and installation time of support, as well in situ stresses, are the same as those mentioned in Sect. 3.1.

Figure 10 shows the radial and tangential displacements along a tunnel wall in rock masses with various joint orientations. For joint sets with a small included acute angle, such as 30° for the case with dip angles of 15°/−15°, the joint-induced anisotropic deformation remains minor. Maximum tangential displacement is 30 mm when $\theta$ is 210°, and radial displacements along the tunnel remain similar. The pre-peak joint displacement contributes only slightly to tunnel surrounding rock deformation, neither does local joint sliding induced by tunnel excavation. As the acute angle of joint sets increases, anisotropic deformation increases. For the case with dip angles of 30°/−30°, both the radial and tangential displacements at $\theta$ near 120° and 300° have local maximums with magnitudes roughly twice those at farther locations. Displacement resulting from joint sliding caused by tunnel excavation dominates surrounding rock deformation. When joint sets have an included angle of 90°, radial displacements dramatically increase when $\theta$ values nearby are 90–180° and 270–360° and tangential displacements increase when $\theta$ values nearby are 0°, 100°, 170° and 270° due to joint sliding. The shear stress in one joint set, which must decrease due to post-peak shear weakening described by the adopted failure criterion of the joint plane, is the normal stress of the other joint set. The decrease in normal stress further reduces shear strength of the joint set. As such, joint sets with an included right angle lead to mutual deterioration after joint sliding, which also accounts for the significant anisotropic deformation in an initially biaxial symmetrical medium.

Fig. 10

The displacement of surrounding rock along a tunnel wall for rock masses containing various joint orientations. a Magnitude of the radial component. b Magnitude of tangential component (color figure online)

4.2 Influence of Joint Strength

A tunnel excavated in a rock mass containing two joint sets with dip angles of 30°/−30° and various joint strengths is simulated to investigate the influence of joint strength on anisotropic deformation. The input parameters are the same as those for the rock mass in Sect. 3.1, except that combinations of the JRC and $\phi_{b}$ are changed to 20° and 43°, 16° and 38°, 12° and 33°, and 8° and 28° representing high, medium, moderate and low joint shear strength, respectively.

Figure 11 shows the radial and tangential displacements of surrounding rock along a tunnel wall in rock masses with various joint strengths. For the rock mass containing joint sets with high shear strength, tunnel excavation causes spares joint sliding, results in minor anisotropic deformation. As joint strength dies down, the area of excavation-induced joint sliding increases in size and give rise to the anisotropic deformation. For the rock mass containing joint sets with moderate shear strength, tunnel excavation induces joint sliding when $\theta$ is 120° and 300° approximately, which cause anisotropic deformation of tunnel surrounding rocks. When joint strength is less than the moderate condition, such as $JRC$ is 8 and $\phi_{b}$ is 28°, the areas of joint sliding around the tunnel wall connect. Tunnel surrounding deformation is then anisotropic and huge, and support failure and subsequent tunnel collapse likely occur.

Fig. 11

Displacement of surrounding rock along a tunnel wall at various joint strengths. A rock mass containing two joint sets with dip angles of 30°/−30° is considered. a Magnitude of the radial component. b Magnitude of the tangential component (color figure online)

4.3 Influence of Overburden and Ratio of Horizontal to Vertical Stress

A tunnel excavated in a rock mass containing two joint sets with dip angles of 30°/−30° with moderate joint shear strength is adopted to investigate the influence of overburden on anisotropic deformation. Overburden in simulations is 200, 400 and 600 m, and in situ horizontal stress equals vertical stress in each case.

Figure 12 shows the radial and tangential displacements along a tunnel wall in rock masses with various overburdens. The magnitudes of radial components of displacement vectors increase at all location on the tunnel wall while tunnel overburden increases. The ratios of maximum to minimum radial components decrease from 2.5 for a 200-m overburden to 2.0 for a 600-m overburden (Fig. 12a). Nevertheless, the magnitudes of tangential components of displacement vectors remain similar for various overburdens (Fig. 12b). Since the tangential components mainly result from joint deformation, these simulating results indicate that no further joint sliding occurs as overburden increase, also implying that for hydrostatic stress conditions, anisotropic deformation of tunnel surrounding rock tends to reduce slightly as overburden increase.

Fig. 12

Displacement of surrounding rock along a tunnel wall for various overburdens. a Magnitude of the radial component. b Magnitude of the tangential component (color figure online)

For the influence of horizontal stress, the ratios of horizontal to vertical stress ($\sigma_{xx} /\sigma_{yy}$) of 0.5, 1.0, and 2.0 are simulated while keeping the first stress invariant constant. Figure 13 shows displacement along a tunnel wall. Both the radial and tangential components are increased significantly due to non-hydrostatic in situ stress. Furthermore, tangential displacement has both positive and negative values instead of always being positive for the hydrostatic condition. These distributions mean that the displacement vectors along a tunnel wall may point in a specific direction inside the tunnel at some locations, and to various directions at other locations, resulting in joint opening and potential tunnel instability. Simulating results indicate that the ratio of horizontal to vertical components of in situ stress can lead to many failure zones surrounding a tunnel, especially that caused by post-peak joint sliding, resulting in considerable anisotropy of deformation.

Fig. 13

Displacement of surrounding rock along a tunnel wall for various ratios of horizontal to vertical in situ stress. a Magnitude of the radial component. b Magnitude of the tangential component (color figure online)

5 Conclusions

Via a constitutive model for a rock mass containing sets of ubiquitous joints and the associated numerical implementation proposed by Wang and Huang (2009), this study validates its application to rock engineering and applies to simulate deformation surrounding a circular tunnel. Simulation results indicate that anisotropic deformation of a tunnel excavated in rock masses is mainly due to closure, shear and dilation deformations of ubiquitous joint sets; particularly, post-peak shear deformation after joint sliding failure. The inherent stress variation caused by tunnel excavation, decreasing in the radial direction and increasing in the tangential direction, decrease shear strength of joints in areas where joint planes are tangential to tunnel wall, leading to joint sliding and considerable shear deformation.

Joint sliding conditions caused by two distinct joint sets may deteriorate reciprocally and generate a large failure zone. Nevertheless, for a rock mass containing three well-distributed joint sets, joint sliding in various joint sets and associated stress variations can balance each other, resulting in less anisotropic deformation than that of rock masses containing one or two joint sets. Furthermore, joint orientation, joint strength, tunnel overburden, and the ratio of horizontal to vertical components of in situ stress affect the anisotropy of deformation surrounding a tunnel. Additionally, the degree of anisotropy depends strongly on the extent of joint sliding failure.