Multi-Region Boundary Element Analysis for Coupled Thermal-Fracturing Processes in Geomaterials

Abstract

This paper describes a boundary element code development on coupled thermal–mechanical processes of rock fracture propagation. The code development was based on the fracture mechanics code FRACOD that has previously been developed by Shen and Stephansson (Int J Eng Fracture Mech 47:177–189, 1993) and FRACOM (A fracture propagation code—FRACOD, User’s manual. FRACOM Ltd. 2002) and simulates complex fracture propagation in rocks governed by both tensile and shear mechanisms. For the coupled thermal-fracturing analysis, an indirect boundary element method, namely the fictitious heat source method, was implemented in FRACOD to simulate the temperature change and thermal stresses in rocks. This indirect method is particularly suitable for the thermal-fracturing coupling in FRACOD where the displacement discontinuity method is used for mechanical simulation. The coupled code was also extended to simulate multiple region problems in which rock mass, concrete linings and insulation layers with different thermal and mechanical properties were present. Both verification and application cases were presented where a point heat source in a 2D infinite medium and a pilot LNG underground cavern were solved and studied using the coupled code. Good agreement was observed between the simulation results, analytical solutions and in situ measurements which validates an applicability of the developed coupled code.

1 Introduction

With increasing concerns about environmental issues related to the mining and energy sectors worldwide, the field of rock mechanics is being advanced and widened to address the complex behavior of mechanical, thermal, and hydraulic responses of rocks. Over the past several decades, coupled mechanical–thermal–hydraulic processes in rock masses have been a focus of research, particularly in the field of underground nuclear waste disposal, and significant advances have been achieved (Min et al. 2005; Rutqvist et al. 2005; Tsang et al. 2005). However, the past studies have mostly treated the rock mass as a continuum or a discontinuum with predefined discontinuities. The process of explicit rock fracturing, which is the dominant mechanism in hard rock failure, has not been adequately addressed during the simulation of complex coupled processes. Understanding and predicting the effects of the interactive processes between explicit rock fracturing, temperature change and fluid flow (coupled fracturing (F)–thermal (T)–hydraulic (H) processes) remain to be a key challenge for industries such as geothermal energy extraction, geological CO₂ sequestration, underground LNG storage, and deep geological disposal of nuclear waste.

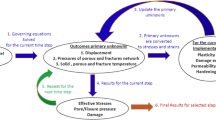
In a fractured rock mass, rock fracturing, fluid flow and rock temperature change are closely correlated (Fig. 1). Rock fractures will enhance the fluid flow by creating new flow channels, whereas the fluid pressure may stimulate fracture growth. Uneven temperature change in rock mass will result in the thermal stress in the rock mass which could lead to fracture propagation. Coupling between these processes are necessary in order to study the above mentioned industrial issues.

Fig. 1

Interactions between rock fracturing, fluid flow and temperature change in rock masses

To deepen the knowledge on the above mentioned issues and to understand the coupled F–T–H processes in rocks in an engineering scale, we developed a numerical tool that is based on boundary element code, FRACOD which has been previously developed by Shen and Stephansson (1993) and FRACOM (2002) and simulates complex fracture propagation in rocks governed by both mode I (tensile) and mode II (shear) mechanisms. FRACOD has been used to model the rock failure field testing in an engineering scale and was proven to be useful in predicting the brittle failure (Rinne et al. 2003), borehole breakouts (Shen et al. 2002; Klee et al. 2011; Barton 2007), stability of large shaft and galleries (Stephansson et al. 2003), pillar spalling (Rinne et al. 2003), fundamental creep behavior of rock samples (Rinne 2008).

For the coupled analysis, we newly implemented an indirect boundary element method, namely the fictitious heat source method to simulate temperature change and thermal stresses in rocks. This paper presents our first development of coupled F–T module in advance to fully coupled F–T–H code development and the verification as well as application cases studies using the developed coupled module were presented. In addition, engineering barriers such as concrete linings and insulation layers are often involved in boreholes and underground caverns in rocks. The coupled code was also extended to simulate multiple region problems where rock mass, concrete linings and insulation layers with different thermal and mechanical properties were present. It should be noted that the thermal coupling and multi-region functions described in this paper have been previously used by many other researchers for stress modeling of intact elastic body. This paper, however, focuses on the coupling of these functions with fracture propagation and hence presents a unique way to predict the complex rock fracturing processes.

2 Development of Coupled Thermal-Fracturing Boundary Element Code

A two-dimensional fracture propagation code, FRACOD developed by Shen and Stephansson (1993) and FRACOM (2002) was taken as a basic code to develop coupled thermal-fracturing boundary element code. FRACOD is capable of modeling explicit fracturing process in rocks which is based on the Displacement Discontinuity Method (DDM). The DDM is an indirect boundary element technique and is very convenient for representing fractures. The DDM has been actively used for fractures related problems since Crouch and Starfield (1983) and its numerical implementation into boundary element method was introduced in many previous publications (Guo et al. 1990; Shen and Stephansson 1993; Tan et al. 1998).

There are two kinds of approaches in boundary element technique: direct approach (direct boundary integration method) and indirect method. The direct method uses the reciprocal theorem and calculates boundary values (stress, displacement, and temperature) at a given boundary by solving a system of equations (Cheng and Detournay 1988). In the direct method, a discretization of time and spatial domain is required which makes the computational process complex (Rajapakse and Senjuntichai 1995).

For the benefit of coupling with FRACOD, we consider an indirect method to simulate the temperature distribution and thermal stresses due to internal and boundary heat sources. In the indirect method, fictitious heat sources with unknown strength over the boundary of domain are used, which is known to be easier to consider the problem with internal heat sources. The indirect approaches have been found efficient in modeling poro-elasticity (Jing 2003) and thermal-poroelasticity (Ghassemi and Zhang 2004) using boundary element methods.

2.1 Fundamentals for Thermo-Elasticity

The theory of thermo-elasticity incorporates the typical linear elastic constitutive equations and linear heat conduction for coupling the temperature and stress fields. The governing equations for the thermo-elasticity can be found in Timoshenko and Goodier (1970) which are briefly reviewed as follows.

2.1.1 Constitutive Equations

In isotropic thermo-elasticity, the constitutive equations can be separated into a deviatoric response and a volumetric one. The deviatoric response is given by ε _ij  = σ _ij /2G (i ≠ j) where ε _ij denotes the components of the deviatoric strain tensor, σ _ij denotes the components of the deviatoric stress tensor, and G is the shear modulus. The volumetric response of the solid contains thermal coupling terms as ε _kk = σ _kk/3 K + αT, where ε _kk is volumetric strain, σ_kk/3 is volumetric stress (mean stress), T is temperature. The constant K is the rock’s bulk modulus. α is the volumetric thermal expansion coefficient of the bulk solid under constant stress, which can also be written as a stress form as $\sigma_{ij} = 2G\varepsilon_{ij} + 2G\nu /(1 - 2\nu ){\kern 1pt} \varepsilon_{ij} \delta_{ij} + K\alpha T\delta_{ij}$ in which ν is Poisson’s ratio. δ _ij is Dirac delta function that represents unit concentrated sources.

2.1.2 Transport Laws

The heat flow is governed by Fourier’s law which is written as $q_{i}^{T} = - \kappa T_{i}$ where $q_{i}^{T}$ is the heat flux, κ ^Τ is the thermal conductivity.

2.1.3 Balance Laws

For local stress balance, the equilibrium equation in elasticity is used as σ _ij  = 0.

2.1.4 Field Equations for Thermo-Elasticity

From the constitutive, transport, and balance equations, the field equations can be derived for temperature T, and displacement u _i by Navier and diffusion equation.

Navier equation: $G\nabla^{2} u_{i} + \frac{1}{3}(G + 3K)\varepsilon_{i}^{{}} = K\alpha T_{i}$

Diffusion equation: $c\nabla^{2} T = \frac{\partial T}{\partial t}$

In the above equation, the constant c represents thermal diffusivity.

2.1.5 Fundamental Solutions

The two-dimensional fundamental solutions for temperature, stresses and displacements induced by a continuous point heat source in thermo-elasticity are given below (Zhang 2004).

$$ T = \frac{1}{4\pi k}Ei(\xi^{2} ) $$

(1)

$$ \sigma_{xx} = \frac{E\alpha }{24\pi k(1 - \nu )}\left\{ {\left( {1 - \frac{{2x^{2} }}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }} - Ei(\xi^{2} )} \right\} $$

(2)

$$ \sigma_{xy} = \frac{E\alpha }{24\pi k(1 - \nu )}\left\{ {\left( { - \frac{2xy}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }}} \right\} $$

(3)

$$ \sigma_{yy} = \frac{E\alpha }{24\pi k(1 - \nu )}\left\{ {\left( {1 - \frac{{2y^{2} }}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }} - Ei(\xi^{2} )} \right\} $$

(4)

$$ u_{x} = \frac{\alpha (1 + \nu )}{4\pi k(1 - \nu )}r\left\{ {\frac{x}{r}\frac{{(1 - e^{{ - \xi^{2} }} )}}{{2\xi^{2} }} + \frac{1}{2}Ei(\xi^{2} )} \right\} $$

(5)

$$ u_{y} = \frac{\alpha (1 + \nu )}{4\pi k(1 - \nu )}r\left\{ {\frac{y}{r}\frac{{(1 - e^{{ - \xi^{2} }} )}}{{2\xi^{2} }} + \frac{1}{2}Ei(\xi^{2} )} \right\} $$

(6)

where T is the temperature (°C), σ _xx , σ _xy , and σ _yy are the stresses (Pa), u _x and u _y are the displacements (m), α is the linear thermal expansion coefficient (1/°C), k is the thermal conductivity (W/m °C), c is the thermal diffusivity (m²/s), ρ is the density (kg/m³), c _p is the specific heat capacity (J/kg °C), and $c = \frac{k}{{\rho c_{p} }}$ and $r = \sqrt {x^{2} + y^{2} } ,\xi^{2} = \frac{{r^{2} }}{4ct},Ei\left( u \right) = \int\nolimits_{u}^{\infty } {\frac{{e^{ - z} }}{z}{\text{d}}z}$ in the above equations.

Equations 1–6 constitute the fundamental equations to be used in all the formulations of the numerical process in this paper. Because FRACOD uses 2D line elements to represent problem boundaries, we will then need to consider a line heat source solution in an infinite medium. This can be done by integrating Eqs. 1–6 over the element length. In FRACOD the integration is done numerically using ten evenly distributed points along each line element.

The applicability of the developed code has been extended to the practical problems where point heat sources are also located inside the region concerned by implementing the formulation by Hemantiyan et al. (2011).

2.2 Fictitious Heat Source Method for Thermo-Elasticity

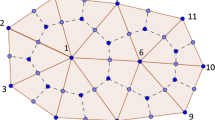
For an internal problem as shown in Fig. 2, the boundary of a finite body has been discretized into n elements. Before any boundary condition is considered, each element is assumed to be in an infinite, isotropic and homogeneous medium. Let’s consider that a constant line heat source with unit heat strength is placed along element j at time t ₀ = 0. At any given time t, the temperature, stresses and displacements at the centre point of another element (element i) is known based on the fundamental solutions given in Eqs. 1–6. Note that these equations are for a point source only. For a line source, the above equations need to be integrated over the entire length of element j. They are given below:

Fig. 2

Elements along a solid body boundary and local coordinate system of the boundary element

$$ T(j \to i) = \frac{1}{4\pi k}\int\limits_{ - a}^{a} {Ei(\xi^{2} ){\text{d}}x^{\prime } } $$

(7)

$$ \sigma_{x'x'} (j \to i) = \frac{E\alpha }{24\pi k(1 - \nu )}\int\limits_{ - a}^{a} {\left\{ {\left( {1 - \frac{{2x\prime^{2} }}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }} - Ei(\xi^{2} )} \right\}{\text{d}}x^{\prime } } $$

(8)

$$ \sigma_{x\prime y\prime } (j \to i) = \frac{E\alpha }{24\pi k(1 - \nu )}\int\limits_{ - a}^{a} {\left\{ {\left( { - \frac{2x'y'}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }}} \right\}{\text{d}}x^{\prime } } $$

(9)

$$ \sigma_{y\prime y\prime } (j \to i) = \frac{E\alpha }{24\pi k(1 - \nu )}\int\limits_{ - a}^{a} {\left\{ {\left( {1 - \frac{{2y^{\prime{2}} }}{{r^{2} }}} \right)\frac{{1 - e^{{ - \xi^{2} }} }}{{\xi^{2} }} - Ei(\xi^{2} )} \right\}{\text{d}}x^{\prime } } $$

(10)

$$ u_{x\prime } (j \to i) = \frac{\alpha (1 + \nu )}{4\pi k(1 - \nu )}\int\limits_{ - a}^{a} {r\left\{ {\frac{x'}{r}\frac{{(1 - e^{{ - \xi^{2} }} )}}{{2\xi^{2} }} + \frac{1}{2}Ei(\xi^{2} )} \right\}{\text{d}}x^{\prime } } $$

(11)

$$ u_{y\prime } (j \to i) = \frac{\alpha (1 + \nu )}{4\pi k(1 - \nu )}\int\limits_{ - a}^{a} {r\left\{ {\frac{y^\prime }{r}\frac{{(1 - e^{{ - \xi^{2} }} )}}{{2\xi^{2} }} + \frac{1}{2}Ei(\xi^{2} )} \right\}{\text{d}}x^{\prime } } $$

(12)

The integrations in Eqs. 7–12 need to be done numerically since a closed form solution is hard to obtain due to the existence of the exponential integral function Ei(ξ ²).

During the numerical integration, element j is divided into ten equal length segments. For each segment, the line heat source is assumed to have “shrunken” to a point source and the point source has the same total strength as the line source over the segment. Therefore, the entire line source over element j is represented by ten point sources evenly distributed over the element. For example, the temperature Eq. 7 is calculated numerically using

$$ T(j \to i) = \sum\limits_{k = 1}^{10} {T\left( {x_{k}^{\prime } ,y^{\prime } } \right)a/5} $$

(13)

where T($x_{k}^{\prime }$, y′) is the temperature at element i calculated from a point source at ($x_{k}^{\prime }$, y′) with strength of a/5. The coordinates of the ten points are given as ($x_{1}^{\prime }$, y′) = (−0.9a, 0), ($x_{2}^{\prime }$, y′) = (−0.7a, 0), ···, ($x_{10}^{\prime }$, y′) = (0.9a, 0).

The results in the above equations are presented for the local coordinates (x′, y′) of the element j as shown in Fig. 2. In the global coordinate system, they need to be transformed. Note that the temperature is independent of direction and hence is not affected by the coordinate transformation:

$$ T = T $$

$$ \begin{gathered} \sigma_{xx}^{ij} = \sigma_{{x^{\prime } x^{\prime } }}^{ij} \cos^{2} \theta - 2\sigma_{{x^{\prime } y^{\prime } }}^{ij} \sin \theta \cos \theta + \sigma_{{y^{\prime } y^{\prime } }}^{ij} \sin^{2} \theta \hfill \\ \sigma_{yy}^{ij} = \sigma_{{x^{\prime } x^{\prime } }}^{ij} \sin^{2} \theta + 2\sigma_{{x^{\prime } y^{\prime } }}^{ij} \sin \theta \cos \theta + \sigma_{{y^{\prime } y^{\prime } }}^{ij} \cos^{2} \theta \hfill \\ \sigma_{xy}^{ij} = (\sigma_{{x^{\prime } x^{\prime } }}^{ij} - \sigma_{y'y'}^{ij} )\sin \theta \cos \theta + \sigma_{{x^{\prime } y^{\prime } }}^{ij} (\cos^{2} \theta - \sin^{2} \theta ) \hfill \\ \end{gathered} $$

(14)

$$ \begin{gathered} u_{x} = u_{x}^{'}\cos \theta - u_{y}^{'}\sin \theta \hfill \\ u_{y} = u_{x}^{'}\sin \theta + u_{y}^{'}\cos \theta \hfill \\ \end{gathered} $$

Since the boundary values (stresses and/or displacements) of the boundary element i are often given in its shear and normal directions, the obtained stresses and displacements should be further transformed to the local co-ordinates of element i. After this process, the temperature, shear and normal stresses, and shear and normal displacements of element i, caused by a unit line heat source at element j are calculated.

In fictitious heat source method, we assume that a line source has been applied along each boundary element. The strength of these line sources are unknowns and need to be solved. The total temperature, stresses and displacements at element i due to the fictitious line sources can be calculated by super-positioning the effect of all individual heat sources as shown below:

$$ T^{i} = \sum\limits_{j = 1}^{n} {T^{ij} H^{j} } \;(t = t_{0} ) $$

(15)

$$ \sigma_{\text{s}}^{i} = \sum\limits_{j = 1}^{n} {\left( {A_{\text{ss}}^{ij} D_{\text{s}}^{j} + A_{\text{sn}}^{ij} D_{\text{n}}^{j} + F_{\text{s}}^{ij} H^{j} } \right)} \;(t = t_{0} ) $$

(16)

$$ \sigma_{\text{n}}^{i} = \sum\limits_{j = 1}^{n} {\left( {A_{\text{ns}}^{ij} D_{\text{s}}^{j} + A_{\text{nn}}^{ij} D_{\text{n}}^{j} + F_{\text{n}}^{ij} H^{j} } \right)} \;(t = t_{0} ) $$

(17)

$$ u_{\text{s}}^{i} = \sum\limits_{j = 1}^{n} {\left( {B_{\text{ss}}^{ij} D_{\text{s}}^{j} + B_{\text{sn}}^{ij} D_{\text{n}}^{j} + G_{\text{s}}^{ij} H^{j} } \right)\;(t = t_{0} )} $$

(18)

$$ u_{\text{n}}^{i} = \sum\limits_{j = 1}^{n} {\left( {B_{\text{ns}}^{ij} D_{\text{s}}^{j} + B_{\text{nn}}^{ij} D_{\text{n}}^{j} + G_{\text{n}}^{ij} H^{j} } \right)} \;(t = t_{0} ) $$

(19)

where H ^j is the strength of the line heat source at element j. T ^ij, A ^ij_ss , A ^ij_sn , A ^ij_ns , A ^ij_nn , B ^ij_ss , B ^ij_sn , B ^ij_ns , B ^ij_nn , F ^ij_s , F ^ij_n , G ^ij_s , G ^ij_n are ‘influence coefficients’, representing the temperature, stress and displacement at the centre of the element i due to a unit line source at element j. They are calculated based on the Eqs. 15–19. For example, the coefficient A ^ij_ns gives normal stress at the midpoint of the ith element ($\sigma_{\text{n}}^{i}$) due to a constant unit shear displacement discontinuity over the jth element ($D_{\text{s}}^{j}$ = 1).

Because the strength (H ^j) of the fictitious heat sources is only dependent upon the thermal boundary conditions, they can be solved using Eq. 15 only. If the temperature along the problem boundary is known, using Eq. 15, we will have n equations with n unknowns. The fictitious heat source strength along each element can then be obtained by solving the system of n equations. Their values can then be used in Eqs. 16–19 to solve the displacement discontinuities $D_{\text{s}}^{j}$ and $D_{\text{n}}^{j}$.

The thermal boundary condition is sometimes defined as heat flux rather than the temperature. In this case, we will need to use the flux equation below to replace Eq. 15 for temperature

$$ Q_{ij} = - k\frac{\partial T}{\partial n} = \frac{{(x_{i} - x_{j} )\cos \theta_{i} + (y_{i} - y_{j} )\sin \theta_{i} }}{{8\pi kt^{2} }}Ei(\xi^{2} ) $$

(20)

where Q _ij is the heat flux in the normal direction of element i due to a unit line source at element j and k is the thermal conductivity.

Other numerical process described before for temperature boundary conditions are also applicable to the flux boundary condition.

2.3 Time Marching Scheme for Transient Heat Flow

The solutions in the previous section have been confined to the cases that the heat sources and the boundary condition are constant over a period of the time t. Here we extend the solution using a time marching scheme to simulate the cases where either the heat source or boundary condition is changing during this period.

There are different approaches to temporal solution of the problem. One approach is solving the problem at the end of a time step and then using the results as the initial conditions for the next time step, marching forward in time. The disadvantage of this method is that it requires discretizing the spatial domain of the problem. The second approach is dividing the heat source into many sub-sources. The sub-sources start to take effect at different times, and hence allows for total strengths of heat source to vary with time. The final solution is the accumulated effect of all the sub-sources. This technique eliminates the need for internal discretization of the spatial domain. But it has the disadvantage that the coefficient matrix must be kept to be used as required.

The implementation of this time marching scheme is possible because it is the time interval between thermal loading and receiving that affects the response rather than the absolute times. This is the so-called ‘time translation’ property of the fundamental solutions. For example, the stress at a point x and time t due to a heat source taking place at point χ and at time τ is equal to the stress at point x and time t − τ due to a heat source occurring at time zero at the point χ. That is

$$ \sigma_{ij} \left( {{\bf{x}},t;\chi ,\tau } \right) = \sigma_{ij} \left( {{\bf{x}},t - \tau ;\chi ,0} \right). $$

(21)

Due to this property of the fundamental solutions, the evaluation time and loading time can be shifted along the time axis without affecting the values of the fundamental solutions. Therefore, the influence coefficient can be calculated only once during the calculation history.

When the time marching scheme is used, Eqs. 15–19 needs to be re-written as:

$$ T^{i} = \sum\limits_{j = 1}^{n} {\sum\limits_{k = 1}^{m} {T^{ij} (t_{k} )H^{j} } } (t_{k} )\;\left( {t = t_{m} } \right) $$

(22)

$$ \sigma_{\text{s}}^{i} = \sum\limits_{j = 1}^{n} {\left( {A_{\text{ss}}^{ij} D_{\text{s}}^{j} + A_{\text{sn}}^{ij} D_{\text{n}}^{j} + \sum\limits_{k = 1}^{m} {F_{\text{s}}^{ij} (t_{\text{k}} )H^{j} (t_{\text{k}} )} } \right)} (t = t_{m} ) $$

(23)

$$ \sigma_{\text{n}}^{i} = \sum\limits_{j = 1}^{n} {\left( {A_{\text{ns}}^{ij} D_{\text{s}}^{j} + A_{\text{nn}}^{ij} D_{\text{n}}^{j} + \sum\limits_{k = 1}^{m} {F_{\text{n}}^{ij} (t_{k} )H^{j} (t_{k} )} } \right)} \;\left( {t = t_{m} } \right) $$

(24)

$$ u_{\text{s}}^{i} = \sum\limits_{j = 1}^{n} {\left( {B_{\text{ss}}^{ij} D_{\text{s}}^{j} + B_{\text{sn}}^{ij} D_{\text{n}}^{j} + \sum\limits_{k = 1}^{m} {G_{\text{s}}^{ij} (t_{k} )H^{j} (t_{k} )} } \right)} \;\left( {t = t_{m} } \right) $$

(25)

$$ u_{\text{n}}^{i} = \sum\limits_{j = 1}^{n} {\left( {B_{\text{ns}}^{ij} D_{\text{s}}^{j} + B_{\text{nn}}^{ij} D_{\text{n}}^{j} + \sum\limits_{k = 1}^{m} {G_{\text{n}}^{ij} (t_{k} )H^{j} (t_{k} )} } \right)} \;\left( {t = t_{m} } \right) $$

(26)

where t _k is the time interval between the evaluation time (t _m ) and the time when the kth sub-source H ^j(t _k ) takes effect t _k  = t _m  − kΔt (k = 0···m).

In Eqs. 22–26, each H ^j(t _k ) is a fictitious heat source and needs to be solved using thermal boundary conditions. For a problem with n boundary elements and m time steps, there are effectively (n × m) unknown fictitious heat sources. They can be solved using Eq. 22 if the boundary condition is temperature. If the boundary condition is heat flux or mixed temperature and flux, then the correspondent flux equation needs to be used.

In some cases, real heat sources with known strength and duration take place inside a rock mass. This can happen, for instance, in nuclear waste disposal where canisters can be considered as a line heat source on large scale. These real heat sources can be considered in the same way as the fictitious heat source except that their strengths are already known. In Eqs. 22–26, the heat sources H ^j(t _k ) also include the real heat sources if there are any.

To demonstrate the time marching process, we consider the situation in Fig. 3 in which evaluation time domain is divided into five equal time steps each with an interval of Δt. The temperature at ith element at the end of each time step is given below:

Fig. 3

Example of time marching scheme with five equal time steps for a continuous heat source H(t)

$$ {\text{Time step }}k = 1:T^{i}_{(t = \Updelta t)} = \sum\limits_{j = 1}^{n} {T^{ij}_{(t = \Updelta t)} H^{j}_{(t = 0)} } $$

$$ {\text{Time step }}k = 2:T^{i}_{(t = 2\Updelta t)} = \sum\limits_{j = 1}^{n} {\left( {T^{ij}_{(t = 2\Updelta t)} H^{j}_{(t = 0)} + T^{ij}_{(t = \Updelta t)} H^{j}_{(t = \Updelta t)} } \right)} $$

$$ {\text{Time step }}k = 3:T^{i}_{(t = 3\Updelta t)} = \sum\limits_{j = 1}^{n} {\left( {T^{ij}_{(t = 3\Updelta t)} H^{j}_{(t = 0)} + T^{ij}_{(t = 2\Updelta t)} H^{j}_{(t = \Updelta t)} + T^{ij}_{(t = \Updelta t)} H^{j}_{(t = 2\Updelta t)} } \right)} $$

$$ {\text{Time step }}k = 4:T^{i}_{(t = 4\Updelta t)} = \sum\limits_{j = 1}^{n} {\left( \begin{gathered} T^{ij}_{(t = 4\Updelta t)} H^{j}_{(t = 0)} + T^{ij}_{(t = 3\Updelta t)} H^{j}_{(t = \Updelta t)} + T^{ij}_{(t = 2\Updelta t)} H^{j}_{(t = 2\Updelta t)} \hfill \\ + T^{ij}_{(t = \Updelta t)} H^{j}_{(t = 3\Updelta t)} \hfill \\ \end{gathered} \right)} $$

$$ {\text{Time step }}k = 5:T^{i}_{(t = 5\Updelta t)} = \sum\limits_{j = 1}^{n} {\left( \begin{gathered} T^{ij}_{(t = 5\Updelta t)} H^{j}_{(t = 0)} + T^{ij}_{(t = 4\Updelta t)} H^{j}_{(t = \Updelta t)} + T^{ij}_{(t = 3\Updelta t)} H^{j}_{(t = 2\Updelta t)} \hfill \\ + T^{ij}_{(t = 2\Updelta t)} H^{j}_{(t = 3\Updelta t)} + T^{ij}_{(t = 2\Updelta t)} H^{j}_{(t = 4\Updelta t)} \hfill \\ \end{gathered} \right)} .$$

To calculate the temperature at the end of a given time step k, the fictitious heat source in the previous step is required. If a uniform time step is used, the influence coefficient calculated from the previous time steps can be saved and re-used during the calculation of time step k. This can significantly reduce the calculation time. The number of time steps is limited to 10 and the time step is uniform in this study. In general, increasing the number of time steps will dramatically increase the size of the system of equations and hence reduce the calculation speed.

2.4 Implementation of Thermal-Fracturing Coupling

The basic principle of the indirect boundary element approach for thermo-elastic analysis is the assumption that a fictitious line heat source exists at each element. The strengths of the line sources are unknown and should be determined based on the boundary conditions. For example, if the temperature at all boundary elements is zero, the combined effect of all the line heat sources on the boundary elements should result in a zero temperature. Once the strength of each fictitious heat source is determined, the temperature, thermal flux, and thermal-induced stresses and displacements at any given location in the rock mass can be calculated using Eqs. 1–6.

The following steps are involved in implementing the thermal function into FRACOD:

Step 1:

Solve the thermal problem separately without mechanical calculations using the fictitious heat source method. Obtain the fictitious heat sources along the boundary, and take into account the real heat sources in a rock mass, if any.

Step 2:

Calculate the thermal stress at the centers of all boundary elements. The thermal stresses are treated as a negative stress on the elements and they are added into the total boundary stresses for the mechanical calculation. The same principle applies to the displacement boundary conditions.

Step 3:

Solve the same problem with mechanical load and obtain the displacement discontinuity (DD)s of each element. The solution has already included the thermal effect.

Step 4:

Calculate the stresses and displacements at any internal point in the rock mass using the resultant DDs. The thermal stresses and displacements need to be added to their mechanical values and they are calculated using fictitious and real heat sources.

In the current coupled thermal-fracturing code, two types of thermal boundary conditions (constant temperature or constant heat flux) can be used. The boundary condition is kept to be constant for the duration of problem time. Fractures can be treated as an internal thermal boundary, and they have constant temperature, constant heat flux or zero thermal resistance (i.e. the derivative of heat flux is constant across the fracture). And internal heat sources are allowed, which include both point sources and line sources in two dimensions. The internal heat sources can have variable strength.

2.5 Fracture Initiation and Propagation Criterion

2.5.1 Fracture Initiation in Intact Solid

The current code considers intact solid as a flawless and homogeneous medium. Thus, any fracture initiation within this medium represents a localized failure of the intact body. For tensile fracture initiation, the tensile failure criterion is used, and Mohr–Coulomb failure criterion is used for a shear fracture initiation.

Tensile fracture criterion: σ _tensile ≥ σ _t

Shear fracture criterion: σ _shear ≥ σ _n · tan ψ + c

Here, σ _tensile and σ _shear are the tensile and shear stress at a given point, respectively, σ _t is the tensile strength of the intact solid body, σ _n is the normal stress to the shear failure plane, ψ is internal friction angle, and c is the cohesion. Direction of tensile and shear failures are calculated θ(σ _tensile) + π/2 and ψ/2 + π/4, respectively, where θ(σ _tensile) is the direction of principal tensile stress.

2.5.2 Fracture Initiation at Boundaries

Fracture initiation at a boundary is not as a straight forward as that is in intact body. Instead of predicting the fracture initiation directly from a boundary, the fracture initiation from the intact body very close to the boundary is examined using the above intact body failure criterion. Once a fracture initiation is predicted from any of the grid points close to the boundaries, a new fracture is created at the grid point in the direction of failure. The code then examines whether the newly formed fracture will link to the boundary or not by using a fracture propagation criterion explained below. An existing fracture is treated to be the same as a boundary.

2.5.3 Fracture Propagation Criterion

In modeling fracture propagation in a solid body where both tensile and shear failure are common, a fracture criterion for predicting both mode I and mode II fracture propagation is needed. In the current code, F-criterion that was proposed by Shen and Stephansson (1993) and is a more general form of strain energy release rate criterion or G-criterion, was used. F value that is calculated as $F(\theta ) = \frac{{G_{\text{I}} (\theta )}}{{G_{{{\text{I}}_{C} }} }} + \frac{{G_{\text{II}} (\theta )}}{{G_{{{\text{II}}_{C} }} }}$ in an arbitrary direction (θ) at a fracture tip, and the fracture tip will propagate when the maximum F value in the direction of θ ₀ reaches 1.0. Here, G _I and G _II are strain energy release rate of Mode I (tensile) and Mode II (shear), respectively, and $G_{{{\text{I}}_{C} }}$ and $G_{{{\text{II}}_{C} }}$ denote a critical strain energy release rate for both modes which is related to the fracture toughness.

3 Implementation of Multi-Region Boundary Element Module

Materials around a rock excavation may have different thermal and mechanical properties. An example problem is a reinforced borehole where three different materials (rock, cement, and steel casing) exist. For application to this case, it is necessary to handle different materials with different thermal and mechanical properties in different regions. A multi-region function for mechanical responses has previous been developed in FRACOD (FRACOM 2002), and the thermal multi-region function is introduced in this section.

The fictitious heat source method discussed before is for a homogenous rock. If a rock mass contains different regions with different material properties, the basic solutions given by Eqs. 1–6 are no longer valid. To solve this problem, the problem region is separated into several individual regions, each being a homogeneous region with the same rock properties (Fig. 4). For each homogeneous region, the basic thermal solutions discussed before are still valid, and systematic equations can be set up for each region to solve for temperature and thermal flux at the internal point and on the boundary. The interfaces between two regions become boundaries in both regions. The boundary temperature and flux values at the interfaces, however, need to meet certain conditions to ensure the thermal continuity of the two regions sharing an interface.

Fig. 4

Treatment of multi-regions with two different material properties by modeling two separate regions (indicated by subscript 1 and 2) of homogeneous property

To demonstrate this process, we consider a basic problem as shown in Fig. 5. The two triangular regions have two different properties. The outer boundaries of each region are represented by displacement discontinuity (DD) elements as Region 1: elements no. 1, 2, 5, 7 and Region 2: elements no. 3, 4, 6, 8. Note that elements 5 and 6, and 7 and 8 are representing the interfaces but in different regions.

Fig. 5

A basic multi-region problem consisting of two triangular regions of eight boundary elements

For the problem with eight elements, the systematic equations can be written

$$ \begin{gathered} T^{1} = T^{11} H^{1} + T^{12} H^{2} + T^{15} H^{5} + T^{17} H^{7} \hfill \\ T^{2} = T^{21} H^{1} + T^{22} H^{2} + T^{25} H^{5} + T^{27} H^{7} \hfill \\ T^{3} = T^{33} H^{3} + T^{34} H^{4} + T^{36} H^{6} + T^{38} H^{8} \hfill \\ T^{4} = T^{43} H^{3} + T^{44} H^{4} + T^{46} H^{6} + T^{48} H^{8} \hfill \\ T^{5} = T^{51} H^{1} + T^{52} H^{2} + T^{55} H^{5} + T^{57} H^{7} \hfill \\ T^{6} = T^{63} H^{3} + T^{64} H^{4} + T^{66} H^{6} + T^{68} H^{8} \hfill \\ T^{7} = T^{71} H^{1} + T^{72} H^{2} + T^{75} H^{5} + T^{77} H^{7} \hfill \\ T^{8} = T^{83} H^{3} + T^{84} H^{4} + T^{86} H^{6} + T^{88} H^{8} \hfill \\ \end{gathered} $$

(27)

For continuity at interfaces, the temperature (T) and thermal flux (Q) at the interface elements have to meet the conditions: T ⁵ = T ⁶, T ⁷ = T ⁸, Q ⁵ = − Q ⁶, Q ⁷ = − Q ⁸.

Using the above conditions, we can then obtain the following equations:

$$ \begin{gathered} T^{1} = T^{11} H^{1} + T^{12} H^{2} + T^{15} H^{5} + T^{17} H^{7} \hfill \\ T^{2} = T^{21} H^{1} + T^{22} H^{2} + T^{25} H^{5} + T^{27} H^{7} \hfill \\ T^{3} = T^{33} H^{3} + T^{34} H^{4} + T^{36} H^{6} + T^{38} H^{8} \hfill \\ T^{4} = T^{43} H^{3} + T^{44} H^{4} + T^{46} H^{6} + T^{48} H^{8} \hfill \\ 0 = T^{51} H^{1} + T^{52} H^{2} - T^{63} H^{3} - T^{64} H^{4} + T^{55} H^{5} - T^{66} H^{6} + T^{57} H^{7} - T^{68} H^{8} \hfill \\ 0 = T^{71} H^{1} + T^{72} H^{2} - T^{83} H^{3} - T^{84} H^{4} + T^{75} H^{5} - T^{86} H^{6} + T^{77} H^{7} - T^{88} H^{8} \hfill \\ 0 = Q^{51} H^{1} + Q^{52} H^{2} + Q^{63} H^{3} + Q^{64} H^{4} + Q^{55} H^{5} + Q^{66} H^{6} + Q^{57} H^{7} + Q^{68} H^{8} \hfill \\ 0 = Q^{71} H^{1} + Q^{72} H^{2} + Q^{83} H^{3} + Q^{84} H^{4} + Q^{75} H^{5} + Q^{86} H^{6} + Q^{77} H^{7} + Q^{88} H^{8} \hfill \\ \end{gathered} $$

(28)

The matrix form of the systematic equations for this simple multi-region problem is then given below:

$$ \left[ {\begin{array}{*{20}c} {T^{11} } & {T^{12} } & {} & {} & {T^{15} } & {} & {T^{17} } & {} \\ {T^{21} } & {T^{22} } & {} & {} & {T^{25} } & {} & {T^{27} } & {} \\ {} & {} & {T^{33} } & {T^{34} } & {} & {T^{36} } & {} & {T^{38} } \\ {} & {} & {T^{43} } & {T^{44} } & {} & {T^{46} } & {} & {T^{48} } \\ {T^{51} } & {T^{52} } & { - T^{63} } & { - T^{64} } & {T^{55} } & { - T^{66} } & {T^{57} } & { - T^{68} } \\ {Q^{51} } & {Q^{52} } & {Q^{63} } & {Q^{64} } & {Q^{55} } & {Q^{66} } & {Q^{57} } & {Q^{68} } \\ {T^{71} } & {T^{72} } & { - T^{83} } & { - T^{84} } & {T^{75} } & { - T^{86} } & {T^{77} } & { - T^{88} } \\ {Q^{71} } & {Q^{72} } & {Q^{83} } & {Q^{84} } & {Q^{75} } & {Q^{86} } & {Q^{77} } & {Q^{88} } \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {H^{1} } \\ {H^{2} } \\ {H^{3} } \\ {H^{4} } \\ {H^{5} } \\ {H^{6} } \\ {H^{7} } \\ {H^{8} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T^{1} } \\ {T^{2} } \\ {T^{3} } \\ {T^{4} } \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right] $$

(29)

where T ^ij, and Q ^ij are the thermal and heat flux influence coefficients, H ⁱ is the strength of fictitious heat source, and T ⁱ is the temperature at boundaries. Thus, Q ^ij denotes the thermal flux of ith element due to the fictitious heat source over the jth element.

After solving the strengths of fictitious heat sources at all boundary and interface elements, the temperature at any internal point can be calculated. Note that only the contributions from elements 1, 2, 5 and 7 are used because the two regions are considered to be separate for an internal point in the Region 1. Elements 3, 4, 6 and 8 of Region 2 will not have contributions to the temperature of the internal point in Region 1.

4 Verification and Application Examples of Coupled Thermal-Fracturing Code

4.1 Verification Examples

4.1.1 Point Heat Source in an Infinite Plane

A point heat source with constant heat strength located in a 2D infinite elastic medium was solved using the developed coupled thermal-fracturing module and compared with analytical solution for a verification purpose of the developed code. The analytical solution to this problem has already been given in Eqs. 1–6.

The material properties as well as initial and boundary conditions for this example are given in Table 1. It was assumed that the material properties were temperature-independent and the thermal output of the source was constant.

Table 1 Material properties, and initial and boundary conditions for a point heat source in 2D infinite medium

We simulated this problem where the point heat source was considered as distributed heat source along a small hole. A constant heat flux was applied to the inner boundary of the hole. The hole radius was assumed to be R = 0.1 m, and the applied flux (q) was 1/2πR = 1.59 W/m². A symmetry condition was used so that only a quarter-section of the model was actually modeled using 15 elements.

The numerically predicted temperature, stresses and displacements after 1 year are shown in Fig. 6, and they were compared with the analytical results along a radial line from the model centre in Fig. 7. We could observe a good agreement between the numerical and analytical results, which verifies the validity of the newly developed thermal calculation module in addition to previous mechanical module.

Fig. 6

Calculated distribution of a temperature, b principal stress, c displacement around a hole-like point heat source after 1 year

Fig. 7

Comparison of a temperature, b stresses and c displacement along a radial line in the numerical model with a hole-like point heat source (dots are the numerical predictions by the coupled FRACOD and lines are the analytical solutions)

4.1.2 Annulus in a Circular Hole in a Plane

A simple case of a boundary value problem in an inhomogeneous elastic body shown in Fig. 8 was solved and compared with analytical solution so as to verify newly implemented multi-region function in the coupled code. The region of interest consists of two different regions with different properties (Young’s modulus, E and Poisson’s ratio, ν): an annulus a ≤ r ≤ b with elastic constants E ₁ and ν₁ inside a circular hole of radius r = b in a sufficiently large plane with elastic constants E ₂ and ν₂. The inside wall of the annulus was subject to a normal stress σ _rr = −p, and the plane was unstressed at infinity. This problem may correspond to the boreholes with cement reinforcement or excavated tunnels with concrete linings in rock engineering problems, where the annulus corresponds to either cement reinforcement or concrete lining and the sufficiently large plane is a rock mass. The normal stress σ _rr = −p is an internal pressure of hydraulic fracturing or pressurized fluid stored inside the annulus.

Fig. 8

Analysis model of the annulus inside a circular hole in plane

The solution to this problem, satisfying continuity of radial stress and displacement at the interface (r = b), can be constructed from standard formulas from thick-walled cylinders (Obert and Duvall 1967):

$$ \sigma_{\text{rr}} = \frac{1}{{1 - \left( {a/b} \right)^{2} }}\left[ {\left( {p\left( {a/b} \right)^{2} - p^{\prime } } \right) - \left( {p - p^{\prime } } \right)\left( {a/r} \right)^{2} } \right]\quad a \le r \le b $$

(30)

$$ \sigma_{\theta \theta } = \frac{1}{{1 - \left( {a/b} \right)^{2} }}\left[ {\left( {p\left( {a/b} \right)^{2} - p^{\prime } } \right) - \left( {p - p^{\prime } } \right)\left( {a/r} \right)^{2} } \right]\quad a \le r \le b $$

(31)

$$ \sigma_{\text{rr}} = - p^{\prime } \quad\left( {b/r} \right)^{2} \quad r \ge b $$

(32)

$$ \sigma_{\theta \theta } = - p^{\prime } \left( {b/r} \right)^{2} \quad r \ge b $$

(33)

in which σ _rr and σ _θθ indicate radial and tangential stresses, respectively, and

$$ p^{\prime } = \frac{{p\left( {a/b} \right)^{2} }}{{1 + \frac{1}{2}\left( {\frac{{E_{1} }}{{E_{2} }}\frac{{1 + \nu_{2} }}{{1 - \nu_{1}^{2} }} - \frac{1}{{1 - \nu_{1} }}} \right)\left( {1 - \left( {a/b} \right)^{2} } \right)}} $$

(34)

In this example, the following geometrical and mechanical parameters were used a = 0.5 m, b = 1.0 m, ν₁ = ν₂ = 0.2, E ₁ = 50 GPa, E ₂ = 25 GPa, and p = 10 MPa.

A total of 60 elements were used for the internal circular boundary and 60 elements for each side of the interface. The modeled stress distribution using the multi-region coupled code was shown in Fig. 9. And a comparison of radial and tangential stresses between the numerical results and the analytical solutions was presented in Fig. 10. A good agreement was obtained, indicating that the developed code accurately simulates the multi-region problem.

Fig. 9

Calculated stress distribution in the annulus inside a circular hole

Fig. 10

Comparison of stresses between the simulation results and analytical solutions for the annulus inside a circular hole (dots and lines indicate the numerical results and analytical solution, respectively)

4.2 Application Examples

4.2.1 A Hypothetical Underground LNG Storage Cavern

A hypothetical underground lined LNG storage cavern was simulated. The cavern size was 5.6 × 5.6 m² after excavation. The cavern has an internal lining system of concrete lining and thermal insulation layer, and both the concrete linings and the insulation layer had a 40 cm thickness (Fig. 11). When filled with LNG during operation, its internal surface temperature was assumed to be −160 °C whereas the rock initial temperature to be 25 °C. This underground lined LNG storage cavern was designed to demonstrate a practical applicability of the developed coupled code with multi-region module, since the thermal shock induced fracturing due to very low temperature of LNG is involved, and insulation layers of different property from surrounding rock mass are required to be considered in the simulation.

Fig. 11

Calculated a temperature and b tensile stress developed in surrounding rock and concrete lining of the hypothetical underground LNG storage cavern after 1 year cooling

The mechanical and thermal properties of the rock mass, the concrete linings and the thermal insulation layer used in the simulation are listed in Table 2. The rock strength parameters are also given in the Table 2. A cooling time of 1 year was considered in this simulation.

Table 2 Mechanical and thermal parameter used in the simulation of the hypothetical underground LNG storage cavern

The temperature and stress distribution around the cavern after 1 year is shown in Fig. 11. It was noted that significant thermal stresses that were induced by the thermal shock of approximately −60 °C in the surrounding rock were concentrating especially at the corner of the floor and the roof of the cavern. These stresses, in this hypothetical simulation conditions, were by far exceeding the tensile strength of the concrete linings and rock mass, so that fracturing that provides an unfavorable leakage for a storage cavern would occur. The results in Fig. 11b were fairly symmetric, minor asymmetry, however, could be seen due to numerical inaccuracy near the boundary. Figure 12 demonstrates the predicted pattern of cooling fractures in the rock. As expected, the fracturing was concentrating at the corner of the floor and roof of the cavern where high stress concentration was observed. It was also noted that the fracturing patterns were different, depending on the properties of inner concrete linings. When the concrete lining was not allowed to fail (Fig. 12a), the fracturing in the rock was comparatively more significant. On the contrary, if the concrete lining was allowed to fail (Fig. 12b), less fracturing in the rock was observed due to the stress relaxation in the concrete linings. However, it should be noted that the fracturing in the concrete lining is more critical and unfavorable in a storage cavern design concept. Figure 13 shows the variation of temperature, stresses and displacement along a monitoring line (Fig. 11a) and we could clearly see that the temperature dropped sharply in the insulation layer. High tensile stresses developed in the concrete lining and surrounding rock mass, which led to the intensive rock fracturing.

Fig. 12

Predicted rock fracturing in surrounding rock due to thermally induced tensile stress of a Case 1: lining is not allowed to fail, and b Case 2: lining is allowed to fail

Fig. 13

Calculated evolution of a temperature, b stresses, and c displacement along the horizontal monitoring line shown in Fig. 11a

Although these results are for hypothetical conditions, it can be clearly seen that the present coupled code can be an effective design tool for predicting a fracturing that is induced by thermal–mechanical coupled processes in concrete linings and rocks.

4.2.2 A Pilot Underground Lined Rock Cavern for LNG Storage

A real pilot lined cavern tested for underground LNG storage was simulated using the coupled code with multi-region module. The design of the underground LNG storage was based on the implementation of a containment system consisting of gas tight steel liners and insulation panels to protect the failure and damage of surrounding rock against thermal shock caused by the extremely low temperature of liquefied LNG (Park et al. 2010). The size of cavern and the thickness of both liners and panels differ from those of the previous hypothetical study of LNG storage cavern in which thermal–mechanical fracturing conditions were intentionally prescribed in order to test the practical applicability of the coupled code. In the present example, however, we mainly focus on the comparison between the calculation and in situ measurements during the pilot test so as to verify the validity of the developed coupled code. The inner dimension of the pilot cavern was 3.5 m × 3.5 m after installing the liners. Figure 14 shows structural concept of the pilot cavern. During the pilot testing, the changes in temperature and displacement in rock mass were monitored and compared with the simulation results.

Fig. 14

Conceptual structures of the pilot lined cavern for underground LNG storage (Park et al. 2010)

In the pilot testing, liquefied nitrogen (LN₂) was used to fill the cavern during the operation of the pilot cavern for safety and practical reasons. The measurements showed that LN₂ had a temperature of −194 °C and gaseous space in the top of the cavern due to boiling of LN₂ was about −100 °C. Thus, two different regions of thermal boundary conditions were explicitly modeled, and initial rock temperature was 17 °C. The mechanical and thermal parameters of the rock mass used in the simulation are summarized in Table 3. The thermal properties of insulation panel and concrete lining in the cavern are listed in Table 4. In the simulation, we considered only the rock stability, and the insulation panel of polyurethane (PU) foam and concrete wall were assumed to have sufficiently high strengths so as not to fail.

Table 3 Mechanical and thermal properties of rock mass in the simulation of the pilot underground LNG storage cavern

Table 4 Thermal properties of the insulation panel and concrete lining in the simulation of the pilot LNG storage cavern

Figure 15 presents the simulated and measured temperature distribution around the pilot cavern. The calculated temperature distribution was generally similar to measurement results, considering that geological heterogeneity in the surrounding rock mass was not considered in the simulation. Figure 16 shows the comparison of the simulated and measured temperature evolution at the floor, where a good agreement was obtained. Figure 17 indicates the modeled major and minor principal stresses distribution after 22 weeks of operation. The simulated tensile stresses in the rock were less than 3 MPa, and hence no tensile fracturing was predicted, considering the tensile strength of concrete and rock that is usually ranging between 5 and 20 MPa. From these results, we may conclude that the current coupled code with multi-region module can be effective in predicting a fracturing that is induced by thermal–mechanical coupled processes in geomaterials.

Fig. 15

Temperature profile a predicted by the simulation, and b estimated from the measurements around pilot LNG cavern after 22 weeks of operation

Fig. 16

Simulated and measured temperature evolution at the floor of the pilot LNG cavern (dot and line indicate the simulation results and measurement, respectively)

Fig. 17

Calculated a major and b minor principal stress distribution around pilot LNG cavern after 22 weeks of operation

5 Concluding Remarks and Discussions

A coupled thermal-fracturing boundary element module has been developed using the existing version of FRACOD to analyze the complex explicit fracturing and thermal responses in geomaterials such as rocks and concretes. FRACOD is the boundary element code based on a displacement discontinuity (DD) method, and has been proven to simulate both tensile and shear fracture propagations.

The coupling was achieved using an indirect method, so called the fictitious heat source method. This coupling method employed the same principle as the DD method, and hence it has been the most appropriate way to implement it into FRACOD code. The coupled code was further extended to deal with multi-regions which enables us to simulate problems where rock mass, concrete linings and insulation layers with different thermal and mechanical properties are all present.

Verification and application examples were presented where good agreement between the simulation results and analytical solution as well as in situ measurement could be observed. Therefore, the developed coupled code can be effectively used in designing structures that are placed under extreme temperature conditions and thermal-fracturing would be significant processes in their stability perspective.

Coupled processes in a fractured rock mass are important in the performance and safety analysis of many rock engineering projects such as CO₂ geosequestration and geothermal industry, but are difficult to be predicted by in situ tests due to many unknown factors affecting the test conditions. From this point of view, the numerical methods to produce predictions under many different conditions could provide valuable information about the coupled processes. Especially, the current coupled code has a good potential to predict the complex behaviors of fractured rock mass realistically due to its capacity to model propagation of discrete fractures. The coupled code is currently under further development to model the mechanical–thermal–hydraulic response of rock and rock fractures, and new application cases with special focus on the CO₂ geosequestration and the geothermal industry would be introduced in the future.