1 Introduction

The stress–strain relationship is the most fundamental part of constitutive relationships. According to Hooke’s Law, which has been generally used to describe this stress–strain relationship for elastic mechanical processes, a stress–strain relationship should be linear. However, this linearity does not always apply to every case, and related moduli are stress-dependent for many applications (e.g., Cazacu 1999; Lionço and Assis 2000; Brown et al. 1989; Johnson and Rasolofosaon 1996; Brady 1969). A number of efforts have been made to relate this stress-dependent behavior to the microstructures of “cracks” in porous rock (Walsh 1965; Nur 1971; Mavko and Nur 1978); an excellent review of these efforts is provided in a chapter entitled “Micromechanical models” in Jaeger et al. (2007). Because it is generally difficult to characterize small-scale structures accurately and then relate their properties to large-scale mechanical properties that are of practical interest, it is desirable to have a macroscopic-scale theory that does not rely on the detailed description of small-scale structures and that can physically incorporate the stress-dependent behavior of relevant mechanical properties. A theory of this kind was recently developed within the framework of Hooke’s law by Liu et al. (2009).

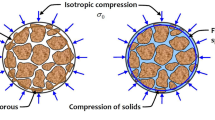
Liu et al. (2009) argued that the natural strain (volume change divided by rock volume at the current stress state), rather than the engineering strain (volume change divided by the unstressed rock volume), should be used in Hooke’s law for accurately modeling elastic deformation, unless the two strains are essentially identical (i.e., as they might be for small mechanical deformations). They indicated that a rock body could be conceptualized into two distinct parts, a “hard” part and a “soft” part. The soft part corresponds to a fraction of the pore volume subject to a relatively large degree of deformation (i.e., cracks or fractures). The complexity of pore structures at different scales has been studied in the literature (e.g., Mavko and Jizba 1991; Damjanac et al. 2007). Deformation is small in the hard part, and, thus, engineering strain can still be used for that part. This approach permits the derivation of constitutive relations between stress and a variety of mechanical and hydraulic rock properties. These theoretically derived relations are generally consistent with empirical expressions and also laboratory experimental data for sandstone rock (Liu et al. 2009). As shown later in this paper, the soft part plays an important role in constitutive relationships and, without considering it, a significant error would occur in describing mechanical deformation. However, the work of Liu et al. (2009) is limited to isotropic stress conditions corresponding to the hydrostatic stress state; in reality, porous rock is generally subject to complex, anisotropic stress conditions. The major objective of this work is to extend the work of Liu et al. (2009) to anisotropic stress conditions.

2 Stress–Strain Relationships

This section presents the theoretical development of the stress–strain relationship under elastic and anisotropic stress conditions. Comparisons between the relationship and relevant experimental observations will be given in the next section.

2.1 Stress–Strain Relationships Under Isotropic Stress Conditions

The new stress–strain relationship to be developed herein is based on the work of Liu et al. (2009) for isotropic (or hydrostatic) stress conditions. For the sake of completeness, the results of Liu et al. (2009) are briefly discussed here.

The major reasoning of Liu et al. (2009) is that the two kinds of strains (natural and engineering) should be carefully distinguished, and the natural (or true) strain should be used in Hooke’s law for accurately describing material deformation (Freed 1995). When a uniformly distributed force is imposed on the surface of a homogeneous and isotropic material body subject to elastic deformation, the natural (or true)-strain-based Hooke’s law can be expressed as:

$$ {\text{d}}\sigma_{\text{h}} = - K\frac{{{\text{d}}V}}{V} = K\,{\text{d}}\varepsilon_{{{\text{v,}}t}} $$
(1)

where V is the total volume of the material body under the current stress state, σ h is the hydrostatic stress, K is the bulk modulus, the subscript h refers to hydrostatic (or isotropic) stress conditions, and \( \varepsilon_{{{\text{v,}}t}} \) is the natural volumetric strain. The engineering-strain-based Hooke’s law can be expressed as:

$$ {\text{d}}\sigma_{\text{h}} = - K\frac{{{\text{d}}V}}{{V_{0} }} = K\,{\text{d}}\varepsilon_{{{\text{v,}}e}} $$
(2)

where V 0 is the unstressed bulk volume and \( \varepsilon_{{{\text{v}},e}} \) is the engineering volumetric strain. Note that the two strains are practically identical for small mechanical deformations.

Engineering strain has been exclusively used in the literature of rock mechanics, considering that the elastic strain is generally small. However, Liu et al. (2009) indicated that the strain could be considerably larger within some portion of a rock body, because of its inherent heterogeneity, and they divide rock mass into two parts in order to consider the impact of heterogeneity. As previously indicated, for the soft part, the natural (or true)-strain-based Hooke’s law is applied. For the hard part, the engineering-strain-based Hooke’s law is applied as a result of small deformation. In this work, we also use subscripts 0, e, and t to denote the unstressed state, the hard part, and the soft part, respectively. According to Liu et al. (2009), the stress–strain relationship for porous and fractured rock under the hydrostatic stress state can be expressed as:

$$ - \frac{{{\text{d}}V}}{{V_{0} }} = \gamma_{e} \frac{{{\text{d}}\sigma_{\text{h}} }}{{K_{e} }} + \gamma_{t} \exp \left( { - \frac{{\sigma_{\text{h}} }}{{K_{t} }}} \right)\frac{{{\text{d}}\sigma_{\text{h}} }}{{K_{t} }} $$
(3)
$$ {\text{d}}V = {\text{d}}V_{e} + {\text{d}}V_{t} $$
(4)
$$ V_{0} = V_{0,e} + V_{0,t} $$
(5)
$$ \gamma_{t} = \frac{{V_{0,t} }}{{V_{0} }} $$
(6)
$$ \gamma_{e} = 1 - \gamma_{t} $$
(7)

where K e and K t refer to the bulk modulus for the hard and soft parts, respectively.

2.2 Stress–Strain Relationship Under Anisotropic Stress Conditions

Without losing generality, we consider stress–strain relationships corresponding to the three principal stresses (Fig. 1).

Fig. 1
figure 1

Principal stresses

Full size image

To extend the work of Liu et al. (2009), we further assume that the principal strain resulting from the soft part is a function of the principal stress along the same direction only and has nothing to do with the other principal stresses. The validity of this assumption will be evaluated by comparing our results with experimental observations.

Following the procedure of Liu et al. (2009) to derive Eq. 3, we derive the expressions for principal strains:

$$ {\text{d}}\varepsilon_{1} = \frac{{\gamma_{e}^{'} }}{{E_{e} }}[{\text{d}}\sigma_{1} - \nu ({\text{d}}\sigma_{2} + {\text{d}}\sigma_{3} )] + \frac{{\gamma_{t}^{'} }}{{E_{t} }}\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right){\text{d}}\sigma_{1} $$
$$ {\text{d}}\varepsilon_{2} = \frac{{\gamma_{e}^{'} }}{{E_{e} }}[{\text{d}}\sigma_{2} - \nu ({\text{d}}\sigma_{1} + {\text{d}}\sigma_{3} )] + \frac{{\gamma_{t}^{'} }}{{E_{t} }}\exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right){\text{d}}\sigma_{2} $$
(8)
$$ {\text{d}}\varepsilon_{3} = \frac{{\gamma_{e}^{'} }}{{E_{e} }}[{\text{d}}\sigma_{3} - \nu ({\text{d}}\sigma_{1} + {\text{d}}\sigma_{2} )] + \frac{{\gamma_{t}^{'} }}{{E_{t} }}\exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right){\text{d}}\sigma_{3} $$
$$ {\text{d}}\varepsilon_{i} = - \frac{{{\text{d}}l^{i} }}{{l_{0}^{i} }}\quad (i \, = 1, 2, 3) $$
(9)
$$ {\text{d}}l^{i} = {\text{d}}l_{e}^{i} + {\text{d}}l_{t}^{i} \quad (i \, = 1, 2, 3) $$
(10)
$$ l_{0}^{i} = l_{0,e}^{i} + l_{0,t}^{i} \quad (i \, = 1, 2, 3) $$
(11)
$$ \gamma_{t}^{'} = \frac{{l_{0,t}^{i} }}{{l_{0}^{i} }}\quad (i \, = 1, 2, 3) $$
(12)
$$ \gamma_{e}^{'} = 1 - \gamma_{t}^{'} \quad (i \, = 1, 2, 3) $$
(13)

where \( \sigma_{1} ,\,\sigma_{2} ,\,\sigma_{3} \) are the principal stresses, \( \varepsilon_{1} ,\,\varepsilon_{2} ,\,\varepsilon_{3} \) are the principal engineering strains, \( \nu \) is the Poisson ratio for the hard part, \( \gamma_{t}^{'} \) is the ratio of the soft part to the entire rock body in one principal direction (under unstressed conditions), \( l^{i} \) is the length in the ith principal direction, and \( E_{e} \) and \( E_{t} \) refer to Young’s (elastic) modulus for the hard and soft parts, respectively.

The first term on the right-hand side of Eq. 8 results from the hard part and the second term from the soft part. Without the second part, our developed strain–stress relationship is reduced to the general engineering-strain-based Hooke’s Law (Jaeger et al. 2007).

To derive the relationship between the \( \gamma_{t} \;{\text{and}}\;\gamma_{t}^{'} \) for the soft part, we consider a rock element and relate the volume of the element \( V_{0} \;{\text{to}}\;l_{0}^{i} \quad (i = 1, 2, 3) \) by:

$$ \begin{aligned} V_{0} \; = & (l_{0,e}^{1} + l_{0,t}^{1} )(l_{0,e}^{2} + l_{0,t}^{2} )(l_{0,e}^{3} + l_{0,t}^{3} ) = l_{0,e}^{1} l_{0,e}^{2} l_{0,e}^{3} + 3\,l_{0}^{1} l_{0}^{2} l_{0}^{3} \gamma_{t}^{'} (1 - \gamma_{t}^{'} )^{2} \\ + 3l_{0}^{1} l_{0}^{2} l_{0}^{3} (\gamma_{t}^{'} )^{2} (1 - \gamma_{t}^{'} ) + l_{0}^{1} l_{0}^{2} l_{0}^{3} (\gamma_{t}^{'} )^{3} \\ \end{aligned} $$
(14)

Because \( \gamma_{t}^{'} \) is generally much smaller than 1, we can neglect it in Eq. 14. Then, \( V_{0} \) can be written as:

$$ V_{0} \; \approx l_{0,e}^{1} l_{0,e}^{2} l_{0,e}^{3} + 3\,\gamma_{t}^{'} l_{0}^{1} l_{0}^{2} l_{0}^{3} = V_{0,e} + 3\,\gamma_{t}^{'} V_{0} $$
(15)

Combining Eqs. 4, 5, 6, and 15 yields:

$$ \gamma_{t}^{'} = \frac{{\gamma_{t} }}{3} $$
(16)

It is well known that the engineering volumetric strain is the sum of three principal strains (Jaeger et al. 2007):

$$ {\text{d}}\varepsilon_{v} = - \frac{{{\text{d}}V}}{{V_{0} }} = {\text{d}}\varepsilon_{1} + {\text{d}}\varepsilon_{2} + {\text{d}}\varepsilon_{3} $$
(17)

where ε v is the volumetric strain. Combining Eqs. 8, 16, and 17 yields:

$$ \begin{aligned} {\text{d}}\varepsilon_{\text{v}} = & \frac{{(3 - \gamma_{t} )(1 - 2\nu )}}{{3E_{e} }}({\text{d}}\sigma_{1} + {\text{d}}\sigma_{2} + {\text{d}}\sigma_{3} ) + \frac{{\gamma_{t} }}{{3E_{t} }}\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right){\text{d}}\sigma_{1} \\ + \frac{{\gamma_{t} }}{{3E_{t} }}\exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right){\text{d}}\sigma_{2} + \frac{{\gamma_{t} }}{{3E_{t} }}\exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right){\text{d}}\sigma_{3} \\ \end{aligned} $$
(18)

To make Eqs. 3 and 18 consistent under isotropic stress conditions, we can relate the Young’s modulus \( E_{e} \) to the bulk modulus \( K_{e} \) by:

$$ K_{e} = \frac{{E_{e} \gamma_{e} }}{{3(1 - 2\nu )\gamma_{e}^{'} }} = \frac{{E_{e} (1 - \gamma_{t} )}}{{3(1 - 2\nu )(1 - \gamma_{t}^{'} )}} $$
(19)

where \( \gamma_{t} \;{\text{and}}\;\gamma_{t}^{'} \) are on the order of 10−1–10−2, much smaller than 1 for most porous rocks and, therefore, can be neglected in Eq. 19. In this case, we obtain:

$$ K_{e} = \frac{{E_{e} }}{3(1 - 2\nu )} $$
(20)

Furthermore, consistency between Eqs. 3 and 18 requires:

$$ K_{t} = E_{t} $$
(21)

With the definitions given in Eqs. 19 and 21, the stress–strain relationship of Liu et al. (2009), or Eq. 3, becomes a special case of Eq. 18.

Based on Eq. 16 and the condition that strains are zero under an unstressed state, principal strains can be solved from Eq. 8 as:

$$ \begin{gathered} \varepsilon_{1} = \frac{{(3 - \gamma_{t} )}}{{3E_{e} }}[\sigma_{1} - \nu (\sigma_{2} + \sigma_{3} )] + \frac{{\gamma_{t} }}{3}\left[ {1 - \exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right)} \right] \hfill \\ \varepsilon_{2} = \frac{{(3 - \gamma_{t} )}}{{3E_{e} }}[\sigma_{2} - \nu (\sigma_{1} + \sigma_{3} )] + \frac{{\gamma_{t} }}{3}\left[ {1 - \exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right)} \right] \hfill \\ \varepsilon_{3} = \frac{{(3 - \gamma_{t} )}}{{3E_{e} }}[\sigma_{3} - \nu (\sigma_{2} + \sigma_{1} )] + \frac{{\gamma_{t} }}{3}\left[ {1 - \exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right)} \right] \hfill \\ \end{gathered} $$
(22)

Note that the second term on the right-hand side is from the soft part in Eqs. 8 and 22. That term, unlike the first term resulting from the hard part, is only a function of the corresponding principal stress and is not related to other stresses. In other words, we ignore Poisson’s ratio for the soft part in Eqs. 8 and 22.

Our treatment of Poisson’s ratio, as the first step, is considered to be a rough approximation, and further research may be needed in order to refine the treatment (by incorporating Poisson’s ratio for the soft part). Poisson’s ratio v is defined as the negative of the ratio of the transverse strain to the longitudinal strain, under conditions of uniaxial stress (Jaeger et al. 2007). Although the use of approximate or typical values in most rock mechanics applications does not create significant problems, Poisson’s ratio plays an undeniably important role in the elastic deformation of rocks and rock masses subjected to static or dynamic stresses. Furthermore, its effects emerge in a wide variety of rock engineering applications, ranging from basic laboratory tests on intact rocks to field measurements for in situ stresses or the deformability of rock masses (Gercek 2007). Poisson (1829) recommended a value for the Poisson’s ratio of 1/4. To make Young’s, shear and bulk, modulus of a material positive, the theoretical value of Poisson’s ratio must lie in the range −1 and 1/2 (Jaeger et al. 2007). According to Gercek (2007), the values of Poisson’s ratio for many elements and materials are between 0 and 0.5. For the case of rock, while one may anticipate that the porosity of rock material will influence the value of Poisson’s ratio, the geometry (size and shape), orientation, distribution, and connectivity of pores are expected to complicate such influence (Gercek 2007). In this study, we assumed that only the hard part has Poisson’s effect. As demonstrated later in this section, this assumption may be adequate for most practical applications in rock mechanics.

Equations developed in this section are for the principal stress/strain coordinate system. The relationships between stress and strain in a general coordinate system (x, y, z) can be obtained from the equations in this section and are given in the “Appendix”.

3 Comparisons with Experimental Observations

To evaluate the validity of the developed stress–strain relationship, we use it to fit the unconfined compression tests presented by Corkum and Martin (2007) and Olalla et al. (1999) for Opalinus Clay rock. In Corkum and Martin (2007), rock samples (83 mm in diameter) were saw-cut core from Boreholes BRA-1 and BRA-2, drilled with oil and air drilling fluids, respectively (Corkum and Martin 2007). In Olalla et al. (1999), rock samples were 78 mm in diameter.

To avoid (as much as possible) the non-uniqueness of parameter values determined from curve fitting, we used a simple procedure to estimate these values from stress–strain data. As shown in Figs. 2 and 3, measured relations between stress and strain are very well represented by a straight line for relatively high stresses. The slope of the straight line is used to determine \( \frac{{E_{e} }}{{\gamma_{e}^{'} }} \) because the exponential terms on the right-hand side of Eq. 22 are negligible for high stress values. The strain value at the intersection between the straight line and the strain axis in Figs. 2 and 3 gives the \( \gamma_{e}^{'} \) value, considering that the straight line represents the first term on the right-hand side of Eq. 22. The above procedure and Eq. 3 allow for the direct determination of values for \( E_{e} , \) \( \gamma_{e}^{'} , \) and \( \gamma_{t}^{'} . \) The remaining parameter \( E_{t} \) can be estimated using a data point at relatively low stress.

Fig. 2
figure 2

Matches between the results calculated from Eq. 22 and experimental data from unconfined compression tests on claystone rock (Corkum and Martin 2007)

Full size image
Fig. 3
figure 3

Matches between the results calculated from Eq. 22 and experimental data from unconfined compression tests on claystone rock (Olalla et al. 1999)

Full size image

As indicted in Figs. 2 and 3, the data are in excellent agreement with our theoretical results, suggesting that our assumption regarding Poisson’s ratio for the soft part seems to be adequate. Fitted parameter values are given in Table 1. As an example, Fig. 4 also shows a comparison between the hard- and soft-part strains for specimen 9963. Several interesting observations can be made when comparing theoretical with experimental results. (1) the soft part has a larger strain than the hard part at an early stage of uniaxial loading, even though the volumetric ratio \( \gamma_{t} \) is much lower than that for the hard part (Fig. 4). It is very likely that the stress sensitivity or the nonlinear responses of the rock can be generally attributed to the deformation or closure of some pores. (2) When applied stress loading on the rock frame increases, the shape of the soft-part pores changes, tending toward complete closure, while the hard-part pores remain hard and resist closure. Note that the Young’s (elastic) modulus for the soft part \( E_{t} \) ranges from 0.2 to 1.2 MPa, which is much smaller than the Young’s (elastic) modulus for the hard part \( E_{e} , \) which ranges from 2,164.5 to 3,345.1 MPa (Table 1). The difference between the Young’s (elastic) moduli indicates that the soft part, as expected, is subject to relatively larger deformation at low stress. (3) The estimated \( \gamma_{t} \) values for the 11 clay rock samples under consideration range from 0.11 to 0.69%, smaller than the typical porosity of Opalinus Clay rock (12–21%) (Corkum and Martin 2007). This difference suggests that the soft part is only a small percentage of the pore volume, if we assume that the soft part results purely from the pore space. The nonlinear response of porous rock mainly depends on the soft part rather than the entire pore space.

Table 1 Fitted parameter values from the experimental data for Opalinus Clay rock
Full size table
Fig. 4
figure 4

Comparisons between the hard-part and soft-part strains for specimen 9963

Full size image

MacBeth (2004) also found that the pressure-sensitivity of sandstone resulted from the closure of intra- and intergranular cracks, small-aspect-ratio pore spaces, and broken grain contacts, none of which consume any significant portion of the pore volume. Shapiro and Kaselow (2005) assumed that the main reason for load-induced changes in the elastic properties of a rock is the load-induced deformation of the pore space, and that a compliant part of the pore space played the more important role. Our work is generally consistent with these previous studies. However, it differs from them in that we are directly based on the reasoning that Hooke’s law should use natural strains, and that rock mass can be divided into hard and soft parts. This notion allows for the derivation of our stress–strain relationship, one that can be further used, in a systematic way, to generate formulations for stress-dependent rock properties with physically defined parameters. In contrast, most of the other studies focus primarily on some specific mechanical parameters, rather than general stress–strain relationships.

To further verify our stress–strain relationship, we compare our theoretical results with data from triaxial compression tests for shale rock (Xu et al. 2006) and conglomerate rock (Hu and Liu 2004). These triaxial tests involve a cylindrical rock sample subjected to confining pressure \( \sigma_{c} \) (corresponding to axial strain \( \varepsilon_{c} ) \) and a constant confining pressure \( \sigma_{c} , \) and then controlled increases in \( \sigma_{1} \) stresses. In these tests, the measured relationship between deviatoric stress \( (\sigma_{1} - \sigma_{c} ) \) and axial strain \( (\varepsilon_{1} - \varepsilon_{c} ) \) are generally reported and used in our evaluation. When the confining pressure is constant, applying Eq. 22 yields:

$$ \varepsilon_{1} - \varepsilon_{c} = \frac{{(3 - \gamma_{t} )}}{{3E_{e} }}(\sigma_{1} - \sigma_{c} ) + \frac{{\gamma_{t} }}{3}\exp \left( { - \frac{{\sigma_{c} }}{{E_{t} }}} \right)\left[ {1 - \exp \left( { - \frac{{\sigma_{1} - \sigma_{c} }}{{E_{t} }}} \right)} \right] $$
(23)

Figures 5 and 6 show the satisfactory matches of Eq. 23 with observed data from rock samples under triaxial compression conditions. The curve-fitted results indicate that the \( \gamma_{t} \) value ranges from 0.9 to 1.02% for the conglomerate rock, and is 1.65% for the shale rock. Because different rock samples are used for different stress conditions during triaxial compression tests, some variation in the fitted values for rock parameters are observed for a given rock type. The fitted parameter values are listed in Table 2.

Fig. 5
figure 5

Matches between results calculated from Eq. 23 and experimental data from triaxial compression tests on a conglomerate rock (Hu and Liu 2004)

Full size image
Fig. 6
figure 6

Matches between results calculated from Eq. 23 and experimental data from triaxial compression tests on shale rock (Xu et al. 2006)

Full size image
Table 2 Fitted parameter values from the experimental data
Full size table

To demonstrate the relative importance of the soft part under a triaxially stressed state, Fig. 7 shows the results of both the soft-part strain and the ratio of the soft-part strain to the hard-part strain as a function of axial stress (R denotes the ratio in the figure). The curve describes the overall deformation behavior of the soft part, showing a significant initial increase in strain with stress and then a slower change later. The shale rock sample shows a decrease in R with increased confining pressure at a given deviatoric stress, and also with increased axial stress at a given deviatoric stress. The conglomerate rock samples show behavior similar to clay rock.

Fig. 7
figure 7

Soft-part strain and R (the ratio of the soft-part strain to the hard-part strain) as a function of axial stress at different confining pressure for shale rock

Full size image

4 Stress-Dependent Mechanical and Hydraulic Rock Properties

Our newly developed stress–strain relationship allows the derivation of a variety of additional constitutive relationships among mechanical and hydraulic properties. This section presents the stress dependence of porosity, compressibility, and shear modulus as illustrative examples.

4.1 Porosity

Rock porosity is an important parameter for modeling coupled hydrological and mechanical processes, because flow processes occur in pore spaces. Following Liu et al. (2009), we assume that the soft part is a fraction of pore space. In this case, the rock porosity is defined by:

$$ {\text{d}}\phi = \frac{{{\text{d}}V^{\text{p}} }}{V} = \frac{{{\text{d}}V_{e}^{\text{p}} + {\text{d}}V_{t} }}{V} \approx \frac{{{\text{d}}V_{e}^{\text{p}} + {\text{d}}V_{t} }}{{V_{0} }} $$
(24)

where V is the bulk volume of rock and the superscript p refers to pore space. Liu et al. (2009) indicated that, for the purpose of calculating porosity, the total rock volume V could be approximated with the unstressed volume V 0, because their differences are small in practical applications.

For the hard part of the pore space, we have:

$$ \frac{{{\text{d}}V_{e}^{\text{p}} }}{{V_{0} }} = \frac{{V_{0,e}^{\text{p}} }}{{V_{0} }}\frac{{{\text{d}}V_{e}^{\text{p}} }}{{V_{0,e}^{\text{p}} }} = - \left( {\varphi_{0} - \gamma_{t} } \right)C_{e} ({\text{d}}\sigma_{1} + {\text{d}}\sigma_{2}^{{}} + {\text{d}}\sigma_{3} ) $$
(25)

To derive the above equation, we use the following relations:

$$ \frac{{V_{0,e}^{\text{p}} }}{{V_{0} }} = \varphi_{0} - \gamma_{t} $$
(26)

and:

$$ C_{e} = - \frac{1}{{3\,V_{0,e}^{\text{p}} }}\frac{{\partial V_{e}^{\text{p}} }}{{\partial \sigma_{i} }}\quad (i = 1, 2, 3) $$
(27)

where \( V_{0,e}^{p} \) is the hard part of the pore volume under unstressed conditions, \( \phi_{0} \) is the porosity under unstressed conditions, and \( C_{e} \) is the pore compressibility (and constant).

From Eq. 18 and its derivation procedure, it can be mathematically shown that the porosity change owing to the soft part, \( \frac{{{\text{d}}V_{t} }}{{V_{0} }} , \) is the same as the last three terms on the right-hand side of Eq. 18. Thus, based on Eqs. 24 and 25, we have:

$$ \begin{aligned} {\text{d}}\phi = & - (\phi_{0} - \gamma_{t} )C_{e} ({\text{d}}\sigma_{1} + {\text{d}}\sigma_{2}^{{}} + {\text{d}}\sigma_{3} ) \\ - \frac{{\gamma_{t}^{{}} }}{{3E_{t} }} \times \left[ {\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right){\text{d}}\sigma_{1} + \exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right){\text{d}}\sigma_{2} + \exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right){\text{d}}\sigma_{3} } \right] \\ \end{aligned} $$
(28)

Using the condition that the unstressed porosity is \( \phi_{0} , \) we obtain:

$$ \begin{aligned} \phi = & \phi_{0} - \gamma_{t} - \left( {\varphi_{0} - \gamma_{t} } \right)C_{e} (\sigma_{1} + \sigma_{2}^{{}} + \sigma_{3} ) \\ + \frac{{\gamma_{t} }}{3}\left[ {\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right) + \exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right) + \exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right)} \right] \\ \end{aligned} $$
(29)

We use the experimental results from uniaxial strain tests to verify our porosity–stress relation, or Eq. 29; relevant data are very limited for more complex stress conditions. Peng and Zhang (2007) reported a data set of porosity (as a function of axial stress) under uniaxial strain conditions for two sandstone specimens cored 1,000 m below the sea floor. Satisfactory matches between results calculated from Eq. 29 and porosity data are shown in Fig. 8. The curve-fitted results indicate that the value for \( \gamma_{t} \) ranges from 1.77 to 2.04% for the sandstone samples under consideration, and the \( E_{t} \) value is 5.0 MPa (Table 3).

Fig. 8
figure 8

Matches between the results calculated from Eq. 29 and experimental data from uniaxial strain tests for two sandstone specimens (Peng and Zhang 2007)

Full size image
Table 3 Fitted parameter values from the experimental data of sandstone samples
Full size table

A similar relationship between stress and porosity was also reported by Shapiro and Kaselow (2005). They assumed that pore space contains the so-called compliant porosity (similar to the “soft part” in this study) and also derived a number of relationships between stress and other mechanical properties under anisotropic conditions (Shapiro and Kaselow 2005). However, several important differences can be observed when comparing our theory with theirs. First, our theory is based on the natural-strain-based Hooke’s law, which is fundamentally different from the physical origin of Shapiro and Kaselow (2005). Second, their theory is theoretically valid only for rocks with moderate or small porosity, on the order of 0.1 or less (Shapiro and Kaselow 2005). As evidenced by the corresponding derivation procedures, our results are not subject to this limitation. Finally, the validity of Shapiro and Kaselow’s (2005) theory requires that their compliant porosity must be a very small part of the total porosity. Again, our theory is not limited by this constraint, largely because our theory has a different physical origin. It can be applied to cases in which the soft porosity is large. For example, Liu et al. (2009) successfully derived a relationship between stress and fracture aperture. Unlike the “soft” part of porous rock, the “soft” part in a fracture corresponds to a much larger portion of fracture voids than the hard part (Liu et al. 2009).

4.2 Bulk Compressibility

Bulk compressibility is often used to quantify the ability of a rock to reduce in volume with applied pressure. It may be defined in different ways. In this study, we define the bulk compressibility (associated with a principal stress \( \sigma_{i} ) \) by:

$$ C_{i} = \frac{{\partial \varepsilon_{v} }}{{\partial \sigma_{i} }}\quad (i = 1, 2, 3) $$
(30)

Based on the above equation and Eq. 18, the compressibility can be readily determined as:

$$ C_{i} = \frac{{(3 - \gamma_{t} )(1 - 2\gamma )}}{{3E_{e} }} + \frac{{\gamma_{t} }}{{3E_{t} }}\exp \left( { - \frac{{\sigma_{i} }}{{E_{t} }}} \right)\quad (i = 1, 2, 3) $$
(31)

Morgenstern and Tamuly Phukan (1969) investigated the relationship between the modulus of compressibility and stress for Bunter sandstone. We use the results from unconfined compression tests of Morgenstern and Tamuly Phukan (1969) to verify our compressibility–stress relation (Eq. 30). For unconfined compression tests, we need only to consider \( C_{1} , \) because \( \sigma_{2} = \sigma_{3} = 0 . \) As shown in Fig. 9, our relationship can satisfactorily match the data, further supporting our overall theoretical results developed for anisotropic conditions. The estimated parameter values for sandstone are presented in Table 4. Note that the compressibility, C, defined by Morgenstern and Tamuly Phukan (1969), is thrice the compressibility given in Eq. 30. In Fig. 9, the former is used. Note that the value for \( E_{t} \) is generally consistent with that reported in Table 3 for sandstone. However, the estimated \( \gamma_{t} \) values are much lower than those given in Table 3, which may be a result of rock porosity values in this part of the study being much lower as well.

Fig. 9
figure 9

Matches between the unconfined compression test data for Bunter sandstone (Morgenstern and Tamuly Phukan 1969) and the compressibility–stress relationship (Eq. 31). Imperial units are used here because of the source of the original data

Full size image
Table 4 Fitted parameter values from the experimental data for Bunter sandstone
Full size table

4.3 Shear Modulus

The shear modulus is an important parameter for various engineering projects. It can be described as:

$$ K_{xy} = \frac{{{\text{d}}\tau_{xy} }}{{{\text{d}}\gamma_{xy} }},\quad K_{xz} = \frac{{{\text{d}}\tau_{xz} }}{{{\text{d}}\gamma_{xz} }},\quad K_{yz} = \frac{{{\text{d}}\tau_{yz} }}{{{\text{d}}\gamma_{yz} }} $$
(32)

where \( \tau \) and \( \gamma \) are the shear stress and strain, respectively, sand x, y, and z are spatial coordinates. Based on the above definitions and the results from the “Appendix”, the shear modulus \( K_{xy} \) can be easily determined as:

$$ K_{xy} = \frac{1}{{\frac{{2(3 - \gamma_{t} )(1 + \nu )}}{{3E_{e} }}\, + \frac{{2\gamma_{t} }}{{3E_{t} }}\left[ {\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right)\frac{{{\text{d}}\sigma_{1} }}{{{\text{d}}\tau_{xy} }}l_{1} m_{1} + \exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right)\frac{{{\text{d}}\sigma_{2} }}{{{\text{d}}\tau_{xy} }}l_{2} m_{2} + \exp \left( { - \frac{{\sigma_{3} }}{{E_{t} }}} \right)\frac{{{\text{d}}\sigma_{3} }}{{{\text{d}}\tau_{xy} }}l_{3} m_{3} } \right]}} $$
(33)

Under the stress condition of \( \sigma_{2} = \sigma_{3} , \) one can obtain:

$$ K_{xy} = \frac{{{\text{d}}\sigma_{1} - {\text{d}}\sigma_{2} }}{{\frac{{2(3 - \gamma_{t} )(1 + \nu )({\text{d}}\sigma_{1} - {\text{d}}\sigma_{2} )}}{{3E_{e} }} + \frac{{2\gamma_{t} }}{{3E_{t} }}\left[ {\exp \left( { - \frac{{\sigma_{1} }}{{E_{t} }}} \right){\text{d}}\sigma_{1} - \exp \left( { - \frac{{\sigma_{2} }}{{E_{t} }}} \right){\text{d}}\sigma_{2} } \right]}} $$
(34)
$$ K_{xy} = K_{yz} = K_{xz} $$
(35)

Stress-dependent data for the shear modulus are relatively limited in the literature. Thus, we use the results calculated from Eq. 34 (with estimated parameters from Table 1) to demonstrate the stress-dependent behavior of the shear modulus in Fig. 10. No comparison is made with experimental observations. However, note that Eq. 34 is the direct result of a mathematical transformation of Eq. 8. The validation of Eq. 8, discussed above, is equivalent to that of Eq. 34. For simplicity, we set \( \sigma_{2} = \sigma_{3} = 0 \) in Fig. 10, which shows the strong stress dependence of the shear modulus at low stress values.

Fig. 10
figure 10

Shear modulus versus \( \sigma_{1} \)for three rock samples with the parameter values given in Table 1

Full size image

5 Conclusions

In this paper, we describe the development of a stress–strain relationship for porous rock under elastic and anisotropic conditions. We showed that this new relationship could satisfactorily represent a number of experimental observations. Furthermore, based on this relationship, we derived additional constitutive relations between stress and selected mechanical and hydraulic properties. The consistency between this relationship and the gathered data further supports its usefulness and validity. However, the work only deals with isotropic rocks and further studies are needed for structurally anisotropic rocks.