1 Introduction

The brittle fracture of many products and construction often seems an unforeseen phenomenon. It is explained by the fact that the process of final fracture is due to the rapid propagation of cracks which happens faster comparing with the durability of the construction. The investigation of the phenomenon of fracture as process evaluating during time is very important for forecasting and estimating of the resource of a construction. Since the time of tests or experiments is limited, while the resource of many constructions must far exceed duration of such tests, it is important to extrapolate the test results for longer periods. It is especially important to study the long-term strength of rocks, since the actual service period of mining objects exceeds any achievable experiment time. Although many building materials and rocks work in compression, knowing the value of the tensile strength is extremely important. A simple calculation shows account the internal structure of the medium and the presence of boundaries leads to the appearance of areas in the specimen that experience tension under unequal compression. In fact, material is fractured by tensile tension under compressive stresses at the macro level (Davis et al. 2017; Shen and Barton 2018).

The study of fracture developing in time from the position of a deterministic models based on the kinetics of the breaking of molecular bonds was initiated by the Busse et al. (1942), Tobolsky and Erying (1943). This model has been seriously developed in the researches of Zhurkov (1984), Betekhtin and Zhurkov (1971) and Zhurkov team. Coleman (1957, 1958) first proposed a statistical model of the lifetime of fibrous materials and Phoenix and Tierney (1983), Schwartz (1987), Ibnabdeljalil and Phoenix (1995), Mahesh and Phoenix (2004) are developed this model for brittle materials. The modern models, based on kinetics of crack growth in quasi-brittle materials for determining lifetime are developed by Amitrano and Helmstetter (2006), Nara (2015), Zhou (2004), Bažant and Pang (2007), Bažant et al. (2009), Le et al. (2009, 2011, 2013), for estimate the dynamic characteristics of fracture by Zhou and Yang (2007), Bhat et al. (2012), Le et al. (2018).

To describe the fracture during time, it is convenient to divide the whole process into separate stages. The researcher divides the process of fracture into two or more stages in order to concentrate and determine consistent patterns in the destruction. Each stage takes its share in durability, although it is conditional. In this paper, the process of fracture is proposed to be divided into two periods: the fracture of solid specimens and cracked specimens. Such a partition makes sense, because the modern phenomenological description of these two stages of the destruction is not carried out uniformly. When a solid sample is fractured damages accumulate in almost the entire volume and are controlled by the applied stress. This process is non-localized (Regel et al. 1974), the process of crack propagation (destruction of the cracked specimens) is extremely localized and controlled by the stress intensity factor of crack tip (Cherepanov 1974; Parton and Morozov 1985). The aim of the presented work is to compare the characteristic parameters of rock fracture in both stages of destruction. One of the possible methods to obtain parameters of long-term strength is tests of the specimens at the corresponding stressed state at different loading rates (Lajtai et al. 1991; Qi et al. 2009; Liang et al. 2015; Yang 2015; Femau et al. 2016; Winner et al. 2018). To determine the parameters of rock fracture in case of the main crack, a similar approach is used to study of dependence of fracture toughness at loading rate. Similar tests of various rocks are described in (Bažant et al. 1993; Zhang et al. 1999; Backers et al. 2003; Zhou et al. 2009, 2010). Many of mentioned authors use interpolation of the fracture rate (damage accumulation, growth of subcritical cracks) by the power law of the stress field. At the same time, the fracture toughness of limestone Bažant et al. (1993), marble and gabbro Zhang et al. (1999), and sandstone Backers et al. (2003) does not depend on the loading rate in the static range, but Zhou et al. (2009, 2010) report the fracture toughness of the Huanglong limestone is proportional to the logarithm of the loading rate in same range. Therefore, the study and analysis of fracture toughness of rocks from the loading rate must be continued.

2 Experimental Methods

Tensile tests of marble, granite and gabbro-diorite were carried out on disk specimens a diameter of 37.6 mm, a thickness of 19–20 mm. All specimens were drilled with a diamond bit from the same plate, after the specimens were kept during long time under the same conditions, in order to minimize the variance of strength. Fracture of all specimens was carried out along a certain direction. To stabilize the contacts of the specimens with loading plates, fluoroplastic membrane (50 μm in thickness) were used. Seven specimens loaded by diameter were fractured at each loading rate. The test scheme is shown in Fig. 1.

Fig. 1
figure 1

The scheme on Brazilian test: 1-specimen

Full size image

The test bench of UME-10TM had 5 rates of displacement from 0.005 to 50 mm min−1, which corresponded to the loading rates from 0.001 to 100 MPa/s. The load F from time was recorded during the tests. The strength was determined according to the maximum load.

Three-point bending applied to study the effect of loading speed on the fracture toughness of marble, gabbro-diorite and dolerite. The specimens, 20 × 20 × 120 mm beams, were cut from the same plates as discs for tensile test. The specimens had a cut-through from 5 to 9 mm, applied by a diamond disk thickness of 1 mm.

The plane of beams and disks fracture coincided. The beams were leaned on rolling bearings on a 100 mm base. The test scheme is shown in Fig. 2. The fracture toughness of rock was measured over a range of loading rates from 5 × 10−4 to 50 MPa m1/2 s−1.

Fig. 2
figure 2

The test scheme on fracture toughness

Full size image

The critical stress intensity factor was calculated according to the fixed maximum load and the initial crack length.

3 Test Results

3.1 Tensile Strength

The Brazilian tests let to construct a graph of the maximum fracture stress at the loading rates. Tensile stress:

$$\sigma = 2F/(\pi Dt),$$
(1)

where D, t—diameter and thickness of the specimen, respectively, F—maximum value of the fracture force was determined at each test. The average values of tensile stress determined from 7 tests at each loading rate, are shown in Fig. 3. For each rock the tests were carried out at 5 rates, differing by an order of magnitude, the average values of the calculated stress and the standard deviation are presented in Table 1. As follows from the diagrams presented in Fig. 3, increasing in the loading rate leads to increasing of the fractured stress, which can be approximated by a linear dependence in semi logarithmic coordinates. The parameters of the approximating lines are also shown in the Fig. 3.

Fig. 3
figure 3

Relationship between tensile stress of rocks and loading rate: 1—marble; 2—granite; 3—gabbro-diorite

Full size image
Table 1 Results of statistical processing of Brazilian tests
Full size table

3.2 Fracture Toughness of Rocks

There are many schemes for testing of fracture toughness. For the purposes of this article it does not matter which one to use. The scheme destruction of the beam with a cut was chosen, because of the ease of preparation of samples. According to the method (Srawley 1977), the determination of the critical stress intensity factor is carried out by testing samples with a through crack of known length at a certain loading rate. The influence of the loading rate on the fracture toughness of rocks was learned on marble, gabbro-diorite and dolerite. The thin through cut simulated a crack. As shown by Ouchterlony (1982) such cut in the rock specimen effectively simulates a crack, and the calculated value of the critical stress intensity factor K1c differs little from the values K1c obtained by real cracked specimens. This is due to the originally defective structure of the rocks. The results of the tests were processed using the following formula for three-point bending (Srawley 1977):

$$K_{1} = \frac{{3F\Delta a^{1/2} }}{{2Wt^{2} }}\left( {1,96 - 2,75\frac{a}{t} + 13.66\left( {\frac{a}{t}} \right)^{2} - 23 , 9 8\left( {\frac{a}{t}} \right)^{3} + 25,22\left( {\frac{a}{t}} \right)^{4} } \right),$$
(2)

where F is the maximum force at the moment of fracture, Δ is the distance between rolling bearings, W, t are the width and thickness of the specimen, respectively, a is the length of the cut.

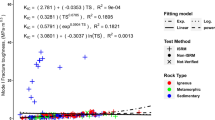
The maximum value of stress intensity factor at the moment of crack start was determined for each test. Tests of gabbro-diorite and dolerite were carried out at three loading rates differing by two orders of magnitude, tests of marble at four rates differing by an order of magnitude. At each loading rate, five samples were tested. The processing of test results (average value and standard deviation) is presented in Table 2. The average calculated fracture toughness values and the approximating line are shown in Figs. 4 and 5, according to loading rate.

Table 2 Results of statistical processing of fracture toughness tests
Full size table
Fig. 4
figure 4

Relationship between fracture toughness of marble and loading rate

Full size image
Fig. 5
figure 5

Relationship between fracture toughness and loading rate: Δ—gabbro-diorite ■—dolerite

Full size image

4 Discussion

The selected range of loading rate corresponds to static tests. Dynamic effects of a sharp increase of strength and fracture toughness from the loading rate in this range are absent. Mainly interest by such tests is due to the possibility of extrapolating the obtained results for significantly longer time periods. For such industries as the construction and service of responsible structures, the extrapolation long-term strength values are necessary for estimating the residual lifetime of the structures. At reduction of loading rate there are trends of the strength and fracture toughness of rocks reduce according to the linear law from loading rate logarithm, that is in consent with researches (Tomashevskaya and Khamidullin 1972; Stavrogin and Pevzner 1974; Belendir et al. 1991; Efimov 2007). This trend allows extrapolation of strength values for a longer period up to a certain limit, estimation of the limit is discussed at the end of the paper.

Approximations, Figs. 3, 4 and 5, have a universal form: an increasing of the values of fracture stresses and fracture toughness according to logarithmic increasing of loading rate, and a high degree of accuracy of approximation. This character of the dependence of strength and fracture toughness at the loading rate confirms the correctness of the kinetic thermofluctuation concept of strength, the principles of which were formulated by Zhurkov (1968). The account of the thermal motion of molecules, and not only of the applied external forces, in the failure, forms the basis of this concept. The kinetics of accumulation of destroyed molecule connections due to thermal fluctuations into applied stresses field leads to a characteristic dependence of the of the sample from the applied external stress and temperature:

$$\tau = A\exp ( - \alpha \sigma ) = \tau_{0} \exp \left( {\frac{{U_{0} - \gamma \sigma }}{RT}} \right),$$
(3)

where τ is the lifetime of the sample, τ0 is the period of the thermal vibrations of the molecules, T is the absolute temperature, R is the universal gas constant, and σ is the effective constant stress, U0 is initial fracture activation energy, γ is structure-sensitive parameter.

At a constant loading rate, this model gives the following relationship between the magnitude of the maximum fracture stress and the loading rate (Regel et al. 1974):

$$\sigma_{tens} = \frac{\ln A\alpha }{\alpha } + \frac{1}{\alpha }\ln \dot{\sigma },$$
(4)

where \(\dot{\sigma }\)—loading rate, the parameters A and α are the same as in (3).

The spread of cracks in the kinetic concept of strength also has a thermo-fluctuation character. According to Cherepanov (1969), the velocity of subcritical main cracks is described by the following equation:

$$\frac{dL}{dt} = \dot{L}_{0} \exp \,\left( { - \frac{{U_{0}^{crack} - \xi {\kern 1pt} K_{1} }}{RT}} \right) = V_{0} \exp \beta K_{1} ,$$
(5)

where L is the length of the main crack, \(\dot{L}_{0}\), V0 are the coefficients of the velocity dimensionality, К1 is the stress intensity factor, \(U_{0}^{crack}\) is the initial activation energy of the fracture, and ξ, β are the proportionality parameters. The stress intensity factor is the characteristic of the local field of stress at the crack tip.

Fracture toughness tests are performed at a constant loading rate. In these conditions, the stress field at the crack tip grows proportionally to a fixed value \(\dot{{\mathcal{K}}}_{1}\). At the moment when the stress intensity factor reaches the critical value K1c, there is a sharp change in the crack propagation mode. The moment of time tp and the corresponding load are fixed on the loading diagram. The condition of transition to the critical mode is written in the following form, which corresponds to the exhaustion of local strength:

$$\frac{1}{\Delta l}\int\limits_{0}^{{t_{p} }} {\frac{dL}{dt}dt} = 1,$$
(6)

where Δl is the crack increasing. The test conditions assume \(\Delta l < < L_{0}\), where L0 is the initial crack length, which is used in the calculation formulas. Substituting (5) into (6) and integrating, we find the connection between К1c and \(\dot{{\mathcal{K}}}_{1}\):

$$V_{0} (\exp (\beta K_{1c} - 1) = \Delta l\beta \dot{K}_{1}$$
(7)

Refusing the small terms and finding the logarithm (7), we obtain an equation that looks like (4) (Efimov 2016):

$$K_{1c} = \frac{{\ln {\text{B}}\beta }}{\beta } + \frac{1}{\beta }\ln \dot{K}_{1} ,$$
(8)

where K1c is the critical stress intensity factor, \(\dot{{\mathcal{K}}}_{1}\) is the rate of change of the stress intensity factor, the parameter B = \({\raise0.7ex\hbox{${\Delta l}$} \!\mathord{\left/ {\vphantom {{\Delta l} {V_{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${V_{0} }$}} = {\raise0.7ex\hbox{${\Delta l}$} \!\mathord{\left/ {\vphantom {{\Delta l} {\dot{L}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\dot{L}}$}}_{0} \exp (U_{0}^{crack} /RT)\).

The coefficient \(\dot{L}_{0}\) corresponds to the crack propagation velocity in a specific case \({{\left( {U_{0}^{crack} - \xi K_{1} } \right)} \mathord{\left/ {\vphantom {{\left( {U_{0}^{crack} - \xi K_{1} } \right)} {RT}}} \right. \kern-0pt} {RT}} \to 0\); such a crack will jump the distance \(\Delta l\) for a period of thermal oscillation. Thus B = \(\tau_{0} \exp (U_{0}^{crack} /RT)\).

The experimental dataset, Fig. 4, 5 confirm this dependence and allow to calculate the parameters β and B from the approximation. Parameters A and α were calculated from the dataset, Fig. 3 and parameters B, β and are presented in Table 3. The calculated values of the initial activation energy of the fracture \(U_{0}^{\text{tens}}\) and \({\text{U}}_{ 0}^{\text{crack}}\) presented in Table 3 do not relate to a molecular connection, but to one mole of medium, are determined at T = 293°K and \(\tau_{0} = 10^{ - 13} s\):

Table 3 Kinetic parameters of rocks fracture, obtained from tests of strength and fracture toughness tests
Full size table
$$A = \frac{{\exp (\alpha \sigma_{p} )}}{{\alpha \dot{\sigma }}};\,\,\,U_{0}^{tens} = RT(\ln A - \ln \tau_{0} ) = 2.3RT(\lg A + 13)$$
(9)
$$B = \frac{{\exp (\beta K_{1c} )}}{{\beta \dot{K}_{1c} }};\,\,\,U_{0}^{crack} = RT(\ln B - \ln \tau_{0} ) = 2.3RT(\lg B + 13)$$
(10)

A comparison of the results of determination of the initial activation energy of fracture obtained from the fracture of solid samples by the Brazilian method (columns 4) and samples of rocks with a crack tested for three-point bending (columns 7) is given in Table 3.

The coefficients of proportionality in (4) and (8) have different dimensions. Since the effective stress at the crack tip is proportional \({\mathcal{K}}_{1} /\sqrt \delta\) (Cherepanov 1969), where δ is the structural parameter of the medium, the proportionality coefficients in (4) and (6) are related by: \(\beta \approx \alpha /\sqrt \delta\). The structural parameter can be represented as a stress averaging site near the crack tip where the average stress is equal to the tensile strength measured in a uniform field (the integral criterion of Novozhilov), (Legan 1993, Efimov 2011):

$$\delta = \frac{2}{\pi }\left( {\frac{{{\mathcal{K}}_{1c} }}{{\sigma_{tens} }}} \right)^{2} ,$$
(11)

where \(\sigma_{tens}\) and \({\mathcal{K}}_{1c}\) are the tensile strength and the critical stress intensity factor, measured according to the standard.

Comparison of columns 8 and 9 of Table 3 confirms this relationship. From Table 3, we can conclude: the characteristic parameters of non-localized and localized rocks fracture are the same.

Extrapolation of strength values for much longer periods of time is closely related to the question of what are the limit strength values for this model. The account of thermal motion leads not only to destroy molecular connections but also to their recombination. The recombination of molecular connections, is not accounted the equation of durability (3). According to (Efimov and Nikiforovsky 2010) there is the stress that determines the equilibrium between the destroyed and recombinant connections and an estimate of this stress called safe is proposed. The value of the safe stress is a horizontal asymptote, to which extrapolated strength values tend.

5 Conclusions

As shown by the experimental results, the loading rate and strength and fracture toughness of the tested rocks are related by the equation: \(\sigma = a + e\ln \dot{\sigma }\) and \({\mathcal{K}}_{1c} = c + d\ln \dot{K}_{1}\) in the range of loading rates of 10−3–102 MPa s−1. The kinetic concept of fracture of Zhurkov S.N. predicts this behavior of strength and fracture toughness.

The presented tests enable to calculate the initial activation energy of fracture, both for tension by the Brazilian method and for rocks fracture toughness. The calculated values of the initial fracture activation energy are practically the same.

The proportionality parameters determined by the angles of slope of the approximation straight lines for tensile tests and fracture toughness are interconnected by means of the structural parameter of the medium.

The obtained experimental results and the calculated constants of rocks, allow predicting the strength values after a long period of time based on the extrapolation of the strength values measured by the standard, as well as the resource.