1 Introduction

Optical approaches such as interferometry techniques have widely been used to measure deformation of a material element (Jones and Wykes 1989; Cloud 1998; Dally and Riley 2005). For example, holographic interferometry, moire interferometry, and speckle interferometry are popular non-contact laboratory methods used in observing surface displacements. Because the wavelength of light is on the order of tenths of microns, it is possible to achieve detailed resolution of displacement measurements. Applications of laser holographic interferometry to brittle materials have generally involved fracture studies, where observations of crack opening displacements (COD) have been reported (Shah 1990; Shah and Choi 1999). In addition, the crack profiles in a center-notched plate were accurately measured using holographic interferometry (Miller et al. 1988), and moire interferometry was used to determine the distribution of COD along the process zone of a stably growing crack (Du et al. 1990; He et al. 1995). Moire interferometry was also used to analyze rapid crack growth in an impact loaded three-point-bend concrete specimen (Yu et al. 1993).

Of particular interest in the area of experimental rock mechanics is electronic speckle pattern interferometry (ESPI), which can be attributed to Leendertz (1970). Butters and Leendertz (1971) and Macovski et al. (1971) simultaneously demonstrated the use of television systems as recording devices, rather than photographic techniques, generating interference fringe patterns based on electronic signal processing. Jones and Wykes (1989) offered a complete description of ESPI principles, and Petzing and Tyrer (1998) provided a summary of ESPI applications for measurement of surface displacements.

A variety of ESPI configurations allows for accurate measurement of in-plane and/or out-of-plane displacements with little or no specimen preparation. Chen and Labuz (2006) demonstrated the utility of ESPI by obtaining high-resolution surface displacements during wedge indentation experiments. Facchini and Zanetta (1995) used ESPI as a tool to setup an in-plane deformation inspection system, which was applied to the evaluation of some mechanical characteristics of masonry components. Other applications of the ESPI technique included monitoring of crack propagation in fracture testing (Horii and Ichinomiya 1991; Maji and Wang 1992; Labuz and Biolzi 2007), and observing the development of microcracks in carbon-fiber-reinforced concrete specimens (Jia and Shah 1994). ESPI has the ability to furnish information about the three-dimensional displacement field, including the measurements of out-of-plane displacements (Hack et al. 1995).

Thus, it is clear that ESPI is a sensitive technique to measure displacement, but its application to rock mechanics studies has been limited. The objective of this paper is to explain the theory of ESPI and demonstrate its usefulness in laboratory testing.

2 Background of ESPI

Electronic (or digital) speckle pattern interferometry involves the analysis of a speckle pattern to obtain information about surface displacements on a test specimen. Speckle correlation infers a comparison between two related speckle images, usually between a reference image and an object image. The method does not yield any information about processes occurring within a specimen, but only displacement at the surface.

2.1 Speckle Patterns

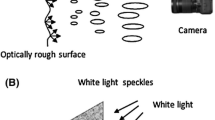
A speckle pattern is created when monochromatic light interacts with an optically rough surface, which is any surface that is not smooth in comparison to a wavelength of light. The phenomenon can be observed by illuminating most common surfaces with a laser, where the resulting digital image is defined by dark and bright spots called speckles (Fig. 1). The speckles are created by the interference of light as it is scattered by the optically rough surface. Each bright or dark speckle is the result of a large number of smaller contributions (superpositions) from a large number of scattered waves. Goodman (1976) compared speckles to a random-walk phenomenon and showed that as long as the number of elementary contributions was large and two criteria were met, the intensity distribution p(I) for a speckle image followed a negative exponential distribution:

$$ p(I) = \left\{ \begin{gathered} \left( {{\frac{1}{{\overline{I} }}}} \right)\exp \left( {{\frac{ - I}{{\overline{I} }}}} \right),\quad I \ge 0 \hfill \\ 0,\quad \quad \quad \quad \quad \quad I < 0 \hfill \\ \end{gathered} \right. $$
(1)

where irradiance I is the intensity of light at a point and \( \overline{I} \) is the mean irradiance. The two criteria are (1) the amplitude and phase of an elementary contribution are independent of each other as well as all other contributing amplitudes and phases, and (2) there is equal probability to find a phase between π and −π anywhere within the field of interest. The intensity distribution means dark speckles are more probable to be observed, but there are always a few bright speckles present (Lehmann 2001). Most solid materials meet the criteria and have sufficient roughness.

Fig. 1
figure 1

Digital image of a speckle pattern captured by a CCD camera

Full size image

The speckle effect was originally thought of as a nuisance, an effect causing laser illuminated surfaces to appear grainy. Butters and Leendertz (1971) and Macovski et al. (1971) showed that the speckle effect could be used as an effective tool to measure surface displacements on a specimen. The superposition of two speckle images double exposed on a single photographic plate produced fringes, which were shown to represent surface displacements. Jones and Wykes (1989) presented a notable description of speckle techniques in their treatise on holographic and speckle interferometry. Methods were developed to increase the measurement clarity and sensitivity of speckle interferometry (Creath 1985; Sirohi and Mohan 1993). As computer processing became more robust, research switched from exposing photographic plates in a dark room to digital frame grabbers, cameras, and real time processing. Computer advances made speckle interferometry a practical experimental technique, where ESPI can be applied to a variety of testing applications.

2.2 In-Plane ESPI Theory

In-plane ESPI displays the surface displacements occurring in two directions, although a simultaneous multi-directional ESPI system increases the setup complexity (Moore and Tyrer 1990; Moore et al. 1996). A single direction, in-plane ESPI system is the focus of this paper and only theory describing this technique will be presented (Jones and Wykes 1989; Cloud 1998; Dally and Riley 2005).

The in-plane ESPI physical configuration requires the specimen surface to be illuminated by two identical plane wavefronts. The two incident beams are considered two individual object beams and no reference beam is used. The two identical wavefronts are created from a single laser beam that is expanded, collimated, and passed through a non-polarizing beam splitter. The two identical beams are then directed by mirrors to illuminate the specimen surface at equal angles (Fig. 2). When each beam, I 1 and I 2, illuminates a surface, the resulting scattering forms a speckle pattern. The pattern can be captured by a charged couple discharge (CCD) camera.

Fig. 2
figure 2

Illumination of a specimen surface by two identical light beams, I 1 and I 2. Note the beams are incident at equal angles to the surface normal

Full size image

The intensity I at any given point in the image plane can be represented by

$$ I_{\text{ref}} = I_{1}^{2} + I_{2}^{2} + I_{1} I_{2} \cos \gamma $$
(2)

where I 1 and I 2 are the amplitudes of each original wave and γ is the phase difference between the two waves. If a displacement \( \overline{u} = u_{x} \overline{i} + u_{y} \overline{j} + u_{z} \overline{k} \) (a bar indicates a vector) occurs, where u x is the horizontal (x-direction) component, u y is the vertical (y-direction) component, and u z is the out-of-plane (z-direction) component, the new intensity I current for the point on the image plane becomes

$$ I_{\text{current}} = I_{1}^{2} + I_{2}^{2} + I_{1} I_{2} \cos \left( {\gamma + \Updelta \phi } \right) $$
(3)

where Δϕ is the phase change caused by the displacement \( \overline{u} . \)

Speckle pattern correlation by subtraction is the method promoted for analysis. The difference between before and after intensities is given as

$$ \left( {I_{\text{ref}} - I_{\text{current}} } \right) = 2I_{1} I_{2} \sin \left( {\gamma + {\frac{1}{2}}\Updelta \phi } \right)\sin \left( {{\frac{1}{2}}\Updelta \phi } \right) $$
(4)

Phase is dependent upon the wavelength of light and the path that the beam of light travels. An important simplifying assumption is that any change in the phase is entirely due to surface displacement. The phase change Δϕ that occurs in each beam (I 1 and I 2) is expressed as

$$ \Updelta \phi_{1} = \left( {\overline{k}_{3} - \overline{k}_{1} } \right) \cdot \overline{u} \quad {\text{and}}\quad \Updelta \phi_{2} = \left( {\overline{k}_{3} - \overline{k}_{2} } \right) \cdot \overline{u} $$
(5)

where propagation vectors \( \overline{k}_{n} \) represent the path over which the beam I n travels. Vectors \( \overline{k}_{1} \) and \( \overline{k}_{2} \) represent the position from the mirror to the specimen surface and vector \( \overline{k}_{3} \) is the position from specimen to the camera. Equation 5 can be expanded for each beam:

$$ \begin{gathered} \Updelta \phi_{1} = {\frac{2\pi }{\lambda }}\left[ {u_{x} \sin \theta + u_{z} \left( {1 + \cos \theta } \right)} \right]\quad \hfill \\ \Updelta \phi_{2} = {\frac{2\pi }{\lambda }}\left[ { - u_{x} \sin \theta + u_{z} \left( {1 + \cos \theta } \right)} \right] \hfill \\ \end{gathered} $$
(6)

where 2π/λ is the magnitude of the propagation vector. The angle θ is the angle of incidence of the two beams, as shown in Fig. 2; note θ 1 = θ 2 = θ. The expressions are derived assuming the beams are contained within the x–z plane. The total phase change Δϕ from Eq. 6 is then determined by subtracting the phase changes on each individual beam:

$$ \Updelta \phi = \Updelta \phi_{1} - \Updelta \phi_{2} = \left( {{\frac{4\pi }{\lambda }}} \right)u_{x} \sin \theta $$
(7)

A dark speckle occurs when the total phase change is zero or a multiple of 2π. The condition is met when

$$ u_{x} = {\frac{n\lambda }{2\sin \theta }} $$
(8)

The system described is sensitive to displacements in the x-direction only. It could also be shown that if the beams were not completely contained within the x–z plane and there was a small angle between the surface normal and the y-axis, the system would still be sensitive to only the x-direction with the condition that the angle in the y–z plane was equal for both beams (I 1 and I 2).

3 Experimental Setup

3.1 Optical Equipment

A unidirectional, in-plane ESPI system was constructed. All of the components were attached to an optical board measuring 749.3 × 1181.0 mm with 25.4 mm spaced holes. Figure 3 shows the layout of the optical setup. A 17 mW laser (Model 25LHP925-249, Melles Griot, Los Angeles, CA) with wavelength of 632.8 nm was used for illumination. The beam path was directed by two mirrors to an expansion and collimating lens combination. Expansion of the beam was necessary to create a beam diameter that illuminated a desired area of the specimen surface. Collimation of the beam created a plane wavefront, which was required for the specific type of ESPI technique utilized. The incident beam, with diameter D i , travels through lens L 1, which focused the beam to a point at its focal length f 1. The beam then expanded over the focal length, f 2, of lens L 2. The beam passed through lens L 2 and emerged as a plane wavefront with diameter D o (Fig. 4).

Fig. 3
figure 3

ESPI schematic of the optics, indicating the beam travel path. M mirror, L lens, NPBS non-polarizing beam splitter

Full size image
Fig. 4
figure 4

Expansion and collimating mechanism for the laser beam

Full size image

After expansion, the beam was directed by a mirror through a filter and then through a non-polarizing beam splitter. The filter allowed for adjustment of the beam intensity, which can become an issue if a highly reflective material is tested and the resulting recorded digital image becomes “washed out” by the light intensity level reflected from the specimen surface. The beam splitter separated the original beam into two identical subsequent beams that were directed with mirrors to the surface of the specimen at equal angles to the normal of the specimen surface.

Of critical importance with any optical testing setup is vibration isolation. To eliminate environmental noise, a table with significant mass was constructed of three legs made from granite blocks and a large limestone slab placed on top of the legs. Foam padding and four partially inflated pneumatic-tubes were placed on top of the limestone block. The optics board was then lowered onto the pneumatic-tubes. A small amount of dead weight (three 20 kg blocks) was then placed on the optical board. The weight of the entire board assembly caused the pneumatic-tubes to become compressed and act as shock absorbers for vibrations.

3.2 Image Processing

To capture the changing speckle intensities during a test, a MicroPix (Ann Arbor, MI) M1024 IEEE-1394 CCD Camera with 1024 × 768 effective square pixels was used in combination with a Computar lens (Model M3Z1228MP, Commack, NY) with manual control of aperture, focus, and zoom. The camera cabling to the computer used an IEEE-1394 or “firewire” connection, which is a standardized specification that allows for data transfer speeds of up to 400 Mb/s. To acquire the digital images, Mathwork’s Matlab Ver. 6.5 with Image Acquisition and Processing Toolboxes (MathWorks, Natick, MA) was utilized. Ten images were acquired at a rate of 7.5 frames/s, with 1 s down time for data transfer of the ten frames.

To process digital images, a reference frame is selected and the pixel intensity values (0–255) are subtracted from another frame. The absolute value of the difference of the intensity values for the images is determined, because negative intensity values have no physical meaning. The video signal is assumed linearly proportional to the actual intensities of the speckle pattern. If speckle intensities are higher than the saturation level of the camera (upper limit of camera detector cells to capture a change in intensity), the original beam could be passed through a filter.

Figure 5 indicates the before and after speckle patterns and the resulting fringe obtained from signal subtraction. The processed image is called an ESPI image, which is different from the digital image taken by CCD camera. The brightness observed on the monitor accurately represented the interference phenomena occurring by subtracting digital images. Knowing the angle θ and the wavelength λ, the sensitivity of the system can be determined.

Fig. 5
figure 5

The ESPI image represents the absolute value difference of intensity values between speckle images I current and I reference

Full size image

3.3 Sensitivity of ESPI

The ESPI system in this work is only sensitive to the horizontal (x-direction) displacements. It is the horizontal displacements that form the fringe pattern in the ESPI image, as shown in Fig. 5. Thus, the fringe pattern can be used to determine the horizontal displacement between two digital image frames, which represent the corresponding loading or stress states in a certain testing configuration. The sensitivity of the ESPI system is the minimum horizontal displacement such that the change of the fringe pattern can be observed on the ESPI image. The spacing of fringes on ESPI image is very sensitive to horizontal displacement. It was shown that the sensitivity of the system S can be represented by Eq. 8:

$$ S = {\frac{\lambda }{2\sin \theta }} $$
(8)

where λ is the wavelength of light (0.6328 μm), and θ is the angle between the incident beam of light and the normal of the specimen surface. The angle θ was determined by measuring the distances, as indicated in Fig. 6, on the optics table:

$$ \tan \theta = {\frac{x}{2l}} $$
(9)

where x is the half-distance between the two mirrors and l is the length between the specimen and the midpoint distance between the two mirrors. Since the mirrors directing the two beams of light to the specimen were not parallel to each other, the maximum and minimum distances were measured for x and the mean, x m , was determined (x m  = 565 mm). The total distance l = 540 mm was the sum of lengths l 1 and l 2. On average, l 1 measured 268 mm, which represented the distance from the specimen to the camera lens. The measurement l 2 is the distance between the front camera edge and the line x, and it remained constant for all tests (l 2 = 272 mm). Substituting x m  = 565 mm and l = 540 mm into Eq. 9, angle θ = 27.6°. Substituting θ into sensitivity equation, the sensitivity S was

$$ S = 0. 6 8\,\mu {\text{m}}/{\text{fringe}} $$

Small changes in the distance l 2 could occur due to focusing and other adjustments, so the effect of any change was determined. An extreme error of ±5 mm was applied to l 2, which resulted in the distance l ranging from 535 to 545 mm. The resulting θ values ranged from 27.4° to 27.8° and the calibration was, respectively, 0.68–0.69 μm/fringe. The expected sensitivity value for the ESPI system was rounded to the nearest tenth of a micron and taken as 0.7 ± 0.05 μm.

Fig. 6
figure 6

Schematic diagram of the optical measurements used to determine the system resolution

Full size image

3.4 Limitations of ESPI

The primary assumption associated with the analysis of surface displacements relies on changes in phase occurring solely due to the displacement of interest, such as that due to deformation. Environmental vibration may contribute to the surface displacement, thereby skewing the resulting data and creating fictitious deformation. Thus, it is important to isolate the optics system from vibrations. In addition, any power fluctuations that occurred at the light source affected the speckle images. This was not a problem, however, as the source was stable.

Another limitation to consider with ESPI is the decorrelation effect. After an amount of displacement occurs with respect to a reference frame, the observed fringes become difficult to discern, that is, fringes became unrecognizable or “decorrelated.” Fringes form by capturing phase changes. If a phase change is large enough, there is no connection between the phase in the reference and current frame. Any alteration of the relative phase relationship within each speckle is the cause for decorrelation (Cloud 1998). Even though the system is sensitive to only in-plane displacements, a large out-of-plane displacement could cause a relative phase relationship alteration.

4 Experimental Results

4.1 Rigid Body Translation

The simplest application of ESPI involved rigid body translation of a block of Berea sandstone over a known distance using a Vernier scale with 1 μm resolution. The block was translated various distances (5, 10, 15, 20, 40 μm) and fringe patterns were observed. The entire translation device was placed on top of the optical table such that the distance between the specimen surface and the camera lens was 284 mm. The ESPI images associated with rigid body translation resulted in a series of parallel horizontal fringes (Fig. 7a), similar to the interference of two identical plane waves produced with a Michelson interferometer. The parallel horizontal fringes with equal spacing indicate that there is no displacement gradient across the field of view in the horizontal direction.

Fig. 7
figure 7

Rigid body translation (rbt) test. a Fringe pattern developed from rbt. b Schematic diagram indicating how β was determined. c Results from five increments of displacement

Full size image

Observations showed that for an increase in rigid body translation the fringes became closer together. The same trend is observed when two plane wavefronts interfere and the angle of interference β is increased (Jones and Wykes 1989):

$$ L = {\frac{\lambda }{2\sin \beta }} $$
(10)

where L is the spacing between parallel fringes and β is the bisector of the angle between the incident wavefronts. Equation 10 is identical to Eq. 8, thus it was used to quantify the spacing of fringes developed from the translation, measured across a vertical line instead of a horizontal one. The angle β was taken as the angle generated by translating the specimen (Fig. 7b). Measuring the length between the specimen surface and the camera, and measuring the spacing of the fringes on the ESPI image (neglecting error in identifying the boundary of the fringes), the angle β was determined. Consequently, the measured displacement was calculated based on the measured fringe spacing, and Fig. 7c shows the results. The measured displacement and the induced translation were in excellent agreement for the five increments of rigid body displacement. The average relative error for the five measurements was 0.19% and the standard error was 2.06%. Using the Student’s t test at the confidence level of 95%, the system accuracy was estimated to be approximately ±5%.

4.2 Stress Intensity Factor

From linear fracture mechanics, it can be shown that crack opening displacement, COD = 2u x , is related to the mode I stress intensity factor K I:

$$ 2u_{x} = K_{\text{I}} {\frac{8}{{E^{'} }}}\sqrt {{\frac{r}{2\pi }}} - A_{1} r^{3/2} $$
(11)

where (Fig. 8a) r is the distance from crack tip along the crack (θ = π), E′ = E for plane stress, E′ = E/(1 − ν 2) for plane strain, ν is Poisson’s ratio, and A 1 is the constant dependent on load and geometry (Sanford 2003). One higher order term (r 3/2) is included in the COD expression because the measurements from ESPI will consider distances outside the singularity dominated region; although ESPI is a very sensitive technique for measuring displacement, not enough information can be gathered near the crack tip to utilize the one term solution. An area of the specimen surface (Fig. 8b), approximately 30 × 30 mm and covering the notch region, was illuminated by the two laser beams; the displacement u x along the notch was be determined by counting fringes on an ESPI image.

Fig. 8
figure 8

a Notation used for determining crack opening displacement for various positions along the crack. b Loading configuration and ESPI illumination area for single edge notch beam specimen

Full size image

A convenient geometry (Fig. 8b) to use in fracture testing is the single edge notched bend (SENB) specimen, and K I is

$$ K_{\text{I}} = {\frac{{Pf\left( {{\frac{a}{H}}} \right)}}{B\sqrt H}} $$
(12a)
$$ f\left( {{\frac{a}{H}}} \right) = {\frac{{3{\frac{s}{H}}\sqrt {{\frac{a}{H}}} }}{{2\left( {1 + 2{\frac{a}{H}}} \right)\left( {1 - {\frac{a}{H}}} \right)^{{{\frac{3}{2}}}} }}}\left[ {1.99 - {\frac{a}{H}}\left( {1 - {\frac{a}{H}}} \right)\left\{ {2.15 - 3.93\left( {{\frac{a}{H}}} \right) + 2.7\left( {{\frac{a}{H}}} \right)^{2} } \right\}} \right] $$
(12b)

where a is crack length, H is the height, s is the span, B is the thickness, and P is the load applied to the beam (Anderson 1995). The material used for the test was aluminum 6061: ν = 0.33, Ε = 70 GPa. The beam dimensions were B = 19.24 mm, H = 38.27 mm, a = 15.3 mm, s = 124.2 mm. For a/H = 0.40, f(a/H) = 6.428.

The displacements observed with ESPI are shown in Fig. 9, where the fringe count provides an estimate of COD. Because an ESPI image gives no information about polarity of displacement, knowledge of the loading configuration is necessary. Based on the symmetry of the SENB specimen, fringe n = 0 was interpreted as the centerline of the beam (coinciding with the notch and the y-axis), and fringes developed more or less symmetrically about the notch (Fig. 9). The high resolution of the ESPI technique showed fringes with a slight asymmetry, probably due to alignment and specimen imperfections. From the n = 0 fringe, which can be either dark or light, other fringes were counted sequentially along both sides of the notch. The dark and light fringes indicated a jump in horizontal displacement at a given position along the notch, since the COD at the notch tip is zero, and either the dark or light fringes can be used to estimate displacement.

Fig. 9
figure 9

Fringe pattern developed from aluminum SENB specimen. a Load increment 2.8–3.2 kN; b load increment 2.8–3.5 kN

Full size image

For example, at position r = 8 mm (Fig. 9a), five light fringes can be identified in moving from the left to the right side of the displacement discontinuity (the notch). Thus, COD = 5 fringes × 0.7 μm/fringe = 3.5 μm. As load was increased and more horizontal displacement was produced, more fringes appeared on the ESPI image with respect to the same reference frame. Thus, at the same position of r = 8 mm, seven dark fringes can be observed in moving from the left to the right side of the notch (Fig. 9b), and COD = 7 fringes × 0.7 μm/fringe = 4.9 μm.

Equation 11 can be written as

$$ 2u_{x} {\frac{E'}{8}}\sqrt {{\frac{2\pi }{r}}} = K_{\text{I}} - B_{1} r $$
(13a)
$$ K_{\text{apparent}} = K_{\text{I}} - B_{1} r $$
(13b)

where B 1 is another constant, and K apparent can be determined from the ESPI measurements of COD and plotted as a function of the distance from the crack tip. Thus, the stress intensity factor is the y-intercept of a best fit line through the data.

Figure 10 shows the measured data from the load increment of 2.8–3.2 kN, with K mI  = 0.623 MPa m1/2; the value calculated using Eq. 12a is K cI  = 0.605 MPa m1/2, a difference of 3%. Similarly, Fig. 10 illustrates the data from the load increment of 2.8–3.5 kN, with K mI  = 0.966 MPa m1/2 and K cI  = 1.058 MPa m1/2, a difference of 9%. The similarity of the measured and calculated K I values indicates that the ESPI system was accurately measuring displacements.

Fig. 10
figure 10

Stress intensity factor determined from ESPI image

Full size image

4.3 Uniaxial Compression

Prismatic specimens of Berea sandstone were machined with height 51.6 mm and cross-section 24.1 × 24.1 mm, and tested in uniaxial compression with appropriate lubrication (Labuz and Bridell 1993). The specimens were instrumented with axial (ε yy ) and lateral (ε xx ) strain gages to provide independent estimates of displacement. Assuming homogeneous deformation, horizontal displacement w x can be determined:

$$ w_{x} = \varepsilon_{xx} \cdot w $$
(14)

where w is width of the prismatic specimen.

Figure 11 shows the development of fringes during different stages of loading. Figure 11a was taken before the start of the test. The line drawn across the images represents the approximate location of the lateral strain gage on the opposite side of the prismatic specimen. By counting the number of inclined fringes that crossed the line, the horizontal deformation can be obtained from the ESPI images. At initial loading stages (30–36% of peak), Fig. 11b indicates a horizontal fringe pattern, which is associated with translation. This horizontal pattern has been observed by other researchers (e.g. Facchini and Zanetta 1995), and it can be attributed to small amounts of rigid body translation. For example, the specimen ends may not have been perfectly parallel; this would result in the specimen translating horizontally. The slight inclination of the fringes would be due to lateral deformation. The spacing of the parallel fringes indicated the rigid body translation was 5 μm. There is almost one fringe inside the horizontal line (Fig. 11b), which means 0.7 μm of horizontal deformation occurred during the load increment.

Fig. 11
figure 11

Development of fringes in a prismatic specimen under uniaxial loading

Full size image

Figure 11c and d indicated horizontal displacements at 64–68% and 71–74% of the maximum load, where fringes started to have a largely vertical trend. The curvature of the lines implies some bending of the specimen, possibly the result of the non-parallelism of the specimen ends. Figure 11e and f were taken near peak load (92–94% and 98–99% of the maximum), and these images indicated a concentration of fringe lines near the upper left corner, and this concentration was associated with an observable fracture.

Table 1 compares the displacements measured from the lateral strain gage and the ESPI fringes. (It was assumed that the level of precision in counting fringes within the cross section was one-half fringe.) Even though the displacements were very small, a reasonable match was obtained from the two techniques.

Table 1 Comparison between strain gage and ESPI data for a uniaxial compression test
Full size table

4.4 Flexural Test

A Berea sandstone beam with a smooth boundary was loaded to failure in a three-point bend test (Fig. 8a). Figure 12a shows the ESPI image and the resulting fringe pattern at 98–99% of peak load. A line, actually a zone shown with a white rectangle, was identified by the convergence of dark and light fringes, indicating localization—a displacement discontinuity—in the specimen. This localized damage zone has been observed using other techniques such as acoustic emission (Labuz and Biolzi 2007). Following a similar approach to the interpretation of the notched-aluminum bend, a fringe n = 0 was identified from the line of symmetry, which was slightly offset from the centerline of the beam, probably due to specimen imperfections in loading and local material heterogeneity.

Fig. 12
figure 12

a ESPI image at 99% of peak. b “Crack” opening profiles at various loading

Full size image

The “crack” opening displacement can be determined by counting the fringes along the localized damage zone, and the opening profiles at four loading stages are shown in Fig. 12b. At 98% peak load, the length of the damage zone was 1–2 mm, with a maximum displacement at the bottom fiber of two fringes or 1.4 μm on one side, for a “crack” opening displacement of 2.8 μm. At 99% peak load, the damage zone grew to 3 mm in length, and the maximum displacement on one side was eight fringes or about 6 μm. At 99% post-peak load, the “intrinsic” damage zone was 6–7 mm long, and the maximum displacement on one side was 28 fringes or approximately 20 μm, for a “crack” opening displacement of 40 μm.

5 Summary

A single direction, in-plane, speckle interferometry system, with a sensitivity of approximately 1 μm, was used for the accurate and precise determination of surface displacements. Acquisition, processing, and storage of digital images allowed for simple signal processing of intensity subtraction to obtain fringes related to horizontal displacement. With knowledge of the testing configuration, the high-resolution displacement measurements can be used to (1) measure deformation of a material element or (2) interpret opening along a displacement discontinuity.