1 Introduction

The importance of morphology in rock mechanics and rock engineering has been highlighted since the 1960s (Rowe 1962; Patton 1966; Ladanyi and Archambault 1969). Later, work of Barton and Bandis and resultant methods—which are among the most used in rock engineering—put the emphasis on the importance of morphology in the hydromechanical response of a rock joint (Barton 1973, 1976; Barton and Choubey 1977; Bandis et al. 1981, 1983, 1986). Other authors showed the importance of morphology on rock joints closure (Tsang and Witherspoon 1983; Brown and Scholz 1985a, b, 1986; Brown 1987; Wang et al. 1988, and others). Field rock engineering practice usually applies empirical methods and/or models. For numerical simulations, it is always better to use improved models for better response and understanding of rock joint behaviour, since most field methods or practices had already been developed in the 1960s. It can be noticed that some failure criteria (Ladanyi and Archambault 1969; Saeb 1990) and constitutive laws (Amadei and Saeb 1990, 1992; Saeb and Amadei 1989; Jing et al. 1993) included in their formulation the quantification of the joint wall surface wear.

Traditionally, wear of natural or man-made joint wall surface roughness subjected to direct shear testing has been characterized in terms of direct quantification of joint wall surface wear, evolution of roughness, or evolution of dilatancy angle (e.g., Plesha 1987; Hutson 1987; Hutson and Dowding 1990; Benjelloun et al. 1990; Jing et al. 1992). However there are no parameters in the literature to directly or indirectly quantify wear or degradation for a set of joint walls during shearing. Wear of joint wall surface was also investigated by Leong and Randolph (1992) using wear theory. They viewed wear in terms of reduction in dilatancy and plough resistance due to surface ploughing by asperities and wear particles. Nevertheless, their model of sheared rock joints lacked an explicit formulation of wear. However, the exact contribution of morphology in rock joint strength properties should be better understood in order to help validate some existing constitutive laws and/or shear strength criteria for sheared rock joints (e.g., Plesha 1987; Jing et al. 1992; Homand et al. 2001; Belem et al. 2002; Grasselli et al. 2002; Grasselli 2006).

This paper aims to characterize the evolution of wear for natural and artificial joint surface textures under monotonic and cyclic shearing. To achieve this, three different joint types were sheared under constant normal stress (CNS) shearing at different normal stress (σ n ) levels ranging from 0.3 to 5 MPa. The sheared joint samples were (i) man-made granite hammered joints, (ii) natural rough and undulated schist joint mortar replicas, and (iii) man-made corrugated mortar joints. The rough and undulated schist joint mortar replicas were sheared under monotonic shearing condition, whereas the granite hammered joints and corrugated mortar joints were sheared under cyclic shearing. Based on already proposed surface roughness parameters (Belem 1997; Belem et al. 2000), two surface roughness parameters and two surface wear parameters were proposed and used for indirect quantification of the evolution of joint surface roughness and the corresponding wear after shearing. Joint wall surface roughness was quantified by joint specific surface roughness SR s and degree of surface relative roughness DR r . Joint surface wear was quantified by the surface wear coefficient Λ and degree of surface wear D w . These two parameters were defined on the basis of joint wall surface actual or true areas calculations prior to and after each shear testing.

2 Background

2.1 Friction and Mechanisms of Wear

Friction and wear occur where two surfaces undergo sliding or rolling contact under load. Friction is a serious cause of energy dissipation, while wear is the main cause of material wastage (Bhushan and Gupta 1991). Frictional heat is also generated at the sliding-contact interface. The imposed stresses and frictional heating at the contact interface are the key driving forces for the occurrence of wear at a sliding-contact interface. Consequently, the wear rates and wear mechanisms are determined in a large part by the magnitude of these driving forces (Erck and Ajayi 2001).

Friction is the resistance to relative motion of contacting surfaces. The degree of friction is quantified by a coefficient of friction (μ), which is expressed as the ratio of tangential force (F t ) required to initiate or sustain relative motion (s), to the normal force (F n ) that presses the two surfaces together. Two modes of friction may occur: sliding or rolling friction. The friction between sliding surfaces (sliding friction) is due to the combined effects of adhesion between flat surfaces, ploughing by wear particles and hard asperities, and asperity deformation. Rolling friction is a complex phenomenon because of its dependence on many factors, including inconsistent sliding (called slip) during rolling, and energy losses during mixed elastic and plastic deformations. Rolling friction may be classified into two types: one in which large tangential forces are transmitted, and another in which small tangential forces are transmitted, often referred to as free rolling (e.g., Bhushan and Gupta 1991; Ramalho and Miranda 2006).

Wear is a process of removal of material from one or both of two solid surfaces in solid-state contact, occurring when two solid surfaces are in sliding or rolling motion together (Bhushan and Gupta 1991). The rate of removal is generally slow, but steady and continuous. Wear may be classified from a fundamental microscale wear mechanism view. The different wear mechanisms often described in the literature are: adhesive wear, abrasive wear, corrosive wear, and surface fatigue wear. Adhesive wear is a type of wear that occurs when wear particles are formed due to the adhesive interaction between the rubbing surfaces (smooth surfaces rub against each other). This type of wear may also be named scuffing, scoring, seizure, and galling due to the appearances and behavior of the worn surfaces. Adhesive wear is often associated with severe wear, but its role in mild wear conditions is unclear. Abrasive wear occurs when a harder surface or particles ploughs a series of groves on a softer surface. Often, wear particles generated by adhesive or corrosive mechanisms will be abrasive particles, which will wear the contact surfaces when they move through the contact. Corrosive wear occurs when the surfaces chemically react with the environment and form reaction layers on the surfaces, which will be worn off due to the mechanical action. Another corrosive wear is fretting, which occurs in contact with small oscillating motions. Corrosive wear generates small, sometimes flake-like, wear particles, which may be hard and abrasive. Surface fatigue wear appears as pits on the surfaces. This type of wear may be found in rolling contacts. The surfaces are fatigued due to repeated high contact stresses.

It seems difficult however to distinguish between the different wear mechanisms, since they often occur together. The different types of wear may also be dependent on each other. An adhesive and corrosive wear process may generate particles that are abrasive in a contact (Olofsson et al. 2000).

2.2 Classical Wear Theory

In classical wear theory, a simple mathematical model for adhesive wear has been developed (Archard 1953) and modified by a number of researchers (e.g., Rabinowicz 1965; Kragelskii 1965). The model is based on the assumption that wear occurs through the shearing of the real contact area (A r ) between two contacting surfaces. The wear volume V produced is given as follows:

$$ \frac{V}{s} = K\frac{{F_{n} }}{H}, $$
(1)

where s is the sliding distance; K is the dimensionless wear coefficient; F n is the applied normal load; and H is the hardness of the softer contact surface.

Furthermore, since each asperity contact during the motion of the surfaces has a statistical probability of producing a wear particle, wear is proportional to total sliding distance. The implication that wear is proportional to load and distance of sliding and inversely proportional to hardness of the material has been verified experimentally (Rabinowicz 1965; Kragelskii 1965; Glaeser 1971; Teer and Arnell 1978). By dividing both sides of Eq. (1) by the apparent contact area A n and by replacing K/H with k, a dimensional wear coefficient, the following wear model is obtained:

$$ \left( {\frac{V}{{sA_{n} }} = \frac{{hA_{n} }}{{sA_{n} }}} \right) = \frac{K}{H}\frac{{F_{n} }}{{A_{n} }} \Rightarrow \frac{h}{s} = kp_{n}, $$
(2)

where h is the wear depth; p n is the applied normal stress.

Queener et al. (1965) showed that wear comprises a transient (nonlinear) and steady (linear) part. For transient wear, the volume increment of wear material ΔG in an increment of slip Δx is considered a linear function of the volume V by which the surface departs from a perfectly flat surface (describing the current surface roughness). This means that total volume of wear is proportional to current volume V (after shearing) and sliding distance s (or accumulated shear displacement).

The possibility to predict the type and amount of wear is limited, although many wear models can be found in the literature (Meng 1994). The models are either simple models describing a wear mechanism from a fundamental point of view, or simple empirical relationships. They are normally not convenient to use or at least very difficult to use in many practical cases (Olofsson et al. 2000).

2.3 Characterization of Surface Morphology

2.3.1 Surface Texture Components

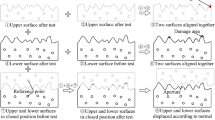
The surface of a geomaterial (natural rocks, mortars, etc.) is made up of a matrix of individual grains, which vary in size and bond strength. Mechanical treatments of surface such as hammering can cause microstructure changes in the bulk material. The surface shape or topology is often seen microscopically as a series of asperities rather than the flat surface seen macroscopically (Bhushan and Gupta 1991). The geometrical texture may be characterized by its surface profile as shown in Fig. 1, and results from three different components of surface texture (roughness, waviness, and lay). In this paper, the roughness component is termed “secondary” or second-order surface roughness, and the waviness component is termed “primary” or first-order surface roughness.

Fig. 1
figure 1

Joint surface morphology components (adapted from Tarr)

Full size image

2.3.2 Surface Roughness Parameters

2.3.2.1 Surface Roughness Coefficient R s

Fracture or joint surface roughness coefficient R s was defined for a single joint wall surface by El Soudani (1978) as the ratio of the joint wall developed surface true area A t (regardless of contacting areas) and its projected flat surface area A n (i.e., apparent surface area of contact or cross-sectional area of measurement), as follows:

$$ R_{s(j)} = \left( {\frac{{A_{t} }}{{A_{n} }}} \right)_{j = l,u} = \left[ {\frac{{\sum {A_{i} } }}{{A_{n} }}} \right]_{j = l,u}, $$
(3)

where j represents the lower wall surface (j = l) or the upper wall surface (j = u); and A i is the elementary surface true area (Fig. 2). When R s  = 1, the fracture surface is perfectly flat and macroscopically smooth (A t  = A n ). According to El Soudani (1978), an upper bound limit value of R s  = 2 is applicable to brittle fractures only.

Fig. 2
figure 2

Entire joint surface showing its developed true area A t , cross-sectional area of measurement (or apparent area of contact or projected surface area) A n , and the ith elementary surface, showing the inclination angle θ i

Full size image
2.3.2.2 Estimating Developed True Surface Area A t

By triangulating a fracture surface topographic data, the developed surface true area A t can be estimated by summing all triangular element areas A i (Fig. 2). However, an alternative method is to estimate the developed surface true area A t from the joint wall surface three-dimensional topographic data z(x,y) using the integral method, according to the following relationship (Belem et al. 2000):

$$ A_{t} = \sum {A_{i} } \approx \Updelta x\Updelta y\sum\limits_{i = 1}^{Nx - 1} {\sum\limits_{j = 1}^{Ny - 1} {\sqrt {1 + \left( {\frac{{z_{i + 1,\ j} - z_{i,\ j} }}{\Updelta x}} \right)^{2} + \left( {\frac{{z_{i,\ j + 1} - z_{i,\ j} }}{\Updelta y}} \right)^{2} } } }, $$
(4)

where Δx and Δy are the sampling steps along the x- and y-axis; N x is the number of data points along the x-axis; N y is the number of data points along the y-axis; and z i, j = z(x i , y j ) is the discrete value of joint surface single asperity height.

2.3.2.3 Specific Surface Roughness Coefficient SR s

To better evaluate the evolution of joint surface roughness during shearing, the roughness coefficient should vary between 1 (intact initial rough surface) and 0 (flattened surface after asperities shearing and surface macroscopically smoothed). The specific surface roughness coefficient SR s has been proposed for a single joint wall (lower or upper) by comparing the roughness specific surface area (ΔA) to the cross-sectional area of measurement (A n ) as follows (Belem et al. 2000):

$$ {\rm SR}_{s(j)} = \left( {\frac{\Updelta A}{{A_{n} }}} \right)_{j = l,u} = \left( {\frac{{A_{t} - A_{n} }}{{A_{n} }}} \right)_{j = l,u} = \left\{ {\left( {\frac{{A_{t} }}{{A_{n} }}} \right)_{j = l,u} - 1} \right\} = R_{s(j)} - 1, $$
(5)

and for a joint interface as follows:

$$ {\rm SR}_{{s({\text{interface}})}} = \frac{{\sum {\left( {A_{t} } \right)_{l,u} - \sum {\left( {A_{n} } \right)_{l,u} } } }}{{\sum {\left( {A_{n} } \right)_{l,u} } }} = \frac{{(A_{t} )_{l} + (A_{t} )_{u} - 2A_{n} }}{{2A_{n} }} = R_{{s({\text{interface}})}} - 1, $$
(6)

where the subscripts l, u indicate the lower wall and upper wall, respectively; ΔA is the joint roughness specific surface area; A t is the joint wall developed surface true area; A n is the projected surface area or apparent contact area. Notice that this specific surface roughness coefficient (SR s ) is comparable to the developed interfacial area ratio (S dr ) proposed by Stout (2000) to address specifically the three-dimensional nature of the surface texture. This parameter was also implemented in the commercial image analysis software named SPIP (scanning probe image processor) under ISO/DIS 25178-2 standard specifications.

2.3.2.4 Degree of Relative Surface Roughness DR r

While the surface roughness parameter SR s (=R s  − 1) is defined with respect to the projected surface area or cross-sectional area of measurement A n , the degree of joint interface relative surface roughness DR r (0 ≤ DR r  ≤ 0.5) was defined as compared with the initial surface area A t in order to describe the possible evolution of surface roughness from its initial state, as follows (Belem et al. 2000):

$$ {\rm DR}_{{r({\text{interface}})}} = \frac{{\sum {\left( {A_{t} } \right)_{l,u} - \sum {\left( {A_{n} } \right)_{l,u} } } }}{{\sum {\left( {A_{t} } \right)_{l,u} } }} = \frac{{(A_{t} )_{l} + (A_{t} )_{u} - 2A_{n} }}{{(A_{t} )_{l} + (A_{t} )_{u} }} = \left( {\frac{{{\rm SR}_{s} }}{{R_{s} }}} \right)_{\text{interface}} = 1 - \frac{1}{{R_{{s({\text{interface}})}} }}, $$
(7)

where the subscripts l, u indicate the lower wall and upper wall, respectively; A n is the projected surface area or apparent contact area, and R s is the surface roughness coefficient; SR s is the specific surface roughness coefficient. Equation (7) shows that, when the joint surface is perfectly flat and macroscopically smooth (ideal plane), DR r  = 0. In contrast, the rougher the joint surface, the more DR r will tend toward 0.5, corresponding to a maximum value of R s  = 2.

2.4 Existing Roughness Degradation Models

Ladanyi and Archambault (1969) proposed a model of shear area ratio a s (0 ≤ a s  ≤ 1) in order to predict the relative degradation of sheared joint surface by the following relationship:

$$ a_{s} = \frac{{A_{s} }}{A} \approx 1 - \left( {1 - \frac{{\sigma_{n} }}{{\sigma_{T} }}} \right)^{{k_{1} }}, $$
(8)

where A s is the projected area of sheared asperities (equivalent to real surface area of contact A r ); A is the total projected area (equivalent to apparent surface area of contact A n ); σ n is the normal stress; σ T is the transitional stress (σ n  ≤ σ T ); and k 1 is the material constant (usually k 1 = 1.5).

Barton and Choubey (1977) proposed a joint damage coefficient M (1 ≤ M ≤ 2) as follows:

$$ M = \frac{JRC}{{d_{n}^{0} }} \times \log_{10} \left( {\frac{JCS}{{\sigma_{n} }}} \right) \approx \frac{JRC}{{12 \times \log_{10} \left( {{\raise0.7ex\hbox{${JCS}$} \!\mathord{\left/ {\vphantom {{JCS} {\sigma_{n} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\sigma_{n} }$}}} \right)}} + 0.70, $$
(9)

where JRC is the joint roughness coefficient; d 0 n is the peak dilation angle; JCS is the compressive strength of the joint wall; and σ n is the normal stress.

Plesha (1987) proposed an exponential law for asperity angle (α) degradation through the deterioration of the dilation angle, based on experimental observations, as follows:

$$ \alpha = \alpha_{0} \exp \left( { - cW_{p} } \right), $$
(10)

where α 0 is the initial asperity angle; c is the damage coefficient determined experimentally; and W p is the plastic work or energy dissipation during frictional sliding.

Hutson and Dowding (1990) later verified experimentally Plesha’s model and proposed that c = −0.141α 0(σ n /σ c ). These authors also suggested a possible hyperbolic equation, as follows:

$$ \alpha = \frac{{\alpha_{0} }}{{1 - a\left( {W_{p} \times \frac{{\sigma_{n} }}{{\sigma_{c} }}} \right)^{b} }}, $$
(11)

where a and b are the material constants; and σ c is the uniaxial compressive strength of material.

Lee et al. (2001) proposed an extended version of Plesha’s model by introducing forward (F) and backward (B) shear displacements and including the second-order roughness effect, as follows:

$$ \left\{ {\begin{array}{*{20}c} {\alpha_{F \to } = \alpha_{0F1} \exp \left( { - c_{1} W_{p} } \right) + \alpha_{0F2} \exp \left( { - c_{2} W_{p} } \right)} \\ {\alpha_{B \leftarrow } = \alpha_{0B1} \exp \left( { - c_{1} W_{p} } \right) + \alpha_{0B2} \exp \left( { - c_{2} W_{p} } \right)} \\ \end{array} } \right., $$
(12)

where c is the damage coefficient determined experimentally; and the subscripts 1 and 2 denote the first- and second-order asperity angle, respectively.

Son et al. (2001) postulated that changes in joint asperity angle occurring in pre- and post-peak ranges of the shear-displacement curve could be approximated by a simple power law of accumulated tangential plastic work, as follows:

$$ \alpha = \alpha_{0} \left( {\frac{1}{{1 + cW_{p} }}} \right)^{a}, $$
(13)

where a and c are constants.

Homand-Etienne et al. (1999) proposed a general roughness degradation model for undulated joint surfaces as follows:

$$ D_{w} = 1 - \left( {1 - \frac{{\sigma_{ni} }}{{\sigma_{c} }}} \right)\exp \left( { - \frac{{k_{a}^{3/2} }}{{\tan \theta_{s} }}\frac{{T \cdot W_{t} }}{{L_{s} \cdot L_{cy} }}\left( {\frac{{\sigma_{ni} }}{{\sigma_{c} }} + \frac{{K_{n} \cdot \tan \theta_{s} \cdot L_{cy} }}{{4\sigma_{c} }}} \right)} \right), $$
(14)

where θ s is the surface mean angle; k a is the apparent anisotropy coefficient; T is the undulation period; L s is the sample length along shear direction; L cy is the total displacement for one shear cycle; W t is the accumulated total displacement; σ c is the uniaxial compressive strength; σ ni is the initial normal stress; and K n is the normal stiffness.

Homand et al. (2001) proposed a roughness degradation model for constant normal stress (CNS) condition based only on roughness parameters, as follows:

$$ D_{w} = 1 - \left( {1 - \frac{{\sigma_{n} }}{{\sigma_{c} }}} \right)\exp \left( { - \frac{{k_{a}^{2} }}{{2{\rm DR}_{r}^{0} }} \cdot \frac{{\sigma_{n} }}{{\sigma_{c} }}} \right), $$
(15)

where σ n is the normal stress; σ c is the uniaxial compressive strength; k a is the apparent anisotropy coefficient; and DR 0 r is the degree of joint relative roughness prior to shearing.

Belem et al. (2007) proposed recently two generalized joint surface asperity degradation models (models 1 and 2) for constant normal stress (CNS), constant normal stiffness (CNSK), monotonic shearing, and cyclic shearing conditions. Model 1 was formulated based on the evolution of surface secondary roughness and Model 2 was developed based on the concept of average asperity probable contact angle, similar to Plesha’s surface roughness damage model and qualitatively comparable to Grasselli et al.’s (2002) model.

Generalized model 1:

$$ D_{w} = 1 - \left( {1 - \frac{{\sigma_{n0} }}{{\sigma_{c} }}} \right)\exp \left( { - \beta_{d} \frac{{\sigma_{n0} + k_{n} u_{s0} \tan (\delta_{ave} )}}{{\sigma_{c} }}} \right) $$
(16a)

Generalized model 2:

$$ D_{w} = \kappa_{w} \left[ {1 - \exp \left( { - \chi \frac{{\sigma_{n0} + k_{n} u_{s0} \tan (\delta_{ave} )}}{{\sigma_{c} }}} \right)} \right] $$
(16b)

and

$$ \beta_{d} = \frac{{3k_{a}^{3} }}{{8{\rm DR}_{r} \tan \theta_{s} }}\log \left( {\frac{{u_{s - tot} }}{{a_{0} k_{a} }}} \right) $$
(17a)
$$ \delta_{ave} = \theta_{s} \left( {\frac{{u_{s0} }}{{5a_{0} }}} \right)\exp \left( { - \log \left( {\frac{{u_{s - tot} }}{{a_{0} }}} \right)\frac{{k_{n} a_{0} }}{{\sigma_{c} }}\sqrt {\frac{{\sigma_{n0} }}{{\sigma_{c} }}} } \right) $$
(17b)
$$ \kappa_{w} \approx \left( {\alpha_{0} - k_{a} } \right)\sqrt {\tan \theta_{s} } \approx 1.13506 + 0.13403 \times \cos \left( {1.55173k_{a} + 1.78383} \right) $$
(17c)
$$ \chi = \frac{{7k_{a}^{3} }}{{15\tan \theta_{s} {\rm DR}_{r} }}\log \left( {\frac{{u_{{s - tot}} }}{{a_{0} k_{a} }}} \right), $$
(17d)

where θ s is the surface asperity average angle; α0 is a constant; k a is the apparent anisotropy coefficient; DR r is the degree of joint surface relative roughness; a0 is the roughness amplitude (equivalent to parameter R t , the peak-to-valley height); σ c is the uniaxial compressive strength; σn0 is the initial normal stress; and k n is the normal stiffness; us0 is the relative or shear displacement; us-tot is the total accumulated shear displacement.

3 Method for Quantification of Wear of Sheared Joints

3.1 Wear Coefficient

The sheared joint interface wear coefficient Λinterface (different from the wear coefficient K defined by Archard 1953) is defined as the ratio of the joint interface roughness specific surface area after shearing (ΔA s ) to its value prior to shearing (ΔA 0), which is given by the following relationship (Belem 1997):

$$ \Uplambda_{\text{interface}} = \left( {\frac{{\Updelta A_{s} }}{{\Updelta A_{0} }}} \right)_{\text{interface}} = \frac{{\sum {(A_{t}^{s} )_{l,u} - } \sum {(A_{n} )_{l,u} } }}{{\sum {(A_{t}^{0} )_{l,u} - } \sum {(A_{n} )_{l,u} } }} = \frac{{(A_{t}^{s} )_{l} + (A_{t}^{s} )_{u} - 2A_{n} }}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }}, $$
(18)

where subscripts l, u indicate the lower wall and upper wall, respectively; A 0 t and A s t are the joint wall surface developed true areas prior to and after shearing, respectively; and A n is the projected surface area or apparent surface area of contact.

Sheared joint interface wear coefficient (Λinterface) varies between 0 (macroscopically entirely flattened joint interface after shearing) and 1 (joint interface not sheared or remained intact after shearing). It was observed that the developed surface true area after shearing (A s t ) can sometimes be higher than the developed surface true area prior to shearing (A 0 t ) in terms of sum of lower and upper walls surface areas (composite surface area or interfacial area). In this case, the sheared joint interface wear coefficient Λinterface is higher than 1 and can be categorized as a negative wear (Λinterface > 1) regarding the datum plane (cross-sectional area of measurement, A n ). This negative wear could be explained either by the wear debris removal from the sheared surface prior to the topographic data acquisition, or the surface geometrical texture (morphological features, asperities distribution, inclination angles, etc.) which favored asperity degradation such as surface flaking or wrenching wear in certain regions (predominant contact areas). Moreover, it should be noted that this negative wear can be captured because this parameter (Λ) quantifies the variation of surface areas (indirect wear) rather than quantifying the wear volume (or wear rate) as performed in tribology (e.g., Archard 1953).

It should also be mentioned that the physical significance of sheared joint interface wear coefficient will not be affected either by wear debris removal or not from the sheared surface. The only thing that will be affected is the calculated numerical value of Λ. From numerous calculations of surface roughness parameters from both removed and nonremoved wear debris after shearing, a minor variation between the two processes was observed. Moreover, the removed wear debris surface roughness parameters were more consistent than the ones from nonremoved wear debris (Lefèvre 1999). Based on these observations, it was chosen to remove all the wear debris prior to surface topographical data measurements. This choice was supported by the fact that the objective of the proposed method is to quantify the amount of surface wear from its initial (or previous) state, but not to properly study the friction properties of rock joints.

The sheared joint wear coefficient for the corresponding single joint lower wall (Λlower) and upper wall (Λupper) surfaces are given as follows (Belem 1997):

$$ \Uplambda_{\text{lower}} = \frac{{(A_{t}^{s} )_{l} - A_{n} }}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }} $$
(19)

and

$$ \Uplambda_{\text{upper}} = \frac{{(A_{t}^{s} )_{u} - A_{n} }}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }}, $$
(20)

where subscripts l, u indicate the lower wall and upper wall, respectively; A 0 t and A s t are the joint wall developed surface true areas prior to and after shearing, respectively; and A n is the projected surface area (cross-sectional area of the measurement) or apparent contact area.

3.2 Degree of Surface Wear

The expression of the parameter a s in Eq. (8) shows that it quantifies a relative degradation or wear of sheared joint wall surfaces (projected areas). However, this parameter also suggests that, since joint wall surface true area can be estimated (by triangulation, integral method or any other method), the parameter D w (degree of surface wear or roughness degradation) can be defined for indirect quantification of the wear or degradation of sheared joint wall surfaces. Based on calculations of numerous joint wall surface true areas by surface triangulation and using Eq. (4) prior to and after different shear tests, the degree of sheared joint interface wear or degradation D w(interface) for an initially rough surface is given by the following relationship:

$$ D_{{w({\text{interface}})}} = \frac{{\left| {\sum {(A_{t}^{0} )_{l,u} } - \sum {(A_{t}^{s} )_{l,u} } } \right|}}{{\sum {(A_{t}^{0} )_{l,u} } - \sum {(A_{n}^{{}} )_{l,u} } }} = \left| {1 - \left( {\frac{{(A_{t}^{s} )_{l} + (A_{t}^{s} )_{u} - 2A_{n} }}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }}} \right)} \right|, $$
(21)

where D w(interface) varies between 0 and 1, and the percentage of wear D w(interface)(%) = D w(interface) × 100. It should be noticed that Eq. (21) is the calculable version of Eqs. (14), (15), and (16), which are predictive models.

Equation (21) shows that D w(interface) is null when the joint interface is not degraded after shearing or when the joint interface is not sheared. When all joint asperities are sheared off at the base (flattened surface up to an ideal macroscopically smooth plane), then \( (A_{t}^{s} )_{l} + (A_{t}^{s} )_{u} = 2A_{n} \) and D w(interface) = 1. For a single joint wall surface (e.g., upper or lower wall), the degree of degradation can be derived from Eq. (19), as follows:

$$ D_{{w({\text{lower}})}} = \frac{{\left| {(A_{t}^{0} )_{l} - (A_{t}^{s} )_{l} } \right|}}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }} $$
(22)

and

$$ D_{{w({\text{upper}})}} = \frac{{\left| {(A_{t}^{0} )_{u} - (A_{t}^{s} )_{u} } \right|}}{{(A_{t}^{0} )_{l} + (A_{t}^{0} )_{u} - 2A_{n} }}. $$
(23)

Combining Eqs. (18) and (21), the degree of degradation can be rewritten as a function of sheared joint interface wear coefficient Λinterface, as follows:

$$ D_{{w({\text{interface}})}} = \left| {1 - \Uplambda_{\text{interface}} } \right| \Rightarrow \left\{ {\begin{array}{*{20}c} {D_{{w({\text{interface}})}} = 1 - \Uplambda_{\text{interface}} \quad {\text{for}}\,\Uplambda_{\text{interface}} \le 1} \\ {D_{{w({\text{interface}})}} = \Uplambda_{\text{interface}} - 1 \quad {\text{for}}\,\Uplambda_{\text{interface}} > 1} \\ \end{array} } \right.. $$
(24)

For a common sense wear (Λ ≤ 1) of a single joint wall (lower or upper), this is

$$ \left\{ {\begin{array}{*{20}c} {D_{{w({\text{lower}})}} = 1 - \Uplambda_{\text{lower}} } \\ {D_{{w({\text{upper}})}} = 1 - \Uplambda_{\text{upper}} } \\ \end{array} } \right. $$
(25)

and for negative wear (Λ > 1) of a single joint wall (lower or upper), as follows:

$$ \left\{ {\begin{array}{*{20}c} {D_{{w({\text{lower}})}} = \Uplambda_{\text{lower}} - 1} \\ {D_{{w({\text{upper}})}} = \Uplambda_{\text{upper}} - 1} \\ \end{array} } \right.. $$
(26)

It should be noted that a plot of D w as a function of Λ[D w  = f(Λ)] allows to visualize the mode of degradation, i.e., common sense wear (0 ≤ Λ ≤ 1) or negative wear (Λ > 1).

3.3 Wear and Roughness Parameters

As seen above, the proposed method of calculation is an indirect method of quantification of sheared joint surfaces wear based on the estimation of surface actual areas. The accuracy of this indirect method of quantification of wear directly depends on the horizontal resolution and the sampling steps of the surface topography measurements. As all the surface roughness parameters are defined based on the surface true area (and its cross-sectional area), it is then possible to express the wear in terms of surface (secondary) roughness parameters.

3.3.1 Wear Coefficient and Surface Roughness Parameters

The surface roughness wear coefficient Λ can be expressed in terms of the surface roughness coefficient R s , the specific surface roughness coefficient SR s , and the degree of surface relative roughness DR r . For the joint interface, this is given by the following relationship:

$$ \Uplambda_{\text{interface}} = \left( {\frac{{{\rm SR}_{s}^{s} }}{{{\rm SR}_{s}^{0} }}} \right)_{\text{interface}} = \left( {\frac{{{\rm DR}_{r}^{s} \cdot R_{s}^{s} }}{{{\rm DR}_{r}^{0} \cdot R_{s}^{0} }}} \right)_{\text{interface}} $$
(27)

and the sheared joint wear coefficient for the corresponding single joint lower wall (Λlower) and upper wall (Λupper) surfaces are given as follows:

$$ \Uplambda_{\text{lower}} = \frac{{{\rm SR}_{{s({\text{lower}})}}^{s} }}{{{\rm SR}_{{s({\text{interface}})}}^{0} }} = \frac{{\left( {{\rm DR}_{r}^{s} \cdot R_{s}^{s} } \right)_{\text{lower}} }}{{\left( {{\rm DR}_{r}^{0} \cdot R_{s}^{0} } \right)_{\text{interface}} }} $$
(28)

and

$$ \Uplambda_{\text{upper}} = \frac{{{\rm SR}_{{s({\text{upper}})}}^{s} }}{{{\rm SR}_{{s({\text{interface}})}}^{0} }} = \frac{{\left( {{\rm DR}_{r}^{s} \cdot R_{s}^{s} } \right)_{\text{upper}} }}{{\left( {{\rm DR}_{r}^{0} \cdot R_{s}^{0} } \right)_{\text{interface}} }}, $$
(29)

where \( {\rm SR}_{{s({\text{interface}})}}^{0} ,\,R_{{s({\text{interface}})}}^{0} \) and \( {\rm DR}_{{r({\text{interface}})}}^{0} \) are the specific surface roughness, surface roughness coefficient, and degree of relative surface roughness of the joint interface prior to shearing, respectively; and \( {\rm SR}_{{s({\text{interface}})}}^{s} ,R_{{s({\text{interface}})}}^{s}, \) and \( {\rm DR}_{{r({\text{interface}})}}^{s} \) are the specific surface roughness, roughness coefficient, and degree of relative surface roughness of the joint interface after shearing, respectively.

3.3.2 Degree of Wear and Surface Roughness Parameters

The degree of surface wear D w can also be expressed in terms of the surface roughness coefficient R s , the specific surface roughness coefficient SR s , and the degree of surface relative roughness DR r . For the joint interface this is given by the following relationship:

$$ D_{{w({\text{interface}})}} = \left| {\mathop {}\limits^{{}} 1 - \frac{{{\rm SR}_{{s({\text{interface}})}}^{s} }}{{{\rm SR}_{{s({\text{interface}})}}^{0} }}\mathop {}\limits_{{}} } \right| = \left| {\mathop {}\limits_{{}} 1 - \frac{{\left( {{\rm DR}_{r}^{s} \cdot R_{s}^{s} } \right)_{\text{interface}} }}{{\left( {{\rm DR}_{r}^{0} \cdot R_{s}^{0} } \right)_{\text{interface}} }}\mathop {}\limits^{{}} } \right| $$
(30)

and the sheared joint wear coefficient for the corresponding single joint lower wall (Λlower) and upper wall (Λupper) surfaces are given as follows:

$$ D_{{w({\text{lower}})}} = \left| {\mathop {}\limits^{{}} 1 - \frac{{{\rm SR}_{{s({\text{lower}})}}^{s} }}{{{\rm SR}_{{s({\text{interface}})}}^{0} }}\mathop {}\limits_{{}} } \right| = \left| {\mathop {}\limits_{{}} 1 - \frac{{\left( {{\rm DR}_{r}^{s} \cdot R_{s}^{s} } \right)_{\text{lower}} }}{{\left( {{\rm DR}_{r}^{0} \cdot R_{s}^{0} } \right)_{\text{interface}} }}\mathop {}\limits^{{}} } \right| $$
(31)

and

$$ D_{{w({\text{upper}})}} = \left| {\mathop {}\limits^{{}} 1 - \frac{{{\rm SR}_{{s({\text{upper}})}}^{s} }}{{{\rm SR}_{{s({\text{interface}})}}^{0} }}\mathop {}\limits_{{}} } \right| = \left| {\mathop {}\limits_{{}} 1 - \frac{{\left( {{\rm DR}_{r}^{s} \cdot R_{s}^{s} } \right)_{\text{upper}} }}{{\left( {{\rm DR}_{r}^{0} \cdot R_{s}^{0} } \right)_{\text{interface}} }}\mathop {}\limits^{{}} } \right|, $$
(32)

where \( {\rm SR}_{{s({\text{interface}})}}^{0} ,R_{{s({\text{interface}})}}^{0}, \) and \( {\rm DR}_{{r({\text{interface}})}}^{0} \) are the specific surface roughness, surface roughness coefficient, and degree of relative surface roughness of the joint interface prior to shearing, respectively; and \( {\rm SR}_{{s({\text{interface}})}}^{s} ,R_{{s({\text{interface}})}}^{s}, \) and \( {\rm DR}_{{r({\text{interface}})}}^{s} \) are the specific surface roughness, roughness coefficient, and degree of relative surface roughness of the joint interface after shearing, respectively.

4 Experimental Program

4.1 Shear Apparatus

Direct shear tests were performed using a computer-controlled bidirectional (forward/reverse shearing mode) and biaxial (along x-axis or y-axis) shear apparatus (Fig. 3a). This apparatus provides different shear loading paths under monotonic and cyclic shearing: (i) constant normal load (CNL), (ii) constant normal stress (CNS), (iii) constant normal stiffness (CNSK), and (iv) constant volume (CV). Normal and shear load capacity was 120 kN.

Fig. 3
figure 3

Schematic diagrams showing (a) a computer-controlled bidirectional and biaxial shear apparatus, and (b) a laser sensor profilometer used for the topographic data measurement

Full size image

4.2 Test Specimens and Topography Measurement

4.2.1 Test Specimens

The direct shear tests were carried out on the test specimens listed in Table 1 (three specimens for series 1, six specimens for series 2, and five specimens for series 3). The first series of experiment was performed on the Lanhelin granite man-made joints with hammered surfaces, which were noninterlocked and unmated (Fig. 4a). The second series of experiment was performed on man-made mortar joints with corrugated surfaces (Fig. 4c). Finally, the third series of experiment was performed on mortar replicas of a natural schist joint with rough and undulated surfaces texture (Fig. 4b). The mechanical properties of the test specimens are listed in Table 2. Compared with the values of granite basic friction angle (ϕ b ) ranging between 29° and 35° reported in the literature (e.g., Hoek and Bray 1981), the ϕ b value of 25° obtained from Lanhelin granite test samples seems low. It should be mentioned that this value was obtained from shear test on saw cut fresh granite samples. Similar values were found on Vietnamese, Tak, and Chinese granite samples (Kemthong 2006). Also from data taken in the literature (Kemthong 2006; Grasselli and Egger 2003), an exponential fitting relationship between ϕ b (in degrees) and the unconfined compressive strength σ c (in MPa) was found with a high coefficient of correlation (r = 0.999): ϕ b  = 1.7608 × exp(0.0172 × σ c ).

Table 1 Test sample characteristics
Full size table
Fig. 4
figure 4

Three-dimensional (3D) plot of test specimen surfaces: (a) granite hammered surface, (b) schist joint replica surface, (c) corrugated mortar joint surface

Full size image
Table 2 Mechanical properties of test samples
Full size table

4.2.2 Topography Data Acquisition

Surface topographical data measurements were performed prior to and after each shearing using a noncontact laser sensor profilometer (Fig. 3b) to quantify the evolution of the surface roughness through its parameters SR s and DR r , the joint wall surface wear through the wear coefficient Λ, and the degree of wear D w of the sheared joints. This equipment allows three-dimensional (3D) measurement of the joint wall surfaces by storing all (x, y, z) data points for each test specimen (Fig. 4). The laser sensor profilometer consists of an optical sensor equipped with a charge coupled device (CCD) camera with 50-μm resolution and 670-nm HeNe laser wavelength. The laser beam was 40 mm in length and 50 μm thick, with z-axis resolution of 50 μm (vertical) and x-axis or y-axis, depending on the sensor position, of 73 μm (horizontal). Standard deviation of white noise error due to mechanical vibration is 5 μm. The measurement system uses the laser triangulation principle, whereby a laser beam plane and a CCD camera are shifted to a 45° angle and both act as reference points (e.g., Sabbadini 1994; Belem 1997). Each surface topographic profile corresponds to a laser beam location on the specimen surface.

First of all, each coordinate z is directly measured from laser triangulation: z = f(x,y). The sampling step along x and y axes was Δx = Δy = 1 mm for hammered joints and Δx = Δy = 2 mm for schist joint replicas and corrugated joints. It should be mentioned that a nonexhaustive parametric study was done on the influence of sampling steps (or square grid step of Δx = Δy = 0.5, 1, and 2 mm) on the values of the calculated surface roughness parameters. It appeared from the corrugated joint samples that calculated parameters with the grid steps of 0.5 and 1 mm were almost identical, but slightly different from those calculated with a grid step of 2 mm. A single sampling step of 1 mm was selected for all the joint types but this sampling step generated vertical drifts for corrugated joint samples. For that reason, a unique sampling or grid step of 2 mm (4 mm2 square grids) was systematically used for calculation of the corrugated joint surface roughness parameters (Belem 1997). It was assumed that this sampling step was able to capture the least variation of surface roughness (minor joint wall degradation).

In the present study wear debris were removed only because it is difficult to maintain them on the surface during the topographical data acquisition procedure due to sample manipulations. It is very difficult, even impossible, to quantify the evolution of surface roughness over time, or with the relative or tangential displacement during shearing. On the other hand, it is easier to quantify the variation of surface roughness between its initial state and a given final state after shearing.

4.3 Testing Procedure

Three series of direct shear tests were carried out under a constant normal stress (CNS) shearing condition at a constant shear rate of 0.5 mm/min and with varying normal stress (σ n ) levels (Table 3). Cyclic shear testing was performed on the hammered and corrugated joint samples, while the natural schist joint sample replicas underwent monotonic shear testing. For cyclic shearing, the testing methodologies consisted of shearing again the “new” joint whose surface was already cleaned between cycles. It is clear that, by doing so, the observed mechanical behavior is not the true response of the same morphology sheared without any debris removal. However, the only bias would arise if one wanted to interpret mechanically the surface wear data and wear mechanisms, which is not the purpose of this paper. The proposed parameters are able to quantify any surface wear after shearing if it is possible to obtain accurate surface topographic data measurements.

Table 3 Constant normal stress shear test program
Full size table

The three hammered joint samples underwent five shearing cycles with three normal stress levels ranging from 0.3 to 4 MPa. For this series of shearing on granite hammered joint samples, it should be mentioned that the shear tests were performed in three stages: stage I (only one cycle of shearing was carried out and corresponds to cycle 1), stage II (two successive cycles of shearing were carried out and correspond to cycles 2 and 3) and stage III (two additional successive cycles of shearing were carried out and correspond to cycles 4 and 5). In other words, the mechanical parameters were calculated from the shearing curves of cycles 1, 2, and 4, while the surface wear parameters were quantified on surfaces after the shearing cycles 1, 3, and 5, which are the final states in terms of surface roughness evolution.

The six mortar corrugated joint specimens underwent ten shearing cycles with six normal stress levels ranging from 0.5 to 5 MPa. Finally, the five natural schist joint replicas underwent monotonic shearing with five normal stress levels ranging from 0.4 to 2.4 MPa.

The total (or accumulated) shear displacement u s_tot was 200 mm for the Lanhelin granite hammered joint surfaces (i.e. u s_tot  = 40 mm/cycle × 5 shearing cycles), 400 mm for the mortar corrugated joint surfaces (u s_tot  = 40 mm/cycle × 10 shearing cycles), and 20 mm (monotonic shearing) for the natural schist joint replicas.

5 Results of Surface Wear Quantification

5.1 Sample Application for Granite Hammered Surfaces

Figure 5 presents the first quadrant of the shear stress–shear displacement curves obtained on the Lanhelin granite hammered joint surfaces after one shearing cycle (cycle 1) under three varying normal stress levels (σ n  = 0.3, 1.2, and 4 MPa). Shear curves show quasiperfect elastoplastic behavior (smooth-like joint behavior), which is typical of nonmated and noninterlocked joint walls. Dilatancy (normal displacement versus shear displacement) curves clearly show the nondilatant nature of these man-made hammered plane joint surfaces (contracting joint). The initial misreporting of dilation for the first 0.2 mm at 4 MPa normal stress shearing curve is due to two combined effects: (i) the two joint walls were unmated, i.e., the wall surfaces were not mirror images and this led to a crushing of surface asperities after the load application, and (ii) a setup problem during this test due to an incorrect installation of the joint sample which had been moved down at the bottom of the shear box immediately after the normal load application. Consequently, there was less compression for 4 MPa due to the depression of the sample and an unusual steel-on-steel friction between the two half-shear boxes.

Fig. 5
figure 5

Constant normal stress (CNS) cyclic shearing curves for granite joint with hammered surfaces after the first shear cycle (σ n  = 1.2 MPa; stage I)

Full size image

Figure 6 presents a sample application of the surface roughness evolution of the granite hammered surfaces. The variation in the specific surface roughness SRs with the number of shearing cycles (for σ n  = 0.3, 1.2, and 4 MPa) is shown in Fig. 6a, while the variation in SR s with the normal stress (σ n ) for the first, third, and fifth shearing cycles is illustrated in Fig. 6b. A progressive decrease in specific surface roughness can be observed with either shearing cycles or normal stress level. In addition, for a given normal stress level, a continuous decrease in surface roughness from the first cycle to the fifth cycle was also observed. Figure 7 shows the evolution of the percentage of wear at the joint interface D w_interface(%) as a function of shearing cycles (Fig. 7a) or the normal stress levels (Fig. 7b). It can be observed that the percentage of wear for the sheared granite hammered joints increases with both the increase of applied normal stress level (σ n ) and the number of shearing cycles.

Fig. 6
figure 6

Evolution of granite hammered joint specific surface roughness coefficient (SR s ) after five nonconsecutive shearing cycles: (a) effect of the shearing cycles, and (b) effect of normal stress

Full size image
Fig. 7
figure 7

Evolution of granite hammered joint surface degree of wear (D w ) after five nonconsecutive shearing cycles: (a) effect of the shearing cycles, and (b) effect of normal stress

Full size image

5.2 Sample Application for the Undulated Natural Schist Joint Mortar Replica

Figure 8 presents the shear stress–shear displacement curves obtained from the natural schist joint mortar replicas subjected to monotonic shearing under five normal stress levels (σ n  = 0.4, 0.8, 1.2, 1.8, and 2.4 MPa). The residual phase (or steady state), which should correspond to a yielding shearing or plastic behavior, was not reached during testing, and the corresponding dilatancy curves indicate dilatant behavior of schist joint mortar replicas having rough and undulated surfaces texture.

Fig. 8
figure 8

Constant normal stress monotonic shearing curves for natural schist joint replicas at different normal stress levels

Full size image

Figure 9 shows the variation in specific surface roughness SR s with normal stress σ n . First of all, it can be observed that, for this particular joint surface texture (rough and undulated), SR s differs between upper and lower walls. This is probably due to the fact that the lower and the upper wall surfaces are matched but not interlocked. Overall, a slight decrease in SR s with increase in normal stress was observed.

Fig. 9
figure 9

Evolution of schist joint mortar replicas specific surface roughness coefficient (SR s ) after monotonic shearing for varying normal stress level

Full size image

Figure 10 presents the evolution of joint surfaces percentage of wear D w(%) as a function of applied normal stress level after monotonic shearing. Once again, the evolution of upper and lower wall percentage of wear differs slightly, with maximum wear at normal stress σ n  = 2.4 MPa of 13% for the lower wall, and 15% for the upper wall. From Fig. 10 a quasilinear evolution of the joint interface percentage of wear D w_interface(%) with the normal stress σ n can also be observed. Maximum percentage of wear for the joint interface is 28%, which is three times lower than that observed for the hammered joints. It can simply be remarked that a visual examination of these rough and undulated joint walls after shearing revealed that surface wear in this case occurred mainly in the central part of the test specimens. This observation however has no incidence on large-scale applications.

Fig. 10
figure 10

Evolution of schist joint mortar replicas surface degree of wear (D w ) after monotonic shearing for varying normal stress level

Full size image

5.3 Sample Application for the Corrugated Mortar Joint Surface

Figure 11 presents a typical shear stress–shear displacement curve obtained from the corrugated mortar joints that underwent ten shearing cycles under a normal stress level of 4 MPa. For this type of joint morphology, which is predominantly characterized by primary roughness (surface waviness), shear stress–shear displacement curves show increasing shear stress (τ) up to peak stress (τ p ), with a subsequent progressive decrease (softening) for the first cycle. It was also observed that for a given normal stress level (σ n ), peak stress (τ p ) increases with the number of shearing cycles with an increase in contact area (including wear debris accumulation and crushing). These curves show a perfect elastoplastic behavior as of shearing cycle 7 (i.e., residual phase was reached after seven shearing cycles) up to shearing cycle 10.

Fig. 11
figure 11

Constant normal stress cyclic shearing curves for mortar corrugated joint after ten shearing cycles (σ n  = 4 MPa)

Full size image

Figure 12 shows that the variation in specific surface roughness SR s with normal stress for theses corrugated joint surfaces is quite similar for the upper and the lower walls after the ten shearing cycles. This seems to confirm that the difference is due to the noninterlocked nature of joint walls. An overall continuous decrease in SR s with an increase in normal stress level is observed.

Fig. 12
figure 12

Evolution of mortar corrugated joint surface roughness coefficient (SR s ) after ten consecutive shearing cycles for varying normal stress levels

Full size image

Figure 13 presents the evolution of the percentage of wear D w(%) of the joint surfaces as a function of normal stress after ten shearing cycles. The evolution of the percentage of wear for the upper and lower walls is again slightly different. The maximum percentage of wear at the joint interfaces is 23%, which is approximately in the same order of magnitude as the schist joint mortar replicas, and is three times lower than that for the hammered joints.

Fig. 13
figure 13

Evolution of mortar corrugated joint surface degree of wear (D w ) after ten consecutive shearing cycles for varying normal stress levels

Full size image

6 Discussion

In the tribology literature, measures of wear have been formulated with respect to changes of the following quantities: (a) mass (m) of the removed material from the solid surface, (b) volume (V) of the removed material, and (c) reduced dimensions of the body. The measures of wear have nonzero values as long as an observable amount of the material is removed. Various models have been developed for the purpose of predicting the volume of wear. Apart from the direct approach of quantification of the volume of wear, there exist possible indirect approaches, namely direct observation of asperity contact and image analysis of contact areas (Dieterich and Kilgore 1994, 1996). In rock mechanics, it is very rare however to specifically carry out wear tests as practised in tribology. Knowing that in rock mechanics and rock engineering the surface morphology plays a crucial role in the normal and tangential behavior of rock joints, it seemed convenient to use its characterization to estimate indirectly the wear (not to predict it). The indirect approach chosen in this study assumes that any rough surface true area A t is made up of mainly two components: a perfect smooth surface area corresponding to the flat cross-sectional area of measurement A n , and the pure roughness area A z which corresponds to the height departure from the flat cross-sectional area (combination of surface roughness and waviness).

$$ A_{t} = A_{n} + A_{z}. $$
(33)

From Eq. (33) it can be observed that the real area of contacts A r , as defined by Bowden and Tabor (1950), will only involve a part of the pure roughness area A z (=A t  − A n ). The interfacial roughness area A * z is the sum of the roughness area of the lower (l) and the upper (u) walls:

$$ A_{z}^{*} = \left( {A_{t} - A_{n} } \right)_{l} + \left( {A_{t} - A_{n} } \right)_{u} = (A_{t} )_{l} + (A_{t} )_{u} - 2A_{n} = (A_{z} )_{l} + (A_{z} )_{u}. $$
(34)

If A *z0 and A * zs are the pure roughness areas prior to shearing (0) and after shearing (s), respectively, the estimated interface real area of contact \( \tilde{A}_{r}^{*} \) can be calculated as follows:

$$ \tilde{A}_{r}^{*} = \left| {A_{z0}^{*} - A_{zs}^{*} } \right|. $$
(35)

The fractional area contacted R c (ratio of estimated interfacial real area of contact \( \tilde{A}_{r}^{*} \) and the projected flat surface area or cross-sectional area A n ) is given as follows:

$$ R_{c} = \frac{{\tilde{A}_{r}^{*} }}{{2A_{n} }} = \frac{{\left| {A_{z0}^{*} - A_{zs}^{*} } \right|}}{{2A_{n} }}. $$
(36)

Knowing also that the wear volume produced per unit of sliding distance (V/s) or wear rate given by Eq. (1) has a unit of area [L 2], this parameter can also be estimated as follows:

$$ \frac{V}{s} = \tilde{W}_{R} \approx \frac{{\left| {\left( {A_{t}^{0} - A_{t}^{s} } \right)_{l} + \left( {A_{t}^{0} - A_{t}^{s} } \right)_{u} } \right|}}{s/2L}, $$
(37)

where \( \tilde{W}_{R}^{{}} \) is the estimated wear rate (in mm2); s is the shear displacement (or sliding distance in mm); L is the joint sample initial length (in mm); subscripts l and u represent the lower and upper joint walls, respectively; A 0 t and A s t are the joint developed surface true areas prior to shearing (0) and after shearing (s), respectively. This formula assumes that wear rate is constant and wear mechanisms are unchanged during the course of shearing, and that the average wear rate is characteristic of the entire test.

According to Lim and Ashby (1987), the wear depth \( \tilde{h} \) can be estimated by dividing both sides of Eq. (37) by the apparent contact area A n as follows:

$$ \frac{V}{{2sA_{n} }} = \tilde{Q}_{R} \approx \frac{L}{s}\frac{{\left| {\left( {A_{t}^{0} - A_{t}^{s} } \right)_{l} + \left( {A_{t}^{0} - A_{t}^{s} } \right)_{u} } \right|}}{{A_{n} }} \approx \frac{{\tilde{h}}}{s}, $$
(38)

where \( \tilde{Q}_{R} \) is the wear depth per unit of shearing displacement or sliding distance \( \left( {\tilde{h}/s} \right). \)

The purpose of this work was not to study in details the frictional behavior of sheared joints, but rather to quantify indirectly its amount. Except for the Lanhelin granite hammered surface joint samples, for which the wear debris were removed between two stages of cyclic shearing, the debris were not removed from the other joint samples until the end of shearing and prior to topographic data measurement (rough and undulated schist joint replicas and corrugated mortar joints). According to Denape and Lamon (1990), when wear debris are removed from the sliding interface, the friction coefficient decreases to a low value and the wear rate correspondingly increases. This implies that, when wear debris accumulate in the sliding interface, the friction coefficient increases and the wear rate decreases. The wear debris have a dual action: (i) they interact with the sliding surfaces by ploughing and abrasion, which increase the friction coefficient; (ii) they present load-carrying capacity, which decreases the wear rate. Consequently, stability of the friction coefficient corresponds to a constant quantity of debris; an increase indicates a debris build-up phase whereas a reduction reflects an elimination phase (Denape and Lamon 1990). For the corrugated mortars joints, the wear debris were not removed and their effect can be seen clearly on the curves shown in Fig. 11. It can be observed that after one cycle of shearing the stress-displacement curve exhibits elastoplastic behavior with softening. After ten cycles of shearing the softening ability of the corrugated mortar joints is fully eliminated due to wear debris accumulation (plasticity-induced damage or wear). However, instead of reducing, the shear resistance increases with the increase in the number of cycle of shearing.

The proposed method of surface wear quantification depends mostly on the accuracy of the calculation of surface true areas. This accuracy in turn depends on the sensitivity of the sampling grid (or step) size on the calculated true area, even if it was assumed that no significant variation was observed between grid size of 1 mm and 2 mm. Also, it can be noticed that when the specific surface roughness coefficient SR s of a mated joint sample differs from the two mirror walls (lower and upper), it is mainly ascribable to a noninterlocking problem. The 2.4 MPa normal stress level shearing curve seemingly exhibits two peaks, but it is mainly the result of the joint initial mismatching and noninterlocking. The same observation was made for σ n  = 0.4 MPa; for example, the natural schist joint replicas were prepared from room temperature vulcanized (RTV) silicone moldings (plaster of Paris) having a high degree of accuracy of reproduction. Even if the calculated surface true area data show a coefficient of variation C v (=standard deviation/mean value) of approximately 0.11% for lower wall or upper wall samples together and a maximum relative variation of approximately 5% between all lower wall samples and all upper wall samples, it was considered that all joint samples were not perfectly interlocked.

For the Lanhelin granite hammered surface joints, the maximum percentage of wear observed was up to 90% after cycle 5 under a normal stress level of 1.2 MPa, which is much higher than the value obtained with 4 MPa. The low values of D w(%) at σ n  = 4 MPa are partly due to the tangential motors exceeding their loading capacity (100 kN) during the CNS shearing tests on the hammered joints. Consequently, it could not be concluded that for this type of roughness the influence of normal stress on the joint surface wear is limited to the low values (σ n  < 4 MPa). It was also observed during shearing of the hammered joint at σ n  = 4 MPa that the lower and upper shear boxes rubbed (steel-on-steel sliding) due to the ratio of thickness of the granite samples (40 mm) and depth of the shear boxes (45 mm).

7 Conclusion

In this study, five monotonic shear tests and ten cyclic shear tests were performed under constant normal stress (CNS) on three types of joint surface textures to better understand their morphomechanical behavior (evolution of surface roughness and joint surface wear). These three surface textures are: Lanhelin granite man-made hammered joints, man-made mortar corrugated joints, and mortar replicas of natural schist joints. Surface topographic data measurements were performed using a noncontact laser sensor profilometer prior to and after each shear test for calculating joint pure or specific interface/surface roughness coefficient SR s and joint interface/surface degree of wear D w(%). Characterization results showed that degree of wear D w(%) is a good parameter for estimating percentage of sheared joint wall surfaces wear. Moreover, from a practical standpoint, D w(%) is more readily estimated than the more commonly used Ladanyi and Archambault’s shear area ratio a s . Evolution of sheared joint surface roughness was quantified by the specific surface roughness SR s . This roughness evolution was directly related to joint wall surface wear.

Degree of wear D w(%) allowed evaluating maximum cumulated wear of more than 90% after five shearing cycles for the granite hammered joints, of approximately 28% after monotonic shearing for the mortar replicas of natural undulated schist joints, and of approximately 23% after ten shearing cycles for the mortar corrugated joints. It was therefore confirmed that the sheared surface wear strongly depends on both geometric texture (morphology and asperities interlocking) and material properties (natural rock or mortar). As it is not easy to quantify sheared joint surface wear directly, the proposed method will allow estimation of the surface wear in a simple way and it will be possible to validate some analytical models and numerical simulations.