1 Introduction

Beams are crucial components in any mechanical structure such as automotive and aircraft components, machine frames, and other mechanical or structural systems that contain beam structures and are designed to carry structural loads. Flexure beams with small thickness have been used widely in micro/nano manipulation mechanisms and grippers. Many studies (Ghafarian et al. 2018, 2019; Zhang et al. 2017; Pinskier and Shirinzadeh 2019; Gu et al. 2018) have been conducted on the design, analysis, and optimization of flexure beams for Micro/Nano electromechanical systems’ (MEMS/NEMS) applications. Dynamic analysis of micro/nano beams is essential as the strength and desired performances of the structure directly related to the dynamic characteristics. Therefore, during the past decade, there have been important insights into the modeling of the vibrational behavior of such micro/nano structures. Nanobeams are an essential component which have been used in biomedical sensors (e-nose), atomic force microscopy (AFM), nanoscale memory devices, photonic crystal nanobeam cavities, resonant Lorentz force magnetic field sensors, and NEMS. CNTs, nanorods, nanoplates, nanowires, nanorings, graphenes and microtubules can also be formulated like a nanobeam. Classical beam theories such as Euler–Bernoulli theory, Rayleigh theory, Timoshenko theory (Ghafarian and Ariaei 2016a, 2019), Reddy theory, and Levinson theory are inappropriate for modeling of small scale effect on nanobeams. Therefore, many size-dependent continuum theories have been established for describing the mechanical behavior of micro/nano scale mechanisms and structures. Among these theories, nonlocal elasticity theory by Eringen (1972, 1983) has been widely used and adopted to explain the behavior of those minuscule mechanical systems (Ghafarian and Ariaei 2016b; Moutlana and Adali 2019; Yayli 2014; Santos and Soares 2012; Wang 2017; Eptaimeros et al. 2020; Jha and Dasgupta 2019). Aranda-Ruiz et al. (2012) calculated the natural frequencies of the flapwise bending vibrations of a non-uniform rotating nano cantilever, considering the true spatial variation of the axial force due to the rotation. The nanobeam’s height was assumed to taper linearly along its length. The problem was formulated using the nonlocal Eringen elasticity theory and it was solved by a pseudospectral collocation method based on Chebyshev polynomials. Aydogdu (2014) studied the axial vibration of double-walled carbon nanotubes (DWCNTs) using nonlocal elasticity theory considering the van der Waals forces in the axial direction. Duan et al. (2007) calibrated the small scaling parameter of the nonlocal Timoshenko beam theory for the free vibration problem of single-walled carbon nanotubes (SWCNTs). The calibration exercise was performed by using vibration frequencies generated from MD simulations at room temperature.

On the other hand, FGMs are regarded as one of the most promising candidates for future advanced composites in many engineering sectors. These materials are deemed to have an advantageous behavior over laminated composites due to the continuous variation of their material properties yet in all three dimensions, which alleviate delamination, de-bonding, and matrix cracking initiation issues. Therefore, the mechanical problems associated with the structures constructed from FGMs have gained a huge deal of attention during recent years (Zhang et al. 2019; Rajasekaran 2013; Aubad et al. 2019; Rastehkenari 2019; Gholipour and Ghayesh 2020). Shahba et al. (2013) studied free vibration analysis of rotating tapered beams made of FGMs using a finite element approach. Karamanli (2018) investigated the free vibration behavior of two-directional FG beams subjected to various sets of boundary conditions by employing a third-order shear deformation theory. The material properties of the beam were assumed to vary exponentially in both directions. Ruocco et al. (2018) presented the buckling and free vibration analyses of nonlocal axially functionally graded Euler nanobeams based on the Hencky bar chain (HBC) model. Gorgani et al. (2019) studied the pull-in behavior of cantilever micro/nano beams made of FGMs with small-scale effects under electrostatic force. The Rayleigh–Ritz method was implemented to approximate analytical solutions for the pull-in voltage and pull-in displacement of the microbeams.

Analytical and semi-analytical solutions of the partial differential equations applied in describing engineering problems are often difficult to obtain. Thus, researchers have used different techniques to solve the differential equations in engineering problems. Some of these applied methods are differential quadrature method (DQM), generalized differential quadrature method (GDQM), homotopy perturbation method (HPM), homotopy analysis method (HAM), optimal homotopy asymptotic method (OHAM), Adomian decomposition method (ADM), finite element method (FEM), and differential transformation method (DTM) which have been used by numerous scholars to solve the governing differential equations describing the behavior of mechanical problems. Each of the mentioned methods has its own advantages over the other methods (Ghafarian and Ariaei 2016a, b, 2019; Ragb et al. 2019; Shishesaz et al. 2019; Noghrehabadi et al. 2012; Aria and Friswell 2019). However, the analytical and semi-analytical solution methods are preferred because of the sense in the physics of the problem and convenience in parametric studies Ghafarian and Ariaei (2016a). DTM is an authentic, effective and precise technique with the ability of simple formulation and implementation and with a low computational cost. DTM employs the polynomial form to estimate the exact solution based on the Taylor series expansion. Throughout this technique, the derived differential equations of motions of the mechanical system as well as the boundary conditions are transformed into algebraic equations. Accordingly, the accurate and reliable results can be obtained throughout solving the resultant algebraic equations, without requiring computational operations. On the whole, the simplicity and high precision are the most distinguished aspects of DTM (Ghafarian and Ariaei 2016a, b, 2019; Semnani et al. 2013; Godara and Joglekar 2017).

As it was discussed in the literature review, so far some research related to the vibration characteristics of the rotating nanobeams made from different materials has been done by the researchers using various theories. However, according to the best knowledge of authors, there is no comprehensive investigation on the vibration characteristics of rotating double-tapered AFGM nanobeams considering two different taper ratios in the formulation and considering a uniform nonlinear distribution of materials throughout the structure. Therefore, in this paper, this issue is investigated to fill the detected gap in the open literature related to the mechanical vibration of rotating nanobeams. It is worth pointing out that AFGM and variable section properties of the considered rotating nanobeam leads to a partial differential equation with variable coefficients. For solving such equation, the DTM is employed as a semi-analytical approach due to reliability, accuracy, and simplicity of implementation.

Herewith, the governing differential equation alongside the boundary conditions describing the dynamic behavior of a rotating double-tapered AFGM nanobeam is derived by adapting the Euler–Bernoulli beam model of nonlocal Eringen elasticity theory. Subsequently, the separation of variables is applied to the equation that yields an equation containing the frequency of the system. Thereafter, dimensionless parameters are defined to obtain the dimensionless form of the governing equation as well as the related boundary conditions. The algebraic equations obtained by means of the transformation rules lead to a characteristic equation which should be solved numerically to gain the dimensionless frequencies. To evaluate the performance of the semi-analytical method, verification and convergence study is adapted. The results show that the presented methodology proves to be accurate. Finally, some detailed numerical results are represented in which the first four dimensionless frequencies and the corresponding mode shapes are investigated. Consequently, the effects of various involved parameters including nonlocal scaling parameter, taper ratios, angular velocity, and hub radius are explored comprehensively. Some important results are revealed which may be useful for efficient designing of the nano-structures benefiting from rotating nanobeams such as nanosensors, biosensors, nano actuators, and other NEMS devices.

2 Nonlocal elasticity theory

Eringen nonlocal elasticity theory has been widely used for modeling of vibration of a nanobeam. Unlike the classic beam theory, a size-dependent term is considered in this theory which makes it compatible to predict vibration of a nano-scale beam. The following nonlocal constitutive stress–strain equation was proposed by Eringen (1983);

$$\left[1-{({e}_{0}a)}^{2}{\nabla }^{2}\right]{\sigma }_{ij}={C}_{ijkl}{\varepsilon }_{kl}$$
(1)

where \({\sigma }_{ij}\), \({C}_{ijkl}\) and \({\varepsilon }_{kl}\) are the nonlocal stress, classical strain, and fourth-order elasticity tensors, respectively. \({e}_{0}\) is a constant determined independently for each material. \(a\) is an internal characteristic length (distance between atoms, lattice parameter, size of grain, granular distance, or distance between the C–C bonds, etc.). The parameter \({e}_{0}\) is estimated that the nonlocal elasticity model predicts satisfactorily the atomic dispersion curves of plane waves compared to that obtained from the atomistic lattice dynamics.

A method of identifying the small scaling parameter \({e}_{0}\) in the nonlocal theory is not known yet. As defined by Eringen (1983), \({e}_{0}\) is a constant specific to each material. Eringen proposed \({e}_{0}=0.39\) by matching the dispersion curves via the nonlocal theory for plane wave and Born–von Karman model of lattice dynamics at the end of the Brillouin zone. On the other hand, Eringen (1972), in his study, proposed \({e}_{0}=0.31\) for Rayleigh surface wave through nonlocal continuum mechanics and lattice dynamics. In general, different values for \({e}_{0}\) have been presented for different types of problems based on the matching of the results obtained with MD simulations to those obtained with the nonlocal continuum mechanics. Araujo dos Santos and Mota Soares (2012) studied the vibration of a SWCNT and found that the values of \({e}_{0}\) vary with the number of natural frequency and the SWCNT length and diameter. Furthermore, Duan et al. (2007) claimed that instead of a constant value, the calibrated \({e}_{0}\) values vary with respect to length-to-diameter ratios, mode shapes, and boundary conditions of the SWCNTs.

3 Nonlocal equations of motion of a rotating double-tapered AFGM nanobeam

3.1 Material properties

In this study, it was assumed that the material properties of the nanobeam such as Young’s Modulus E and mass density r vary continuously according to power law form. Therefore, the material properties were considered to vary through the nanobeam axis and the material characteristics can also be assumed to vary based on power law distribution, and thus can be described using the following formulas;

$$E\left(x\right)={E}_{L}+({E}_{R}-{E}_{L}){\left(\frac{x}{L}\right)}^{n}$$
(2)
$$\rho \left(x\right)={\rho }_{L}+({\rho }_{R}-{\rho }_{L}){\left(\frac{x}{L}\right)}^{n}$$
(3)

where subscripts L and R are the corresponding material properties of the left and the right side of the nanobeam, respectively, and n is the non-negative power law exponent which dictates the material variation profile through the axis of the nanobeam. Table 1 shows the materials which were used for describing the nanobeam. To have a uniform distribution of both material, \(n\)=2 is chosen as the exponent.

Table 1 Material properties of an AFGM nanobeam
Full size table

3.2 Equation of motion

Nanotubes are central components to new rotating devices such as miniature motors. The rotating CNT can be represented as a cantilevered nanobeam which is assumed to be slender and satisfied Euler–Bernoulli beam theory. In this section, the nonlocal equation of motion is obtained based on the Euler–Bernoulli beam deformation theory for one rotating double-tapered AFGM nanobeam.

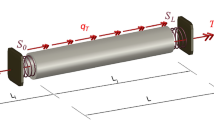
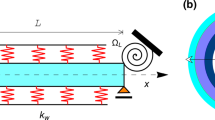
Figure 1 shows a nanobeam of length L which is fixed to a rigid molecular hub. The molecular hub has radius R and rotates in a counter-clockwise direction at a constant rotational speed, Ω. The nanobeam tapers through its breadth and height by the coefficients of \({c}_{b}\) and \({c}_{h}\), respectively. Further, the material properties of the nanobeam change through its length.

Fig. 1
figure 1

Configuration of a rotating double-tapered nanobeam

Full size image

Based on the Euler–Bernoulli beam theory, the axial and transverse displacement fields are represented as;

$$u(x,y,z,t)=-z\frac{\partial w(x,t)}{\partial x}$$
(4)
$$w(x,y,z,t)=w(x,t)$$
(5)

where w is the transverse displacement of the neutral axis of the nanobeam. It is noteworthy that, based on some studies in the literature which considered longitudinal displacement as an independent variable for linear vibration (Lin and Wu 2005; Lin and Ro 2003), no effect was observed on the results obtained for other displacements. Considering Eqs. (4) and (5), the only non-zero strain term of the Euler–Bernoulli beam theory is described by;

$${\varepsilon }_{xx}=\frac{\partial u}{\partial x}=-z\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(6)

The equation of motion of a rotating nanobeam based on the Euler–Bernoulli beam theory is presented as;

$$\frac{\partial V}{\partial x}+q+\frac{\partial }{\partial x}\left(T\left(x\right)\frac{\partial w}{\partial x}\right)=\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}$$
(7)

where;

$$V=\frac{\partial M}{\partial x}$$
(8)
$$M=\underset{A}{\overset{}{\int }}z{\sigma }_{xx}dA$$
(9)

where V is the shear force, q is the external force per unit of length, T(x) is the axial force due to centrifugal acceleration, r is the mass density, A is the nanobeam cross-sectional area, M is the bending moment, and \({\sigma }_{xx}\) is the axial stress on the yz-section in the direction of x.

By considering Eqs. (1) and (6), it can be found that only one equation exists to describe the stress–strain behavior of the nanobeam;

$${\sigma }_{xx}-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}{\sigma }_{xx}}{\partial {x}^{2}}=E{\varepsilon }_{xx}$$
(10)

By performing surface integration of \({\int }_{A}z\left(\right)dA\) from both sides of Eq. (10), and noting that the moment of inertia of the nanobeam cross-section is \({I}_{y}={\int }_{A}{z}^{2}dA\), the following equation was derived;

$$M-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}M}{\partial {x}^{2}}=-E{I}_{y}\frac{{\partial }^{2}w}{\partial {x}^{2}}$$
(11)

By differentiating Eq. (8) with respect to x and substituting into Eq. (7), finding the term \(\frac{{\partial }^{2}M}{\partial {x}^{2}}\), and substituting it into Eq. (11), Eq. (12) was resulted as follows;

$$M=-E{I}_{y}\frac{{\partial }^{2}w}{\partial {x}^{2}}+{\left({e}_{0}a\right)}^{2}\left[\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}-\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)-q\right]$$
(12)

Now, by having the moment of inertia and using Eq. (8), the shear force of the nanobeam was derived;

$$V=-\frac{\partial }{\partial x}\left(E{I}_{y}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)+{\left({e}_{0}a\right)}^{2}\frac{\partial }{\partial x}\left[\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}-\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)-q\right]$$
(13)

Using the shear force, Eq. (13), and substituting it back into the Euler–Bernoulli equation of motion of a rotating nanobeam, Eq. (7), the final version of the equation of motion of a rotating nanobeam was obtained as;

$$\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}+\frac{{\partial }^{2}}{\partial {x}^{2}}\left(E{I}_{y}\frac{{\partial }^{2}w}{\partial {x}^{2}}\right)-\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}}{\partial {x}^{2}}\left\{\rho A\frac{{\partial }^{2}w}{\partial {t}^{2}}-\frac{\partial }{\partial x}\left(T\frac{\partial w}{\partial x}\right)\right\}=q-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}q}{\partial {x}^{2}}$$
(14)

As the nanobeam tapers linearly from its breadth and height, the following assumptions were made;

$${c}_{b}=1-\frac{{b}_{L}}{{b}_{0}}$$
(15)
$${c}_{h}=1-\frac{{h}_{L}}{{h}_{0}}$$
(16)
$$A={A}_{0}(1-{c}_{b}\frac{x}{L})(1-{c}_{h}\frac{x}{L})$$
(17)
$${I}_{y}={I}_{{y}_{0}}(1-{c}_{b}\frac{x}{L}){(1-{c}_{h}\frac{x}{L})}^{3}$$
(18)

where \({c}_{b}\) and \({c}_{h}\) should be considered lower than 1 to avoid having zero nanobeam’s height and breadth between its ends.

According to Ghafarian and Ariaei (2016a, b), the centrifugal force \(T\left(x\right)\) at a distance x from the clamped end of nanobeam can be expressed as follows;

$$T\left(x\right)={\int }_{x}^{L}\rho A{\Omega }^{2}\left(R+\Lambda \right)d\Lambda ={A}_{1}\left(L-x\right)+{A}_{2}\left({L}^{2}-{x}^{2}\right)+{A}_{3}\left({L}^{3}-{x}^{3}\right)+{A}_{4}\left({L}^{4}-{x}^{4}\right)+{A}_{5}\left({L}^{5}-{x}^{5}\right)+{A}_{6}\left({L}^{6}-{x}^{6}\right)$$
(19)

where Ai (i = 1,…,6) are constants and were formulated and presented in “Appendix A”. Substituting the FGM formulations, Eqs. (2) and (3), the centrifugal force, Eq. (19), and the taper assumptions, Eqs. (15)-(18), into the Eq. (14), the equation of motion of a rotating Euler–Bernoulli double-tapered AFGM nanobeam was obtained as follows;

$${B}_{1}\frac{{\partial }^{2}w}{\partial {t}^{2}}+{B}_{2}\frac{{\partial }^{4}w}{\partial {x}^{4}}+{B}_{3}\frac{{\partial }^{3}w}{\partial {x}^{3}}+{B}_{4}\frac{{\partial }^{2}w}{\partial {x}^{2}}+{B}_{5}\frac{\partial w}{\partial x}+{B}_{6}\frac{{\partial }^{3}w}{\partial x\partial {t}^{2}}+{B}_{7}\frac{{\partial }^{4}w}{\partial {x}^{2}\partial {t}^{2}}=q-{\left({e}_{0}a\right)}^{2}\frac{{\partial }^{2}q}{\partial {x}^{2}}$$
(20)

Bi (i = 1,…,7) are functions of x and were shown in “Appendix B”.

3.3 Boundary conditions

Boundary conditions of a cantilever nanobeam are described as below;

Transverse displacement and angle of bending are zero at the fixed end of nanobeam;

$$w = 0,\;\;{\text{At}},\quad x = 0$$
(21)
$$\frac{\partial w}{{\partial x}} = 0,\;\;{\text{At}},\quad x = 0$$
(22)

Bending moment and shear force are zero at the free end of nanobeam;

$$M = 0,\;\;{\text{At}},\quad x = L$$
(23)
$$V = 0,\;\;{\text{At}},\;\;x = L$$
(24)

4 Free vibration analysis of the system

4.1 Free vibration analysis

In this section, free vibration analysis of a rotating double-tapered AFGM nanobeam is investigated. For this purpose, initially, the external force was neglected, and later a harmonic motion was assumed as the following form;

$$w\left(x,t\right)=u(x){e}^{i\omega t}$$
(25)

where \(u(x)\) is the amplitude functions of transverse displacement, and \(\omega\) is the circular natural frequency.

4.2 Dimensionless parameters, nonlocal equation of motion, and boundary conditions

For convenience and also comparing the results with other articles, the following dimensionless parameters are introduced:

$$\begin{aligned} \overline{x} & = \frac{x}{L} \\ \overline{w} & = \frac{w}{L} \\ \overline{u} & = \frac{u}{L} \\ \tau & = \frac{{e_{0} a}}{L} \\ \delta & = \frac{R}{L} \\ \overline{E} & = \frac{{E_{L} - E_{R} }}{{E_{L} }} \\ \overline{\rho } & = \frac{{\rho_{L} - \rho_{R} }}{{\rho_{L} }} \\ {\overline{\Omega }} & = {\Omega }\sqrt {\frac{{\rho_{L} A_{0} }}{{E_{L} I_{{y_{0} }} }}} L^{2} \\ {\overline{\omega }} & = {\upomega }\sqrt {\frac{{\rho_{L} A_{0} }}{{E_{L} I_{{y_{0} }} }}} L^{2} \\ \end{aligned}$$
(26)

where \(\overline{x}\) is the dimensionless location along the length of nanobeam, \(\overline{w}\) is the dimensionless transverse displacement,\(\overline{u}\) is the dimensionless amplitude functions of transverse displacement, \(\tau\) is the dimensionless nonlocal scaling parameter, \(\delta\) is the dimensionless hub radius, \(\overline{E}\) is the dimensionless Young’s modulus, \(\overline{\rho }\) is the dimensionless density, \(\overline{\Omega }\) is the dimensionless rotational speed, and \(\overline{\omega }\) is the dimensionless natural frequency. Substituting Eq. (25) and dimensionless parameters (26) into Eqs. (20) and (21)–(24), the dimensionless form of the nonlocal equation of motion, along with the nonlocal boundary conditions were obtained, respectively, as explained in the following.

5 Dimensionless nonlocal equation of motion

The dimensionless nonlocal equation of motion was derived and shown in Eq. (27);

$${C}_{0}\overline{u}+{C}_{1}\frac{d\overline{u}}{d\overline{x}}+{C}_{2}\frac{{d}^{2}\overline{u}}{d{\overline{x}}^{2}}+{C}_{3}\frac{{d}^{3}\overline{u}}{d{\overline{x}}^{3}}+{C}_{4}\frac{{d}^{4}\overline{u}}{d{\overline{x}}^{4}}=0$$
(27)

Ci (i = 0,…,4) are functions of \(\overline{x}\) and were shown in “Appendix C”. Equation (27) is a linear forth order homogenous ordinary differential equation that describes the behavior of the nanobeam system.

6 Dimensionless nonlocal boundary conditions

The dimensionless nonlocal boundary conditions were derived and shown in Eqs. (28)–(31);

Dimensionless transverse displacement at the fixed end of nanobeam;

$$\overline{u} = 0,\;{\text{At}},\quad \overline{x} = 0$$
(28)

Dimensionless angle of bending at the fixed end of nanobeam;

$$\frac{{d\overline{u}}}{{d\overline{x}}} = 0,\;{\text{At}},\quad \overline{x} = 0$$
(29)

Dimensionless nonlocal bending moment at the free end of nanobeam;

$$\overline{M} = D_{2} \frac{{d^{2} \overline{u}}}{{d\overline{x}^{2} }} + D_{1} \frac{{d\overline{u}}}{{d\overline{x}}} + D_{0} \overline{u} = 0,\;{\text{At}},\quad \overline{x} = 1$$
(30)

Dimensionless nonlocal shear force at the free end of nanobeam;

$$\overline{V} = E_{3} \frac{{d^{3} \overline{u}}}{{d\overline{x}^{3} }} + E_{2} \frac{{d^{2} \overline{u}}}{{d\overline{x}^{2} }} + E_{1} \frac{{d\overline{u}}}{{d\overline{x}}} + E_{0} \overline{u} = 0,\;{\text{At}},\quad \overline{x} = 1$$
(31)

Di (i = 0,1,2) and Ei (i = 0,1,2,3) are functions of \(\overline{x}\) and were shown in “Appendices D” and “E”.

6.1 Differential transform method (DTM)

DTM is a beneficial and appropriate semi-analytical method for finding the solution of a differential equation. Generally, this technique consists of two differential and inverse differential transformations. If function \(\overline{u}(\overline{x})\) is analytic in domain D, and \(\overline{x}={\overline{x}}_{0}\) represents any point in this domain, the differential transformation of the function \(\overline{u}(\overline{x})\) is then presented by;

$$U\left(m\right)={\left.\frac{1}{m!}\left[\frac{{d}^{m}\overline{u}(\overline{x})}{d\overline{x}^{m}}\right]\right|}_{\overline{x}={\overline{x}}_{0}}$$
(32)

where, \(\overline{u}(\overline{x})\) is the original function and \(U\left(m\right)\) is the \({m}^{\mathrm{t}\mathrm{h}}\) order differential transformation of \(\overline{u}(\overline{x})\).

On the other hand, the inverse differential transformation of \(U\left(m\right)\) is also defined as;

$$\overline{u}\left(\overline{x}\right)=\sum_{m=0}^{\infty }U(m){(\overline{x}-{\overline{x}}_{0})}^{m}$$
(33)

In practical applications, the function \(\overline{u}\left(\overline{x}\right)\) is expressed by a finite series and Eq. (33) can be rewritten as follows;

$$\overline{u}\left(\overline{x}\right)=\sum_{m=0}^{s}U(m){(\overline{x}-{\overline{x}}_{0})}^{m}$$
(34)

Equation (34) implies that \(\overline{u}\left(\overline{x}\right)=\sum_{m=s+1}^{\infty }U(m){(\overline{x}-{\overline{x}}_{0})}^{m}\) is negligibly small. The number of terms, s, is chosen as the convergence of natural frequencies is satisfied. Also, \({\overline{x}}_{0}\) is considered as zero.

The properties that are useful in the transformation of the differential equation and the boundary conditions are tabulated in Tables 2 and 3, respectively.

Table 2 DTM theorems used for the equation of motion
Full size table
Table 3 DTM theorems used for the boundary conditions
Full size table

By applying the DTM technique from Table 2, the nonlocal equation of motion for a rotating double-tapered AFGM nanobeam, Eq. (27), can be rewritten as follows;

$${F}_{1}U(m-4)+{F}_{2}U(m-3)+{F}_{3}U(m-2)+{F}_{4}U(m-1)+{F}_{5}U(m)+{F}_{6}U(m+1)+{F}_{7}U(m+2)+{F}_{8}U(m+3)+{F}_{9}U(m+4)=0$$
(35)

In addition, by implementing the DTM technique from Table 3, the nonlocal boundary conditions can also be rewritten as follows;

$$U\left( 0 \right) = 0,\;{\text{At}},\quad \overline{x} = 0$$
(36)
$$U\left( 1 \right) = 0,\;{\text{At}},\quad \overline{x} = 0$$
(37)
$$\overline{\overline{M}} = \mathop \sum \limits_{m = 0}^{\infty } \left\{ {G_{1} m\left( {m - 1} \right) + \left( {e_{0} a} \right)^{2} \left[ {G_{2} + G_{3} m} \right]} \right\}U\left( m \right) = 0,\;{\text{At}},\quad \overline{x} = 1$$
(38)
$$\overline{\overline{V}} = \mathop \sum \limits_{m = 0}^{\infty } \left\{ {H_{1} m\left( {m - 1} \right)\left( {m - 2} \right) + H_{2} m\left( {m - 1} \right) + \left( {e_{0} a} \right)^{2} \left[ {H_{3} + H_{4} m\left( {m - 1} \right) + H_{5} m} \right]} \right\}U\left( m \right) = 0,\;{\text{At}},\quad \overline{x} = 1$$
(39)

Coefficients \({F}_{i}\) (\(i\) = 1,…,9), \({G}_{i}\) (\(i\quad\)= 1, 2, 3), and \({H}_{i}\) (\(i\quad\)= 1,…,5) were derived and shown in “Appendices F, G”, and “H”, respectively. It is worthy of mention that the function coefficients represented in “Appendices C, D, E, F, G”, and “H” are dimensionless. \(\overline{\overline{M}}\) and \(\overline{\overline{V}}\) are the transformed dimensionless nonlocal bending moment and shear force at the free end of the nanobeam, respectively. Applying the nonlocal boundary conditions expressed in Eqs. (36)–(39) in Eq. (35) and considering \(U\left(2\right)={C}_{1}\) and \(U\left(3\right)={C}_{2}\), the following expression was obtained;

$${A}_{i1}\left(\overline{\omega }\right){C}_{1}+{A}_{i2}\left(\overline{\omega }\right){C}_{2}=0, i=\mathrm{1,2}$$
(40)

where \({C}_{1}\) and \({C}_{2}\) are constant, and \({A}_{i1}\left(\overline{\omega }\right)\) and \({A}_{i2}\left(\overline{\omega }\right)\) are polynomials with respect to \(\overline{\omega }\). The dimensionless natural frequencies are the eigenvalues of Eq. (40) and they were calculated by solving the following determinant when equals to zero;

$$\left|\begin{array}{cc}{A}_{11}\left(\overline{\omega }\right)& {A}_{12}\left(\overline{\omega }\right)\\ {A}_{21}\left(\overline{\omega }\right)& {A}_{22}\left(\overline{\omega }\right)\end{array}\right|=0$$
(41)

This determinant provides a single polynomial equation for determining the dimensionless natural frequencies, \(\overline{\omega }\). To determine the value of the jth natural frequency, the following convergence criterion may be used;

$$\left| {\overline{\omega }_{j}^{\left( q \right)} - \overline{\omega }_{j}^{{\left( {q - 1} \right)}} } \right| \le {\upvarepsilon }\;\;\;,\quad j = 1,{ }2,{ }3, \ldots$$
(42)

where \(q\) is the iteration counter, \(\overline{\omega }_{j}\) is the estimated value of the jth dimensionless natural frequency, and ε is a tolerance parameter and a sufficiently small number. After calculating the natural frequencies, the mode shapes can be obtained by deriving the following relation from Eq. (40);

$${C}_{2}=-\frac{{A}_{11}\left({\overline{\omega }}_{j}\right)}{{A}_{12}\left({\overline{\omega }}_{j}\right)}{C}_{1}$$
(43)

Applying Eq. (43), \({U}_{j}\left(m\right)\) can be expressed in terms of \({\overline{\omega }}_{j}\) and \({C}_{1}\) as follows;

$${U}_{j}\left(m\right)=U({\overline{\omega }}_{j},{C}_{1})$$
(44)

Having \({U}_{j}\left(m\right)\) related to each natural frequency and implementing inverse of DTM, the mode shape related to that natural frequency was obtained by the following equation;

$${\overline{u}}_{j}\left(\overline{x}\right)=\sum_{m=0}^{s}{U}_{j}\left(m\right){\overline{x}}^{m}$$
(45)

7 Results and discussions

In this section, the obtained results of the mathematical modeling are presented and comparisons are made to the previous studies to prove the accuracy of modeling and results.

7.1 FGM properties

The proposed nanobeam system is made of FGM. This means that the mechanical properties of the nanobeam are dependent on the specific position in itself and are changing by position. This trend in the proposed modeling was formulated by Eqs. (2) and (3), which \(n=2\) was assumed. Figures 2, 3 and 4 show how the mechanical properties are changing by changing in the exponent and the position along the length of the nanobeam. Figure 2 is the 3D model of this trend with respect to \(\overline{x}\) and \(n\). Figure 3 is the contour of this 3D model and numbers inside of the left figure show the Young’s Modulus and the numbers inside of the right figure show the mass density. It is obvious that at the very left side of the nanobeam (\(\overline{x}=0\)) the only material is Zirconia and at the very right side of the nanobeam (\(\overline{x}=L\)) the only material is Aluminium. Figure 4 shows the trend of changing of E and r along the length of the nanobeam for the exponent equals to 2. According to Fig. 4, the local Young’s modulus and mass density decrease when becoming closer to the end x = L. The Young’s modulus reduces faster than the mass density as getting closer to the end x = L. Reasons for that are the dimensionless Young’s modulus reduction (\(\frac{{E}_{L}-{E}_{R}}{{E}_{L}}\times 100=65\mathrm{\%}\)) is higher than the dimensionless density reduction (\(\frac{{\rho }_{L}-{\rho }_{R}}{{\rho }_{L}}\times 100\cong 52.6\mathrm{\%}\)).

Fig. 2
figure 2

Variation of Young’s modulus and mass density with respect to the exponent and dimensionless location along the length of nanobeam

Full size image
Fig. 3
figure 3

The contour of Young’s modulus and mass density with respect to the exponent and dimensionless location along the length of nanobeam

Full size image
Fig. 4
figure 4

Variation of Young’s modulus and mass density with respect to the dimensionless location along the length of nanobeam (\(n=2\))

Full size image

7.2 Validation of results

For validation purposes, the results are compared with Shahba et al. (2013) and Aranda-Ruiz et al. (2012). Shahba et al. (2013) investigated the vibration analysis of an AFGM tapered rotating beam. Material and geometry properties of the analysis were chosen as shown in Tables 1 and 4, respectively. Table 5, shows the first five dimensionless natural frequencies obtained from the presented study and Shahba et al. (2013). It can be seen that good accuracy was achieved.

Table 4 Geometry properties of an AFGM tapered rotating beam
Full size table
Table 5 First five dimensionless natural frequencies of an AFGM tapered rotating beam
Full size table

Investigation of a rotating nanobeam was done by Aranda-Ruiz et al. (2012) and the results are compared with the presented study. The geometry properties of the analysis were chosen as shown in Tables 6. Figure 5 shows the result of this comparison which the first three dimensionless natural frequencies were plotted against different dimensionless rotational speeds. It can be noted that the results had a good overlap and the accuracy of the modeling was guaranteed.

Table 6 Geometry properties of a rotating ZrO2 nanobeam
Full size table
Fig. 5
figure 5

Variation of dimensionless natural frequency against the dimensionless rotational speed of a rotating nanobeam, filled (Present); unfilled (Aranda-Ruiz et al. 2012)

Full size image

7.3 Results of the presented nanobeam system and mathematical modeling

All numerical results presented in this section are based on the numerical data tabulated in Tables 1 and 7.

Table 7 Geometry properties of an AFGM double-tapered rotating nanobeam
Full size table

Slenderness Ratio (SR) is defined as the length of the nanobeam to the smallest size of the cross-section of it. The behavior of a nanobeam is closer to the nonlocal Euler–Bernoulli beam theory by a larger SR quantity due to the fact that the effects of shear deformation and rotatory inertia become negligible. In the presented work, the smallest size of the cross-section (\(h\)) is changing through the nanobeam’s length from \({h}_{0}\)=2 nm to \({h}_{L}\)=1.2 nm. Consequently, the SR changes from 125 to 208.3. Therefore, as a result of having large SR (meaning slender nanobeam), it can be concluded that there is no significant difference between the vibrational frequencies of Euler–Bernoulli and Timoshenko nanobeams and the nonlocal Euler–Bernoulli beam theory can be used to describe the behavior of the considered nanobeam system (Kikidis and Papadopoulos 1992; Aydin 2013).

In Fig. 6, the convergence of the first four dimensionless natural frequencies is introduced. Here, it was necessary to take 95 terms to evaluate up to the fourth dimensionless natural frequency to four-digit precision. Therefore, the number of the terms, s, mentioned in Eq. (34) is 95 for the first four dimensionless natural frequencies. Additionally, here it is seen that higher modes appear when more terms are taken into account in DTM application. Thus, depending on the order of the required mode, one must try a few values for the term number at the beginning of the numerical calculations in order to find an adequate number of terms.

Fig. 6
figure 6

Convergence of the first four dimensionless natural frequencies

Full size image

Table 8 shows the first four dimensionless natural frequencies of a rotating double-tapered AFGM nanobeam. Figure 7 shows the corresponding mode shapes of those natural frequencies obtained from Eq. (45).

Table 8 First four natural frequencies of an AFGM double-tapered rotating nanobeam
Full size table
Fig. 7
figure 7

Mode shapes of an AFGM double-tapered rotating nanobeam

Full size image

Figure 8 shows the importance of considering the nonlocal Eringen theory and specifically the nonlocal scaling parameter in analyzing a nanobeam system. It can be seen that increasing \(\tau\) causes an increase in the first natural frequency and a decrease in the remaining three. As \(\tau =0\), shows the behavior of the nanobeam with classical Euler–Bernoulli theory, the natural frequencies are different when the nonlocal parameter is being counted and it shows the importance of this parameter. The most interesting result is that the importance of this parameter becomes clearer when the attention is directed towards the higher natural frequencies.

Fig. 8
figure 8

Effect of the dimensionless nonlocal scaling parameter on the natural frequencies of an AFGM double-tapered rotating nanobeam

Full size image

The effects of rotational speed and hub radius on natural frequencies were investigated and the results are shown in Figure 9. It was seen that by increasing rotational speed, the natural frequencies increase and this trend is also occurring when the hub radius increases. In addition, rotational speed and hub radius have more impact on the higher natural frequencies than the lower ones and the rate of changing the natural frequencies due to changing those two parameters is more evident on the higher natural frequencies as well. It is noted that natural frequencies remain constant by changing hub radius for a non-rotating double-tapered AFGM nanobeam which makes sense, because without rotation there is no centrifugal force applied to the nanobeam, and the only important relationship between the hub and the nanobeam is the boundary conditions between them.

Fig. 9
figure 9

Effect of rotational speed and hub radius on the natural frequencies of a rotating double-tapered AFGM nanobeam

Full size image

The proposed nanobeam tapered linearly from both its height and breadth. The results of this tapering effect from its height are plotted in Figure 10. As it is very obvious from Eq. (16), \({c}_{h}\) can be between 0 to 1. From the results, it can be understood that by increasing the height taper ratio, or in the other words by making it tapered quicker, the first natural frequency increases but the other ones decrease. This trend of changing in the value of natural frequencies due to the changing in height taper ratio is more evident when it gets to the higher natural frequencies.

Fig. 10
figure 10

Effect of the height taper ratio on the natural frequencies of a rotating double-tapered AFGM nanobeam

Full size image

Based on Eq. (15), \({c}_{b}\) can be between 0 to 1. Therefore, the effect of the breadth taper ratio on the natural frequencies is shown in Fig. 11. It must be emphasized that by increasing the breadth taper ratio the natural frequencies increase.

Fig. 11
figure 11

Effect of the breadth taper ratio on the natural frequencies of a rotating double-tapered AFGM nanobeam

Full size image

Looking at the results of the effect of height and breadth taper ratio on the natural frequencies, it can be concluded that by increasing mode number, the effect of height taper ratio on the natural frequencies becomes more dominant than the effect of breadth taper ratio. In other words, the height taper ratio plays a key role compared to the breadth taper ratio when the mode number increases.

8 Conclusion

In this article, free vibration analysis of a rotating double-tapered AFGM nanobeam was presented. It was assumed that the height and the breadth of nanobeam taper linearly along its length and moreover, the mechanical properties of it change nonlinearly along its length. Using the nonlocal Eringen theory, the equation of motion of the proposed system and the boundary conditions were developed. Afterward, the separation of variables solution was applied to obtain an equation containing the frequency. Then, DTM and related rules were employed to convert the obtained equation as well as the boundary conditions to the form of algebraic equations, from which, a characteristic equation was extracted. Solving the resultant characteristic equation yielded the dimensionless natural frequencies. Additionally, the corresponding mode shapes were obtained and the effect of several parameters such as nonlocal scaling parameter, rotational speed, hub radius, height and breadth taper ratios were investigated on the natural frequencies and the results were presented. Finally, the results were compared with those reported in the literature and an excellent agreement was observed. Moreover, the following results were obtained for a rotating double-tapered AFGM nanobeam system;

  • The value of the first natural frequency is increased by increasing the nonlocal scaling parameter and the rest is decreased.

  • The importance of the nonlocal scaling parameter becomes clearer when the attention is directed towards the higher natural frequencies.

  • Increasing rotational speed and hub radius cause an increase in the natural frequencies.

  • Rotational speed, hub radius, and height taper ratio have more impact on the higher natural frequencies than the lower ones and the rate of changing the natural frequencies due to changing those parameters is more evident.

  • Increasing the breadth taper ratio causes an increase in the natural frequencies. Moreover, increasing the height taper ratio causes an increase in the first natural frequency but a decrease in the rest.

The results given in this paper present some complementary information about the exact size-dependent vibration behavior of the rotating cantilever double-tapered AFGM nanobeams. Therefore, the paper and its results can be applicable in an efficient design of the nano-structures in which the rotating nanobeams play a pivotal role.