1 Introduction

The motion of heat for a viscous fluid has numerous industrialized, biomedical and engineering demands for instance capacity generator, petroleum productions, plasma research, cancer therapy, the laminar boundary layer dominance in aerodynamics and numerous others. But this concept takes a long journey to shape up for this position. In 1904, Prandtl suggested the laminar boundary layer theory which humor that the viscous impact would be limited to thin shear surfaces adjacent borders in the case of the flow of fluids with very small viscosity (Schlichting et al. 1960). Sakiadis (1961ab) has studied the boundary layer Blasius motion due to surface supplying with constant speed from a slit into a liquid at relaxes. Crane (1970) has investigated the flow over a stretching sheet. Numerous researchers for instance Dutta et al. (1985), Char (1988), Gupta and Gupta (1977) expanded the research of Crane (1970). Varied features of such problems have been studied by different researchers for instance Hayat et al. (2008). Hayat et al. (2006), Xu and Liao (2005) and Cortell (2005, 2006).Motion past a cylinder is assumed to be 2-D boundary layer flow across a stretching cylinder was invoked by Datta et al. (2006). Elbarbary was analyzed by heat transfer effects on micropolar across a stretching cylinder (Elbarbary and Elgazery 2005). Wang (1988) has investigated the steady two dimensional flow of a fluid across a stretching cylinder. Ishak et al. (2008) have studied the MHD motion and transfer of heat past a stretching cylinder. Ishak et al. (2008) have numerical investigation on the effect of suction/blowing on the motion across a stretching cylinder. Butt et al. (2016) have explored Heat transfer effects on hydromagnetic entropy generation flow over a horizontal stretching cylinder. They are obtaining solutions by using bvp4c technique in MATLAB.

Radiation plays very important role in engineering, industry, and humankind also. In human kinds radiation is used for medicines, excavation, radiology lab, MRI scans etc. Akinshilo (2019) was scrutinized the flow of hydromagnetic fluid flow across vertical micro channel with radiation effects, in this paper they are obtaining solution by implementing Runge–Kutta scheme. A steady 3D non-linear radiation on flow of a carreau fluid across a bidirectional stretching sheet was studied by Khan et al. (2018). They concluded that by escalating values of Hartmann number the velocity profile is declines and opposite behaviour is seen in temperature profile. Khan et al. (2018) was deliberated by impact of linear radiation on third grade fluid for coating analysis. In this paper they are obtaining solution by using HAM. Hashim et al. (Hamid et al. 2018) studied by heat and mass transfer effects on non-Newtonian fluid over a circular cylinder.

Magnetohydrodynamic plays a key role in industry, engineering, heat transfers etc. Hydromagnetics is the revise of the magnetic premises of electrically conducting fluid. There are several applications in magneto hydrodynamics they are cosmology, seismology, metal detectors etc.Heat transfer effects on hydromagnetic nano fluid by using Buongiorno’s model were analyzed by Ajam et al. (2018).they are obtaining solution by using OHAM. Durga Prasad et al. (2018) was scrutinized by analytical approximation on MHD nano fluid across a semi-infinite plate. Khan et al. (2018) was invoked by homogenious –hetrogenious reactions on hydromagnetic non-newtonian fluid across a cylinder. Siti et al. (2018) was investigated by MHD flow past a stretching disk. Heat and fluid flow along a stretching cylinder was studied by Vikas et al. (2018). In this paper they are presenting graphical presentations along with stability analysis. Ismail et al. (2019) analyzed the study of stability analysis on an unsteady hydromagnetic flow across a shrinking sheet. Gholinia et al. (2019) was analyzed by heat and mass transfer effects on hydromagnetic nano fluid across a stretching sheet. In this paper they are presenting graphical representations by using Runge–Kutta method. Heat transfer effects on hydromagnetic natural convection in Darcy-Forchhimer were scrutinized by Sajjadi et al. (2019).

In modern days the abnormal trend of nanofluid is due to its unexpected thermal properties and have dynamic role in heat transfer enhancement of material processing and industrial thermal managements. Free convection flows permanently faced in engineering tools and nuclear reactor technology. Prasannakumara et al. (Prasannakumara et al. 2017) deliberate effort on radiative heat transfer of nanofluids using magnetic field over a plate. They perceive that the Nusselt number and Sherwood number are enhanced for nonlinear stretching sheet. Kumar et al. (2018) represented the Marangoni effects on nanofluid in the presence of heat. Recently various researchers studied heat transfer of nanofluids (Kumar et al. 2018; Kumar and Chamkha 2019; Kumar 2019; Usman et al. 2018; Anwar and Rasheed 2017; Mebarek-Oudina 2019; Mebarek-Oudina 2017; Raza et al. 2019; Gourari et al. 2019; Verma and Sinha 2015; Verma et al. 2017; Ganesh et al. 2020; Nadeem et al. 2020; Rashid et al. 2020; Abbas et al. 2020; Kahshan et al. 2019; Uddin et al. 2019; Akermi et al. 2019; Ganesh Kumar et al. 2019).

The above literature analysis discloses that no work occurs on incompressible tangent hyperbolic nanoliquid flow past a permeable surface. The combined effect of magnetic field and nanofluid across a permeable surface are accounted. By using similarity transformations PDE’S can be transformed into ODE’S and explained numerically. Outcomes are represented through graphs for the parameters of concern.

2 Mathematical formulation

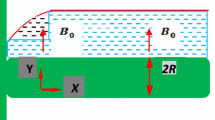
Here firstly assume that flow is steady and the incompressible tangent hyperbolic nanoliquid flow past a permeable surface is considered. The flow occupies to \( y > 0 \), velocity of the sheet is \( u_{w} (x) = bx,b > 0 \) and further x-axis taken along the sheet (Fig. 1).

Fig. 1
figure 1

Physical model and coordinate system

Full size image

The constitutive equation of tangent hyperbolic fluid is,

$$ \bar{\tau } = \left[ {\mu_{0} + \left( {\mu_{0} + \mu_{\infty } } \right)\tanh \left( {\varGamma \bar{\dot{\gamma }}} \right)^{n} } \right]\bar{\dot{\gamma }} , $$
(a)

in which, \( \bar{\tau } \) is the extra stress tensor, \( \mu_{\infty } \) the infinite shear rate viscosity, \( \mu_{0} \) the zero shear rate viscosity, \( \varGamma \) is the time dependent material constant, n the power law index i.e. flow behavior index and \( \bar{\dot{\gamma }} \) is defined as,

$$ \bar{\dot{\gamma }} = \frac{1}{2}\sqrt {\frac{1}{2}\mathop \sum \limits_{i} \mathop \sum \limits_{j} \bar{\dot{\gamma }}_{ij} \bar{\dot{\gamma }}_{\text{ji}} } = \sqrt {\frac{1}{2}\varPi } . $$
(b)

Consider the equation (a), for the case when \( \mu_{\infty } = 0 \) because it is not possible to discuss the problem for the infinite shear rate viscosity and since we are considering tangent hyperbolic fluid that describing shear thinning effects so \( \varGamma \bar{\dot{\gamma }} < 1. \) Then equation (a) will takes the form,

$$ \begin{aligned} \bar{\tau } = \mu_{0} \left[ {\left( {\varGamma \bar{\dot{\gamma }}} \right)^{n} } \right] \hfill \\ \bar{\tau } = \mu_{0} [1 + n(\varGamma \bar{\dot{\gamma }} - 1)]\bar{\dot{\gamma }}. \hfill \\ \end{aligned} $$
(c)

Governing equations for tangent hyperbolic fluid model after applying the boundary layer approximations can be defined as Abdul Maleque (2013), Dhlaminia et al. (2019), Kumar et al. (2017),

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \nu \left( {1 - n} \right)\frac{{\partial^{2} u}}{{\partial y^{2 } }} + \sqrt 2 \nu n\varGamma \left( {\frac{\partial u}{\partial y}} \right)\frac{{\partial^{2} u}}{{\partial y^{2} }}{-}\frac{{\sigma B_{0}^{2} }}{\rho }u, $$
(2)
$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)\, + \tau \left\{ {D_{B} \left( {\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}} \right) + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left[ {\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]} \right\} - \frac{1}{{\rho C_{p} }}\frac{{\partial q_{r} }}{\partial y},\,\,\,\, $$
(3)
$$ u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{B} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - k_{r}^{2} (C - C_{\infty } )\left( {\frac{T}{{T_{\infty } }}} \right)^{m} \exp \left( {\frac{ - Ea}{\kappa T}} \right) $$
(4)

The following imposed conditions of the model are;

$$ u = u_{w} \left( x \right),v = v_{w} ,T = T_{w} \,,\,\,D_{B} \frac{\partial C}{\partial y} + \frac{{D_{T} }}{{T_{\infty } }}\frac{\partial T}{\partial y}{ = 0}\,({\text{passive}}\,\,{\text{control}}\,{\text{of}}\,\phi )\,\,\,\,{\text{at}}\,\,\,y = 0 $$
$$ u \to 0,T \to T_{\infty } ,C \to C_{\infty } \,as\,\,y \to \infty $$
(5)

Here \( v_{w} > 0 \) notes as injection, \( v_{w} < 0 \) noted as suction. The third term on RHS of Eq. (5) denotes modified Arrhenius formula in which \( k_{r}^{2} \) for rate of reaction, Ea for activation energy, \( \kappa \) for Boltzmann constant and m dimensionless fitted rate constant which lies in the range \( - 1 < m < 1 \).

Implementation Rosseland approximation \( q_{r} \) defined as,

$$ q_{r} = - \frac{{4\sigma^{*} }}{{3k^{*} }}\frac{{\partial T^{4} }}{\partial y} = \frac{{16\sigma^{*} }}{{3k^{*} }}T^{3} \frac{\partial T}{\partial y}, $$
(6)

use of (6) in (3), we get;

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{\partial }{\partial y}\left[ {\left( {\alpha + \frac{{16\sigma^{*} }}{{3k^{*} }}T^{3} \frac{\partial T}{\partial y}} \right)\frac{\partial T}{\partial y}} \right] + \tau \left\{ {D_{B} \left( {\frac{\partial C}{\partial y}\frac{\partial T}{\partial y}} \right) + \left( {\frac{{D_{T} }}{{T_{\infty } }}} \right)\left[ {\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right]} \right\} , $$
(7)

To obtain the similarity result use the following variables

$$ \eta = \left( {\frac{{u_{w} }}{\nu x}} \right)^{1/2} y,\,\,f(\eta ) = \frac{\psi }{{(x\nu u_{w} )^{1/2} }},\,\theta (\eta ) = \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\phi (\eta ) = \frac{{C - C_{\infty } }}{{C_{\infty } }}({\text{passive}}\,{\text{control}}\,{\text{of}}\,\phi ) $$
(8)

where \( T = T_{\infty } \left( {1 + \left( {\theta_{w} - 1} \right)\theta (\eta )} \right) \) and \( \theta_{w} = {\raise0.7ex\hbox{${T_{w} }$} \!\mathord{\left/ {\vphantom {{T_{w} } {T_{\infty } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{\infty } }$}},\theta_{w} > 1 \) being temperature ration parameter.

Applying (8) in (1, 2, 4 and 7), one can have;

$$ \left( {1 - n} \right)f^{{{\prime \prime \prime }}} \left( \eta \right){-}\left[ {f^{{\prime }} \left( \eta \right)} \right]^{2} + f^{{\prime \prime }} \left( \eta \right)f\left( \eta \right) + n W_{e} f^{{{\prime \prime }2}} \left( \eta \right)f^{{{\prime \prime \prime }}} (\eta ) {-}Mf^{{\prime }} \left( \eta \right) = 0, $$
(9)
$$ \left( {\left[ {\left( {1 + Nr(\theta_{w} - 1)} \right)\theta } \right]^{3} \theta^{{\prime }} } \right)^{{\prime }} + \Pr \left( {f\theta^{{\prime }} + Nb\theta^{{^{{\prime }} }} \phi^{{\prime }} + Nt\theta^{{{\prime 2}}} } \right) = 0 , $$
(10)
$$ \phi^{{\prime \prime }} + Scf\phi^{{\prime }} + \frac{Nt}{Nb}\theta^{{\prime \prime }} - Sc\sigma (1 + \delta \theta )^{m} \phi \,\exp \left( {\frac{ - E}{1 + \delta \theta }} \right) = 0 , $$
(11)

COresponding boundary conditions are;

$$ f(0) = S,f^{\prime } (0) = 1,\theta (0) = 1,Nb\phi^{\prime } (0) + Nt\theta^{\prime } (0) = 0({\text{passive}}\,{\text{control}}\,{\text{of}}\,\phi ),f^{'} (\infty ) \to 0,\theta (\infty ) \to 0,\phi (\infty ) \to 0. $$
(12)

The dimentionless numbers in Eqs. (9–12) are\( \lambda = \lambda_{2}^{2} a^{2} \) for material parameter, \( Nr\left( { = \frac{{16\sigma^{*} T_{\infty }^{3} }}{{3kk^{*} }}} \right) \) for radiation parameter, \( Nb\left( { = \frac{{\tau D_{B} C_{\infty } }}{\nu }} \right) \) for Brownian movement. \( Nt\left( { = \frac{{\tau D_{T} (T_{f} - T_{\infty } )}}{{\nu T_{\infty } }}} \right) \) for thermophoretic, \( \Pr \left( { = \frac{\nu }{\alpha }} \right) \) for Prandtl number, \( Sc\left( { = \frac{\nu }{{D_{B} }}} \right) \) for Schmidt number, \( \sigma \left( { = \frac{{k_{r}^{2} }}{b}} \right) \) for reaction rate, \( \delta \left( { = \frac{{T_{f} - T_{\infty } }}{{T_{\infty } }}} \right) \) for temperature difference, \( E\left( { = \frac{Ea}{{\kappa T_{\infty } }}} \right) \) for activation energy, \( W_{e} = \frac{{\sqrt {2b} \varGamma u_{w} }}{\sqrt \nu } \) is the Weissenberg number and n is the power law index parameter and \( S = - \frac{{v_{w} }}{{\sqrt {b\nu } }} \) for mass transfer parameter.

The physical quantities of interest like skin friction coefficient \( \left( {C_{f} } \right) \) and local Nusselt number (Nux), and Sherwood number are defined as,

$$ c_{f} = \frac{{\tau_{w} }}{{\rho u_{w}^{2} }},Nu_{x} = \frac{{u_{w} q_{w} }}{{bk\left( {T_{\infty } - T_{w} } \right)}}\quad {\text{and}}\quad Sh_{x} = \frac{{u_{w} q_{m} }}{{aD_{b} (C_{w} - C_{\infty } )}}, $$
(13)

where \( \tau_{w} \) is known as shear stress along the wall, \( q_{w} \) is known as heat flux, \( q_{m} \) is nano particle mass flux,

$$ \tau_{w} = \mu_{0} \left( {\left( {1 - n} \right)\frac{\partial u}{\partial y} + \frac{n\varGamma }{\sqrt 2 }\left( {\frac{\partial u}{\partial y}} \right)^{2} } \right), \quad q_{w} = - k\frac{\partial T}{\partial y}\left. \right|_{y = 0 } \quad {\text{and}}\quad q_{m} = - D\frac{\partial C}{\partial y}\left. \right|_{y = 0} . $$
(14)

Finally the expression of drag friction \( (C_{f} ) \), local Nusselt number \( (Nu) \) and Sherwood number \( (Sh) \) written as,

$$ \begin{aligned} \sqrt {Re} C_{f} = \left[ {\left( {1 - n} \right)f^{{\prime \prime }} \left( \eta \right) + \frac{n}{2}W_{e} \left( {f^{{\prime \prime }} \left( \eta \right)} \right)^{2} } \right]_{\eta = 0} ,Nu{\text{Re}}_{x}^{ - 1/2} = - \left( {1 + Nr\theta_{w}^{3} } \right)\theta^{{\prime }} (0)\;{\text{and}} \hfill \\ Sh{\text{Re}}_{x}^{ - 1/2} = \frac{Nt}{Nb}\theta^{{\prime }} (0)({\text{passive}}\,{\text{control}}\,{\text{of}}\,\phi ) \hfill \\ \end{aligned} $$
(15)

where \( \text{Re}_{x} = {\raise0.7ex\hbox{${u_{w} x}$} \!\mathord{\left/ {\vphantom {{u_{w} x} \nu }}\right.\kern-0pt} \!\lower0.7ex\hbox{$\nu $}} \) for local Reynolds number.

3 Numerical method

The dimensionless arrangement of Eqs. (9)–(11) with the conditions (12) are profoundly coupled differential conditions. One needs to turn towards numerical strategies to acquire the arrangement of such conditions. In this investigation, we have utilized the method Runge–Kutta–Fehlberg fourth–fifth order with shooting system. The calculations have been done utilizing the representative programming Maple.

The algorithm of Runge–Kutta–Fehlberg –forth- fifth order method is given by;

$$ \begin{aligned} k_{0} = & F\left( {\bar{x}_{m} ,\bar{y}_{m} } \right), \\ k_{1} = & F\left( {\bar{x}_{m} + \frac{h}{4},\bar{y}_{m} + \frac{{hk_{0} }}{4}} \right), \\ k_{2} = & F\left( {\bar{x}_{m} + \frac{3}{8}h,\bar{y}_{m} + \left( {\frac{3}{32}k_{0} + \frac{9}{32}k_{1} } \right)h} \right), \\ k_{3} = & F\left( {\bar{x}_{m} + \frac{12}{13}h,\bar{y}_{m} + \left( {\frac{1932}{2197}k_{0} - \frac{7200}{2197}k_{1} + \frac{7296}{2197}k_{2} } \right)h} \right), \\ k_{4} = & F\left( {\bar{x}_{m} + h,\bar{y}_{m} + \left( {\frac{439}{216}k_{0} - 8k_{1} + \frac{3860}{513}k_{2} - \frac{845}{4104}k_{3} } \right)h} \right), \\ k_{5} = & F\left( {\bar{x}_{m} + \frac{h}{2},\bar{y}_{m} + \left( { - \frac{8}{27}k_{0} + 2k_{1} - \frac{3544}{2565}k_{2} + \frac{1859}{4104}k_{3} - \frac{11}{40}k_{4} } \right)h} \right), \\ \bar{y}_{m + 1} = & \bar{y}_{m} + h\left( {\frac{25}{216}k_{0} + \frac{1408}{2565}k_{2} + \frac{2197}{4109}k_{3} - \frac{1}{5}k_{4} } \right), \\ \bar{y}_{m + 1} = & \bar{y}_{m} + h\left( {\frac{16}{135}k_{0} + \frac{6656}{12825}k_{2} + \frac{28561}{56430}k_{3} - \frac{9}{50}k_{4} + \frac{2}{55}k_{5} } \right), \\ \end{aligned} $$

4 Results and discussion

The flawless perception of the physical problem is discussed in this section. The prominent characteristics of the impact of a combination of nanofluids on velocity, temperature and concentration augmentation are evaluated through graphical representation of numerical data and tables. Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 represent the fluid flow, temperature and concentration profiles. For this computation we choose the parameter values \( Nb = Nt = 0.3, Nr = 3, Pr = 3, n = 0.5, W_{e} = 0.8, \theta_{w} = 1.2, \sigma = \delta = E = 1 \) and \( Sc = 0.5. \)

Fig. 2
figure 2

Impact of M on \( f^{{\prime }} \left( \eta \right) \)

Full size image
Fig. 3
figure 3

Impact of We on \( f^{{\prime }} \left( \eta \right) \)

Full size image
Fig. 4
figure 4

Impact of Nr on \( \theta \left( \eta \right) \)

Full size image
Fig. 5
figure 5

Impact of \( \theta_{w} \) on \( \theta \left( \eta \right) \)

Full size image
Fig. 6
figure 6

Impact of \( \delta \) on \( \phi \left( \eta \right) \)

Full size image
Fig. 7
figure 7

Impact of E on \( \phi \left( \eta \right) \)

Full size image
Fig. 8
figure 8

Impact of Sc on \( \phi \left( \eta \right) \)

Full size image
Fig. 9
figure 9

Impact of Nt on \( \theta \left( \eta \right) \)

Full size image
Fig. 10
figure 10

Impact of Nb on \( \theta \left( \eta \right) \)

Full size image
Fig. 11
figure 11

Impact of Nt on \( \phi \left( \eta \right) \)

Full size image
Fig. 12
figure 12

Impact of Nb on \( \phi \left( \eta \right) \)

Full size image
Fig. 13
figure 13

Influence of Nb and Nt on \( - NuRe_{x}^{{ - \frac{1}{2}}} \)

Full size image
Fig. 14
figure 14

Influence of \( Sc \) and E on \( - ShRe_{x}^{{ - \frac{1}{2}}} \)

Full size image
Fig. 15
figure 15

Stream lines for when \( M = 0.5 \)

Full size image
Fig. 16
figure 16

Stream lines for when \( M = 2.0 \)

Full size image
Fig. 17
figure 17

Stream lines for when \( W_{e} = 0.1 \)

Full size image
Fig. 18
figure 18

Stream lines for when \( W_{e} = 1.0 \)

Full size image

Figure 2 captured the impact of M on velocity profiles against similarity variable \( \eta \) respectively. We perceived from Fig. 2 that by enhancing magnetic number M the fluid flow diminished progressively. Because the Lorentz force is an opposite force for strengthen magnetic number which resists the liquid motion. The influence of Weissenberg parameter \( W_{e} \) can be seen in Fig. 3. From these figures show that the velocity profile enhances with boost up values of \( W_{e} \). Furthermore, the thickness of hydrodynamic boundary layer is high for rising values of \( W_{e} \).

The behaviour of Radiation parameter Nr is illustrated in Fig. 4 An increase in Radiation parameter Nr shows the significant enhancement in the fluid temperature function. Physically speaking, by strengthening Nr yields more heat into the liquid, as a consequence the thickness of associated the energy boundary layer enhanced. Thus, Nr effects plays a key role in magnify the rate of heat transfer.

The influence of temperature ratio parameter \( \theta_{w} \) on \( \theta (\eta ) \) is illustrated in Fig. 5. The temperature and species profiles rises by improving values of \( \theta_{w} \) thickness of boundary layer increased. From Figs. 6, 7 illustrates that for escalating values of \( \delta \) and E concentration profile declines for \( \delta \) and opposite behaviour is seen in E.

From Fig. 8 shows that for boost up values of Schmidt number Sc concentration decreases for both the phases. Physically, enhancing values of Schmidt number Scthe mass diffusivity declines. Figures 9 and 10 are demonstrates the influence of Nt and Nb on \( \theta \left( \eta \right) \). It shows that an increase in Nt and Nb enhances the \( \theta \left( \eta \right) \) and hence, the associated thickness of the boundary layer also enhances.

Figure 11 elucidates the effect of Nb on \( \phi \) field. A reduction in \( \phi \) field is obtained for the larger values of Nb parameter. Correspondingly thickness of boundary layer exhibits the same behavior as that of nanoparticle concentration profile. This is because of the larger Brownian motion of the suspended particle, due to its increment in its corresponding parameter.

In the boundary layer region Nt plays a vital role on the \( \phi \) field. This effect is captured in Fig. 12. From this figure it is clear that for gradually increasing values of Nt concentration profile is increased. Physically, the thermophoretic is a force that one particle exerts on the other particle. Due to which the particles in the hotter region are moved to the colder region. As a result an acclivity in the concentration is noted. The effects of Nb and Nt on \( - NuRe_{x}^{{ - \frac{1}{2}}} \) is established in Fig. 13. It shows that the \( - NuRe_{x}^{{ - \frac{1}{2}}} \) decreases for both injection and suction case for large values of Nb and Nt. Figure 14 IS prepared to establish the influence of \( Sc \) verses E on \( - ShRe_{x}^{{ - \frac{1}{2}}} \). It is clear that, \( - ShRe_{x}^{{ - \frac{1}{2}}} \) decays for enlarged values of \( Sc \) verses E.

Finally, to get a clear view of the flow field patterns, the stream line dynamics are reported in Figs. 15, 16, 17 and 18 for with peculiar values of Magnetic parameter M and Weissenberg number \( W_{e} \) For Magnetic parameter M and Weissenberg number \( W_{e} \) is strengthened, the fluid particle traces a definite curve along x-direction where the surface is present. But it is clear that the there is a retardation in the flow pattern.

5 Conclusion

Fully developed steady of flow and heat transfer of tangent hyperbolic nanofluid fluid over a stretching sheet is considered. In this paper the effect of zero mass flux, activation energy and impact of applied magnetic field is taken into consideration. The outcome of the present work is as follows:

  • Velocity of the fluid increases as \( W_{e} \) parameter increases.

  • Both concentration and temperature profiles enhance for increasing values of Nb parameter.

  • Temperature and velocity profiles shows reverse trend in rising values of Nt.

  • Momentum boundary layer thickness decreases for rising values of M.

  • The concentration profile and corresponding boundary layer thickness decreases for enhancing values of \( \delta \) and E.

  • Higher Nr plays a key role in magnify the rate of heat transfer. This is because, higher Nr enhances the temperature profile and also enhances the corresponding boundary layer thickness.