1 Introduction

Heat transport phenomenon plays a major role in many geographical processes, engineering and industrial domain. Particular types of such processes incorporate space cooling, cooling of electronic devices, heat conduction in tissues, cooling of nuclear reactor etc. Heat is transferred due to temperature difference within a body or between two bodies. In the last two centuries, heat transfer is studied via Fourier’s heat conduction law. In fact, conventional law of Fourier is a parabolic type equation which illustrates that heat is transferred with infinite speed. The law is also known as conduction paradox. To correct this issue Cattaneo (1948) presented the non-Fourier theory. He added time relaxation factor in classical law of Fourier so that the heat transfers in a normal way with limited speed. Later on, Christov (2009) refined Cattaneo’s idea for material-invariant formulation using Oldroyd’s upper-convected derivatives. This model is utilized by many researchers Transportation of heat in squeezed Jeffrey fluid via non-Fourier approach is demonstrated by Hayat et al. (2016a). Reddy et al. (2016) elaborated the characteristics of cross diffusion on magnetohydrodynamic flow through a plate and cone wedge utilizing non-Fourier approach. Salient features of non-Darcian flow of the Oldroyd-B material via modified version of Fourier law with variable fluid features is described by Shehzad et al. (2016). The dynamics of the viscous fluid through linearly stretched sheet embedded in a Darcian medium using non-Fourier theory is exposed by Nadeem and Muhammad (2016). Hayat et al. (2016b) exposed the impact of non-Fourier theory and influence of auto-catalyst and reactant in the stagnation flow over a non-linear thicked stretchable plate.

Newton’s law of viscosity is not obeyed by certain materials. Such material are known as non-Newtonian. Dyes, ketchup, shampoo, paints, lubricants, blood at low shear rate, mud, and personal care products are few examples of such materials. These fluids play impactful role in many engineering processes and industrial domain. The non-Newtonian fluid cannot be demonstrated through a constitutive expression between shear stress and rate due to the diverse nature of the fluid. Thus, the rheological properties of these materials are analyzed by modelling governing laws for such fluids. Sutterby flow model is one of these models which show very dilute polymeric aqueous solutions. Scientists have paid a little attention so far in exploration of Sutterby fluid flows. Hayat et al. (2016c) investigated the magnetic effects on peristalsis of Sutterby fluid flow in a vertical channel. In another investigation, Hayat et al. (2017d) analyzed slip effects on peristaltic Sutterby fluid through a curved channel. Tetsu et al. (1974) elaborated the convective flow of a Sutterby fluid along a vertical sheet.

The heat source (or sink) in flowof fluid have gained more importance amongs investigators now a days. Internal heat generation and natural convection has attracted the attention of investigators because of extensive range of engineering and industrial applications include disposal of radioactive waste material, heat removed from the nuclear fuel debris, food stuff storage and exothermic reactions in reactors. Many researchers are investigating the characteristics of heat source (or sink) in the fluid flows. Hussain et al. (2018) exposed the convective CNTs nanomaterial flow along with heat source/sink. Hayat et al. (2017a) disclosed the impact of heat generation (or absorption) on radiative magneto Maxwell nanomaterial towards shrinking sheet. Gaffar et al. (2017) elaborated the nonlinear boundary layer flow, mass and heat transport of Jeffrey fluid through vertical surface. Qayyum et al. (2018) concentrated on transportation of radiative and heat generative phenomenon in the stagnant region via Newtonian conditions with magnetic buoyancy effects caused by stretchable surface. Eid and Mahny (2017) addressed the magnetic and generative heat phenomena on convective mass and heat transport of a nanoliquid towards stretchable sheet. Khan et al. (2017) considered the auto-catalyst reactant features on Maxwell fluid flow with heat absorption/generation. Ganga et al. (2016) mathematically analyzed the behavior of heat source /sink on radiative nanoliquid through vertical surface with magnetic field effects.

Recently, exploration of flow through stagnant region has attaracted the engineers and researchers. The flow phenomenon past the edges of submarines, rockets, aircrafts and oil ships, are the examples of this type of flow. Morover, there exist two different categories of stagnation point, termed as oblique and orthogonal. The flow in the region of stagnation point may occur as inviscid (or viscous), steady (or unsteady) and in many other forms. In this regard, Hiemenz (1911) initiated the analysis on stagnation point flow and developed its exact solution. Mahapatra and Gupta (2002) explored the flows about stagnation point through stretchable plate under the analysis of heat transfer. Haq et al. (2015) disclosed the stagnation point radiative slip flow in MHD nanomaterial through stretchable sheet. Hayat et al. (2017b) depicted the Dufour-Soret impacts in hyperbolic-tangent fluid flow neat stagnation point. Hayat et al. (2018) explained the viscoelastic nanoliquid flow over the stretched sheet saturated in stagnation point. Tian et al. (2018) studied the magneto non-Newtonian nanomaterial flow deformed by stretching phenomenon in the region of stagnation point. Shafiq et al. (2018) illustrated the stagnation-point radiative flow of Walters’ B liquid caused by stretchable Riga plate. Ismail et al. (2019) discussed the dissipative effects in stagnation-point magneto flow caused by shrinking plate. Khan et al. (2019) explored the chemically reactive CNTs flow in the region of stagnation-point. Raza (2019) discussed the radiative slip flow of hydro-magneto Casson fluid caused by stretching sheet around the stagnation point.

In thermally stratified flow, different layers of the fluid are formed with diverse densities due to temperature differences. In nature, stratification process controls the oxygen and hydrogen ratio which controls species growth rate in lakes and ponds. Thermal and solutal stratification have vital role in various chemical process, agriculture, oceanography and geophysical flows. In literature most of studies were carried out to discuss the stratification phenomena considering different physical aspects. Daniel et al. (2018) exposed the radiative magneto nanofluid flow through shrinking sheet embedded in stratified medium. Muhammad et al. (2017) discussed thermally stratified ferromagnetic liquid through stretchable surface. Rehman et al. (2017a) elaborated the radiative effects on stratified hyperbolic tangent liquid flow via flat and cylindrical channels both. Kandasamy et al. (2018) described stratification effects on MHD nanomaterial flow over a porous surface. Hayat et al. (2017c) disclosed convective flow of a dual stratified Oldroyd-B nanofluid.

Literature survey reveals that no investigation has ever been made to explore the heat generation/absorption effects on stagnation flow of Sutterby fluid due to linearly stretchable sheet using non-Fourier approach. Generally, when fluid flows, heat is produced continuously due to active metabolism process. Therefore it is accounted. Heat transport involve thermal stratification and heat generation/absorption. Thus, this study is conducted to fill the gap. Homotopic procedure (Liao 2012; Cui et al. 2015; Abbasi et al. 2016; Farooq et al. 2016; Asad et al. 2016; Rehman et al. 2017b is utilized to evaluate the resulting non-linear differential system and to figure out the non-linear analysis. Influence of important embedded parameters are sketched and elaborated graphically. Graphical exposure for drag force (skin friction coefficient) are also demonstrated very carefully. The paper is organized as follows. The Sect. 1 belongs to introductry part. The Sect. 2 is describing the mathematical formulation of the flow problem. The Sect. 3 elaborates the Homotopic method utilized for the flow analysis. The acquired results are analyzed and discussed in Sect. 4. The Sect. 5 gives the outcomes of the considered study.

2 Mathematical modelling

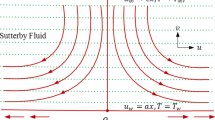
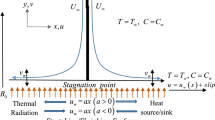
Consider incompressible and steady flow of Sutterby fluid in the region of stagnation-point over a linearly stretched plate. Cartesian coordinate system (x,y) is utilized in such a way that x-axes is along the stretched plate where as y is normal to it. The fluid occupies the region \(y\succeq 0\) (See Fig. 1). Heat generation (or absorption) and stratification effects are taken into consideration,in order to analyze heat transfer phenomena. Cattaneo–Christove theory is also accounted in present flow analysis. The temperature outside the boundary layer \(T_{\infty }\) is assumed to be less than that of sheet. (i.e. \(T_{\infty }<T).\)

Fig. 1
figure 1

Flow diagram

Full size image

Boundary layer approximation reduces the fundamental laws as Hayat et al. (2016a, c):

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial \upsilon }{\partial y}=0 \end{aligned}$$
(1)
$$\begin{aligned}&u\frac{\partial u}{\partial x}+\upsilon \frac{\partial u}{\partial y}\nonumber \\&\quad =U_{e} \frac{dU_{e}}{dx}+\nu \left( 1-\frac{\beta ^{2}}{6}\frac{\partial u}{ \partial y}\right) ^{n}\frac{\partial ^{2}u}{\partial y^{2}}\nonumber \\&\qquad -\frac{n\beta ^{2}}{6}\nu \left( 1-\frac{\beta ^{2}}{6}\frac{\partial u}{\partial y} \right) ^{n-1}\frac{\partial u}{\partial y}\frac{\partial ^{2}u}{\partial y^{2}}\end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial T}{\partial x}+\upsilon \frac{\partial T}{\partial y}-\frac{ Q_{0}}{\rho c_{p}}\left( T-T_{\infty }\right) \nonumber \\&\quad +\tau _{0}\left[ \begin{array}{c} u^{2}\frac{\partial ^{2}T}{\partial x^{2}}+\left( u\frac{\partial u}{ \partial x}+\upsilon \frac{\partial u}{\partial y}\right) \frac{\partial T}{ \partial x}+\left( u\frac{\partial \upsilon }{\partial x}+\upsilon \frac{ \partial \upsilon }{\partial y}\right) \frac{\partial T}{\partial y} +2u\upsilon \frac{\partial ^{2}T}{\partial x\partial y} \\ +\upsilon ^{2}\frac{\partial ^{2}T}{\partial y^{2}}+\frac{Q_{0}}{\rho c_{p}} \left( u\frac{\partial (T-T_\infty)}{\partial x}+\upsilon \frac{\partial (T-T_\infty)}{\partial y} \right) \end{array} \right] \nonumber \\&\qquad =\lambda \frac{\partial ^{2}T}{\partial y^{2}}, \end{aligned}$$
(3)

with boundary conditions

$$\begin{aligned} u & = {} U_{w}\left( x\right) =ax; \ T=T_{0}+Bx,\ \ \text { at }\ y=0, \end{aligned}$$
(4)
$$\begin{aligned} u & = U_{e}=bx\,;\ \,T=T_{\infty }=T_{0}+B_{1}x\text {, as y} \rightarrow \infty , \end{aligned}$$
(5)

where u and \(\upsilon\) represent horizontal ad vertical components of velocity, \(U_{e}\) represent the free stream velocity; \(\nu\) represents the kinematic viscosity, a, b, B, B1 represent the positive dimensional constants, \(Q_{0}\) represents heat generation/absorption coefficient; \(U_{w}\) represent the stretching velocity, T represents the temperature of fluid; \(\tau _{0}\) denotes the relaxation time of heat flux, \(T_{\infty }\) represents the ambient temperature; \(\lambda =\kappa /\rho c_{p}\) represents the thermal diffusivity; \(\kappa\) represents the thermal conductivity, \(T_{0}\) represents the reference temperature, \(\rho\) represents the fluid density; \(\mathbf {\tau }\) represents Cauchy stress tensor; \(c_{p}\) represents the specific heat capacity and \(Q_{0}\) represents the heat generation/absorption coefficient.

Employing the similarity transformation of the form

$$\begin{aligned} \psi & = \sqrt{a\nu }f(\xi ),\,\xi =\sqrt{\frac{a}{\nu }}y \end{aligned}$$
(6)
$$\begin{aligned} u & = axf^{\prime }(\xi ),\upsilon =-\sqrt{a\nu }f(\xi ) \end{aligned}$$
(7)
$$\begin{aligned} \theta \left( \xi \right) & = \frac{T-T_{\infty }}{T_{w}-T_{0}}. \end{aligned}$$
(8)

The incompressibility condition (1) identically satisfied and the flow Eqs. (2–5) are reduced below

$$\begin{aligned}&\left[ 1-\frac{\alpha }{6}f^{\prime \prime }\right] ^{n}f^{\prime \prime \prime }-\frac{n}{6}\alpha \left[ 1-\frac{\alpha }{6}f^{\prime \prime } \right] ^{n-1}f^{\prime \prime }f^{\prime \prime \prime }\nonumber \\&\quad -f^{\prime 2}+ff^{\prime \prime }+A^{2}=0 \\&\frac{1}{{\mathrm{Pr}}\,}\theta ^{\prime ^{\prime }}\left( \eta \right) +Q\theta \left( \eta \right) +f(\eta )\theta ^{\prime }\left( \eta \right) -f^{\prime }(\eta )\theta \left( \eta \right) -s1f^{\prime }(\eta )\nonumber \\&\quad -\gamma \left( \begin{array}{c} \begin{array}{c} s1\left( f^{\prime }(\eta )\right) ^{2}+\left( f^{\prime }(\eta )\right) ^{2}\theta \left( \eta \right) -s1f(\eta )f^{\prime ^{\prime }}(\eta ) \\ -f(\eta )\theta \left( \eta \right) f^{\prime ^{\prime }}(\eta )-f(\eta )f^{\prime }(\eta )\theta ^{\prime }\left( \eta \right) +\left( f(\eta )\right) ^{2}\theta ^{\prime ^{\prime }}\left( \eta \right) \end{array}\\ +Q\left( f(\eta )\theta ^{\prime }\left( \eta \right) -f^{\prime }(\eta )\theta \left( \eta \right) \right) \end{array} \right) =0. \nonumber \end{aligned}$$
(9)

The associated boundary conditions are expressed below:

$$\begin{aligned}&f(0)=0,\ f^{\prime }(0)=1,\,f^{\prime }(\infty )=A \end{aligned}$$
(10)
$$\begin{aligned}&\theta (0)=1-s1,\ \theta (\infty )=0. \end{aligned}$$
(11)

The prime represents differentiation w.r.t ‘\(\xi\)’ . \({\mathrm{Pr}}\) stands for Prandtl number, A denotes the ratio parameter, s1 represents the thermal stratification parameter, Q denotes the heat generation (or absorption) parameter. \(\gamma\) represents the thermal relaxation parameter.

The nondimentional quantities can be written in the form:

$$\begin{aligned}&\alpha =\beta ^{2}x\sqrt{\frac{a^{3}}{\nu }},\,\gamma =\tau _{0}a \, ,\nonumber \\&{\mathrm{Pr}}\,=\frac{\mu c_{p}}{k},\,A= \frac{b}{a},\, s1=\frac{B_{1}}{B}, Q=\frac{Q_{0}}{\rho c_{p} a}, \end{aligned}$$
(12)

Skin friction coefficient is

$$\begin{aligned} C_{f}=\frac{\tau _{w}}{\rho U_{w}^{2}}, \end{aligned}$$
(13)

here the shear stress \(\tau _{w}\) is given by

$$\begin{aligned} \tau _{w}=\mu \left[ 1-\frac{\beta ^{2}}{c}\left( \frac{\partial u}{\partial y}\right) |_{\text {y}=0}\right] ^{n}\left( \frac{\partial u}{\partial y} \right) |_{\text {y}=0}. \end{aligned}$$
(14)

In dimensionless variables

$$\begin{aligned} C_{f}\sqrt{\hbox {Re}_{x}}=\left[ 1-\frac{\alpha }{6}f^{\prime \prime }(0) \right] ^{n}f^{\prime \prime }(0), \end{aligned}$$
(15)

where \(\hbox {Re}_{x}=ax^{2}/\nu\) represents the local Reynolds number.

3 Solution procedure

Here homotopic technique is utilized which was initiated by Liao (2012) in 1992. This method facilitates to adopt and construct the convergent series solution for given flow equations. This mathematical method comprises in finding the approximate solutions of the problem. Zeroth order problem is defined for the nonlinear governing equations, which consists of deformed function, embedding parameter, auxiliary parameter and nonlinear operator. One time differentiation of zeroth order problem corresponding to embedding parameter is known as first order of approximation. Similarly, two times differentiation corredponding to embedding parameter is known as second order of approximation and so on. Further, this method is highly depends upon the embedding parameter q which belongs to the specified interval [0, 1]. Using \(q\in [0,1]\), from homotopy theory, family of equations is constructed which is called the zeroth-order deformation equation, whose solution varies continuously with respect to the embedding parameter \(q\in [0,1]\). It means that as q enhances from 0 to 1, the solution of the zeroth-order deformation equation varies from the selected initial guess to the solution of the considered equation. Thus, zeroth-order approximation is the term, which is used by researchers for a first basic ideology towards the solution of the problem throughout this technique. In that way, the approximations of the problem is expected to carry in order to increase the accuracy in the series solution. Therefore, from the zeroth-order deformation equation, one can directly extract the constitutive equation of mth order called mth-order deformation problem. In this way, the earliest equation is transferred into an infinite number of linear ones, but without the assumption of any small/large physical parameters. For this purpose, it is crucial to have initial guesses and linear operators satisfying the following definitions.

$$\begin{aligned} f_{0}\left( \xi \right) & = A\xi +1-A+(A-1)\exp [-\xi ] \end{aligned}$$
(16)
$$\begin{aligned} \theta _{0}\left( \xi \right)= & {} \exp [-\xi ]-s1\exp [-\xi ] \end{aligned}$$
(17)
$$\begin{aligned} \mathcal {L}_{f}\left( f\right)= & {} \frac{d^{3}f}{d\xi ^{3}}-\frac{df}{d\xi }, \,\mathcal {L}_{\theta }\left( \theta \right) =\frac{d^{2}\theta }{d\xi ^{2}}-\theta . \end{aligned}$$
(18)

The operators have the properties given below:

$$\begin{aligned} \mathcal {L}_{f}\left[ A_{1}+A_{2}\exp (\xi )+A_{3}\exp (-\xi )\right]= 0 \end{aligned}$$
(19)
$$\begin{aligned} \mathcal {L}_{\theta }\left[ A_{4}\exp (\xi )+A_{5}\exp (-\xi )\right]= 0, \end{aligned}$$
(20)

where \(A_{i}\)\(\left( i=1-5\right)\) are the arbitrary constants. The zeroth and mth order deformation problems are:

3.1 Zeroth-order problems

$$\begin{aligned}&\left( 1-q\right) \mathcal {L}_{f}\left[ \widehat{f}\left( \xi ;q\right) -f_{0}\left( \xi \right) \right] =q\hbar _{f}\mathcal {N}_{f}\left[ \widehat{f }\left( \xi ;q\right) ,\widehat{\theta }\left( \xi ;q\right) \right] \end{aligned}$$
(21)
$$\begin{aligned}&\left( 1-q\right) \mathcal {L}_{\theta }\left[ \widehat{\theta }\left( \xi ;q\right) -\theta _{0}\left( \xi \right) \right] =q\hbar _{\theta }\mathcal {N }_{\theta }\left[ \widehat{\theta }\left( \xi ;q\right) ,\widehat{f}\left( \xi ;q\right) \right] \end{aligned}$$
(22)
$$\begin{aligned}&\widehat{f}\left( 0;q\right) =0,\quad \widehat{f}^{\prime }\left( 0;q\right) =1\,,\,\widehat{f}^{\prime }\left( \infty ;q\right) =A \end{aligned}$$
(23)
$$\begin{aligned}&\widehat{\theta }\left( 0;q\right) =1-s1,\quad \widehat{\theta } \left( \infty ;q\right) =0, \end{aligned}$$
(24)

for \(\hbox {n}=1\)

$$\begin{aligned}&\mathcal {N}_{f}\left[ \widehat{f}\left( \xi ,q\right) ,\widehat{\theta } \left( \xi ;q\right) \right] \nonumber \\&\quad =\frac{\partial ^{3}\widehat{f}\left( \xi ;q\right) }{\partial \xi ^{3}}-\frac{\alpha }{3}\frac{\partial ^{2}\widehat{f }\left( \xi ;q\right) }{\partial \eta ^{2}}\frac{\partial ^{3}\widehat{f} \left( \xi ;q\right) }{\partial \xi ^{3}} \nonumber \\&\qquad -\left( \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \right) ^{2}+\widehat{f}\left( \xi ;q\right) \frac{\partial ^{2}\widehat{f} \left( \xi ,q\right) }{\partial \xi ^{2}}+A^{2}, \end{aligned}$$
(25)
$$\begin{aligned}&\mathcal {N}_{\theta }\left[ \widehat{f}\left( \xi ;q\right) ,\widehat{\theta }\left( \xi ;q\right) \right] \nonumber \\&\quad =\frac{\partial ^{2}\widehat{\theta }\left( \xi ;q\right) }{\partial \xi ^{2}}\nonumber \\&\qquad -{\mathrm{Pr}}\,\left[ \frac{\partial \widehat{f} \left( \xi ;q\right) }{\partial \xi }\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) -\widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{ \theta }\left( \xi ;q\right) }{\partial \xi }-Q\widehat{\theta }\left( \xi ;q\right) \right] \nonumber \\&\qquad -{\rm Pr}\gamma \left[ \begin{array}{c} \left( \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \right) ^{2}\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) - \widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi }\frac{\partial \widehat{\theta }\left( \xi ;q\right) }{\partial \xi } \\ -\widehat{f}\left( \xi ;q\right) \frac{\partial ^{2}\widehat{f}\left( \xi ;q\right) }{\partial \xi ^{2}}\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) +\left( \widehat{f}\left( \xi ;q\right) \right) ^{2}\frac{ \partial ^{2}\widehat{\theta }\left( \xi ;q\right) }{\partial \xi ^{2}} \\ +Q\left( -\frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \left(\widehat{\theta }\left( \xi ;q\right) \right) +\widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{\theta }\left( \xi ;q\right) }{ \partial \xi }\right) \end{array} \right] \end{aligned}$$
(26)

For \(\hbox {n}=2\)

$$\begin{aligned}&\mathcal {N}_{f}\left[ \widehat{f}\left( \xi ,q\right) ,\widehat{\theta } \left( \xi ;q\right) \right] \nonumber \\&\quad =\frac{\partial ^{3}\widehat{f}\left( \xi ;q\right) }{\partial \xi ^{3}}-\frac{2\alpha }{3}\frac{\partial ^{2}\widehat{ f}\left( \xi ;q\right) }{\partial \eta ^{2}}\frac{\partial ^{3}\widehat{f} \left( \xi ;q\right) }{\partial \xi ^{3}}\nonumber \\&\qquad +\frac{1}{12}\alpha ^{2}\left( \frac{\partial ^{2}\widehat{f}\left( \xi ;q\right) }{\partial \eta ^{2}} \right) ^{2}\frac{\partial ^{3}\widehat{f}\left( \xi ;q\right) }{\partial \xi ^{3}} \nonumber \\&\qquad -\left( \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \right) ^{2}+\widehat{f}\left( \xi ;q\right) \frac{\partial ^{2}\widehat{f} \left( \xi ,q\right) }{\partial \xi ^{2}}+A^{2}, \end{aligned}$$
(27)
$$\begin{aligned}&\mathcal {N}_{\theta }\left[ \widehat{f}\left( \xi ;q\right) ,\widehat{\theta }\left( \xi ;q\right) \right] \nonumber \\&\quad =\frac{\partial ^{2}\widehat{\theta }\left( \xi ;q\right) }{\partial \xi ^{2}}\nonumber \\&\qquad -{\mathrm{Pr}}\,\left[ \frac{\partial \widehat{f} \left( \xi ;q\right) }{\partial \xi }\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) -\widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{ \theta }\left( \xi ;q\right) }{\partial \xi }-Q\widehat{\theta }\left( \xi ;q\right) \right] \nonumber \\&\qquad -{\rm Pr} \gamma \left[ \begin{array}{c} \left( \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \right) ^{2}\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) - \widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi }\frac{\partial \widehat{\theta }\left( \xi ;q\right) }{\partial \xi } \\ -\widehat{f}\left( \xi ;q\right) \frac{\partial ^{2}\widehat{f}\left( \xi ;q\right) }{\partial \xi ^{2}}\left( s1+\widehat{\theta }\left( \xi ;q\right) \right) +\left( \widehat{f}\left( \xi ;q\right) \right) ^{2}\frac{ \partial ^{2}\widehat{\theta }\left( \xi ;q\right) }{\partial \xi ^{2}} \\ +Q\left( -\frac{\partial \widehat{f}\left( \xi ;q\right) }{\partial \xi } \left( \widehat{\theta }\left( \xi ;q\right) \right) +\widehat{f}\left( \xi ;q\right) \frac{\partial \widehat{\theta }\left( \xi ;q\right) }{ \partial \xi }\right) \end{array} \right] , \end{aligned}$$
(28)

where \(q\in [0,1]\) is embedding parameter and \(\hbar _{f}\), \(\hbar _{\theta }\) the non-zero auxiliary parameters.

3.2 mth-order problems

$$\begin{aligned}&\mathcal {L}_{f}\left[ f_{m}\left( \xi \right) -\chi _{m}f_{m-1}\left( \xi \right) \right] =\hbar _{f}\mathcal {R}_{m}^{f}\left( \xi \right) \end{aligned}$$
(29)
$$\begin{aligned}&\mathcal {L}_{\theta }\left[ \theta _{m}\left( \xi \right) -\chi _{m}\theta _{m-1}\left( \xi \right) \right] =\hbar _{\theta }\mathcal {R}_{m}^{\theta }\left( \xi \right) \end{aligned}$$
(30)
$$\begin{aligned}&f_{m}\left( 0\right) =0,\quad f_{m}^{\prime }\left( 0\right) =0,\quad f_{m}^{\prime }\left( \infty \right) =0 \end{aligned}$$
(31)
$$\begin{aligned}&\theta _{m}\left( 0\right) =0,\quad \theta _{m}\left( \infty \right) =0, \end{aligned}$$
(32)

for \(\hbox {n}=1\)

$$\begin{aligned} \mathcal {R}_{m}^{f}\left( \eta \right) & = f_{m-1}^{\prime \prime \prime }- \frac{\alpha }{3}\sum _{k=0}^{m-1}f_{m-1-k}^{\prime ^{^{\prime \prime }}}f_{k}^{^{\prime \prime \prime }}\nonumber \\ & \quad -\sum _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }\right) +\sum _{k=0}^{m-1}\left( f_{m-1-k}f_{k}^{\prime \prime }\right) +A^{2} \end{aligned}$$
(33)
$$\begin{aligned} \mathcal {R}_{m}^{\theta }\left( \eta \right)= & {} \theta _{m-1}^{\prime \prime }\nonumber \\&-{\mathrm{Pr}}\,\left( s1f_{m-1}^{\prime }-\sum _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }\theta _{k}\right) -\sum _{k=0}^{m-1}\left( f_{m-1-k}\theta _{k}^{\prime }\right) -Q\theta _{m-1}\right) \nonumber \\&-{\rm Pr} \gamma\left( \begin{array}{c} s1\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }\right) +\sum \nolimits _{k=0}^{m-1}f_{m-1-k}^{\prime }\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime }\theta _{l}\right) \\ -\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime }\theta _{l}^{\prime }\right) -s1\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}f_{k}^{\prime \prime }\right) \\ -\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime \prime }\theta _{l}\right) +\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}\theta _{l}^{\prime \prime }\right) \\ +Q\left( -\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }\theta _{k}\right) +\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}\theta _{k}^{\prime }\right) \right) \end{array} \right) . \end{aligned}$$
(34)

For \(\hbox {n}=2\)

$$\begin{aligned} \mathcal {R}_{m}^{f}\left( \eta \right) & = f_{m-1}^{\prime \prime \prime }- \frac{2\alpha }{3}\sum _{k=0}^{m-1}f_{m-1-k}^{\prime ^{\prime }}f_{k}^{^{\prime \prime \prime }}\nonumber \\& \quad +\frac{1}{12}\alpha ^{2}\sum _{k=0}^{m-1}\sum _{l=0}^{k-1}\left( f_{k-1-l}^{\prime ^{\prime }}f_{l}^{\prime ^{\prime }}\right) f_{m-k}^{^{\prime \prime \prime }}-\sum _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }\right) \nonumber \\& \quad +\sum _{k=0}^{m-1}\left( f_{m-1-k}f_{k}^{\prime \prime }\right) +A, \end{aligned}$$
(35)
$$\begin{aligned} \mathcal {R}_{m}^{\theta }\left( \eta \right)= & {} \theta _{m-1}^{\prime \prime }\nonumber \\&-{\mathrm{Pr}}\,\left( s1f_{m-1}^{\prime }-\sum _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }\theta _{k}\right) -\sum _{k=0}^{m-1}\left( f_{m-1-k}\theta _{k}^{\prime }\right) -Q\theta _{m-1}\right) \nonumber \\& - {\Pr }\gamma \left( \begin{array}{c} s1\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }f_{k}^{\prime }\right) +\sum \nolimits _{k=0}^{m-1}f_{m-1-k}^{\prime }\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime }\theta _{l}\right) \\ -\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime }\theta _{l}^{\prime }\right) -s1\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}f_{k}^{\prime \prime }\right) \\ -\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}^{\prime \prime }\theta _{l}\right) +\sum \nolimits _{k=0}^{m-1}f_{m-1-k}\sum \nolimits _{l=0}^{k}\left( f_{k-l}\theta _{l}^{\prime \prime }\right) \\ +Q\left(-\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}^{\prime }\theta _{k}\right) +\sum \nolimits _{k=0}^{m-1}\left( f_{m-1-k}\theta _{k}^{\prime }\right) \right) \end{array} \right) \end{aligned}$$
(36)
$$\begin{aligned} \chi _{m}= & {} \left\{ \begin{array}{cc} 0,&{} m\le 1 \\ 1,&{} m>1 \end{array} \right. . \end{aligned}$$
(37)

Obviously for \(q=0\) and \(q=1\), one may write

$$\begin{aligned} \widehat{f}\left( \xi ;0\right)= f_{0}\left( \xi \right) ,\quad \widehat{f}\left( \xi ;1\right) =f\left( \xi \right) \end{aligned}$$
(38)
$$\begin{aligned} \widehat{\theta }\left( \xi ;0\right)= \theta _{0}\left( \xi \right) ,\quad \widehat{\theta }\left( \xi ;1\right) =\theta \left( \xi \right) , \end{aligned}$$
(39)

and with variation of q from 0 to 1, \(\widehat{f}\left( \xi ;q\right)\) and \(\widehat{\theta }\left( \xi ;q\right)\) vary from the initial solutions \(f_{0}\left( \xi \right)\) and \(\theta _{0}(\xi )\) to the final solutions \(f\left( \xi \right)\) and \(\theta (\xi )\) respectively. Using Taylor series for \(q=1\)

$$\begin{aligned} f\left( \xi \right)& = f_{0}\left( \xi \right) +\sum \limits _{m=1}^{\infty }f_{m}\left( \xi \right) \end{aligned}$$
(40)
$$\begin{aligned} \theta \left( \xi \right)& = \theta _{0}\left( \xi \right) +\sum \limits _{m=1}^{\infty }\theta _{m}\left( \xi \right) . \end{aligned}$$
(41)

The general solutions \(\left( f_{m},\,\theta _{m}\,\right)\) of Eqs. (34)–(35) in terms of special solutions \(\left( f_{m}^{*}\,and \,\theta _{m}^{*}\,\right)\) are

$$\begin{aligned} f_{m}\left( \xi \right)& = f_{m}^{\star }\left( \xi \right) +A_{1}+A_{2}e^{\xi }+A_{3}e^{-\xi } \end{aligned}$$
(42)
$$\begin{aligned} \theta _{m}\left( \xi \right)& = \theta _{m}^{\star }\left( \xi \right) +A_{4}e^{\xi }+A_{5}e^{-\xi }, \end{aligned}$$
(43)

where the constants \(A_{i}\)\((i=1-5)\) are computed through the boundary conditions (39)–(40) which is given below:

$$\begin{aligned} A_{2}= A_{4}=0,\,A_{1}=-f_{m}^{\star }\left( 0\right) -f_{m}^{\star ^{\prime }}\left( 0\right) \end{aligned}$$
(44)
$$\begin{aligned} A_{3}= -f_{m}^{\star ^{\prime }}\left( 0\right) \text {,}\ A_{5}=-\theta _{m}^{\star }\left( 0\right) . \end{aligned}$$
(45)

3.3 Convergence analysis

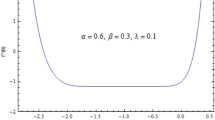
HAM provides an easy approach to control and adjust the region of convergence for the iterative solutions. Now the solution of Eqs. (37)–(38) with the boundary conditions in Eqs. (39)–(40) are calculated using HAM. HAM ensures the convergence in the region which is sketched parallel to \(\hbar -axis\) (See Fig. 2a, b). The Fig. 2 exhibits the allowable ranges of the convergence control parameters \(\hbar _{f}\) and \(\hbar _{\theta }\) are \(-0.7\le \hbar _{f}\le -0.1\) and \(-0.6\le \hbar _{\theta }\le -0.2.\)The h-curves for the square residual errors have been ploted in Fig. 3 (See Fig. 3a, b). The square residual errors is defined as follows:

$$\begin{aligned} \triangle _{m}^{f}= & {} \int _{0}^{1}\left[ R_{m}^{f}\left( \eta ,\hslash _{f}\right) \right] ^{2}d\eta \\ \triangle _{m}^{\theta }= & {} \int _{0}^{1}\left[ R_{m}^{\theta }\left( \eta ,\hslash _{\theta }\right) \right] ^{2}d\eta . \end{aligned}$$

It is found from Fig. 3a that the lowest possible error for f is obtained for \(\hslash _{f}\)\(\in\)\(\left[ -0.7,-0.4\right]\). Figure 3b gives the confirmation that the lowest possible error for \(\theta\) is achieved for \(\hslash _{\theta }\in\)\(\left[ -0.6,-0.3\right]\). Figure 3a, b provide a verification of the convergence analysis in the Fig. 2.

Fig. 2
figure 2

a h-curve for velocity, b h-curve for temperature

Full size image
Fig. 3
figure 3

a Residual error for \(\hslash _f\). b Residual error for \(\hslash _\theta\)

Full size image

4 Discussion

In this segment, the analytical technique known as Homotopy analysis method is used to solve nonlinear system of ordinary differential equations given in Eqs. (2–3) with boundary conditions given in Eqs. (4–5) and results depicting the impact of eminent parameters on flow and heat transfer features are discussed through graphs. A well-known commuting package “Mathematica software” has been utilized in order to develop the parametric study of considered flow problem. Moreover, the numerical accuracy 64 bit of the system is used. The detail of this scheme can be found from the book written by Liao (2012). The graphical interpretations are developed for two different values of power law index i.e. \(n=1\) and \(n=2.\) The horizontal velocity distribution at \(n=1\) and \(n=2\) for diverse values of velocity ratio parameter A is sketched in Fig. 4. This figure highlights an increment in horizontal velocity by dominating A. However, the fluid velocity dominates in case of \(n=2\). The associated thickness of boundary layer exhibits decreasing trend for larger A. Further \(A=1\) corresponds to no boundary layer thickness. It means that the fluid and sheet both have the same velocity. The cases \(A<1\) and \(A>1\) correspond to higher velocity at surface and away from the wall. Figure 5 depicts the Sutterby fluid parameter \(\alpha\) effects on the velocity field for two fixed values of n. It is noticed that velocity for both values of n increases with increasing fluid parameter. However, for \(n=2\), it shows a dominating trend with increasing Sutterby fluid parameter. Physically increasing fluid parameter \(\alpha\) reduces the kinematics viscosity which helps in more fluid deformation and resultantly, horizontal velocity increases. It is also observable here that for small Sutterby fluid parameter, the Newtonian curve is founded. The variation of temperature field at two fixed values of n i.e. \(n=1\) and \(n=2\) for various values of Prandtl number Pr is illustrated in Fig. 6. Here the temperature follows diminishing trend by growing Pr for both cases i.e. \(n=1\) and \(n=2\). In fact greater Prandtl number is corresponding to low thermal diffusivity which causes the reduction in temperature field. Moreover, a decrease in thickness of associated boundary layer is noted for larger Pr. Comparing both solutions reveal that temperature for \(n=2\) is greater than the fluid temperature for \(n=1\). Figure 7 discloses the impacts of heat generation / absorption parameter Q on the fluid temperature when \(n=1\) and \(n=2\). The case \(Q>0\) corresponds to the heat generation whereas the case \(Q<0\) describes the heat absorption phenomenon. Generally it is noticed that fluid temperature increases with dominating heat generation parameter (\(Q>0\)). In fact positive values of Q result maximum in temperature due to more heat is generated which consequently strengthens the temperature field. The boundary layer correspond to temperature field is thicker when heat generation parameter rises. However opposite trend is evident in the magnitude of the fluid temperature and associated thickness of thermal boundary layer with heat absorption parameter (\(Q<0\)). Fig. 8 shows the impact of stratification parameter s1 on temperature field for both the cases \(n=1\) and \(n=2\). Higher intensity of stratification parameter causes in decrement of temperature field for both solutions. Also for both solutions i.e. for \(n=1\) and \(n=2\), thermal boundary layer in stretching case is thinner. Physically dominating values of stratification parameter minimizes the difference in temperature between surface fluid and ambient, so temperature profile diminishes. On comparison, the fluid temperature secure greater magnitude in case of \(n=2\). Fig. 9 illustrates temperature field for some values of thermal relaxation parameter \(\gamma 1\) for both \(n=1\) and \(n=2\). It reveals that variation of reduces both the temperature and associated boundary layer thickness for both the solutions. Physically liquid particles need more time in transporting heat to the nearby particles when \(\gamma 1\) rises. Moreover, it is interesting to notice that the fluid temperature is lower in case of \(n=2\). Figure 10 represents the effects of Sutterby fluid parameter \(\alpha\) and velocity ratio parameter A on surface drag. It is examined that surface drag grows as enhance \(\alpha\) and A for both the cases \(n=1\) and \(n=2\) (see Table 1).

Fig. 4
figure 4

Effect of A on \(f^{\prime }\)

Full size image
Fig. 5
figure 5

Effect of \(\alpha\) on \(f^{\prime }\)

Full size image
Fig. 6
figure 6

Effect of Pr on \(\theta\)

Full size image
Fig. 7
figure 7

Effect of Q on \(\theta\);

Full size image
Fig. 8
figure 8

Effect of s1 on \(\theta\);

Full size image
Fig. 9
figure 9

Effect of \(\gamma\) on \(\theta\)

Full size image
Fig. 10
figure 10

Effect of A and \(\alpha\) on Cf

Full size image
Table 1 Analysis of surface drag coefficient (\(f^{\prime \prime }(0)\)) with published works of Mahapatra and Gupta (2002), Pop et al. (2004) and Sharma and Singh (2009) for various values of A when \(\alpha =0\)
Full size table

The above table reflects that all the results are matched in excellent order.

5 Closing remarks

Heat generation/absorption in thermally stratified flow of stagnant Sutterby fluid through linearly stretched plate is analyzed in this atricle. The key points listed below:

  • Temperature shows decreasing trend for dominant Prandtl number, thermal stratification parameter, thermal relaxation parameter and heat generation parameter.

  • Sutterby fluid parameter \(\alpha\) enhances the velocity field.

  • Skin friction coefficient grows for enlarge ratio parameter A and Sutterby fluid parameter \(\alpha\).