Characterization of a vortex-induced vibrating thin plate energy harvester with particle image velocimetry

Abstract

Energy of turbulent wakes can be harnessed using vortex induced vibration harvesters. The unequal pressure distribution due to turbulence on the device generates vibrations which can be converted to electricity through piezoelectric transduction mechanism. The energy harvester concept that is investigated here consists in a polymeric thin flexible plate (that can host piezoelectric elements on each side) placed in the wake of a rigid bluff body. The motion of the plate is similar to that of a swimming eel and can be approximated using a cantilever beam model. Experiments were carried out in a water tunnel, different polyethylene plates were clamped to a square cylinder and a high speed camera was used to simultaneously capture both the plate deflection and the flow pattern. Plates were varied in slenderness; the Reynolds number based on the square cylinder ranged between 1500 and 20,000. From each captured frame, the deflection was computed and used to perform modal decomposition and strain energy calculation. The plate deflection pattern evolves from splitter plate oscillations at low Reynolds number or high flexural rigidity into travelling waves at high Reynolds number or low flexural rigidity. Those travelling waves lead to higher strain energy. The measured velocity vectors show that when the normal flow simultaneously impinges at different locations on both sides of the plate, complex bending shapes result. The frequency delay observed with longer plates show that there is more plate-wake interaction sustaining the turbulence in the wake and thus optimizing the energy transfer.

1 Introduction

The core principle of flow induced vibration harvesters is that the unequal pressure distribution due to turbulence around the device will generate vibrations (Eloy et al. 2011; Tang et al. 2003, 2009), which can be converted to electricity through either piezoelectric or electromagnetic or even both transduction mechanisms. When a non-turbulent flow impinges on a square cylinder at low Reynolds number, periodic vortex shedding occurs in the wake. Vortices are shed alternatively from the upper and lower surface of the body leading to an oscillatory wake. This unsteady flow pattern comes from the separation at the leading edges. For sharp edged bodies, the Strouhal number and other wake properties are relatively insensitive to the Reynolds number (Okajima 1982). Therefore, a square cylinder is the most basic bluff body when it comes to generate an oscillatory wake. The resulting sinusoidal wave pattern of the dynamic pressure behind the square can then be used to generate oscillatory motion of a piezoelectric plate (Allen and Smits 2001) or other electrostrictive material (Giacomello and Porfiri 2011).

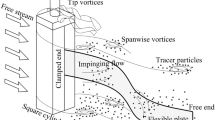
For a square cylinder having a length/diameter ratio H/D ≥ 5, (Wang et al. 2004) the flow structures can be schematized as in Fig. 1. Periodic spanwise vortex shedding occurs over the whole span except close to the cylinder top and bottom walls where flow is strongly tridimensional. In the present study, a slender square cylinder is to be the vortex generating bluff body; allowing to further simplify the study into a quasi-two dimensional fluid–structure interaction problem.

Fig. 1

Wake structures behind a square cylinder

Long strips of piezoelectric polymers can be placed in the wake of a bluff body (Taylor et al. 2001); the vortices shed by the bluff body create a pressure differential on the surface of the strips which will in turn cause oscillatory motion. Taylor et al. named their device “The Energy Harvesting Eel” because those undulating strips in water flow recall the swimming motion of an eel. The “eel” has one central non-active layer made of flexible polymer and active layers made of piezoelectric or electrostrictive material on each side. When strained, the active layers release a low frequency ac voltage signal along the electroded segment. The design criterion is to maximize the strain in the active layers with the bluff body and eel geometry as key parameters (Shi et al. 2013, 2014). Taylor et al. carried out experiments in a flow tank and also successfully simulated the Eel motion using the fluid structure interaction software NEKTAR; which was further used to understand the influence of different bluff body widths, eel lengths and Reynolds numbers. The strain was determined through records of the curvature and also the open circuit voltage of the Eel segment electrode was measured using eight electrode pairs. The “eel” motion was described as a sum of the modes of an ideal cantilever beam and also as a travelling wave.

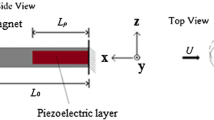
The present study focuses on a flexible thin polyethylene plate clamped to a slender square cylinder immersed in water (Fig. 2). Through water tunnel experiments, we aim to investigate the flapping motion, the modal contributions, the strain energy and the wake flow pattern for several distinct deflected shapes.

Fig. 2

Concept of the present study

2 Theory

2.1 Modal contributions

We assume that the bending of the flexible plate can be modeled as the bending of a cantilever beam. This assumption is valid in the case of slender thin plates where torsion is not significant. As a matter of fact, the swimming motion of slender fish happens to be almost two-dimensional because of the superior efficiency (Shelton et al. 2014; Lighthill 1960). The one dimensional plate equation describing the motion of the plate centerline (Dowell 1975) is expressed as:

$$- EI\frac{{\partial^{4} w}}{{\partial x^{4} }} - N_{x} \frac{{\partial^{2} w}}{{\partial x^{2} }} - m\frac{{\partial^{2} w}}{{\partial t^{2} }} + \Delta p \cdot b = 0$$

(1)

$$I = \frac{{b \times t_{p}^{3} }}{12}$$

(2)

In this one dimensional model, $N_{x}$ represents the tension induced by stretching, $EI$ is the flexural rigidity in which $E$ is the Young’s modulus and I accounts for the second moment of inertia, $m$ is the mass per unit length of the plate, $w$ is the lateral displacement, $\Delta p$ is the resultant of the local pressure acting on the both sides, $b$ is the width and $t_{p}$ the thickness.

Because one end of the plate is free and due to the inextensibility of the centerline: we assume that no stretching occurs at the neutral axis (Lighthill 1971). As a result, the tension term $N_{x}$ can be neglected. Considering the differential equation for the free vibration of the beam described as:

$$EI\frac{{d^{4} w}}{{dx^{4} }} + \rho_{p} A\frac{{d^{2} w}}{dt} = 0,$$

(3)

where $A$ is the cross-sectional area, $\rho_{p}$ is the mass per unit volume of the beam. The solution for the free undamped vibration displacement (Sonalla 1989) can generally be expressed by

$$w(x,t) = \mathop \sum \limits_{m = 1}^{\infty } X_{m} (x)B_{m} \cos \omega_{m} t$$

(4)

In which $\omega_{m}$ is the natural frequency of the mode $m$ associated with modeshape $X_{m} (x)$ with an amplitude determined by $B_{m}$. The natural frequencies are calculated from:

$$\omega_{m} = \alpha^{2} \sqrt {\frac{EI}{{\rho_{p} A}}}$$

(5)

in which $\alpha \cdot L_{0}$ represents the eigenvalues ($L_{0}$ accounts for the length of the plate at rest) with an eigenfunction expressed as:

$$\begin{aligned} X_{m} (x) & = (\cosh \alpha_{m} x - \cos \alpha_{m} x) \\ & \quad - \gamma_{m} (\sinh \alpha_{m} x - \sin \alpha_{m} x) \\ \end{aligned}$$

(6)

Hence, the vibratory motion of the beam is represented as a superposition of the different modes, each vibrating at its own frequency. In the present study, only the first four mode shapes of an ideal cantilever beam have been considered and are illustrated in Fig. 3.

Fig. 3

Cantilever beam first four mode shapes, strain energy of each mode scaled to mode 1

The complex shape of the plate at any time is composed of a certain contribution of each of these fundamental shapes. With the measurement of the deflected shape, each modal contribution $B_{m}$ can be computed. Supposing that we can rewrite the solution for the free undamped displacement as:

$$f(x) = \sum\limits_{m = 1}^{\infty } {X_{m} (x)B_{m} }$$

(7)

Integrating both sides and multiplying by $X_{n}$ with $X_{m}$ and $X_{n}$ being orthogonal with each other:

$$\mathop \int \limits_{0}^{{L_{0} }} f(x)X_{n} dx = \int_{0}^{{L_{0} }} {\sum\limits_{m = 1}^{\infty } {X_{m} B_{m} X_{n} dx} }$$

(8)

Hence, from the measurements of the deformed shape, one can calculate numerically to obtain modal contributions $B_{m}$ according to:

$$B_{m} = \frac{{\sum\nolimits_{i = 1}^{n} {w_{i} \cdot X_{{m_{i} }} \cdot \Delta x} }}{{\sum\nolimits_{i = 1}^{n} {X_{{m_{i} }}^{2} \cdot \Delta x} }}$$

(9)

This allows us to sort the deflected shapes into categories according to their modal contributions.

2.2 Strain energy

Electrostrictive and Piezoelectric materials convert strain into electricity, therefore we use the strain energy as a criterion to compare the harvesting potential of the different plates (Binyet et al. 2017). In the present study we do not take into consideration the actual mean of further conversion to electricity.

From the theory of elasticity (Timoshenko and Goodier 2018), the potential (strain) energy for the whole beam is expressed as:

$$U = \frac{1}{2}\frac{{Et^{3} }}{12}\mathop \int \limits_{0}^{{L_{0} }} \left( {\frac{1}{\rho }} \right)^{2} dx$$

(10)

$\rho$ is the radius of curvature which is linked to the derivatives of the lateral displacement by:

$$\frac{{w^{\prime \prime } }}{{(1 + (w^{\prime } )^{2} )^{3/2} }} = \frac{1}{\rho }$$

(11)

Including the expression for the radius of curvature (11), we obtain the final expression for the beam strain energy:

$$U = \frac{1}{2}D\mathop \int \limits_{0}^{{L_{0} }} \left( {\frac{{w^{\prime \prime } }}{{(1 + (w^{\prime } )^{2} )^{3/2} }}} \right)^{2} dx$$

(12)

$$D = \frac{{Et^{3} }}{12}.$$

(13)

$D$ represents the flexural rigidity with the thickness $t.$ The strain energy integral can be computed numerically using the composite trapezoidal rule with finite difference schemes once the plate deflection is known:

$$\mathop \int \limits_{0}^{{L_{0} }} \left( {\frac{{w^{\prime \prime } }}{{(1 + (w^{\prime } )^{2} )^{3/2} }}} \right)^{2} dx \approx \frac{{L_{0} }}{n}\left( {\frac{{\left( {\frac{{\Delta_{2,i = 1} }}{{(1 + \Delta_{i = 1}^{2} )^{3/2} }}} \right)^{2} }}{2} + \mathop \sum \limits_{i = 2}^{n - 1} \left( {\frac{{\Delta_{2,i} }}{{(1 + \Delta_{i}^{2} )^{3/2} }}} \right)^{2} + \frac{{\left( {\frac{{\Delta_{2,i = n} }}{{(1 + \Delta_{i = n}^{2} )^{3/2} }}} \right)^{2} }}{2}} \right)$$

(14)

The strain increases with smaller radius of curvature (11). Therefore, bending modes 3 and 4 are more interesting for a strain based harvester (piezoelectric). On the other hand, bending modes 1 and 2 are of interest in the case of a displacement based harvester (electromagnetic transduction). To illustrate that, Fig. 3 displays the strain energy integral computed for each basic mode shape. The strain energy is expressed as a factor from the first bending mode, in which case the strain is localized mostly near the cantilevered end and there is no bending further along the beam. The strain energy increases drastically when bending develops further along the beam because of the resulting decrease in the radius of curvature.

3 Experimental setup

3.1 Water tunnel

The experiments were carried out in a water tunnel with the flow velocity ranging from 0.1 to 1.3 m/s giving a Reynolds number range (based on the square cylinder) of 1500–19,770 and a vortex shedding frequency range of 0.9–12 Hz when calculated using a Strouhal number of 0.14. As shown in Fig. 4, the flexible plate was placed at mid-depth and on the center plane in the water tunnel. The plate was clamped to the square cylinder at one end and free at the other. The square cylinder has dimensions of 15 mm × 15 mm × 105 mm; the water tunnel has a cross section of 160 mm (width) × 250 mm (depth) thus giving a blockage of 4%. The test section is 0.75 m long. The fluid flow parameters were all set by the free stream velocity as the bluff body size is kept constant. The plates are made of polyethylene having approximately a Young’s modulus of 2 GPa and a density of 1475 kg/m³. Those material properties are fairly similar with the piezoelectric polymer polyvinylidene fluoride (PVDF). The width and length of the plates were varied and the thickness was of 100 or 120 μm depending on the plate. The plate parameter under investigation was the slenderness (width and length).

Fig. 4

Experimental setup a water tunnel layout, b flexible plate and square cylinder, c captured frame before and after image processing

At an early stage a high speed camera at a frame rate of 476 frames per second in a 640 × 480 pixels resolution was used to capture the plate shapes evolutions with the free stream velocity. In a second phase, a 5000 frames per second high speed camera in a resolution of 640 × 1150 was used to be able to analyze the wake flow using Particle Image Velocimetry methods (PIV). The laser sheet impinging at mid-span illuminates the fully transparent plate and the seeding particles in the wake flow. The laser used is a 3000 mw 532 nm green laser; a cylindrical lens is placed on the laser beam to create a thin laser sheet. The seeding particles are 3 μm diameter PVC spheres.

3.2 Image processing

Frames are captured and converted into gray scale as shown in Fig. 4c, using MATLAB’s image processing toolbox, we applied a filter that emphasizes horizontal edges in order to remove the seeding particles used for further PIV analysis. The grayscale image was then converted into a binary image according to a certain threshold level. The resulting binary image is actually a matrix where black pixels take the 0 value and white pixels are assigned with the value of 1. Hence, we can evaluate the plate’s deformation by measuring the vertical distance between the horizontal axis line and the deformed plate by looking for the position of the series of 1 (white pixels) in each column of the matrix containing mostly 0. A sweep of the matrix is performed to look for series of 1 on both sides of the horizontal axis line to determine the position in number of pixels in each column. The conversion of the distance in number of pixels to mm is done with the help of a calibration image.

3.3 Curve fitting

Once the deformed plate’s raw deflection data are obtained, they are first filtered and then fitted with a polynomial to ease further analysis. The raw data of the deflection are first separated into segments of 5 mm each along the plate. Then, the most representative value of each segment is taken and stored into a new vector. Next, we apply the compatibility condition test between each segment value which means that the first derivatives should be continuous at mid points, to ensure continuation, the values that don’t meet the compatibility criterion are filtered out. Finally, the continuous data points are fitted with a polynomial that is the best fit in the least-squares sense. The final polynomial form for the plate is then used for strain energy computation and modal analysis.

3.3.1 Modal contributions and strain energy

For each frame, the modal contributions of the first four bending modes are computed and then stored into a table. The strain energy is also computed. The aim is to associate a certain range of strain energy to each family of deflected shapes.

3.4 Flow characterization

The flow around the square cylinder and the plate can be described by carrying out PIV experiments which aim to measure the velocity vectors of the tracer particles. The vectors are determined by cross-correlating pairs of images, each pair is composed of two frames recorded at fixed time interval (Fig. 4c). The time elapsed between each frame being known, the velocity vector is computed by measuring the displacement vector of identical particles between the paired frames (Raffel et al. 2018). Statistic methods such as cross-correlation functions are used to determine the identical particles between these two frames. The particles locations in the second frame at time ${\text{t}}^{\prime } = t + \Delta {\text{t}}$ can be expressed as:

$$\overrightarrow {{X_{i}^{\prime } }} = \overrightarrow {{X_{i} }} + \vec{D} = \left( {\begin{array}{*{20}c} {X_{i} + D_{x} } \\ {Y_{i} + D_{y} } \\ \end{array} } \right)$$

(15)

where $\vec{D}$ is the displacement vector from which the velocity vectors components can be deducted (Fig. 5).

Fig. 5

Particle image velocimetry, velocity vector field calculation principle

Interrogation windows at time $t$ and time ${\text{t}}^{\prime } = t + \Delta {\text{t}}$ are cross-correlated to obtain the most probable particle displacement $\vec{D}$ within the windows. The discrete cross-correlation function as mentioned by Thielicke is expressed as (Thielicke 2014):

$${\text{C(}}m,n )= \mathop \sum \limits_{i} \mathop \sum \limits_{j} A(i,j)B(i - m,j - n)$$

(16)

where $A,B$ correspond to the image intensity distribution of the interrogation windows at time $t$ and $t^{\prime }$. $m$ and $n$ represent the pixel offset between the two images. ${\text{C(}}m,n )$ measures the agreement between $A,B$ for a given particle displacement. In the correlation matrix, the cross correlation function peaks for the $i = j$ terms (identical particles) whereas the $i \ne j$ terms form a noise floor. The location of the maximum in the correlation matrix ${\text{C(}}m,n )$ yields the average in-plane displacement $\vec{D}$ of the particles from $A$ to $B$. Most commonly, Eq. (16) is computed in the frequency domain using the discrete Fourier transform in order to reduce the computation effort.

The software PIVlab was used with MATLAB to carry out the PIV analysis. Each frame is subdivided into interrogation windows within which the software proceeds to the cross-correlation analysis to determine the identical particles between each pairs. Setting the window size is critical as a narrow size might let the particle “escape” from the window in the second frame and therefore the program would not be able to determine the change in the position vector. On the other hand, setting a too large window size would yield a coarse resolution of the velocity field.

4 Results

The presence of the bluff body triggers the oscillatory motion of the plate and therefore the plate’s undulating frequency is closely related to the vortex shedding frequency $f_{v}$. The plate motion can be seen as a combination of two distinct categories: splitter plate oscillations and travelling waves. Splitter plate oscillations refer to an up down motion with relatively low bending along the length of the plate (first and second bending modes); travelling waves refer to the plate bending into sine wave-like shapes (third and fourth bending modes). The response of the plate to the wake flow is determined by its bending stiffness; travelling waves occur mostly under a low bending stiffness. In Fig. 6, the plate follows the vortex shedding frequency: $f_{plate} \approx f_{v}$; its motion is of the splitter plate oscillation type with seldom occurrence of dominant mode 2 shapes.

Fig. 6

PE plate 1 cm × 5 cm 100 μm u = 0.95 m/s Re = 14,300, $f_{v} = 8.9 {\text{Hz}}$, $T_{v} = 0.11 {\text{s}}$, several plate shapes

The strain energy is displayed as a factor of the lowest value which take 1. Figure 6c has the most strain energy because of its dominant mode 2 contribution. Figure 6d has the least strain energy due to its smallest mode 2 contribution. The factor of nearly 28 is not surprising when considering the values in Fig. 3.

The undulating frequency of the 125 mm plate shown in Fig. 7 is half of the vortex shedding frequency: $f_{plate} \cong 4 Hz$. This frequency delay in the plate undulating motion is due to the increased interaction between the wake and the deflected plate; the bent shapes being more complex, they occur less frequently as they require distinct flow patterns.

Fig. 7

PE plate 1 cm × 12.5 cm 100 μm u = 0.95 m/s Re = 14,300, $f_{v} = 8.9 {\text{Hz}}$, $T_{v} = 0.11 {\text{s}}$, several plate shapes

Figure 7b has the most strain energy because of its dominant mode 3 contribution. With this plate length, the difference in strain energy between the frames is much smaller because shapes are more complex with significant contributions from each mode. Comparing Figs. 6a and 7a shows that increasing the length of the plate and consequently lowering its bending stiffness allows travelling waves to occur. Strain energy increases drastically due to the occurrence of dominant mode 3 shapes and the resulting plate-wake interaction is also more significant as shown by the delay in undulating frequency. The average modal ratio is the average ratio of the modal contribution to the overall biggest modal contribution. The overall biggest modal contribution is mode 1, averaging is done among more than 10,000 captured frames for each data point. Figure 8 shows the evolution of modes 3 and 4 contributions following increasing Reynolds numbers for two different plates having the same wetted surface area. We see that the slenderer plate has greater contributions overall and that his mode 4 contributions increase more significantly with the Reynolds number than its counterpart. Hence, for slender plates travelling waves occur at lower Reynolds numbers and are more prominent.

Fig. 8

PE plate 120 μm modes 3 and 4 contributions

Figure 9 shows the median values of the strain energy computed for different plates at several Reynolds numbers. The strain energy increases with the Reynolds number, resulting from the increase in mode 3 and 4 contributions (Fig. 8). Figure 9 shows that the increase in length tremendously increases the strain energy, owing to the dominant travelling wave shapes. It is noticed that the strain energy is inversely proportional to the plate width. Hence, one can deduce that an array of strips would produce more strain energy than a single wide ribbon. This can be explained by the fact that the observation of significant torsion in this study when the width of the plate increases. Indeed, fluid flow energy conveyed to the plate is more efficiently converted into harvestable strain energy when the motion of the plate is two-dimensional; the occurrence of torsion modes is not wanted in this application since we tend to mimic anguilliform swimming motion.

Fig. 9

PE plate 120 μm strain energy

Figure 10 shows a dominant mode 2 shape in the velocity profile of a PE plate of 1 cm × 7.5 cm (width × length) and 100 μm thick acquired at flow velocity of 0.95 m/s (Re = 14300), Fig. 11 a dominant mode 3 shape with the PE plate of 1 cm × 10 cm, and Fig. 12 a dominant mode 4 shape with the PE plate of 1 cm × 12.5 cm. From Fig. 10, it can be seen that the mode 2 shape is a consequence of normal flow impinging at mid-length on one side and normal flow impinging near the free end on the other side. Hence, rolling the plate in a concave/convex shape. Mode 1 occurs when the normal flow impinges only on one side of the plate. In Fig. 11, normal flow from the vortices on both side of the plate simultaneously impinges on the plate but at different locations along the length. This flow pattern is precisely what creates complex bending shapes. The velocity vector components u = 0.53 m/s and v = 0.91 m/s, mean that there is a local acceleration; the plate absorbs fluid momentum for its motion but it also sheds momentum back into the wake flow. The velocity vector components show mostly important deceleration which shows how the plate extracts energy from the flow to generate its bending and undulating motion. It is important to notice that the wake of the ensemble square cylinder and plate is different than the wake of a square cylinder alone. Figure 12 shows that when the length of the plate increases, there are more occurrences of normal flow impinging simultaneously at different locations on both side of the plate resulting in more complex shapes. This is also because the plate prevents reattachment of the shear layers and thus helps sustaining turbulence in the wake. Indeed, interacting more with the wake allows to extract more momentum. The asymmetry in the normal flow distribution on both sides is what yields the plate deformation. When the curvature changes from concave to convex along the plate, the strain energy is greatly magnified. This eel-like swimming motion ensures an optimum energy transfer from the flow to the plate.

Fig. 10

Velocity profile of the PE plate of 1 cm × 7.5 cm

Fig. 11

Velocity profile of the PE plate of 1 cm × 10 cm (width × length)

Fig. 12

Velocity profile of the PE plate of 1 cm × 12.5 cm (width × length)

5 Conclusion

A flexible cantilever plate in the wake flow of a bluff body undergoes periodic oscillations, the resulting deflection generates strain within the body which can be converted to electric energy through Electrostriction or Piezoelectricity. The water tunnel experiments were carried out in this study with different polyethylene plates clamped to a square cylinder. The plate deflection as well as the flow field were recorded using a high speed camera. The undulating motions and flow patterns yielding the most strain energy have been identified. Slender plates bending into a travelling wave pattern extract more efficiently the energy from the flow due to the complex plate-wake interaction. Moreover, plates should be slender because two-dimensional plate motion is more efficient. Indeed, the plate should tend to mimic the eel swimming motion. There is potential for further research as the optimum thickness of the plate under a certain flow regime has not been yet determined.