1 Introduction

Mechanical tuning is an attractive alternative to conventional thermo-optic or free carrier injection methods for an optical filter, with the benefit of minimal standing power consumption (Hah et al. 2011; Kauppinen et al. 2011; Ikeda and Hane 2013; Shoman and Dhalem 2014). Its mechanism is based on control of evanescent coupling between a microring resonator and a waveguide (index modulator) running parallel to it. As the distance between two adjacent waveguides is varied, the evanescent coupling between them also changes so that effective indices of the modes propagating through the waveguides are altered (Lukosz and Pliska 1991; Haronian 1998; Chollet et al. 1999). In this way, by controlling the distance between the resonator and the index modulator, resonant wavelengths of the resonator can be tuned.

The mechanically tunable filter devices reported so far employ a single resonator and a single index modulator. The main constraint of such devices is a limited tuning range. A tuning range of a single-resonator filter is determined by the free spectral range (FSR) of its resonator, which is inversely proportional to the perimeter length of the resonator. Therefore, one can extend the tuning range of a filter by making the resonator small. When the perimeter length of the resonator is made too small, however,—for example, as small as 10 µm (in the case of silicon) to cover the entire C-band from 1530 to 1565 nm—the resonator loss increases drastically due to scattering and junction mismatch, and degrades the quality factor of the resonator significantly (Van et al. 2001). Moreover, as the resonator size shrinks, although the FSR becomes wider, tuning itself becomes more challenging because the length of the waveguide where modulation is to be applied is also reduced. These two issues applied to all the tuning methods mentioned above.

Therefore, a different approach is needed to realize wide-band tuning in optical filters other than reduction of the resonator sizes. One such approach explored by several research groups is utilization of the Vernier effect (Kaminow et al. 1987, 1988). Series (Fig. 1) or parallel coupling of multiple resonators is one of the typical methods employed in general filter design for improved filter characteristics such as a box-shape pass-band. Such coupling among resonators of different sizes brings about the so-called Vernier effect by which the tuning range of the filter can be extended as its principle is illustrated in Fig. 2. When resonators of two different FSRs are coupled together, the FSR of the overall filter becomes the least common multiple of the FSRs of the individual resonators. Several groups have demonstrated this expansion of FSR in microring resonator configurations through the Vernier effect, both as fixed filters (Yanagase et al. 2002; Melloni and Martinelli 2002; Grover et al. 2002; Boeck et al. 2013) and as tunable filters (Choi et al. 2005; Goebuchi et al. 2006; Fegadolli et al. 2012; Prabhathan et al. 2012; Jayatilleka et al. 2016), mostly by thermo-optic tuning. In this paper, the Vernier effect is examined in the case of micromechanical (evanescent coupling) tuning. In the next section, the detailed optical analysis for the series-coupled microring resonators will be presented based on both a finite-difference time-domain (FDTD) method and analytical methods.

Fig. 1
figure 1

A schematic diagram of an optical add-drop filter with mechanical tuning and series-coupled microring resonators. Arrowheads indicate the direction of light traveling at resonance (color online)

Full size image
Fig. 2
figure 2

Principle of the Vernier effect explained with the output spectra at the DROP port. 36 nm FSR of the cascaded resonator is the least common multiple of 9 and 12 nm of the individual resonators

Full size image

Meanwhile, it is desirable to design a filter to have linear tuning characteristics for more straightforward drop channel control. Recently, the author reported a shaped-finger design method to achieve such characteristics in a filter with a single resonator (Hah and Bordelon 2015; Hah 2017). Shaped-finger comb-drive actuators have been reported previously by several research groups (Ye et al. 1998; Jensen et al. 2003; Lee et al. 2008; Engelen et al. 2010), who calculated finger shapes from a desired straightforward force profile by using either an optimization algorithm or a closed-form equation. Author’s approach can be regarded more general where a numerical solution is found for an application-specific differential equation. In the current work where several resonators as well as several index modulators are employed, the actuator design must become more complicated than for the one with a single resonator. Section 3 will explain the shaped-finger design in the case of series-coupled resonator filters as well as the design verification through three-dimensional (3D) finite element analysis. Effects of fabrication imperfections to the filter characteristics will be described as well based on the numerical simulation results.

2 Optical analysis

2.1 Operation principle

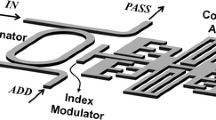
The basic configuration of the filter as illustrated in Fig. 1 works as an optical add-drop filter. It has two input ports, IN and ADD, and two output ports, PASS and DROP. Light of wavelength that satisfies the resonance conditions of all the microring resonators in the filter travels from IN to DROP and ADD to PASS. Arrowheads over the resonators indicate the direction of the light at resonance. At off resonance, light travels from IN to PASS and ADD to DROP without much coupling through the resonators. Resonant wavelengths of a resonator are determined by its perimeter length and the effective index of the mode propagating through the resonator. In order for the resonance condition to be obtained for the entire filter, resonant wavelengths of all the resonators have to coincide to one another. By coupling resonators with different FSRs in series as depicted in Fig. 1, one can extend the FSR of the filter as illustrated in Fig. 2. In this work, a resonator (large) with an FSR of 9 nm and two resonators (small) with an FSR of 12 nm are cascaded in series to result in a filter with an overall FSR of 36 nm to cover the entire C band.

The resonant wavelength of a resonator is tuned by an index modulator, which is a movable waveguide placed in parallel to the straight section of the resonator. The presence of the index modulator incurs evanescent coupling between itself and the resonator. Such coupling results in change in the effective index, which brings in shift in resonant wavelength. By varying the gap between the index modulator and the resonator, one can control the evanescent coupling, and hence, the resonant wavelength. Such control, i.e. translational motion of the index modulator is rendered by a comb-drive actuator that is attached to it. Since a comb-drive actuator is an electrostatic actuator, it requires most of the power consumption during the tuning. Once the desired channel is set, minimal power is needed to maintain the tuning so that the filter can be operated with little standing power consumption.

First, the optical analysis of the filter through analytical methods will be presented. Then, analysis using a finite-difference time-domain (FDTD) method will be explained.

2.2 Analytical methods

For analytical methods, the normal mode theory (Marom et al. 1984; Ribot et al. 1990) and the resonator coupling theory (Yariv 2000) were used. The normal mode theory was used to compute profiles (eigenmodes) and effective indices (eigenvalues) of the modes that are supported by multilayer slabs. Then, the resonator coupling theory was used to model the coupling and the propagation of light through the bus waveguides and the resonators. The detailed procedure used for the analysis can be found from the author’s previous work (Hah et al. 2011). According to the resonator coupling theory, fields at a coupling region (Fig. 3) can be described by,

$$ \left[ {\begin{array}{*{20}c} {b_{m + 1} } \\ {b_{m}^{\prime } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {t_{m}^{*} } & { - \kappa_{m}^{*} } \\ {\kappa_{m} } & {t_{m} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {a_{m + 1} } \\ {a_{m}^{\prime } } \\ \end{array} } \right], $$
(1)

where κ m and t m are dimensionless coupling and transmission coefficient, respectively, which satisfy the relationship of |κ m |2 + |t m |2 = 1. m is an integer from 0 to 3. Inside a resonator, \( a_{m}^{\prime } \) and b m , and a m and \( b_{m}^{\prime } \) are related as below:

$$ a_{m}^{\prime } = \sqrt {\alpha_{msb} } \alpha_{im} b_{m} \exp ({{ - j\varphi_{1r} } \mathord{\left/ {\vphantom {{ - j\varphi_{1r} } 2}} \right. \kern-0pt} 2}), $$
(2a)
$$ a_{m} = \sqrt {\alpha_{msb} } \alpha_{im} b_{m}^{\prime } \exp ({{ - j\varphi_{1r} } \mathord{\left/ {\vphantom {{ - j\varphi_{1r} } 2}} \right. \kern-0pt} 2}), $$
(2b)

where α msb , α im , and ϕ 1r are unloaded (material, scattering, and bending) loss in one roundtrip, loss caused by evanescent coupling to the index modulator in one roundtrip, and phase shifts incurred during one roundtrip, respectively. α im depends on the gap (g, see Fig. 1) between the resonator and the index modulator. α im is 1 if there is no index modulator in the corresponding section. ϕ 1r includes the additional phase shift caused by evanescent coupling to the index modulators, again function of g. When a IN is 1 and a ADD is 0, from (1) and (2a, 2b), the optical power at the DROP port, P DROP can be derived to become,

$$ P_{DROP} = \left| {b_{DROP} } \right|^{2} = \left| {\frac{{\alpha_{msb\_sr} \sqrt {\alpha_{msb\_lr} } \left( {1 - |t_{rr} |^{2} } \right)\left( {1 - |t_{br} |^{2} } \right)}}{{(1 - C_{1} t_{rr} - C_{2} t_{rr}^{*} + C_{1} C_{2} )(1 - C_{1} D)}}} \right|^{2} , $$
(3a)

where

$$ C_{1} = \alpha_{msb\_sr} \alpha_{im\_sr} t_{br}^{*} \exp ( - j\varphi_{1r\_sr} ), $$
(3b)
$$ C_{2} = \alpha_{msb\_lr} \alpha_{im\_lr} t_{rr}^{*} \exp ( - j\varphi_{1r\_lr} ), $$
(3c)
$$ D = \frac{{|t_{rr} |^{2} - C_{1} t_{rr} |t_{rr} |^{2} - C_{2} t_{rr}^{*} + C_{1} C_{2} }}{{t_{rr}^{*} - C_{1} |t_{rr} |^{2} - C_{2} (t_{rr}^{*} )^{2} + C_{1} C_{2} t_{rr}^{*} }}. $$
(3d)
Fig. 3
figure 3

Field notations for the filter (top view). Dimensions of the resonators used in the simulation are as follows. R SR : 2.92 µm, R LR : 2.92 µm, L SR : 18.35 µm, L LR : 27.53 µm

Full size image

In (3a, 3b, 3c), sr and lr in the subscripts indicate those related to the small resonator and to the large resonator, respectively. t rr is the transmission coefficient between the resonators, and t br is the one between a bus waveguide and a small ring resonator.

In the author’s previous work (Hah et al. 2011), a material with a low refractive index (n = 2.2) was considered for an index modulator for its low power coupling characteristics. In this work, it is replaced by silicon (n = 3.48), which offers an advantage of simpler fabrication processes because all the main structures can be made out of the same material. Since high refractive index of the silicon modulator incurs high coupling loss (α im ) to the resonator, the modulator was designed with narrower width (W IM , see Fig. 1)—two different values of 50 nm and 100 nm were considered in this work—than the one with low refractive index. The width of the index modulator plays a significant role in the filter characteristics. A narrower (50 nm) index modulator does not incur substantial coupling loss, but its range of continuous wavelength tuning is limited due to moderate influence to the effective indices. Therefore, tuning of a full FSR of the filter has to be realized by stitching of (or hopping among) multiple bands, which will be further described in the next paragraph. A wider index modulator (100 nm) allows full-FSR tuning within one band without the necessity of band hopping. However, it results in substantial coupling loss.

Figure 4 shows the calculated resonant wavelengths (λ r ) of the single resonators, both small and large, with respect to the gap (g) between the resonator and the index modulator for each of the index modulator widths, 50 nm and 100 nm. In the graphs, the results calculated with the analytical methods are presented with lines. To have an FSR of 12 nm for the small resonator and of 9 nm for the large resonator, perimeters were designed as 55.1 and 73.4 µm, respectively. The detailed dimensions of the resonators are presented in Fig. 3. The ring perimeter pairs were selected carefully so that their resonant wavelengths coincide at both ends of the extended FSR of the cascaded-ring filter. This can be seen from the curves indicated by LB (lower bound) and UB (upper bound) in Fig. 4. From Fig. 4a, it can be seen that one cannot achieve tuning of entire range by staying in just one curve in the case of 50-nm-wide modulator. For example, if the gaps (g) for the small resonator and the large resonator are changed by the same amount, i.e. if one stays on the curve marked by LB, the tuning can be only obtained from 1529 to 1554 nm. Therefore, to cover the entire range of C-band, one has to match the wavelengths from different bands (band hopping). In other words, the index modulator gap of a large resonator has to be controlled separately from those of small resonators. For example, to tune the wavelength at 1558 nm (indicated by a dashed line in Fig. 4a), the index modulator gap for the small resonator has to be set at 90 nm on the SR2 curve while it has to be at 140 nm on the LR3 curve for the large resonator. To the contrary, the entire C-band can be covered without band hopping in the case of the 100-nm-wide modulator, as can be seen from Fig. 4b. In other words, identical modulator gaps can be used for all the rings for tuning in the case of 100-nm-wide modulator. The drawback of the 100-nm-wide modulator device is the significant power loss to the index modulator as will be shown in the next subsection.

Fig. 4
figure 4

Calculated resonant wavelength (λ r ) of a single resonator with respect to the gap (g) between the index modulator and the resonator. Red: small ring resonator. Black: large ring resonator. Symbols: FDTD results. Lines: analytical method results. Curves marked with LB (lower bound) and UB (upper bound) indicate spectra coincidence of a small ring resonator and a large ring resonator. Width of the index modulator (W IM ): a 50 nm, and b 100 nm (color online)

Full size image

2.3 Finite-difference time-domain (FDTD) analysis

In the analytical methods used in the previous subsection, some aspects are not taken into consideration, such as curved sections of resonators and mode mismatch at the junction between the curved section and the straight section. Therefore, for more accurate analysis of the filter, two-dimensional (2D) finite-difference time-domain (FDTD) simulation was performed with the same filter structure. RSoft’s FullWAVE™ was used for this simulation. Figure 5 shows snapshots of the computed fields, taken at certain instances, with a single wavelength at resonance launched to the IN port. Figure 5a is with the 50-nm-wide modulator, and Fig. 5c is with the 100-nm-wide modulator. Images in Fig. 5b, d are magnification of the areas near the index modulators, respectively. It is shown that stronger light coupling occurs with the wider modulator as expected.

Fig. 5
figure 5

Snapshots from 2D FDTD analysis of the series-coupled filter. Single wavelength at resonance is launched to IN port. Top view. a Wavelength: 1535.9 nm. Index modulator width: 50 nm. g for the small ring/large ring: 70 nm/69 nm. b Magnified view of a around the modulator section. c Wavelength: 1537.5 nm. Index modulator width: 100 nm. g for both the small ring and the large ring: 97 nm. d Magnified view of c around the modulator section. Normalized electric field strength is plotted in a color scale (color online)

Full size image

The resonant wavelength versus index modulator gap (g) calculated by using FDTD simulation is plotted as symbols in Fig. 4. It is shown that the results with simple analytical methods agree very well with those by FDTD simulation. Figure 6 shows the spectra of the filter at the DROP port, calculated at various index modulator gaps (g), in the case of 50-nm-wide-modulator device. Solid lines are results by the FDTD method and dotted lines are from the analytical methods. It can be seen that the spectra by two methods agree relatively well to each other except that the one with the analytical methods underestimates the DROP power compared to the one with the FDTD method. It can be also seen that the filter has an FSR of 36 nm as designed. As explained earlier, band hopping was used to cover the entire C-band. Figure 7 shows the spectra at the DROP port in the case of 100-nm-wide-modulator device. It can be seen that the variation in P DROP at different index modulator positions is significantly more compared to the case of 50-nm-wide-modulator device, which is a drawback. In either case, the simulation results show that the entire FSR can be tuned with the designed filter.

Fig. 6
figure 6

Calculated spectra of series-coupled filters at the DROP port (P DROP ) for various index modulator positions (or gaps g). Solid lines: FDTD results. Dotted lines: analytical method results. Width of the index modulator (W IM ): 50 nm. g for the small ring/large ring are a 1 : 350 nm/350 nm, a 2 : 70 nm/69 nm, a 3 : 111 nm/77 nm, a 4 : 50 nm/99 nm, and a 5 : 90 nm/140 nm, respectively (color online)

Full size image
Fig. 7
figure 7

Calculated spectra of series-coupled filters at the DROP port (P DROP ) for various index modulator positions (or gaps g). Solid lines: FDTD results. Dotted lines: analytical method results. Width of the index modulator (W IM ): 100 nm. g for both the small ring and the large ring is b 1 : 350 nm, b 2 : 97 nm, b 3 : 62 nm, b 4 : 40 nm, and b 5 : 24 nm, respectively (color online)

Full size image

3 Actuator design

The lateral movement of the index modulator is controlled by comb-drive actuators as illustrated in Fig. 8. Just for the sake of movement, a single comb on the left hand side is sufficient. However, due to a couple of nonlinear relationships: (1) the exponential relationships between the resonant wavelength and the distance of the index modulator from the resonator (λ r  − g), and (2) the direct square relationships between the comb-drive actuator displacement and the applied voltage (x − V), the wavelength-voltage (λ r  − V) characteristics of a single comb device is highly nonlinear (see Fig. 11, open square). By adding the second comb (on the right hand side) as a control comb and by using the first comb as a bias comb, one can make the λ r  − V characteristics more linear (see Fig. 11, open circle) by reversing the convexity of the x − V curve. Employment of dual electrostatic actuators has been proposed by other groups previously for linearization of actuator movement (Tang et al. 1990; Toshiyoshi et al. 2001). Since the dual comb-drive configuration by itself turned out to be insufficient for linearization of λ r  − V characteristics, a shaped comb finger design was proposed by the author (Hah and Bordelon 2015; Hah 2017), as summarized as follows.

Fig. 8
figure 8

Schematic drawing of a shaped-finger comb-drive actuator (top view)

Full size image

The governing equation of the comb-drive actuator illustrated in Fig. 8 can be described as,

$$ \frac{1}{2}\frac{d}{dx}\left\{ {2N_{f} \left[ {\int_{0}^{x} {C_{bias} (u)du} + C_{const} } \right]} \right\}V_{bias}^{2} + \frac{1}{2}\frac{d}{dx}\left\{ {2N_{f} \left[ {\int_{0}^{{x_{max} - x}} {C_{ctrl} (v)dv} + C_{const} } \right]} \right\}V^{2} - k_{s} x = 0, $$
(4a)
$$ N_{f} C_{bias} (x)V_{bias}^{2} - N_{f} C_{ctrl} (x_{max} - x)V^{2} - k_{s} x = 0, $$
(4b)

where N f , C const , and k s are the number of fingers in one comb, the capacitance of the section with constant finger gaps near the fixed finger tips, and the spring constant. x, u, and v are defined in Fig. 8. C bias and C ctrl are the 2D (y − z plane) capacitances of the bias comb and of the control comb, respectively, as functions of positions (u or v) within the combs, and designed intuitively to be complementary to each other as described by,

$$ C_{ctrl} (v) = - C_{bias} (x_{max} - v) + C_{bias} (0) + C_{bias} (x_{max} ). $$
(5)

V bias is the bias voltage on the bias comb. When V = 0, x is to be x max , the displacement of the maximum finger engagement by the bias comb. From (4b),

$$ V_{bias}^{2} = \frac{{k_{s} x_{max} }}{{N_{f} C_{bias} (x_{max} )}}. $$
(6)

The objective of the finger shape design, linear λ r -V relationships can be expressed by using the linear constant c 0 as,

$$ \frac{{d\lambda_{r} }}{dV} = \frac{{d\lambda_{r} }}{dx} \cdot \frac{dx}{dV} = c_{0} , $$
(7a)
$$ c_{0} = \frac{{\lambda (x_{max} ) - \lambda (0)}}{{V(x_{max} ) - V(0)}} \, = \frac{{\lambda (0) - \lambda (x_{max} )}}{V(0)}. $$
(7b)

λ r (x) is obtained from Fig. 4 for each of the resonators. By combining (4a, 4b)–(7a, 7b), one can obtain the following objective differential equation:

$$ \frac{{dC_{bias} }}{dx} = \frac{{2N_{f} V(x)\left[ {C_{bias} (0) + C_{bias} (x_{max} ) - C_{bias} (x)} \right] \cdot \frac{{d\lambda_{r} }}{dx} + k_{s} c_{0} }}{{c_{0} \left[ {N_{f} \left\{ {V(x)} \right\}^{2} + \frac{{k_{s} x_{max} }}{{C_{bias} (x_{max} )}}} \right]}}, $$
(8a)
$$ V(x) = \sqrt {\frac{{k_{s} }}{{N_{f} C_{ctrl} (x_{max} - x)}}\left[ {\frac{{C_{bias} (x)x_{max} }}{{C_{bias} (x_{max} )}} - x} \right]} . $$
(8b)

Since (8a) is a nonlinear differential equation, the Euler’s method is used to find the approximate solution as below:

$$ C_{bias,k + 1} = C_{bias,k} + h \cdot \left. {\frac{{dC_{bias} }}{dx}} \right|_{{x = x_{k} ,C_{bias} = C_{bias,k} }} , $$
(9a)
$$ x_{k} = h \cdot k. $$
(9b)

h is the uniform step size in x, and k is an index.

The shaped-finger design method described above was applied for the series-coupled-resonator filter. First, C bias (u) and C ctrl (v) are found by using (5) and (9a, 9b). Then, the finger gaps, d bias (u) and d ctrl (v) (see Fig. 8) are found based on the 2D electrostatic simulation results using finite element analysis with COMSOL Multiphysics® software. d min which is d bias (x max ) and d ctrl (x max ), and d max which is d bias (0) and d ctrl (0) are designed to be 50 nm and 80 nm, respectively, in this study. Figure 9 shows the designed finger gaps of the comb-drive actuators for both devices with index modulator widths (W IM ) of 50 nm and of 100 nm. The calculated λ r  − V characteristics using (4a, 4b)–(9a, 9b) are almost perfect straight lines as those of the previous report (Hah 2016). However, those calculations are based on one assumption: a 3D capacitance equals to a stack of 2D capacitances. In other words, it is assumed that all the field lines are perpendicular to the x − z plane. This is not exactly the case in reality. Therefore, it is necessary to verify the design through 3D finite element analysis (FEA), which will be described in the following subsection.

Fig. 9
figure 9

Calculated finger gaps, d bias (red) and d ctrl (blue) for linear wavelength-voltage relationships in a series-coupled filter. Width of the index modulator W IM : 50 nm (dashed lines) and 100 nm (solid lines) (color online)

Full size image

3.1 3D finite element analysis

For the 3D FEA, COMSOL Multiphysics® was used as an example snapshot is given in Fig. 10. Calculated field lines and electric potential distributions in a half unit of a bias comb are presented in the figure. Figure 11 shows the calculated λ r  − V characteristics for the 100-nm-wide-modulator filter device, with an assumption of a linear spring. This assumption is reasonable since the whole range of displacement is merely less than 350 nm. For comparison, the characteristics of the devices with the conventional constant-gap design, both with (○) and without (□) a bias comb are presented together. For clearer comparison, voltages are normalized using the maximum and the minimum values for each case. In the case of the shaped-finger design (×), the region-of-interest extension method was used as reported before (Hah 2017) to exclude the nonlinear regions at the both ends of the characteristic curve.

Fig. 10
figure 10

Calculated field lines (arrows) and electric potential distributions (contour map) in a half unit of a bias comb. Symmetric boundary conditions are used (color online)

Full size image
Fig. 11
figure 11

Wavelength-voltage characteristics (λ r  − V) of series-coupled filters, calculated with 3D electrostatic simulation and assuming a linear spring. Shaped finger: × . Constant-gap (single comb): white square. Constant-gap (double comb): white circle. Design parameters: number of fingers (N f ) = 50, spring constant (k s ) = 0.27 N/m, period of a comb: 400 nm, thickness of a finger = 200 nm, and width of the index modulator (W IM ) = 100 nm. Voltages are normalized with respect to the maximum and the minimum values for each case

Full size image

In the case of the 100-nm-wide index modulator, the channel selection is straightforward because a single λ r  − V curve can cover the entire C band, and hence, the same λ r  − V curve can be shared by the small and the large resonators. The control becomes a bit more complicated in the case of the 50-nm-wide-modulator device because it involves band hopping. If typical comb-drive actuators with constant finger gaps are used, the control becomes complicated due to combination of nonlinear characteristics and band hopping. As can be seen from the characteristics presented in Fig. 12, hopping among different bands becomes more manageable due to the linear control obtained through shaped-finger design. The characteristics given in Fig. 12 are again with the region-of-interest extension method; the bias voltages on the control combs are 1.90 and 2.53 V for the small and the large resonator, respectively. In both cases of index modulator widths, it was verified through 3D FEA that reasonable linearization can be achieved by using the shaped-finger design method.

Fig. 12
figure 12

Wavelength-voltage characteristics (λ r  − V) of series-coupled filters, calculated with 3D electrostatic simulation and assuming a linear spring. Red lines: small ring resonator. Black lines: large ring resonator. Bias voltage applied to the control comb: 1.90 V (small ring) and 2.53 V (large ring). Design parameters: number of fingers (N f ) = 50, spring constant (k s ) = 0.27 N/m, period of a comb: 400 nm, thickness of a finger = 200 nm, and width of the index modulator (W IM ) = 50 nm (color online)

Full size image

3.2 Effect of fabrication error

The effect of fabrication imperfections to the device characteristics designed with the shaped fingers was studied for the 100-nm-wide-modulator device, as presented in Fig. 13. Fabrication offset was considered as an example of deviation from the ideal design. Due to various issues such as over-exposure, etch bias, and so on, the fabricated finger gaps can become larger than the original design. In addition, the widths of the optical components, i.e. resonators, waveguides, and index modulators, can become smaller due to the fabrication imperfections. The fabrication offset was defined as the deviation from one side. For example, 10 nm offset from the designed gap of 80 nm makes the fabricated gap of 100 nm. At the same time, it decreases the width of an index modulator from 100 to 80 nm. To examine the individual effect of the changes made in the actuator part and the optical part separately, simulation study was conducted by considering individual changes first, and then combined later.

Fig. 13
figure 13

Effect of fabrication offset to the tuning characteristics. 3D analysis. Width of the index modulator (W IM ): 100 nm. a When the dimension changes only in the shaped fingers are considered. Voltages are normalized with respect to the maximum and the minimum values for each offset. b When the dimension changes only in the optical components are considered. c When the dimension changes both in the shaped fingers and in the optical components are considered. Fabrication offset: 20 nm. d When the dimension changes both in the shaped fingers and in the optical components are considered. Only the parts of the characteristic curves, which are determined for more linear tuning, are shown (color online)

Full size image

Figure 13a shows the effect of the fabrication offset to the tuning characteristics when only the gap changes to the shaped fingers are considered. For clearer comparison, the control voltages are normalized according to the maximum and the minimum values for each offset. The results show that nonlinearity increases as the offset increases because the finger shapes deviates more from the designs based on meticulous calculation. Figure 13b shows the effect of the fabrication offset, just by the changes made to the widths of the optical components. One may anticipate that the tunability will be significantly reduced because of the narrowing in the index modulator widths as was shown by difference between the 50-nm-width index modulator and the 100-nm-width index modulator. However, the results in Fig. 13b show that such an effect is not as significant as one would expect. This can be understood in terms of the compensation originated from looser confinement of light in the waveguide as the waveguide width shrinks. Due to the narrowing in the resonator widths, evanescent field becomes stronger so that its interaction with the index modulators becomes more enhanced. In the case of 10 and 20 nm offset, which means 80 nm width and 60 nm width, respectively, coverage of the whole tuning range of 35 nm is shown possible. However, in the case of 30 nm offset (40 nm width), the index modulator narrowing effect outruns that of the resonator so that whole 35 nm cannot be covered. It can be also seen that the nonlinearity increases as the fabrication imperfection increases when only the changes in the optical components are considered even though the increase of nonlinearity is not as severe as in the case of changes in the finger shape only. The more critical issue in the effect of fabrication offset to the characteristics of the optical components is the shift in the resonant wavelengths. As the resonator width is decreased, the effective index changes, which alters the resonant wavelengths as a result. As the resonant wavelengths repeat every FSR, one can find shifted resonant wavelength within one FSR from the original resonant wavelength even if the shift is more than one FSR, as can be seen from Fig. 13b. However, this is still an issue because the filter is designed to be used in the C-band. One way to address this issue is band hopping as in the case of a 50-nm-width index modulator.

Figure 13c shows the example of band hopping in the case of 20 nm fabrication offset. In the results shown, fabrication offset was considered both for the shaped fingers and for the optical components. The sections indicated by solid lines can be selected to be used for tuning. Those sections are determined to maximize the linearity. Figure 13d shows just the sections chosen for more linear tuning for various fabrication offsets, considering changes in both shaped fingers and optical components. By comparing the results in Fig. 13d to those of Fig. 13a, b, one can see that nonlinearity mainly comes from the changes in the shaped fingers. In summary, it was learned that the fabrication offset brings about two major effects: (1) increase in nonlinearity and (2) shift in the resonant wavelengths, and the latter can be overcome by employment of band hopping.

4 Conclusion

36-nm-FSR band-pass tunable optical filters were designed for the optical C band by series coupling of multiple microring resonators based on the Vernier effect. 2D finite-difference time-domain method was used to study the optical behavior of the proposed filter devices, and showed good agreement with the results from the analytical methods, reported previously. Once again, it was shown that the C-band optical filter can be designed, which is based on the micromechanical tuning. Width of the index modulator was found to be one of the important design parameters. Its effects to the continuous tuning range and the evanescent coupling loss were discussed. The shaped-comb finger design method was applied to the series-coupled filters for linear drop channel control. 3D finite element analysis was carried out to verify the design outcomes.