1 Introduction

A laterally driven comb-drive actuator is one of the most frequently used electrostatic actuators in microelectromechanical systems (MEMS) (Tang et al. 1989). It has been widely utilized in various applications including sensors—accelerometers (Su et al. 2005), angular rate sensors (Mochida et al. 2000), force sensors (Sun et al. 2005), magnetic field sensors (Bahreyni and Shafai 2007); RF MEMS—RF filters (Nguyen 1995), variable capacitors (Li and Tien 2002), RF switches (Kang et al. 2009); optical MEMS—microlens scanners (Kwon et al. 2002), variable optical attenuators (Hou et al. 2008), shutters (Grade et al. 2003), optical switches (Marxer and de Rooij 1999); and other areas such as micro-tweezers (Harouche and Shafai 2005), micro transportation systems (Pham et al. 2007), and so on.

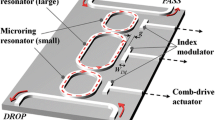
Electrostatic actuation has shown advantages for tunable optical filters with microring resonators, a recent development by several research groups including the author’s (Kauppinen et al. 2011; Hah et al. 2011; Ikeda and Hane 2013; Shoman and Dhalem 2014; Errando-Herranz et al. 2015a, b), especially with the minimal standing power consumption. In the author’s previous report, two types of designs were proposed—one with out-of-plane actuation and one with in-plane actuation (Hah et al. 2011). The latter with a comb-drive actuator is the main focus of this paper, which is illustrated in Fig. 1.

Fig. 1
figure 1

A schematic diagram of a mechanically tunable optical add-drop filter with a microring resonator and a laterally-driven comb-drive actuator

Full size image

The original design of the proposed filter device employs a single comb-drive actuator—the same as one in Fig. 1 excluding the comb on the right hand side. The operation principle of the filter device is as follows. The actuator varies the gap between an index modulator (a movable waveguide) and a microring resonator. The gap change affects evanescent coupling between the modulator and the resonator, and, at the same time, effective indices of the modes propagating along the resonator, and therefore, it shifts the resonant wavelengths, i.e. the add/drop channel of the filter. The major issue with the original design with a single comb-drive actuator is the severe nonlinearity in a relationship between the resonant wavelength and the voltage applied to the comb-drive actuator as presented in the curve indicated as single-comb constant-gap (SC-CG) in Fig. 2. This nonlinearity stems from two effects: (1) the exponential relationship between the gap between two waveguides and the evanescent coupling (Yariv and Yeh 2007; Hah et al. 2011) as depicted in Fig. 2 in the inset, and (2) the direct square relationship between the displacement and the applied voltage in a conventional constant-finger-gap comb-drive actuator. Such high nonlinearity is undesirable because it may require high complexity in control electronics.

Fig. 2
figure 2

Tuning characteristics of the filter with a single-comb constant-gap (SC-CG) actuator and those with a dual-comb varying-gap (DC-VG) actuator, calculated with the parallel-plate capacitance approximation. Inset resonant wavelength (λ r ) versus gap between the index modulator and the resonator, obtained by 2D finite-difference time-domain (FDTD) analysis

Full size image

One method to achieve more linear tuning characteristics was proposed by the author recently (Hah and Bordelon 2015). The essence of the method is (1) to employ a dual comb-drive actuator as illustrated in Fig. 1, in order to reverse the convexity of the direct square relationship in the comb-drive actuator, and (2) to derive the comb finger shapes from the differential equation that determines the tuning characteristics of the filter. The dual comb-drive actuator configuration shares a common concept with previous works where multiple electrostatic actuators were employed in a balanced way for various purposes (Tang et al. 1990; Toshiyoshi et al. 2001). Optimization of finger shapes in comb-drive actuators has been investigated previously by several research groups as well. Ye et al. (1998) utilized an optimization algorithm to find proper coefficients for polynomials in comb drives with polynomial gap profiles in order to produce linear, quadratic or cubic driving force profiles. Other groups reported on curved comb fingers designed by solving closed-form equations that are specific for individual goals such as frequency-tunable micromechanical resonators (Jensen et al. 2003; Lee et al. 2008) and shock-resistant actuation (Engelen et al. 2010). All those previous works start from a desired straightforward force profile, and calculate the corresponding finger shapes by using either an optimization algorithm or a solution to a closed-form equation. As the more general approach, the current work tries to find an approximate solution to an application-specific objective equation which can be often complicated.

The comb-drive on the left hand side in Fig. 1 is used as a bias, and the one on the right as a control. The combs are designed so that the tips of the moving fingers on the bias comb are placed at the beginning of the gap-varying section of the bias comb when fabricated (minimum engagement), and those on the control comb are at the end of the gap-varying section of the control comb (maximum engagement) as depicted in Fig. 3. The bias voltage is applied so that the tips of the moving fingers on the bias comb are drawn to the end of the gap-varying section of the bias comb—this is when the index modulator will be the closest to the resonator, which means that those on the control-comb are shifted to the beginning of the gap-varying section of the control comb. In this condition, when the control voltage is applied to the control comb, the movable part moves towards the control comb, i.e. the index modulator is pulled away from the resonator. The original version of the finger shape design method is detailed in (Hah and Bordelon 2015), of which results are presented by the curve indicated as dual-comb varying-gap (DC-VG) in Fig. 2, and show perfectly linear relationship.

Fig. 3
figure 3

Conceptual drawing of a part of the comb-drive actuator for linear tuning characteristics of the filter. Top view u and v are the distances from the boundary between the constant gap section and the gap-varying section for a bias comb and a control comb, respectively

Full size image

This perfect linearity, however, was obtained with a simple model based on the parallel-plate approximation. For the real applications, therefore, it is necessary to refine the method, taking the actual electric field lines into consideration including fringe fields. This paper will present the revised design method. Section 2 will provide theoretical explanations for the revised design method as well as the effects of some design parameters to the design procedure. The revised design method will be assessed by three-dimensional (3D) numerical analysis in Sect. 3. Section 3 will also discuss about additional methods to achieve further improvement in linearity.

2 Design method

The goal to be achieved by using the revised design method is the same as the original one (Hah and Bordelon 2015), i.e. linear resonant wavelength–control voltage (λ r –V) characteristics, which can be expressed by the following objective equation.

$$\frac{{d\lambda_{r} }}{dV} = \frac{{d\lambda_{r} }}{dx} \cdot \frac{dx}{dV} = C_{0} ,$$
(1)

where x is the displacement of the index modulator. C 0 is the linear constant, which is determined by the ranges of λ r and V, and can be expressed as,

$$C_{0} = - \frac{{\lambda_{\hbox{max} } - \lambda_{\hbox{min} } }}{{V_{\hbox{max} } - V_{\hbox{min} } }} \, .$$
(2)

Due to the biasing configuration described in Sect. 1, the index modulator is closest to the resonator when V is minimum on the control comb, which means λ r is at the upper limit (λ max , the longest within one free spectral range or FSR of consideration), and λ r is at the lower limit (λ min , the shortest) when V is maximum. λ r has an exponential relationship with the displacement of the index modulator, and can be modeled by,

$$\lambda_{r} \left( x \right) = \lambda_{\hbox{min} } + \frac{{\lambda_{\hbox{max} } - \lambda_{\hbox{min} } }}{{\exp \left( {a_{0} } \right) - 1}}\left[ {\exp \left( {a_{0} \frac{x}{{x_{\hbox{max} } }}} \right) - 1} \right] \, ,$$
(3)

where x max is the displacement of the index modulator, which corresponds to λ max . a 0 is the exponential fitting parameter acquired from the filter characteristics obtained by the FDTD simulation (Hah et al. 2011). Its value along with values of other parameters in (3) is given in Table 1. The governing equation of the comb-drive actuator shown in Fig. 1 is,

$$\frac{1}{2}\frac{{dC_{BIAS} }}{dx}V_{bias}^{2} + \frac{1}{2}\frac{{dC_{CTRL} }}{dx}V^{2} - k_{s} x = 0 ,$$
(4)

where V bias and k s are the bias voltage on the bias comb and the spring constant, respectively. C BIAS and C CTRL are the capacitances of the bias comb and the control comb, respectively, as a function of displacement of the index modulator x. Those capacitances can be approximated by integration of two-dimensional (2D) cross-sectional capacitances, C bias and C ctrl , along the finger length as follows.

$$C_{BIAS} \left( x \right) = 2N_{f} \left[ \int_{0}^{x} {C_{bias} \left( u \right)du + C_{const} } \right]\;{\text{and}}$$
(5)
$$C_{CTRL} \left( x \right) = 2N_{f} \left[ {\int_{0}^{{x_{\hbox{max} } - x}} {C_{ctrl} \left( v \right)dv} + C_{const} } \right] ,$$
(6)

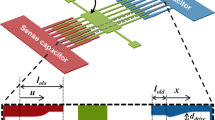
where N f is the number of fingers on one comb, and C const is the capacitance of the section with constant finger gaps near the tips of the fixed fingers. (5) and (6) are based on the configuration of Fig. 3, where u and v are defined as well. (5) and (6) are valid for 0 ≤ x ≤ x max . By using (5) and (6), (4) becomes,

$$C_{bias} \left( x \right)V_{bias}^{2} - C_{ctrl} \left( {x_{\hbox{max} } - x} \right)V^{2} - \frac{{k_{s} x}}{{N_{f} }} = 0 .$$
(7)

When V = 0, x is to be x max , and when V = V max , x is to be 0. Therefore,

$$V_{bias}^{2} = \frac{{k_{s} x_{max} }}{{N_{f} C_{bias} \left( {x_{max} } \right)}},\;{\text{and}}$$
(8)
$$V_{\hbox{max} }^{2} = V_{bias}^{2} \frac{{C_{bias} \left( 0 \right)}}{{C_{ctrl} \left( {x_{\hbox{max} } } \right)}} = \frac{{k_{s} x_{\hbox{max} } C_{bias} \left( 0 \right)}}{{N_{f} C_{bias} \left( {x_{\hbox{max} } } \right)C_{ctrl} \left( {x_{\hbox{max} } } \right)}} .$$
(9)

k s , N f , C bias (0), C bias (x max ), C ctrl (0), and C ctrl (x max ) are the actuator design parameters that decide the level of the operation voltage. Since the value of dλ r /dx is small at small x and large at large x (near x max ), in order to achieve linear tuning characteristics, it is reasonable to expect that the designed combs will have slow-changing gaps for the near side (i.e. close to the index modulator) and fast-changing gaps for the far side (i.e. away from the index modulator) as illustrated in Fig. 3. The signs of gap changes for the two combs, however, have to be opposite from each other—positive for the bias comb and negative for the control comb as one moves from the near side to the far side. Based on these trends, one can intuitively arrive at a design where capacitances for the two combs are complementary to each other, which can be expressed by the following equation.

$$C_{ctrl} \left( x \right) = - C_{bias} \left( { - x + x_{\hbox{max} } } \right) + C_{bias} \left( 0 \right) + C_{bias} \left( {x_{\hbox{max} } } \right)$$
(10)

(10) is arranged so that C ctrl (0) is equal to C bias (0) and C ctrl (x max ) is equal to C bias (x max ). By taking the first derivative of (7) with respect to x (denoted by ′ throughout the paper) and utilizing (8) and (10), one can reach the following differential equation.

$$C^{\prime}_{bias} \left( x \right) = \frac{{2N_{f} V\left( x \right)\left[ {C_{bias} \left( 0 \right) + C_{bias} \left( {x_{\hbox{max} } } \right) - C_{bias} \left( x \right)} \right] \cdot \lambda^{\prime}_{r} \left( x \right) + k_{s} C_{0} }}{{C_{0} \left[ {N_{f} \left\{ {V\left( x \right)} \right\}^{2} + \frac{{k_{s} x_{\hbox{max} } }}{{C_{bias} \left( {x_{\hbox{max} } } \right)}}} \right]}}$$
(11)

(11) is a nonlinear differential equation, which does not have a closed-form solution. Instead, Euler’s method can be used to find the approximate solution, where a series of C bias,k is calculated by the following approximation with initial conditions of x 0  = 0 and C bias,0  = C bias (0).

$$C_{bias,k + 1} = C_{bias,k} + h \cdot C_{bias}^{\prime } \left( {x_{k} , C_{bias,k} } \right)\;{\text{and}}$$
(12)
$$x_{k} = h \cdot k ,$$
(13)

where h is the uniform step size in x. The series of capacitance values calculated from (12) can then be converted into the finger gaps of the comb by using the curve of Fig. 4, 2D cross-sectional capacitance versus finger gap, calculated by electrostatic numerical analysis with ANSYS®. The geometries of the comb-drive actuators used to create Fig. 4 are summarized in Table 2. This 2D capacitance calculation was conducted for a device structure where a substrate is sufficiently away from the actuator or even eliminated completely underneath the actuator region (see Fig. 8). For a device structure where a grounded substrate is in close proximity to the actuator, the proposed method has to be significantly modified due to the well-known levitation effect (Tang et al. 1992). Even in the case of presence of a grounded substrate nearby, however, the proposed design method can be used with the new calculation of 2D cross-sectional capacitances according to the new device structure if the method with alternating polarity voltage application is adopted (Tang et al. 1992).

Table 1 Parameters of the tunable filter used in the simulation
Full size table
Fig. 4
figure 4

Cross-sectional capacitance versus finger gap, calculated by 2D electrostatic numerical analysis (ANSYS®) with the finger geometries given in Table 2

Full size image
Table 2 Geometrical dimensions and other parameters of the comb-drive actuator used in the simulation
Full size table

In the process of finding optimum finger geometries using (12), h is one of the critical parameters. It is important to use a sufficiently small value for h to find a solution that is close enough to the real solution. If a chosen value for h is too coarse, it will result in λ r –V characteristics deviating far from a straight line. Figure 5 shows the effect of using different values for h to the λ r –V characteristics. Since the λ r –V characteristics, when plotted for the entire range as in Fig. 5a, are not clearly distinguishable from one another except for the case of h = 10 nm, the central region is magnified and presented in Fig. 5b. It shows that 0.01 nm is small enough for h. For the real fabrication of the device with the state-of-the-art equipment, however, h of 0.01 nm is too small to be practical. Instead, the capacitance values and the corresponding finger gaps can be obtained by sampling according to the minimum precision limit of the equipment to be used, from the results with smaller h, such as 0.01 nm.

Fig. 5
figure 5

Calculated tuning characteristics with 2D approximation for various h, step size in x. a Entire range and b central region magnified

Full size image

Other important design parameters are C bias (0) and C bias (x max ), in other words, the finger gaps d bias at the both ends of the gap-varying section. Figure 6 presents the effect of different d bias (0) to the calculated d bias (x) with d bias (x max ) fixed at 50 nm. It shows that the shape of the curve varies according to the value of d bias (0), especially near x max . When d bias (0) is smaller than a certain value, d bias (x) becomes smaller than d bias (x max ) for some range. For the rest of the paper, d bias (0) of 80 nm will be used. Figure 7 shows the calculated finger gaps for the both combs. In the next section, the revised design method will be examined with 3D electrostatic numerical analysis using ANSYS®.

Fig. 6
figure 6

Designed bias comb finger gaps for various d bias (0), calculated with (11)

Full size image
Fig. 7
figure 7

Designed finger gaps for the bias comb (red) and the control comb (blue) (color online)

Full size image

3 3D simulation

The revised design method described in the previous section is still based on an approximation—total 3D capacitance of a comb is approximated by integration of 2D capacitances as in (5) and (6). This approximation, however, ignores fringe fields at the tips of the fingers (indicated by an oval in Fig. 8) as well as the fact that the field lines are not exactly perpendicular to the sidewall of the moving finger. Therefore, it is imperative to investigate the revised method with 3D electrostatic numerical analysis to understand the proximity of the approximation to the real solution. The analysis was conducted with the device geometries given in Fig. 7 and Table 2 by using ANSYS®. Figure 8 shows the calculated field lines of the control comb when x is 0. A symmetric boundary condition—the plane of symmetry is parallel to the sidewall of the moving finger—was used in the simulation to calculate the 3D capacitances, C BIAS,3D (x) and C CTRL,3D (x). Then, the index modulator displacement versus the applied voltage (x–V) characteristics were obtained by using (4) and (8), with an assumption of a linear spring, which is valid since the whole range of displacement is quite small (<300 nm). Figure 9 shows the calculated x–V characteristics, where V bias of 5.74 V was used. These x–V characteristics were combined with the λ r –x characteristics given in the inset of Fig. 2 to produce the λ r –V characteristics which are presented in Fig. 10. Figure 10 also shows the λ r –V characteristics of the one with constant finger gaps (dual comb) for comparison, simulated by the same procedure. The values of the applied voltages in Fig. 10 were normalized with the maximum voltages in order to facilitate the comparison. It is shown that although the device designed with the proposed method does not show perfectly linear λ r –V characteristics, there is a considerable improvement from the conventional design. For quantitative comparison of linearity among different designs, the maximum deviation from linearity (MDL) was calculated as the following equation.

$$MDL = \frac{{\hbox{max} \left( {\left| {\lambda_{real} - \lambda_{ideal} } \right|} \right)}}{{\lambda_{\hbox{max} } - \lambda_{\hbox{min} } }} \times 100 \, \left( \% \right)$$
(14)
Fig. 8
figure 8

Top a solid model and bottom calculated electric field lines of the control comb. Symmetric boundary condition is used. The red oval points out the fringe fields near the moving finger tip (color online)

Full size image
Fig. 9
figure 9

Index modulator displacement versus applied control voltage, calculated by using 3D capacitances. Dimensions and parameters of Table 2 and Fig. 7 are used. V bias  = 5.74 V

Full size image
Fig. 10
figure 10

Tuning characteristics, calculated with 3D capacitances, of one with varying finger gaps (red) and one with constant finger gaps (blue). This was obtained by combining Fig. 9 and the inset of Fig. 2. The black dashed line indicates the ideal straight line (color online)

Full size image

MDL was reduced by 17.2 % points from 25.7 % of the one with constant finger gaps to 8.5 % of the one with the proposed design method.

The linearity can be further improved by making modifications in the design. First, the improvement can be achieved by excluding the sections of the curve near the both ends (Fig. 10) where the deviation from the ideal line is more pronounced. In those end sections, the effect of fringe field around the tip of the moving finger is stronger due to an abrupt transition from the gap-varying section to the constant gap section. Exclusion of those end sections shortens the free spectral range. Therefore, pre-adjustment needs to be made; the gap-varying section has to be slightly extended beyond x max . For instance, the range of the gap-varying section can be extended to 290 nm instead of 286.75 nm. Then, the region of interest can be cut out from the entire range. For example, the range of [30, 287 nm] can be considered out of [0, 290 nm]. Then, the free spectral range can be still maintained to be 11.2 nm as before. This change in the region of interest implies requirement of another (smaller) dc bias to the control comb apart from the original dc bias to the bias comb. In this particular example, 0.6 V of bias needs to be added to the control comb. As can be seen from Fig. 11, this modification reduces MDL from 8.5 to 7.8 %. The shift in the wavelength range caused by shifting of the region of interest is noticeable in Fig. 11, but relatively small.

Fig. 11
figure 11

Tuning characteristics by different design approaches. Red the same as Fig. 10 (varying finger gaps). Green with control bias (shift in the region of interest in x, and therefore, in λ r ) but without the finger gap adjustment. Blue with control bias as well as the finger gap adjustment using (15). The black dashed line indicates the ideal straight line (color online)

Full size image

Second, the linearity can be further improved by adjusting the finger gaps according to the difference between the designed capacitances (C bias and C ctrl ) and the first derivatives of the 3D capacitances (C BIAS,3D and C CTRL,3D ) calculated by the simulation. Following equations are used to recalculate the 2D capacitances (\(C_{bias}^{ * }\) and \(C_{ctrl}^{ * }\)) and then the revised finger gaps.

$$C_{bias}^{*} \left( x \right) = \frac{{\left\{ {C_{bias} \left( x \right)} \right\}^{2} }}{{C^{\prime}_{BIAS,3D} \left( x \right)}},\quad C_{ctrl}^{*} \left( x \right) = \frac{{\left\{ {C_{ctrl} \left( x \right)} \right\}^{2} }}{{C^{\prime}_{CTRL,3D} \left( x \right)}} \,$$
(15)

The idea of this approach is to pre-adjust the finger gaps, taking the difference between the 2D approximation and the real 3D calculation into account. Figure 11 also shows the simulated tuning characteristics by using the revised finger gaps, with a diminution of MDL to 4.4 % (the control bias was also used here).

3.1 Consideration of fabrication limit

One thing that has to be taken into consideration in relation to the realization of the proposed actuator design is the fabrication imperfections. Among various imperfections, in this paper, the precision limit in the lithography tool used is considered. The simulations in the previous sections were conducted with the precision limit of 0.01 nm, which is beyond the capability of the typical tools used currently. Therefore, simulation was repeated with more practical precision limits (1 and 10 nm), i.e. the finger gaps (d bias and d ctrl ) were adjusted by rounding to the precision limits. For instance, 75.43 nm of d ctrl at x = 140 nm was rounded to 75 and 80 nm, respectively. Figures 12 and 13 show d ctrl and simulated tuning characteristics, respectively, for various precision limits. For the simulation, the design with both the control bias and the finger gap adjustment was used. It can be seen that the tuning characteristics with 1 nm precision limit is almost the same as the one with 0.01 nm limit. The effect of much poorer precision limit (10 nm), however, is clearly noticeable. The calculated MDLs for 0.01, 1, and 10 nm precision limit are 4.4, 4.5, and 7.5 %, respectively. Since the state-of-the-art lithography tools have precision limit better than 1 nm, it is considered that substantial effect of the lithography tool precision limit to the linearity of the tuning characteristics can be avoided. However, as the deviation of the finger shapes from the ideal at the order of several nanometers can affect the linearity appreciably, it is crucial to precisely control the fabrication steps to minimize imperfections in order to achieve the desired characteristics.

Fig. 12
figure 12

Control comb finger gaps d ctrl , recalculated according to the precision limit in the lithography tool used in the fabrication. The design with control bias and the finger gap adjustment was used (color online)

Full size image
Fig. 13
figure 13

Effect of the precision limit in the lithography tool used in the fabrication to the tuning characteristics. The design with control bias and the finger gap adjustment was used. Blue the same as Fig. 11. The black dashed line indicates the ideal straight line (color online)

Full size image

4 Conclusion

The revised method of comb-drive actuator design was presented and applied to mechanically tunable optical filters for linear tuning characteristics. The design method was examined by 3D electrostatic numerical analysis. Significant improvement in linearity was achieved with the proposed design method. Methods to obtain further improvement in linearity were discussed as well. The proposed design method can be also used in various applications to achieve specific characteristics, where comb-drive actuators are used.