Effect of rotation on a micropolar magneto-thermoelastic solid in dual-phase-lag model under the gravitational field

Abstract

The purpose of this paper is to study the effect of rotation and gravitational field on a micropolar magneto-thermoelastic solid in the context of the dual-phase-lag model (DPL). The normal mode analysis is used to obtain the exact expressions for displacement components, force stresses, the micro-rotation and temperature. The variations of the considered variables with the horizontal distance are illustrated graphically. Comparisons are made in the presence and absence of rotation, gravity and magnetic field in the context of the dual-phase-lag model and the Lord-Shulman theory.

1 Introduction

The linear theory of micropolar elasticity is introduced to represent the behavior of such materials. For ultrasonic waves, i.e. in the case of elastic vibrations characterized by high frequencies and small wavelengths, the effect of the body microstructure becomes significant. This influence of microstructure results in the development of new types of waves, not found in the classical theory of elasticity. Metals, polymers, composites, soils, rocks, concrete is typical media with microstructures. More generally, most of the natural and man-made materials, including engineering, geological and biological media possess a microstructure. Eringen and Şuhubi (1964a, b) and Eringen (1966) introduce a modern formulation of thermoelasticity equations which became known as the equations of the micropolar theory of elasticity or the theory of asymmetric elasticity. These equations were also developed by (Treusdell and Toupin 1960). Micropolar elasticity was extended to include the thermal effects, Eringen (1970), Nowacki (1966) and Iesan (1968).

(Tzou 1995a, b, 1996) proposed the dual-phase-lag (DPL) model, which describes the interactions between photons and electrons on the microscopic level as retarding sources causing a delayed response on the macroscopic scale. For macroscopic formulation, it would be convenient to use the (DPL) model for investigation of the micro-structural effect on the behavior of heat transfer. The physical meanings and the applicability of the (DPL) model have been supported by the experimental results. The (DPL) proposed by Tzou is such a modification of the classical thermoelastic model in which the Fourier law is replaced by an approximation to a modified Fourier law with two different time translations: a phase-lag of the heat flux $\tau_{q}$ and a phase-lag of temperature gradient $\tau_{\theta }$. A Taylor series approximation of the modified Fourier law, together with the remaining field equations leads to a complete system of equations describing a (DPL) thermoelastic model. The model transmits thermoelastic disturbance in a wavelike manner if the approximation is linear with respect to $\tau_{q}$ and $\,\tau_{\theta }$, and 0 ≤ $\tau_{\theta }$ < $\tau_{q}$; or quadratic in $\tau_{q}$ and linear in $\tau_{\theta }$, with $\tau_{q}$ > 0 and $\tau_{\theta }$ > 0. This theory is developed in a rational way to produce a fully consistent theory which is able to incorporate thermal pulse trans-mission in a very logical manner. The investigation of interaction between a magnetic field, stress, and strain in a thermoelastic solid is very important due to its many applications in the fields of geophysics, plasma physics, and relevant topics, especially in the nuclear field, where the extremely high temperature and temperature gradients, as well as the magnetic fields originating inside nuclear reactors, influence their design and operation. The theory of magneto-thermoelasticity is concerned with the influence of a magnetic field on the elastic and thermoelastic deformations of a solid body. This theory has aroused much interest in recent years, because of its applications in various branches of science and technology.

In the classical theory of elasticity, the gravity effect is generally neglected. The effect of gravity field in the problem of propagation of waves in solids, in particular on an elastic globe, was first studied by Bromwich (1898). Subsequently, an investigation of the effect of the gravity field was discussed by Love (1911), who showed that the velocity of Rayleigh waves increased to a significant extent by gravitational field when wavelengths are large. Othman et al. (2013) studied the influence of gravitational field and rotation on generalized thermoelastic solid with voids under Green-Naghdi theory. One can find some studies on the theory of thermoelasticity by Kumar and Ailawalia (2005a, b), Othman and Atwa (2012) and Othman et al. (2014, 2015).

In this paper, the (DPL) theory is applied to study the influence of the rotation and gravitational field on the plane waves of a linearly magneto-micropolar thermoplastic isotropic medium. Numerical results for the temperature, the displacement components, the normal micro-rotation and the stresses are performed and illustrated graphically. A complete and comprehensive analysis of the results is presented for the (DPL) and (L-S) theories.

2 Formulation of the problem and basic equations

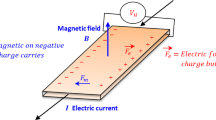
We consider a homogeneous and magneto-micropolar thermoelastic half-space under gravitational field and rotating uniformly with angular velocity $\varvec{\varOmega}= \varOmega \hat{n}$, where $\hat{n}$ is a unit vector representing the direction of the axis of rotation. Schoenberg and Censor (1973) show that, the displacement equation of motion in the rotating frame has two additional terms: the centripetal acceleration $\varvec{\varOmega}\times (\varvec{\varOmega}\times \varvec{u})$ due to the time-varying motion only and the Coriolis acceleration $2\varvec{\varOmega}\times \dot{\varvec{u}}$, where $\varvec{u} = \left( {u,0,w} \right)$ is the dynamic displacement vector, the micro-rotation vector is $\varvec{\phi}= (\text{0},\phi_{2} ,\text{0})$ and $\varvec{\varOmega}= \left( {\text{0},\varOmega ,\text{0}} \right)$ is the angular velocity. A magnetic field with constant intensity is $\varvec{H} = (0,H_{0} ,0),$ (taken as the direction of the y-axis). All quantities considered are functions of the time t and the coordinates $x$ and $z.$.

Let $\varvec{g}$ be the acceleration due to gravity. Here states of initial stress, due to gravity effect, are given by

$$ \left. \begin{aligned} \sigma_{ij} = \chi \,\;;i = j \hfill \\ \quad \,\,{\kern 1pt} = 0\,\;;i \ne j \hfill \\ \end{aligned} \right\} $$

(1.)

Where $\chi$ is a function of $z.$ The equilibrium conditions of initial field are

$$ \chi_{,j} + \rho g\delta_{3j} = 0 $$

(2)

.

The Lorentz force is given by:

$$ \varvec{F}_{i} = \mu_{0} (\varvec{J}{\mathbf{ \times }}\varvec{H})_{i} $$

(3)

.

The system of governing equations and constitutive relation of a linear magneto-micropolar thermoelasticity under the influences of rotation and gravity and without body forces and heat sources in a (DPL) thermoelastic model and in view of Eqs. (1), (2), and (3), take the following form (Eringen 1970; Mukherjee et al. 1991 and Schoenberg and Censor 1973).

2.1 Equations of motion

$$ (\lambda + \mu )\frac{\partial e}{\partial x} + (k + \mu )\nabla^{2} u - \gamma_{1} \frac{\partial T}{\partial x} - k\frac{{\partial \phi_{2} }}{\partial z} + \rho g\frac{\partial w}{\partial x} + F_{1} = \rho [\frac{{\partial^{2} u}}{{\partial t^{2} }} - \varOmega^{2} u + 2\varOmega \frac{\partial w}{\partial t}] $$

(4)

$$ (\lambda + \mu )\frac{\partial e}{\partial z} + (k + \mu )\nabla^{2} w - \gamma_{1} \frac{\partial T}{\partial z} + k\frac{{\partial \phi_{2} }}{\partial x} - \rho g\frac{\partial u}{\partial x} + F_{3} = \rho [\frac{{\partial^{2} w}}{{\partial t^{2} }} - \varOmega^{2} w - 2\varOmega \frac{\partial u}{\partial t}] $$

(5)

$$ \varepsilon_{ijk} \sigma_{jr} + m_{ji,j} = j\rho [\phi_{i,\,tt} + \varOmega \times \phi_{,\,t} ]. $$

(6)

2.2 The constitutive laws

$$ \sigma_{ij} = \lambda u_{r,r} \delta_{ij} + \mu (u_{i,j} + u_{j,i} ) + k(u_{j,i} - \varepsilon_{ijk} \phi_{r} ) - \gamma_{1} T\delta_{ij} $$

(7)

$$ m_{ij} = \alpha \phi_{r,r} \delta_{ij} + \beta \phi_{i,j} + \gamma \phi_{j,\,i} $$

(8)

.

2.3 The generalized heat conduction equation in the DPL model (Tzou 1995a, b)

$$ K(1 + \tau_{\theta } \frac{\partial }{\partial t})T_{,jj} = (\frac{\partial }{\partial t} + \tau_{q} \frac{{\partial^{2} }}{{\partial t^{2} }})(\rho \,C_{E} T + T_{0} \gamma_{1} e) $$

(9)

.

Where $e = \frac{\partial u}{\partial x} + \frac{\partial w}{\partial y}$, $T$ is the temperature above the reference temperature $T_{0}$ chosen so that $\left| {(T - T_{0} )/T_{0} } \right| \ll 1$, $\lambda ,\mu$ are the counterparts of Lame’ constants, $t$ is the time, $\sigma_{ij}$ are the components of the stress tensor, $e$ is the dilatation, $j$ is the micro-inertia moment, $k,\alpha ,\beta ,\gamma$ are the micropolar constants, $m_{ij}$ is the couple stress tensor, $\delta_{ij}$ is the Kronecker delta, $\varepsilon_{ijk}$ is the alternate tensor, $\rho$ is the mass density, $C_{E}$ is the specific heat at the constant strain, $K$ is the thermal conductivity, $\tau_{q}$ is the heat flux parameter, $\tau_{\theta }$ is the temperature gradient parameter and $\gamma_{1} = (3\lambda + 2\mu + k)\alpha_{t} ,$ $\alpha_{t}$ is the linear expansion. The simplified linear equations of electrodynamics for a slowly moving perfectly conducting medium given by Maxwell’s equations

$$ \varvec{J} = \nabla {\mathbf{ \times }}\varvec{h} - \varepsilon_{0} \varvec{E}_{{\varvec{,}t}} $$

(10)

$$ \nabla {\mathbf{ \times }}\varvec{E} = - \mu_{0} \varvec{h}_{,t} $$

(11)

$$ \varvec{E} = - \mu_{0} (\varvec{u}_{{\varvec{,}t}} {\mathbf{ \times }}\varvec{H}) $$

(12)

$$ \nabla \cdot \varvec{h} = 0 $$

(13)

.

Where $\mu_{0}$ is the magnetic permeability, $\varepsilon_{0}$ is the electric permeability, $\varvec{J}$ is the current density vector and $\varvec{u}_{{\varvec{,}t}} s$ is the particle velocity of the medium and the small effect of the temperature gradient on $\varvec{J}$ is also ignored. The dynamic displacement vector is actually measured from a steady state deformed position and the deformation is supposed to be small. Due to the application of the initial magnetic field $\varvec{H},$ there results an induced magnetic field $\varvec{h} = \text{(0,}h\text{,0)},$ and an induced electric field $E,$ as well as the simplified equations of electro-dynamics of slowly moving medium for a homogeneous, thermal and electrically conducting elastic solid. In the above equations a dot denotes differentiation with respect to time, and a comma followed by a subscript denotes partial differentiation with respect to the corresponding coordinates.

Express components of the vector $\varvec{J} = (J_{\text{1}} \text{,}J_{\text{2}} \text{,}J_{\text{3}} )$ in terms of the displacement by eliminating the.

quantities $h$ and $E$ from Eqs. (10)–(13), thus yields

$$ \varvec{J} = H_{0} (\tfrac{\partial e}{\partial z},\,0,\, - \tfrac{\partial e}{\partial x}) - \varepsilon_{0} \tfrac{{\partial \varvec{E}}}{\partial t},\;\;h = - H_{0} {\kern 1pt} e,\;\varvec{E} = - \mu_{0} H_{0} ( - \tfrac{\partial w}{\partial t},0,\tfrac{\partial u}{\partial t}) $$

(14)

Substituting from Eq. (14) in Eq. (3), we get

$$ F_{\text{1}} = - \mu_{0} H_{\text{0}} \frac{\partial h}{\partial x} - \varepsilon_{0} \mu_{0}^{2} H_{\text{0}}^{\text{2}} \frac{{\partial^{2} u}}{{\partial t^{2} }},\;F_{\text{2}} = 0,\;\;F_{3} = - \mu_{0} H_{\text{0}} \frac{\partial h}{\partial z} - \varepsilon_{0} \mu_{0}^{2} H_{\text{0}}^{\text{2}} \frac{{\partial^{2} w}}{{\partial t^{2} }} $$

(15.)

The constitutive equations can be written as

$$ \sigma_{xx} = \lambda e + (2\mu + k)\frac{\partial u}{\partial x} - \gamma_{1} T $$

(16)

$$ \sigma_{zz} = \lambda e + (2\mu + k)\frac{\partial w}{\partial z} - \gamma_{1} T $$

(17)

$$ \sigma_{xz} = \mu \frac{\partial u}{\partial z} + (k + \mu )\frac{\partial w}{\partial x} + k\phi_{2} $$

(18)

$$ \sigma_{zx} = \mu \frac{\partial w}{\partial x} + (k + \mu )\frac{\partial u}{\partial z} - k\phi_{2} $$

(19)

$$ m_{xy} = \gamma \frac{{\partial \phi_{2} }}{\partial x} $$

(20)

$$ m_{zy} = \gamma \frac{{\partial \phi_{2} }}{\partial z} $$

(21.)

For convenience, the following non-dimensional variables are used:

$$ \left( {x^{\prime},{\kern 1pt} \,z^{\prime}} \right) = \frac{{\eta_{0} }}{{C_{0} }}\left( {x,\,z} \right),\;\,\left( {u^{\prime},\,w^{\prime}} \right) = \frac{{\rho \eta_{0} C_{0} }}{{\gamma_{1} T_{0} }}\left( {u,\,w} \right),\;\,\left( {t^{\prime},\,\tau^{\prime}_{q} ,\,\tau^{\prime}_{\theta } } \right) = \eta_{0} \,\left( {t,\,\tau_{q} ,\tau_{\theta } } \right),h^{\prime} = \frac{h}{{H_{0} }},T^{\prime} = \frac{T}{{T_{\text{0}} }},\sigma^{\prime}_{ij} = \frac{{\sigma_{ij} }}{{\gamma_{\text{1}} T_{\text{0}} }},\phi_{2}^{\prime } = \frac{{\rho C_{\text{0}}^{\text{2}} }}{{\gamma_{\text{1}} T_{\text{0}} }}\phi ,\varOmega^{\prime} = \frac{\varOmega }{{\eta_{{_{\text{0}} }} }},m^{\prime}_{ij} = \frac{{\eta_{{_{\text{0}} }} }}{{C_{\text{0}} \gamma_{\text{1}} T_{\text{0}} }}m_{{_{ij} }} ,g^{\prime} = \frac{g}{{C_{0} \eta_{0} }},E^{\prime} = \frac{E}{{\mu_{0} H_{0} C_{0} }},\eta_{0} = \frac{{\rho C_{E} C_{0}^{2} }}{K},C_{0}^{2} = \frac{\mu }{\rho } $$

(22)

Using Eq. (22) into Eqs. (4)–(6) and (9), taking into account that; $\varvec{\varOmega}$ and $\varvec{\phi}$ have the same direction, then $\varvec{\varOmega}\times\varvec{\phi}_{,\,t} = 0,$(dropping the dashed for convenience), we get;

$$ a_{1} \nabla^{2} u + a_{2} \frac{\partial e}{\partial x} - a_{3} \frac{{\partial \phi_{2} }}{\partial z} - \frac{\partial T}{\partial x} + g\frac{\partial w}{\partial x} = (a_{4} \frac{{\partial^{2} u}}{{\partial t^{2} }} - \varOmega^{2} u + 2\varOmega \frac{\partial w}{\partial t}) $$

(23)

$$ a_{1} \nabla^{2} w + a_{2} \frac{\partial e}{\partial z} + a_{3} \frac{{\partial \phi_{2} }}{\partial x} - \frac{\partial T}{\partial z} - g\frac{\partial u}{\partial x} = [a_{4} \frac{{\partial^{2} w}}{{\partial t^{2} }} - \varOmega^{2} w + 2\varOmega \frac{\partial u}{\partial t}] $$

(24)

$$ \nabla^{2} \phi_{2} - a_{5} \phi_{2} + a_{6} (\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}) = a_{7} \frac{{\partial^{2} \phi_{2} }}{{\partial t^{2} }} $$

(25)

$$ (1 + \tau_{\theta } \frac{\partial }{\partial t})\nabla^{2} T = (\frac{\partial }{\partial t} + \tau_{q} \frac{{\partial^{2} }}{{\partial t^{2} }})T + a_{8} (\frac{\partial }{\partial t} + \tau_{q} \frac{{\partial^{2} }}{{\partial t^{2} }})e $$

(26)

where $a_{1} = \frac{\mu + k}{{\rho C_{0}^{2} }},$ $a_{2} = \frac{{\mu + \lambda + \mu_{0} H_{0}^{2} }}{{\rho C_{0}^{2} }},$ $a_{3} = \frac{k}{{\rho C_{0}^{2} }},$ $a_{4} = \frac{{\mu_{0}^{2} H_{0}^{2} \varepsilon_{0} + \rho }}{\rho },$ $a_{5} = \frac{{2kC_{0}^{2} }}{{\gamma \eta_{0}^{2} }},$ $a_{6} = \frac{{kC_{0}^{2} }}{{\gamma \eta_{0}^{2} }},$ $a_{7} = \frac{{j\rho C_{0}^{2} }}{\gamma },$ $a_{8} = \frac{{\gamma_{1}^{2} T_{0} }}{{\rho \eta_{0} K}}.$.

Introducing the scalar and vector potentials $q\left( {x,\,z,\,t} \right)$ and $\psi \left( {x,\,z,\,t} \right)$ defined by

$$ u = \frac{\partial q}{\partial x} + \frac{\partial \psi }{\partial z},\;\quad w = \frac{\partial q}{\partial z} - \frac{\partial \psi }{\partial x} $$

(27.)

Using Eq. (27) into Eqs. (23)–(26), we obtain:

$$ [(a_{1} + a_{2} )\nabla^{2} - a_{4} \frac{{\partial^{2} }}{{\partial t^{2} }} + \varOmega^{2} ]q + (2\varOmega \frac{\partial }{\partial t} - g\frac{\partial }{\partial x})\psi - T = 0, $$

(28)

$$ (a_{1} \nabla^{2} - a_{4} \frac{{\partial^{2} }}{{\partial t^{2} }} + \varOmega^{2} )\psi - (2\varOmega \frac{\partial }{\partial t} - g\frac{\partial }{\partial x})q - a_{3} \phi_{2} = 0, $$

(29)

$$ (\nabla^{2} - a_{5} - a_{7} \frac{{\partial^{2} }}{{\partial t^{2} }})\phi_{2} + a_{6} \nabla^{2} \psi = 0, $$

(30)

$$ [(1 + \tau_{\theta } \frac{\partial }{\partial t})\nabla^{2} - (\frac{\partial }{\partial t} + \tau_{q} \frac{{\partial^{2} }}{{\partial t^{2} }})]\,T = a_{8} (\frac{\partial }{\partial t} + \tau_{q} \frac{{\partial^{2} }}{{\partial t^{2} }})\nabla^{2} q. $$

(31.)

3 Normal mode analysis

The solution of the considered physical variables can be decomposed in terms of normal mode as the following form:

$$ \text{[}u,w,T,\phi_{\text{2}} ,q,\psi ,\sigma_{ij} ,m_{ij} \text{](}x,z,t\text{)} = \text{[}u^{*} ,w^{*} ,T^{*} ,\phi_{\text{2}}^{*} ,q^{*} ,\psi^{*} ,\sigma_{ij}^{*} ,m_{ij}^{*} \text{](}z\text{)}\;exp\text{(}b{\kern 1pt} t + iax\text{)} $$

(32.)

where $[u^{ * } ,w^{ * } ,T^{ * } ,\phi_{2}^{ * } ,q^{ * } ,\psi^{ * } ,\sigma_{ij}^{ * } ,m_{ij}^{ * } ](z)$ are the amplitude of the physical quantities, $b$ is a complex and $a$ is the wave number in the x-direction.

Using Eq. (32), Eqs. (28)–(31), became respectively

$$ (b_{1} \text{D}^{2} - b_{2} )q^{ * } - b_{3} \,\psi^{ * } - T^{ * } = 0 $$

(33)

$$ (a_{1} \text{D}^{2} - b_{4} )\psi^{ * } + b_{3} \,q^{ * } - a_{3} \phi_{2}^{ * } {\kern 1pt} = 0 $$

(34)

$$ (\text{D}^{2} - b_{5} )\phi_{2}^{ * } + a_{6} ({\text{D}}^{2} - a^{2} )\psi^{ * } = 0 $$

(35)

$$ (b_{6} \text{D}^{2} - b_{9} )T^{ * } - b_{8} (\text{D}^{2} - a^{2} )q^{ * } = 0 $$

(36.)

where $\text{D = }\tfrac{\text{d}}{{\text{dz}}},$ $b_{1} = a_{1} + a_{2} ,$ $b_{2} = b_{1} a^{2} + a_{4} b^{2} - \varOmega^{2} ,$ $b_{3} = iag - 2\varOmega b,$ $b_{9} = b_{6} a^{2} + b_{7} ,$ $b_{4} = a_{1} a^{2} + a_{4} b^{2} - \varOmega^{2} ,$ $b_{5} = a^{2} + a_{5} + a_{7} b^{2} ,$ $b_{6} = 1 + \tau_{\theta } b,$ $b_{7} = b + \tau_{q} b^{2} ,$ $b_{8} = a_{8} b_{7} .$.

Eliminating $\phi_{2}^{ * } ,\psi^{ * } ,q^{ * }$ and $T^{ * }$ between Eqs. (33)–(36) we obtain:

$$ (\text{D}^{\text{8}} - A\,\text{D}^{\text{6}} \text{ + }B\,\text{D}^{\text{4}} - C\,\text{D}^{\text{2}} + F)\{ q^{ * } (z),\psi^{ * } (z),\phi_{2}^{ * } (z),T^{ * } (z)\} = 0 $$

(37.)

Where $s_{1} = b_{1} b_{6} ,$ $s_{2} = b_{1} b_{9} + b_{2} b_{6} + b_{8} ,$ $s_{3} = b_{2} b_{9} + a^{2} b_{8} ,$ $s_{4} = a_{1} b_{5} + b_{4} - a_{3} a_{6} ,$ $s_{6} = b_{3}^{2} b_{6} ,$ $s_{5} = b_{4} b_{5} - a_{3} a_{6} a^{2} ,$ $s_{7} = b_{3}^{2} (b_{5} b_{6} + b_{9} ),$ $s_{8} = b_{3}^{2} b_{5} b_{9} ,$ $r = \tfrac{1}{{s_{1} a_{1} }},$ $A = r(s_{1} s_{4} + s_{2} a_{1} ),$ $B = r(s_{1} s_{5} + s_{2} s_{4} + s_{3} a_{1} + s_{6} ),$ $C = r(s_{2} s_{5} + s_{3} s_{4} + s_{7} ),$ $F = r(s_{3} s_{5} + s_{8} ).$.

Equation (37) can factored as

$$ (\text{D}^{2} - k_{1}^{2} )(\text{D}^{2} - k_{2}^{2} )(\text{D}^{2} - k_{3}^{2} )(\text{D}^{2} - k_{4}^{2} )\{ \psi^{ * } (z),\,\,q^{ * } (z),\,\,\phi_{2}^{ * } (z),\;T^{ * } (z)\} = 0 $$

(38)

.

where $k_{n}^{2} \,(n = 1, \,2,\,3,\,4)$ are the roots of the characteristic equation of Eq. (38).

The solutions of Eq. (37), bounded as $(z \to \infty )$ are given by

$$ (\psi^{ * } ,\phi_{2}^{ * } ,q^{ * } ,T^{ * } )(z) = \sum\limits_{n = 1}^{4} {(1,H_{1n} ,H_{2n} ,H_{3n} )M_{n} \exp ( - k_{n} z)} $$

(39)

.

Substituting from Eq. (39) into Eq. (27) we obtain the components of displacements

$$ u^{ * } (z) = \sum\limits_{n = 1}^{4} {M_{n} H_{4n} \exp ( - k_{n} z)} $$

(40)

$$ w^{ * } (z) = \sum\limits_{n = 1}^{4} {M_{n} H_{5n} \exp ( - k_{n} z)} $$

(41)

Substituting from Eq. (22) in Eqs. (16)–(21) and with the help of Eqs. (39)–(41) we obtain the components of stresses and tangential couple stress

$$ (\sigma_{xx}^{ * } ,\sigma_{zz}^{ * } ,\sigma_{xz}^{ * } ,\sigma_{zx}^{ * } )(z) = \sum\limits_{n = 1}^{4} {(H_{6n} ,H_{7n} ,H_{8n} ,H_{9n} )M_{n} \exp ( - k_{n} z)} $$

(42)

$$ m_{xy}^{ * } (z) = \sum\limits_{n = 1}^{4} {\frac{{\gamma \eta_{0}^{2} }}{{\rho C_{0}^{4} }}iaM_{n} H_{1n} \exp ( - k_{n} z)} $$

(43)

$$ m_{zy}^{ * } (z) = \sum\limits_{n = 1}^{4} {\frac{{ - \;\gamma \eta_{0}^{2} }}{{\rho C_{0}^{4} }}k_{n} M_{n} H_{1n} \exp ( - k_{n} z)} $$

(44)

where $M_{n} (n = 1,2,3,4)$ are some parameters and:

$$\begin{aligned}H_{1n} &= \frac{{ - \;a_{6} (k_{n}^{2} - a^{2} )}}{{k_{n}^{2} - b_{5} }}, \quad H_{2n} = (b_{4} + a_{3} H_{1n} - a_{1} k_{n}^{2} )/b_{3}, \\ H_{3n} &= \frac{{b_{8} (k_{n}^{2} - a^{2} )H_{2n} }}{{b_{6} k_{n}^{2} - b_{9} }}, \quad H_{4n} = iaH_{2n} - k_{n}, \\ H_{5n} &= - k_{n} H_{2n} - ia, \quad H_{6n} = \frac{k + 2\mu }{{\rho C_{0}^{2} }}iaH_{4n} + \frac{{\lambda (k_{n}^{2} - a^{2} )}}{{\rho C_{0}^{2} }}H_{2n} - H_{3n}, \\ H_{7n} &= \frac{{\lambda (k_{n}^{2} - a^{2} )}}{{\rho C_{0}^{2} }}H_{2n} - \frac{k + 2\mu }{{\rho C_{0}^{2} }}k_{n} H_{5n} - H_{3n}, \quad H_{8n} = \frac{1}{{\rho C_{0}^{2} }}[ia(\mu + k)H_{5n} - \mu k_{n} H_{4n} + kH_{1n} ], \\ H_{9n} &= \frac{1}{{\rho C_{0}^{2} }}[ia\mu H_{5n} - (\mu + k)k_{n} H_{4n} - kH_{1n} ].\end{aligned}$$

.

4 The boundary conditions

In order to determine the parameters $M_{n} (n = 1,\,2\,,3\,,4)$ we need to consider the boundary conditions at $z = 0$ as follows:

a) Thermal boundary condition as:

$$ T = p_{1} \,\exp (bt + iax) $$

(45.)

b) Mechanical boundary condition as:

$$ \sigma_{xx} = - p_{2} \exp (bt + iax),\;\sigma_{xz} = 0,\quad m_{xy} = 0 $$

(46)

where $p_{1}$ is the magnitude of thermal source and $p_{2}$ is the magnitude of mechanical force.

Substituting the expression of the variables considered into the above boundary conditions, we can obtain the following equations satisfied by the parameters $M_{n} (n = 1,\,2\,,3\,,4)$ as:

$$ \sum\limits_{n = 1}^{4} {H_{3n} M_{n} = p_{1} } $$

(47)

$$ \sum\limits_{n = 1}^{4} {H_{6n} M_{n} = } \; - p_{2} $$

(48)

$$ \sum\limits_{n = 1}^{4} {H_{8n} M_{n} } = 0 $$

(49)

$$ \sum\limits_{n = 1}^{4} {H_{1n} M_{n} = 0} $$

(50)

To get the values of the constants$M_{n} (n = 1,\ldots,4)$ , solving Eqs. (47)–(50) for $M_{n} (n = 1,\ldots,4)$ by using the inverse of matrix method as follows:

$$ \left( \begin{aligned} M_{1} \hfill \\ M_{2} \hfill \\ M_{3} \hfill \\ M_{4} \hfill \\ \end{aligned} \right) = \left( \begin{aligned} H_{31} \quad H_{32} \quad \;H_{33} \quad \;H_{34} \hfill \\ H_{61} \;\;\,\;H_{62} \quad \;H_{63} \quad \;H_{64} \hfill \\ H_{81} \quad H_{82} \quad \,\;H_{83} \quad \,H_{84} \hfill \\ H_{11} \,\;\,\,\,H_{12} \;\,\quad H_{13} \;\;\,\,\,\,H_{14} \hfill \\ \end{aligned} \right)^{ - 1} \left( \begin{aligned} p_{1} \hfill \\ - p_{2} \hfill \\ \;\,\,0 \hfill \\ \;\,\,0 \hfill \\ \end{aligned} \right) $$

(51.)

5 Numerical results and discussions

The analysis is conducted for a magnesium crystal-like material. Following reference Eringen (1984), the values of physical constants are $T_{0} = 298K^{ \circ } ,$ $k = 1.0 \times 10^{10} Nm^{ - 2} ,$ $\gamma = 0.779 \times 10^{ - 9} N,$ $\lambda = 9.4 \times 10^{10} Nm^{ - 2} ,\mu = 4.0 \times 10^{10} Nm^{ - 2} ,$ $C_{E} = 1.04 \times 10^{3} \;kg\;m^{ - 3} ,$ $\rho = 1.74 \times 10^{3} \;kg/m^{3} ,$ $j = 0.2 \times 10^{ - 15} m^{2} ,$ $\alpha_{t} = 7.4033 \times 10^{ - 7} K^{ - 1} ,$ $K = 1.7 \times 10^{2} Jm^{ - 1} s^{ - 1} \deg^{ - 1} ,$ $b = b_{0} + i\,\xi ,$ $b_{0} = 1.9,$ $\xi = 1,$ $a = 0.6,$ $p_{1} = p_{2} = 3.$.

Where $\,b_{0}$ is the complex time constant. The computations are carried out for the non-dimensional time $\,t = 0.2$, and on the surface plane $\,x = 0.2$. The numerical technique outlined above is used for the distribution of the real part of the non-dimensional displacements u, the non-dimensional temperature T, the distributions of non-dimensional stresses $\sigma_{xx}$,$\sigma_{xz}$, the non-dimensional micro-rotation $\phi_{2}$ and the non-dimensional couple stress $m_{xy}$ for the problem. To study the effects of the gravity, the rotation and the magnetic field on the solutions, we now present our results of the numerical evaluation in the form of graphs.

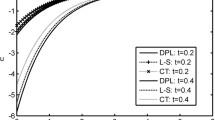
The Figs. 1, 2, 3, 4, 5, 6 are plotted to show the variation of the above quantities against the distance z in both the (L-S) and (DPL) models for ($g = 0,\,\,9.8$) where, the solid lines represent results for the (DPL) model for $g = 0,\,$ the large dash line represent results for the (DPL) model for $g = 9.8$, the large dashes line with dot represent results for the (L-S) theory for $g = 0$, the small dashes line represent results for the (L-S) theory for $g = 9.8.$ In Fig. 1 the thermal displacement u is plotted against the distance z, it is observed that the displacement u for $g = 9.8$ begin from positive and begin from negative for $\,g = 0$. It is clear that the values of solutions for the (L-S) model and the (DPL) model in the case of $g = 9.8$ are large in comparison with those for $g = 0$ in the range $\,0 \le z \le 2.5$; small in the range $\,2.5 \le z \le 4.2$; while the values are the same for two cases as $\,z \ge 4.2$. Figure 2 exhibits the distribution of the temperature $T$ and demonstrates that it begins from positive values. In the context of the two theories, the values of the temperature $T$ increase in the beginning to a maximum value in the range $\,0 \le z \le 0.4$, then decrease to a minimum value in the range $\,0.4 \le z \le 4$, and also move in wave propagation. Figure 3 displays that the distribution of the stress component $\sigma_{xx}$ always begins from negative values for $g = 0$. It is clear that the values of solutions for the (L-S) model and the (DPL) model in the case of $g = 9.8$ are small in comparison with those for $g = 0$ in the range $0 \le z \le 1.8;$ large in the range $\,1.8 \le z \le 4$; while the values are the same for the two cases as $\,z \ge 4$. Figure 4 shows the distribution of the stress component $\sigma_{xz}$ against the distance z, this figure indicates that the all curves start from the zero at $z = 0,$ which agrees with the boundary conditions. It is clear that the values of solutions for the (L-S) model and the (DPL) model in the case of $g = 9.8$ are large in comparison with those for $g = 0$ in the range $\,0 \le z \le 1.2$; small in the range $\,1.2 \le z \le 3.4$; while the values are the same for two cases as $\,z \ge 3.4$. Figure 5 depicts the variation of the normal micro-rotation $\phi_{2}$ against the distance z, from this figure we see that, the all curves start from the same value (zero) at $z = 0$ for $g = 0$. It is clear that the values of solutions for the (L-S) model and the (DPL) model in the case of $g = 9.8,$ being small in comparison with those for $g = 0$ in the range $\,0 \le z \le 7.5$; while the values are the same for two cases as $z \ge 7.5.$ Fig. 6 exhibits the values of the tangential couple stress $m_{xy}$ against the distance z; this figure shows that all the curves start from the zero at $z = 0,$ which agree with the boundary conditions for $g = 0$. It is clear that the values of solutions for the (L-S) model and the (DPL) model in the case of $g = 9.8$ are large in comparison with those for $g = 0$ in the range $0 \le z \le 2.4$; small in the range $2.4 \le z \le 5,$ while the values are the same for two cases as $z \ge 5.$.

Fig. 1

The thermal displacement u against horizontal distance $z$

Fig. 2

The temperature T against horizontal distance $z$

Fig. 3

The normal stresses $\sigma_{xx}$ with horizontal distance $z$

Fig. 4

The tangential stresses $\sigma_{xz}$ with horizontal distance $z$

Fig. 5

The micro-rotation $\phi_{2}$ with horizontal distance $z$

Fig. 6

The couple stress $m_{xy}$ with horizontal distance $z$

Figures 7, 8, 9, 10, 11, 12 show comparisons among the displacement component u, the temperature T, and the force stress components $\sigma_{xx} ,$ $\sigma_{xy}$, the micro-rotation $\phi_{2}$ and the couple stress $m_{xy}$ for different values of $\varOmega$($\varOmega = \text{0,}\;\text{ 0}\text{.5}$) in the presence of the gravity $g = 9.8$ and magnetic field $H_{0} = 100$.

Fig. 7

The thermal displacement u with horizontal distance $z$

Fig. 8

The temperature T with horizontal distance $z$

Fig. 9

The normal stresses $\sigma_{xx}$ with horizontal distance $z$

Fig. 10

The tangential stresses $\sigma_{xz}$ with horizontal distance $z$

Fig. 11

The micro-rotation $\phi_{2}$ with horizontal distance $z$

Fig. 12

The couple stress $m_{xy}$ with horizontal distance $z$

Figure 7 explains that the distribution of the horizontal displacement u against the distance z and in all two theories (DPL) and (L-S), the values of the horizontal displacement u for ($\varOmega =$ 0) are large compared to those for $\varOmega = \text{0}\text{.5}$ in the range $\text{0} \le z \le 0.6$; small in the range $\,0.6 \le z \le 2.4$; large in the range $\,2.4 \le z \le 4.4$; while the values are the same for two theories as $\,z \ge 4.4$.

Figure 8 exhibits the distribution of temperature $T$ against the distance z; this figure shows the similar behaviors as those in Fig. 2. In Fig. 9 the stress component $\sigma_{xx}$ begins from a negative values for ($\varOmega = \text{0,}\;\text{ 0}\text{.5}$) and it is clear that, the values of stress component $\sigma_{xx}$ for ($\varOmega = \text{0}$) are large compared to those for ($\varOmega = \text{0}\text{.5}$) in the range $\,\text{0} \le z \le 2.2,$ but small in the range $\,2.2 \le z \le 4$; while the values are the same for two theories at $\,z \ge 4$. Figure 10 displays that the distribution of the stress component $\sigma_{xz}$ with distance $z$ for ($\varOmega = \text{0, 0}\text{.5}$), and the values of stress component $\sigma_{xz}$ for ($\varOmega = \text{0}$) are small compared to those for $\text{(}\varOmega = \text{0}\text{.5)}$ in the range $\text{0} \le z \le 1.8$; large in the range $1.8 \le z \le 3.4$; small in the range $3.4 \le z \le 5.2$; while the values are the same for two theories as $z \ge 5.2$. Figure 11 depicts the variation of the normal micro-rotation $\phi_{2}$ against the distance z, from this figure we see that, all curves start from the same value at $z = 0$ then decreases to maximum value in the range $0 \le z \le 2$ after that increases until attaining zero, and the values of normal micro-rotation $\phi_{2}$ for ($\varOmega = \text{0}$) are large compared to those for ($\varOmega = \text{0}\text{.5}$) in the range $0 \le z \le 4$; while the values are the same for two cases as $z \ge 4$. Figure 12 exhibits the variations of the tangential couple stress $m_{xy}$ against the distance z; this figure shows that, all curves start from the zero at $z = 0,$ which agree with the boundary conditions. In the context of the two theories, the values of the tangential couple stress $m_{xy}$ for ($\varOmega = \text{0}$) are small compared to those for ($\varOmega = \text{0}\text{.5}$) in the range $\,\text{0} \le z \le 2.4$; large in the range $2.4 \le z \le 4.8$ while the values are the same for two theories as $z \ge 4.8.$.

Figures 13, 14, 15, 16, 17, 18 show comparisons among the displacement component u, the temperature T, and the force stress components $\sigma_{xx} ,$ $\sigma_{xy}$ the micro-rotation $\phi_{2}$ and the couple stress $m_{xy}$ for different values of $H_{0}$($H_{0} = 0,\;100$) in the presence of the rotation and gravity $\varOmega = \text{0}\text{.5,}$ $g = 9.8.$ Fig. 13 depicts that the distribution of the horizontal displacement $u,$ in the context of the two theories, begins from positive values. In the context of the two theories, $u$ increases to a maximum value in the range $\text{0} \le z \le 1$ then decreases to a minimum value in the range $\,1 \le z \le 3$, and moves in wave propagation. Figure 14 demonstrates that the temperature $\,T$ begins from positive values. In the context of the two theories, $\,T$ increases to a maximum value in the range $\,0 \le z \le 0.3$, then decreases to a minimum value in the range $\,0.3 \le z \le 3$, while the values are the same for the two cases as $z \ge 3,$ also, this figure shows the similar behaviors as those in Fig. 2. Figure 15 displays that the distribution of the stress component $\sigma_{xx}$ always begins from negative values for ($H_{0}$ = 0, 100). In the context of the two theories, $\sigma_{xx}$ decreases to a minimum value in the range $0 \le z \le 0.5$ then increases to a maximum value in the range $0.5 \le z \le 2.5,$ while the values are the same for two theories as $z \ge 2.5.$ Fig. 16 investigates the distribution of the stress component $\sigma_{xz}$ against the distance z, this figure shows that, all curves start from the zero at $z = 0,$ which agrees with the boundary conditions, and for the two cases all curves move in wave propagation. Figure 17 exhibits the variation of the normal micro-rotation $\phi_{2}$ against the distance $z,$ the all curves start from the zero at $z = 0.$ In the context of the two theories, $\phi_{2}$ decreases to a minimum value in the range $0 \le z \le 1.7$ then increases to a maximum value in the range $2.5 \le z \le 3.8,$ while the values are the same for two theories at $z \ge 3.8.$ Fig. 18 explains the distribution of the tangential couple stress $m_{xy}$ against the distance z, this figure shows that all the curves start from the zero at $z = 0,$ which agree with the boundary conditions. In the context of the two theories, the values of the tangential couple stress $m_{xy}$ for ($H_{0}$ = 0, 100) increases to a maximum value in the range $0 \le z \le 0.9$ then decreases to a minimum value in the range $0.9 \le z \le 3$ while the values are the same for two theories as $z \ge 3.$.

Fig. 13

The thermal displacement u with horizontal distance $z$

Fig. 14

The temperature T with horizontal distance $z$

Fig. 15

The normal stresses $\sigma_{xx}$ with horizontal distance $z$

Fig. 16

The tangential stresses $\sigma_{xz}$ with horizontal distance $z$

Fig. 17

The micro-rotation component $\phi_{2}$ with horizontal distance $z$

Fig. 18

The couple stress $m_{xy}$ with horizontal distance $z$

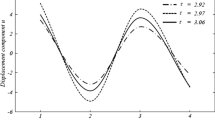
Figure 19 is giving 3D surface curves for the normal micro-rotation $\phi_{2}$ for the thermal shock problem in the presence of rotation, magnetic field and gravity at $t = 0.2,$ in the context of the (DPL) theory. This figure is very important to study the dependence of these physical quantities on the vertical component of distance. The curves obtained are highly depending on the vertical distance from origin, all the physical quantities are moving in wave propagation.

Fig. 19

Distribution of micro-rotation $\phi_{2}$ against both components of distance based on dual-phase-lag theory

6 Conclusions

According to the above results, we can conclude that:

• The rotation, the magnetic field and the gravity have a significant effect on all the field quantities.

• The comparison of the different theories of thermoelasticity, i.e. (L-S) theory and (DPL) model is carried out.

• Deformation of the body depends on the nature of the applied force as well as the type of boundary conditions.

• Analytical solutions based upon normal mode analysis for thermoelastic problem in solids have been developed and utilized.

• All the curves converge to zero as distance from surface of medium increases; this satisfies the condition for surface wave propagation.