Deformation in a micropolar material under the influence of Hall current and initial stress fields in the context of a double-temperature thermoelastic theory involving phase lag and higher orders

Abstract

This work aims to propose a generalized micropolar thermoelastic model for the study of semisolid space. Essentially, it is intended to develop the generalized theory of thermoelasticity combined with the framework of a linear two-temperature theory to present the thermal and mechanical analysis of micropolar magneto-thermoelastic media influenced by initial stress. The higher-order derivatives thermoelasticity model has been applied to establish the model based on two-phase lags under the influence of magnetic Hall current. The normal mode analysis technique was used to solve specific boundary-value problems in the applied theory of magneto-thermostatic micropolar systems. The constitutive equations are constructed, and two distinct temperatures are obtained, respectively, conductive temperature and thermodynamic temperature, as well as displacements, partial rotation, thermal stresses and couple stresses. In addition, the critical values of the physical parameters of the Hall current and initial stress are determined, as is their influence on the wave fields, and the characteristics of such media are determined. Some points of interest highlighting the effects of the magnetic Hall current in the current context have been completed. A comparison was made between different models of thermoelastic theories of higher-order time derivatives.

1 Introduction

Micropolar continuum mechanics is a scientific discipline concerned with the mechanics of vector objects whose primitive elements (in the rough sense) consist of solid particles. In contrast to classical continuum mechanics, intrinsic orientations and rotational inertia connect the physical points of a micropolar continuum. From a physical point of view, each physical point (or particle) in a micropolar continuum is phenotypically equivalent to a small solid body. Therefore, the rotation of nearby particles is taken into account independently. It should be noted that the gap between general mechanics and the strength of materials has been narrowed by the introduction of independent translations, rotations and similarities between classical mechanics force couples, moment strength and stresses in continuum mechanics [1].

For a homogeneous material in classical elasticity, we should know two Lamé moduli, whereas, in the linear micropolar elasticity of isotropic solids, the material is determined by six material parameters. Three degrees of freedom are translational, as in classic elasticity, and the other three are orientational or rotational. These additional degrees of freedom are believed to provide the proper physical mechanism to discuss and predict certain phenomena inherently due to the granular and molecular nature of materials. Micropolar theory applications are found, and more are expected in the fields of composite materials, liquid crystals, granular solids, etc. It is of current and emerging interest to mechanicians, physicians, materials scientists and engineers, as its limits and possibilities are not fully established, which is a severe application constraint. The micropolar theory addressed here is primarily based on the efforts of Eringen and colleagues. Eringen introduced the laws of equilibrium in 1962 [2], and the complete approach was published as a particular case of a general idea of microelasticity by Eringen and Suhubi in 1964 [3]. Eringen [4] also introduced the theory of micropolar elasticity, discussed the complex microstructure and derived the constitutive relations of the micropolar medium. Also, Eringen and Nowacki extended the micropolar idea by including thermal effects [5, 6]. Boschi and Ieşan (1973) established a general theory of micropolar linear thermoelasticity that acknowledges the possibility of "second sound" effects [7].

Dost and Tabarrok [8] used the Green–Lindsay theory to present another generalized micropolar thermoelasticity model. Pouget et al. [9] used the micropolar theory to calculate the micropolar elastic moduli of other ferroelectric crystals. Based on the entropy inequality of Green and Laws [10], Scalia came up with a micropolar theory of thermoelasticity that is grade-consistent and has holes in it. Ciarletta et al. [11, 12] investigated plane waves and vibration theory in void-distributed micropolar thermoelasticity. Deswal and Kalkal have recently analyzed plane wave propagation in a fractional-order micropolar magneto-thermoelastic medium [13]. Marin and Florea [14] considered the temporal behavior of solutions in the thermoelasticity of porous micropolar bodies. Othman et al. [15] investigated the effect of rotation on a micropolar thermoelastic medium with a void problem. Also, Othman et al. [16, 17] used normal mode analysis to study the effect of rotation on micropolar generalized thermoelasticity with two temperatures using a dual-phase-lag and three-phase-lag model. Fahmy et al. [18] proposed a new boundary element modeling technique to simulate and optimize three-temperature micropolar magneto-thermo-viscoelastic problems in anisotropic porous intelligent structures. Recently, it is worth mentioning that one can refer to Othman et al. [19], Singh and Kaur [20], Meline et al. [21] and Sheoran et al. [22] for their efforts and their overview of utilizing micropolar materials in scientific research and their applications as well.

Any vibrating structure experienced a change in internal energy due to the strain field, with compressed regions becoming hotter (assuming a positive coefficient of thermal expansion) and stretched parts becoming cooler. The consequent lack of thermal balance between various components of the vibrating structure is the reason for thermoelastic damping. Energy dissipates when the temperature gradient causes irreversible heat flow. Duhamel first discussed this heat phenomenon in elasticity [23], and one can call it the classical thermoelasticity theory. In this theory, the equations of motion or equilibrium contain the temperature term, but the heat conduction equation is independent of the strain field, which contradicts the physical experiments. In 1938, Zener [24] studied the thermoelastic damping phenomenon. He looked at thermoelastic damping in vibrating beams due to flexural forces. A thermal imbalance results from the alternating tensile and compressive strains that flexural vibrations generate on the opposite sides of the neutral axis. Vibrational energy is lost due to irreversible heat transfer that is brought on by temperature gradients.

The concept of uncoupled thermoelasticity theory was developed when Biot [25] introduced the coupled thermoelastic theory. This theory consists of two coupled partial differential equations, one of which is hyperbolic and the other is parabolic. Due to the nature of the parabolic-type equation, this theory predicts an infinite speed for heat propagation; that is, if a material conducting heat is subjected to thermal disturbance, the effects of the disturbance will be felt instantaneously at distances infinitely far from the source. This prediction is unrealistic from a physical point of view, particularly for problems like those concerned with sudden heat inputs. To remove the contradiction in the paired Biot theory, the traditional theories of thermal elasticity have been generalized in the sense that these theories include a hyperbolic heat transfer equation. Experiments support these models and show the occurrence of heat transfer wave types in solids. To eliminate the second sound paradox of classical thermoelasticity theory, Lord and Shulman [26] established a generalized thermoelasticity theory based on the Maxwell and Cattaneo–Vernotte heat conduction equation in 1958 [27, 28], which is often referred to as the Lord–Shulman (LS) model and is widely used in the case of high heat flux and low temperature. Green and Lindsay [29] introduced another theory, the GL theory, which involves two relaxation times. Later, Green and Naghdi [30,31,32] later developed three models for generalized thermoelasticity of homogeneous isotropic materials, labeled as GN models I, II and III. Detailed information regarding these theories can be found in Chandrasekharaiah [33].

The following generalization of thermoelasticity is known as the dual-phase-lag (DPL) model developed by Tzou [33]. He considered microstructural effects on the delayed response in macroscopic formulation by assuming that the lattice temperature is delayed due to phonon electron interactions at the macroscopic level. Two-phase lags [34] were introduced to both the heat flux vector and the temperature gradient and used as constitutive equations to describe lagging behavior in solid heat conduction. The photothermal interactions in semiconductor microbeams during the photo-thermoelastic process have been investigated using the generalized photothermal theory by Zakaria et al. [35]. It must be noted that some previous models have been generalized and many studies have been presented in this field [36,37,38,39,40,41,42,43], which can be said to have a strong trend in opening horizons for researchers interested in the field of thermoelasticity.

Initial stress is defined by pressures already present or developed in a medium before being studied. The earth is an initially stressed medium because of external loading, gravitational field, weight, overburden layer, hydrostatic tension or compression and largeness, differential external forces and so on. Incorporating initial stresses in wave reflection, transmission and propagation studies is essential due to their impacts on the different reactions of considered materials. Initial stress is inevitable due to machining, non-uniform material properties, quenching processes, enhancing fracture toughness, shrinkage and growth during processing and cooling down to operating or room temperature, slow creep deformation, thermal or chemical influences, etc. Also, prestress is imposed on layered piezoelectric structures during manufacturing processes to prevent brittle fracture, which may lead to microcracking, degradation, debonding and delamination of the considered layer. As a result, it is critical to thoroughly investigate the effects of initial stresses, as has been done by several eminent researchers [44,45,46,47,48,49,50,51,52]. However, it is found from most of the previous work in the extant literature that only the influences of normal initial stresses were taken into consideration. But in reality, initial stresses affect the considered structures from all sides and are not just normal. During the second half of the twentieth century, great attention was devoted to studying combined and coupled electro-magneto-thermoelastic problems based on generalized thermoelastic theories.

The study of electro-magneto-thermoelastic interactions deals with the interactions among strain, temperature and electromagnetic fields in a thermoelastic material. It is of great practical importance due to its extensive uses in diverse fields, such as geophysics, damping of acoustic waves in a magnetic field, designing machine elements like heat exchangers and boiler tubes where temperature-induced elastic deformation occurs, biomedical engineering (problems involving thermal stress), emissions of electromagnetic radiation from nuclear devices, development of a highly sensitive superconducting magnetometer, electrical power engineering and plasma physics. Using computational analysis, Abouelregal et al. [53] investigated a magneto-thermoelastic problem for an isotropic, perfectly conducting half-space medium. Tiwari et al. [54] have studied the non-local behavior of a magnetically permeated piezoelectric half-space in the context of three-phase lag heat conduction with a memory-dependent derivative. A new modified heat conduction model with fractional order that includes the Caputo–Fabrizio differential operator (CF) and the thermal relaxation time has been established by Abouelregal et al. [55].

In the late 1960s, Chen and Gurtin [56] and Chen et al. [57] formulated what soon became known as the two-temperature theory. This theory proposes that heat conduction in a material body depends upon two distinct temperatures: the conductive temperature and the thermodynamic temperature. Under certain conditions, both of these two temperatures are equal. However, for time-dependent problems, particularly those involving wave propagation, they are generally different. In this theory, the two temperatures refer to the electron temperature and the lattice temperature. Electron temperature: This represents the average energy of the electrons in the material. When a heat pulse interacts with a material, it can cause rapid heating of the electrons due to their strong interaction with the electromagnetic field. The electron temperature describes the energy distribution among the electrons and characterizes their thermal behavior. Lattice temperature refers to the average power of the atoms or ions that make up the material's crystal lattice. While the heat pulse can rapidly heat the electrons, the energy transfer to the lattice occurs slower due to the weaker interaction between the lattice and the heat field. Therefore, the lattice temperature typically remains lower than the electron temperature. The two-temperature theory describes the non-equilibrium dynamics that occur during heat-material interactions. It allows for understanding phenomena such as ultrafast heating and cooling processes, energy transfer between the electrons and lattice and the subsequent relaxation of the system toward thermal equilibrium. It is worth noting that this theory has been applied in many thermoelastic studies in recent years and has given distinguished results [58, 59].

If an electric current flows through a conductor in a magnetic field, the magnetic field exerts a transverse force on the moving charge carriers, which tends to push them to one side of the conductor. This is most evident in a thin, flat conductor, as illustrated. A buildup of charge at the sides of the conductors will balance this magnetic influence, producing a measurable voltage between the two sides of the conductor. The presence of this measurable transverse voltage is called the Hall effect after Edwin H. Hall, who discovered it in 1879 [60].

After describing the discovery and early history of the Hall effect, it is worth mentioning that it played a vital role in developing theories of electronic conduction; the application of the Hall effect to semiconductor research is discussed. Experimental techniques for measuring the Hall coefficient and the procedures for interpreting the results are described. Also, it is shown that the Hall effect provides a valuable tool for measuring magnetic flux density and for several other applications where other electronic devices are less suitable. Lata and Singh [61] investigated the Stoneley wave propagation at the interface of two dissimilar homogeneous non-local magneto-thermoelastic media under the effect of Hall current applied to multi-dual-phase-lag heat transfer. The development of initial stress on a thermoelastic porous medium with a microtemperature in the presence of a magnetic field, taking Hall current into account, is studied by Othman and Abd-Elaziz [62].

In the present work, an extensive study was carried out that included synthesizing many theories related to thermoelasticity and micropolarity and integrating them into a single generalized thermal model. Through this model, many critical physical problems in scientific research, especially biological studies, as well as the fabrication process of microdevices, engineering and micro/nanostructures in medicine and technology, can be addressed. The introduced model also included formulating the governing equations for a thermoelastic model for a micropolar semisolid material in the context of the two-temperature DPL with higher-order time-derivative concepts. The general solution to the system equations was obtained using the normal mode approach. A micropolar magnesium material that was subjected to initial stress and a magnetic field's influence was used to study the mathematical model. The numerical analysis was presented by plotting the data as a function of several physical parameters, such as the initial stress and the magnetic Hall parameter. Finally, a comparison of various thermoelasticity theory models was conducted, and the outcomes of the current model were evaluated in light of earlier research in the same field.

2 Mathematical formulation and basic equations

Eringen was the first to present the mathematical equations for the micropolar thermoelastic system [4, 5]. By accounting for the initial stress and two temperatures, the governing equations are [63]:

$$ \sigma_{ij} = \lambda u_{k,k} \delta_{ij} + \mu \left( {u_{j,i} + u_{i,j} } \right) + k_{0} \left( {u_{j,i} - \varepsilon_{ijk} \phi_{k} } \right) - \gamma_{1} \theta \delta_{ij} - S\left( {\delta_{ij} + \omega_{ij} } \right), $$

(1)

$$ m_{ij} = \alpha \phi_{k,k} \delta_{ij} + \beta \phi_{i,j} + \gamma \phi_{j,i} , $$

(2)

$$ \varepsilon_{ij} = \frac{1}{2}\left( {u_{j,i} + u_{i,j} } \right), \omega_{ij} = \frac{1}{2}\left( {u_{j,i} - u_{i,j} } \right). $$

(3)

In the above equations, $\sigma_{ij}$ stands for stress tensor, $\omega_{ij}$ the rotation tensor, $u_{i}$ the displacement components, $\phi_{k}$ the microrotation components, $\phi_{ji}$ the microcurvature tensor, $m_{ij}$ the couple stress components, $\alpha$, $\beta ,$ $\gamma$ and $k_{0}$, are micropolar material parameters, $\lambda$, and $\mu$ are Lame’s constants, $\varepsilon_{ijk}$ alternate tensor, $\delta_{ij}$ the Kronecker delta, $\varepsilon_{ij}$ strain-tensor, $\theta = T - T_{0}$ the thermodynamic temperature from the reference temperature $T_{0}$, and $\gamma_{1} = \left( {3\lambda + 2\mu + k_{0} } \right)\alpha_{t}$.

It can be shown that the equations for motion and couple stress have the following forms:

$$ \sigma_{ij,j} + F_{i} = \rho \mathop u\limits^{..}_{i} , $$

(4)

$$ \varepsilon_{ijk} \sigma_{jk} + m_{ji,j} = \rho j\ddot{\phi }_{,i}\quad i,j,k = 1,2,3, $$

(5)

where $\rho$ the density and $j$ the microinertia coefficient.

By using Eqs. (1) and (2) in (4) and (5), one can get

$$ \left( {\mu + k_{0} } \right)\nabla^{2} {\vec{\text{u}}} + \left( {\lambda + \mu } \right)\nabla \left( {\nabla .{\vec{\text{u}}}} \right) + k_{0} \nabla \times \vec{\phi } - \gamma_{1} \nabla \theta + \vec{F} = \rho \frac{{\partial^{2} {\vec{\text{u}}}}}{{\partial t^{2} }}, $$

(6)

$$ \left( {\alpha + \beta + \gamma } \right)\nabla \left( {\nabla .\vec{\phi }} \right) - \gamma \nabla \times \left( {\nabla \times \vec{\phi }} \right) + k_{0} \nabla \times \vec{u} - 2k_{0} \vec{\phi } = \rho j\frac{{\partial^{2} \vec{\phi }}}{{\partial t^{2} }}. $$

(7)

The energy equation can be written as follows:

$$ \rho C_{E} \frac{\partial \theta }{{\partial t}} + \gamma_{1} T_{0} \frac{\partial }{\partial t}\left( {{{div\vec{u}}}} \right) = - \nabla .\vec{H} + \rho Q, $$

(8)

where $C_{E}$ denotes the specific heat while the strain is held constant, and ${\vec{\text{H}}}$ denotes the heat flow density. Fourier's law states that the rate of heat transport through a substance depends on the internal heat gradient. It can be written in mathematical form as:

$$ {\vec{\text{H}}}\left( {{\vec{\text{r}}},t} \right) = - K\nabla \theta \left( {{\vec{\text{r}}},t} \right), $$

(9)

where $K$ represents the heat conductivity and ${\vec{\text{r}}}$ represents the position vector.

In heat transfer theory, conductive temperature, symbolically represented by $\varphi$, is a fundamental concept in those non-simple materials in which the temperature dispersion is not uniform and helps describe the temperature field. But in thermodynamics, a key idea known as thermodynamic temperature $\theta$ relates temperature to the kinetic energy of particles. This temperature ($\theta$) is considered a technique to determine the average thermal energy of the molecules that make up the system.

It should be mentioned that the assumed equality of conduction temperature $\varphi$ and the thermodynamic temperature $\theta$ was canceled out for the two-temperature theory by Gurtin and Williams in their proposed papers published in 1966 and 1967 [64, 65]. By considering the two-temperature concepts, Ahmadi [66] introduced a new modified formula of the conventional Fourier law (9) to be

$$ {\vec{\text{q}}}\left( {{\vec{\text{x}}},t} \right) = - K\nabla \varphi \left( {{\vec{\text{x}}},t} \right). $$

(10)

Conduction and thermodynamic temperature domains are related by:

$$ \varphi - \theta = a\nabla^{2} \varphi , $$

(11)

where $a > 0$ is a formative factor (two-temperature parameter). The key element that sets the two-temperature theory apart from the classical theory is the material parameter $(a > 0)$. Specifically, in the limit as $a \to 0$, $\varphi \to \theta$ and the classical theory is recovered. Specifically, in the limit as $a \to 0, \varphi \to \theta$ and the classical theory is recovered.

Under specific circumstances, there may be a disparity between the conductive heat temperature and the thermodynamic temperature. A single temperature often regulates the process of heat conduction, whereas a separate temperature controls the provision of heat. However, the equality of these two temperatures might no longer be true in the case of a non-simple material because the conductive temperature and its spatial variations affect the thermodynamic properties. The distinction between conductive heat and thermodynamic temperatures has special significance within the realm of thermal conductivity research. Thermal conductivity measurement, a material property, is commonly conducted using electricity as an indirect indicator since direct measurement of heat movement is not feasible. Hence, the dissimilarity between the conductive heat and thermodynamic temperatures can vary based on the material and the measuring methodology.

Building on the concepts of the two-temperature theories, Quintanilla [67] and Mukhopadhyay et al. [68] presented a modified version of Fourier's law by keeping in mind the idea of the time delays as follows:

$$ {\vec{\text{H}}}\left( {{\vec{\text{r}}},t + \tau_{q} } \right) = - K\nabla \varphi \left( {{\vec{\text{r}}},t + \tau_{\varphi } } \right), $$

(12)

where the parameters $\tau_{q}$ and $\tau_{\varphi }$ are the heat flux phase and the conductive temperature gradient lags, respectively.

The Taylor series expansion method will be applied independently to each side of Eq. (12) on the phase delays $\tau_{q}$ and $\tau_{\varphi }$ until the terms $l$ and $n$ reach a sufficiently high order to obtain [69]

$$ \left( {1 + \mathop \sum \limits_{r = 1}^{l} \frac{{\tau_{q}^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\vec{q} = - K\left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\tau_{\varphi }^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla \varphi . $$

(13)

When the energy Eq. (8) is combined with the modified Fourier Eq. (13), the optimized formula for the higher-order heat transfer model at two temperatures is as follows:

$$ K\left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\tau_{\varphi }^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \varphi = \left( {1 + \mathop \sum \limits_{r = 1}^{l} \frac{{\tau_{q}^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\left( {\rho C_{E} \frac{\partial \theta }{{\partial t}} + \gamma_{1} T_{0} \frac{\partial }{\partial t}\left( {{{div\vec{u}}}} \right) - \rho Q} \right). $$

(14)

The use of higher orders $m$ and $n$ has several restrictions, as demonstrated by Chiriţă et al. [70,71,72], such as when $l \ge 5$ results in an unstable system that cannot describe an actual physical characteristic. When the approximation orders are fewer than or equal to four, it is necessary to consider whether the second law of thermodynamics is in effect.

The simplified linear equations of the electromagnetic theory (Maxwell’s equations) for a solid with homogeneous and isotropic, thermally, and electrical properties can be written as:

$$ \begin{array}{*{20}c} {\nabla \times \vec{h} = \vec{J} + \frac{{\partial \vec{D}}}{\partial t},{ }\nabla \times \vec{E} = - \frac{{\partial \vec{B}}}{\partial t},\nabla \cdot \vec{B} = 0,{ }} \\ {\nabla \cdot \vec{D} = \rho_{e} ,{ }\vec{D} = \varepsilon_{0} \vec{E},{ }\vec{B} = \mu_{0} \left( {\vec{H}_{0} + \vec{h}} \right).} \\ \end{array} $$

(15)

The following formula represents modified Ohm's law for medium with finite conductivity, which includes the Hall current effect [73]:

$$ \vec{J} = \frac{{\sigma_{0} }}{{1 + m^{2} }}\left[ {\vec{E} + \mu_{0} \frac{{\partial {\vec{\text{u}}}}}{\partial t} \times \left( {\vec{H}_{0} + \vec{h}} \right) - \frac{{\mu_{0} }}{{e_{c} n_{e} }}\vec{J} \times \left( {\vec{H}_{0} + \vec{h}} \right)} \right], $$

(16)

where

$$ \sigma_{0} = \frac{{e_{c}^{2} n_{e} t_{e} }}{{m_{e} }},{ }\omega_{e} = \frac{{e_{c} \mu_{0} H_{0} }}{{m_{e} }},{ }m = \omega_{e} t_{e} . $$

(17)

In Eqs. (15–17), $\vec{B}$ is the total magnetic field vector, $\vec{h}$ is the induced magnetic field vector, $\vec{J}$ is the current density vector, $\vec{E}$ denotes the electric field intensity tensor, $\vec{D}$ represents the electric displacement vector, $\mu_{0}$ is the magnetic permeability, $\rho_{e}$ indicates the charge density, $\varepsilon_{0}$ is the electric permittivity, $\vec{H}_{0}$ is the externally applied magnetic field vector, $\sigma_{0}$ is the electric conductivity, $t_{e}$ symbolizes the electron collision time, $e_{c}$ denotes the electron charge, $m$ is the Hall parameter, $n_{e}$ is the electron number density, $\omega_{e}$ designates the electron frequency, $m_{e}$ signifies the electron mass and $t_{e}$ is the electron collision time.

In Eq. (16), the term $\frac{{\sigma_{0} }}{{1 + m^{2} }}{\vec{\text{E}}}$ denotes the electric field contribution to the current density. It follows the original Ohm's law, where the conductivity $\sigma_{0}$ determines the proportionality between the electric field and the resulting current density, and the term $\frac{{\sigma_{0} \mu_{0} }}{{1 + m^{2} }}\frac{{\partial \vec{u}}}{\partial t} \times \left( {{\vec{\text{H}}}_{0} + {\vec{\text{h}}}} \right)$ represents the Hall effect contribution to the current density. It accounts for the cross product of the time derivative of the charge carrier velocity and the total magnetic field (the sum of the applied magnetic field and any additional magnetic field). This term captures the deflection of charge carriers due to the Lorentz force acting on them in the presence of a magnetic field, resulting in the Hall current. Finally, the term $\frac{{\sigma_{0} \mu_{0} }}{{\left( {1 + m^{2} } \right)e_{c} n_{e} }}{\vec{\text{J}}} \times \left( {{\vec{\text{H}}}_{0} + {\vec{\text{h}}}} \right)$ represents the contribution of the Hall current to the current density. It accounts for the cross product of the current density and the total magnetic field. This term describes the feedback effect of the Hall current itself on the current density distribution.

In summary, this modified Ohm's law accounts for the effects of both the applied electric field and the magnetic field, including the Hall current and its feedback on the current density in a medium with finite conductivity.

When $E = 0$ inside the conductor, there is no contradiction, because this assertion is valid for stationary charges where $J = 0$. Moreover, for perfect conductors $E = J/\sigma = 0$ even if current is flowing. In practice, metals are such good conductors that the electric field required to drive current in them is negligible. Thus, we routinely treat the connecting wires in electric circuits as equipotential.

3 Problem formulation

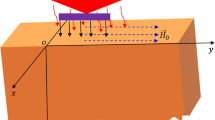
In the current section, we suppose a semi-spaced area filled with polar homogeneous refractory material. The reference temperature is $T_{0}$ throughout the entire medium. Additionally, it was assumed that the boundary of a traction-free, heat-exposed material at $z = 0$ would eventually cause the $2L$ bandwidth to become smaller next to the $x$-axis. For simplicity, Cartesian coordinates ($x,y,z$) will be used to investigate the problem, assuming that its origin is at the top of the plane at $z = 0$ and that the z-axis is usually halfway deep. All particles in a line perpendicular to the $y$-axis are displaced by the same amount when considering planar waves in the plane. For this reason, changes in the direction of the y-coordinate will be ignored, and all fields studied will be functions in the variables $x$, $z$ and $t$ only.

The components of the displacement and microrotation vectors will be described by the following expressions under the circumstances above:

$$ u_{x} = u\left( {x,z,t} \right),\quad u_{y} = 0,{ }u_{z} = w\left( {x,z,t} \right),\quad \vec{\phi } = \left( {0,\phi \left( {x,z,t} \right),0} \right). $$

(18)

Therefore, the expression for dilatation $e = e_{kk}$ in the $x$–$z$ plane is given by

$$ e = e_{kk} = {\text{div}}\left( {{\vec{\text{u}}}} \right) = \varepsilon_{xx} + \varepsilon_{zz} = \frac{\partial u}{{\partial x}} + \frac{\partial w}{{\partial z}}. $$

(19)

A tremendously strong magnetic field $\vec{H}_{0} = \left( {0,H_{0} ,0{ }} \right)$ has been applied along the positive $y$-axis and perpendicular to the plane surface. Because of this uniform magnetic field and the assumption $E = 0$, the modified Ohm’s law (Eq. (16)) gives $J_{y} = 0$ everywhere in the medium. Then the current density $\vec{j}$ components by using Maxwell’s Eqs. (15) can be written in the formula:

$$ \vec{j} = \left( {J_{x} ,J_{y} ,J_{y} } \right) = \frac{{\sigma_{0} \mu_{0} H_{0} }}{{1 + m^{2} }}\left( {m\frac{\partial u}{{\partial t}} - \frac{\partial w}{{\partial t}},0,\frac{\partial u}{{\partial t}} + m\frac{\partial w}{{\partial t}}} \right). $$

(20)

The point charge under the influences of the electromagnetic fields is exposed to an electric and magnetic force called the Lorentz force. By using Eqs. (15–17), one can find the Lorentz force components as follows:

$$ \vec{F} = \left( {F_{x} ,F_{y} ,F_{z} } \right) = \frac{{\sigma_{0} \mu_{0}^{2} {\text{H}}_{0}^{2} }}{{1 + m^{2} }}\left( { - m\frac{\partial w}{{\partial t}} - \frac{\partial u}{{\partial t}},0,m\frac{\partial u}{{\partial t}} - \frac{\partial w}{{\partial t}}} \right). $$

(21)

In the case of situations involving two dimensions, the equations of motion (6) and equilibrium momentum (7) are simplified to

$$ \left( {\lambda + \mu + \frac{S}{2}} \right)\frac{\partial e}{{\partial x}} + \left( {\mu + k_{0} - \frac{S}{2}} \right)\nabla^{2} u + k_{0} \frac{\partial \phi }{{\partial z}} - \frac{{\sigma_{0} \mu_{0}^{2} {\text{H}}_{0}^{2} }}{{1 + m^{2} }}\left( {m\frac{\partial w}{{\partial t}} + \frac{\partial u}{{\partial t}}} \right) = \rho \frac{{\partial^{2} u}}{{\partial t^{2} }} + \gamma_{1} \frac{\partial \theta }{{\partial x}}, $$

(22)

$$ \left( {\lambda + \mu + \frac{S}{2}} \right)\frac{\partial e}{{\partial z}} + \left( {\mu + k_{0} - \frac{S}{2}} \right)\nabla^{2} w - k_{0} \frac{\partial \phi }{{\partial x}} + \frac{{\sigma_{0} \mu_{0}^{2} {\text{H}}_{0}^{2} }}{{1 + m^{2} }}\left( {m\frac{\partial u}{{\partial t}} - \frac{\partial w}{{\partial t}}} \right) = \rho \frac{{\partial^{2} w}}{{\partial t^{2} }} + \gamma_{1} \frac{\partial \theta }{{\partial z}}, $$

(23)

$$ \gamma \nabla^{2} \phi + k_{0} \left( {\frac{\partial u}{{\partial z}} - \frac{\partial w}{{\partial x}}} \right) - 2k_{0} \phi = \rho j\frac{{\partial^{2} \phi }}{{\partial t^{2} }}. $$

(24)

The higher-order heat transport Eq. (14) with two unequal temperatures can be considered as follows:

$$ K\left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\tau_{\varphi }^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \varphi = \left( {1 + \mathop \sum \limits_{r = 1}^{m} \frac{{\tau_{q}^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\left( {\rho C_{E} \frac{\partial \theta }{{\partial t}} + \gamma_{1} T_{0} \frac{\partial e}{{\partial t}}} \right). $$

(25)

In a two-dimensional problem, the constitutive relations (1) and (2) in the $x$–$z$ plane can be reduced to

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{zz} } \\ {\sigma_{yy} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\lambda + 2\mu + k_{0} } & \lambda & { - \gamma_{1} } \\ \lambda & {\lambda + 2\mu + k_{0} } & { - \gamma_{1} } \\ \lambda & \lambda & { - \gamma_{1} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ {\frac{\partial w}{{\partial z}}} \\ \theta \\ \end{array} } \right] - S\left[ {\begin{array}{*{20}c} 1 \\ 1 \\ 1 \\ \end{array} } \right], $$

(26)

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{zx} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mu + \frac{S}{2}} & {\mu + k_{0} - \frac{S}{2}} & {k_{0} } \\ {\mu + k_{0} - \frac{S}{2}} & {\mu + \frac{S}{2}} & { - k_{0} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial w}{{\partial x}}} \\ {\frac{\partial u}{{\partial y}}} \\ \phi \\ \end{array} } \right], $$

(27)

$$ \left[ {\begin{array}{*{20}c} {m_{xy} } \\ {m_{zy} } \\ \end{array} } \right] = \gamma \left[ {\begin{array}{*{20}c} {\frac{\partial \phi }{{\partial x}}} \\ {\frac{\partial \phi }{{\partial z}}} \\ \end{array} } \right], $$

(28)

$$ \varphi - \theta = a\nabla^{2} \varphi ,{ }\nabla^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }} + \frac{{\partial^{2} }}{{\partial z^{2} }}. $$

(29)

Under any boundary conditions that can be imposed, the problem of solving fundamental differential equations can be resolved. The thermally semi-elastic zone with an initially stressed surface that is susceptible to a band of time-dependently fluctuating temperature will be taken into consideration in the current study. This micropolar half-space body is $2L$ wide and affects a small area surrounding the $x$-axis. In light of this, the following boundary conditions will be supposed:

The mechanical boundaries conditions

$$ \sigma_{zz} \left( {x,z,t} \right) = \sigma_{xz} \left( {x,z,t} \right) = 0\;{\text{at}}\;z = 0, $$

(30)

$$ m_{xy} \left( {x,z,t} \right) = 0{\text{ at }}z = 0. $$

(31)

Boundary conditions related to the temperature at the free surface

$$ \varphi \left( {x,z,t} \right) = \varphi_{0} H\left( {L - \left| x \right|} \right){\text{exp}}\left( { - bt} \right){\text{a}}t{ }z = 0, $$

(32)

where $\varphi_{0}$ represents a constant function, and $H\left( . \right)$ represents the well-known Heaviside unit step function. This equation also reveals that the width of the applied thermal and mechanical shock is $2L$ on a surface that is half the area of the x-axis but that its value is zero elsewhere. This is because the shock width decreases with increasing distance from the origin.

4 Dimensionless system of equations

Through the use of dimensionless variables, the PDE control system can be converted into equations without any measurable quantities. Let us define some dimensionless variables to facilitate discussion:

$$ \begin{array}{*{20}c} {\left\{ {x^{\prime},z^{\prime}} \right\} = \frac{{\omega^{*} }}{{c_{1} }}\left\{ {x,z} \right\}, \left\{ {u^{\prime},w^{\prime}} \right\} = \frac{{\rho c_{1} \omega^{*} }}{{\gamma_{1} T_{0} }}\left\{ {u,v} \right\}, \left\{ {t^{\prime},\tau_{q}{\prime} ,\tau_{\varphi }{\prime} } \right\} = \omega^{*} \left\{ {t,\tau_{q} ,\tau_{\varphi } } \right\},} \\ {\left\{ {\theta^{\prime},\varphi^{\prime}} \right\} = \frac{\gamma }{{\rho c_{1}^{2} }}\left\{ {\theta ,\varphi } \right\},\sigma_{ij}{\prime} = \frac{{\sigma_{ij} }}{{\gamma_{1} T_{0} }}, m_{ij}{\prime} = \frac{{\omega^{*} }}{{c_{1} \gamma_{1} T_{0} }}m_{ij} , \phi{\prime} = \frac{{\rho c_{1}^{2} }}{{\gamma_{1} T_{0} }}\phi , } \\ \end{array} $$

(33)

where $c_{1}^{2} = \frac{{\lambda + 2\mu + k_{0} }}{\rho }$ and $\omega^{*} = \frac{{\rho c_{1}^{2} C_{E} }}{K}$.

By deleting primes from Eqs. (22–25) and applying Eq. (33), we obtain the following non-dimensional equations:

$$ \left( {\lambda + \mu + \frac{S}{2}} \right)\frac{\partial e}{{\partial x}} + \left( {\mu + k_{0} - \frac{S}{2}} \right)\nabla^{2} u + k_{0} \frac{\partial \phi }{{\partial y}} - \frac{M}{{1 + m^{2} }}\left( {m\frac{\partial w}{{\partial t}} + \frac{\partial u}{{\partial t}}} \right) = \rho c_{1}^{2} \frac{{\partial^{2} u}}{{\partial t^{2} }} + \rho c_{1}^{2} \frac{\partial \theta }{{\partial x}}, $$

(34)

$$ \left( {\lambda + \mu + \frac{S}{2}} \right)\frac{\partial e}{{\partial z}} + \left( {\mu + k_{0} - \frac{S}{2}} \right)\nabla^{2} w - k_{0} \frac{\partial \phi }{{\partial x}} + \frac{M}{{1 + m^{2} }}\left( {m\frac{\partial u}{{\partial t}} - \frac{\partial w}{{\partial t}}} \right) = \rho c_{1}^{2} \frac{{\partial^{2} w}}{{\partial t^{2} }} + \rho c_{1}^{2} \frac{\partial \theta }{{\partial z}}, $$

(35)

$$ \gamma \nabla^{2} \phi + \frac{{c_{1}^{2} k_{0} }}{{\omega^{*} }}\left( {\frac{\partial u}{{\partial z}} - \frac{\partial w}{{\partial x}}} \right) - \frac{{2c_{1}^{2} k_{0} }}{{\omega^{*} }}\phi = \rho c_{1}^{2} j\frac{{\partial^{2} \phi }}{{\partial t^{2} }}, $$

(36)

$$ \left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\tau_{\varphi }^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \varphi = \left( {1 + \mathop \sum \limits_{r = 1}^{l} \frac{{\tau_{q}^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\left( {\frac{\partial \theta }{{\partial t}} + g\frac{\partial e}{{\partial t}}} \right), $$

(37)

where $g = \frac{{\gamma_{1}^{2} T_{0} }}{{\rho \omega^{*} Kc_{1}^{2} }}$ and $M = \frac{{\sigma_{0} \left( {\mu_{0} H_{0} } \right)^{2} }}{{\omega^{*} \rho c_{1}^{2} }}$.

Additionally, in a similar way, by utilizing (33), the non-dimensional constitutive Eqs. (26–29) can be expressed as

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{zz} } \\ {\sigma_{yy} } \\ \end{array} } \right] = \frac{1}{{\rho c_{1}^{2} }}\left[ {\begin{array}{*{20}c} {\lambda + 2\mu + k_{0} } & \lambda & { - 1} \\ \lambda & {\lambda + 2\mu + k_{0} } & { - 1} \\ \lambda & \lambda & { - 1} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial x}}} \\ {\frac{\partial w}{{\partial z}}} \\ \theta \\ \end{array} } \right], $$

(38)

$$ \left[ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{zx} } \\ \end{array} } \right] = \frac{1}{{\rho c_{1}^{2} }}\left[ {\begin{array}{*{20}c} \mu & {\mu + k_{0} } & {k_{0} } \\ {\mu + k_{0} } & \mu & { - k_{0} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\frac{\partial u}{{\partial z}}} \\ {\frac{\partial w}{{\partial x}}} \\ \phi \\ \end{array} } \right], $$

(39)

$$ \left[ {\begin{array}{*{20}c} {m_{xy} } \\ {m_{zy} } \\ \end{array} } \right] = \frac{{\rho c_{1}^{2} \gamma }}{{K^{2} }}\left[ {\begin{array}{*{20}c} {\frac{\partial \phi }{{\partial x}}} \\ {\frac{\partial \phi }{{\partial z}}} \\ \end{array} } \right], $$

(40)

$$ \varphi - \theta = a_{1} \nabla^{2} \varphi , $$

(41)

where $a_{1} = \frac{{c_{1}^{2} }}{{\eta^{2} }}a$.

There are a significant number of differential equations as well as field variables, so it is possible to introduce the potential functions ${\Phi }\left( {x,y,t} \right)$ and ${\vec{\Psi }}\left( {x,y,t} \right)$, both of which are determined by the relations

$$ {\vec{\text{u}}} = \nabla {\Phi } + \nabla \times {\vec{\Psi }}, {\vec{\Psi }} = \left( {0,0,{\Psi }} \right). $$

(42)

Using (42), the displacement components $u\left( {x,y,t} \right)$ and $w\left( {x,y,t} \right)$ can be expressed as:

$$ u = \frac{{\partial {\Phi }}}{\partial x} + \frac{{\partial {\Psi }}}{\partial z},\;w = \frac{{\partial {\Phi }}}{\partial z} - \frac{{\partial {\Psi }}}{\partial x}. $$

(43)

By inserting Eq. (43) into Eqs. (34–37), we can derive the corresponding system of equations:

$$ \left( {\beta_{1}^{2} \nabla^{2} - \frac{{\partial^{2} }}{{\partial t^{2} }} - \frac{{M^{2} }}{{1 + m^{2} }}\frac{\partial }{\partial t}} \right){\Phi } = \theta - \frac{{mM^{2} }}{{1 + m^{2} }}\frac{{\partial {\Psi }}}{\partial t}, $$

(44)

$$ \left( {\beta_{2}^{2} \nabla^{2} - \frac{{\partial^{2} }}{{\partial t^{2} }} + \frac{{M^{2} }}{{1 + m^{2} }}\frac{\partial }{\partial t}} \right){\Psi } = - \frac{{k_{0} }}{{\rho c_{1}^{2} }}\phi + \frac{{mM^{2} }}{{1 + m^{2} }}\frac{{\partial {\Phi }}}{\partial t}, $$

(45)

$$ \left( {\nabla^{2} - \beta_{3}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }} - 2k_{0} } \right)\phi = - k_{0} \nabla^{2} {\Psi ,} $$

(46)

$$ \left( {1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\tau_{\varphi }^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\nabla^{2} \varphi = \left( {1 + \mathop \sum \limits_{r = 1}^{l} \frac{{\tau_{q}^{r} }}{r!}\frac{{\partial^{r} }}{{\partial t^{r} }}} \right)\left( {\frac{\partial \theta }{{\partial t}} + g\frac{\partial }{\partial t}\nabla^{2} {\Phi }} \right), $$

(47)

where

$$ \beta_{1}^{2} = \frac{{\lambda + 2\mu + k_{0} - \frac{S}{2}}}{{\rho c_{1}^{2} }},{ }\beta_{2}^{2} = \frac{{\mu + k_{0} - \frac{S}{2}}}{{\rho c_{1}^{2} }}{ },{ }\beta_{3}^{2} = \frac{\rho j}{\gamma }.{ } $$

(48)

5 Method of solution

To address system Eqs. (44–47), according to boundary constraints (30–32), we assume that the studied field variables that are being examined can be prescribed as:

$$ \left( {\theta ,\varphi ,u,v,\sigma_{ij} , \Phi ,m_{ij} , \Psi ,\omega } \right) = \left( {\overline{\theta },\overline{\varphi },\overline{u},\overline{v},\overline{\sigma }_{ij} ,\overline{\Phi },\overline{m}_{ij} ,\overline{\Psi },\overline{\phi }} \right)\left( z \right)\exp \left( {i\zeta x + \varpi t} \right), $$

(49)

where $\varpi$ represents the complex unchanging angular frequency, and $\zeta$ represents the wave number parallel to the longitudinal x-axis, respectively. The quantities $\overline{\theta }$, $\overline{\varphi }$, $\overline{u}$, $\overline{v}$, $\overline{\sigma }_{ij}$, ${\overline{\Phi }}$, ${\overline{\Psi }}$ and $\overline{\phi }$ are all indefinite magnitude functions in the variable $z$ only. These variables are entirely distinct from the time t and the location $x$.

It is possible to construct the following equations by inserting Eq. (49) into Eqs. (44–47)

$$ \left( {D^{2} - L_{1} } \right)\overline{\Phi } = \frac{1}{{\beta_{1}^{2} }}\overline{\theta } - L_{2} \overline{\Psi }, $$

(50)

$$ {\text{L}}_{4} {\overline{\Phi }} = \left( {{\text{D}}^{2} - {\text{L}}_{3} } \right){\overline{\Psi }} + {\text{L}}_{5} \overline{\phi }, $$

(51)

$$ \left( {D^{2} - L_{6} } \right)\overline{\phi } = - k_{0} \left( {D^{2} - \zeta^{2} } \right)\overline{\Psi }, $$

(52)

$$ \left( {D^{2} - \zeta^{2} } \right)\overline{\varphi } = {\text{L}}_{7} \left( {\overline{\theta } + g\left( {D^{2} - \zeta^{2} } \right){\overline{\Phi }}} \right), $$

(53)

$$ \overline{\theta } = - \left( {a_{1} D^{2} - a_{1} \zeta^{2} - 1} \right)\overline{\varphi }, $$

(54)

where

$$ \begin{array}{*{20}c} {{\text{L}}_{1} = \frac{1}{{\beta_{1}^{2} }}\left( {\beta_{1}^{2} \zeta^{2} - \varpi^{2} - \frac{{M^{2} \varpi }}{{1 + m^{2} }}} \right),{\text{ L}}_{2} = \frac{1}{{\beta_{1}^{2} }}\left( {\frac{{\varpi mM^{2} }}{{1 + m^{2} }}} \right),{\text{L}}_{3} = \frac{1}{{\beta_{2}^{2} }}\left( {\beta_{1}^{2} \zeta^{2} - \varpi^{2} - \frac{{M^{2} \varpi }}{{1 + m^{2} }}} \right),{ }} \\ {{\text{L}}_{4} = \frac{1}{{\beta_{2}^{2} }}\left( {\frac{{\varpi mM^{2} }}{{1 + m^{2} }}} \right), {\text{L}}_{5} = \frac{{k_{0} }}{{\beta_{2}^{2} \rho c_{1}^{2} }}, {\text{L}}_{6} = \zeta^{2} + \beta_{3}^{2} \varpi^{2} - 2k_{0} , {\text{ L}}_{7} = \frac{{\varpi L_{q} }}{{L_{\varphi } }}, } \\ {L_{q} = 1 + \mathop \sum \limits_{r = 1}^{l} \frac{{\varpi^{r} \tau_{q}^{r} }}{r!}, L_{\varphi } = 1 + \mathop \sum \limits_{r = 1}^{n} \frac{{\varpi^{r} \tau_{\varphi }^{r} }}{r!}, {\text{D}} = \frac{d}{dz}.} \\ \end{array} $$

(55)

We may simplify Eqs. (50–54) to get the following differential equation of the eighth order:

$$ \left( {D^{8} - \eta_{1} D^{6} - \eta_{2} D^{4} + \eta_{3} D^{2} - \eta_{4} } \right)\left\{ {\overline{\theta },\overline{\varphi },{\overline{\Phi }},{\overline{\Psi }},\overline{\phi }} \right\}\left( z \right) = 0, $$

(56)

where

$$ \begin{array}{*{20}c} {\eta_{1} = \displaystyle\frac{{\beta_{1}^{2} \alpha_{3} + \beta_{1}^{2} \alpha_{6} + \alpha_{4} a_{1} + \alpha_{6} \alpha_{4} }}{{\beta_{1}^{2} + \alpha_{4} a_{1} }}, \eta_{2} = \displaystyle\frac{{\beta_{1}^{2} \alpha_{6} \alpha_{3} + \beta_{1}^{2} \alpha_{7} + \zeta^{2} \alpha_{6} \alpha_{4} + \alpha_{10} \alpha_{4} }}{{\beta_{1}^{2} + \alpha_{4} a_{1} }},} \\ {\eta_{3} = \displaystyle\frac{{\alpha_{3} \beta_{1}^{2} \alpha_{7} + \beta_{1}^{2} \alpha_{8} + \zeta^{2} \alpha_{10} \alpha_{4} + \alpha_{11} \alpha_{4} }}{{\beta_{1}^{2} + \alpha_{4} a_{1} }}, \eta_{4} = \displaystyle\frac{{\alpha_{3} \beta_{1}^{2} \alpha_{8} + \zeta^{2} \alpha_{11} \alpha_{4} }}{{\beta_{1}^{2} + \alpha_{4} a_{1} }} ,} \\ \end{array} $$

(57)

with

$$ \begin{array}{*{20}c} {\alpha_{1} = L_{6} + L_{3} + k_{0} { }L_{5} ,\alpha_{2} = L_{6} L_{3} + \zeta^{2} k_{0} { }L_{5} ,\alpha_{3} = \frac{{\zeta^{2} + \zeta^{2} a_{1} { }L_{7} + L_{7} }}{{1 + a_{1} { }L_{7} }},} \\ {\alpha_{4} = \frac{{gL_{7} }}{{1 + a_{1} { }L_{7} }}, \alpha_{5} = \zeta^{2} a_{1} + 1,\alpha_{6} = L_{1} + \alpha_{1} ,\alpha_{7} = L_{1} \alpha_{1} + \alpha_{2} + L_{2} L_{4} , } \\ {\alpha_{8} = L_{1} \alpha_{2} + L_{2} L_{4} L_{6} ,\alpha_{9} = \alpha_{5} + a_{1} \alpha_{1} ,\alpha_{10} = \alpha_{5} \alpha_{1} + a_{1} \alpha_{2} ,\alpha_{11} = \alpha_{5} \alpha_{2} .} \\ \end{array} $$

(58)

By satisfying the consistency criteria, the solutions of Eq. (56) can be written as, where $\overline{\theta }$, $\overline{\varphi }$, $\overline{u}$, $\overline{v}$, $\overline{\sigma }_{ij}$, ${\overline{\Phi }}$, ${\overline{\Psi }}$ and $\overline{\omega }$ are functions that tend to zero as $z$ approaches infinity

$$ \overline{\Phi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(59)

$$ \overline{\Psi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} B_{j} \;e^{{ - \lambda_{j} z}} , $$

(60)

$$ \overline{\phi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} C_{j} \;e^{{ - \lambda_{j} z}} , $$

(61)

$$ \overline{\varphi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} D_{j} \;e^{{ - \lambda_{j} z}} , $$

(62)

$$ \overline{\theta }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} E_{j} \;e^{{ - \lambda_{j} z}} , $$

(63)

where $A_{j} ,$ $B_{j}$, $C_{j}$, $D_{j}$ and $E_{j}$, and $i = 1,2,3$ and 4 are a set of parameters whose values are determined by $\zeta$ and $\varpi$, respectively. Additionally, the values of the parameters $\lambda_{i}$ and $i = 1,2,3$ and 4, which are positive, make up the positive roots of the following equation:

$$ \lambda^{8} - \eta_{1} \lambda^{6} - \eta_{2} \lambda^{4} + \eta_{3} \lambda^{2} - \eta_{4} = 0. $$

(64)

When Eqs. (59–63) are substituted into Eqs. (50–54), one can derive the following relations:

$$ \begin{aligned} & {B_{j} = \frac{{L_{4} \left( {\lambda_{j}^{2} - L_{6} } \right)}}{{\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} }}A_{j} = M_{j} A_{j} ,{ } C_{j} = \frac{{L_{4} k_{0} \left( {\lambda_{j}^{2} - \zeta^{2} } \right)}}{{\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} }}A_{j} = N_{j} A_{j} ,{ }} \\ & {D_{j} = \frac{{\alpha_{4} \left( {\lambda_{j}^{2} - \zeta^{2} } \right)}}{{\left( {\lambda_{j}^{2} - \alpha_{3} } \right)}}A_{j} = P_{j} A_{j} ,E_{j} = \frac{{\alpha_{4} \left( {\lambda_{j}^{2} - \zeta^{2} } \right)\left( {a_{1} \lambda_{j}^{2} - a_{1} \zeta^{2} - 1} \right)}}{{\left( {\lambda_{j}^{2} - \alpha_{3} } \right)}}A_{j} = Q_{j} A_{j} .} \\ \end{aligned} $$

(65)

After incorporating relations (65) into the Eqs. (60–63), we get

$$ \overline{\Psi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} M_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(66)

$$ \overline{\phi }\left( z \right) = - \mathop \sum \limits_{j = 1}^{4} N_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(67)

$$ \overline{\varphi }\left( z \right) = \mathop \sum \limits_{j = 1}^{4} P_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(68)

$$ \overline{\theta }\left( z \right) = - \mathop \sum \limits_{j = 1}^{4} Q_{j} \;e^{{ - \lambda_{j} z}} . $$

(69)

In order to obtain the displacement variables $\overline{u}$ and $\overline{w}$, we first insert Eq. (49) into Eq. (43), and then we apply Eqs. (59) and (66) to obtain

$$ \overline{u} = \mathop \sum \limits_{j = 1}^{4} R_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(70)

$$ \overline{w} = - \mathop \sum \limits_{j = 1}^{4} S_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(71)

where

$$ R_{j} = \frac{{i\zeta \left( {\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} } \right) - L_{4} \lambda_{j} \left( {\lambda_{j}^{2} - L_{6} } \right)}}{{\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} }}, S_{j} = \frac{{\lambda_{j} \left( {\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} } \right) + i\zeta L_{4} \left( {\lambda_{j}^{2} - L_{6} } \right)}}{{\lambda_{j}^{4} - \alpha_{1} \lambda_{j}^{2} + \alpha_{2} }} . $$

(72)

The thermal and coupling stress components $\overline{\sigma }_{ij}$ and $\overline{m}_{ij}$, respectively, can be expressed in the following forms using the normal mode solution technique:

$$ \overline{\sigma }_{xx} = \frac{1}{{\rho c_{1}^{2} }}\mathop \sum \limits_{j = 1}^{4} 2\left[ {i\zeta \left( {\lambda + 2\mu + k_{0} } \right)R_{j} + \lambda \lambda_{j} S_{j} - Q_{j} } \right]A_{j} \;{\text{e}}^{{ - \lambda_{j} z}} , $$

(73)

$$ \overline{\sigma }_{yy} = \frac{1}{{\rho c_{1}^{2} }}\mathop \sum \limits_{j = 1}^{4} \left[ {i\zeta \lambda R_{j} + \lambda \lambda_{j} S_{j} - Q_{j} } \right]A_{j} \;e^{{ - \lambda_{j} z}} , $$

(74)

$$ \overline{\sigma }_{zz} = \frac{1}{{\rho c_{1}^{2} }}\mathop \sum \limits_{j = 1}^{4} 2\left[ {i\zeta \lambda R_{j} + \left( {\lambda + 2\mu + k_{0} } \right)\lambda_{j} S_{j} - Q_{j} } \right]A_{j} \;{\text{e}}^{{ - \lambda_{j} z}} , $$

(75)

$$ \overline{\sigma }_{xz} = - \frac{1}{{\rho c_{1}^{2} }}\mathop \sum \limits_{j = 1}^{4} \left[ {i\zeta \left( {\mu + k_{0} } \right)S_{j} + \mu \lambda_{j} R_{j} - k_{0} N_{j} } \right]A_{j} \;e^{{ - \lambda_{j} z}} , $$

(76)

$$ \overline{\sigma }_{zx} = - \frac{1}{{\rho c_{1}^{2} }}\mathop \sum \limits_{j = 1}^{4} \left[ {\lambda_{j} \left( {\mu + k_{0} } \right)R_{j} + i\zeta S_{j} + k_{0} N_{j} } \right]A_{j} \;{\text{e}}^{{ - \lambda_{j} z}} , $$

(77)

$$ \overline{m}_{xy} = - \frac{{i\zeta \rho c_{1}^{2} \gamma }}{{K^{2} }}\mathop \sum \limits_{j = 1}^{4} N_{j} A_{j} \;e^{{ - \lambda_{j} z}} , $$

(78)

$$ \overline{m}_{zy} = \frac{{\rho c_{1}^{2} \gamma }}{{K^{2} }}\mathop \sum \limits_{j = 1}^{4} \lambda_{j} N_{j} A_{j} \;e^{{ - \lambda_{j} z}} . $$

(79)

Using Eq. (49), it is possible to write the boundary conditions (30–32) as

$$ \overline{\sigma }_{zz} \left( {x,z,t} \right) = 0,{ }\overline{\sigma }_{xz} \left( {x,z,t} \right) = 0,{ }\overline{m}_{xy} \left( {x,z,t} \right) = 0{\text{ at }}z = 0, $$

(80)

$$ \overline{\varphi }\left( {x,z,t} \right) = \varphi_{0} H\left( {L - \left| x \right|} \right){\text{e}}^{{\left( { - \left[ {i\zeta x + \left( {\varpi + b} \right)t} \right]} \right)}} = \overline{f}\left( {t,\zeta , {\Omega }} \right){\text{ at }}z = 0. $$

(81)

Using the respective functions of the boundary conditions (80) and (81), we can get the following system of equations:

$$ \mathop \sum \limits_{j = 1}^{4} 2\left[ {i\zeta \lambda R_{j} + \left( {\lambda + 2\mu + k_{0} } \right)\lambda_{j} S_{j} - Q_{j} } \right]A_{j} = 0, $$

(82)

$$ \mathop \sum \limits_{j = 1}^{4} 0\left[ {i\zeta \left( {\mu + k_{0} } \right)S_{j} + \mu \lambda_{j} R_{j} - k_{0} N_{j} } \right]A_{j} = 0, $$

(83)

$$ \mathop \sum \limits_{j = 1}^{4} N_{j} A_{j} = 0, $$

(84)

$$ \mathop \sum \limits_{j = 1}^{4} P_{j} A_{j} = \overline{f}\left( {t,\zeta , \Omega } \right)., $$

(85)

The constants $A_{j}$ and $i = 1,2,3$ and 4 can be set after solving the system above of equations. Thus, the complete system of equations was solved, and the various physical fields in question were obtained.

6 Particular cases

The equations in Sect. 2 of this article can be used to make a number of models of dual-temperature and single-temperature micropolar thermoelasticity that can be used with or without a micropolar effect. The three categories into which special instances can be divided are as follows:

6.1 Single/two-temperature thermoelastic models

When the micropolar impact is neglected ($k_{0} = \alpha = \beta = \gamma = 0$), we can obtain:

The conventional theory (CTE) [25] states that if $\tau_{q} = \tau_{\varphi } = 0$, $a_{1} = 0$ and ${ }\theta = \varphi$.

The single Lord–Shulman model (1LS) [26] if $\tau_{q} > 0,$ $a_{1} = 0$, $\tau_{\varphi } \to 0$ and $l = 1$.

The single dual-phase-lag theory (1DPL) [34] if $a_{1} = 0$, $\tau_{q} ,\tau_{\varphi } > 0$, $n = 1$ and $l = 2$.

The single thermoelastic model with high order (1HLS) [74] is obtained when $a = 0$, $\tau_{q} > 0$, $n,l \ge 1$ and $\tau_{\varphi } \to 0$.

The two-temperature Lord–Shulman model (2LS) [75] is used when $\tau_{q} > 0,$ $a_{1} > 0$, $\tau_{\varphi } \to 0$ and $l = 1$.

The two-temperature dual-phase-lag theory (2DPL) [68] if $a_{1} > 0$, $\tau_{q} ,\tau_{\varphi } > 0$, $n = 1$ and $l = 2$.

The single-temperature model with high order and phase lags (1HDPL) is obtained when $a_{1} = 0$, $\tau_{q} ,\tau_{\varphi } > 0$, $n,l \ge 1$.

The two-temperature model with high order and phase lags (2HDPL) [76] is obtained when $a_{1} > 0$, $\tau_{q} ,\tau_{\varphi } > 0$, $n,l \ge 1$.

6.2 Single/two-temperature micropolar thermoelastic models

In the case of the micropolarity effect ($k_{0} ,\alpha ,\beta ,\gamma > 0$), a similar set of two-temperature thermoelastic models can be derived based on the values of phase lag parameters ($\tau_{q}$ and $\tau_{\varphi }$) and high order ($n$ and $l$). When the conductive temperature $\varphi$ and thermodynamic temperature $\theta$ are equal, one-accurate thermoplastic models ($a_{1} = 0$) can also be generated.

7 Numerical results and discussion

The validity of the proposed model is investigated by introducing some numerical computations.

We kept the values of some parameter’s constant throughout the calculations, such as time $t$, thermal relaxation time $\tau_{q}$ and $\tau_{\varphi }$ when the position $x = 0.1$. In numerical calculations, the real part of the amplitude of the field variables represented along the $z$-axis in the period $0 \le z \le 5$ will be considered. For this section objective, the values of the involved physical parameters for magnesium (Mg) are taken as follows [77]:

$$ \lambda = 4.76 \times 10^{9} \left( {{\text{N}}/{\text{m}}^{2} } \right), \mu = 9.86 \times 10^{10} \left( {{\text{N}}/{\text{m}}^{2} } \right),{ }\rho = 1.74 \times 10^{3} {\text{kg}}/{\text{m}}^{3} , $$

$$ k_{0} = 1 \times 10^{11} \left( {{\text{kg}}/{\text{m}}.{\text{s}}^{2} } \right), \varphi_{0} = 1, j = 2 \times 10^{ - 12} {\text{m}}^{2} ,{ }C_{E} = 1.04 \times 10^{3} \left( {{\text{J}}/{\text{kgK}}} \right), $$

$$ \gamma = 7.79 \times 10^{ - 8} {\text{ N}}, K = 156\left( {{\text{W}}/{\text{m}}.{\text{K}}} \right), \alpha_{t} = 1.78 \times 10^{ - 3} \left( {1/{\text{K}}} \right), $$

$$ \sigma_{0} = 9.36 \times 10^{5} \left( {{\text{Col}}^{2} /{\text{Cal s}}} \right), H_{0} = 10^{7} /4\pi \left( {{\text{A}}/{\text{m}}} \right),\mu_{0} = 4\pi \times 10^{ - 7} \left( {{\text{H}}/{\text{m}}} \right), $$

$$ L = 2,b = 1,{ }\varpi = \varpi_{Re} + {\text{i}}\varpi_{im} ,\varpi_{Re} = 0.3, \varpi_{im} = 0.3,\zeta = 2,T_{0} = 293{\text{K}}. $$

The effect of changing some important parameters, such as the two-temperature theory parameter (discrepancy coefficient) $a_{1}$ and higher orders $m$ and $l$ of the fractional time derivative on the temperatures ($\varphi$ and $\theta$) distributions, micropolar stresses ($\sigma_{xx}$, $\sigma_{zz}$ and $\sigma_{xz}$) and displacement elements ($u$ and $v$) will be explained in detail. The microrotation $\phi$ and couple stress elements $m_{xy}$ are also discussed (Figs. 1 and 2).

Fig. 1

Magnetic Hall effect ($V_{H}$ is the Hall voltage)

Fig. 2

Schematic of a micropolar thermoelastic solid half-space

7.1 The effect of Hall current parameter

The first subsection of the study deals with elucidating the effects of the Hall magnetic current parameter on different fields such as the two dynamic temperatures, displacements, thermal stress components, microrotation and couple stress distributions. The results are displayed graphically in Figs. 3, 4, 5, 6, 7, 8, 9, 10 and 11. The profiles were done for five different values of $m$; one of them refers to the absence of the Hall effect when $m = 0$, and the others refer to the presence of the Hall effect when $m = { }0.2$, 0.4, 0.6 or 0.8. Figures have been computed for fixed values of $a_{1} = 1$, $S = 10$ and $\tau_{q} = 0.03, \tau_{\varphi } = 0.5$.

Fig. 3

Dynamical temperature $\theta$ profile with distance $z$ for various values of Hall current parameter

Fig. 4

Conductive temperature $\varphi$ profile with distance $z$ for various values of Hall current parameter

Fig. 5

Displacement $u$ profile with distance $z$ for various values of Hall current parameter

Fig. 6

Displacement $w$ profile with distance $z$ for various values of Hall current parameter

Fig. 7

Thermal pressure $\sigma_{zz}$ profile with distance $z$ for various values of Hall current parameter

Fig. 8

Thermal pressure $\sigma_{xz}$ profile with distance $z$ for various values of Hall current parameter

Fig. 9

Thermal pressure $\sigma_{xx}$ profile with distance $z$ for various values of Hall current parameter

Fig. 10

Microrotation $\phi$ profile with distance $z$ for various values of Hall current parameter

Fig. 11

Couple's stress $m_{xy}$ profile with distance $z$ for various values of Hall current parameter

The curves of Fig. 3 show the temperature distributions in the body starting from the surface ($z = 0$) until it reaches the damping state within the thermoelastic half-space. As can be seen from the figure, the temperature distributions take their highest value at $z = 0$, then they decrease rapidly in an area near the surface until they disappear at $z$ equal to approximately 2.5. As shown in Figs. 3 and 4, the Hall parameter has a noticeable effect on the two-temperature distributions. The dynamic temperature distributions $\theta$ and conductive temperature $\varphi$ take their minimum in the absence of the effect of the Hall parameter, i.e., when $m = 0$ and then increase with increasing values of the Hall parameter $m$. The explanation is attributed to the alternative mutual influence between the magnetic and thermal fields in the dynamic system.

It can be seen from the curves of Figs. 5 and 6, the displacement distributions $u$ reach the steady state monotonically in contrast to the component $w$. It can be seen from Fig. 5 that the displacement $u$ has a maximum value at the surface $z = 0$, and then gradually decreases to reach the steady state in the region close to $z \approx 4$, but, through a different behavior, the displacement $w$ increases with values of $z$ until the maximum value at the point $z \approx 0.6$. It decreases until the steady state due to the effect of the deteriorating pressure gradient. It is also easy to notice the significant effect of the presence and absence of Hall current on the displacement components and also their different behaviors depending on the presence of the parameter $m$ with different values.

Figures 7, 8 and 9 show the distributions of different thermal stresses ($\sigma_{zz}$, $\sigma_{xz}$ and $\sigma_{xx}$) as functions of the Hall effect $m$ along the $z$-axis. The distribution curves show a clear variation in shapes under the influence of the Hall effect. As it appears, all values of thermal stress distributions increase with increasing values of Hall parameter $m$. But according to the $z$-axis, the axial and shear thermal stress distributions showed different behaviors from the vertical thermal stress distributions. Both the axial thermal stress and the thermal shear stress took a zero value at $z = 0$, thus satisfying the imposed boundary conditions, in contrast to the vertical thermal stress, whose minimum nonzero value was recorded at $z = 0$.

The vertical thermal stress curves in Fig. 9 show that its wave continues to increase with gradually increasing $z$ values until it reaches zero, which is a stable state. In contrast, the axial and shear stress continued to decrease until it reached its minimum value at $z \approx 0.45$. It started to increase again until it reached the stage of stabilization and functional damping with a value close to $z = 5$, as in Fig. 2. 7 and 8.

Figures 10 and 11 show the microrotation $\phi$ and the coupled pressure profile $m_{xy}$ for different values of the Hall current parameter $m$. Figure 10 shows that the microrotation field remains negative and decreases as the Hall current parameter inside the domain increases from 0 to 5, in contrast to the couple stress in Fig. 11. Moreover, we see from Fig. 10 that the microrotation field has a minimum value at $z = 0$. Then it gradually increases along the $z$-axis until it reaches zero at $z \approx 5$. But in Fig. 11, the couple stress has its maximum value at $z = 0$ and then gradually decreases along the z-axis until it reaches zero at $z = 5$.

7.2 Effect of initial stress

The present subsection discusses the initial stress parameterization of the physical field variables along the $z$-axis with the initial stress $S$. Figures 12 and 13 present the numerical results of the mathematical model under different values of the initial stress, and in the absence of the initial stress, we consider $S$ equal to zero. The initial stress values were assumed to be 0, 10, 15, 20 and 25, and the values of the other effective parameters were considered constant.

Fig. 12

Dynamic temperature $\theta$ changes across $z$ for different values of initial stress $S$

Fig. 13

Conductive temperature $\varphi$ changes across $z$ for different values of initial stress $S$

In Figs. 12 and 14, it is shown how the dynamic and conductive temperature distributions change, respectively, with the initial stress $S$ in the absence and presence cases. From the figures, it can be seen that the temperature distribution curves decrease with increasing values of the initial stress $S$. It is also clear that the two-temperature distribution curves start at the maximum value at the surface $z = 0$ and then decrease with increasing $z$ to reach zero. Moreover, from Fig. 14, we observed that the initial stress has little effect on the junction temperature.

Fig. 14

Displacement component $u$ changes across $z$ for different values of initial stress $S$

The behavior of the displacement components $u$ and $w$ is presented graphically in Figs. 15 and 16, respectively, under the influence of initial stress. It was noted that the behaviors of the curves differed in the cases of the presence and absence of the initial stress, but the curves of the variables recorded the lowest rate in the case of the absence of the initial stress ($S = 0$) and it increased with increasing values of that parameter. To display the effect of the initial stress $S$ on the behavior of the thermal stress components, Figs. 17, 18 and 19 are represented along $z$-axis. Figures. 17 and 18 show that the axial and shear thermal stresses are zero at the surface of the thermoelastic micropolar body ($z = 0$) and reach their lowest levels at the point $z = 0.6$. Then the values increase in the vanishing direction, with z increasing until a steady state is reached. It is worth noting here the physical effect resulting from the presence of initial stress on the system’s physical variables. Figures 20 and 13 show the partial rotation parameter $\phi$ and couple stress $m_{xy}$ for different values of initial stress $S$ at the interval [0, 5]. One can notice by comparing the curves that the initial pressure $S$ has a prominent effect on these areas.

Fig. 15

Displacement ${\text{w}}$ changes across distance ${\text{z}}$ for different values of initial stress ${\text{ S}}$

Fig. 16

Thermal stress $\sigma_{zz}$ changes across distance $z$ for different values of initial stress $S$

Fig. 17

Thermal stress $\sigma_{xz}$ changes across distance $z$ for different values of initial stress $S$

Fig. 18

Thermal stress $\sigma_{xx}$ changes across distance $z$ for different values of initial stress $S$

Fig. 19

Microrotation $\phi$ changes across distance $z$ for different values of initial stress $S$

Fig. 20

Couple of stress $m_{xy }$ changes across distance $z$ for different values of initial stress $S$

7.3 Comparison of different micropolar thermoelastic models

This case study looks at how different physical variables behave by comparing the proposed micropolar thermoelastic model with two temperatures and some other thermoelastic models that can be used as special cases from the main model that is being shown. We looked at the thermoelastic interactions in a micropolar thermoelastic half-space medium and compared them to the theory of double-phase delay when magnetic and thermal fields are present at the edges. The results are presented graphically in Figs. 21 and 22 in the z-axis direction for the different models. By referring to the governing equations, it becomes clear that these models depend on the magnetic field parameter $M$, the temperature variation parameter $a_{1}$ and the higher-order derivative parameters $n$ and $l$. These models can be referred to as the dual-phase-lag two-temperature model with no higher-order derivatives (2DPL), the magneto-thermoelastic two-phase lag model without higher-order derivatives (2MDPL) and the two-phase double-phase delay model with one temperature and higher-order time derivatives (1HDPL), the two-phase higher-order time-derivative dual-phase delay model 2HDPL and the two-temperature higher-order time-derivative dual-phase delay model 2HMDPL. These different models are referred to in detail in the sixth section of this work.

Fig. 21

Dynamic temperature variations $\theta$ for different thermoelastic and micropolar models

Fig. 22

Conductive temperature variations $\varphi$ for different thermoelastic and micropolar models

The field variables $\theta$, $\varphi$ and $m_{xy}$ for different models are shown in Figs. 23, 24 and 22. These distributions take positive values, starting with their maximum values at an interval of half the micropolar area and eventually decreasing to reach zero, with the exception of the displacement component $u$, which begins with a gradual decrease and then a rapid decrease in the case of all the different models. Figures 25 and 26 show that the values of the stress distributions $\sigma_{zz}$ and $\sigma_{xz}$ remain negative and start with the value 0 at the boundaries, fulfilling the boundary conditions. In Figs. 27 and 28, the vertical thermal stress $\sigma_{xx}$ and the partial rotation $\phi$ start at the lowest values and increase along the $z$-axis to reach zero inside the elastic medium.

Fig. 23

Variations in the displacement $u$ for different thermoelastic and micropolar models

Fig. 24

Variations in the displacement $w$ for different thermoelastic and micropolar models

Fig. 25

Stress $\sigma_{zz}$ variation for different thermoelastic and micropolar models

Fig. 26

Stress variation $\sigma_{xz}$ for different thermoelastic and micropolar models

Fig. 27

Stress variation $\sigma_{xx}$ for different thermoelastic and micropolar models

Fig. 28

Variations of the microrotation $\phi$ for different thermoelastic and micropolar models

By comparing the models in Figs. 21 and 23, we found that the presence of the magnetic parameter $M$ in the model 2MDPL (green curve) leads to a decrease in distributions than in the case of its absence in the 2DPL model (black curve), and this is the same as what happened with the two models 2HMDPL (blue curve) and 2HDPL (yellow curve). Also, by taking into consideration the two-temperature model, with $a_{1} > 0$, the distributions become less than in the case of a single temperature with $a_{1} = 0$, and one can see that in Figs. 24 and 29 for the displacement distributions as well.

Fig. 29

Variations of the couple stresses $m_{xy}$ for different thermoelastic and micropolar models

Finally, for all models, the behavior of the system tends to be stabilized. One can say that the model of micropolar magneto-thermoelastic dual-phase lag with a two-temperature model in the context of an advanced higher-order time derivative and all its special cases predict a finite speed of propagation, which is in agreement with the previously introduced results [19, 22, 62].

8 Conclusions

The main objective of this study is to investigate the behavior of a thermoelastic micropolar half-space material under initial stress by looking at how it behaves thermally and dynamically. The micropolar elasticity equations of motion and the modified hyperbolic heat equation are considered in the context of a two-temperature two-phase lag model. Also, Maxwell's equations were applied, which are used to express the components of the Lorentz magnetic force. The effects of the Hall effect parameter, the initial compressive pressure and the Hartmann number on the dynamic and thermal wave propagation and temperature distributions are explained. The effect of all parameters affecting the responses of the physical field variables was also presented in illustrative figures. Here are some conclusions that can be drawn:

• Changes in the Hall current parameter and initial stress led to the emergence of variation in the behavior of all the physical variables studied inside the micropolar body.

• The current and initial stress parameters greatly influence all studied areas and in the cases of micropolar thermoelastic theories that are compared.

• • The Hartmann number (magnetic variable) greatly affects all mechanical and thermal field variables studied.

• Since elemental stresses are widely prevalent in inert and animate materials, the proposed foundational model can be used in many applications toward the nondestructive quantification of primary stresses in solids.

• Based on the proposed model, future research can be expanded to include a broader class of heterogeneous material behaviors and relate initial stress to thermal and mechanical elastic wave velocities.

• The proposed model was verified, and it was shown that if the two-phase generalized thermoelastic theory is applied, it turns out that there is a limited speed of heat wave propagation in a micropolar body. In other words, the region of turbulence is limited in the material near the external forces and sources affecting the medium.

• Based on the results obtained, it was shown that the proposed model can be used to determine how well the thermoelectric material performs based on the selection of phase delay selection times.