1 Introduction

Functionally graded materials (FGMs) are the advanced materials in the family of engineering composites whose composition varies continuously as a function of position usually along the thickness of a structure. Typically, these materials are made from the combination of two materials, usually metal and ceramics that provides many advantages including high-temperature resistance, higher fracture toughness, and reduced stress intensity factors. In recent years, in order to improve the functionalities of nano-electro-mechanical systems (NEMS), FGM are broadly spread into synthesize these systems (Witvrouw and Mehta 2005; Rahaeifard et al. 2009; Fu et al. 2003; Lee et al. 2006). In the study of mechanical behavior of micro/nanoplates, the effects of structure size play a significant role in the correct examination of such structures in small scales. Since the classical continuum theory fails to capture the size effect, the various non-classical continuum theories, such as couple surface elasticity theory (Toupin 1962; Mindlin and Tiersten 1962), modified couple stress theory (MCST) (Yang et al. 2002), strain gradient elasticity theory (SGT) (Aifantis 1999) and nonlocal elasticity theory (Eringen and Edelen 1972; Eringen 1972) have been proposed. In these theories some additional material constants are employed to account the size effects on the mechanical behaviors of microstructures. Based on the couple stress theory, two additional material constants is considered and strain energy is a function of both strain and curvature tensors (Akgöz and Civalek 2012). Whereas, according to the MCST, an additional length scale parameter is used to predict size effects in the mechanical properties of nano-structures. Furthermore, the strain energy is expressed by a function of the strain and only the symmetric part of the curvature tensor based on the MCST (Yang et al. 2002). Also, based on the SGT, three additional material constants exist to capture the size effects of mechanical relations in nano-structures and the strain energy is assumed to be a function of strain tensor and gradient of the strain tensor (Aifantis 1999). The nonlocal elasticity theory is introduced by Eringen (Eringen and Edelen 1972; Eringen 1972). Based on this theory, the stress at a point is a function of strains at all other points in the domain. The nonlocal elasticity theory contains two additional material length scale parameters. Recently, Chen et al. (2004) reported that among the size-dependent continuum theories (Micromorphic theory, Microstructure theory, Micropolar theory, Cosserat theory, nonlocal theory and couple stress theory), the nonlocal elasticity theory can achieve a correspondence with atomistic lattice dynamics and molecular dynamics. Also, Sun et al. (2007) reported that there is a noticeable difference between atomistic simulation and the strain gradient elasticity solution for the bending response of micro/nano-scale structures. Generally, the nonlocal elasticity theory is simple and quick in contrast to the other non-classical continuum theories (Chen et al. 2004; Golmakani and Rezatalab 2014). Thus, the nonlocal elasticity theory is the most commonly used theory to analyze the mechanical behavior of nanostructures such as nano-plates. Peddieson et al. (2003) first used the nonlocal elasticity theory to develop a nonlocal Bernoulli/Euler beam model. Sudak (2003) considered the column buckling of multi-walled carbon nanotubes based on nonlocal elasticity theory and Euler–Bernoulli beam model. Lu et al. (2007) proposed a nonlocal plate model for bending and free vibration analysis of a rectangular plates with simply supported edges. Duan and Wang (2007) obtained a closed form solution for the axisymmetric bending of circular nanoplates based on nonlocal elasticity theory. Using Navier’s approach, Pradhan (2009) studied the buckling behavior of SLGS based on nonlocal elasticity and higher order shear deformation theory. Pradhan and Murmu (2009) investigated the small scale effect on the buckling of orthotropic nanoplate under biaxial compression. Aghababaei and Reddy (2009) analyzed the bending and free vibration behaviors of a simply supported isotropic rectangular nanoplate based on nonlocal third-order shear deformation theory of Reddy. Radic et al. (2014) studied the buckling of double-orthotropic nanoplates based on nonlocal elasticity theory. Farajpour et al. (2011) obtained explicit expressions for buckling analysis of the circular graphene sheet under uniform radial compression based on nonlocal elasticity theory. Mohammadi et al. (2014) presented the closed-form solution to study the vibration behavior of annular and circular SLGS embedded in an elastic medium under thermal loads. Ravari and Shahidi (2013) analyzed the buckling behavior of circular and annular nanoplate under uniform compression using finite difference method and nonlocal elasticity theory. According to the literature, some research works have been presented for the buckling analysis of isotropic/orthotropic nanoplates based on nonlocal elasticity theory. However, investigations on buckling behavior of functionally graded (FG) nanoplates are limited in number. Among those, considering surface effects and using Kirchhoff hypothesis, Lu et al. (2009) presented a thin plate theory for nano-scaled functionally graded films. Using Navier’s procedure, Lei et al. (2013) investigated the static bending and free vibration of FG micro-beams by employing the strain gradient elasticity theory (SGT) and sinusoidal shear deformation theory. Zhang et al. (2015) studied the free vibration analysis of functionally graded cylindrical micro-shells based on the strain gradient elasticity and a four-unknown shear deformation theory. Using the Navier’s approach, Tadi Beni et al. (2015) studied the free vibration analysis of size-dependent FG cylindrical shell based on FSDT and modified couple stress theory. More recently, Salehipour et al. (2015) presented a closed-form solution for the free vibration of simply supported FG rectangular nanoplate. They used the three-dimensional nonlocal elasticity theory of Eringen. Nami and Janghorban (2014) studied the resonance behaviors of FG micro/nano rectangular plate with two size-dependent theory, nonlocal elasticity theory and strain gradient theory. They compared each results of theories. Using nonlocal elasticity theory, the buckling behavior of functionally graded circular/annular nanoplates were studied by Bedroud et al. (2013) for clamped and simply supported boundary conditions. Also, they presented the analytical approach for buckling behavior of FG annular nanoplates under radial compressive load based on nonlocal elasticity theory and FSDT (Bedroud et al. 2016). In recent decades, many researchers have presented various techniques to improve numerical methods for structural analysis. Differential quadrature method (DQM) was presented by Bellman and Casti (1971) in 1988 and since then, owing to its low computational cost and accuracy, DQM has been widely used and developed in many fields of macro and micro/nanoscale structures. For example, Striz et al. (1995) presented harmonic differential quadrature (HDQ) and this method was used in various studies by Civalek (2003, 2004) and Civalek and Ulker (2004). Wu and Liu (2000) proposed a generalized differential quadrature (GDQ). Karami and Malekzadeh (2002) presented a new differential quadrature methodology for beam analysis. Civalek and his coworkers (Civalek et al. 2010) employed the DQM to consider the free vibration and bending behaviors of cantilever microtubules based on nonlocal continuum model. Danesh et al. (2012) studied axial vibration of a tapered nanorod based on nonlocal elasticity theory and differential quadrature method. Furthermore, similar works have been done to study the mechanical behaviors of micro- and nanoscale structures using DQM (Farajpour et al. 2013; Ke et al. 2012; Beni and Malekzadeh 2012; Janghorban and Zare 2011; Ansari et al. 2011; Farajpour et al. 2012; Mohammadi et al. 2014). From the literature review, despite significant contributions to investigation of SLGS buckling behavior in previous years, few studies have focused on the elastic buckling of FG nanoplate embedded in an elastic medium. Thus, this work focuses on the buckling of FG annular graphene sheets in an elastic medium based on nonlocal mindlin plate theory. The material properties of the FG graphene sheets are assumed to vary in the thickness direction according to a power-law distribution in terms of the volume fraction of the constituents. The small scale effects are introduced using the nonlocal elasticity theory. Both Winkler-type and Pasternak-type foundation models are employed to simulate the interaction between the graphene sheet and the surrounding elastic medium. Using the principle of virtual work, the nonlocal equilibrium equations are obtained for axisymmetric FG annular graphene sheets and the stability equations are established by using the adjacent equilibrium criterion technique. The created eigenvalue problem is then solved by the DQM for simply supported, clamped and free boundary conditions and various combinations of them. The formulation and method of solution are verified by comparing the results, in limited cases, with those available in the open literature. Excellent agreement between the obtained and available results is observed. Finally, the influences of the length scale parameter, annularity, elastic medium, grading index and boundary conditions are investigated on the buckling load of FG single-layered annular graphene sheets.

2 Formulation

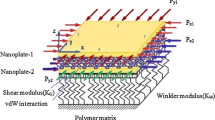
In this section, the nonlocal governing equations are presented for the buckling analysis of FG annular graphene sheet. Figure 1 shows the FG annular graphene sheet with thickness \(h\), inner radius \(r_{i}\) and outer radius \(r_{o}\) resting on Winkler springs (\(k_{w}\)), shear layer (\(k_{g}\)) and subjected to uniform radial compression load \(N\). Considering axial symmetry in geometry and loading, the cylindrical coordinates system \((r,\theta ,z)\) is chosen for deriving the equilibrium equations.

Fig. 1
figure 1

A continuum model of FG annular nanoplate in an elastic medium under uniform radial compression

Full size image

The properties of the nanoplate are assumed to vary through the thickness of the nanoplate with a power-law distribution of the volume fractions of the constituent materials. In fact, the top surface (z = h/2) of the nanoplate is metal-rich whereas the bottom surface (z = −h/2) is ceramic-rich. Poisson’s ratio ν is assumed to be constant and is taken as 0.3 throughout the analysis. Young’s modulus is assumed to vary continuously through the nanoplate thickness as

$$E = E(z) = E_{m} + (E_{c} - E_{m} )\left( {\frac{1}{2} + \frac{z}{h}} \right)^{n} ,$$
(1)

where the subscripts m and c represent the metallic and ceramic constituents and n is the grading index and takes only non-negative values. According to the nonlocal continuum theory of Eringen (Eringen and Edelen 1972; Eringen 1972) which accounts for the small scale effects by assuming the stress at a reference point as a function of the strain field at every point of the continuum body, the nonlocal constitutive equations of a Hookean solid can be written by the following differential constitutive relation

$$(1 - \mu \nabla^{2} )\sigma^{nl} = \sigma^{l} ,$$
(2)

where \(\sigma^{nl}\) and \(\sigma^{l}\) express the nonlocal stress and local (classical) stress tensors, respectively. Also \(\mu = (e_{0} a)^{2}\) is the nonlocal parameter, which incorporates the small-scale effect (\(e_{0} a\)) into the formulation, \(a\) is an internal characteristic length and \(e_{0}\) is Eringen’s nonlocal elasticity constant. Wang and Wang (2007) reported that small-scale effect of carbon nanotubes (CNTs) must be smaller than 2.0 nm. Thus, the value of nonlocal parameter must be less than 4.0 nm2. Moreover, \(\nabla^{2}\) is the Laplacian operator that in axisymmetric polar coordinate is given by \(\nabla^{2} = \frac{{d^{2} }}{{dr^{2} }} + \frac{d}{rdr}\). The macroscopic (local) stress tensor (\(\sigma^{l}\)) at a given point is related to strain tensor of the point by the generalized Hooke’s law

$$\sigma^{l} = C:\varepsilon ,$$
(3)

where \(C\) and \(\varepsilon\) are the stiffness and local strain tensors, respectively; and the symbol ‘:’ indicates the double dot product. Using Eqs. (1), (2) and (3), the plane stress nonlocal constitutive relation of annular FG nanoplate in polar coordinates are expressed by

$$\left\{ {\begin{array}{*{20}c} {\sigma_{r}^{nl} } \\ {\sigma_{\theta }^{nl} } \\ {\sigma_{rz}^{nl} } \\ \end{array} } \right\} - \mu \nabla^{2} \left\{ {\begin{array}{*{20}c} {\sigma_{r}^{nl} } \\ {\sigma_{\theta }^{nl} } \\ {\sigma_{rz}^{nl} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{12} } & {Q_{22} } & 0 \\ 0 & 0 & {C_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{r} } \\ {\varepsilon_{\theta } } \\ {\gamma_{rz} } \\ \end{array} } \right\},$$
(4)

where the stiffness coefficients for the FG layer are defined as bellow

$$Q_{11} = \frac{E(z)}{{1 - \nu^{2} }},\quad Q_{22} = \frac{E(z)}{{1 - \nu^{2} }},\quad Q_{12} = \frac{{v E(z)}}{{1 - \nu^{2} }},\quad C_{55} = G(z) = \frac{E(z)}{2(1 + \nu )}.$$
(5)

Here, \(G\) and ν are the shear modulus and Poisson’s ratio, respectively. Furthermore, \(\varepsilon_{r}\) and \(\varepsilon_{\theta }\) are normal strains and \(\gamma_{rz}\) expresses the shear strain. According to the assumption of axisymmetric buckling and based on first-order shear deformation theory, the displacement field of an annular plate is defined as follows

$$\begin{aligned}&U(r,\theta ,z) =u(r,\theta ) + z\phi \hfil\\&V(r,\theta ,z) = 0 \hfill \\&W(r,\theta ,z) = w(r), \hfill \\ \end{aligned}$$
(6)

where (U, V, W) are the displacement components of an arbitrary point (x, θ, z) of the plate, and u and w are displacements of the mid-plane in the r and z directions, respectively. Also, \(\phi\) is rotation of the middle surface of plate in θ direction. Based on the FSDT and nonlinear von Karman theory, the strain-displacement relations can be written as

$$\left\{ {\begin{array}{*{20}l} {\varepsilon_{r} } \\ {\varepsilon_{\theta } } \\ {\gamma_{rz} } \\ \end{array} } \right\} = \left\{ \begin{aligned} &\frac{du}{dr} + \frac{1}{2}\left( {\frac{dw}{dr}} \right)^{2} + z\frac{d\phi }{dr} \hfill \\ &\frac{u}{r} + z\frac{\phi }{r} \hfill \\ &\phi + \frac{dw}{dr} \hfill \\ \end{aligned} \right\}.$$
(7)

The force, moment and shear stress resultants N i (i = r, θ), M i (i = r, θ) and Q r of nonlocal elasticity defined by

$$(N_{r} ,N_{\theta } ,Q_{r} )^{nl} = \int_{ - h/2}^{h/2} ( \sigma_{r} ,\sigma_{\theta } ,k.\sigma_{rz} )^{nl} dz$$
$$(M_{r} ,M_{\theta } )^{nl} = \int_{ - h/2}^{h/2} ( \sigma_{r} ,\sigma_{\theta } )^{nl} zdz.$$
(8)

In which \(k\) is the transverse shear correction coefficient and taken as 5/6. Using Eqs. (4), (7), and (8), the stress resultants can be written in terms of displacements as

$$\left\{ \begin{aligned} N_{r} \hfill \\ N_{\theta } \hfill \\ Q_{r} \hfill \\ M_{r} \hfill \\ M_{\theta } \hfill \\ \end{aligned} \right\}^{nl} - \mu \nabla^{2} \left\{ \begin{aligned} N_{r} \hfill \\ N_{\theta } \hfill \\ Q_{r} \hfill \\ M_{r} \hfill \\ M_{\theta } \hfill \\ \end{aligned} \right\}^{nl} = \left\{ \begin{aligned}&A\frac{du}{dr} + A\frac{1}{2}\left( {\frac{dw}{dr}} \right)^{2} + A\nu \frac{u}{r} + B\frac{d\phi }{dr} + B\nu \frac{\phi }{r} \hfill \\&A\nu \frac{du}{dr} + A\nu \frac{1}{2}\left( {\frac{dw}{dr}} \right)^{2} + A\frac{u}{r} + B\nu \frac{d\phi }{dr} + B\frac{\phi }{r} \hfill \\&Ak\left( {\frac{1 - \nu }{2}} \right)\phi + Ak\left( {\frac{1 - \nu }{2}} \right)\frac{dw}{dr} \hfill \\&B\frac{du}{dr} + B\frac{1}{2}\left( {\frac{dw}{dr}} \right)^{2} + B\nu \frac{u}{r} + C\frac{d\phi }{dr} + C\nu \frac{\phi }{r} \hfill\\&B\nu \frac{du}{dr} + B\nu \frac{1}{2}\left( {\frac{dw}{dr}} \right)^{2} + B\frac{u}{r} + C\nu \frac{d\phi }{dr} + C\frac{\phi }{r} \hfill \\ \end{aligned} \right\},$$
(9)

where

$$(A,B,C) = \int {\frac{E(z)}{{1 - \nu^{2} }}\,(1,z,z^{2} )dz.}$$
(10)

Principle of virtual work is used to derive the governing equations of an annular nanoplate on an elastic foundation under uniform radial compressive load. The principle of virtual work can be written as

$$\delta \prod = \delta (U + V) = 0,$$
(11)

where Π, U and V are the total potential energy, total strain energy and virtual work done by applied forces. Also, \(\delta\) is a variation with respect to r. The variation of the total strain energy, \(\delta U\), is expressed by:

$$\delta U = \int_{{r_{i} }}^{{r_{o} }} {\int_{0}^{2\pi } {\int_{ - h/2}^{h/2} {(\sigma_{r} \delta \varepsilon_{r} + \sigma_{\theta } \delta \varepsilon_{\theta } + \sigma_{rz} \delta \varepsilon_{rz} )rdzd\theta dr} } } .$$
(12)

Also, the variation of virtual work done by applied forces is as follows:

$$\delta V = \int_{{r_{i} }}^{{r_{o} }} {\int_{0}^{2\pi } {(k_{w} w\delta w + k_{g} \frac{\partial w}{\partial r}\delta (\frac{\partial w}{\partial r}))rd\theta dr} } + \frac{N}{h}\int_{{r_{i} }}^{{r_{o} }} {\int_{0}^{2\pi } {\int_{ - h/2}^{h/2} {\frac{\partial (r\delta u)}{\partial r}dzd\theta dr} } } .$$
(13)

Using the principle of virtual work, the following equilibrium equations can be obtained (Naderi and Saidi 2011; Sepahi et al. 2010):

$$\begin{aligned}&\frac{{dN_{r} }}{dr} + \frac{{N_{r} - N_{\theta } }}{r} = 0 \hfill \\& \frac{{dM_{r} }}{dr} + \frac{{M_{r} - M_{\theta } }}{r} - Q_{r} = 0 \hfill \\& \frac{{dQ_{r} }}{dr} + \frac{{Q_{r} }}{r} + (1 - \mu \nabla^{2} )N_{r}^{{}} \frac{{d^{2} w}}{{dr^{2} }} + (1 - \mu \nabla^{2} )N_{\theta } \left( {\frac{1}{r}\frac{dw}{dr}} \right) \hfill \\& - k_{w} (1 - \mu \nabla^{2} )w + (1 - \mu \nabla^{2} )k_{g} (\nabla^{2} w) = 0. \hfill \\ \end{aligned}$$
(14)

The stability equations are derived from the adjacent equilibrium criterion (Naderi and Saidi 2011; Sepahi et al. 2010; Jones 2006). Let us assume that the state of equilibrium of annular nanoplate under loads is defined in terms of the displacement components u 0, w 0 and ϕ 0. The displacement components of a neighboring state of the stable equilibrium differ by u 1, w 1 and ϕ 1 with respect to the equilibrium position. Thus, the total displacements of a neighboring state can be expressed by:

$$\begin{aligned} u=&\,u^{0} + u^{1} \hfill\\w=&\,w^{0} + w^{1} \hfill \\ \phi =&\,\phi^{0} + \phi^{1}.\hfill \\ \end{aligned}$$
(15)

Substituting the displacement components (15) into relations (8) yields

$$\eqalign{ & {N_r} = N_r^0 + N_r^1\quad {M_r} = M_r^0 + M_r^1 \cr & {N_\theta } = N_\theta ^0 + N_\theta ^1\quad {M_\theta } = M_\theta ^0 + M_\theta ^1 \cr & {Q_r} = Q_r^0 + Q_r^1. \cr}$$
(16)

By substituting Eqs. (15) and (16) in Eq. (14) and performing proper simplifications, the stability equations are obtained as (Sepahi et al. 2010; Bedroud et al. 2013)

$$\begin{aligned}&\frac{{dN_{r}^{1} }}{dr} + \frac{{N_{r}^{1} - N_{\theta }^{1} }}{r} = 0 \hfill \\& \frac{{dM_{r}^{1} }}{dr} + \frac{{M_{r}^{1} - M_{\theta }^{1} }}{r} - Q_{r}^{1} = 0 \hfill \\& \frac{{dQ_{r}^{1} }}{dr} + \frac{{Q_{r}^{1} }}{r} + (1 - \mu \nabla^{2} )N_{r}^{0} \frac{{d^{2} w^{1} }}{{dr^{2} }} \hfill \\\quad&+(1 - \mu \nabla^{2} )N_{\theta }^{0} (\frac{1}{r}\frac{{dw^{1} }}{dr}) - k_{w} (1 - \mu \nabla^{2} )w^{1} + (1 - \mu \nabla^{2} )k_{g} (\nabla^{2} w^{1} ) = 0, \hfill \\ \end{aligned}$$
(17)

where \(N_{r}^{0}\) and \(N_{\theta }^{0}\) are pre-buckling in-plane stress resultant defined as follows for uniform radial compression:

$$N_{\theta }^{0} = N_{r}^{0} = - N_{p} .$$
(18)

Thus, the stability equations of axisymmetric nanoplates in terms of the displacements can be written as:

$$A\left( {r^{2} \frac{{d^{2} u^{1} }}{{dr^{2} }} + r\frac{{du^{1} }}{dr} - u^{1} } \right) + B\left( {r^{2} \frac{{d^{2} \phi^{1} }}{{dr^{2} }} + r\frac{{d\phi^{1} }}{dr} - \phi^{1} } \right) = 0$$
$$\begin{aligned}&B\left( {r^{2} \frac{{d^{2} u^{1} }}{{dr^{2} }} + r\frac{{du^{1} }}{dr} - u^{1} } \right) + C\left( {r^{2} \frac{{d^{2} \phi^{1} }}{{dr^{2} }} + r\frac{{d\phi^{1} }}{dr} - \phi^{1} } \right) \hfill \\&- Akr^{2} \left( {\frac{1 - \nu }{2})(\phi^{1} + \frac{{dw^{1} }}{dr}} \right) = 0 \hfill \\ \end{aligned}$$
$$\begin{aligned}&kA\left( {\frac{1 - \nu }{2}} \right)\left( {\frac{{d\phi^{1} }}{dr} + \frac{{\phi^{1} }}{r} + \frac{{dw^{1} }}{rdr} + \frac{{d^{2} w^{1} }}{{dr^{2} }}} \right) - N_{p} (1 - \mu \nabla^{2} )(\nabla^{2} w^{1} ) \hfill \\&- K_{w} (1 - \mu \nabla^{2} )w^{1} + K_{g} (1 - \mu \nabla^{2} )(\nabla^{2} w^{1} ) = 0. \hfill \\ \end{aligned}$$
(19)

The following boundary conditions are employed in this study for both inner and outer edges of annular nanoplate (Sepahi et al. 2010; Bedroud et al. 2013):Simply supported (S):

$$w^{1} = 0,\quad N_{r}^{1} = M_{r}^{1} = 0$$
(20)

Clamped (C):

$$w^{1} = \phi^{1} = 0,N_{r}^{1} = 0$$

Free (F):

$$\begin{aligned}&P_{r}^{1} = 0 \quad :\;N_{p} (1 - \mu \nabla^{2} )\frac{{dw^{1} }}{dr} + k_{g} (1 - \mu \nabla^{2} )\frac{{dw^{1} }}{dr} + Q_{r}^{1} = 0\,\,\, \hfill \\& N_{r}^{1} = M_{r}^{1} = 0. \hfill \\ \end{aligned}$$

3 Solution methodology

In order to solve the equilibrium equations, the differential quadrature method (Shu 2000) is used. The DQM is a numerical technique for the solution of initial and boundary value problems. It follows that the partial derivative of a function with respect to a variable is approximated by taking a weighted linear sum of the functional values at all grid points in the whole domain (Shu 2000). Therefore, every partial differential equation system can be simplified to a set of linear algebraic equations using DQM. According to the DQ method, the partial derivatives of a function f(x) as an example, at the point (x i ) can be expressed by (Mohammadi et al. 2014):

$$\frac{{\partial^{s} f(x_{i} )}}{{\partial x^{s} }} = \sum\limits_{j = 1}^{N} {C_{ij}^{s} f(x_{j} )\quad } i = 1,2, \ldots ,N,$$
(21)

where N is the total number of grid points in the x-direction and \(C_{ij}^{s}\) represents the weighting coefficient related to the sth-order derivative and is obtained as follows (Mohammadi et al. 2014; Murmu and Pradhan 2009):

$$\begin{aligned} C_{ij}^{1} =&\frac{{R(x_{i} )}}{{(x_{i} - x_{j} )R(x_{j} )}}\quad i \ne j\, - i,\,\,j =&1,\,2,\, \ldots ,\,N \hfill \\ C_{ii}^{1} =&-\sum\limits_{j = 1,i \ne j}^{N} {C_{ij}^{1} }\quad i =1,\,2,\, \ldots ,\,N, \hfill \\ \end{aligned}$$
(22)

where \(R(x)\) is defined as:

$$R(x_{i} ) = \prod\limits_{j = 1, \ne i}^{N} {(x_{i} - x_{j} ).}$$
(23)

Also, for higher order partial derivatives the weighting coefficients are obtained by:

$$\begin{aligned} C_{ij}^{2} = \sum\limits_{k = 1}^{N} {C_{ik}^{1} } C_{kj}^{1}\quad C_{ij}^{3} = \sum\limits_{k = 1}^{N} {C_{ik}^{1} } C_{kj}^{2} \hfill \\ C_{ij}^{4} = \sum\limits_{k = 1}^{N} {C_{ik}^{1} } C_{kj}^{3}\quad i,j = 1,2, \ldots N. \hfill \\ \end{aligned}$$
(24)

In order to obtain the suitable number of discrete grid points and a better mesh point distribution, Gauss–Chebyshev–Lobatto technique has been employed as follows (Bert and Malik 1996)

$$x_{i} = \frac{1}{2}\left( {1 - \cos \frac{i - 1}{n - 1}\pi } \right)\quad i = 1,2, \ldots ,N.$$
(25)

Using the DQ method, Eq. (19)

$$i = 2,3, \ldots ,N - 1$$
$$Ar_{i}^{2} \sum\limits_{j = 1}^{n} {C_{ij}^{2} } u_{j} + Ar_{i} \sum\limits_{j = 1}^{n} {C_{ij}^{1} } u_{j} - Au_{i} + Br_{i}^{2} \sum\limits_{j = 1}^{n} {C_{ij}^{2} } \phi_{j} + Br_{i} \sum\limits_{j = 1}^{n} {C_{ij}^{1} } \phi_{j} - B\phi_{i} = 0$$
$$\begin{aligned}&Br_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{2} } u_{j} + Br_{i} \sum\limits_{j = 1}^{N} {C_{ij}^{1} } u_{j} - Bu_{i} + Cr_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{2} } \phi_{j} + Cr_{i} \sum\limits_{j = 1}^{N} {C_{ij}^{1} } \phi_{j} \hfill \\\quad& - \left( {C + Akr^{2} \frac{1 - \nu }{2}} \right)\phi_{i} - Akr^{2} \frac{1 - \nu }{2}\sum\limits_{j = 1}^{N} {C_{ij}^{1} } w_{j} = 0 \hfill \\ \end{aligned}$$
$$\begin{aligned} &\left( {Ak\frac{1 - \nu }{2}} \right)\left( {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{1} } \phi_{j} + r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } + r_{i}^{2} \phi_{i} } \right) \hfill \\&+N_{p} \mu \left\{ {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{4} w_{j} } + 2r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{3} w_{j} } + r_{i} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\} \hfill \\&-N_{p} \left\{ {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\}-k_{w} w_{i} \hfill \\\quad&+ k_{w} \mu \left\{ {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\} + k_{g} \left\{ {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\} \hfill \\\quad&- k_{g} \left\{ {r_{i}^{3} \sum\limits_{j = 1}^{N} {C_{ij}^{4} w_{j} } + 2r_{i}^{2} \sum\limits_{j = 1}^{N} {C_{ij}^{3} w_{j} } + r_{i} \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } + \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\} = 0. \hfill \\ \end{aligned}$$
(26)

Also, the DQ form of different types of boundary conditions at boundary point i = 1, N can be written as

$$w_{i} = 0$$
$$\phi_{i} = 0$$
$$(N_{r}^{1} )_{i} = 0 - :A\sum\limits_{j = 1}^{N} {C_{ij}^{1} } u_{j} + A\nu \frac{{u_{i} }}{{r_{i} }} + B\sum\limits_{j = 1}^{N} {C_{ij}^{1} } \phi_{j} + B\nu \frac{{\phi_{i} }}{{r_{i} }} = 0$$
$$(M_{r}^{1} )_{i} = 0 - :B\sum\limits_{j = 1}^{N} {C_{ij}^{1} } u_{j} + B\nu \frac{{u_{i} }}{{r_{i} }} + C\sum\limits_{j = 1}^{N} {C_{ij}^{1} } \phi_{j} + C\nu \frac{{\phi_{i} }}{{r_{i} }} = 0$$
$$\begin{aligned} (P_{r}^{1} )_{i} = 0\quad :&- N_{p} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } + N_{p} \mu \left\{ {\sum\limits_{j = 1}^{N} {C_{ij}^{3} w_{j} } + \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } } \right\} \hfill \\\quad &+k_{g} \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } + k_{g} \mu \left\{ {\sum\limits_{j = 1}^{N} {C_{ij}^{3} w_{j} } + \sum\limits_{j = 1}^{N} {C_{ij}^{2} w_{j} } } \right\} \hfill \\\quad &+Ak(\frac{1 - \nu }{2})\left\{ {\phi_{i} + \sum\limits_{j = 1}^{N} {C_{ij}^{1} w_{j} } } \right\} = 0. \hfill \\ \end{aligned}$$
(27)

By employing the DQ technique and assembling the stability equations and boundary conditions, the differential equations system has changed to set of linear algebraic equations following as (Farajpour et al. 2012; Mohammadi et al. 2014; Tornabene et al. 2009)

$$\left[ {\begin{array}{*{20}c} {\left[ {K_{bb} } \right]} & {\left[ {K_{bi} } \right]} \\ {\left[ {K_{ib} } \right]} & {\left[ {K_{ii} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d_{i} } \\ {d_{b} } \\ \end{array} } \right\} = N_{p} \left[ {\begin{array}{*{20}c} 0 & 0 \\ {\left[ {KN_{ib} } \right]} & {\left[ {KN_{ii} } \right]} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {d_{b} } \\ {d_{i} } \\ \end{array} } \right\},$$
(28)
$$\begin{aligned}&(\left[ {[KN_{ib} ][K_{bb} ]^{ - 1} [K_{bi} ] + [KN_{ii} ]} \right]^{ - 1} \left[ { - [K_{ib} ][K_{bb} ]^{ - 1} [K_{bi} ] + [K_{ii} ]} \right])\left\{ {d_{i} } \right\}^{T} - N_{p} [I]\left\{ {d_{i} } \right\}^{T} = 0 \hfill \\&([K_{total} ] - N_{p} [I])\{ d_{i} \} = 0 \hfill \\& N_{p} = {\text{Eigenvalue}}.[K_{toal} ] \hfill \\& d_{i} = \{ w_{2} , \ldots ,w_{n - 1} ,\phi_{2} , \ldots ,\phi_{n - 1} \} \hfill \\&d_{b} = \{ w_{1} ,w_{n} ,\phi_{1} ,\phi_{n} \} . \hfill \\ \end{aligned}$$
(29)

After implementation of the boundary conditions into formulation, the discretized governing Eq. (18) can be expressed by the following matrix form

$$\begin{aligned}&(\left[ {K_{total} } \right] - N_{p} I)\{ W\}=0 \hfill \\& \{ W\} =[u - \phi - w]^{T} , \hfill \\ \end{aligned}$$
(30)

where I denotes identity matrix and N p is the critical buckling load which can be calculated from Eq. (29) using a standard eigenvalue solver.

4 Results and discussion

In this section, the numerical results are presented for investigating the effects of small scale parameter, grading index, surrounding elastic medium and geometrical parameters on the buckling behavior of the annular FG nanoplate with various boundary conditions, namely clamped–clamped (CC), clamped–simply (CS), simply–clamped (SC), simply–simply (SS), clamped–free (CF) and free–clamped (FC) supports at inner and outer edges, respectively. The material properties of FG nanoplate are taken as that of E m = 70 Gpa, E c = 380 Gpa, ν = 0.3 (Hosseini-Hashemi et al. 2013). The outer and inner radii of the FG nanoplate are r o  = 20 nm and r i  = 0.5r o , respectively, unless stated otherwise. The results are defined and presented in terms of the following non-dimensional quantities, \(\varOmega = N_{r} r_{0}^{2} /D\), \(R = r_{i} /r_{o}\), \({\text{K}}_{\text{w}} = k_{w} r_{0}^{4} /D\), \({\text{K}}_{\text{g}} = k_{g} r_{0}^{2} /D\) which are the critical buckling load, annularity, Winkler and shear foundations, respectively, and \(D = E_{c} h^{3} /12(1 - \nu^{2} )\). Moreover, in order to measure the influence of small scale effect on the buckling behavior, buckling load ratio is defined as:

$$Buckling \, load \, ratio = \frac{Buckling\,load\,calculated\,using\,nonlocal\,theory}{Buckling\,load\,calculated\,using\,local\,theory}.$$

First, it is required to carry out a convergence test because the results of DQ procedure depend on the number of grid points. Thus, the non-dimensional buckling loads of CC, CS, SC and SS FG annular graphene sheet are tabulated in Table 1 for various numbers of grid points. As indicated in Table 1, ten grid points along the radial direction are sufficient to gain converge solution.

Table 1 Convergence and accuracy of the non-dimensional buckling load for various boundary conditions (r o  = 10 nm, n = 1, h/r o  = 0.1)
Full size table

In order to verify the accuracy of the formulation and results, the DQ solutions are compared with the ones reported for the buckling analysis of FG annular macroplate (Koohkan et al. 2010) and also those obtained by (Bedroud et al. 2013) for the buckling of isotropic annular nanoplate in Table 2 and Fig. 2, respectively, for different boundary conditions, grading indices, annularity and nonlocal parameters. As seen in Table 2 and Fig. 2, the present results are in excellent agreement with the ones obtained by Refs. (Bedroud et al. 2013; Koohkan et al. 2010) and current solutions are validated.

Table 2 Comparison of the DQM results with those calculated by Koohkan and Kimiaeifar (Koohkan et al. 2010) for the buckling of FG annular plate under uniform compression load
Full size table
Fig. 2
figure 2

Comparison of the DQM results with those calculated by Bedroud et al. (2013b) for the buckling of isotropic annular nanoplate under uniform compressive load

Full size image

Figure 3a–f illustrate the non-dimensional critical buckling load in terms of nonlocal parameters for different values of annularity (R) and grading index (n) with various types of boundary conditions (r o  = 20 nm, h = 0.5 nm). As seen, with respect to the type of boundary condition, the lowest to the highest differences of buckling load caused by increasing the nonlocal parameter are as follows: CF < FC < SS < CS < SC < CC. Also, it is obvious that with increase of grading index the buckling load decreases. So that differences of buckling load caused by changing the grading index are constant for all types of boundary conditions and annularity ratios in a specified nonlocal parameter. It is also observed that with increase of nonlocal parameter from 0 to 4 the differences of buckling loads remain constant for isotropic (n = 0) and FG nanoplate in different ratios of annularity and boundary conditions. Moreover, with decrease of R the difference of buckling loads between µ = 0 and µ = 4 decreases as well.

Fig. 3
figure 3

Non-dimensional critical buckling load in terms of nonlocal parameters, different values of annularity (R) and grading index (n) for (a) CF, (b) FC, (c) SS, (d) CS, (e) SC, (f) CC boundary conditions (r o  = 20 nm, h = 0.5 nm)

Full size image

Figure 4 illustrates the non-imensional critical buckling load versus grading index in different values of nonlocal parameters with and without presence of elastic medium for different boundary conditions (R = 0.5, h/r o  = 0.1). As seen in Fig. 4, the difference of buckling loads caused by changing the nonlocal parameter decreases by rising the coefficient of elastic foundation in all values of material grading indices. So that, in presence of elastic foundation, the effect of increasing nonlocal parameter on the decrease of buckling load varies as follows CF > FC > SS > CS > SC > CC. Furthermore, as observed in Fig. 3, it is shown in Fig. 4 that difference of buckling loads remains constant between two values of nonlocal parameter for all grading indices and boundary conditions of FG nanoplate without elastic foundation. However, in presence of elastic medium this behavior is not seen and the difference of buckling load caused by changing the nonlocal parameter decreases with increase of grading index.

Fig. 4
figure 4

Non-dimensional critical buckling load versus grading index with and without presence of elastic medium (Kw, Kg) and different values of nonlocal parameters (µ) for (a) SS, (b) CS, (c) SC, (d) CC, (e) CF, (f) FC boundary conditions (R = 0.5, h/r o  = 0.1)

Full size image

Figure 5 illustrates the buckling load in terms of Winkler and Pasternak elastic foundations for SS boundary condition. As depicted, for all values of grading indices and nonlocal parameter, the variation of buckling load caused by increasing the Winkler and Pasternak foundations is linear. In other words, the effects of elastic foundations on buckling loads are independent of nonlocal parameter and grading index. Also, as observed in Fig. 5, the effect of grading index on buckling load increases when the elastic foundation exists.

Fig. 5
figure 5

Non-dimensional critical buckling load of SS annular nanoplate versus the (a) Winkler module and (b) shear elastic foundation (Kw = 50) for different values of grading index (R = 0.5, h/r o  = 0.1)

Full size image

Figure 6 shows the variation of buckling load in terms of thickness to radius ratio for two cases of with and without elastic foundation and all types of boundary conditions. As seen, for both cases of with and without elastic medium by increasing the thickness-to-radius ratio the buckling load raises significantly. Also, comparing the results of Fig. 6a and b shows that effects of thickness-to-radius ratio on buckling loads are independent of elastic foundation for all boundary conditions. Furthermore, in specified radiuses with increase of the nanoplate’s thickness the difference of buckling load between two values of grading index remains constant for the nanoplate without elastic foundation. However, if the elastic foundation exists, by increasing the thickness of the nanoplate the difference of buckling load between two values of grading index decreases.

Fig. 6
figure 6

Critical buckling load of annular FG nanoplate versus the (a) Without elastic foundation (b) Elastic foundation (Kw = 100, Kg = 10) for different boundary condition and different values of nonlocal parameter (µ = 1 nm2, R = 0.5, r o = 20 nm)

Full size image

In Fig. 7, the values of buckling load ratio is illustrated in terms of grading index for two different values of nonlocal parameter and various types of boundary conditions. As shown, the buckling load ratio is constant for different values of grading indices. Also, by increasing the nonlocal parameter the buckling load ratio decreases for all types of boundary conditions. Furthermore, with respect to the type of boundary condition, the greatest to the lowest difference of buckling load ratio between two values of nonlocal parameter are as follows FC < CF < SS < CS < SC < CC.

Fig. 7
figure 7

Buckling load ratio of annular FG nanoplate versus grading index for different boundary conditions and nonlocal parameters (h = 0.5 nm, R = 0.5, r o = 20 nm)

Full size image

Figure 8 shows the effect of outer radius on the buckling load ratio in different values of grading indices for CC boundary condition. As seen, in a specified inner radius by raising the outer radius the buckling load ratio increases. Moreover, in higher values of the outer radius the effect of nonlocal parameter on the buckling load ratio goes up.

Fig. 8
figure 8

Buckling load ratio of CC annular FG nanoplate versus grading index for different values of outer radius and nonlocal parameter (r i  = 10, h = 0.5 nm)

Full size image

Similar to Fig. 8, the influence of inner radius on the buckling load ratio is considered in Fig. 9 for CC annular FG nanoplate with different nonlocal parameters. As indicated, with increase of inner radius the buckling load ratio decreases.

Fig. 9
figure 9

Buckling load ratio of CC annular FG nanoplate versus grading index for different values of inner radius and nonlocal parameter (r o  = 20, h = 0.5 nm)

Full size image

Figure 10 shows effect of mod numbers on the non-dimensional buckling load in different values of nonlocal parameters and grading indices for SS and CC boundary conditions. It can be inferred that decrease of buckling loads caused by increasing the nonlocal parameters from 0 to 4, goes up by raising the mod numbers. Furthermore, this behavior is independent of grading index for all boundary conditions.

Fig. 10
figure 10

Non-dimensional critical buckling load versus the nonlocal parameter in different of buckling mod number (m) and different values of grading index (n = 2,5) for (a) SS (b) CC boundary conditions (R = 0.5, r o = 20 nm)

Full size image

In Table 3, non-dimensional buckling load is presented for different values of outer and inner radiuses of SS annular FG nanoplate. As indicated, with increase of outer radius and decrease of inner radius the difference of buckling load between two values of nonlocal parameter falls. In other words, the difference of buckling load between two values of nonlocal parameter is dependent to the both inner and outer radiuses.

Table 3 Non-dimensional critical buckling load for different values of outer and inner radiuses of SS annular FG nanoplate (n = 1, h = 0.5 nm)
Full size table

In Tables 4 and 5, the non-dimensional critical buckling load is presented for different values of nonlocal parameters and grading indices of FG nanoplate with and without presence of elastic medium and various boundary conditions. As observed previously, with increase of nonlocal parameter the effect of grading index on the buckling load is constant. Also, by increasing the Winkler and Pasternak elastic foundations the effect of grading index on the buckling load decreases.

Table 4 Non-dimensional critical buckling load in terms of nonlocal parameters for different grading indices (n) and various boundary conditions with and without Winkler elastic medium (R = 0.5 nm, h/r o  = 0.1)
Full size table
Table 5 Non-dimensional critical buckling load in terms of nonlocal parameters for different grading indices (n) and various boundary conditions in presence of Pasternak elastic medium (Kw, Kg) (R = 0.5 nm, h/r o  = 0.1)
Full size table

5 Conclusions

In this study, the axisymmetric buckling of FG annular nanoplate embedded in an elastic medium is investigated under uniform in-plane loading. The material properties of the FG nanoplate are assumed to vary in the thickness direction according to a power-law distribution in terms of the volume fraction of the constituents. Using the principle of virtual work, the equilibrium equations are obtained through Mindlin orthotropic plate models, and Eringen nonlocal elasticity theory was applied to consider the small scale effect parameter. Differential quadrature method is used to solve the governing equations for free, simply supported or clamped boundary conditions and various combinations of them. The presented formulation and method of solution are validated by comparing the results with those available in the literature. Finally, a detailed parametric study is carried out to investigate the influences of the length scale parameter, annularity, elastic medium, grading index and boundary conditions on the buckling load of FG annular nanoplate. Some general inferences are mentioned below:

  • In a specified nonlocal parameter, differences of buckling load caused by changing the grading index are constant for all types of boundary conditions and annularity ratios.

  • The lowest to the highest differences of buckling load caused by increasing the nonlocal parameter are related to CF < FC < SS < CS < SC < CC boundary conditions.

  • In presence of elastic medium, the highest and lowest effect of increasing nonlocal parameter on the decrease of buckling load are related to CF and CC boundary conditions, respectively.

  • Difference of buckling loads remains constant between two values of nonlocal parameter for all grading indices and boundary conditions of FG nanoplate without elastic medium.

  • For all values of grading indices and nonlocal parameter, the variation of buckling load caused by increasing the Winkler and Pasternak foundations is linear.

  • For both cases of with and without elastic medium, by increasing the thickness-to-radius ratio of the FG nanoplate buckling load raises significantly and this increase is independent of boundary conditions and grading index.