1 Introduction

Electrothermal microactuators in microelectromechanical systems (MEMS) are gaining increasing attention over the past several decades (Steiner et al. 2015; Phan et al. 2015; Shen et al. 2014). Amongst the family of various actuation approaches such as electro-static (Gupta et al. 2012), electro-magnetic (Pawinanto et al. 2013), and piezoelectric (Moussa et al. 2014), etc., electrothermal (Lott et al. 2002; Ogando et al. 2012) actuators that work on the principle of Joule heating and resulting thermal expansions, have been demonstrated to be compact, stable, large displacement and force actuation techniques (Sameoto et al. 2004; Mayyas et al. 2009). Owing to these virtues, they have been used in a wide spectrum of applications, such as switch (Li et al. 2010), nano-positioners (Rakotondrabe et al. 2014; Oak et al. 2011), micro-grippers (Shivhare et al. 2015; Wang et al. 2015), micro-testing devices (Zhu et al. 2006), micro-pump (Karajgikar et al. 2010), and terahertz metamaterials (Lalas et al. 2014), etc. Electrothermal principle can also be combined with other principles, such as piezoelectric effect, to achieve both coarse and fine actuation (Micky and Ioan 2011). In general, electrothermal actuators can be categorized in light of their motion directions as, in-plane and out-of-plane (Ogando et al. 2012; Li and Uttamchandani 2009; Kim et al. 2013) actuations. The in-plane actuators are dominant in real-world applications due to its ease of fabrications using the surface micromachining technologies. In contrast, the bulk micromachining technologies have been rarely used for the out-of-plane actuators due to its limited fabrication processes. As a result, the most efficient methods in constructing out-of-plane actuators is to utilize existing in-plane actuators (Chen and Lee 2015).

The U- (Wang et al. 2015), V- (Enikov et al. 2005), and Z-shaped (Guan and Zhu 2010) beam electrothermal actuators are three fundamental types capable of generating in-plane motion. The U-shaped beam is capable of generating arc circular motion, whereas the V- and Z-shaped actuators offer rectilinear motion. In decades, extensive research effort has focused on different aspects of interest including fabrication (Kim et al. 2013; Feng et al. 2016), design (Oak et al. 2011; Suen et al. 2011; Choi et al. 2015; Li et al. 2015), control (Borovic et al. 2005), modeling (Zhang et al. 2015a, b), buckling (Wittwer et al. 2006; So and Pisano 2015), and scaling effect (Jungen et al. 2006), etc. And various configurations derived from the three basic types have been created to allow for all kinds of applications (Zhu et al. 2006; Torres et al. 2015). Compared to the arc circular motion the U-shaped actuator offers, rectilinear motion is preferred and widespread in a wide range of MEMS devices as it would benefit the development of more complex systems by combining the actuators with compliant mechanisms (Shi et al. 2015; Xi et al. 2016), and therefore in recent years V- and Z-shaped actuators have attracted extensive attention.

Despite the advantages over other actuation approaches, electrothermal actuations have shown disadvantages of slow response and large power consumptions, and easy to be over-heated resulting in thermal failure when driven periodically. Previous efforts have partially addressed these issues in static terms (Enikov et al. 2005; Guan and Zhu 2010; Hickey et al. 2003). However, few research efforts have been made to dynamic modeling and analysis which addresses the control and design that concerns the microactuators with fast response.

In practice, it is desired to drive the actuator periodically usually with step input excitations (Mayyas et al. 2009). It is evidenced by experimental results that the overall dynamic response is dominated by the electrothermal response due to the fact that the mechanical frequency is much faster than thermal frequency (Hussein et al. 2015). And, in general, the electrothermal response has a dynamic cycle that consists of heating, dwell (engaging), and cooling times (Mayyas et al. 2009) when it is driven periodically. Hence, the maximum operating frequency, excluding the dwell time, is measured from the heating and cooling rates. To make fast actuation possible, on one hand, it is desirable to increase operating frequency via decreasing the heating and cooling times. On the other hand, the actuators have to be operated below a frequency that the actuator is able to completely dissipate the heat during each dynamic cycles such that it will neither cause a static offset nor in a worst case thermal failure due to accumulation of heat. Therefore, an analytical model is primarily needed to provide not only predictions on the dynamic response for each cycle, but also offers insight and guidance on design of the structures with aims of increasing heating and cooling rates.

To this objective, a number of works have focused on the dynamic modeling (Borovic et al. 2005; Hussein et al. 2015, 2016; Walle et al. 2010), simulation analysis (Hickey et al. 2003; Mallick et al. 2012; Li et al. 2007), and experimental studies (Hussein et al. 2015) of the U-shaped actuators. But for the V-shaped and Z-shaped actuators featured by a symmetric beam structure supporting a shuttle in the middle, which differs the U-shaped beam completely, few research efforts have been reported on dynamic issues. Our preliminary work (Zhang et al. 2016) has developed a common dynamic electrothermal model of the V- and Z-shaped actuators for the first time, and proved that the electrothermal response is significantly different from that of the line-shaped beam case due to existence of the shuttle. In that work, only: (1) the heating process, (2) the “in vacuum” working condition, and the electrothermal behaviors, were considered. As a result, the model cannot be applied to: (1) a complete dynamic cycle incorporating both the heating and the cooling process, (2) the “in air” working conditions, where heat also dissipated to the substrate via the air gap, and (3) overall electro-thermo -mechanical dynamic behaviors.

In this paper, we establish a dynamic model of the V- and Z-shaped electrothermal actuators capable of predicting dynamic cycle behaviors, i.e., heating and cooling, under step excitations. The model also takes into account both the “in air” and “in vacuum” conditions. The overall system model is composed of dynamic electrothermal and static thermomechanical sub-models with considerations that the electrothermal dominates the overall dynamics of the system due to the significant higher mechanical frequency over the thermal frequency. The electrothermal behaviors are described by partial differential equations (PDE) and is solved subjected to appropriate boundary, continuity, and initial conditions for each segments. Different from the line-shaped beam in which the method of Fourier series can be utilized directly, a modified Fourier series method is used for solving the PDEs. The thermomechanical behaviors are treated as quasi-static and previous work results are thus applied in which the Castigliano’s theorem is used to predict the displacement and force given the average temperature rise of the beams. The final solution, combining the electrothermal and thermomechanical solutions, is conveniently written as sum of the steady-state and transient responses. The verification of the model is conducted using the finite element analysis via the ANSYS software, in which both the temperature and displacement are discussed.

With a proposed comparison benchmark, distinct dynamic behaviors between the U-shaped actuator and the V/Z-shaped actuators are illustrated using finite-element simulations. Finally, influences of the structural and material parameters on the dynamic behaviors are discussed with aims to provide insight and guidance on improving the design and optimization of dimension of the V- and Z-shaped beams.

2 Dynamic modeling

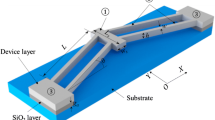
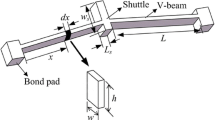
The working principle of the V- and Z-shaped actuators is simple. When applying a voltage difference on the anchors, heat is generated due to Joule heating effect, and the shuttle will be pushed forward outputting displacement and force thanks to the symmetric thermal expansion of beams. The input is the voltage, and the output is displacement/force for the actuator system. The schematic diagram as well as dimension notations of V- and Z-shaped electrothermal microactuators is depicted in Fig. 1 is the thickness of air gap between the structure and the substrate. \( L_{0} \), called half span of beams, is the distance between the anchor and the shuttle. \( L_{b} \) denotes beam length measured along the beam shape (i.e., for V-shaped beam, \( L_{b} = L_{0} /cos\theta \), and for Z-shaped beam, \( L_{b} = L_{2} + L_{0} \)). In addition, \( b \) denotes the thickness of the structure, i.e., \( b = b_{0} = b_{1} \).\( h_{0} \) and \( h_{1} \) are width of the beam and the shuttle respectively. \( L_{s} \) denotes the length of the shuttle.

Fig. 1
figure 1

Schematic diagram of V- and Z-shaped electrothermal microactuator

Full size image

As evidenced by simulation and experiment results that mechanical frequency is much higher than the thermal frequency (Hussein et al. 2015), the mechanical inertia is considered to be quasi-static. The overall dynamic modeling can therefore be divided into two sub-modeling, i.e., the dynamic electrothermal modeling on the evolution of the temperature distribution caused by the voltage applied to the anchors, and the static thermomechanical modeling on the output displacement and force driven by temperature rise inside the beams, as shown in Fig. 2 below.

Fig. 2
figure 2

Block diagram of dynamic modeling

Full size image

In practice, electrothermal actuators are desired to work periodically in each dynamic cycles consisting of heating, dwell (engaging), and cooling times (Mayyas et al. 2009). This is often realized by applying a step voltage to the anchors (i.e., heating and dwell) and then switched off (i.e., cooling). Heating time allows the generation and dissipation of heat inside the structure until it reaches a dynamic balanced state (i.e., dwell) resulting in the shuttle being pushed forward and kept at a static deflection. Cooling time allows the dissipation of heat by switching off the voltage. In order to increase the operating frequency, on one hand, heating time must be reduced to achieve fast response. On the other hand, the cooling time also has to be compressed to make sure the heat is completely dissipated so that the actuator neither retain a perturbed static deflection nor heat will accumulate in the structure causing the temperature keep rising and eventually thermal failure (Mayyas et al. 2009).

In what follows, the model will incorporate both heating and cooling dynamics for the V- and Z-shaped actuators under a step voltage. In addition, as the working conditions affects significantly the heat dissipation, both “in vacuum” and “in air” working environments are taken into account.

2.1 Electrothermal modeling

Since the beams are typically slender and one-dimensional (1-D) heat transfer is assumed. Heat conduction is considered to be the only heat transfer mode in this paper due to the fact that the heat convection and radiation are weak and thus is omitted. Because the shape of beams, i.e., V- and Z-shaped beams, is unrelated to the heat generation and transfer, it is convenient to use a general structure with two line-shaped beams supporting a shuttle for the electrothermal modeling, as in Fig. 3. Based on our simulation results, direct heat transfer analysis is sufficient for simple structures like the V- and Z-shaped beams. However, for some complex structures, the thermal networks techniques can be used to largely facilitate the analysis of heat transfer problem through treating heat transfer to be equivalent to electric circuit analysis (Micky and Ioan 2010).

Fig. 3
figure 3

General line-shaped model in dynamic electrothermal modeling of V- and Z-shaped actuators

Full size image

With assumptions of 1-D heat transfer and constant material properties, the partial differential equation (PDE) that governs the heat conduction process is given by

$$ \rho C_{p} \frac{\partial u}{\partial t} - k\frac{{\partial^{2} u}}{{\partial x^{2} }} + \varepsilon_{0} \left( {u - T_{0} } \right) = \dot{q}, $$
(1)

where the first term on the left describes the rate of energy stored in the structure, the second term indicates the heat conduction in the structure, the third term is the heat dissipation to the substrate though the air gap, and the term on the right side is the input power due to Joule heating. \( u \) and \( T_{0} \) represent the temperature of the structure (at position \( x \) and time \( t \)) and room temperature, respectively. Noted that in (1) the temperature of the substrate is assumed to be remained at room temperature during operation. \( \rho \), \( C_{p} \), and \( k \) are density, specific heat, and thermal conductivity of the structure respectively.\( \varepsilon_{0} \) is calculated as \( \varepsilon_{0} = k_{a} S_{F} /\left( {bh_{a} } \right) \), in which \( k_{a} \) and \( S_{F} \) denote the thermal conductivity of air and the shape factor that accounts for the influence of the beam geometry in the conduction of heat to the substrate.\( S_{F} \) is obtained empirically as \( S_{F} = S_{0} \cdot \frac{{bh_{a} }}{{h_{0} \left( {b + h_{a} } \right)}} + 1 \) in which \( S_{0} \approx \) 161/180. (1) is written in compact form as in (2).

$$ \frac{\partial u}{\partial t} - \hat{k}\frac{{\partial^{2} u}}{{\partial x^{2} }} + \varepsilon u = f, $$
(2)

where \( \varepsilon = \varepsilon_{0} /(\rho C_{p} ) \), \( f = \varepsilon T_{0} + \dot{f} \) and \( \dot{f} = \dot{q}/(\rho C_{p} ) \). (1) and (2) govern the heat balance in differential segment \( dx \) and is used for both line-shaped beam and the actuators cases. The existence of the shuttle makes the actuator different structure in terms of heat generation and conduction compared to the simple line-shaped beams. Therefore, three separate equations are needed to describe the behavior of each segments of the actuator, that is, the left beam, shuttle, and the right beam, as follows

$$ \frac{{\partial u_{k} }}{\partial t} - \hat{k}\frac{{\partial^{2} u_{k} }}{{\partial x^{2} }} + \varepsilon u_{k} = f_{k} , $$
(3)

where the subscript \( k \) represents each segments of the structure, i.e., \( k = 1,s, 2 \) denotes the left beam, shuttle, and the right beam, respectively. The term on the right side \( f_{k} \) is calculated as \( f_{k} = \varepsilon T_{0} + \dot{f}_{k} \), in which \( \dot{f}_{k} = \dot{q}_{k} /(\rho C_{p} ) \). \( \dot{q}_{k} \) is obtained as

$$ \dot{q}_{s} = \frac{1}{{\hat{\rho }(2L_{b} H + L_{s} )^{2} }}U^{2} , $$
(4)
$$ \dot{q}_{b} = H^{2} \dot{q}_{s} , $$
(5)

where, \( H = A_{s} /(mA_{b} ) \), and \( m \) represents the number of pairs of beams. Clearly, due to the symmetric of the structure, the input power in the two beams are the same, and hence we have \( \dot{q}_{b} = \dot{q}_{1} = \dot{q}_{2} \) and \( \dot{f}_{b} = \dot{f}_{1} = \dot{f}_{2} . \)

Clearly, (2) applies for the following cases: (1) V- and Z-shaped beams, (2) actuator \( \left( {H \ne 1} \right) \) and line-shaped beams \( \left( {H = 1} \right) \), (3) heating (\( \dot{f} \ne 0 \)) and cooling (\( \dot{f} = 0 \)), and (4) “in air” (\( \varepsilon \ne 0 \)) and “in vacuum” (\( \varepsilon = 0 \)) conditions.

It is convenient to treat the temperature \( u(x,t) \) as sum of the steady-state \( w(x) \) and transient \( v(x,t) \) solutions as in (6).

$$ u\left( {x,t} \right) = w\left( x \right) + v\left( {x,t} \right), $$
(6)

Substituting (6) into (2) allows one to obtain the ODE of \( w\left( x \right) \) and PDE of \( v\left( {x,t} \right) \) respectively as in (7) and (8)

$$ \frac{{d^{2} w}}{{dx^{2} }} - \frac{\varepsilon }{{\hat{k}}}w = - \frac{f}{{\hat{k}}}, $$
(7)
$$ \frac{\partial v}{\partial t} - \hat{k}\frac{{\partial^{2} v}}{{\partial x^{2} }} + \varepsilon v = 0 . $$
(8)

In order to use the method of separation of variables, the following transform is used

$$ v\left( {x,t} \right) = v_{0} \left( {x,t} \right)e^{ - \varepsilon t} . $$
(9)

Substituting (9) into (8), we obtain

$$ \frac{{\partial v_{0} }}{\partial t} - \hat{k}\frac{{\partial^{2} v_{0} }}{{\partial x^{2} }} = 0 . $$
(10)

To solve the steady-state and transient responses, the following two boundary (B.C.) and four continuity conditions (C.C.), and one initial condition (I.C.) are utilized, listed in Table 1.

Table 1 Boundary, continuity, and initial conditions for actuators
Full size table

The boundary conditions indicate that the temperature at the two ends of the actuator is assumed to be remained at room temperature during operation. The continuity conditions demonstrate the fact that the temperature and heat flux at \( x = L_{b} \) and \( x = L_{b} + L_{s} \) for the shuttle and the beam are the same. Besides the boundary and continuity conditions, initial conditions are needed for solving the transient responses. That is, for heating process, the temperature of the actuator is initially at room temperature, and for the cooling stage, the initial temperature is at the steady-state temperature (i.e., the temperature in dwell time) after heating. The accent markers of “hat” and “check” represent the heating and cooling processes respectively. For the initial conditions, for instants, \( \hat{w}_{k} \) and \( \check{w}_{k} \) represent the steady-state temperatures for heating and cooling processes respectively, and \( \hat{v}_{k} \) and \( \check{v}_{k} \) represent the transient temperature for the heating and cooling processes, respectively. The steady-state response for heating process in vacuum and in air cases take the forms as in (11) and (12) respectively

$$ \hat{w}_{k} \left( x \right) = a_{k} x^{2} + b_{k} x + c_{k} , $$
(11)
$$ \hat{w}_{k} \left( x \right) = a_{k} e^{rx} + b_{k} e^{ - rx} + c_{k} , $$
(12)

where \( r = \sqrt {\frac{\varepsilon }{{\hat{k}}}} = \sqrt {\frac{{\varepsilon_{0} }}{k}} \). The unknown coefficients are obtained combining (7) and using the boundary and continuity conditions. The results can be found in our previous work on static modeling of V- and Z-shaped actuators (Zhang et al. 2015a, b).

In Table 1, the steady-state temperature response for the cooling process in both in vacuum (\( \varepsilon = 0 \)) and in air \( \left( {\varepsilon \ne 0} \right) \) conditions is returned to the room temperature \( T_{0} \), i.e., \( \check{w}_{k} = T_{0} \) which can be proved using the boundary and continuity conditions listed in Table I. Note that for the cooling process, \( \dot{f} = 0 \) and thus \( f = \varepsilon T_{0} \).

Using the method of separation of variables, \( v_{0} \left( {x,t} \right) \) can be decomposed into two functions with separated variables

$$ v_{0} \left( {x,t} \right) = X\left( x \right)T\left( t \right). $$
(13)

Substituting the separated functions (13) into the PDE (10) allows one to obtain

$$ \hat{k}X^{{\prime \prime }} + \lambda X = 0 , $$
(14)
$$ T^{{\prime }} + \lambda T = 0, $$
(15)

where \( \lambda \) is a positive non-zero constant assigned to \( X(x) \) and \( T(t) \). The general solution of \( v_{0} \left( {x,t} \right) \) has the following form

$$ v_{0} \left( {x,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } e^{{ - \hat{k}\lambda_{n}^{2} t}} \left[ {A_{n} \cos \left( {\lambda_{n} x} \right) + B_{n} { \sin }(\lambda_{n} x)} \right], $$
(16)

where \( \lambda_{n} = \sqrt {\lambda /\hat{k}} \). For the actuator, \( v_{0} \left( {x,t} \right) \) is decomposed into three separated functions, in which the subscript k refers to each segments of the actuator as

$$ v_{0k} \left( {x,t} \right) = \mathop \sum \limits_{n = 1}^{\infty } e^{{ - \hat{k}\lambda_{n}^{2} t}} \left[ {A_{kn} \cos \left( {\lambda_{n} x} \right) + B_{kn} { \sin }(\lambda_{n} x)} \right]. $$
(17)

It is clear that, to obtain \( v_{0k} \left( {x,t} \right) \), \( \lambda_{n} \), \( A_{kn} \), and \( B_{kn} \) need to be calculated.

The first step is to find \( \lambda_{n} \). Introducing the boundary and continuity conditions summarized in Table 1 to (17), we obtain

$$ \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 & {} & {} \\ {} & {s_{1} } & { - c_{1} } \\ {} & {} & { - \bar{c}} \\ \end{array} } & {\begin{array}{*{20}c} {} & {} & {} \\ { - s_{1} } & {} & {} \\ { - \bar{s}} & {\bar{c}} & {\bar{s}} \\ \end{array} } \\ {\begin{array}{*{20}c} {} & {c_{1} } & {Hs_{1} } \\ {} & {} & {H\bar{s}} \\ {} & {} & {} \\ \end{array} } & {\begin{array}{*{20}c} { - Hc_{1} } & {} & {} \\ { - H\bar{c}} & { - \bar{s}} & {\bar{c}} \\ {} & {c_{2} } & {s_{2} } \\ \end{array} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{1n} } \\ {B_{1n} } \\ {A_{sn} } \\ \end{array} } \\ {\begin{array}{*{20}c} {B_{sn} } \\ {A_{2n} } \\ {B_{2n} } \\ \end{array} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ \end{array} } \\ \end{array} } \right), $$
(18)

where \( s_{1} = { \sin }(\lambda_{n} L_{b} ) \), \( c_{1} = { \cos }(\lambda_{n} L_{b} ) \), \( s_{2} = { \sin }(\lambda_{n} L) \), \( c_{2} = { \cos }(\lambda_{n} L) \), \( {\bar{\text{s}}} = { \sin }[\lambda_{n} (L_{b} + L_{s} )] \), \( {\bar{\text{c}}} = { \cos }[\lambda_{n} (L_{b} + L_{s} )] \), \( \overline{{{\bar{\text{s}}}}} = { \sin }(\lambda_{n} L_{s} ) \), and \( \overline{{{\bar{\text{c}}}}} = { \cos }(\lambda_{n} L_{s} ) \). In order that the coefficients \( A_{kn} \) and \( B_{kn} \) are nonzero, the determinant of the matrix on the left must equal to zero. Thus, the characteristic equation of \( \lambda_{n} \) concluded from (18) is as follows

$$ s_{1}^{2} \overline{{\bar{s}}} H^{2} - 2s_{1} c_{1} \overline{{\bar{c}}} H - c_{1}^{2} \overline{{\bar{s}}} = 0. $$
(19)

Unlike the case of a line-shaped beam as in appendix section, the transcendental Eq. (19) does not allow one to obtain a simple analytical form of \( \lambda_{n} \).The value of \( \lambda_{n} \) for the actuator must be then calculated numerically using (19).

Next step is to find coefficients \( A_{kn} \) and \( B_{kn} \). For the heating case, applying the initial conditions to (17), we obtain

$$ T_{0} - \hat{w}_{k} \left( x \right) = \mathop \sum \limits_{n = 1}^{\infty } \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} \sin \left( {\lambda_{n} x} \right)} \right]. $$
(20)

Unlike the line-shaped case, where Fourier series method is utilized to solve (49), the Fourier series method cannot be used for solving (20) due to the existence of the shuttle. Here, we use a modified Fourier series method by multiplying both sides of (20) dy \( H_{k} \left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} { \sin }(\lambda_{m} x)} \right] \), and integrating it over the length of the structure, as follows

$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {T_{0} - \hat{w}_{k} \left( x \right)} \right]\left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} { \sin }(\lambda_{m} x)} \right]dx \hfill \\ &\quad = \mathop \sum \limits_{n = 1}^{\infty } \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]\\&\qquad\times\,\left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} { \sin }(\lambda_{m} x)} \right]dx , \hfill \\ \end{aligned} $$
(21)

where \( H_{1} = H_{2} = 1 \) and \( H_{s} = H \). The right side in (21) can be decomposed into two parts

$$ \begin{aligned} &\mathop \sum \limits_{n = 1}^{\infty } \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]\left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} { \sin }(\lambda_{m} x)} \right]dx \hfill \\ &\quad = \mathop \sum \limits_{n \ne m}^{\infty } \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} \sin \left( {\lambda_{n} x} \right)} \right]\left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} \sin \left( {\lambda_{m} x} \right)} \right]dx \hfill \\ &\qquad + \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} { \sin }(\lambda_{m} x)} \right]^{2} dx , \hfill \\ \end{aligned} $$
(22)

Considering the boundary and continuity conditions allows the cancellation of the first part of (22) for \( n \ne m \) as

$$ \mathop \sum \limits_{n \ne m}^{\infty } \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} \sin \left( {\lambda_{n} x} \right)} \right] \times\left[ {\hat{A}_{km} \cos \left( {\lambda_{m} x} \right) + \hat{B}_{km} \sin \left( {\lambda_{m} x} \right)} \right]dx = 0. $$
(23)

Therefore, (21) can be written as

$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {T_{0} - \hat{w}_{k} \left( x \right)} \right]\left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]dx \hfill \\ &\quad = \mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]^{2} dx. \hfill \\ \end{aligned} $$
(24)

Considering the boundary and continuity conditions, the left and right sides in (24) are expressed respectively in (25) and (26) as follows

$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {T_{0} - \hat{w}_{k} \left( x \right)} \right]\left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]dx \hfill \\ &\quad = \frac{{H\dot{f}_{s} }}{{\lambda_{n} \left( {\varepsilon + \lambda_{n}^{2} \hat{k}} \right)}}\left[ {H\hat{B}_{1n} \left( {c_{1} - 1} \right) + \left( {\hat{B}_{sn} {\bar{\text{c}}} - \hat{A}_{sn} {\bar{\text{s}}}} \right) - \left( {\hat{B}_{sn} c_{1} - \hat{A}_{sn} s_{1} } \right) + H\left( {\hat{B}_{2n} c_{2} - \hat{A}_{2n} s_{2} } \right) - H\left( {\hat{B}_{2n} {\bar{\text{c}}} - \hat{A}_{2n} {\bar{\text{s}}}} \right)} \right], \hfill \\ \end{aligned} $$
(25)
$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]^{2} dx \hfill \\ &\quad = \frac{1}{2}\hat{B}_{1n}^{2} L_{b} + \frac{H}{2}\left( {\hat{A}_{sn}^{2} + \hat{B}_{sn}^{2} } \right)L_{s} + \frac{1}{2}\left( {\hat{A}_{2n}^{2} + \hat{B}_{2n}^{2} } \right)L_{b} . \hfill \\ \end{aligned} $$
(26)

According to (18), \( A_{kn} \) and \( B_{kn} \) can be expressed in terms of \( B_{1n} \) as follows

$$ \lambda_{k} = \frac{{B_{kn} }}{{B_{1n} }} = \left\{ {\begin{array}{*{20}c} { 1, \quad k = 1} \\ {\frac{{Hs_{1}^{2} + c_{1}^{2} }}{H}, \quad k = s} \\ {\frac{{c_{2} \left( {Hs_{1} \overline{{{\bar{\text{c}}}}} + c_{1} \overline{{{\bar{\text{s}}}}} } \right)}}{{ - s_{1} H}}, \quad k = 2} \\ \end{array} } \right. , $$
(27)
$$ \eta_{k} = \frac{{A_{kn} }}{{B_{1n} }} = \left\{ {\begin{array}{*{20}c} {0, \quad k = 1} \\ {\frac{{s_{1} c_{1} \left( {H - 1} \right)}}{H}, \quad k = s} \\ {\frac{{s_{2} \left( {Hs_{1} \overline{{{\bar{\text{c}}}}} + c_{1} \overline{{{\bar{\text{s}}}}} } \right)}}{{s_{1} H}}, \quad k = 2} \\ \end{array} } \right.. $$
(28)

Introducing (27), (28) into (25) and (26) respectively, allows the expressions of (25) and (26) in terms of \( \hat{B}_{1n} \) as follows

$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {T_{0} - \hat{w}_{k} \left( x \right)} \right]\left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]dx \hfill \\ &\quad = \frac{{H\dot{f}_{s} \hat{B}_{1n} }}{{\lambda_{n} \left( {\varepsilon + \lambda_{n}^{2} \hat{k}} \right)}}\left[ {H\left( {c_{1} - 1} \right) + \lambda_{s} \left( {{\bar{\text{c}}} - c_{1} } \right) + \eta_{s} \left( {s_{1} - {\bar{\text{s}}}} \right) +\, H\lambda_{2} \left( {c_{2} - {\bar{\text{c}}}} \right) + H\eta_{2} \left( {{\bar{\text{s}}} - s_{2} } \right)} \right], \hfill \\ \end{aligned} $$
(29)
$$ \begin{aligned} &\mathop \int\limits_{0}^{L} H_{k} \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} { \sin }(\lambda_{n} x)} \right]^{2} dx \hfill \\ & \quad = \frac{1}{2}\hat{B}_{1n}^{2} \left[ {L_{b} + H\left( {\eta_{s}^{2} + \lambda_{s}^{2} } \right)L_{s} + \left( {\eta_{2}^{2} + \lambda_{2}^{2} } \right)L_{b} } \right]. \hfill \\ \end{aligned} $$
(30)

Combining (29) and (30) with (24), \( \hat{B}_{1n} \) is expressed as

$$ \hat{B}_{1n} = \frac{1}{{k\hat{\rho }\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n} }} \cdot D \cdot U^{2} , $$
(31)

where \( D = \frac{{2s_{1} H^{2} \left[ {\left( {c_{1} - 1} \right)\left( {\overline{{\bar{c}}} + 1} \right)s_{1} H^{2} + \left( {c_{1}^{2} - s_{1}^{2} - c_{1} } \right)\overline{{\bar{s}}} H + \left( {\overline{{\bar{c}}} - 1} \right)c_{1} s_{1} } \right]}}{{(2L_{b} H + L_{s} )^{2} \left[ {s_{1}^{2} H^{2} L_{b} + \left( {H^{2} s_{1}^{2} + c_{1}^{2} } \right)s_{1}^{2} HL_{s} + \left( {Hs_{1} \overline{{\bar{c}}} + c_{1} \overline{{\bar{s}}} } \right)^{2} L_{b} } \right]}}, \) \( r = \sqrt {\frac{\varepsilon }{{\hat{k}}}} = \sqrt {\frac{{\varepsilon_{0} }}{k}} \).

Thus \( \hat{A}_{kn} \) and \( \hat{B}_{kn} \) is derived using (31), (27) and (28). For the cooling cases, applying the initial condition to (17), we have

$$ \hat{w}_{k} \left( x \right) - T_{0} = \mathop \sum \limits_{n = 1}^{\infty } \left[ {\hat{A}_{kn} \cos \left( {\lambda_{n} x} \right) + \hat{B}_{kn} \sin \left( {\lambda_{n} x} \right)} \right]. $$
(32)

Comparing with (20), it is clear that \({\check{B}}_{1n} \) is negative to \( \hat{B}_{1n} \), and thus

$$ {\check{A}}_{kn} = - \hat{A}_{kn} , $$
(33)
$$ \check{B}_{kn} = - \hat{B}_{kn} . $$
(34)

Now, it is possible to derive the transient responses of the temperature \( v_{k} \left( {x,t} \right) \) for both the heating \( \hat{v}_{k} \left( {x,t} \right) \) and cooling \({\check{v}}_{k} \left( {x,t} \right) \) cases

$$ \hat{v}_{k} \left( {x,t} \right) = \frac{{U^{2} }}{{k\hat{\rho }}} \cdot \left\{ {\mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n} }} \cdot D \cdot \left[ {\eta_{k} \cos \left( {\lambda_{n} x} \right) + \lambda_{k} \sin \left( {\lambda_{n} x} \right)} \right]} \right\}. $$
(35)
$${\check{v}}_{k} \left( {x,t} \right) = - \hat{v}_{k} \left( {x,t} \right) $$
(36)

Based on (6), the temperature response for the actuator is derived. Note that the temperature for the case of in vacuum conditions is calculated simply by letting \( \varepsilon = 0 \). The average temperature of the (left) beam can thus be obtained as

$$ \Delta T_{{u_{1} }} = \frac{1}{{L_{b} }}\mathop \int\limits_{0}^{{L_{b} }} u_{1} \left( {x,t} \right)dx - T_{0} = \Delta T_{{w_{1} }} + \Delta T_{{v_{1} }} , $$
(37)

where \( \Delta T_{{w_{1} }} = \frac{1}{{L_{b} }}\mathop \int\limits_{0}^{{L_{b} }} w_{1} \left( x \right)dx - T_{0} \); \( \Delta T_{{v_{1} }} = \frac{1}{{L_{b} }}\mathop \int\limits_{0}^{{L_{b} }} v_{1} \left( {x,t} \right)dx \).

For heating process

$$ \Delta T_{{\hat{w}_{1} }} = Q \cdot T \cdot U^{2} , $$
(38)
$$ \Delta T_{{\hat{v}_{1} }} = \frac{{U^{2} }}{{k\hat{\rho }}} \cdot \mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n}^{2} L_{b} }} \cdot D_{0} . $$
(39)

For cooling process

$$ \Delta T_{{\check{w}}_{1}} = 0, $$
(40)
$$ \Delta T_{{\check{v}}_{1}} = - \Delta T_{{\hat{v}}_{1}} , $$
(41)

where \( D_{0} = D\left( {1 - {\text{c}}_{1} } \right) \). Detailed calculation of (38) is seen in our previous work (Zhang et al. 2015a, b).

2.2 Thermomechanical modeling

Generally, in micro-structures the natural frequency is higher (Mayyas et al. 2009; Hussein et al. 2015, 2016). In addition, simulations in Sects. 3 and 4 of this paper show that the electrothermal response dominates the overall dynamic responses and the thermomechanical response only introduces local low-amplitude high-frequency vibrations which is hard to be noticed in practice. Therefore, the mechanical inertia is considered to be quasi-static and thermomechanical modeling is conducted in static level in this work.

As the thermal elongation is small, the deformation of the actuator can be assumed linear and thus the tip displacement is obtained using Castigliano’s theorem. Detailed modeling process can be found in our preliminary work (Zhang et al. 2015a, b). The tip displacements of V- and Z-shaped beams are expressed in one common formula as in (42)

$$ y(t) = \left( {\begin{array}{*{20}c} {\alpha B_{1} } & {} \\ {} & { - \frac{1}{2mE}B_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\Delta T_{{u_{1} }} } \\ P \\ \end{array} } \right), $$
(42)

where for V-shaped beam: \( B_{1} = L_{b} B\sin \theta \), \( B_{2} = BL_{b} /A_{b} \),\( B = L_{0}^{2} /(h_{0}^{2} cos^{4} \theta + L_{0}^{2} sin^{2} \theta ) \), and for Z-shaped beam: \( B_{1} = L_{b} (\beta_{2} \omega_{2} + \beta_{13} \omega_{13} G_{1} ) \), \( B_{2} = L_{2} (1 + G_{2} )/ \,A_{b} \),\( \omega_{2} = L_{2} /L_{b} \), \( \omega_{13} = L_{0} /L_{b} \), \( G_{1} = 3L_{2} (2L_{1}^{2} L_{3} + L_{1}^{2} L_{2} +\, 2L_{1} L_{3}^{2} + L_{2} L_{3}^{2} )/[h_{0}^{2} L_{0} L_{b} + L_{2}^{2} (L_{2}^{2} + 12L_{1} L_{3} + 4L_{1} L_{2} + 4L_{2} L_{3} )], \)and \( G_{2} = \frac{{36L_{2} (2L_{1}^{2} L_{3} + L_{1}^{2} L_{2} + 2L_{1} L_{3}^{2} + L_{2} L_{3}^{2} )^{2} }}{{\left\{ {L_{b} ( - 4h_{0}^{2} )[h_{0}^{2} L_{0} L_{b} + L_{2}^{2} (L_{2}^{2} + 12L_{1} L_{3} + 4L_{1} L_{2} + 4L_{2} L_{3} )]} \right\}}} +\, [4/(h_{0}^{2} L_{2} )][L_{1}^{3} + 3\left( {L_{2} + L_{3} } \right)L_{1}^{2} + 3L_{1} L_{3}^{2} + L_{3}^{3} ] - [3(L_{1}^{2} + 2L_{1} L_{2} + 2L_{1} L_{3} + L_{3}^{2} )^{2} ]/(h_{0}^{2} L_{2} L_{b} ) \). \( \alpha \) and \( E \) denote the coefficient of thermal expansion (CTE) and Young’s modulus of the beam material respectively. The output force \( F(t) \) is written as (43) as follows

$$ F(t) = \left( {\begin{array}{*{20}c} {2\alpha mE \cdot \frac{{B_{1} }}{{B_{2} }}} & {} \\ {} & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {\Delta T_{{u_{1} }} } \\ P \\ \end{array} } \right) . $$
(43)

Note that the output displacement \( y(t) \) and force \( F(t) \) obtained in (42) and (43) are functions of time. When the actuator is heated up till steady-state the displacement reaches maximum value, the output force decreases to be zero from the maximum at the initial position.

The obtained expressions allow one to obtain directly the evolution of the temperature distribution, displacement, and force of V- and Z-shaped actuators with determined dimensions and material properties. More importantly, the dynamic model allows one to identify the influence of the dimensions and material properties on the dynamic response, which will be the focus in Sect. 5.

2.3 Complete model

Combing the electrothermal and thermomechanical models, a complete model from electrical input \( U \) to the displacement and force outputs can be summarized, as in (44) and (45). This is useful for simulating the actuator or designing a controller.

$$ y(t) = \left( {\begin{array}{*{20}c} {W(t)} & {} \\ {} & { - \frac{1}{2mE}B_{2} } \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {U^{2} } \\ P \\ \end{array} } \right), $$
(44)
$$ F(t) = \left( {\begin{array}{*{20}c} {V(t)} & {} \\ {} & { - 1} \\ \end{array} } \right)\left( {\begin{array}{*{20}c} {U^{2} } \\ P \\ \end{array} } \right), $$
(45)

where \( W(t) \) is calculated as \( \hat{W}(t) \) and \({\check{W}} (t) \) for heating and cooling respectively, and \( V(t) \) is calculated as \( \hat{V}(t) \) and \( {\check{V}} (t) \) for heating and cooling respectively, as in (46)–(49).

$$ \hat{W}(t) = \alpha B_{1} \left( {QT + \frac{1}{{k\hat{\rho }}} \cdot \mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n}^{2} L_{b} }} \cdot D_{0} } \right) $$
(46)
$${\check{W}} \left( t \right) = - \alpha B_{1} \left( {\frac{1}{{k\hat{\rho }}} \cdot \mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n}^{2} L_{b} }} \cdot D_{0} } \right) $$
(47)
$$ \hat{V}\left( t \right) = 2\alpha mE\frac{{B_{1} }}{{B_{2} }} \cdot \left( {QT + \frac{1}{{k\hat{\rho }}}\mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n}^{2} L_{b} }} \cdot D_{0} } \right) $$
(48)
$${\check{V}} (t) = - 2\alpha mE\frac{{B_{1} }}{{B_{2} }} \cdot \left( {\frac{1}{{k\hat{\rho }}} \cdot \mathop \sum \limits_{n = 1}^{\infty } \frac{{e^{{ - \hat{k}\left( {r^{2} + \lambda_{n}^{2} } \right)t}} }}{{\left( {r^{2} + \lambda_{n}^{2} } \right)\lambda_{n}^{2} L_{b} }} \cdot D_{0} } \right). $$
(49)

3 Model verification

The numerical results with the analytical model in this section is compared with the results of FEM simulations (using ANSYS, version 14.0) in terms of evolution of output displacement and temperature rise for both the V- and Z-shaped beams operating in air and in vacuum conditions. The simulation is focused on step response only, and the step input is the voltage. Its value as well as the actuator dimensions and room temperature are listed in Table 2. The dimensions are chosen the same as the ones of the fabricated actuators in the reference (Guan and Zhu 2010).

Table 2 Actuator dimensions, voltage, and room temperature (unit of length: μm)
Full size table

The coupled-field analysis of the actuators is used in ANSYS simulations. It involves a single analysis from electrical inputs directly to mechanical outputs using the 3-D SOLID227 element which has the coupled-field capability. SOLID227 element allows for both static and transient analysis in electrical, thermal and mechanical domains. (Pant et al. 2012). The material properties of the actuator and the air used in analytical calculation and simulations are listed in Tables 3 and 4 respectively.

Table 3 Material properties of actuator
Full size table
Table 4 Material properties of air (units: same as Table 3)
Full size table

The 3-D simulation models in ANSYS software are shown in Fig. 4. To avoid lengthy presentations, we only present two of the models, i.e., the Z-shaped beam in vacuum and the V-shaped beam in air conditions. It is seen in Fig. 4b, the actuator is embedded in air environment which was modeled using the material properties of air listed in Table 4 and glued to the actuator so that the heat can dissipate via the air to the substrate.

Fig. 4
figure 4

ANSYS models: a Z-shaped beam in vacuum; b V-shaped beam in air

Full size image

The verification of the analytical model is depicted in Fig. 5. The simulations are conducted with transient analysis type in which the time at end of load step is set to be 0.008 s for the heating and 0.016 s for the cooling process, to make sure the actuators have sufficient time to reach the steady state. The temperature and output displacement are measured at the middle of the shuttle. It is seen from Fig. 5 that, the results from the dynamic model and the ANSYS simulations agree well with each other in both temperature and displacement terms within a dynamic cycle for V- and Z-shaped actuators operating in vacuum or in air conditions. Clearly, the displacement and temperature evolutions for the cooling process are simply the reverse of that for the heating process, and return to the initial states. That is, the cooling time is always the same as the heating time. This fact can be explained with the analytical model, seen from (36) that, the transient response of the cooling process is always negative to that of the heating stage. It is therefore beneficial to the design and optimization of the actuator, for one does not have to make compromise when considering reducing both heating and cooling times.

Fig. 5
figure 5

Model verification: a temperature of V-shaped beam; b temperature of Z-shaped beam; c displacement of V-shaped beam; d displacement of Z-shaped beam. The dashed line and solid line refer to the analytical and simulation results respectively

Full size image

Contrary to the almost perfect agreement in evaluations of temperature and for the “in vacuum” case, of the displacement, small derivations are found in displacement estimation for the “in air” conditions. This is mainly due to an empirically-based calculation of the shape factor which accounts for the extra heat conduction to the substrate for particular structural geometries, and it is not likely to acquire an accurate expression. Fortunately, the shape factor does not affect the transient response and only relates to the steady-state predictions. It is also noticed that, the transient response for the actuator operating in air conditions is much faster compared to the “in vacuum” case. This is because the existence of the air accelerates the heat dissipation resulting in quick heat balance. It is also seen from (35) that, for the “in air” conditions, \( r \ne 0 \), it takes shorter time to reach steady-state, whereas for the “in vacuum” conditions, i.e., \( r = 0 \), clearly, it takes longer time to reach steady-state value.

The nonlinearity is an important issue in the design and control of electrothermal microactuators. To reveal the nonlinear characteristics, the input–output maps are given in Fig. 6a: displacement and force vs voltage, and Fig. 6b: average temperature vs voltage. The nonlinearity is clearly demonstrated in Fig. 6, and agrees to the nonlinearity in (44) and (45) of the complete actuator model.

Fig. 6
figure 6

Input-output maps. a Displacement and force vs. voltage in vacuum; b average temperature increase of beam

Full size image

4 Dynamic characteristic analysis and comparison between U-shaped and V/Z-shaped actuators

In this section, the dynamic characteristics of U-shaped and V/Z-shaped actuators are investigated and compared using ANSYS simulations. Compared to the symmetric configuration of V- and Z-shaped actuators, the U-shaped actuator is asymmetric configured consisting of the thick and thin beams and when heated, the thin beam overcomes the thick beam and output displacement and force. Because of the difference in structures, the U-shaped beam offers the arc circular motions whereas the V- and Z-shaped beams can produce rectilinear motions. It is therefore necessary to compare the behavior and performances between the two distinct in-plane electrothermal actuators.

Here, we propose a comparison benchmark, shown in Fig. 7, to compare the performances and behaviors between the asymmetric U-shaped actuators and the symmetric V- and Z-shaped actuators. First, the comparison must be conducted with same input voltage/current, material properties, and same room temperature to rule out the structural-irrelevant factors. Second, the height of air gap, the span of beams \( L_{0} \) and the cross-sectional areas for the thin beams must be the same to eliminate the structural parameters that unrelated to the beam shape, ensuring the same degree of ability for the structure to generate and dissipate heat. Based on the two comparison rules, the performance of the actuators is only determined by the topological structures. Now it is possible to find which type of beams performs better. Note that, the comparison between V- and Z-shaped beams follows the comparison benchmark proposed in our previous work in (Zhang et al. 2015a, b) which is initially used for comparison in static terms. With the benchmark, the comparison of V- and Z-shaped beams must be conducted with the end-to-end structure shown in Fig. 7. The dimensions of the thick beam for the U-shaped actuator and the short beam length for the Z-shaped actuator (or the inclined angle for the V-shaped actuator) are changeable to make the comparison in a wide range of dimensions.

Fig. 7
figure 7

Comparison benchmark of U-, V-, and Z-shaped beams

Full size image

Figure 8 shows comparison results of the three types of actuators using ANSYS simulations. The dimensions, material properties, and input voltages etc. are chosen from an actual U-shaped actuator in (Hussein et al. 2016). For both U- and V-shaped beams (and Z-shaped beams), different temperature evolution rates in the thick and thin beams (for the V-shaped beams, the shuttle and the beam) are observed in Fig. 8a, b. For the heating process, due to lower width, faster initial temperature evolution, i.e., higher local Joule heating, is found in the thin beams. For the cooling process, because the thick beam (shuttle) is farthest to the anchors, the temperature drops faster in the thin beam than in the thick beam (shuttle) at the beginning. Considering the same dynamic electrothermal responses for the V- and Z-shaped beams, only the V-shaped actuator is presented in Fig. 8a.

Fig. 8
figure 8

Dynamic behaviors of U-shaped and V- and Z-shaped actuators. a Temperature evolution with time of the shuttle and beam at mid points of V-shaped actuator; b temperature evolution with time of the thick and thin beam at mid points of U-shaped actuator; c evolution of displacement with time of U-, V- and Z-shaped actuators; d high-frequency and low-amplitude vibrations of V- and Z-shaped actuators

Full size image

It is seen from Fig. 8c that, the displacement of U-shaped actuator undergoes an over-shoot before it reaches the steady state, whereas the displacement of V- and Z-shaped actuators increases without the overshoot feature to reach the steady state. It is clear that for the U-shaped beams, the expansion of the thin beam has to overcome the expansion of the thick beam to output displacement. Therefore, the initial faster temperature evolution in the thin beam results in a short-time positive displacement which is diminished shortly with the expansion of the thick beam in opposite direction. For the V- and Z-shaped beams, however, both the expansion of the shuttle and the beams result in positive displacement, and therefore no overshoot occurs despite the different rates of temperature evolution in the beams and in the shuttle as the U-shaped beams. Figure 8c also suggests that the U-shaped beam is less capable in producing large displacement (and force as well) compared to the V- and Z-shaped beams. This is also can be explained that for the U-shaped beams, the thin beam is expanded in opposite direction to the thick beam, and in order to produce motion, the thin beam has to overcome the negative motion produced by the thick beam, whereas, in V- and Z-shaped beam situations, both the expansions of the shuttle and the beams contributed to the output displacement.

Another fact that for particular dimensions such as longer beam length, smaller beam width, and shorter beam steps (i.e., incline angle for the V-shaped beam and middle beam length for the Z-shaped beam), high-frequency and low-amplitude vibrations occur along the displacement evolution, is observed for the V- and Z-shaped actuators, as shown in Fig. 8d. For the U-shaped actuators, similar local vibrations may also occur for particular geometries (Hickey et al. 2003). Obviously, the vibration is caused by the mechanical inertia, which is not included in our model due to the quasi-static assumption. However, for the most part, the vibration will not occur or it is quite small, which does not influence the overall dynamics and only affects the local responses. The dynamic model established in this paper is therefore sufficient to produce good estimations. The vibrations, as shown in Fig. 8d, are the structural vibration caused by the axial thermal stress in the beams (Marakala et al. 2010). The vibration frequency is high as the beams have high longitudinal stiffness. Our ongoing efforts will work on the analytical mechanical vibration analysis of the V- and Z-shaped microactuators.

5 Parameter analysis

The aim of this paper is to provide analytical tool and guidance on increasing the operation frequency of the V- and Z-shaped actuators. To achieve this, the heating time (as well as the cooling time, which is the same as the heating time) must be reduced. As clear when comparing Figs. 5 and 8 that, the V- and Z-shaped actuators can response quite fast or slow depending on the choice of the structural parameters as well as material properties. Thus, in this section, a variety of factors that may influence the response rate will be studied to provide insight and guidance on improving the dynamic behaviors.

It is evident from (35) that, the input voltage \( U \) and room temperature \( T_{0} \) are irrelevant to the transient responses, and only contributed to the steady-state response. For the material properties, larger the value of thermal conductivity of the actuator \( k \). and the air \( k_{a} \) (\( k_{a} \) only work for the in air case) results in shorter the response time, larger the value of the density \( \rho \) and specific heat \( C_{p} \) of the actuators results in longer the response ti, and the resistivity of the structure \( \hat{\rho } \) only related to the steady-state response. Clearly, the increase of thermal conductivity of the actuator and the air means less resistance for the heat conduction and therefore it is faster to reach the steady state. In addition, the larger value of density and specific heat of the actuators means it needs longer time for the heat to be stored in the actuator, which slower the actuator response.

The influences of the structural parameters on the response rate are summarized in Table 5 based on parameter analyses using the established dynamic model, in which “+”, “−”, and “0” refer to respectively the positive-, negative-, and non-correlation between the values of those structural parameters and the response rate. It is seen that increasing the values of lengths of beams \( L_{b} \) and shuttle \( L_{s} \) and the shuttle width \( h_{1} \) result in slower responses, whereas increasing the number of pairs of beams \( m \) and width of the beams \( h_{0} \) results in quicker the response. The thicknesses of the structure \( b \) and the air gap \( h_{a} \). have no impacts on the response rate when operating in vacuum conditions, whereas for the in air cases, the increase of \( b \). and \( h_{a} \) result in slower responses. It is obvious that according to the comparison benchmark proposed in our previous work (Zhang et al. 2015a, b), the V-shaped beam responses a little faster than the Z-shaped beams due to the shorter beam length.

Table 5 Structural parameter analysis
Full size table

Figures 9 and 10 show the rise time for the actuator as functions of beam dimensions, i.e., beam length and cross-sectional shapes, in order to give more specific insight and guidance on the design and optimization of the beams. Figure 9 shows the rise time versus beam length \( L_{b} \) with cross-sectional areas \( A_{b} \) to be 20 μm2 (\( b_{0} = 10 \) μm and \( h_{0} = 2 \) μm) and 80 μm2 (\( b_{0} = 20 \) μm and \( h_{0} = 4 \) μm) respectively. Figure 10 gives the rise time as function of beam shapes, i.e., the ratio of beam thickness to width \( b_{0} /h_{0} \) with constant cross-sectional areas (the beam length \( L_{b} \) is 180 μm).

Fig. 9
figure 9

Rise time vs beam length

Full size image
Fig. 10
figure 10

Rise time vs ratio of beam thickness to width

Full size image

Figures 9 and 10 show that: (1) the rise time increases with increases of beam length \( L_{b} \) and ratio of beam thickness to width \( b_{0} /h_{0} \) resulting in slower responses. (2) Larger the cross-sectional area of the beam results in quicker response for “in vacuum” conditions, whereas for “in air” conditions, the actuator responses slower.

6 Conclusion

In this work, an analytical electro-thermo-mechanical model has been established to obtain the dynamic solutions of the V- and Z-shaped electrothermal microactuators. This model describes the dynamic behaviors for the heating and cooling processes under step input voltage, and can be applied to both the “in vacuum” and “in air” working conditions. Verification of the model has been conducted with finite element analysis using the ANSYS software. Good agreements are obtained between the analytical and simulation results. A comparison benchmark has been proposed and utilized to compare and reveal the different dynamic characteristics between the U-shaped and V- and Z-shaped actuators. With aims of increasing response rates and for design and optimization purpose, influences of the working conditions, material properties, input voltage, room temperature, and structural parameters on the dynamic behaviors have been investigated based on the established model.