1 Introduction

The rapid progress in microsystems technology is increasingly supported by MEMS-specific modeling methodologies and dedicated simulation tools (Senturia 1998; Fedder 2003; Bechtold et al. 2005). System-level simulation is a way to simulate complete systems consisting of the subsystems where several physical domains must be taken into account. The hierarchical circuit-level representation of the MEMS devices for the system-level simulation has been developed during the past years. Behavioral models and nodal simulation of the MEMS elements are implemented in Analogy MAST with simulation in Saber (Vandemeer et al. 1998; Vandemeer 1998; Jing 2003) or in SPICE-like representation with simulation in MATLAB (Clark et al. 1998; Zhou 2002). The advantages of the hierarchical circuit-level methodology for MEMS are the reusability of the parametric models, and the interoperability with electronic circuit representations. Surface micromachined MEMS devices can be simply decomposed into anchors, beams, plates and gaps. This set of elements was chosen because they all occur commonly and their behavior can be accurately approximated with a simple lumped parameter model (Mukherjee et al. 2000). A circuit simulation environment for micromachined devices based on this element library with parametrized behavior models has been developed (Vandemeer et al. 1998; Vandemeer 1998; Jing 2003; Clark et al. 1998; Zhou 2002), which is possible to simulate electromechanical devices.

The application of a voltage difference between two points of an arbitrary, electrically conducting and elastic continuum produces Joule heating. The topology and shape of the continuum give rise to non-uniform Joule heating and hence non-uniform thermal expansion. Based on this consideration, electrothermal microactuators have been developed as a compact, high-force actuation technique which complements electrostatic, magnetostatic, or piezoelectric actuation. Guckel et al. (1992) first adopted LIGA technology to produce nickel based U-shaped flexure actuators and analyzed the arcing motion at the tip of the actuator. Comtois et al. (1995) developed a polysilicon microactuator with a similar topology using a commerical foundry process (MUMPs). Similarly, Pan and Hsu (1997) developed an electrothermal microactuator with different lengths of two beams rather than the variable cross-sections of the microstructure. To improve the mechanical efficiency of the electrothermal actuators, Burns and Bright (1997) developed a double hot arm polysilicon thermal actuator. Moreover, Que et al. (1999, 2001) developed electrothermal actuators based on bent-beam suspensions that have been used very successfully for strain sensing (Gianchandani and Najafi 1996). Jonsmann et al. (1999) have applied topology optimization techniques to the design of electrothermal microactuators. Properties of these kinds of electrothermal microactuators strongly depend on its geometric structure and material properties as well as applied voltage or current. It is therefore important to model the electrothermal microactuator so that its design may be improved or optimized. Generally, modeling of the electrothermal microactuator has to take electro-thermal-mechanical couples into account. Efforts to model the electrothermal actuators have focused on finite-element (FEM) (Lerch et al. 1996; Mankame and Ananthasuresh 2001; Chen et al. 2002; Geisberger et al. 2003; Borovic et al. 2005), finite difference (FDM) (Kuang et al. 2002; Lott et al. 2002), lumped parameter (Huang and Lee 1999a, b, 2000; Hickey et al. 2003; Yan et al. 2003), and model order reduction (Yang and Yu 2004).

It is the most common way to perform numerical simulation utilizing meshing in the analyses of MEMS devices (Wong 2004; Hsu and Quoc 1996). However, the computing cost to simulate using meshing is extremely high which makes it impossible to take it as a system-level simulation method. A completely different method without meshing is proposed to build the model of the thermal electrothermal microactuator in this paper. Its computing effect is much higher than the traditional methods using meshing. The surface micromachined electrothermal microactuators can be decomposed into essential elements of beams and anchors. By using the properties of the spatial distribution of the temperature, this paper first presents a nonlinear lumped parameter model for them. Based on the general nodal analysis, this paper takes then noncoaxial joints of the beams for the electrothermal microactuators into account. Three types of the electrothermal microactuators are finally simulated with the model inserted into the nodal analysis method by SPICE. The results are validated by ANSYS simulation under nonlinear options. The proposed nodal analysis method for the electrothermal microactuators would find applications in the design of related MEMS devices.

2 Model

The anchor of the electrothermal actuator would keep a low temperature shift while actuating in reasonable temperature. So it is assigned as an ideal heat sink in the nodal analysis. In this section, an electrothermal model of the beam is first developed based on the heat-transfer governing equation. And then, a thermomechanical model of beam with the effects that should be considered in the electrothermal microactuators is introduced to construct a complete model of beam along with the electrothermal model.

2.1 Heat-transfer governing equation

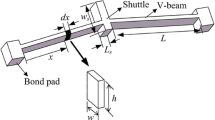
According to the typical structures of the laterally-driven electrothermal microactuators (Guckel et al. 1992; Comtois et al. 1995; Pan and Hsu 1997; Burns and Bright 1997; Que et al. 1999, 2001), these actuators are composed of the basic beam with properly-jointed structures. The beam in Fig. 1 is the schematic view of the basic element of the thermal microactuator. It shows that less than 1% of the heat is lost to the surroundings by radiation even at high temperature (1,000°C) (Huang and Lee 1999). So the radiation effect is not considered in this model. The temperature at any location along the cross-section of the beam is assumed to be uniform. This is proper if the Biot number, Bi, is less than 0.1. The Biot number Bi =  (κair /κ)(w/t air), where w and κ are the width and the thermal conductivity of the beam, respectively. κair is the thermal conductivity of the air layer between the beam and the silicon substrate, and t air is the lift of the beam. For a beam with κair =  0.026 W m− 1 K− 1, κ =  131 W m− 1 K− 1, w =  2 μm and t air =  2 μ m, the calculated Biot number is 0.0002. Therefore the temperature gradients along the cross-section are very small in the most part and the model in this paper is one-dimensional.

Fig. 1
figure 1

Schematic view of a beam

Full size image

With the simplification presented above, the heat-tranfer governing equation of the beam is an 1-D PDE. If the ambient temperature is assumed to be equal to that of the substrate, according to the coordination illustrated in Fig. 1, the PDE is written as

$$\rho cwb\frac{{\partial T_{b} (x,t)}}{{\partial t}} - wb\frac{\partial}{{\partial x}}{\left[ {\kappa \frac{{\partial T_{b} (x,t)}}{{\partial x}}} \right]} = - {\left({hw + \frac{{wS}}{{R_{T}}}} \right)}{\left[ {T_{b} (x,t) - T_{\infty}} \right]} + \frac{{i^{2} (t)\rho_{e}}}{{wb}}$$
(1)

where T b (x,t) is the temperature distribution along the beam, T ∞ is the temperature of the substrate (the ambient temperature is assumed to be the same as that of the substrate), κ is the thermal conductivity of the beam, h is the convection coefficient, ρ e is the electrical resistivity of the beam, i(t) is the electric current through the beam, w and b are the width and thickness of the beam, respectively, S is the shape factor which accounts for the impact of the shape of the element on heat conduction to the substrate. If the beam is wide enough, R T would be the thermal resistance between the beam and the substrate and given by the following equation (Huang and Lee 1999; Lin and Chiao 1996)

$$R_{T} = \frac{{t_{{air}}}}{{\kappa_{{air}}}} + \frac{{t_{N}}}{{\kappa_{N}}} + \frac{{t_{O}}}{{\kappa_{O}}}$$
(2)

where κ N and κ O are the thermal conductivity of Si3N4 and SiO2, respectively, t N and t O are the thickness of the Si3N4 and SiO2, respectively, as shown in Fig. 1. The following equation gives the shape factor for heat conduction (Huang and Lee 1999; Lin and Chiao 1996)

$$S = \frac{b}{w}\left(\frac{{2t_{{air}}}}{b} + 1\right) + 1$$
(3)

In order to make the following model easy for nodal analysis, the left end of the beam in Fig. 1 is defined as Node 1 and the right end as Node 2.

2.2 Coupling electrothermal model with temperature-dependent parameters of the material

The variation of the thermal conductivity and electrical resistivity is up to 100% when the temperature ranges from 300 to 800 K (Geisberger et al. 2003). For simplicity, only the thermal conductivity and electrical resistivity are considered here to vary linearly with the temperature. The two parameters can approximately be written as a functions of the relative temperature (Geisberger et al. 2003).

$$\kappa = \kappa_{0} + \kappa_{1} T,\quad \rho_{e} = \rho_{{e0}} (1 + \zeta T)$$
(4)

where κ0 was the thermal conductivity of the beam at the ambient temperature, κ1 the first-order coefficient of κ; ρ e0 is the electrical resistivity of the beam, ζ the temperature coefficient of electrical resistivity. For simplicity, it is assumed that

$$T(x,t) = T_{b} (x,t) - T_{\infty}$$
(5)

where T(x,t) is the temperature difference between the beam at the point x the ambient.

Substituting Eq. 4 into 1, the governing equation may be written as

$$\begin{aligned}& {\underbrace {{\left[ {\frac{1}{\alpha}\frac{{\partial T(x,t)}}{{\partial t}} - \frac{{\partial^{2} T(x,t)}}{{\partial x^{2}}} + {\left({\frac{h}{{\kappa_{0} b}} + \frac{S}{{\kappa_{0} bR_{T}}}} \right)}T(x,t) - i^{2} {\left({\frac{{\rho_{{e0}}}}{{\kappa_{0} w^{2} b^{2}}}} \right)}} \right]}}_{A}} \\& \quad - {\underbrace {{\left[ {\frac{{\kappa_{1}}}{{\kappa_{0}}}\frac{\partial}{{\partial x}}{\left({T(x,t)\frac{{\partial T(x,t)}}{{\partial x}}} \right)} + {\left({\frac{{\rho_{{e0}} \zeta}}{{\kappa_{0} w^{2} b^{2}}}} \right)}i^{2} T(x,t)} \right]}}_{B}} = 0 \\\end{aligned}$$
(6)

where \({\alpha \big(\alpha = \frac{\kappa}{{\rho c}}}\big)\) is the heat diffusivity. In Eq. 6, item A is the main part and Item B is introduced due to variational material parameters. When the temperature-dependent parameters are assumed constant, Item B could be neglected. In Item B, the first item is due to temperature-dependent thermal conductivity and the second due to temperature-dependent electrical resistivity. The boundary conditions of Eq. 6 were

$$\left\{\begin{aligned}\,& T(x,t)|_{{x = 0}} = T_{1} (t) \\& T(x,t)|_{{x = l}} = T_{2} (t) \\& T'(x,t)|_{{x = 0}} = \eta_{1} (t) \\& T'(x,t)|_{{x = l}} = \eta_{2} (t) \\\end{aligned} \right.$$
(7)

where η1(t) and η2(t) are the derivative of the temperature with respect to x at x = 0 and x = l, respectively.

To solve the PDE shown in Eq. 6, the solution format should be assigned in advance. The temperature along the beam is fitted with the Hermit’s polynomial of the temperature and the derivative of temperature of the two nodes, and the residual of the fit is then offset by the Fourier series. In the electrothermal microactuator, the temperature of most part changes smoothly due to the uniform heat source distribution and relatively high thermal conductivity. Therefore few stages of the Fourier series should be taken. The stage is determined as 3 which is optimized with numerical simulations. The solution is assigned as

$$\begin{aligned}T(x,t) &= u(x,t) + v(x,t) \\ &= {\left\{{\frac{{2{\left[ {T_{1} (t) - T_{2} (t)} \right]}}}{{l^{3}}} + \frac{{{\left[ {\eta_{1} (t) + \eta_{2} (t)} \right]}}}{{l^{2}}}} \right\}}x^{3} - {\left\{{\frac{{3{\left[ {T_{1} (t) - T_{2} (t)} \right]}}}{{l^{2}}} + \frac{{{\left[ {2\eta_{1} (t) + \eta_{2} (t)} \right]}}}{l}} \right\}}x^{2} \\ &\quad + \eta_{1} (t)x + T_{1} (t) + {\left[ {1 - \cos {\left({\frac{{2\pi x}}{l}} \right)}} \right]}\beta (t)\\ \end{aligned}$$
(8)

where β (t) is a undetermined function.

Substituting Eq. 8 into 6 followed with even continuation of the functions about x, and then performing spatial Fourier transformation along the beam, Eq. 6 could be converted into a set of ODEs, as the format in Eq. 9. The same as the Fouier series taken above, only the first 3 stages of the equation are taken.

$$\Upsilon_{n} - \Psi_{n} - \Phi_{n} = 0 \quad n \in \{0,1,2\}$$
(9)

Equation 9 stands for three ODEs about the undetermined functions, T 1, T 2, η1, η2 and β, where \({\Upsilon_{n}}\) is the item which is independent of temperature, − Ψ n and − Φ n are the items introduced by the variational thermal conductivity and electrical resistivity, respectively. The format of them is too complex and not listed here.

The heat flow out of the two nodes of the beam is

$$f_{1} (t) = \kappa wb\eta_{1} (t) = \kappa_{0} wb\eta_{1} (t) + \kappa_{1} wbT_{1} (t)\eta_{1} (t), \quad \hbox{Node}\;1$$
(10)
$$f_{2} (t) = - \kappa wb\eta_{2} (t) = - \kappa_{0} wb\eta_{2} (t) - \kappa_{1} wbT_{2} (t)\eta_{2} (t), \quad \hbox{Node}\;2$$
(11)

The electrical current through the beam in above equations is assumed to know. But it is actually a function of the temperature-dependent electrical resistance when working. It should be expressed as a function of the temperature as below.

$$\begin{aligned}R &= {\int_0^l {\frac{{(1 + \zeta T)\rho_{{e0}}}}{{wb}}{\rm d}x}} \\ &= \frac{{\rho_{{e0}} l}}{{wb}} + \frac{{\zeta \rho_{{e0}}}}{{wb}}{\int_0^l {(u + v){\rm d}x}} \\ &= \frac{{\rho_{{e0}} l}}{{wb}} + \frac{{\zeta \rho_{{e0}} l}}{{wb}}{\left[ {\frac{{T_{1} + T_{2}}}{2} + \frac{{l{\left({\eta_{1} - \eta_{2}} \right)}}}{{12}} + \beta} \right]} \\\end{aligned}$$
(12)

With Eqs. (9)–(12) and Ohm’s Law, one can build the coupling electrothermal model of the beams with the linearly variational thermal conductivity and electrical resistivity.

2.3 Coupling thermomechanical model

The nodal analysis equation of the mechanical beam for small lateral displacement with rectangular cross-section in the global coordination was (Jing 2003)

$$F_{g} + H^{T} F_{l} = \left[H^{T} MH\right]U_{g} '' + \left[H^{T} BH\right]U_{g} ' + \left[H^{T} KH\right]U_{g}$$
(13)

where F g is the global force vector; F l is the local force vector; U g is the global displacement; M is the mass matrix; K is the stiffness matrix; B is the damp matrix; T stands for the transpose operator. In this paper, F g and F l are defined as “through” qualities and U g the “across” quality. H is the matrix by which the local vector could be converted to global vector. The effect of damping was not involved in this paper, so B =  0.

In the laterally-driven electrothermal microactuator, the displacement is generally induced by the axial force of each beam. So the relative large axial stress makes the ordinary beam method not keep accurate. The bending of these beams will be governed by the Euller–Bernoulli equation. In this case, the lateral displacement of the nodes depends on the axial displacement, which modifies the stiffness matrix (Jing 2003), K, as a function of the axial force, N. N is expressed as (tensile force as positive)

$$N = \frac{{EA}}{l}{\left({x_{{l2}} - x_{{l1}} + \Delta l - {\int_0^l {\varepsilon_{t} {\rm d}x}}} \right)}$$
(14)

where ɛ t is the thermal strain in the axial direction which is induced by thermal expansion. x l1 and x l2 are the axial displacement of each node in its local coordination. Δl is the change of the effective axial length of the beam introduced by the lateral displacement (Jing 2003). A is the area of the cross-section of the beam, A =  wb.

The thermal expansion coefficient is generally a function of the temperature (Okada and Tokumaru 1984). If it is assumed to be a linear one, the thermal strain may be written as

$$\varepsilon_{t} = \alpha_{m} T(x,t) = \alpha_{{m0}} T(x,t) + \alpha_{{m1}} T^{2} (x,t)$$
(15)

where α m0 is the expansion coefficient at the ambient temperature and α m1 is the first-order coefficient. Δl is given by

$$\Delta l = l' - l = {\int_0^l {{\sqrt {1 + {\left({\frac{{{\rm d}y}}{{{\rm d}x}}} \right)}^{2}}}{\rm d}x}} - l \approx {\int_0^l {\frac{1}{2}{\left({\frac{{{\rm d}y}}{{{\rm d}x}}} \right)}^{2} {\rm d}x}}$$
(16)

where y is the lateral displacement along the beam; l′ is the effective axial length after bending without axial force; l is the original axial length. Substituting the shape function of the beam into Eq. 16, the change of the effective axial length would be obtained.

The effect of thermal strain could be equivalent with the lumped tensile axial force applied at the two nodes of the beam. The magnitude of the equivalent force is

$$F_{{eqv}} = \frac{{EA}}{l}{\left({{\int_0^l {\varepsilon_{t} {\rm d}x}} - \Delta l} \right)}$$
(17)

So the equivalent force vector representing the effect of thermal strain is given by

$$F_{l} = {\left[ {\begin{array}{*{20}c}{{- F_{{{\rm eqv}}}}}& {0}& {0}& {{F_{{{\rm eqv}}}}}& {0}& {0} \\\end{array}} \right]}^{T}$$
(18)

In the electrothermal microactuator, there are some noncoaxial joints of beams as shown in Fig. 2. Due to the relative large axial force in the beams of the electro-thermal actuators, the additional moment caused by the axial force cannot be neglected. The relation between the force and displacement at node 1 and 2 in Fig. 2 is

$$F_{{2g}} + H^{T} {\left({\begin{array}{*{20}c}{1}& {0}& {0} \\ {0}&{1}& {0} \\ {-d}& {0}& {1} \\ \end{array}} \right)}HF_{{1g}} = 0, \quad U_{{1g}} = H^{T} {\left[ {\begin{array}{*{20}c}{1}& {0}& {{- d}} \\ {0}&{1}& {0} \\ {0}& {0}& {1} \\ \end{array}} \right]}HU_{{2g}}$$
(19)
Fig. 2
figure 2

Schematic view of the noncoaxial joint

Full size image

Here, due to neglecting the 2-D temperature distribution, the temperature of nodes 1 and 2 in Fig. 2 is assumed to be the same.

3 Representation of the equivalent circuit for the beam

Here is used SPICE as a general ODE solver which makes it easy to co-simulate with other control circuits in the same system. A node of a coupling electro-thermo-mechanical beam corresponds to five sub-nodes in the representation of the equivalent circuit: one sub-node in electrical domain at which the “across” quality is voltage and the “through” quality is electric current; one sub-node in thermal domain at which the “across” quality is temperature and the “through” quality is heat flux; and three sub-nodes in mechanical domain at which the “across” qualities are axial displacement, transverse displacement and the angle rotation of the node, respectively, and the “through” quality are axial and transverse force and moment. Therefore, one node of the beam can be represented by five nodes in the equivalent circuit model.

3.1 Equivalent circuit of the coupling electro-thermal model of the beam

In order to solve the model built in ODE format as listed in Eq. 9 by using SPICE, one should build the equivalent circuit for the model. The equivalent circuit of the coupling electro-thermal model for the beam is shown in Fig. 3 where the solid square points mark the electrical and thermal node, and the solid circular points mark the reference variable. N e1 and N e2 are the electrical nodes; N th1 and N th2 are the thermal nodes. The equivalent circuit is mainly composed of nonlinear controlled source as shown in Fig. 3. The variables in the parenthesis near each controlled source represent the controller of the source.

Fig. 3
figure 3

Equivalent circuit of the coupling electro-thermal model of the beam

Full size image

In the equivalent circuit, there are five auxiliary voltage sources, V e, V ref01, V ref02, V ref11 and V ref21, of which 0 V is used to supply the current reference for other CCCSs (current controlled current source). In Sect. 2, it indicates that there are five undetermined functions, T 1, T 2, η1, η2 and β. To simplify the problem, T 1 and T 2 are first assumed as determined when interacting with other beams. Then there are three undetermined functions left, so the three reference variables, β, ηplus and ηsub, in the equivalent circuit can determine all the three undetermined functions. It should be pointed out that the assumption taken above is only for simplicity. Actually, all the five undetermined functions depend upon each other simultaneously. But in a practical electro-thermal actuator, the number of undetermined functions always equals that of ODEs due to sharing nodes of the beams and the anchors, which assures the solvability of the model.

3.2 Equivalent circuit of the coupling thermomechanical model of the beam

There are some second derivatives in Eq. 13. In order to use ODE solvers, the equation should be converted firstly. One could eliminate the second derivatives by defining a variable \({\tilde{U}_{g}}\) and letting \({\tilde{U}_{g} = U_{g}'}\) (Levitan et al. 2003):

$${\left({\begin{array}{*{20}c} {0}& {{H^{T} MH}} \\ {H^{T} MH}& {{H^{T}BH}} \\ \end{array}}\right)} {\left({\begin{array}{*{20}c} {{\tilde{U}_{g}}} \\ {{U_{g}}}\\ \end{array}} \right)}^{\prime} + {\left({\begin{array}{*{20}c} {{- H^{T}MH}}& {0} \\ {0}& {{H^{T} KH}} \\ \end{array}} \right)} {\left({\begin{array}{*{20}c} {{\tilde{U}_{g}}} \\ U_{g}\\ \end{array}} \right)} = {\left({\begin{array}{*{20}c}{0} \\ {F_{g} +H^{T} F_{l}} \\ \end{array}} \right)}$$
(20)

The equivalent circuit of coupling thermomechanical model for the beam is illustrated in Fig. 4 where the solid square points mark the mechanical node and the solid circular points mark the reference variable. The reference variables, V af and V exp in Fig. 4, stand for the axial force and thermal expansion, respectively.

Fig. 4
figure 4

Equivalent circuit of the coupling thermomechanical model of the beam

Full size image

The mechanical effects mentioned in Sect. 2, including thermal expansion, large axial stress, and the change of effective axial length, all act in the local coordination which resulted that all the controlled sources are applied at the local nodes of the beam model, as can be seen in Fig. 4. The component of the simple linear beam in Fig. 4 is the traditional one without the effects of the large axial stress and change of the effective axial length (Jing 2003). The simple linear beam is modified by introducing the 6 VCCSs (voltage controlled current source) connected with the local nodes to add the three effects mentioned above.

4 Simulation and verification

In this section, three examples of electro-thermal microacutators are presented. The static and dynamic behavior as well as the frequency response of them is simulated here. Some results are verified by ANSYS. In the following simulations, the temperature of the silicon substrate and the ambient was assumed to be fixed at 300 K. All the data of the temperature was given with respect to 300 K. The mechanical, electrical and thermal parameters of the actuator used in the simulations are listed in Table 1.

Table 1 Material properties of the beam used in this paper
Full size table

4.1 Case study I: V-shaped electro-thermal microactuator

Figure 5 shows the schematic top view of a V-shaped electro-thermal microactuator. The geometrical dimension of it is listed in Table 2. The nodal representation of this kind of microactuator is very simple as shown in Fig. 6. This microactuator consists of two beams and two anchors. The equivalent circuit is simulated with HSPICE of Synopsys Corp. ANSYS is utilized to verify the simulated data with sequentially coupled SOLID69 and SOLID45 element. The command of “NLGEOM, ON” was used to include the large-deflection effects in the static and full-transient analysis to take account of the effects of large axial stress and the change of effective axial length and some other effects.

Fig. 5
figure 5

Schematic top view of the bent-beam thermal actuator

Full size image
Table 2 The dimensions of the V-shaped thermal microactuator
Full size table
Fig. 6
figure 6

Nodal representation of the bent-beam thermal microactuator

Full size image

Figure 7 compares the tip temperature as a function of the applied voltage for the different thermal conductivity. One curve shows the results of variational thermal conductivity as listed in Table 1, the other shows the results of constant thermal conductivity, 38.6, which is the average value in the range from 300 to 1,000 K. It is shown that the results of the variational thermal conductivity agree well with the results of ANSYS. The maxim relative error is below 0.6% in this simulation.

Fig. 7
figure 7

Comparison of simulation results of the tip temperature of the V-shaped microactuator with constant and variational κ

Full size image

Figure 8 compares the tip stroke with and without the effect of the change of the effective axial length of the beam. When the tip stroke is small, there is little difference between the two results. Their difference increases as the applied voltage rising because the change of the effective axial length is a function of the lateral bending. The increase of the axial length of the beam releases the axial stress due to thermal strain significantly. The results with this effect agree well with that of ANSYS. The maxim relative error is below 1.4% in this simulation.

Fig. 8
figure 8

Comparison of simulation results of the tip stroke of the V-shaped microactuator with and without the change of effective axial length introduced by lateral bending (A) with the change of the effective axial length and (B) without the change of the effective axial length

Full size image

Figure 9 compares the tip stroke with and without the effect of large axial stress as a function of the tilt angle. Opposite to the model without this effect, there is not a peak value when the tilt angle is about 0.6° in the model with the effect. It is caused by the increasing axial stress while the angle decreasing. The maximum relative error between the results with this effect and that of ANSYS is below 2.9% in this simulation.

Fig. 9
figure 9

Comparison of the simulation results of the tip stroke of the V-shaped microactuator with and without the large axial stress with (A) without (B) the large axial stress

Full size image

4.2 Case study II: U-shaped electro-thermal microactuator

Figure 10 shows the schematic top view of an U-shaped electro-thermal microactuator. The geometric dimensions used in this analysis are listed in Table 3. The nodal representation of the actuator is shown in Fig. 11. The U-shaped microactuator consists of four beams, four nodes, and one joint. The simulation of the nodal analysis model was performed with HSPICE. The configuration and element used for ANSYS are the same as case study I.

Fig. 10
figure 10

Schematic top view of the U-shaped polysilicon thermal microactuator

Full size image
Table 3 The dimensions of the U-shaped microactuator
Full size table
Fig. 11
figure 11

Nodal representation of the U-shaped thermal actuator

Full size image

Figure 12 presents the comparison of the simulation results for the three different effects: the change of the effective axial length, large axial stress, and additional moment introduced by the noncoaxial joint. The results of all the three effects are verified with ANSYS. The maxim relative error is below 4.8% in this simulation.

Fig. 12
figure 12

Comparison of the simulation results of the U-shaped microactuator of different effects: (A) with all the 3 effects, (B) without the noncoaxial component, (C) without the change of the effective axial length and (D) without the large axial stress

Full size image

The transient response of the U-shaped microactuator is presented in Figs. 13, 14. We use an ideal step voltage stimulus of 4.5 V applied across the two anchors of the actuator when TIME = 0. Figure 13 shows the temperature response. The 2-D temperature distribution in this case is the most obvious in the three case studies of this paper, which giving rise to the difference of the time constant of the temperature. Figure 14 shows the response of the nodes deflection. The time step of simulation in ANSYS was set to be much larger than in SPICE due to the long simulation time, which may account for the fluctuation of the simulation results. The results of the two simulators agree well with each other.

Fig. 13
figure 13

Simulation results of the nodes temperature response of the U-shaped microactuator with an ideal step stimulus of the applied voltage

Full size image
Fig. 14
figure 14

Simulation results of the nodes deflection response of the U-shaped microactuator with an ideal step stimulus of the applied voltage

Full size image

Figure 15 illustrates the frequency response of Node 2 of the U-shaped microactuator. The −3 dB frequency of the temperature and deflection are about 720 Hz and 1.7 kHz, respectively. When the frequency of applied AC stimulus is much larger than the −3 dB frequency, the microactuator would behave the same as the case where a DC stimulus of the same effective value is applied.

Fig. 15
figure 15

Frequency response of the U-shaped microactuator

Full size image

4.3 Case study III: long-short beam electro-thermal microactuator

Figure 16 shows the schematic top view of a long-short beam thermal microactuator. The geometrical dimension is listed in Table 4. The nodal representation of the actuator is shown in Fig. 17. As seen in Fig. 17, this microactuator consists of three beams and two nodes. The nodal analysis was also performed by HSPICE. The configuration and element used for ANSYS is the same as case study I.

Fig. 16
figure 16

Schematic top view of the long-short beam thermal microactuator

Full size image
Table 4 The dimension of the long–short beam thermal microactuator
Full size table
Fig. 17
figure 17

Nodal representation of the long–short beam thermal microactuator

Full size image

Figure 18 illustrates the pulse response of the long-short beam microactuator. The pulse width and period are 1 and 2 ms, respectively. The voltage amplitude of pulse is 5 V. The results is also verified with ANSYS. The maximum relative error is below 2%.

Fig. 18
figure 18

Simulation results of the nodes deflection of the long–short beam microactuator with the pulse voltage stimulus

Full size image

5 Summary

Based on the traditional nodal analysis method, this paper presents a novel approach which may calculate the temperature of nodes of in-plane electrothermal microactuator with the electro-thermal model developed by fit and Fourier transformation. This kind of novel coupling electro-thermal model was performed by a widely-used circuit simulation software HSPICE. The simulated results have been verified by the full-meshed model of FEM by ANSYS. Through the study of the three typical electrothermal microactuators, it shows that this approach can provide rapid simulation in the design with fairly high accuracy.