1 Introduction

MEMS vibrational gyroscopes operate based on a transfer of energy between two of the gyro’s modes of vibration caused by the Coriolis effect (Shkel 2006). Compared with the traditional mechanical gyros, optical fiber gyros and laser gyros and so on, MEMS gyros are widely used in the fields of consumer electronics, automobile, inertial navigation, other military and civilian areas, due to their small size, low cost, low power consumption, and batch production. With the improvement of the performance of the gyros characteristic such as the resolution, sensitivity, and bandwidth (Prikhodko et al. 2011; Cho et al. 2012; Zotov et al. 2012), the vibration (acceleration) applied to the gyros has a prominent impact on the reliability and robustness of the gyroscope because of the high quality factor ranging from 45 in air to tens of thousands in vaccum (Geen et al. 2002; Zaman et al. 2006), which causes an output error, referred as ‘acceleration sensitivity’ or ‘acceleration output’. As the acceleration output errors are unpredictable and very hard to compensate using electronics, the short-term errors and systemic problems can be induced (Kazinczi et al. 2002). MEMS vibrational gyros can be divided into the single mass gyro, dual mass gyro, and quadruple mass gyro according to the types of structure (Alper and Akin 2004; Azgin et al. 2007; Prikhodko et al. 2012). For the single mass gyro, the response caused by the Coriolis force cannot be distinguished from the vibration along the sense direction (Palaniapan et al. 2003). For the quadruple mass gyro, it is hard to realize a higher performance owing to the more complex structure and higher technological requirements. Therefore, more and more researches focus on the acceleration sensitivity of the dual mass gyro.

To cancel the vibration-induced output errors, TFG operates differentially and employs two identical masses that vibrate out of phase, which is believed to be insensitive to vibrations due to countering the common-mode noise (Xie and Fedder 2003; Geen 2004; Schofield et al. 2007). However, Schofield et al. (2007) and Yoon et al. (2007) found that TFGs could still experience an output error caused by applying the linear acceleration along the sense axis to the gyros. The reason why the error occurred was not yet to be understood. Yoon et al. (2012) identified three major error sources causing the acceleration output in ideal fabricated TFGs that arise from (1) the asymmetric electrostatic force along the sense direction of the drive electrodes, (2) the asymmetric electrostatic force along the drive direction of the drive electrodes, and (3) the capacitive nonlinearity of the parallel plate sense electrodes. The most significant error source was caused by the acceleration along the sense direction. However, the analysis was based on the ideal fabricated TFG without considering the mismatch during fabrication. Due to the limitation of the technology, there does not exist any perfectly ideal TFGs. Singh et al. (2012, 2013) investigated the acceleration sensitivity of MEMS TFGs using FEM simulations and experimental verification. They assumed the central point of the coupled spring is steady, established a single DOF model, and studied on the effect of stiffness imbalance on the acceleration sensitivity. And they reported that increasing the decoupled ratio and anti-phase frequency can reduce the acceleration output. In fact, the central point of the coupled spring is unsteady caused by the stiffness imbalance. Therefore, a new model needs to be established to quantitatively analyze the common-mode acceleration output errors

In this paper, we design the fully decoupled symmetric TFG operating the linearly coupled, anti-phase oscillation as the sense mode. Since the acceleration output along the drive direction can be eliminated effectively by the related electronics, we focus on the acceleration output along the sense direction. Therefore, besides simplifying the TFG structure into the two linearly coupled sense tines, we assume the central point of the coupled spring is unsteady and establish the two DOFs coupled model. The matrix perturbation technique is used to approximately calculate the acceleration output caused by the fabrication defects. And the FEM simulations are carried out to compare with the theoretical calculations. Meanwhile, the analytical expressions coincide with the experimental results from the other researches. Our results reveal that the stiffness imbalance leads to the in-phase and anti-phase displacement and phase differences between two tines. This paper is organized as follows: Sect. 2 describes the theoretical study on the acceleration output of the ideal symmetric TFG. The frequency response caused by the stiffness imbalance is calculated using the matrix perturbation technique in Sect. 3. In Sects. 4, 5, and 6 we carry out the FEM simulations by intentional changing the sense beams widths and coupled springs stiffness, and experimentally verify the analytical expressions. Conclusions are given in Sect. 7.

2 Theoretical study on the frequency response of the ideal TFG

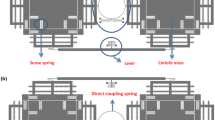
The TFG structure is simplified into the two DOFs coupled model, as shown in Fig. 1.

Fig. 1
figure 1

Two DOFs model of the ideal TFG

Full size image

The dynamics of the sense tines of the left and right gyroscopes are governed by:

Left gyroscope:

$$ \begin{aligned} m\mathop {x_{1} }\limits^{{ \bullet \bullet }} + c\mathop {x_{1} }\limits^{ \bullet } + c^{\prime}\left( {\mathop {x_{1} }\limits^{ \bullet } - \mathop {x_{2} }\limits^{ \bullet } } \right) \hfill + kx_{1} + k^{\prime}\left( {x_{1} - x_{2} } \right) = F\sin wt \hfill \\ \end{aligned} $$
(1)

Right gyroscope:

$$\begin{aligned} && m\mathop {x_{2} }\limits^{{ \bullet \bullet }} + c\mathop {x_{2} }\limits^{ \bullet } + c^{\prime}\left( {\mathop {x_{2} }\limits^{ \bullet } - \mathop {x_{1} }\limits^{ \bullet } } \right) \hfill + kx_{2} + k^{\prime}\left( {x_{2} - x_{1} } \right) = F\sin wt \hfill \\ \end{aligned} $$

The Eq. (1) can be expressed as matrix form:

$$ M\mathop x\limits^{ \bullet \bullet } + C\mathop x\limits^{ \bullet } + Kx = F_{0} \sin wt $$
(2)

where m, k and c denote the mass, stiffness and damping of the left and right sense tines, respectively, k′ denotes the coupled stiffness, c′ denotes the coupled damping, x 1 and x 2 denote the displacement of the left and right sense tines, respectively, F 0 sin wt denotes the external force induced by the acceleration applied to the TFG, which can be expressed as

$$ M = \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right],$$
$$ C = \left[ {\begin{array}{*{20}c} {c + c^{\prime}} & { - c^{\prime}} \\ { - c^{\prime}} & {c + c^{\prime}} \\ \end{array} } \right], $$
$$ K = \left[ {\begin{array}{*{20}c} {k + k^{\prime}} & { - k^{\prime}} \\ { - k^{\prime}} & {k + k^{\prime}} \\ \end{array} } \right], $$
$$ F_{0} = \left[ {\begin{array}{*{20}c} F \\ F \\ \end{array} } \right], $$
$$ x = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right]. $$

We take advantage of the mode superposition method to solve Eq. (2). And we obtain the steady-state response induced by the common-mode acceleration:

$$ x\left( t \right) = \frac{{Q_{1} }}{k}\left[ {\begin{array}{*{20}c} F \\ F \\ \end{array} } \right]\sin \left( {w_{1} t - \frac{\pi }{2}} \right) $$
(3)

Substituting F = ma, Eq. (3) can be rewritten as:

$$ x\left( t \right) = \frac{{aQ_{1} }}{{w_{1}^{2} }}\left[ {\begin{array}{*{20}c} 1 \\ 1 \\ \end{array} } \right]\sin \left( {w_{1} t - \frac{\pi }{2}} \right) $$
(4)

where, w 1 denotes the first-order (in-phase) angular frequency (\( w_{1} = \root \of {\frac{k}{m}} \)), Q 1 denotes the in-phase mode quality factor. Therefore,

$$ x_{1} \left( t \right) = x_{2} \left( t \right) $$
(5)

The Eq. (5) shows that the amplitude and phase of the left and right sense tines are completely identical, so the ideal TFG can resist the common-mode acceleration. Meanwhile, the single DOF model is proved right and we identify the required condition of using the single DOF model is that the TFG structure is totally symmetric.

3 Theoretical study on the frequency response of the non-ideal TFG using the matrix perturbation technique

Due to limitations of the current fabrication technology, the mass, stiffness and damping of two sense tines are not identical (Walther et al. 2013). Considering the actual deviation is tiny and the analytical solution of the second-order vibration system is so tedious, we take advantage of the matrix perturbation technique to approximately calculate the dynamic responses of the two DOFs vibration system. This paper focuses on the dynamic responses caused by the stiffness imbalance. The two DOFs model with stiffness imbalance is shown in Fig. 2. The governing equation may be expressed as:

$$ M_{0} \mathop x\limits^{ \bullet \bullet } + C_{0} \mathop x\limits^{ \bullet } + K_{0} x + \varepsilon K_{1} x = F_{0} \sin wt $$
(6)

where, ɛ is a small parameter representing the deviations between the actual and original value of the stiffness,the other parameters can be expressed as

$$ M_{0} = \left[ {\begin{array}{*{20}c} m & 0 \\ 0 & m \\ \end{array} } \right], $$
$$ C_{0} = \left[ {\begin{array}{*{20}c} {c + c^{\prime}} & { - c^{\prime}} \\ { - c^{\prime}} & {c + c^{\prime}} \\ \end{array} } \right], $$
$$ K_{0} = \left[ {\begin{array}{*{20}c} {k + k^{\prime}} & { - k^{\prime}} \\ { - k^{\prime}} & {k + k^{\prime}} \\ \end{array} } \right], $$
$$ K_{1} = \left[ {\begin{array}{*{20}c} k & 0 \\ 0 & 0 \\ \end{array} } \right], $$
$$ F_{0} = \left[ {\begin{array}{*{20}c} F \\ F \\ \end{array} } \right], $$
$$ x = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {x_{2} } \\ \end{array} } \right]. $$

The structural vibration eignproblems of discrete systems may be written as:

$$ \left[ K \right]\left\{ u \right\} = \lambda \left[ M \right]\left\{ u \right\} $$
(7)

where, [K] and [M] denote the stiffness matrix and the mass matrix, respectively. {u} denotes the modal vector, λ denotes the eigenvalue, and λ = w 2, w denotes the modal frequency.

Fig. 2
figure 2

Two DOFs model of the non-ideal TFG

Full size image

The mass matrix and the stiffness matrix of the updated structure (Chen and Wada 1977) can be expressed as:

$$ \left[ M \right] = \left[ {M_{0} } \right] + \varepsilon \left[ {M_{ 1} } \right],\;\left[ K \right] = \left[ {K_{0} } \right] + \varepsilon \left[ {K_{ 1} } \right] $$
(8)

where, ɛ is a small parameter representing the deviations between the updated and the original system, and when ɛ = 0, the system is the original one. Here, [M 0] and [K 0] denote the original mass and stiffness matrices, ɛ[M 1] and ɛ[K 1] are the corresponding changes. As the deviations approach zero, the updated values approach the original values, [M] → [M 0], [K] → [K 0].

If ɛ[M 1] and ɛ[K 1] are tiny, the eigenvalues and the eigenvectors (modal vectors) only have small changes. According to the perturbation theory, the updated eigenvalues λ and eigenvectors {u} can be expressed as the analytical function of ɛ,

$$ \lambda^{\left( i \right)} = \lambda_{0}^{\left( i \right)} + \varepsilon \lambda_{1}^{\left( i \right)} + \cdots \cdots $$
(9)
$$ \left\{ {u^{\left( i \right)} } \right\} = \left\{ {u_{0}^{\left( i \right)} } \right\} + \varepsilon \left\{ {u_{1}^{\left( i \right)} } \right\} + \cdots \cdots $$

Since the parameter change is very small, we calculate the updated eigenvalues and eigenvectors using the first-order perturbation method (Chen et al. 1984). That is

$$ \lambda_{1}^{\left( i \right)} = \left\{ {u_{0}^{\left( i \right)} } \right\}^{T} \left[ {K_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\} - \lambda_{0}^{\left( i \right)} \left\{ {u_{0}^{\left( i \right)} } \right\}^{T} \left[ {M_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\} $$
(10)
$$ \left\{ {u_{1}^{\left( i \right)} } \right\} = \sum\limits_{\begin{subarray}{l} s = 1 \\ s \ne i \end{subarray} }^{n} {\frac{1}{{\lambda_{0}^{\left( i \right)} - \lambda_{0}^{\left( s \right)} }}} \left( {\left\{ {u_{0}^{\left( s \right)} } \right\}^{T} \left[ {K_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\} - \lambda_{0}^{\left( i \right)} \left\{ {u_{0}^{\left( s \right)} } \right\}^{T} \left[ {M_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\}} \right)\left\{ {u_{0}^{\left( s \right)} } \right\} - \frac{1}{2}\left( {\left\{ {u_{0}^{\left( i \right)} } \right\}^{T} \left[ {M_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\}} \right)\left\{ {u_{0}^{\left( i \right)} } \right\} $$

The mass matrices have no any change, so [M 1] is zero. Upon substitution, the Eq. (10) can be rewritten as

$$ \lambda_{1}^{\left( i \right)} = \left\{ {u_{0}^{\left( i \right)} } \right\}^{T} \left[ {K_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\} $$
(11)
$$ \left\{ {u_{1}^{\left( i \right)} } \right\} = \sum\limits_{\begin{subarray}{l} s = 1 \\ s \ne i \end{subarray} }^{n} {\frac{1}{{\lambda_{0}^{\left( i \right)} - \lambda_{0}^{\left( s \right)} }}} \left( {\left\{ {u_{0}^{\left( s \right)} } \right\}^{T} \left[ {K_{1} } \right]\left\{ {u_{0}^{\left( i \right)} } \right\}} \right)\left\{ {u_{0}^{\left( s \right)} } \right\} $$

Using the Eq. (7), one obtains

$$ \lambda_{0}^{\left( 1 \right)} = \frac{k}{m},\;\lambda_{0}^{\left( 2 \right)} = \frac{{k + 2k^{\prime}}}{m} $$
(12)
$$ \left\{ {u_{0}^{\left( 1 \right)} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt {2m} }}} \\ {\frac{1}{{\sqrt {2m} }}} \\ \end{array} } \right],\;\left\{ {u_{0}^{2} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt {2m} }}} \\ { - \frac{1}{{\sqrt {2m} }}} \\ \end{array} } \right] $$

where, λ (1)0 and λ (2)0 denote the original eigenvalues, {u (1)0 } and {u 20 } denote the original regular modal vectors.

Substituting Eq. (12) and [K 1] into Eq. (11), one obtains

$$ \lambda_{1}^{\left( 1 \right)} = \frac{k}{2m},\;\lambda_{1}^{\left( 2 \right)} = \frac{k}{2m} $$
(13)
$$ \left\{ {u_{1}^{\left( 1 \right)} } \right\} = - \frac{k}{{4k^{\prime}}}\left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt {2m} }}} \\ { - \frac{1}{{\sqrt {2m} }}} \\ \end{array} } \right],\;\left\{ {u_{1}^{2} } \right\} = \frac{k}{{4k^{\prime}}}\left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt {2m} }}} \\ {\frac{1}{{\sqrt {2m} }}} \\ \end{array} } \right] $$

Upon substitution of the Eqs. (12) and (13) into Eq. (9), one obtains

$$ \lambda^{\left( 1 \right)} = \frac{k}{m} + \varepsilon \frac{k}{2m},\;\lambda^{\left( 2 \right)} = \frac{{k + 2k^{\prime}}}{m} + \varepsilon \frac{k}{2m} $$
(14)
$$ \left\{ {u^{\left( 1 \right)} } \right\} = \frac{1}{{\sqrt {2m} }}\left[ {\begin{array}{*{20}c} {1 - \varepsilon \frac{k}{{4k^{\prime}}}} \\ {1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ \end{array} } \right],\;\left\{ {u^{\left( 2 \right)} } \right\} = \frac{1}{{\sqrt {2m} }}\left[ {\begin{array}{*{20}c} {1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ { - 1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ \end{array} } \right] $$

Using Eq. (14), one obtains

$$ \varLambda = \left[ {\begin{array}{*{20}c} {\lambda^{\left( 1 \right)} } & 0 \\ 0 & {\lambda^{\left( 2 \right)} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\frac{k}{m} + \varepsilon \frac{k}{2m}} & 0 \\ 0 & {\frac{{k + 2k^{\prime}}}{m} + \varepsilon \frac{k}{2m}} \\ \end{array} } \right] $$
$$ u = \left[ {\begin{array}{*{20}c} {\left\{ {u^{\left( 1 \right)} } \right\}} & {\left\{ {u^{\left( 2 \right)} } \right\}} \\ \end{array} } \right] = \frac{1}{{\sqrt {2m} }}\left[ {\begin{array}{*{20}c} {1 - \varepsilon \frac{k}{{4k^{\prime}}}} & {1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ {1 + \varepsilon \frac{k}{{4k^{\prime}}}} & { - 1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ \end{array} } \right] $$
(15)

where Λ denotes the spectral matrix and u denotes the modal shape matrix.

Using the model analysis method, the principal mass matrix M p , the principal stiffness matrix K p , and the principal damping matrix C p can be expressed as

$$ M_{p} = u^{T} Mu,\;K_{p} = M_{p} \varLambda ,\;C_{p} = u^{T} Cu $$
(16)

Substituting Eq. (15) into Eq. (16) and ignoring the second-order and above terms, one obtains

$$ \begin{gathered} M_{p} = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right],K_{p} = \left[ {\begin{array}{*{20}c} {\frac{k}{m} + \varepsilon \frac{k}{{2m}}} & 0 \\ 0 & {\frac{{k + 2k^{\prime}}}{m} + \varepsilon \frac{k}{{2m}}} \\ \end{array} } \right], \hfill \\ C_{p} = \left[ {\begin{array}{*{20}c} {\frac{c}{m}} & { - \frac{{\varepsilon k}}{{2k^{\prime}}} \cdot \frac{{c^{\prime}}}{m}} \\ { - \frac{{\varepsilon k}}{{2k^{\prime}}} \cdot \frac{{c^{\prime}}}{m}} & {\frac{{c + 2c^{\prime}}}{m}} \\ \end{array} } \right] \hfill \\ \end{gathered} $$
(17)

Considering the non-diagonal damping coefficient is far less than the main diagonal damping coefficient, the non-diagonal one can be ignored, so C p becomes decoupled.

$$ C_{p} = \left[ {\begin{array}{*{20}c} \frac{c}{m} & 0 \\ 0 & {\frac{{c + 2c^{\prime}}}{m}} \\ \end{array} } \right] $$

From Eq. (17) and the new C p , the damping ratios ξ 1 and ξ 2 can be expressed as

$$ \xi_{1} = \frac{{C_{{p_{1} }} }}{{2w_{1} M_{{p_{1} }} }} = \frac{c}{{2\sqrt {\left( {k + \varepsilon \frac{k}{2}} \right)m} }},\;\xi_{2} = \frac{{C_{{p_{2} }} }}{{2w_{2} M_{{p_{2} }} }} = \frac{{c + 2c^{\prime}}}{{2\sqrt {\left( {k + 2k^{\prime} + \varepsilon \frac{k}{2}} \right)m} }} $$
(18)

We obtain the steady-state response using the mode superposition method. That is

$$ x\left( t \right) = \sum\limits_{i = 1}^{2} {\frac{{\beta_{i} u_{i} u_{i}^{T} }}{{K_{{p_{i} }} }}F_{0} \sin \left( {wt - \psi_{i} } \right)} $$
(19)

where, the amplitude amplification factor \( \beta_{i} = \frac{1}{{\sqrt {\left( {1 - l_{i}^{2} } \right)^{2} + \left( {2\xi_{i} l_{i} } \right)^{2} } }} \), the phase angle \( \psi_{i} = \arctan \frac{{2\xi_{i} l_{i} }}{{1 - l_{i}^{2} }} \), and the angular frequency ratio \( l_{i} = \frac{w}{{w_{i} }} \).

Upon substitution, the final solution will be

$$ x\left( t \right) = \frac{{\beta_{1} F}}{{K_{{p_{1} }} m}}\left[ {\begin{array}{*{20}c} {1 - \varepsilon \frac{k}{{4k^{\prime}}}} \\ {1 + \varepsilon \frac{k}{{4k^{\prime}}}} \\ \end{array} } \right]\sin \left( {wt - \psi_{1} } \right) + \frac{{\beta_{2} F}}{{K_{{p_{2} }} m}}\left[ {\begin{array}{*{20}c} {\varepsilon \frac{k}{{4k^{\prime}}}} \\ { - \varepsilon \frac{k}{{4k^{\prime}}}} \\ \end{array} } \right]\sin \left( {wt - \psi_{2} } \right) $$
(20)

When w = w 1 (the excitation frequency is equal to the in-phase frequency), from Eq. (20)

$$ x_{1} \left( t \right) = \frac{{\beta_{1} F}}{{K_{{p_{1} }} m}}\left( {1 - \varepsilon \frac{k}{{4k^{\prime}}}} \right)\sin \left( {wt - \psi_{1} } \right), \quad \;x_{2} \left( t \right) = \frac{{\beta_{1} F}}{{K_{{p_{1} }} m}}\left( {1 + \varepsilon \frac{k}{{4k^{\prime}}}} \right)\sin \left( {wt - \psi_{1} } \right) $$
(21)

Substituting F = ma, \( c = \frac{{mw_{1} }}{{Q_{1} }} \) into the Eq. (21), we obtain

$$ \begin{aligned} x_{1} \left( t \right) - x{}_{2}\left( t \right) &= \frac{{\varepsilon F\sqrt {\frac{m}{{\left( {k + \varepsilon \frac{k}{2}} \right)}}} }}{2c} \times \frac{k}{{k^{\prime}}}\cos w_{1} t \\&\,= - \frac{{aQ_{1} }}{{w_{1}^{2} }} \times \frac{\varepsilon }{2} \times \frac{k}{{k^{\prime}}}\cos w_{1} t \end{aligned} $$
(22)

where, a denotes the amplitude of the common-mode acceleration, Q 1 denotes the first-order modal quality factor.

When w = w 2 (the excitation frequency is equal to the anti-phase frequency), from Eq. (20)

$$ \begin{gathered} x_{1} \left( t \right) = \frac{{\beta _{2} F}}{{4K_{{p_{2} }} m}}\varepsilon \frac{k}{{k^{\prime}}}\sin \left( {wt - \psi _{2} } \right), \hfill \\ x_{1} \left( t \right) = \frac{{\beta _{2} F}}{{4K_{{p_{2} }} m}}\varepsilon \frac{k}{{k^{\prime}}}\sin \left( {wt - \psi _{2} - \pi } \right) \hfill \\ \end{gathered} $$
(23)

Substituting F = ma, \( c + 2c^{\prime} = \frac{{mw_{2} }}{{Q_{2} }} \) into the Eq. (23), we obtain:

$$ \begin{aligned} x_{1} \left( t \right) - x{}_{2}\left( t \right) &= \frac{{\varepsilon F\sqrt {\frac{m}{{\left( {k + 2k^{\prime} + \varepsilon \frac{k}{2}} \right)}}} }}{{2 \times \left( {c + 2c^{\prime}} \right)}} \times \frac{k}{{k^{\prime}}}\cos w_{2} t \\&\quad = - \frac{{aQ_{2} }}{{w_{2}^{2} }} \times \frac{\varepsilon }{2} \times \frac{k}{{k^{\prime}}}\cos w_{2} t \end{aligned}$$
(24)

where, Q 2 denotes the second-order modal quality factor.

The ratio of the coupled stiffness k ′ to the sense stiffness k is termed the coupled stiffness ratio (CSR), which is given by:

$$ CSR = \frac{{k^{\prime}}}{k} $$
(25)

From Eq. (22), we conclude that increasing the CSR, square of the in-phase frequency, and decreasing the stiffness imbalance and the acceleration amplitude and the quality factor can improve the synchronism of two tines.

The Eq. (23) shows that the two tines operate out of phase and double the acceleration output error.

From Eq. (24), we obtain that increasing the CSR, square of the anti-phase frequency, and decreasing the stiffness imbalance and the acceleration amplitude and the quality factor can reduce the anti-phase movement of two tines.

4 Structural design and FEM simulations

4.1 Structural design

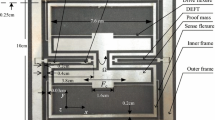
We design the symmetrically fully decoupled structure based on the published TFG from Trusov et al. (2011), two tines are coupled with a linearly coupled spring. The schematic of the design is shown in Fig. 3.

Fig. 3
figure 3

Schematic of the designed TFG

Full size image

The linearly coupled direction is the sense mode direction and the sense electrodes are lateral comb capacitance. We decouple the drive mode and sense mode by the central sensitive mass, and the structural type of the elastic beams is identical to ensure the symmetry and mode-match of TFG. The lever can improve the anti-phase motion synchronism of the drive mode, and increase the frequency of the spurious drive mode. The designed sense beam and coupled beam are shown in Fig. 4

Fig. 4
figure 4

Sense beam (a) and coupled beam (b)

Full size image

The sense spring k s and coupled spring k c are given by:

$$ k_{s} = E \times h \times \left( {\frac{{w_{s} }}{{l_{s} }}} \right)^{3} ,\;k_{c} = E \times h \times \left( {\frac{{w_{c} }}{{l_{c} }}} \right)^{3} $$
(26)

where, E is 169 GPa and h, w, and l are the thickness, width, and length of the spring beam.

We design the structures of three different CSR values (which are 0.038, 0.075, and 0.15) by the cascade of the coupled spring, which comprises three identical springs, two identical springs and one spring, respectively. The stiffness imbalance is varied by intentional changing the left tine sense spring width, to realize three different values, respectively (which are 0.97, 1.83, and 4.0 %).

4.2 FEM simulations

In this study, the harmonic responses simulations are carried out using the finite element software Ansys. The central sensitive masses are meshed with triangular elements; larger linear elements are used for the frames while smaller quadratic elements are used to form the suspension springs. The amplitude of the acceleration applied to the model is 1 g (g = 9.8 m/s2) and the Q-factor is 200. To reduce the calculation time and ensure the calculation accuracy, we sweep frequency of 3,600–4,000, 3,600–4,200, and 3,600–4,500 Hz for 0.038, 0.075, and 0.15 CSR structures, respectively. The simulation parameters are listed in Table 1.

Table 1 Model parameters used in the simulation model shown in Fig. 3
Full size table

We simulate the modals of 0.075 CSR TFG, as shown in Fig. 5. And we compare the simulated frequency response of 0.075 CSR symmetric TFG with the 0.075 CSR asymmetric TFG of 4.0 % stiffness imbalance, as shown in Fig. 6.

Fig. 5
figure 5

Modal analysis of the in-phase mode (a) and anti-phase mode (b)

Full size image
Fig. 6
figure 6

Frequency response of 0.075 CSR symmetric coupled tines (a), frequency response of 0.075 CSR asymmetric coupled tines of 4.0 % stiffness imbalance (b)

Full size image

The simulation results in Fig. 6a show that simulations coincide with the theoretical analysis, which reveals that two tines have a completely synchronized movement to suppress the common-mode acceleration. The acceleration output will appear when the stiffness is imbalanced (Fig. 6b), which demonstrates that two tines displacement difference is large in the in- and anti-phase modal frequencies while the phases of two tines have an out of phase trend in the anti-phase modal frequency.

From Fig. 7a, c and e, we obtain that as the coupled stiffness ratio increases the two tines in-phase and anti-phase displacement difference decreases, and as the stiffness imbalance decreases the displacement difference decreases. Fig. 7b, d and f demonstrate increasing CSR may reduce the phase difference and decreasing the stiffness imbalance may have a smaller phase difference and narrower bandwidth.

Fig. 7
figure 7

a Displacement difference and b phase difference of 4.0 % stiffness imbalanced coupled tines; c Displacement difference and d phase difference of 1.83 % stiffness imbalanced coupled tines; e Displacement difference and f phase difference of 0.97 % stiffness imbalanced coupled tines

Full size image

5 Simulations and analytical comparisons

To achieve a fair comparison, we use the same parameters with the simulation models. The in-phase and anti-phase modal frequencies of all designed structures are listed in Table 2.

Table 2 In-phase and anti-phase modal frequencies of all designed models
Full size table

We compute the two tines displacement difference using the previous theoretical formulas, Eqs. (22) and (24) (described in Sect. 3), and compare with the simulation results. The error rates are calculated, as shown in Table 3.

Table 3 Simulations and analytical comparisons
Full size table

Table 3 clearly shows that theoretical values are in line with simulation results within a small stiffness imbalance verifying the theoretical model. We conclude the in-phase and anti-phase displacement differences between two tines are inversely proportional to CSR and proportional to the stiffness imbalance.

To describe the phenomenal more clearly, the displacement difference of 0.97 and 4.0 % stiffness imbalance are plotted against the different CSR, as shown in Fig. 8.

Fig. 8
figure 8

Theoretical and simulation displacement difference of a 0.97 % and b 4.0 % stiffness imbalanced coupled tines

Full size image

The effect of the coupled stiffness ratio and stiffness imbalance on the acceleration output is clearly demonstrated. In the case of 4.0 % stiffness imbalance, the error rate between the theoretical values and simulation results is a little large. The reason is that as the stiffness imbalance increases the accuracy of the first-order perturbation method decreases. But we believe that the accuracy can be guaranteed in the case of small stiffness imbalance caused by the practical fabrication imperfections.

6 Experimental verification

According to the experimental conclusions from Singh et al. (2013), the expression is:

$$ V_{0} \propto \frac{\varDelta k}{{DR \times f_{\text{anti}}^{2} }} $$
(27)

where, V 0 is the anti-phase differential output voltage, Δk is the stiffness imbalance, f anti is the anti-phase modal frequency, and DR is the frequency decoupling ratio.

The DR is defined as follows:

$$ DR = \frac{{f_{{s_{\text{anti}} }} - f_{{s_{\text{in}} }} }}{{f_{{s_{\text{anti}} }} }} $$
(28)

where, \( f_{{s_{\text{anti}} }} \) and \( f_{{s_{\text{in}} }} \) denote the anti- and in-phase modal frequency in the sense direction, respectively.

Substituting Eq. (15) (derived in Sect. 3) into Eq. (28), we obtain that:

$$ CSR = \frac{{\left( {1 - \left( {1 - DR} \right)^{2} } \right) \times \left( {1 + \frac{\varDelta k}{2}} \right)}}{{2 \times \left( {1 - DR} \right)^{2} }} $$
(29)

The capacitance sensitivity S c and the displacement sensitivity S d can be expressed as follows:

$$ S_{c} = \frac{{V_{0} }}{\varDelta c},\;S_{d} = \frac{\varDelta c}{\varDelta x} $$
(30)

From the Eq. (30), the displacement difference can be written as:

$$ \varDelta x = \frac{{V_{0} }}{{S_{c} \cdot S_{d} }} $$
(31)

Since the type of TFG we designed is the same to Type-B from Singh, we select the Type-B experimental results to make a comparison.

The case is as follows:

$$ f_{{s_{\text{anti}} }} = 16.5\;{\text{kHz}}, $$

Q anti = 330, Δk = 1 %, DR = 0.09, S c  = 3.77 mV/fF, S d  = 66 aF/nm, V 0 = 4 mV,a = 9.8 m/s 2

From Eq. (29), we obtain:

CSR = 0.10

From Eq. (31), we calculate the experimental displacement difference:

$$ \varDelta x = 1.61 \times 10^{ - 8} m $$

According to the theoretical formula Eq. (24) (derived in Sect. 3), we obtain the analytical displacement difference Δx ′:

$$ \varDelta x^{\prime} = \frac{{a \times Q_{\text{anti}} }}{{\left( {2\pi \times f_{{s_{\text{anti}} }} } \right)^{2} }} \times \frac{\varDelta k}{2} \times \frac{1}{CSR} $$

So,

$$ \varDelta x^{\prime} = 1.51 \times 10^{ - 8} \;m $$

Considering the error of the calculation of Δk and the nonlinearity of the parallel plate electrodes, our analytical solution coincides with the experimental result. So, the analytical expression is verified. Since the in-phase displacement difference between two tines has not been studied, we will fabricate these TFGs and experimentally verify in the future studies.

7 Conclusions

This paper analyzes the acceleration sensitivity of the non-ideal (stiffness imbalance) MEMS tuning fork gyroscopes (TFGs). We establish two degrees of freedom coupled model by simplifying TFG into two linearly coupled sense tines, and take advantage of the first-order matrix perturbation method to compute the differential acceleration output, which coincides with the FEM simulation results. Additionally, we verify the analytical expressions using the experimental data from the other researches. The main conclusion is that the differential output displacement caused by the stiffness imbalance becomes larger in the in- and anti-phase modal frequencies, which is inversely proportional to the coupled stiffness ratio and square of the modal frequency, and is proportional to the stiffness imbalance, the quality factor and the amplitude of common-mode acceleration. The displacement and phase differences arise from the unsynchronized motion of two tines due to the stiffness imbalance. Therefore, the acceleration sensitivity of TFGs can be reduced by increasing coupled stiffness ratio, modal frequency and sense beam widths which are insensitive to the technological imperfections.