1 Introduction

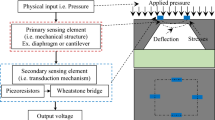
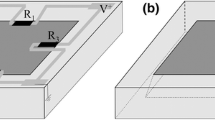
Micro electro mechanical system (MEMS) contains components of sizes ranging from few micrometers to few millimeters. MEMS combine mechanical and electrical aspects via transducer action. MEMS systems can sense, control and actuate on the micro scale, and can generate effects on the macro scale. The interdisciplinary nature of MEMS utilizes design, engineering and manufacturing expertise from a wide range of technical areas including integrated circuit fabrication technology, mechanical engineering, materials science, electrical engineering, chemistry and chemical engineering, as well as fluid engineering, optics, instrumentation and packaging. The complexity of MEMS is also shown in the extensive range of applications that incorporate MEMS devices. Micro-sensors are a subclass of MEMS which are built to sense and measure certain physical, chemical or biological quantities such as temperature, pressure, force, sound, magnetic flux and chemical compositions, to name a few. Micro-sensors can be found in systems like automotive, medical, electronic, communication and defense applications (Wisitsoraat et al. 2007). Most of the MEMS sensors use silicon for diaphragm and piezoresistive property of silicon or polycrystalline silicon as sensing mechanism (Wisitsoraat et al. 2007; Bao and Wang 1987; Jevti and Smiljani 2008). There are mainly three types of pressure sensors for sensing the deformation of diaphragm when a pressure is being applied. They are the capacitive, resonant and piezoresistive pressure sensors (Clausen and Sveen 1987). MEMS piezoresistive pressure sensors belong to the category of micro-sensors which are widely used in automotive and aerospace industries. Silicon pressure sensors have become very popular due to miniaturization, mechanical stability, compatibility with integrated circuit fabrication and micromachining as well as the price (Tian et al. 2010). Piezoresistivity is a common pressure sensing principle for micro-machined sensors. Silicon is an ideal material for designing MEMS systems. Doped silicon, in particular, exhibits remarkable piezoresistive response characteristics among all known piezoresistive materials. Boron doped silicon is normally used as the material for making the micro piezoresistors which are used in MEMS piezoresistive pressure sensors. The resistance change in piezoresistors is proportional to the applied pressure which can be measured using a suitable measurement theory (Tai-Ran-Hsu 2000; Suja et al. 2013a; Tufte et al. 1962). Schematic view of a MEMS pressure sensor is as shown in Fig. 1. Top view of a MEMS pressure sensor diaphragm is shown in Fig. 1a. The cross sectional view of diaphragm at cut line position AA′ shown in Fig. 1a is shown in Fig. 1b. The electrical schematic of Wheatstone bridge configuration in which resistors R1 to R4 are electrically connected is shown in Fig. 1c. When there is no applied pressure the bridge will be in balanced condition and there will not be any output. When the diaphragm is subjected to pressure P, due to induced stress, the diaphragm will deform and there will be a change in resistance ΔR in all of the four resistors. The bridge is out of balance and an input voltage Vi to Wheatstone bridge results in an output voltage Vout. If all the change in resistance is equal then the output voltage can be expressed in Eq. (1)

Fig. 1
figure 1

a Schematic of silicon pressure sensor; b top view of pressure sensor; c schematic of electrical links forming the Wheatstone bridge

Full size image
$$V_{out} = V_{i} \frac{\Delta R}{R}$$
(1)

The sensitivity (S) of the pressure sensor is then expressed in Eq. (2).

$$S = \frac{{V_{out} }}{{V_{i} }} \times \frac{1}{P}$$
(2)

In a piezoresistive pressure sensor the variation in the length (l) of the piezoresistor plays a greater role in determining the sensitivity of the sensor than width (w) or thickness (t) variations (Madhavi et al. 2013). Considerable improvement in the sensitivity is possible when the size of the piezoresistor is optimized. The effect of size of piezoresistors on the sensitivity of silicon on insulator piezoresistive pressure sensor has been reported (Suja et al. 2013b). However, the reasons for the change in the sensitivity of the pressure sensor due to the change in piezoresistor dimensions are not clearly understood.

In this work, the dimensions of piezoresistors are varied by keeping the electrical resistance constant. Other important condition on which the performance of a MEMS pressure sensor depends on is its operating conditions, mainly the ambient temperature. Therefore, design should be such that the performance has to be stable over wide temperature range. Here an analysis for the same is being done, which considers the variation in material properties of boron piezoresistors with temperature which will particularly affects the performance of the system. The sensitivity of the system depends on the electrical conductivity of the micro piezoresistors. The main objective is to suggest a model for electrical conductivity of boron doped silicon which depends on temperature and acceptor doping. The temperature and doping dependent factors which effect electrical conductivity are energy band gap, intrinsic carrier concentration, electron and hole mobility and ionization factor (Sze 1981; Streetman and Banarjee 2002). The variation of electron and hole mobility with respect to temperature and doping concentration estimated using the Caughey-Thomas model and Arora model (Sze 1981; Streetman and Banarjee 2002; Caughey and Thomas et al. 1967; Selberherr 1984). Using the derived models, the electrical conductivity as a function of temperature and variation in electrical conductivity with temperature at various doping concentrations are studied.

2 Design criteria of piezoresistive MEMS pressure sensors

The load deflection method that describes the relation between displacement and applied pressure for a flat square diaphragm is given by Eq. (3) (Linlin et al. 2006)

$$\frac{{Pa^{4} }}{{Eh^{4} }} = \frac{4.2}{{\left( {1 - v^{2} } \right)}}\left( \frac{y}{h} \right) + \frac{1.58}{{\left( {1 - v^{2} } \right)}}\left( \frac{y}{h} \right)^{3}$$
(3)

E is Young’s modulus, ν is Poisson’s ratio of the diaphragm material, ‘a’ is the side length of the diaphragm in μm, h is diaphragm thickness in μm. According to the load-deflection method, the deflection range is divided into two regions namely, a small deflection region (deflection <25 % of the diaphragm thickness) described by the linear term in Eq. (3). Large deflection region (deflection >25 % of the diaphragm thickness) is described by the non-linear, cubic term in Eq. (3). The governing equation for determining the deflection can be derived from small scale deflection theroy as described in (Timoshenko and Woinowsky-Krieger 1959). Due to symmetry, square diaphragm has the highest induced stress for a given applied pressure. Analytical model for diaphragm size, burst pressure and sensitivity is reported (Gong and Lee 2001). Thus, the square diaphragm is preferred for the design of pressure sensor. For a square plate clamped at the edges, the maximum stress (σmax) at the center of the each edge is given by Eq. (4).

$$\sigma_{\hbox{max} } = \frac{{0.308Pa^{4} }}{{h^{2} }}$$
(4)

The maximum deflection in the diaphragm is given by Eq. (5).

$$w_{\hbox{max} } = \frac{{ - 0.013\,Pa^{4} }}{{Eh^{3} }}$$
(5)

The deflection and stress in the diaphragm play an important role in analyzing the performance of the diaphragm. The piezoresistive effect was first discovered by Lord Kelvin in 1856 when he reported that certain metallic conductors under mechanical strain exhibited a corresponding change in electrical resistance. Piezoresistivity is the dependence of electrical resistivity on strain. The resistivity of a material depends on the internal atom positions and their motions. Strain changes these arrangements and hence the resistivity. If a strip of elastic material is subjected to tension (force), its longitudinal dimension will increase while there will be a reduction in a lateral dimensions. So when the strain is positive the length of the material increases and area of cross section decreases. Thus the resistance of the material under consideration will feel a change (increase) in resistance. This change in the resistance value of a conductor due to applied strain is called piezoresistive effect. The piezoresistive effect in single crystal silicon was first reported in 1954. The piezoresistive effect causes change in the resistance of certain doped materials when they are subjected to stress. The resistivity of a piezoresistive material is a function of stress that is also direction dependent due to the anisotropic crystal structure. The fact that silicon doping type and anisotropic structure has made the relationship between the change in resistance and the existent stress field more complex and is given by Eq. (6) (Chaurasia and Chaurasia 2012)

$$\left\{ {\Delta R} \right\} = \left[ \varPi \right]\left\{ \sigma \right\}$$
(6)

where {∆R} = {∆Rxx ∆Ryy ∆Rzz ∆Rxy ∆Rxz ∆Ryz}T represents the change of resistance in a small cubic piezo resistive crystal element with corresponding stress elements {σ} = {σxx σyy σzz σxy σxz σyz}T for the six crystallographic directions in silicon. σxx, σyy, σzz represent the normal stresses and σxy, σxz, σyz are the shear stresses. The vector [π] is referred to as piezoresistive coefficient matrix. These piezoresistive coefficients depend strongly on doping type, which relate the fractional change in resistance to the applied stress. For a diffused resistor subjected to longitudinal and transverse stress components σl and σt respectively the resistance change is given by Eq. (7) (Arora et al. 1982). Properties of materials used for the analysis are shown Table 1.

Table 1 Material properties of n-type piezo resistive silicon used in the simulation studies
Full size table
$$\frac{\Delta R}{R} = \sigma_{l} \varPi_{l} + \sigma_{t} \varPi_{t} = \left( {\varPi_{l} + \nu \,\varPi_{t} } \right)$$
(7)

3 Sensitivity analysis

In this section, the sensitivity of MEMS piezoresistive pressure sensor is analyzed. In the analysis, the dimensions of piezoresistors are varied while the resistance of the piezoresistor is kept constant at 1 kΏ. The diaphragm dimensions length (l) and width (w) of the piezoresistor are varied while the thickness (t) is maintained at 1 μm. In these studies, the applied pressure is 0.1 MPa.

The sensitivity of a pressure sensor is highly depended on the piezoresistor dimensions. The arrangement of four piezoresistors used in simulation along with various cases is shown in Fig. 2. The resistors are divided into two groups––Group-A (R1 and R3) and Group-B (R2 and R4). In order to identify the effect of resistor size on the sensitivity, three options have been analyzed. In option-I, as shown in Fig. 2a, the dimension of Group-A resistors and Group-B resistors are same. In option-II, as shown in Fig. 2b, the dimension of Group-A resistor is varied while the dimension of Group-B resistor is fixed. In option-III, as shown in Fig. 2c, the dimension of Group-A resistor is fixed while the dimensions of Group-B resistors are varied. Table 2 indicates various dimensions considered in each of the three options. The simulated sensitivity values of all the three options are tabulated in Table 2. From Table 2 it can be observed that, in option-I and option-III, the sensitivity decreases drastically as the dimension of Group-B resistors increases. The sensitivity is fairly constant in case of Option-II, in which dimension of Group-B resistor is kept constant while the dimension of Group-A resistors increases.

Fig. 2
figure 2

Arrangement of piezoresistors for different cases

Full size image
Table 2 Sensitivity estimated for different size (l × w) options of piezoresistor
Full size table

Thus it can be concluded that the dimension of Group-B resistors play a significant role in the sensitivity and a smaller Group-B resistor dimensions are preferred for better sensitivity. The cut line along with the stress is observed which is indicated by line AA′ in Fig. 2c. From the stress profile in Fig. 3, it is evident that the stress becomes compressive between −166 to −250 and 166 to 250 μm. Therefore the maximum length of the resistor sensing the compressive stress cannot be more than 84 μm. The resistors of Group-B (R2 and R4) sense the compressive stress. Therefore, their size should be kept small. In order to confirm this point, performance of the sensor is analyzed for various resistor sizes by maintaining the size of Group-B resistors to minimum possible size (option-II).

Fig. 3
figure 3

Longitudinal stress profile along X = ± a and Y = 0

Full size image

The reduction in sensitivity as resistor size increases is due to the reduction in average stress induced in a given area of the resistor. Thus, it is important to select the design on resistors that feel the compressive stress to optimum size to attain better sensitivity. The comparison between the sensitivities for the three cases shown in Fig. 4 indicates that the resistors that sense the tensile stress does not contribute to change in sensitivity while the resistors that sense the compressive stress contribute to significant change in sensor sensitivity.

Fig. 4
figure 4

Comparison of sensitivity vs. length for various cases

Full size image

4 Optimization of doping concentration on piezoresistor performance

Temperature affects the properties of electronic systems in a number of fundamental ways. Since the change in electrical conductivity can affect the sensitivity of the system, here the focus is on the change in electrical conductivity of piezoresistors with respect to temperature is considered. In the analysis, the acceptor doping of p-type piezoresistor is also considered which significantly contributes to the resistance and thus needs to be considered in design optimization. The fundamental relation that describes the conductivity (σ) in silicon as a function of mobility and carrier concentration is given by Eq. (8).

$$\sigma = q\left( {n\mu_{n} + p\mu_{p} } \right)$$
(8)

In Eq. (8), q is unit charge, n is electron density, p is hole density μn and μp are electron mobility and hole mobility respectively. The conductivity from Eq. (8) as a function of absolute temperature and doping concentration can be written as in Eq. (9).

$$\sigma \left( {T,N_{A} } \right) = q\left[ {n\left( {T,N_{A} } \right)\mu_{n} \left( {T,N_{A} } \right) + p\left( {T,N_{A} } \right)\mu_{p} \left( {T,N_{A} } \right)} \right]$$
(9)

From Eq. (9), it can be seen that to estimate conductivity and hence the resistance of a piezoresistor, the carrier concentration and the mobility need to be modeled accurately.

4.1 Estimation of carrier concentration

Carrier concentration in a semiconductor depends on doping concentration and temperature of operation. If a semiconductor piezoresistor is doped with acceptor impurities (NA), the electrical neutrality results in the number of holes as in Eq. (10).

$$p = N_{A}^{ - } + n$$
(10)

where p is the hole density in the valence band and n is the electron density in the conduction band and N − A is the ionized acceptor concentration. Electrical conductivity of implanted resistor depends on another important factor, ionization factor. The ionization of the impurities depends on the thermal energy and the position of the impurity level within the energy band gap. The position of impurity level is a function of dopant material. Shallow impurities readily ionize so that the free carrier density equals the impurity concentration. For acceptor impurities this implies that the hole density equals the acceptor concentration whereas deep impurities require energies larger than the thermal energy to ionize so that only a fraction of the impurities present in the semiconductor contributes to free carriers. Deep impurities which are more than five times the thermal energy away from either band edge are very unlikely to ionize. Due to ionization, the hole concentration in the piezoresistor can be written as in Eq. (11).

$$p = \eta \left( {T,N_{A} } \right)N_{A}$$
(11)

where η(T, N A ) is ionization factor which indicates the fraction of acceptor impurities (N − A ) that contribute to the conductivity and is given by Eq. (12).

$$\eta \left( {T,N_{A} } \right) = \frac{{N_{A}^{ - } }}{{N_{A} }}$$
(12)

The ionized acceptors are given by Eq. (13)

$$N_{A}^{ - } = \frac{{N_{A} }}{{1 + ge^{{\frac{{E_{A} - E_{F} }}{kT}}} }}$$
(13)

In Eq. (13), g is ground state degeneracy factor equal to four in case of holes, EA is acceptor energy level of dopant atom in the semiconductor, EF is Fermi level, which is related as described in Eq. (14). The acceptor energy level of Boron in silicon is 0.045 eV.

$$E_{A} - E_{F} = \left[ {E_{i} \left( T \right) - E_{F} } \right] - \left[ {E_{i} \left( T \right) - E_{A} } \right]$$
(14)

Thus, the ionization factor can be re-written as in Eq. (15).

$$\eta \left( T \right) = \frac{{N_{A}^{ - } }}{{N_{A} }} = \frac{1}{{1 + 4e^{{\frac{{E_{A} - E_{F} }}{kT}}} }}$$
(15)

The intrinsic energy level as a function of temperature is given by Eq. (16).

$$E_{i} \left( T \right) = \frac{{E_{g} }}{2} + \frac{3}{4}kTln\left( {\frac{{m_{p}^{*} }}{{m_{n}^{*} }}} \right)$$
(16)

Using the charge neutrality condition np = n 2 i , electron concentration can be estimated by Eq. (17).

$$n = \frac{{n_{i}^{2} \left( T \right)}}{{\eta \left( {T,N_{A} } \right)N_{A} }}$$
(17)

Here ni(T) is the intrinsic carrier concentration of silicon which is a temperature dependent parameter [10–11], given by Eq. (18).

$$n_{i} \left( T \right) = 2\left( {\frac{2\pi kT}{{h^{2} }}} \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} \left( {m_{n}^{*} m_{p}^{*} } \right)^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}} e^{{{\raise0.7ex\hbox{${ - E_{g} }$} \!\mathord{\left/ {\vphantom {{ - E_{g} } {2kT}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${2kT}$}}}}$$
(18)

In Eq. (18), h is Planck’s constant, k is Boltzmann’s constant, Eg is band gap, m *n and m *p are effective mass of electron and hole in silicon respectively. In order to study the effect of temperature on ionization factor, the ionization factor at different doping concentrations in a piezoresistor is studied as a function if temperature. To estimate ionization factor, Eq. (12) is used for computing the ionization factor along with Eq. (13) through Eq. (16).

The variation of ionization factor with respect to various doping concentration (NA) are shown in Fig. 5. It is observed from Fig. 5 that the ionization factor decreases with temperature and doping concentration. As the doping concentration increases, the ionization factor decreases at a given temperature. Thus, it is important to note that, if the sensor is going to operate in a low temperature regime, it is important to dope it high so that the conductivity is sufficiently large to produce a significant at the output of Wheatstone bridge.

Fig. 5
figure 5

Ionization factor vs. temperature for different acceptor concentrations

Full size image

4.2 Estimation of mobility

Mobility describes the ease of carriers to move when a unit electric field is applied. Generally the term mobility can be expressed as in Eq. (19), in terms of low electric field the drift velocity (v d) and electric field strength (E).

$$v_{d} = \mu \epsilon$$
(19)

Carrier mobility is affected by scattering mechanisms. There are two important scattering mechanisms that affect the carrier mobility significantly. The first one is scattering due to acoustic phonons described by Eq. (20) which decreases with temperature.

$$\mu_{l} \propto \left( {m^{*} } \right)^{{{\raise0.7ex\hbox{${ - 5}$} \!\mathord{\left/ {\vphantom {{ - 5} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} T^{{{\raise0.7ex\hbox{${ - 3}$} \!\mathord{\left/ {\vphantom {{ - 3} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(20)

The second mechanism that affects mobility is due to ionized impurity scattering as described by Eq. (21).

$$\mu_{i} \approx \left( {m^{*} } \right)^{{{\raise0.7ex\hbox{${ - 1}$} \!\mathord{\left/ {\vphantom {{ - 1} 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} N_{I}^{ - 1} T^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$
(21)

NI is ionized impurity density and in this case equal to NA. The mobility is expected to increase with temperature. Using Matthiessen’s rule, the effective mobility (Sze 1981; Streetman and Banarjee 2002) can be estimated using by Eq. (22).

$$\mu = \left( {\frac{1}{{\mu_{l} }} + \frac{1}{{\mu_{i} }}} \right)^{ - 1}$$
(22)

From Eq. (22), it can be observed that as the temperature increases, the effective mobility will increase till a particular temperature and then decreases. The mobility models of electrons and holes that consider doping concentration variation and temperature variation considered in this work are Arora low field mobility model and Caughey–Thomas model.

4.2.1 Arora low field mobility model

Arora low field mobility model is an empirical model developed in Caughey and Thomas et al. (1967). The electron mobility and hole mobility in Eq. (23) explain the mobility as a function temperature and doping concentration. This model is an empirical model. This model agrees with experimental data at 300 K for any doping concentration. Various parameters that fully describe Arora low field mobility are shown in Table 3.

Table 3 Various parameters used in Arora mobility model (Atlas 2006)
Full size table
$$\mu_{n,p} = \mu_{n,p1} \left( \frac{T}{300} \right)^{{\alpha_{n,p} }} + \frac{{\mu_{n,p2} \left( \frac{T}{300} \right)^{{\beta_{n,p} }} }}{{1 + \frac{{N_{D} }}{{N_{critn,p} \left( \frac{T}{300} \right)^{{\gamma_{n,p} }} }}}}$$
(23)

Using Arora model, electron mobility and hole mobility in silicon as a function of temperature are plotted as shown in Fig. 6. The maximum value of electron mobility and hole mobility are about 1,400 and 450 cm2/V s respectively. However, Arora model overestimates the mobility especially in the low temperature regime. Thus, the conductivity estimated using Arora model might erroneous at low temperatures. Even though Arora model overestimates the mobility at low temperatures, this model agrees extremely well with experiments in the vicinity of 300 K.

Fig. 6
figure 6

Electron mobility and hole mobility as a function of temperature in Arora model

Full size image

4.2.2 Caughey–Thomas low field mobility model

Caughey–Thomas low field mobility model is an empirical model based on data (Sze 1981) and fitting parameters (Selberherr 1984). The model has been developed using the experimental data and an empirical relationship is formed. The expression for electron mobility and hole mobility which depend on temperature and doping concentration are is given by Eq. (24). Various parameters used in Eq. (24) are listed in Table 4.

Table 4 Various parameters used in Caughey–Thomas model (Atlas 2006)
Full size table
$$\mu_{\text{n,p}} = \mu_{n,p1} \left( {\frac{\text{T}}{300}} \right)^{{\alpha_{n,p} }}\, + \frac{{\left( {\mu_{\text{n,p2}} \left( \frac{T}{300} \right)^{{\beta_{n,p} }} } \right) - \left( {\mu_{\text{n,p1}} \left( \frac{T}{300} \right)^{{\alpha_{n,p} }} } \right)}}{{1 + \left[ {\left( \frac{T}{300} \right)^{{\gamma_{n,p} }} \left( {\frac{N}{{N_{\text{critn,p}} }}} \right)^{{\Delta_{n,p} }} } \right]}}$$
(24)

Using Caughey–Thomas model, electron mobility and hole mobility in silicon as a function of temperature are plotted as shown in Fig. 7. The mobility values estimated by Caughey–Thomas model agree well over a wide doping concentration range and temperature range.

Fig. 7
figure 7

Electron mobility and hole mobility as a function of temperature in Caughey–Thomas model

Full size image

4.2.3 Estimation of electrical conductivity

The electrical conductivity in Eq. (9) incorporating carrier concentration using ionization factor in Eq. (11) and Eq. (18) and Caughey–Thomas mobility model in Eq. (24) is computed and analyzed. Electrical conductivity as a function of temperature for different values of acceptor concentration (NA) is computed and shown in Fig. 8. Since the Arora model results in erroneous mobility estimations, this model is not used in computing the electrical conductivity of the piezoresistor. As observed from Fig. 8, as the doping concentration decreases, the conductivity of the piezoresistor decreases and approaches a limiting value as the temperature increases. This is due to the fact that at lower doping concentrations, the intrinsic carrier concentration will be determining factor of conductivity. Thus the resistance of the piezoresistor (for a given dimensions), over a wide higher temperature region is constant at lower doping concentrations. The differential change in electrical conductivity as a function of temperature is estimated which is plotted in Fig. 9. The differential conductivity strongly depends on temperature at higher doping concentrations. Thus it is beneficial to use low-doped piezoresistors if the temperature range is very wide. However, if the temperature is too high, then the intrinsic carrier concentration increases and dominates the doping concentration, as described by Eq. (18). As the intrinsic carrier concentration is influenced by thermal noise, at high temperatures, the output signal will be very noisy. As it can be observed from Fig. 9, the change in conductivity can be treated as constant at higher larger doping concentrations (sigmoid fit). Thus, if the doping concentration of the piezo resistor is high, then the random error can be reduced as the conductivity is still controlled by the dopant atoms rather intrinsic carriers. As a result, piezoresistors will be less affected by random thermal noise and leaving behind the systematic error which can be corrected. Thus, it is evident that at higher temperatures, piezoresistors should be doped heavily to reduce the noise.

Fig. 8
figure 8

Electrical conductivity as a function of temperature for different acceptor concentration in Caughey–Thomas model

Full size image
Fig. 9
figure 9

Change in electrical conductivity as a function of temperature for different acceptor concentration in Caughey–Thomas model

Full size image

5 Conclusion

The performance of the piezoresistive pressure sensor is evaluated for its sensitivity. The implanted resistor plays an important role in optimizing the sensitivity and decreasing noise. The sensitivity of a piezoresistive pressure sensor can be increased by optimization of resistor size. To obtain improved sensitivity one method is to optimize the size of the piezoresistor in such a way that piezoresistor that are affected by compressive stress should be of small size when compared to the piezoresistors that sense the tensile stress. The sensitivity of the sensor can change drastically if the size of the resistor that senses compressive stress is very large.

The effect of piezoresistor doping concentration is evaluated. It is observed that if the sensor needs to be operated over very large temperature range, then the doping concentration should be small and if the sensor needs to be operated at elevated temperatures, then the doping concentration of the sensor should be large. Thus, the selection of doping of piezoresistor becomes important role in determining the sensitivity and noise immunity.