1 Introduction

The tensor form as the natural representation of an image has emerged in various applications. For example, in gray image data mining, the data, such as faces [1] or handwritten digits [2], are usually represented in the form of 2D tensor. Additionally, in color image data mining [3], the data is a 3D tensor in all color channels. How to classify this kind of data is an important topic for both image processing and machine learning. Nevertheless, traditional classification methods are usually vector-based representation [4–6], such as K-nearest neighborhood classifier [7], support vector machine (SVM) [8, 9], and ridge regression (RR) [10]. These methods must transform each image data into a vector which is reformulated by concatenating each row (or column) of a tensor. This makes image classification unable to fully use the neighborhood relationship between pixels. Some important spatial information is discarded in these vector-based representation methods.

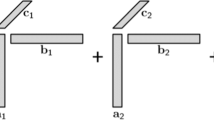
In order to make full use of the spatial information by treating image as itself without vectorization, tensor representations have been proposed to tackle the mentioned challenge. In [11], a novel, tensor face for face recognition has been proposed. Other traditional vector-based representation subspace learning methods have been extended to tensor representation, such as tensor principal component analysis [12], tensor linear discriminant analysis [13], and multi-linear discriminant analysis [14]. However, we can not directly classify the image as tensor data by using these methods because their purposes are to learn a subspace of tensor data and then employ another vector-based classifier. In [15], the images are represented as 2D matrices and directly used to learn two groups of classification vectors. The 2D matrix represents an image in its natural matrix form. Thus, this method can preserve the spatial correlation of an image and avoid the curse of dimensionality. However, we cannot handle the 3D or higher order image data by using this method. In [16], a supervised tensor learning framework (STL) framework has been presented. In STL, the higher order parameter was decomposed based on CANDECOMP/PARAFAC (CP) decomposition [17] and the tensor is directly considered as input data. Based on STL, several researchers have extended some traditional vector-based representation methods to their tensor patterns, such as tensor least square classifier [18], tensor SVM [19], tensor ridge regression (TRR) and support tensor regression [3]. As shown in Fig. 1a, the tensor was decomposed into a sum of \(N\) rank-1 tensors according to the CP decomposition [20]. After CP decomposition, the rank of tensor is \(N\). An important issue of tensor CP decomposition is that the rank \(N\) cannot be confirmed. If the number of rank-1 tensor is too many, the included information may be noise and redundancy, otherwise this representation is incomplete. So tensor CP decomposition is difficult to retain exact structural information for image classification. Moreover, these methods require many labeled training data but collecting these are high labor and time cost. It is not practical to provide sufficient labeled training data for these method in the real word [21].

Fig. 1
figure 1

Two widely used tensor decompositions: a CP decomposition and b Tucker decomposition

Full size image

To solve these problems, there are two advanced researches: (1) the first one is the Tucker decomposition [22], which is considered as higher-order principal component analysis. As shown in Fig. 1b, each tensor is represented as the product of a core tensor and matrices along all orders in the Tucker decomposition. There are two advantages in Tucker decomposition. First, compared with the CP decomposition that need to evaluate the rank to approximate the initial tensor, we can obtain the more exact decomposition result of tensor by using Tucker decomposition. The other benefit is that we can achieve the goal of dimension reduction by adjusting the dimension of the core tensor. (2) The second method is semi-supervised learning [15, 23, 24], which utilizes the manifold structure of both labeled and unlabeled training data to attain improved performance. In [24], a semi-supervised ranking scheme is proposed by introducing the local regression and global alignment into the objective function. In [23], a semi-supervised dimensionality reduction algorithm called semi-supervised discriminant analysis is presented. In [15], the graph Laplacian based semi-supervised learning is added into the compound matrix regression for image classification. The experiments in [15, 23, 24] have shown that simultaneously leveraging labeled and unlabeled images is beneficial for many applications.

Motivated by the advantages of tensor Tucker decomposition and semi-supervised learning, we propose a new semi-supervised classification frame for image tensors. The proposed frame utilizes the tensor regression model with Tucker decomposition, and graph Laplacian based semi-supervised learning jointly for classification. Tucker decomposition can efficiently preserve the spatial information of image data during the learning process. Semi-supervised learning enables our algorithm to overcome the deficiency of limited labeled training samples. The classification performance of proposed method thereby is enhanced subsequently.

In the proposed frame, the input image and parameter are regarded as tensor form directly. For the \(M\)-order parameter tensor, we decompose it into a core tensor multiplied by matrices along \(M\) orders at first. Then in each round of the alternating optimization algorithm utilized in this paper, the core tensor is transformed into the core matrix along one order and the decomposed matrix associated with this order can be estimated by solving the the RR problem while fixing other and core matrix. After solving for matrices along \(M\) orders, we can compute the core tensor by using the same process. The procedure is repeated until convergence.

We name the proposed method semi-supervised Tucker ridge regression (STuRR). The contributions of this paper are as follows:

  • 1. In order to exploit the spatial structure of the image data, we propose the Tucker decomposition to decompose the parameter tensor, which is more robust than that using the CP decomposition of parameter tensor. Moreover, the efficiency is guaranteed by avoiding the generation of high-dimensional vectors.

  • 2. The proposed approach embeds the semi-supervised learning into tensor regression model, which improves the performance in image classification by utilizing the unlabeled data.

  • 3. The experiments on different gray and color image datasets show that our method yields good results when only amount of labeled training data are available.

The rest of the paper is organized as follows: In Sect. 2, we introduce the novel semi-supervised Tucker ridge regression that is able to directly handle tensor representation of image and utilize the unlabeled images. The efficiency of the proposed algorithm is demonstrated on nine publicly available image databases in Sect. 3. Finally, conclusions are drawn in Sect. 4.

2 Semi-supervised tensor learning for image classification

In this section, we present the objective function of STuRR followed by a detailed optimization method for investigating the solution.

2.1 Semi-supervised Tucker ridge regression

When the appropriate regularization is added, the least squares loss function gains comparable performance to other complicated loss functions [25]. The least squares loss function therefore is considered in this paper for the problem of regression. When the \(\ell _2\)-norm is used for regularization in the vector space, the typical ridge regression can be formulated as:

$$\begin{aligned} \mathop {\min }\limits _{w,b} \sum \limits _{i = 1}^n {( \langle x _i ,w \rangle - y_i + b)^2 } + \lambda \left\| w \right\| _2^2 \end{aligned}$$
(1)

where \(x_i\) is the vector representation of input image, \(w\) is the parameter vector, \(b\) is the bias, and \(y_i\) is the regression output of \(x_i\).

In order to extend the ridge regression from vector to tensor space and classify image tensor directly, let \(\chi = [ \chi _1 ,\chi _2 ,\ldots ,\chi _n ]\in IR^{d_1 \times d_2 \times \cdots d_M \times n} \) as the set of training images where the \(i\)th image \(\chi _i\) is an \(M\)-order tensor and \(n\) is the total number of the training images. We denote the associated class label vectors as: \(y=[y_1,y_2,\ldots ,y_n]^T \in \{0,1\}^{n \times 1}\). \(y_i=1\) if the \(i\)th image is a positive example, whereas \(y_i=0\) otherwise. The TRR can be written as:

$$\begin{aligned} \mathop {\min }\limits _{\varvec{\omega },b} \sum \limits _{i = 1}^n {( \langle\chi _i ,\varvec{\omega } \rangle - y_i + b)^2 } + \lambda \left\| \varvec{\omega } \right\| _F^2 \end{aligned}$$
(2)

where \(\varvec{\omega }\in IR^{d_1 \times d_2 \cdots \times d_M }\) is the parameter tensor, \(\lambda \) denotes the regularization parameter and \(b\) is the bias term. We focus on learning the parameter tensor \(\varvec{\omega }\) and bias term \(b\). In this paper, in order to capture the underlying structure of image tensor, the parameter tensor \(\varvec{\omega }\) is decomposed according to the Tucker tensor decomposition firstly. That is:

$$\begin{aligned} \varvec{\omega }&= \mathcal {G} \times _1 U_1 \times _2 U_2 \cdots \times _M U_M \nonumber \\&= [\![{\mathcal {G} ;U_1 ,U_2 , \ldots ,U_M } ]\!]\end{aligned}$$
(3)

where \(\mathcal {G}\in IR^{R_1 \times R_2 \cdots \times R_M }\) is a core tensor and \(\{U_1,U_2,\ldots ,U_M\}\) are a set of matrices which are multiplied to the core tensor \(\mathcal {G}\) along each order. According to [17], \(R_i \le d_i\) for all \(i = 1,2,\ldots , M\). Compared with the CP decomposition, Tucker decomposition does not need pre-evaluate the rank \(N\). The \(\times _l\) is the \(l\)th order product between the tensor \(\mathcal {G}\) and the matrix \(U_l\in IR^{ I_l \times R_l } \). So \(\mathcal {G}\times _l U_l\) yields a new tensor \(\mathcal {Q}\in IR^{R_1\cdots \times R_{l-1}\times d_l\times R_{l+1}\cdots \times R_M }\) [17]. After Tucker decomposition, the Eq. (2) can be rewritten as:

$$\begin{aligned}&\mathop {\min }\limits _{\mathcal {G},U_1,\ldots ,U_M,b} \sum \limits _{i = 1}^n {( \langle \chi _i ,[\![{\mathcal {G} ;U_1 ,U_2 , \ldots ,U_M } ]\!]\rangle - y_i + b)^2 } \nonumber \\&\quad + \lambda \left\| [\![{\mathcal {G} ;U_1 ,U_2 , \ldots , U_M }]\!]\right\| _F^2. \end{aligned}$$
(4)

Compared with traditional ridge regression, using Tucker tensor decomposition enables our method to learn the spatial information along each order.

Now we show how to extend the Eq. (4) to a semi-supervised mode using the graph Laplacian. We first calculate the affinity matrix \(G\) by estimating the similarity between the training data. \(G_{ij}=1\) if \(\chi _i\) and \(\chi _j\) are the \(k\) nearest neighbors, whereas \(G_{ij}=0\) otherwise. The graph Laplacian matrix \(L\in IR^{n\times n}\) is constructed according to \(L=D-G\) where \(D\) is a diagonal matrix with its diagonal element \(D_{ii}=\sum _j{G_{ij}}\).

Suppose the first \(l\) images are labeled samples. If \(\chi _i\) is not labeled image, \(y_i=0\). The ground truth labels of the training images is \(y=[y_1,y_2,\ldots ,y_l,0,\ldots ,0]^T\in \{0,1\}^{n\times 1}\). In semi-supervised learning, \(l \ll n\), that is only a small mount of training data are labeled. Following [26], we define \(f=[f_1,f_2,\ldots ,f_n]^T\in IR^{n\times 1}\) as the predicted label vector of training data. A large value of \(f_i\) indicates a higher possibility that \(\chi _i\) is positive example. We propose our objective function as:

$$\begin{aligned}&\mathop {\min }\limits _{f, \left. {U_k } \right| _{k = 1}^M, b} \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y )) \nonumber \\&\quad + \lambda \sum \limits _{i = 1}^n {( \langle \chi _i ,[\![{\mathcal {G} ;U_1 ,U_2 , \ldots ,U_M } ]\!]\rangle - f_i + b)^2 } \nonumber \\&\quad + \beta \left\| [\![{\mathcal {G} ;U_1 ,U_2 , \ldots ,U_M } ]\!]\right\| _F^2 \end{aligned}$$
(5)

where Tr(.) is the trace operator. \(S\in IR^{n\times n}\) denotes a diagonal matrix. If \(\chi _i\) is a labeled image \(S_{ii}=\infty \) and \(S_{ii}=1\) otherwise. \(\mathrm{Tr}((f - y )^T S(f - y ))\) ensures that \(f\) is consistent with the known part of \(y\), and \(\mathrm{Tr}((f )^T Lf)\) makes \(f\) be smooth on the graph Laplacian.

2.2 Optimizing the objective function

We present our solution for obtaining the image tensor classifier. The objective function in Eq. (5) is not jointly convex for all items of \(\varvec{\omega } \) after Tucker decomposition. In order to solve the problem, we follow a alternating optimization algorithm, where at each iteration, the convex optimization problem with respect to one item of the parameters is solved, while all the other parameters are kept fixed.

To obtain \(U_k\), the tensor \(\varvec{\omega }\), \(\mathcal {G}\) and \(\chi _i\) should be unfolded along the \(k\)-order, namely \(\varvec{\omega } \rightarrow W_k ,\mathcal {G} \rightarrow G_k\) and \(\varvec{\chi }_i \rightarrow X_i^k\). The matrix representation along \(k\)-order of Eq. (3) can be written as:

$$\begin{aligned} W_k&= U_k G_k (U_M \otimes \cdot \cdot \cdot \otimes U_{k + 1} \otimes U_{k - 1} \otimes \cdot \cdot \cdot U^1 )^T \nonumber \\&= U_k G_k \widetilde{U}_k^T. \end{aligned}$$
(6)

So the Eq. (5) can be rewritten as:

$$\begin{aligned}&\mathop {\min }\limits _{f, {W_k } ,b} \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y ))\nonumber \\&\quad + \lambda \sum \limits _{i = 1}^n {\left( Tr\left( W_k {X_i^k} ^T \right) - f_i + b\right) ^2 } + \beta \left\| {W_k } \right\| _F^2. \end{aligned}$$
(7)

Substituting \(W_k\) in Eq. (7) with Eq. (6), and fixing \(\left. {U_l } \right| _{l = 1,l \ne k}^M ,G_k\), f, it becomes:

$$\begin{aligned}&\mathop {\min }\limits _{{U_k } ,b} \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y )) \lambda \sum \limits _{i = 1}^n {\left( \mathrm{Tr}\left( U_k G_k \widetilde{U}_k^T {X_i^k} ^T \right) - f_i + b\right) ^2 }\nonumber \\&\quad + \beta \mathrm{Tr}\left( U_k G_k \widetilde{U}_k^T \widetilde{U}_k G_k^T U_k^T\right) . \end{aligned}$$
(8)

We set \(\widetilde{X}_i^{kT} = G_k \widetilde{U}_k^T {X_i^k}^T\) and \(D_k = G_k \widetilde{U}_k^T \widetilde{U}_k G_k^T\), then Eq. (8) is rewritten as:

$$\begin{aligned}&\mathop {\min }\limits _{U_k ,b} \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y ))\nonumber \\&\quad +\lambda \sum \limits _{i = 1}^n {\left( \mathrm{Tr}\left( U_k \widetilde{X}_i^{kT}\right) - f_i + b\right) ^2 } + \beta \mathrm{Tr}\left( U_k D_k U_k^T\right) . \end{aligned}$$
(9)

We define \(\widetilde{D}_k = \left[ {\begin{array}{cc} {D_k \otimes I_{d_k \times d_k } } &{} 0 \\ 0 &{} 1 \\ \end{array}} \right] \), \(\mathrm{Tr}(U_k \widetilde{X}_i^{kT} ) = [\mathrm{vec}(U_k )^T\;b] [\mathrm{vec}(\widetilde{X}_i^k )^T\;1]^T= V_k^T \widehat{X}_i\). In definition, \(\mathrm{vec}(.)\) is the vectorization operation and \(\otimes \) is matrix Kronecker product. Then, Eq. (9) can be rewritten as:

$$\begin{aligned}&\mathop {\min }\limits _{V_k } \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y ))\nonumber \\&\quad +\lambda \sum \limits _{i = 1}^n {\left( V_k^T \widehat{X}_i - f_i \right) ^2 } + \beta \mathrm{Tr}\left( V_k^T \widetilde{D}_k V_k \right) . \end{aligned}$$
(10)

By letting \(\widehat{X} = [\widehat{X}_1 ,\widehat{X}_2 ,\ldots ,\widehat{X}_n ]\), Eq. (10) is rewritten as:

$$\begin{aligned}&\mathop {\min }\limits _{V_k} \mathrm{Tr}\left( V_k^T (\lambda XX^T + \beta \widetilde{D})V_k \right) - 2\lambda \mathrm{Tr}\left( V_k^T Xf^{T} \right) \nonumber \\&\quad + \mathrm{Tr}(f L(f )^T + (f - y^r )S(f - y^r )^T +\lambda (f )^T f )). \end{aligned}$$
(11)

Thus, the optimization problem for \(U_k,b\) in Eq. (8) is formulated as a ridge regression problem with respect to \(V_k\). Setting the derivative of Eq. (11) w.r.t. \(V_k\) to 0, we have:

$$\begin{aligned} 2(\lambda XX^T + \beta \widetilde{D})V_k - 2\lambda Xf^{T} = 0 \Rightarrow V_k = \lambda (\lambda XX^T + \beta \widetilde{D})^{ - 1} Xf^{T}. \end{aligned}$$
(12)

Denoting \(G_k = (\lambda XX^T + \beta \widetilde{D})^{ - 1}\), we get:

$$\begin{aligned} V_k = \lambda G_k Xf^{rT}. \end{aligned}$$
(13)

Substituting \(V_k\) in Eq. (11) with Eq. (13), we obtain:

$$\begin{aligned}&\mathop {\min }\limits _{f } \mathrm{Tr}(f L(f )^T) + \mathrm{Tr}((f - y )S(f - y )^T) \nonumber \\&\quad - \lambda ^2 \mathrm{Tr}(f X^T G_k^T Xf^{T} ) + \lambda \mathrm{Tr}((f )^T f )). \end{aligned}$$
(14)

Setting the derivative of Eq. (14) w.r.t. \(f\) to 0, we have:

$$\begin{aligned}&2f L + 2(f - y )S - 2\lambda ^2 f X^T G_k^T X + 2\lambda f = 0 \nonumber \\&\quad \Rightarrow f = y S\left( L + S - \lambda ^2 X^T G_k^T X + \lambda I_k \right) ^{ - 1} \end{aligned}$$
(15)

where \(I_k\in IR^{n\times n}\) is an identity matrix. Denoting \(E_k = (L + S - \lambda ^2 X^T G_k^T X + \lambda I_k )^{ - 1}\), we have:

$$\begin{aligned} f = y SE_k. \end{aligned}$$
(16)

After obtaining the closed form solution of \(\{U_1,U_2,\ldots ,U_M\}\), because the core tensor \(\mathcal {G}\) can be unfolded along arbitrary order, we solve for \(\mathcal {G}\) along the \(1\)th order, namely \(G_1\). Firstly, we define \(\mathrm{vec}(W_1 ) = U_ \otimes \mathrm{vec}(G_1 )\) where \(U_ \otimes = U_M \otimes \cdots \otimes U_1 \). According to Eq. (5), we can solve for \(G_1 \) by

$$\begin{aligned}&\mathop {\min }\limits _{G_1,b, f} \mathrm{Tr}((f )^T Lf) + \mathrm{Tr}((f - y )^T S(f - y ))\nonumber \\&\quad +\lambda \sum \limits _{i = 1}^n {\left( \mathrm{vec}(G_1 )^T U_ \otimes ^T \mathrm{vec}(X_i^k ) - f_i + b\right) ^2 } \nonumber \\&\quad + \beta \mathrm{vec}(G_1 )^T U_ \otimes ^T U_ \otimes \mathrm{vec}(G_1 ). \end{aligned}$$
(17)

Similarly, we denote \(\overline{X}_i = [(U_ \otimes \mathrm{vec}(X_i^k ))^T \;1]\), \(g_1 = [(\mathrm{vec}(G_1 ))^T\;b]\), \(D = \left[ {\begin{array}{cc} {U_ \otimes ^T U_ \otimes } &{} 0 \\ 0 &{} 1 \\ \end{array}} \right] \) and \(\overline{X} = [\overline{X}_1 ,\overline{X}_2 ,\ldots ,\overline{X}_n ]\). Eq. (17) can be represented as ridge regression problem about \(g_1\), as follows:

$$\begin{aligned}&\mathop {\min }\limits _{g_1, f} \mathrm{Tr}\left( g_1^T \left( \overline{X}\;\overline{X}^T + \beta D\right) g_1 \right) - 2\lambda \mathrm{Tr}\left( g_1^T \overline{X}f^T \right) \nonumber \\&\quad + \lambda \mathrm{Tr}((f )^T Lf+(f - y )^T S(f - y )+\lambda (f)^T f)). \end{aligned}$$
(18)

Setting the derivative of Eq. (18) w.r.t. \(g_1\) to 0, it becomes:

$$\begin{aligned} 2\left( \lambda \overline{X}\overline{X}^T + \beta D\right) g_1 - 2\lambda \overline{X}f^{T} = 0 \Rightarrow g_1 = \lambda \left( \lambda \overline{X}\overline{X}^T + \beta D\right) ^{ - 1} \overline{X}f^{T}. \end{aligned}$$
(19)

Denoting \(Q = (\lambda \overline{X}\overline{X}^T + \beta D)^{ - 1}\), we get:

$$\begin{aligned} g_1 = \lambda Q \overline{X}f^{T}. \end{aligned}$$
(20)

Substituting \(g_1\) in Eq. (18) with Eq. (10), we obtain:

$$\begin{aligned} \mathop {\min }\limits _{f } \mathrm{Tr}(f L(f )^T) + \mathrm{Tr}((f - y )S(f - y )^T) - \lambda ^2 \mathrm{Tr}\left( f \overline{X}^T Q^T \overline{X}f^{T} \right) + \lambda \mathrm{Tr}((f )^T f )). \end{aligned}$$
(21)

Setting the derivative of Eq. (14) w.r.t. \(f\) to 0, we have:

$$\begin{aligned} 2f L + 2(f - y )S - 2\lambda ^2 f \overline{X}^T Q^T \overline{X}+ 2\lambda f = 0 \Rightarrow f = y S\left( L + S - \lambda ^2 \overline{X}^T Q^T \overline{X}+ \lambda I_k \right) ^{ - 1}. \end{aligned}$$
(22)

Denoting \(P = (L + S - \lambda ^2 \overline{X}^T Q^T \overline{X}+ \lambda I_k )^{ - 1}\), we have:

$$\begin{aligned} f = y SP. \end{aligned}$$
(23)

The optimization of \(\{\mathcal {G}; U_1,U_2,\ldots ,U_M, b\}\) is iterated until convergence. The detailed iteration process is given in Algorithm 1.

figure a

Once the \(U_1,U_2,\ldots ,U_M,\mathcal {G},b\) for \(c\) classes are obtained, we can easily get \(c\) groups of classification parameters \(\{U_1^r,U_2^r,\ldots ,U_M^r,\mathcal {G}^r,b^r\}\left| {_{r = 1}^c } \right. \). Then we propose Algorithm 2 to predict the labels of the testing image tensor.

figure b

By fixing \(\left. {U_l } \right| _{l = 1,l \ne k}^M, G_k\) and \(f\), the objective function in Eq. (5) is converted to the problem in Eq. (11). It can be seen that Eq. (11) is a convex optimization problem for \(V_k\). Therefore, we can obtain the global solutions for \(U_k\) by setting the derivative of Eq. (11) w.r.t. \(V_k\) to zero. Based on the similar theory, we also prove that we can obtain the global solutions for \(G_1\) and \(f\). Thus, when we alternately fix the values of parameters, the optimal solutions obtained from Algorithm 1 make the value of objective functions decreased and Algorithm 1 is guaranteed to be converged.

In this paper, the parameter tensor \(\varvec{\omega }\) is decomposed as \(\{U_1,..,U_k,..,U_M, \mathcal {G}\}\). The dimensions of \(U_k\) and \(\mathcal {G}\) are \(d\times R\) and \(\prod \limits _{k = 1}^M {{R}}\) respectively. Because \(R\) is much smaller than \(d\) in practice, the most time consuming operation is to solve the ridge regression problem associated with \(V_k\) (i.e., vectorized form of \(U_k\)). The complexity of our algorithm is roughly \(O((d*R)^3)\).

3 Experiments

In the experiment, we compare STuRR with several supervised tensor algorithms [3], namely, support Tucker machines (STuM) [22], higher rank support tensor regression (hrSTR), higher rank tensor ridge regression (hrTRR), optimal-rank support tensor regression (orSTR) and optimal-rank tensor ridge regression (orTRR). STuM adopts Tucker decomposition to decompose parameter tensor. hrTRR, hrSTR, orTRR and orSTR employ CP decomposition to realize parameter tensor decomposition. The purpose is to investigate if STuRR exploits the structural knowledge of image tensors. We also include comparison with the semi-supervised vector algorithms anchor graph regularization (AnGR) [27], cost-sensitive semi-supervised support vector machine (CS4VM) [28]. AnGR and CS4VM have better performance on large datasets. The purpose is to evaluate if STuRR exploits the information in the unlabeled data. The average accuracy over all image categories is chosen as the evaluation metric.

The details of experiments setting are as follows:

  1. 1.

    The pixel values of the gray and color images are directly used as features. Algorithm STuRR, hrSTR, hrTRR, orSTR, orTRR and STuM deal with image tensors while other methods utilize vectors.

  2. 2.

    To fairly compare different classification algorithms, we use a “grid-research” strategy from \(\{10^-6,10^-5,\ldots ,10^5,10^6,\}\) to tune all the parameters for all the algorithms, we report the best results obtained from different parameters. Moreover, we fix the parameter \(k=10\), which is used in the k-nearest neighbors of Laplacian matrix \(L\).

  3. 3.

    We randomly split each dataset into two subsets, one as the training set and the other as the testing set. To evaluate the performance of image classification for the cases when only a few labeled data per class are available, we set the number of labeled data per class to 5 and randomly sample these labeled data from the training set. The split is repeated five times and we report the average results.

3.1 Datasets

In our experiment, we have collected a diversity of six gray (UMISTFootnote 1, YaleBFootnote 2, PIEFootnote 3, USPSFootnote 4, binary alpha digits (BAd)Footnote 5, and MNISTFootnote 6) and three color (Flower-17Footnote 7, CIFAR-10Footnote 8 and STL-10Footnote 9) images datasets to compare different algorithms. Each gray image is reshaped into \(16\times 16\) pixels and each color image is resized as \(16\times 16\times 3\) pixels in our experiments. The brief description of image datasets is listed in Table 1.

Table 1 Dataset description
Full size table

For each image dataset (CIFAR-10 excepted), we randomly select 10 images per class as the training set and the remaining images as the testing set. In CIFAR-10 dataset, we randomly select 20 images per class as the training set and the remaining images as the testing set. For color image datasets, in order the exploit to the information of R, G, and B channels, we set the dimension of the core tensor in the third order to 3.

3.2 Experimental results and discussion

In Table 2, we report the comparisons of different algorithms on nine datasets. For all these algorithms, the number of labeled data per class is set to 5. From the Table 2, we observe that: (1) AnGR gains the top performance for all datasets, which indicates that semi-supervised learning do benefit much from the usage of unlabeled data. (2) STuM over other tensor CP decomposition based algorithms. The phenomenon demonstrates that Tucker decomposition is much robust to preserve the image tensor structure. (3) STuRR consistently gains the best performances among all the comparing algorithms. It indicates that tensor Tucker decomposition and semi-supervised learning both contribute to the performance. The STuRR gains around performance improvement 1.4, 1.5, 3.7, 5.7, 11.6, 4.1, 2.2, 9.9 and 12.8 % over these algorithms for each dataset, respectively. These results demonstrate the proposed STuRR obtain better performance for the cases when only a few labeled data are available.

Table 2 Classification results of different datasets
Full size table
Fig. 2
figure 2

Classification results of STuM, AnGR, and STuRR when the numbers of labeled data per class are different, respectively. a UMIST, b YaleB, c PIE, d USPS, e BAd, f MNIST, g Flower-17, h STL-10 and i CIFAR-10

Full size image

To further investigate the effectiveness of proposed STuRR when a small amount of labeled data are available. We compare the performance of STuM, AnGR and STuRR when the numbers of labeled data per class are different. The result are plotted in Fig. 2. Figure 2 shows that the performance of STuRR is generally better than that of STuM and AnGR for all the number of labeled data per class. As the number of labeled data per class are small (compared to the sizes of nine datasets, see Table 1), the results in Fig. 2 further validates the effectiveness of STuRR in big datasets when small labeled data are available.

3.3 Parameter sensitivity and convergence

The dimension of core tensor is set to 4 for gray and color image datasets, respectively. Each decomposed core tensor of the gray and color images is \(4\times 4\) and \(4\times 4\times 3\) tensor. We tune the two parameters \(\lambda \) and \(\beta \) of STuRR for each dataset. The parameter tuning results are shown in Fig. 3. The best performance on nine datasets was obtained when when \(\{\lambda = 0.0001, \beta = 100\}, \{\lambda = 0.0001, \beta = 10\},\{\lambda = 0.0001, \beta = 10\},\{\lambda = 0.0001, \beta = \text {10,000}\},\{\lambda = 0.0001, \beta = 0.1\},\{\lambda = 0.0001, \beta = \text {1,000}\},\{\lambda = 0.001, \beta = \text {10,000}\},\{\lambda = 0.001, \beta = \text {1,000}\},\{\lambda = 0.001, \beta = \text {10,000}\},\) respectively. According to [17], the dimension of core tensor is equal to or less than initial tensor. In the following, we fix the value of \(\lambda \) and \(\beta \) to be the values with which the best performance is obtained and tune the dimension of core tensor \(R\) from \(1\) to \(20\). In Fig. 4, we plot the classification accuracy against dimension of core tensor for all the datasets. In this paper, the initial tensor images are \(16\times 16\) and \(16\times 16\times 3\) for gray images and color images, respectively. The dimension of initial tensor \(d\) is \(16\). It is clear that the performances are almost stable when \(R>4\), especially for \(R>d\). The best classification accuracy rate is achieved when \(R<d\). It indicates that the choice of a smaller dimension core tensor lead to dimension reduction tailored to the classification problem and if the \(R\) is properly chosen, the most significant principal components will be retained.

Fig. 3
figure 3

Parameter sensitivity. a UMIST, b YaleB, c PIE, d USPS, e BAd, f MNIST, g Flower-17, h STL-10 and i CIFAR-10

Full size image
Fig. 4
figure 4

Dimension of core tensor \(R\) versus classification accuracy for all the datasets. a UMIST, b YaleB, c PIE, d USPS, e BAd, f MNIST, g Flower-17, h STL-10 and i CIFAR-10

Full size image
Fig. 5
figure 5

Convergence curves of the objective function value in Eq. (5) using Algorithm 1. The figure show that the objective function value monotonically decreases until converged by applying the proposed algorithm. a UMIST, b YaleB, c PIE, d USPS, e BAd, f MNIST, g Flower-17, h STL-10 and i CIFAR-10

Full size image

Moreover, we study the convergence of the proposed STuRR in Algorithm 1. Figure 5 shows the convergence curves of our STuRR algorithm according to the objective function value in Eq. (5) on all the datasets. The figure shows that the objective function value monotonically decreases until converged by applying the proposed algorithm. It can be seen that our algorithm converges within a few iterations. For example, it takes no more than 10 iterations for UMIST, YaleB, PIE, USPS BAd, MNIST, and STL-10 and no more than 20 iterations for Flower-17 and CIFAR-10.

4 Conclusions

Representing images with tensors is better in preserving the spatial correlation. In this work, we addressed the gray and color images classification problem within the tensor classification framework, which is realized by learning parameter tensor for image tensors. Our method is a semi-supervised algorithm which uses both labeled and unlabeled data. An efficient alternative optimization algorithm has also been proposed to solve our objective function. Our method processes the image tensors directly to capture the spatial correlation and achieves good results when using few labeled training samples, which is cost-saving. In order to exploit the structure information of image tensor, the parameter tensor are obtained using the Tucker tensor decomposition. By using Tucker tensor decomposition, we can adjust the dimension of core tensor for the optimal solution, resulting in improved performance. Experiments on different image datasets were further conducted to evaluate the efficacy of our method. The results are encouraging and have demonstrated that our method is especially competitive when only few labeled training data are available.