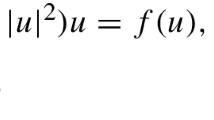Existence and multiplicity of solutions for Schrödinger–Poisson equations with sign-changing potential

Abstract

In this paper, we study the existence and multiplicity of solutions for the Schrödinger–Poisson equations

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+\lambda V(x)u+K(x)\phi u=f(x,u)\ \ \ \ \ &{} \ \text{ in }\mathbb {R}^3,\\ -\Delta \phi =K(x)u^2\ \ \ \ \ \ &{} \ \text{ in } \mathbb {R}^3, \end{array}\right. \end{aligned}$$

where $\lambda >0$ is a parameter, the potential $V$ may change sign and $f$ is either superlinear or sublinear in $u$ as $|u|\rightarrow \infty$.

1 Introduction and main results

Consider the following Schödinger–Poisson equations:

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+\lambda V(x)u+K(x)\phi u=f(x,u)\ \ \ \ \ &{} \ \text{ in } \mathbb {R}^3,\\ -\Delta \phi =K(x)u^2\ \ \ \ \ \ &{} \ \text{ in } \mathbb {R}^3, \end{array}\right. \qquad \qquad \qquad (SP)_{\lambda } \end{aligned}$$

where $\lambda \ge 1$ is a parameter, $V\in C(\mathbb {R}^3,\mathbb {R})$ and $f\in C(\mathbb {R}^3\times \mathbb {R},\mathbb {R})$.

Problem $(SP)_\lambda$ (also called Schrödinger–Maxwell equation) arises in applications from mathematical physics, such as in quantum electrodynamics, to describe the interaction of a charged particle with the electromagnetic field, and also in semiconductor theory, in nonlinear optics and in plasma physics. For more details in physical aspects, we refer to [9, 12].

There has been a vast literature on the study of existence and multiplicity of solutions of system $(SP)_\lambda$ under various hypotheses on the potential $V(x)$ and the nonlinearity $f(x,u)$, see [1–3, 5, 9–14, 18, 19, 21, 22, 24–28, 31, 34–37] and the references therein. Most of them dealt with the situation where $V(x)$ is a positive constant or being radially symmetric and $f(x,u)=|u|^{p-1}u$, $1<p<5$. In [25] the case $p=5/3$ was studied. The authors applied a minimization procedure in an appropriate manifold to find a positive solution (possibly non-radial) for system $(SP)_1$ (i.e. $(SP)_\lambda$ with $\lambda =1$). In [11, 12], a radial positive solution of $(SP)_1$ was obtained for $3\le p<5$, by taking advantage of the mountain pass theorem due to Ambrosetti and Rabinowitz [4]. In [13], a related Pohozǎev identity was found, and with this in hand, the authors proved that problem $(SP)_1$ has no nontrivial solutions for $p\le 1$ or $p>5$. This result was completed in [24], where Ruiz showed that if $p\le 2$, problem $(SP)_1$ does not admit any nontrivial solution, and if $2<p<5$, there exists a positive radial solution of $(SP)_1$. Ambrosetti and Ruiz [2] and Ambrosetti [3] considered problem $(SP)_1$ with a parameter, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+u+\lambda \phi u=|u|^{p-1}u\ \ \ \ \ \ &{} \text{ in } \mathbb {R}^3,\\ -\Delta \phi =u^2\ \ \ \ \ \ \ &{} \text{ in } \mathbb {R}^3. \end{array}\right. \ \ \ \ \ \ \ \qquad \qquad \qquad (A)_{\lambda } \end{aligned}$$

Using variational methods, they constructed the existence of infinitely many pairs of radial solutions of problem $(A)_\lambda$, where $2<p<5$, for all $\lambda >0$, and also multiple solutions (but not infinitely many) of $(A)_\lambda$, where $1<p\le 2$, for $\lambda >0$ small sufficiently. In addition, the existence of infinitely many non-radial solutions of system $(SP)_1$ was constructed in d’Avenia et al. [14], when $1<p<5$ and $K(x)$ is a positive radial function decaying at infinity. See also [5, 19, 34, 37] for the critical case.

The case of positive and non-radial potential $V$ has been discussed in [10, 22, 26, 28, 31, 35]. In particular, supposing that $V(x)$ satifies:

$(V_1)$ :

$V\in C(\mathbb {R}^3, \mathbb {R})$ and $\inf _{x\in \mathbb {R}^3}V(x)\ge a>0$, where $a$ is a positive constant;

$(V_2)$ :

For any $b>0$, meas$\left\{ x\in \mathbb {R}^3:V(x)\le b\right\} <+\infty$, where meas denotes the Lebesgue measure in $\mathbb {R}^3$;

[10, 22, 31] established the existence of infinitely many high-energy solutions of problem $(SP)_1$, where $f$ is 4-superlinear at infinity, while the existence of infinitely many small-energy solutions was proved in Sun [26] with sublinear nonlinearity. The proofs in [10, 22, 31] were based on the (variant) fountain theorem. It is worth mentioning that conditions $(V_1)$–$(V_2)$ were first introduced by Bartsch and Wang [8] to guarantee the compact embedding of the functional space (see [8, Remark 3.5]). If replacing $(V_2)$ by a more general assumption:

$(V_3)$ :

There is $b>0$ such that meas$\left\{ x\in \mathbb {R}^3:V(x)\le b\right\} <+\infty$,

the compactness of the embedding fails and this situation becomes more delicated.

Recently, [32, 35] considered this case. Yang et al. [32] investigated the semiclassical solutions of the Schrödinger–Poisson equations

$$\begin{aligned} \left\{ \begin{array}{ll} -\varepsilon ^2\Delta u+ V(x)u+\phi u=f(x,u)\ \ \ \ \ &{} \ \text{ in }\mathbb {R}^3,\\ -\Delta \phi =4\pi u^2\ \ \ \ \ \ &{} \ \text{ in } \mathbb {R}^3. \end{array}\right. \ \ \ \ \ \qquad \qquad \qquad (B)_{\varepsilon } \end{aligned}$$

They assumed that $(V_3)$ holds, $V(0)=$ min$V=0$ and $f(x,u)$ satisfies:

$(g_1)$ :

$f(x,u)=o(u)$ as $u\rightarrow 0$ uniformly in $x$;

$(g_2)$ :

There are $c_0>0$ and $q<6$ such that $|f(x,u)|\le c_0(1+|u|^{q-1})$ for all $(x,u)$;

$(g_3)$ :

There are $a_0>0$, $p>4$ and $\mu >4$ such that $F(x,u)\ge a_0|u|^p$ and $\mu F(x,u)\le f(x,u)u$ for all $(x,u)$, where $F(x,u):=\int _0^u f(x,s)ds$.

They showed that for any $\sigma >0$ there exists $\varepsilon _\sigma >0$ such that $(B)_\varepsilon$ has at least one solution when $\varepsilon \le \varepsilon _\sigma$; and if additionally $f(x,u)$ is odd in $u$, then given any $\varepsilon >0$ small enough $(B)_\varepsilon$ has at least $m$ pairs of solutions. Zhao et al. [35] studied the existence of nontrivial solution and concentration results (as $\lambda \rightarrow +\infty$) of $(SP)_\lambda$, provided that $V$ satisfies $(V_3)$ and

$(V_4)$ :

$V\in C(\mathbb {R}^3,\mathbb {R})$ and $V$ is bounded below,

$(V_5)$ :

$\Omega =int V^{-1}(0)$ is nonempty and has smooth boundary and $\overline{\Omega }=V^{-1}(0)$,

and $f(x,u)=|u|^{p-2}u$ $(2<p<6)$.

We also note that if $K\equiv 0$, $(SP)_\lambda$ reduces to the Schödinger equation

$$\begin{aligned} -\Delta u+\lambda V(x)u=f(x,u),\ \ \ \ \ \ \ \ x\in \mathbb {R}^N,\ \ \ \qquad \qquad \qquad \qquad (C)_{\lambda } \end{aligned}$$

which has been the object of interest for many authors, see e.g. [15, 16, 29] and their references. In [16], Ding and Szulkin studied the existence and the number of decaying solutions of problem $(C)_\lambda$ when $V$ may change sign, satisfies $(V_4)$ and

$(V_6)$ :

There exists $b>0$ such that the set $\left\{ x\in \mathbb {R}^N:V(x)<b\right\}$ is nonempty and has finite measure;

and $f$ is either asymptotically linear or superlinear (but subcritical) in $u$ as $|u|\rightarrow \infty$. Wang and Zhou [29] dealt with the ground states of problem $(C)_\lambda$, where $V(x)$ changes sign and may vanish at infinity, $f(x,u)=K_1(x)g(u)$ and $g$ is either of the form $g(u)=|u|^{p-1}u$ with $1<p<\frac{N+2}{N-2}$ or asymptotically linear.

Motivated by the works mentioned above, in the present paper, we are mostly interested in sign-changing potentials though in a few cases we need to have $V\ge 0$. Under $(V_3)$–$(V_4)$ and some more generic 4-superlinear conditions on $f(x,u)$, we prove the existence and multiplicity of solutions of problem $(SP)_\lambda$ when $\lambda >0$ large, using variational method. Furthermore, we investigate the situation where the nonlinearity $f(x,u)$ is sublinear with mild assumptions different from those studied previously. Infinitely many small-energy solutions are obtained for problem $(SP)_1$ by applying a new version of symmetric mountain pass lemma developed by Kajikiya. The main results are the following theorems.

First, we handle the 4-superlinear case, and hence make the following assumptions:

$(f_1)$ :

$F(x,u)\ge 0$ for all $(x,u)$ and $f(x,u)=o(u)$ uniformly in $x$ as $u\rightarrow 0$.

$(f_2)$ :

$F(x,u)/u^4\rightarrow +\infty$ as $|u|\rightarrow \infty$ uniformly in $x$.

$(f_3)$ :

$\mathcal {F}(x,u):=\frac{1}{4}f(x,u)u-F(x,u)\ge 0$ for all $(x,u)\in \mathbb {R}^3\times \mathbb {R}$.

$(f_4)$ :

There exist $a_1$, $L_1>0$ and $\tau \in (3/2,2)$ such that

$$\begin{aligned} |f(x,u)|^\tau \le a_1\mathcal {F}(x,u)|u|^\tau ,\ \ \ \ \ \ \forall x\in \mathbb {R}^3,\ \ |u|\ge L_1. \end{aligned}$$

$(K)$ :

$K\in L^2(\mathbb {R}^3)\cup L^\infty (\mathbb {R}^3)$ and $K(x)\ge 0$ for all $x\in \mathbb {R}^3$.

Remark 1.1

It follows from $(f_2)$ and $(f_4)$ that $|f(x,u)|^\tau \le \frac{a_1}{4}|f(x,u)||u|^{\tau +1}$ for large $u$. Thus, by ($f_1$), for any $\varepsilon >0$, there is $C_\varepsilon >0$ such that

$$\begin{aligned} |f(x,u)|\le \varepsilon |u|+C_\varepsilon |u|^{p-1},\ \ \ \ \ \ \ \forall (x,u)\in \mathbb {R}^3\times \mathbb {R} \end{aligned}$$

(1.1)

and

$$\begin{aligned} |F(x,u)|\le \varepsilon u^2+C_\varepsilon |u|^p,\ \ \ \ \ \ \forall (x,u)\in \mathbb {R}^3\times \mathbb {R}, \end{aligned}$$

where $p=2\tau /(\tau -1)\in (4,2^*)$, $2^*=6$ is the critical exponent for the Sobolev embedding in dimension 3.

Theorem 1.1

(Superlinear) Assume that $(V_3)$–$(V_4)$, $(K)$ and $(f_1)$–$(f_4)$ are satisfied.

• (i) If $V(x)<0$ for some $x\in \mathbb {R}^3$, then for each $k\in \mathbb {N}$, there exist $\lambda _k>k$ and $b_k>0$ such that problem $(SP)_\lambda$ has a nontrivial solution $(u_\lambda ,\phi _\lambda )\in H^1(\mathbb {R}^3)\times \mathcal {D}^{1,2}(\mathbb {R}^3)$ for every $\lambda =\lambda _k$ and $|K|_2<b_k$ (or $|K|_\infty <b_k$).

• (ii) If $V^{-1}(0)$ has nonempty interior, then there exist $\Lambda >0$ and $b_\lambda >0$ such that problem $(SP)_\lambda$ has a nontrivial solution $(u_\lambda ,\phi _\lambda )\in H^1(\mathbb {R}^3)\times \mathcal {D}^{1,2}(\mathbb {R}^3)$ for every $\lambda >\Lambda$ and $|K|_2<b_\lambda$ (or $|K|_\infty <b_\lambda$).

Remark 1.2

Theorem 1.1 (ii) generalizes [35, Theorem 1.1], which is the special case of Theorem 1.1 (ii) corresponding to $f(x,u)=|u|^{p-2}u$ $(4<p<6)$.

If $V\ge 0$, the restriction on the norm of $K$ can be removed and we have the following theorem.

Theorem 1.2

(Superlinear) Assume that $V\ge 0$, $(V_3)$–$(V_4)$, $(K)$ and $(f_1)$–$(f_4)$ are satisfied, and $V^{-1}(0)$ has nonempty interior $\Omega$. Then there exist $\Lambda _*>0$ such that problem $(SP)_\lambda$ has at least one nontrivial solution $(u_\lambda ,\phi _\lambda )\in H^1(\mathbb {R}^3)\times \mathcal {D}^{1,2}(\mathbb {R}^3)$ whenever $\lambda >\Lambda _*$. Moreover, if $f$ is odd in $t$, then for each $k\ge 1$ there exists $\Lambda _k>0$ such that problem $(SP)_\lambda$ has at least $k$ pairs of nontrivial solutions whenever $\lambda >\Lambda _k$.

Remark 1.3

Theorem 1.2 can be viewed as an improvement of the results in Yang et al. [32] and Zhao et al. [35]. Comparing with [32, Theorems 1.1 and 1.2], our hypotheses on $f$ are much weaker. Indeed, assumption $(g_3)$ implies

$$\begin{aligned} 0<\mu F(x,u)\le f(x,u)u \ \ \ \ \text{ for } \text{ some } \mu >4 \text{ and } \text{ all } (x,u) \text{ with } u\ne 0. \end{aligned}$$

So, if $f$ satisfies $(g_1)$ and $(g_3)$, it is easy to see that $(f_2)$–$(f_3)$ hold, and it will be showed as in the proof of [16, Lemma 2.2 $(i)$] that so does $(f_4)$. As for [35], we consider a larger class of nonlinearities and discuss the multiplicity result.

Remark 1.4

There are functions $f$ which match conditions $(f_1)$–$(f_4)$ but not satisfying the results in [32, 35]. For example, let

$$\begin{aligned} f(x,t)=h(x)t^3\left( 2\ln (1+t^2)+\frac{t^2}{1+t^2}\right) ,\ \ \ \ \ \forall (x,t)\in \mathbb {R}^3\times \mathbb {R}, \end{aligned}$$

where $h$ is a continuous bounded function with $\inf _{x\in \mathbb {R}^3}h(x)>0$.

Next, we treat the sublinear case. Assume that:

$(f_5)$ :

There exist constants $\sigma$, $\gamma \in (1,2)$ and functions $m\in L^{2/(2-\sigma )}(\mathbb {R}^3,\mathbb {R}^+)$, $h\in L^{2/(2-\gamma )}(\mathbb {R}^3,\mathbb {R}^+)$ such that

$$\begin{aligned} |f(x,u)|\le m(x)|u|^{\sigma -1}+h(x)|u|^{\gamma -1},\ \ \ \ \ \ \forall (x,u)\in \mathbb {R}^3\times \mathbb {R}. \end{aligned}$$

$(f_6)$ :

There exist $x_0\in \mathbb {R}^3$, two sequences $\left\{ \varepsilon _n\right\}$, $\left\{ M_n\right\}$ and constants $a_2$, $\varepsilon$, $\delta >0$ such that $\varepsilon _n>0$, $M_n>0$ and

$$\begin{aligned}&\lim _{n\rightarrow \infty }\varepsilon _n=0,\ \ \ \ \ \lim _{n\rightarrow \infty }M_n=+\infty ,\nonumber \\&\varepsilon _n^{-2}F(x,u)\ge M_n\ \ \ \ \ \ \ \text{ for } |x-x_0|\le \delta \text{ and } |u|=\varepsilon _n, \nonumber \\&F(x,u)\ge -a_2u^2\ \ \ \ \ \ \ \text{ for } |x-x_0|\le \delta \text{ and } |u|\le \varepsilon . \end{aligned}$$

(1.2)

Theorem 1.3

(Sublinear) Assume that $V\ge 0$, $(V_3)$, $(K)$ and $(f_5)$–$(f_6)$ are satisfied and that $f(x,u)$ is odd in $u$. Then problem $(SP)_1$ possesses infinitely many nontrivial solutions $\left\{ (u_k,\phi _k)\right\}$ such that

$$\begin{aligned} \frac{1}{2}\int \limits _{\mathbb {R}^3}(|\nabla u_k|^2+V(x)u_k^2)dx+\frac{1}{4}\int \limits _{\mathbb {R}^3}K(x)\phi _k u_k^2dx-\int \limits _{\mathbb {R}^3}F(x,u_k)dx\rightarrow 0^-\ \ \ \text{ as } \ \ k\rightarrow \infty . \end{aligned}$$

Remark 1.5

In Sun [26], the existence of infinitely many small-energy solutions was obtained for $(SP)_1$, where $K\equiv 1$, under assumptions $(V_1)$–$(V_2)$ and:

$(f')$ :

$f(x,u)=b(x)|u|^{\sigma -1}$, where $b:\mathbb {R}^3\rightarrow \mathbb {R}^+$ is a positive continuous function such that $b\in L^{2/(2-\sigma )}(\mathbb {R}^3,\mathbb {R})$ and $1<\sigma <2$ is a constant.

Observing $(f')$ implies that there is an open set $J\subset \mathbb {R}^3$ such that

$$\begin{aligned} F(x,t)/t^2\rightarrow +\infty \ \ \ \ \ \ \ \text{ as } t\rightarrow 0\ \ \text{ uniformly } \text{ for } x\in J, \end{aligned}$$

it is stronger than $(f_5)$–$(f_6)$. Hence Theorem 1.3 improves [26, Theorem 1.1] by weakening hypotheses on $V$, $K$ and $f$. There are functions $V$, $K$ and $f$ which match our setting but not satisfying the results in [21, 26]. For example, let

$$\begin{aligned} V\equiv c(>0),\ \ \ \ \ \ \ \ K(x)=|x|^{-4}, \end{aligned}$$

and

$$\begin{aligned} f(x,u)=\left\{ \begin{array}{ll} |x|e^{-|x|^2}\left[ \sigma |u|^{\sigma -2}u\sin ^2\left( \frac{1}{|u|^\varrho }\right) -\varrho |u|^{\sigma -\varrho -2}\sin \left( \frac{2}{|u|^\varrho }\right) \right] , \ \ \ \ &{} t\ne 0,\\ 0,\ \ \ \ &{} t=0, \end{array} \right. \end{aligned}$$

where $\varrho >0$ small enough and $\sigma \in (1+\varrho ,2)$. Simple calculation shows that

$$\begin{aligned} F(x,u)=\left\{ \begin{array}{ll} |x|e^{-|x|^2}|u|^\sigma \sin ^2\left( \frac{1}{|u|^\varrho }\right) , \ \ \ \ &{} t\ne 0,\\ 0,\ \ \ \ &{} t=0. \end{array} \right. \end{aligned}$$

It is easy to check that $(V_3)$–$(V_4)$, $(K)$ and $(f_5)$–$(f_6)$ are satisfied with $\varepsilon _n=\left( \frac{2}{(2n+1)\pi }\right) ^{1/\varrho }$. However, in this case, $(V_2)$ and $(f')$ fail.

The paper is organized as follows. In Sect. 2 we introduce the variational setting and recall some related preliminaries. Section 3 is concerned with the 4-superlinear case and Sect. 4 with the sublinear case. In Sect. 5, concentration of solutions to problem $(SP)_\lambda$ on the set $V^{-1}(0)$ as $\lambda \rightarrow +\infty$ is discussed.

Notation

• $H^1(\mathbb {R}^3)$ is the usual Sobolev space endowed with the standard scalar and norm

  $$\begin{aligned} ( u,v)_{H^1}=\int \limits _{\mathbb {R}^3}(\nabla u\cdot \nabla v+uv)dx;\ \ \ \ \ \ \Vert u\Vert _{H^1}=(u,u)_{H^1}^{1/2}. \end{aligned}$$

• $\mathcal {D}^{1,2}(\mathbb {R}^3)$ is the completion of $C_0^\infty (\mathbb {R}^3)$ with respect to the norm $\Vert u\Vert _{\mathcal {D}^{1,2}}^2:=\int _{\mathbb {R}^3}|\nabla u|^2dx.$

• $L^s(\Omega )$, $1\le s\le +\infty$, $\Omega \subset \mathbb {R}^3$, denotes a Lebesgue space; the norm in $L^s(\Omega )$ is denoted by $|u|_{s,\Omega }$, where $\Omega$ is a proper subset of $\mathbb {R}^3$, by $|\cdot |_s$ when $\Omega =\mathbb {R}^3$.

• $\bar{S}$ is the best Sobolev constant for the Sobolev embedding $\mathcal {D}^{1,2}(\mathbb {R}^3)\hookrightarrow L^6(\mathbb {R}^3)$, i.e.,

  $$\begin{aligned} \bar{S}=\inf _{u\in H^1(\mathbb {R}^3)\backslash \left\{ 0\right\} }\frac{\Vert u\Vert _{\mathcal {D}^{1,2}}}{|u|_6}. \end{aligned}$$

• For any $r>0$ and $z\in \mathbb {R}^3$, $B_r(z)$ denotes the ball of radius $r$ centered at $z$.

• The letter $c$ will be used to denote various positive constants which may vary from line to line and are not essential to the problem.

2 Variational setting and preliminaries

Let

$$\begin{aligned} E:=\left\{ u\in H^1(\mathbb {R}^3):\int \limits _{\mathbb {R}^3}V^+(x)u^2dx<+\infty \right\} , \end{aligned}$$

where $V^\pm (x)=\max \left\{ \pm V(x),0\right\}$. Then $E$ is a Hilbert space with the inner product and norm

$$\begin{aligned} (u,v)=\int \limits _{\mathbb {R}^3}(\nabla u\cdot \nabla v+V^+(x)uv)dx,\ \ \ \ \ \ \Vert u\Vert =(u,u)^{1/2}. \end{aligned}$$

We also need the following inner product

$$\begin{aligned} (u,v)_\lambda =\int \limits _{\mathbb {R}^3}(\nabla u\cdot \nabla v+\lambda V^+(x)uv)dx, \end{aligned}$$

and the corresponding norm is denoted by $\Vert u\Vert _\lambda =( u,u)_\lambda ^{1/2}$ (so $\Vert \cdot \Vert =\Vert \cdot \Vert _1$). Set $E_\lambda =(E,\Vert \cdot \Vert _\lambda )$. It follows from $(V_3)$, $(V_4)$ and the Poincaré inequality that the embedding $E_\lambda \hookrightarrow H^1(\mathbb {R}^3)$ is continuous, and hence, for $s\in [2,2^*]$, there exists $\nu _s>0$ (independent of $\lambda$) such that

$$\begin{aligned} |u|_s\le \nu _s\Vert u\Vert _\lambda ,\ \ \ \ \ \ \ \forall u\in E_\lambda . \end{aligned}$$

(2.1)

Let

$$\begin{aligned} F_\lambda :=\left\{ u\in E_\lambda :\text{ supp }u\subset V^{-1}([0,+\infty ))\right\} , \end{aligned}$$

and $F_\lambda ^\bot$ denote the orthogonal complement of $F_\lambda$ in $E_\lambda$. Clearly, $F_\lambda =E_\lambda$ if $V\ge 0$, otherwise $F_\lambda ^\bot \ne \left\{ 0\right\}$. Define

$$\begin{aligned} A_\lambda :=-\Delta +\lambda V, \end{aligned}$$

then $A_\lambda$ is formally self-adjoint in $L^2(\mathbb {R}^3)$ and the associated bilinear form

$$\begin{aligned} a_\lambda (u,v):=\int \limits _{\mathbb {R}^3}(\nabla u\cdot \nabla v+\lambda V(x)uv)dx \end{aligned}$$

is continuous in $E_\lambda$. As in [16], we consider the eigenvalue problem

$$\begin{aligned} -\Delta u+\lambda V^+(x)u=\mu \lambda V^-(x)u,\ \ \ \ \ \ \ u\in F_\lambda ^\bot . \end{aligned}$$

(2.2)

In view of $(V_3)$–$(V_4)$, the functional $I(u)=\int _{\mathbb {R}^3}V^-(x)u^2dx$ for $u\in F_\lambda ^\bot$ is weakly continuous. Hence, as a result of [30, Theorems 4.45 and 4.46], we deduce the following proposition, which is the spectral theorem for compact self-adjoint operators jointly with the Courant-Fischer minimax characterization of eigenvalues.

Proposition 2.1

Assume that $(V_3)$–$(V_4)$ hold, then for any fixed $\lambda >0$, problem (2.2) has a sequence of positive eigenvalues $\left\{ \mu _j(\lambda )\right\} _{j=1}^\infty$, which may be characterized by

$$\begin{aligned} \mu _j(\lambda )=\inf _{\text{ dim }M\ge j,M\subset F_\lambda ^\bot }\sup \left\{ \Vert u\Vert _\lambda ^2:u\in M,\int \limits _{\mathbb {R}^3}\lambda V^-(x)u^2dx=1\right\} ,\ \ \ \ \ j=1,2,\dots . \end{aligned}$$

Furthermore, $\mu _1(\lambda )\le \mu _2(\lambda )\le \dots \le \mu _j(\lambda )\mathop {\longrightarrow }\limits ^{j} +\infty$ and the corresponding eigenfunctions $\left\{ e_j(\lambda )\right\} _{j=1}^\infty$, which may be chosen so that $(e_i(\lambda ),e_j(\lambda ))_\lambda =\delta _{ij}$, are a basis of $F_\lambda ^\bot$.

For the eigenvalues $\left\{ \mu _j(\lambda )\right\}$ defined above, we have the following properties.

Proposition 2.2

(see Lemma 2.1 in [16]) Assume that $(V_3)$–$(V_4)$ hold and $V^-\not \equiv 0$. Then, for each fixed $j\in \mathbb {N}$,

• (i) $\mu _j(\lambda )\rightarrow 0$ as $\lambda \rightarrow +\infty$.

• (ii) $\mu _j(\lambda )$ is a non-increasing continuous function of $\lambda$.

Remark 2.1

By Proposition 2.2 $(i)$, there exists $\Lambda _0>0$ such that $\mu _1(\lambda )\le 1$ for all $\lambda > \Lambda _0$.

Take

$$\begin{aligned} E_\lambda ^-:=\text{ span }\left\{ e_j(\lambda ):\mu _j(\lambda )\le 1\right\} \ \ \ \ \ \text{ and }\ \ \ \ \ E_\lambda ^+:=\text{ span }\left\{ e_j(\lambda ):\mu _j(\lambda )>1\right\} . \end{aligned}$$

Then we have the following orthogonal decomposition:

$$\begin{aligned} E_\lambda =E_\lambda ^-\bigoplus E_\lambda ^+\bigoplus F_\lambda . \end{aligned}$$

From Remark 2.1, we have that dim$E_\lambda ^-\ge 1$ when $\lambda >\Lambda _0$. Moreover, dim$E_\lambda ^-<+\infty$ for every fixed $\lambda >0$ since $\mu _j(\lambda )\mathop {\longrightarrow }\limits ^{j} +\infty$.

It is well known that problem $(SP)_\lambda$ can be transformed into a Schrödinger equation with a nonlocal term (see e.g. [24]). Indeed, the Lax-Milgram theorem implies that for all $u\in E_\lambda$, there exists a unique $\phi _u\in \mathcal {D}^{1,2}(\mathbb {R}^3)$, which can be expressed as $\phi _u(x)=\frac{1}{4\pi }\int _{\mathbb {R}^3}\frac{K(y)u^2(y)}{|x-y|}dy$, satisfying

$$\begin{aligned} -\Delta \phi _u=K(x)u^2. \end{aligned}$$

(2.3)

If $K\in L^\infty (\mathbb {R}^3)$, by Hölder and Sobolev inequality, we get

$$\begin{aligned} \Vert \phi _u\Vert _{\mathcal {D}^{1,2}}^2=\int \limits _{\mathbb {R}^3}K(x)\phi _u u^2dx\le \bar{S}^{-2}\nu _{12/5}^4|K|_\infty ^2\Vert u\Vert _\lambda ^4. \end{aligned}$$

Similarly, if $K\in L^2(\mathbb {R}^3)$,

$$\begin{aligned} \Vert \phi _u\Vert _{\mathcal {D}^{1,2}}^2=\int \limits _{\mathbb {R}^3}K(x)\phi _u u^2dx\le \bar{S}^{-2}\nu _6^4|K|_2^2\Vert u\Vert _\lambda ^4. \end{aligned}$$

Thus, there exists $C_0>0$ such that

$$\begin{aligned} \Vert \phi _u\Vert _{\mathcal {D}^{1,2}}^2=\int \limits _{\mathbb {R}^3}K(x)\phi _u u^2dx\le C_0 \Vert u\Vert _\lambda ^4,\ \ \ \ \ \ \ \ \ \forall K\in L^2(\mathbb {R}^3)\cup L^\infty (\mathbb {R}^3). \end{aligned}$$

(2.4)

Take

$$\begin{aligned} N(u)=\int \limits _{\mathbb {R}^3}K(x)\phi _u u^2dx=\frac{1}{4\pi }\int \int \limits _{\mathbb {R}^3\times \mathbb {R}^3}\frac{K(x)K(y)u^2(x)u^2(y)}{|x-y|}dxdy \end{aligned}$$

We recall some important properties of the functional $N$.

Lemma 2.1

Let $K\in L^\infty (\mathbb {R}^3)\cup L^2(\mathbb {R}^3)$. If $u_n\rightharpoonup u$ in $H^1(\mathbb {R}^3)$ and $u_n(x)\rightarrow u(x)$ a.e. $x\in \mathbb {R}^3$, then

• (i) $\phi _{u_n}\rightharpoonup \phi _u$ in $\mathcal {D}^{1,2}(\mathbb {R}^3)$, and $N(u)\le \liminf _{n\rightarrow \infty }N(u_n)$;

• (ii) $N(u_n-u)=N(u_n)-N(u)+o(1)$;

• (iii) $N'(u_n-u)=N'(u_n)-N'(u)+o(1)$ in $H^{-1}(\mathbb {R}^3)$.

Proof

A straightforward adaption of [37, Lemma 2.1] shows that (i) holds. If $K\equiv 1$, the proofs of (ii) and (iii) have been given in [36], and it is easy to see that the conclusions remain valid if $K\in L^\infty (\mathbb {R}^3)$. Hence we only consider the case $K\in L^2(\mathbb {R}^3)$.

We claim that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(K(x)\phi _{u_n}u_n^2-K(x)\phi _uu^2)dx\mathop {\longrightarrow }\limits ^{n}0 \end{aligned}$$

(2.5)

and

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(K(x)\phi _{u_n}u_n\psi -K(x)\phi _uu\psi )dx\mathop {\longrightarrow }\limits ^{n}0 \end{aligned}$$

(2.6)

uniformly for $\psi \in H^1(\mathbb {R}^3)$ with $\Vert \psi \Vert _{H^1}\le 1$. It follows from (i) and Hölder’s inequality that

$$\begin{aligned}&\lim _{n\rightarrow \infty }\int \limits _{\mathbb {R}^3}(K(x)\phi _{u_n}u_n^2-K(x)\phi _uu^2)dx\nonumber \\&\quad \le \lim _{n\rightarrow \infty }\int \limits _{\mathbb {R}^3}\left[ K(x)\phi _{u_n}(u_n^2-u^2)+K(x)(\phi _{u_n}-\phi _u)u^2\right] dx\nonumber \\&\quad \le \lim _{n\rightarrow \infty }|\phi _{u_n}|_6|u_n+u|_6|K(x)(u_n-u)|_{3/2}\nonumber \\&\qquad +\lim _{n\rightarrow \infty }\int _{\mathbb {R}^3}K(x)u^2(\phi _{u_n}-\phi _u)dx. \end{aligned}$$

(2.7)

The first limit on the right is 0 by the fact $K^{3/2}\in L^{4/3}(\mathbb {R}^3)$ and $(u_n-u)^{3/2}\rightharpoonup 0$ in $L^4(\mathbb {R}^3)$, and so is the second limit because $(\phi _{u_n}-\phi _u)\rightharpoonup 0$ in $L^6(\mathbb {R}^3)$ and $K(x)u^2\in L^{6/5}(\mathbb {R}^3)$. Thus (2.5) holds. Moreover, observing that $|K(x)u|^{6/5}\in L^{5/4}(\mathbb {R}^3)$ and $(\phi _{u_n}-\phi _u)^{6/5}\rightharpoonup 0$ in $L^5(\mathbb {R}^3)$, we obtain

$$\begin{aligned}&\int \limits _{\mathbb {R}^3}(K(x)\phi _{u_n}u_n\psi -K(x)\phi _uu\psi )dx\nonumber \\&\quad \le \int \limits _{\mathbb {R}^3}\left[ K(x)\phi _{u_n}(u_n-u)\psi +K(x)(\phi _{u_n}-\phi _u)u\psi \right] dx\\&\quad \le |\phi _{u_n}|_6|\psi |_6|K(x)(u_n-u)|_{3/2}+|\psi |_6|K(x)u(\phi _{u_n}-\phi _u)|_{6/5}\\&\quad \le c|K(x)(u_n-u)|_{3/2}+c|K(x)u(\phi _{u_n}-\phi _u)|_{6/5}\\&\quad \rightarrow 0 \end{aligned}$$

uniformly with respect to $\psi$, i.e., (2.6) is satisfied. Now (ii) and (iii) follow from (2.5) and (2.6), respectively. $\square$

By (1.1) and the above lemma, the functional $\varphi _\lambda : E_\lambda \rightarrow \mathbb {R}$,

$$\begin{aligned} \varphi _\lambda (u)=\frac{1}{2}\int \limits _{\mathbb {R}^3}(|\nabla u|^2+\lambda V(x)u^2)dx+\frac{1}{4}\int \limits _{\mathbb {R}^3}K(x)\phi _uu^2dx-\int \limits _{\mathbb {R}^3}F(x,u)dx, \end{aligned}$$

is of class $C^1$ with derivative

$$\begin{aligned} \langle \varphi _\lambda '(u),v\rangle =\int \limits _{\mathbb {R}^3}(\nabla u\cdot \nabla v+\lambda V(x)uv+K(x)\phi _uuv-f(x,u)v)dx \end{aligned}$$

for all $u$, $v\in E_\lambda$. It can be proved that the pair $(u,\phi )\in E_\lambda \times \mathcal {D}^{1,2}(\mathbb {R}^3)$ is a solution of problem $(SP)_\lambda$ if and only if $u\in E_\lambda$ is a critical point of $\varphi _\lambda$ and $\phi =\phi _u$ (see [9]).

To conclude this section, we state the following propositions, which will be applied to prove Theorems 1.1–1.3. Recall that a $C^1$ functional $I$ satisfies Cerami condition at level $c$ ($(C)_c$ condition for short) if any sequence $(u_n)\subset E$ such that $I(u_n)\rightarrow c$ and $(1+\Vert u_n\Vert )\Vert I'(u_n)\Vert \rightarrow 0$ has a converging subsequence; such a sequence is then called a $(C)_c$ sequence.

Proposition 2.3

(see [17]) Let $E$ be a real Banach space and $I\in C^1(E,\mathbb {R})$ satisfying

$$\begin{aligned} \max \left\{ I(0),I(e)\right\} \le a<b\le \inf _{\Vert u\Vert =\rho }I(u) \end{aligned}$$

for some $a<b$, $\rho >0$ and $e\in E$ with $\Vert e\Vert >\rho$. Let $c\ge b$ be characterized by

$$\begin{aligned} c=\inf _{\gamma \in \Gamma }\max _{t\in [0,1]}I(\gamma (t)), \end{aligned}$$

where $\Gamma =\left\{ \gamma \in C([0,1],E):\gamma (0)=0,\gamma (1)=e\right\}$ is the set of continuous paths jointing 0 and $e$, then $I$ possesses a $(C)_c$ sequence.

If $V(x)$ is sign-changing, we need the following linking theorem.

Proposition 2.4

(see [23]) Let $E=X\bigoplus Y$ be a Banach space with $\dim Y<+\infty$, $I\in C^1(E,\mathbb {R})$. If there exist $R>\rho >0$, $\alpha >0$ and $e_0\in X$ such that

$$\begin{aligned} \alpha :=\inf I(X\cap S_\rho )>\sup I(\partial Q) \end{aligned}$$

where $S_\rho =\left\{ u\in E:\Vert u\Vert =\rho \right\}$, $Q=\left\{ u=v+te_0:v\in Y, t\ge 0, \Vert u\Vert \le R\right\}$. Then $I$ has a $(C)_c$ sequence with $c\in [\alpha ,\sup I(Q)]$.

Proposition 2.5

(see [6]) Suppose that $I\in C^1(E,\mathbb {R})$ is even, $I(0)=0$ and there exist closed subspaces $E_1$, $E_2$ such that codim$E_1<+\infty$, $\inf I(E_1\cap S_\rho )\ge \alpha$ for some $\rho$, $\alpha >0$ and $\sup I(E_2)<+\infty$. If $I$ satisfies the $(C)_c$-condition for all $c\in [\alpha ,\sup I(E_2)]$, then $I$ has at least $\dim E_2-$codim$E_1$ pairs of critical points with corresponding critical values in $[\alpha ,\sup I(E_2)]$.

To establish the existence of infinitely many solutions in the sublinear case, we require the new version of symmetric mountain pass lemma of Kajikiya (see [20]). Let $E$ be a Banach space and

$$\begin{aligned} \Gamma :=\left\{ A\subset E\backslash \left\{ 0\right\} : A \text{ is } \text{ closed } \text{ and } \text{ symmetric } \text{ with } \text{ respect } \text{ to } \text{ the } \text{ origin }\right\} . \end{aligned}$$

We define

$$\begin{aligned} \Gamma _k:=\left\{ A\in \Gamma :\gamma (A)\ge k\right\} , \end{aligned}$$

where $\gamma (A):=\inf \left\{ m\in \mathbb {N}:\exists h\in C(A,\mathbb {R}^m\backslash \left\{ 0\right\} ), -h(x)=h(-x)\right\}$. If there is no such mapping $h$ for any $m\in \mathbb {N}$, we set $\gamma (A)=+\infty$.

Proposition 2.6

(Symmetric mountain pass lemma) Let $E$ be an infinite dimensional Banach space and $I\in C^1(E,\mathbb {R})$ be even, $I(0)=0$ and satisfies the following conditions:

• (i) $I$ is bounded from below and satisfies the Palais-Smale condition (PS), i.e., $(u_n)\subset E$ has a converging subsequence whenever $\left\{ I(u_n)\right\}$ is bounded and $I'(u_n)\rightarrow 0$ as $n\rightarrow \infty$.

• (ii) For each $k\in \mathbb {N}$, there exists an $A_k\in \Gamma _k$ such that $\sup _{u\in A_k}I(u)<0$.

Then either (1) or (2) holds.

• (1) There exists a sequence $\left\{ u_k\right\}$ such that $I'(u_k)=0$, $I(u_k)<0$ and $\left\{ u_k\right\}$ converges to zero.

• (2) There exist two sequence $\left\{ u_k\right\}$ and $\left\{ v_k\right\}$ such that $I'(u_k)=0$, $I(u_k)=0$, $u_k\ne 0$, $\lim _{k\rightarrow \infty }u_k=0$, $I'(v_k)=0$, $I(v_k)<0$, $\lim _{k\rightarrow \infty }I(v_k)=0$ and $\left\{ v_k\right\}$ converges to a non-zero limit.

Remark 2.2

From Proposition 2.6, we deduce a sequence $\left\{ u_k\right\}$ of critical points such that $I(u_k)\le 0$, $u_k\ne 0$ and $\lim _{k\rightarrow \infty }u_k=0$.

3 Proofs of Theorems 1.1–1.2

We first discuss the $(C)_c$ sequence. We only consider the case $K\in L^2(\mathbb {R}^3)$, the other case $K\in L^\infty (\mathbb {R}^3)$ is similar.

Lemma 3.1

Let $(V_3)$–$(V_4)$, $(K)$, $(f_1)$–$(f_4)$ be satisfied. Then each $(C)_c$-sequence ($c\in \mathbb {R}$) of $\varphi _\lambda$ is bounded in $E_\lambda$.

Proof

Let $(u_n)\subset E_\lambda$ be a $(C)_c$ sequence of $\varphi _\lambda$. Arguing indirectly, we can assume that

$$\begin{aligned} \varphi _\lambda (u_n)\rightarrow c,\ \ \ \ \ \Vert \varphi _\lambda '(u_n)\Vert (1+\Vert u_n\Vert _\lambda )\rightarrow 0,\ \ \ \ \ \ \ \Vert u_n\Vert _\lambda \rightarrow \infty \end{aligned}$$

(3.1)

as $n\rightarrow \infty$ after passing to a subsequence. Take $w_n:=u_n/\Vert u_n\Vert _\lambda$. Then $\Vert w_n\Vert _\lambda =1$, $w_n\rightharpoonup w$ in $E_\lambda$ and $w_n(x)\rightarrow w(x)$ a.e. $x\in \mathbb {R}^3$ after passing to a subsequence.

We first consider the case $w=0$. Combining this with (3.1), $(f_3)$ and the fact $w_n\rightarrow 0$ in $L^2(\left\{ x\in \mathbb {R}^3:V(x)<0\right\} )$, we obtain

$$\begin{aligned} o(1)&= \frac{1}{\Vert u_n\Vert _\lambda ^2}\left( \varphi _\lambda (u_n)-\frac{1}{4}\langle \varphi _\lambda '(u_n),u_n\rangle \right) \\&\ge \frac{1}{4}\Vert w_n\Vert _\lambda ^2-\frac{\lambda }{4}\int \limits _{\mathbb {R}^3}V^-(x)w_n^2dx +\frac{1}{\Vert u_n\Vert _\lambda ^2}\int \limits _{\mathbb {R}^3}\mathcal {F}(x,u)dx\\&\ge \frac{1}{4}-\frac{\lambda }{4}|V^-|_\infty \int \limits _{supp V^-}w_n^2dx\\&= \frac{1}{4}+o(1), \end{aligned}$$

a contradiction.

If $w\ne 0$, then the set $\Omega _1=\left\{ x\in \mathbb {R}^3:w(x)\ne 0\right\}$ has positive Lebesgue measure. For $x\in \Omega _1$, one has $|u_n(x)|\rightarrow \infty$ as $n\rightarrow \infty$, and then, by $(f_2)$,

$$\begin{aligned} \frac{F(x,u_n(x))}{u_n^4(x)}w_n^4(x)\rightarrow +\infty \ \ \ \ \text{ as } n\rightarrow \infty , \end{aligned}$$

which, jointly with Fatou’s lemma (see [33]), shows that

$$\begin{aligned} \int \limits _{\Omega _1}\frac{F(x,u_n)}{u_n^4}w_n^4dx\rightarrow +\infty \ \ \ \ \text{ as } n\rightarrow \infty . \end{aligned}$$

(3.2)

We see from $(f_1)$, (2.4), (3.2) and the first limit of (3.1) that

$$\begin{aligned} \frac{C_0}{4}&\ge \limsup _{n\rightarrow \infty }\int \limits _{\mathbb {R}^3}\frac{F(x,u_n)}{\Vert u_n\Vert _\lambda ^4}dx \ge \limsup _{n\rightarrow \infty }\int \limits _{\Omega _1}\frac{F(x,u_n)}{u_n^4}w_n^4dx=+\infty . \end{aligned}$$

This is impossible.

In any case, we deduce a contradiction. Hence $(u_n)$ is bounded in $E_\lambda$. $\square$

Lemma 3.2

Suppose that $(V_3)$–$(V_4)$, $(K)$ and (1.1) are satisfied. If $u_n\rightharpoonup u$ in $E_\lambda$, $u_n(x)\rightarrow u(x)$ a.e. in $\mathbb {R}^3$, and we denote $w_n:=u_n-u$, then

$$\begin{aligned} \varphi _\lambda (u_n)=\varphi _\lambda (w_n)+\varphi _\lambda (u)+o(1) \end{aligned}$$

(3.3)

and

$$\begin{aligned} \varphi _\lambda '(u_n)=\varphi _\lambda '(w_n)+\varphi _\lambda '(u)+o(1) \end{aligned}$$

(3.4)

as $n\rightarrow \infty$. In particular, if $\varphi _\lambda (u_n)\rightarrow d$ $(\in \mathbb {R})$ and $\varphi _\lambda '(u_n)\rightarrow 0$ in $E_\lambda ^*$ (the dual space of $E_\lambda$), then $\varphi _\lambda '(u)=0$, and

$$\begin{aligned} \varphi _\lambda (w_n)\rightarrow d-\varphi _\lambda (u),\ \ \ \ \ \ \ \varphi _\lambda '(w_n)\rightarrow 0 \end{aligned}$$

(3.5)

after passing to a subsequence.

Proof

Since $u_n\rightharpoonup u$ in $E_\lambda$, one has $(u_n-u,u)_\lambda \rightarrow 0$ as $n\rightarrow \infty$, which implies that

$$\begin{aligned} \Vert u_n\Vert _\lambda ^2=(w_n+u,w_n+u)_\lambda =\Vert w_n\Vert _\lambda ^2+\Vert u\Vert _\lambda ^2+o(1). \end{aligned}$$

(3.6)

Recall $(V_3)$ and $w_n\rightharpoonup 0$, we have

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}V^-(x)w_nudx\right| = \left| \int \limits _{supp V^-}V^-(x)w_nudx\right| \le |V^-|_\infty \left( \int \limits _{supp V^-}w_n^2dx\right) ^{1/2}|u|_2\mathop {\longrightarrow }\limits ^{n} 0 \end{aligned}$$

by the Hölder inequality. Thus

$$\begin{aligned} \int \limits _{\mathbb {R}^3}V^-(x)u_n^2dx=\int \limits _{\mathbb {R}^3}V^-(x)w_n^2dx +\int \limits _{\mathbb {R}^3}V^-(x)u^2dx+o(1). \end{aligned}$$

Combining this with (3.6) and Lemma 2.1 (ii), we obtain

$$\begin{aligned} \frac{1}{2}a_\lambda (u_n,u_n)+\frac{1}{4}N(u_n)&= \left( \frac{1}{2}a_\lambda (w_n,w_n) +\frac{1}{4}N(w_n)\right) +\left( \frac{1}{2}a_\lambda (u,u)+\frac{1}{4}N(u)\right) +o(1). \end{aligned}$$

Similarly, by Lemma 2.1 (iii),

$$\begin{aligned} a_\lambda (u_n,h)+\int \limits _{\mathbb {R}^3}K(x)\phi _{u_n}u_nhdx&= \left( a_\lambda (w_n,h)+\int \limits _{\mathbb {R}^3}K(x)\phi _{w_n}w_nhdx\right) \\&+\left( a_\lambda (u,h)+\int \limits _{\mathbb {R}^3}K(x)\phi _uuhdx\right) +o(1),\ \ \ \ \ \ \forall h\in E_\lambda . \end{aligned}$$

Therefore, to obtain (3.3) and (3.4), it suffices to check that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(F(x,u_n)-F(x,w_n)-F(x,u))dx=o(1) \end{aligned}$$

(3.7)

and

$$\begin{aligned} \sup _{\Vert h\Vert _\lambda =1}\int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,w_n)-f(x,u))h dx=o(1). \end{aligned}$$

(3.8)

Here, we only prove (3.8), the verification of (3.7) is similar. Inspired by [1], we take ${\lim _{n\rightarrow \infty }\sup _{\Vert h\Vert _\lambda =1}}\big |\int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,w_n)-f(x,u))h dx\big |=A$. If $A>0$, then, there is $h_0\in E_\lambda$ with $\Vert h_0\Vert _\lambda =1$ such that

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,w_n)-f(x,u))h_0dx\right| \ge \frac{A}{2} \end{aligned}$$

(3.9)

for $n$ large enough. It follows form (1.1) and the Young inequality that

$$\begin{aligned} |(f(x,u_n)-f(x,w_n))h_0|&\le \varepsilon (|w_n+u|+|w_n|)|h_0|+C_\varepsilon (|w_n+u|^{p-1}+|w_n|^{p-1})|h_0|\\&\le c(\varepsilon |w_n||h_0|+\varepsilon |u||h_0|+C_\varepsilon |w_n|^{p-1}|h_0|+C_\varepsilon |u|^{p-1}|h_0|)\\&\le c(\varepsilon w_n^2+\varepsilon h_0^2+\varepsilon u^2+\varepsilon |w_n|^p+C_{\varepsilon ,1}|u|^p+C_{\varepsilon ,2}|h_0|^p) \end{aligned}$$

for all $n$. Hence

$$\begin{aligned} |(f(x,u_n)\!-\!f(x,w_n)\!-\!f(x,u))h_0|\!\le \! c(\varepsilon w_n^2\!+\!\varepsilon h_0^2\!+\!\varepsilon u^2\!+\!\varepsilon |w_n|^p\!+\!C_{\varepsilon ,1}|u|^p\!+\!C_{\varepsilon ,2}|h_0|^p). \end{aligned}$$

Letting

$$\begin{aligned} g_n(x):=\max \left\{ |(f(x,u_n)-f(x,w_n)-f(x,u))h_0|-c\varepsilon ( w_n^2+|w_n|^p),0\right\} , \end{aligned}$$

we have

$$\begin{aligned} 0\le g_n(x)\le c(\varepsilon h_0^2+\varepsilon u^2+C_{\varepsilon ,1}|u|^p+C_{\varepsilon ,2}|h_0|^p)\in L^1(\mathbb {R}^3), \end{aligned}$$

which implies that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}g_n(x)dx\rightarrow 0\ \ \ \ \ \text{ as } \ \ n\rightarrow \infty \end{aligned}$$

(3.10)

because of the Lebesgue dominated convergence theorem and the fact $w_n\rightarrow 0$ a.e. in $\mathbb {R}^3$. The definition of $g_n(x)$ implies that

$$\begin{aligned} |(f(x,u_n)-f(x,w_n)-f(x,u))h_0|\le g_n(x)+c\varepsilon ( w_n^2+|w_n|^p), \end{aligned}$$

which, together with (3.10) and (2.1), shows that

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,w_n)-f(x,u))h_0 dx\right| \le c\varepsilon \end{aligned}$$

for $n$ sufficiently large. This contradicts (3.9). Hence $A=0$ and (3.8) holds.

If moreover $\varphi _\lambda '(u_n)\rightarrow 0$ as $n\rightarrow \infty$, then $\varphi _\lambda '(u)=0$. Indeed, for each $\psi \in C_0^\infty (\mathbb {R}^3)$, we have

$$\begin{aligned} (u_n-u,\psi )_\lambda \mathop {\longrightarrow }\limits ^{n} 0, \end{aligned}$$

(3.11)

and

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}V^-(x)(u_n-u)\psi dx\right| \le |V^-|_\infty \left( \int \limits _{supp \psi }(u_n-u)^2dx\right) ^{1/2}|\psi |_2 \mathop {\longrightarrow }\limits ^{n} 0, \end{aligned}$$

(3.12)

since $u_n\rightarrow u$ in $L_{loc}^2(\mathbb {R}^3)$. By Lemma 2.1 (i), $u_n\rightharpoonup u$ in $E_\lambda$ yields $\phi _{u_n}\rightharpoonup \phi _u$ in $\mathcal {D}^{1,2}(\mathbb {R}^3)$. So

$$\begin{aligned} \phi _{u_n}\rightharpoonup \phi _u\ \ \ \ \ \text{ in } L^6(\mathbb {R}^3), \end{aligned}$$

and hence

$$\begin{aligned} \int \limits _{\mathbb {R}^3}K(x)(\phi _{u_n}-\phi _u)u\psi dx\rightarrow 0 \end{aligned}$$

since $K(x)u\psi \in L^{6/5}(\mathbb {R}^3)$. Combining this with Hölder’s inequality, we obtain

$$\begin{aligned}&\left| \int \limits _{\mathbb {R}^3}(K(x)\phi _{u_n}u_n\psi -K(x)\phi _uu\psi )dx\right| \nonumber \\&\quad \le \int \limits _{\mathbb {R}^3}|K(x)\phi _{u_n}(u_n-u)\psi |dx+\int \limits _{\mathbb {R}^3}\left| K(x)(\phi _{u_n}-\phi _u)u\psi \right| dx\nonumber \\&\quad \le |\psi |_\infty |K|_2|\phi _{u_n}|_6|u_n-u|_{3,supp \psi }+\int _{\mathbb {R}^3}|K(x)(\phi _{u_n}-\phi _u)u\psi |dx\nonumber \\&\quad =o(1). \end{aligned}$$

(3.13)

Furthermore, it follows from (1.1) and the dominated convergence theorem that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,u))\psi dx=\int \limits _{supp \psi }(f(x,u_n)-f(x,u))\psi dx=o(1). \end{aligned}$$

This, jointly with (3.13), (3.12) and (3.11), shows that

$$\begin{aligned} \langle \varphi _\lambda '(u),\psi \rangle =\lim _{n\rightarrow \infty }\langle \varphi _\lambda '(u_n),\psi \rangle =0,\ \ \ \ \ \ \ \ \forall \psi \in C_0^\infty (\mathbb {R}^3). \end{aligned}$$

Consequently, $\varphi _\lambda '(u)=0$ and (3.5) follows from (3.3)–(3.4). The proof is complete. $\square$

Lemma 3.3

Let $V\ge 0$, $(V_3)$–$(V_4)$, $(K)$, $(f_1)$–$(f_4)$ be satisfied. Then, for any $M>0$, there exists $\Lambda =\Lambda (M)>0$ such that $\varphi _\lambda$ satisfies $(C)_c$ condition for all $c<M$ and $\lambda >\Lambda$.

Proof

Let $(u_n)\subset E_\lambda$ be a $(C)_c$ sequence with $c< M$. According to Lemma 3.1, $(u_n)$ is bounded. Hence we may assume that

$$\begin{aligned} u_n\!\rightharpoonup \!u\ \ \text{ in } E_\lambda ,\ \ u_n\!\rightarrow \!u \text{ in } L_{loc}^s(\mathbb {R}^3)\ \ (2\le s<2^*),\ \ u_n(x)\!\rightarrow \!u(x) \text{ a.e. } x\in \mathbb {R}^3 \end{aligned}$$

(3.14)

after passing to a subsequence. Denote $w_n:=u_n-u$, we claim that $w_n\rightarrow 0$ in $E_\lambda$ for $\lambda >0$ large. In fact, Lemma 3.2 yields that $\varphi _\lambda '(u)=0$, and

$$\begin{aligned} \varphi _\lambda (w_n)\rightarrow c-\varphi _\lambda (u),\ \ \ \ \varphi _\lambda '(w_n)\rightarrow 0\ \ \ \ \ \ \ \text{ as } n\rightarrow \infty . \end{aligned}$$

(3.15)

Noting $V\ge 0$ and using $(f_3)$, we get

$$\begin{aligned} \varphi _\lambda (u)=\varphi _\lambda (u)-\frac{1}{4}\langle \varphi _\lambda '(u),u\rangle =\frac{1}{4}\Vert u\Vert _\lambda ^2+\int \limits _{\mathbb {R}^3}\mathcal {F}(x,u_n)dx\ge 0, \end{aligned}$$

and then, by (3.15),

$$\begin{aligned} \int \limits _{\mathbb {R}^3}\mathcal {F}(x,w_n)dx&\le \varphi _\lambda (w_n)-\frac{1}{4}\langle \varphi _{\lambda }'(w_n),w_n\rangle =c-\varphi _{\lambda }(u)+o(1)\le M+o(1).\qquad \qquad \end{aligned}$$

(3.16)

Since $V(x)<b$ on a set of finite measure and $w_n\rightharpoonup 0$,

$$\begin{aligned} |w_n|_2^2\le \frac{1}{\lambda b}\int \limits _{V\ge b}\lambda V^+(x)w_n^2dx+\int \limits _{V<b}w_n^2dx\le \frac{1}{\lambda b}\Vert w_n\Vert ^2_\lambda +o(1). \end{aligned}$$

(3.17)

For $2<s<2^*$, by (3.17) and the Hölder and Sobolev inequality, we obtain

$$\begin{aligned} |w_n|_s^s&\le \left( \int \limits _{\mathbb {R}^3}w_n^2dx\right) ^{\frac{2^*-s}{2^*-2}} \left( \int \limits _{\mathbb {R}^3}w_n^{2^*}dx\right) ^\frac{s-2}{2^*-2}\nonumber \\&\le \left( \frac{1}{\lambda b}\Vert w_n\Vert _\lambda ^2\right) ^\frac{2^*-s}{2^*-2}\bar{S}^{-\frac{2^*(s-2)}{2^*-2}}\left( \int \limits _{\mathbb {R}^3}|\nabla w_n|^2dx\right) ^\frac{2^*(s-2)}{2(2^*-2)}+o(1)\nonumber \\&\le \bar{S}^{-\frac{2^*(s-2)}{2^*-2}}\left( \frac{1}{\lambda b}\right) ^\frac{2^*-s}{2^*-2}\Vert w_n\Vert _\lambda ^s+o(1). \end{aligned}$$

(3.18)

By $(f_1)$, for any $\varepsilon >0$, there exists $\delta =\delta (\varepsilon )>0$ such that $|f(x,t)|\le \varepsilon |t|$ for all $x\in \mathbb {R}^3$ and $|t|\le \delta$, and $(f_4)$ is satisfied for $|t|\ge \delta$ (with the same $\tau$ but possibly larger $a_1$). Hence we obtain

$$\begin{aligned} \int \limits _{|w_n|\le \delta }f(x,w_n)w_ndx\le \varepsilon \int \limits _{|w_n|\le \delta }w_n^2dx\le \frac{\varepsilon }{\lambda b}\Vert w_n\Vert _\lambda ^2+o(1), \end{aligned}$$

(3.19)

and

$$\begin{aligned} \int \limits _{|w_n|\ge \delta }f(x,w_n)w_ndx&\le \left( \int _{|w_n|\ge \delta }\left| \frac{f(x,w_n)}{w_n}\right| ^\tau dx\right) ^{1/\tau }|w_n|_s^2\nonumber \\&\le \left( \int _{|w_n|\ge \delta }a_1\mathcal {F}(x,w_n)dx\right) ^{1/\tau }|w_n|_s^2\nonumber \\&\le (a_1M)^{1/\tau }\bar{S}^{-\frac{2^*(2s-4)}{s(2^*-2)}}\left( \frac{1}{\lambda b}\right) ^\theta \Vert w_n\Vert _\lambda ^2+o(1) \end{aligned}$$

(3.20)

by $(f_4)$, (3.16), (3.18) with $s=2\tau /(\tau -1)$ and the Hölder inequality, where $\theta =\frac{2(2^*-s)}{s(2^*-2)}>0$. Therefore, using (3.20), (3.19) and the second limit of (3.15),

$$\begin{aligned} o(1)&= \langle \varphi _\lambda '(w_n),w_n\rangle \nonumber \\&\ge \Vert w_n\Vert _\lambda ^2-\int \limits _{\mathbb {R}^3}f(x,w_n)w_ndx\nonumber \\&\ge \left[ 1-\frac{\varepsilon }{\lambda b}-(a_1M)^{1/\tau }\bar{S}^{-\frac{2^*(2s-4)}{s(2^*-2)}}\left( \frac{1}{\lambda b}\right) ^\theta \right] \Vert w_n\Vert _\lambda ^2+o(1). \end{aligned}$$

(3.21)

So, there exists $\Lambda =\Lambda (M)>0$ such that $w_n\rightarrow 0$ in $E_\lambda$ when $\lambda >\Lambda$. Since $w_n=u_n-u$, it follows that $u_n\rightarrow u$ in $E_\lambda$. $\square$

Lemma 3.4

Suppose that $(V_3)$–$(V_4)$, $(K)$, $(f_1)$–$(f_4)$ are satisfied, and $(u_n)\subset E_\lambda$ be a $(C)_c$ ($c>0$) sequence of $\varphi _\lambda$ satisfying $u_n\rightharpoonup u$ as $n\rightarrow \infty$. Then, for any $M>0$, there exists $\Lambda =\Lambda (M)>0$ such that, $u$ is a nontrivial critical point of $\varphi _\lambda$ and $\varphi _\lambda (u)\le c$ for all $c<M$ and $\lambda >\Lambda$.

Proof

By Lemma 3.2, we have $\varphi _\lambda '(u)=0$ and

$$\begin{aligned} \varphi _\lambda (w_n)\rightarrow c-\varphi _\lambda (u),\ \ \ \ \ \ \varphi _\lambda '(w_n)\rightarrow 0\ \ \ \ \ \ \text{ as } n\rightarrow \infty . \end{aligned}$$

(3.22)

Since $V$ is allowed to be sign-changing, from

$$\begin{aligned} \varphi _\lambda (u)=\varphi _\lambda (u)-\frac{1}{4}\langle \varphi _\lambda '(u),u\rangle =\frac{1}{4}\Vert u\Vert _\lambda ^2- \frac{\lambda }{4}\int \limits _{\mathbb {R}^3}V^-(x)u^2dx+\int \limits _{\mathbb {R}^3}\mathcal {F}(x,u)dx, \end{aligned}$$

it cannot deduce $\varphi _\lambda (u)\ge 0$. We consider two possibilities:

• (i) $\varphi _\lambda (u)<0$,

• (ii) $\varphi _\lambda (u)\ge 0$.

If $\varphi _\lambda (u)<0$, then $u\ne 0$ and the proof is done. If $\varphi _\lambda (u)\ge 0$, following the same lines as the proof of Lemma 3.3, we can deduce $u_n\rightarrow u$ in $E_\lambda$. Indeed, using $(V_2)$ and the fact $w_n\rightarrow 0$ in $L^2(\left\{ x\in \mathbb {R}^3:V(x)<b\right\} )$, we have

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}V^-(x)w_n^2dx\right| \le |V^-|_\infty \int \limits _{supp V^-}w_n^2 dx=o(1). \end{aligned}$$

Combining this with (3.22), we obtain

$$\begin{aligned} \int \limits _{\mathbb {R}^3}\mathcal {F}(x,w_n)dx&= \varphi _\lambda (w_n)-\frac{1}{4}\langle \varphi _\lambda '(w_n),w_n\rangle +\frac{1}{4}\int \limits _{\mathbb {R}^3}\lambda V^-(x)w_n^2dx-\frac{1}{4}\Vert w_n\Vert _\lambda ^2\\&\le c-\varphi _\lambda (u)+o(1)\\&\le M+o(1). \end{aligned}$$

It follows that (3.20) and (3.21) remain valid. Hence $u_n\rightarrow u$ in $E_\lambda$ and $\varphi _\lambda (u)=c$ $(>0)$. This completes the proof. $\square$

Next, we give some preliminary results, i.e., Lemmas 3.5 to 3.8, which ensure that the functional $\varphi _\lambda$ has the linking structure.

Lemma 3.5

Suppose that $(V_3)$–$(V_4)$, $(K)$ and (1.1) with $p\in (4,2^*)$ are satisfied. Then, for each $\lambda >\Lambda _0$ ($\Lambda _0$ is the constant given in Remark 2.1), there exist $\alpha _\lambda$, $\rho _\lambda >0$ such that

$$\begin{aligned} \varphi _\lambda (u)\ge \alpha _\lambda \ \ \ \ \ \ \text{ for } \text{ all } u\in E_\lambda ^+\bigoplus F_\lambda \text{ with } \Vert u\Vert _\lambda =\rho _\lambda . \end{aligned}$$

(3.23)

Furthermore, if $V\ge 0$, we can choose $\alpha$, $\rho >0$ independent of $\lambda$.

Proof

For any $u\in E_\lambda ^+\bigoplus F_\lambda$, writing $u=u_1+u_2$ with $u_1\in E_\lambda ^+$ and $u_2\in F_\lambda$. Clearly, $(u_1,u_2)_\lambda =0$, and

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(|\nabla u|^2+\lambda V(x)u^2)dx=\int \limits _{\mathbb {R}^3}(|\nabla u|_1^2+\lambda V(x)u_1^2)dx+\Vert u_2\Vert ^2_\lambda . \end{aligned}$$

(3.24)

For each fixed $\lambda >\Lambda _0$, noticing $\mu _j(\lambda )\mathop {\longrightarrow }\limits ^{j} +\infty$, there exists a positive integer $n_\lambda$ such that $\mu _j(\lambda )\le 1$ for $j\le n_\lambda$ and $\mu _j(\lambda )>1$ for $j\ge n_\lambda +1$. For $u_1\in E_\lambda ^+$, we set $u_1=\sum _{j=n_\lambda +1}^\infty a_j(\lambda )e_j(\lambda )$. Thus

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(|\nabla u_1|^2+\lambda V(x)u_1^2)dx=\Vert u_1\Vert ^2_\lambda -\int \limits _{\mathbb {R}^3}\lambda V^-(x)u_1^2dx \ge \left( 1-\frac{1}{\mu _{n_\lambda +1}(\lambda )}\right) \Vert u_1\Vert _\lambda ^2\nonumber \\ \end{aligned}$$

(3.25)

Now, using (3.24), (3.25) and (2.1), we obtain

$$\begin{aligned} \varphi _\lambda (u)&\ge \frac{1}{2}\left( 1-\frac{1}{\mu _{n_\lambda +1}(\lambda )}\right) \Vert u\Vert _\lambda ^2-\varepsilon |u|_2^2-C_\varepsilon |u|_p^p\\&\ge \left[ \frac{1}{2}\left( 1-\frac{1}{\mu _{n_\lambda +1}(\lambda )}\right) -\varepsilon \nu _2^2\right] \Vert u\Vert ^2_\lambda -C_\varepsilon \nu _p^p\Vert u\Vert ^p_\lambda , \end{aligned}$$

consequently the conclusion follows because $p>2$ and $\varepsilon$ has been chosen arbitrarily.

If $V\ge 0$, since $E_\lambda =F_\lambda$, and

$$\begin{aligned} \int \limits _{\mathbb {R}^3}(|\nabla u|^2+\lambda V(x)u^2)dx=\Vert u\Vert ^2_\lambda , \end{aligned}$$

we can choose $\alpha$, $\rho >0$ (independent of $\lambda$) such that (3.23) holds. $\square$

Lemma 3.6

Let $(V_3)$–$(V_4)$, $(K)$, $(f_1)$ and $(f_2)$ be satisfied. Then, for any finite dimensional subspace $\widetilde{E}_\lambda \subset E_\lambda$, there holds

$$\begin{aligned} \varphi _\lambda (u)\rightarrow -\infty \ \ \ \ \ \ \ \ \text{ as }\ \ \ \ \ \Vert u\Vert _\lambda \rightarrow \infty ,\ \ u\in \widetilde{E}_\lambda . \end{aligned}$$

Proof

Assuming the contrary, there is a sequence $(u_n)\subset \widetilde{E}_\lambda$ with $\Vert u_n\Vert _\lambda \rightarrow \infty$ such that

$$\begin{aligned} -\infty <\inf _{n}\varphi _\lambda (u_n). \end{aligned}$$

(3.26)

Take $v_n:=u_n/\Vert u_n\Vert _\lambda$. Since dim$\widetilde{E}_\lambda <+\infty$, there exists $v\in \widetilde{E}_\lambda \backslash \left\{ 0\right\}$ such that

$$\begin{aligned} v_n\rightarrow v \text{ in } \widetilde{E}_\lambda ,\ \ \ \ \ \ \ \ \ \ \ \ \ v_n(x)\rightarrow v(x) \text{ a.e. } x\in \mathbb {R}^3 \end{aligned}$$

after passing to a subsequence. If $v(x)\ne 0$, then $|u_n(x)|\mathop {\rightarrow }\limits ^{n} +\infty$, and hence by $(f_2)$,

$$\begin{aligned} \frac{F(x,u_n(x))}{u_n^4(x)}v_n^4(x)\rightarrow +\infty \ \ \ \ \ \ \ \text{ as } n\rightarrow \infty . \end{aligned}$$

Combining this with $(f_1)$, (2.4) and Fatou’s lemma, we obtain

$$\begin{aligned} \frac{\varphi _\lambda (u_n)}{\Vert u_n\Vert _\lambda ^4}&\le \frac{1}{2\Vert u_n\Vert _\lambda ^2}+\frac{C_0}{4}-\int \limits _{\mathbb {R}^3}\frac{F(x,u_n)}{\Vert u_n\Vert _\lambda ^4}dx\\&= \frac{1}{2\Vert u_n\Vert _\lambda ^2}+\frac{C_0}{4}-\left( \int \limits _{v=0}+\int \limits _{v\ne 0}\right) \frac{F(x,u_n)}{u_n^4}v_n^4dx\\&\le \frac{1}{2\Vert u_n\Vert _\lambda ^2}+\frac{C_0}{4}-\int \limits _{v\ne 0}\frac{F(x,u_n)}{u_n^4}v_n^4dx\\&\rightarrow -\infty , \end{aligned}$$

a contradiction with (3.26). $\square$

Lemma 3.7

Suppose that $(V_3)$–$(V_4)$, $(K)$, $(f_1)$ and $(f_2)$ are satisfied. If $V(x)<0$ for some $x$, then, for each $k\in \mathbb {N}$, there exist $\lambda _k>k$, $w_k\in E_{\lambda _k}^+\bigoplus F_{\lambda _k}$, $R_{\lambda _k}>\rho _{\lambda _k}$ ($\rho _{\lambda _k}$ is the constant given in Lemma 3.5) and $b_k>0$ such that, for $|K|_2<b_k$ (or $|K|_\infty <b_k$),

• (a) $\sup \varphi _{\lambda _k}(\partial Q_k)\le 0$,

• (b) $\sup \varphi _{\lambda _k}(Q_k)$ is bounded above by a constant independent of $\lambda _k$,

where $Q_k:=\left\{ u=v+tw_k:v\in E_{\lambda _k}^-, t\ge 0, \Vert u\Vert \le R_{\lambda _k}\right\}$.

Proof

We adapt an argument in Ding and Szulkin [16]. For each $k\in \mathbb {N}$, since $\mu _j(k)\rightarrow +\infty$ as $j\rightarrow \infty$, there is $j_k\in \mathbb {N}$ such that $\mu _{j_k}(k)>1$. By Proposition 2.2, there is $\lambda _k>k$ such that

$$\begin{aligned} 1<\mu _{j_k}(\lambda _k)<1+\frac{1}{\lambda _k}. \end{aligned}$$

Taking $w_k:=e_{j_k}(\lambda _k)$ be an eigenvalue of $\mu _{j_k}(\lambda _k)$, then $w_k\in E_{\lambda _k}^+$ as $\mu _{j_k}(\lambda _k)>1$. Since dim$E_{\lambda _k}^- \bigoplus \mathbb {R}w_k<+\infty$, it follows directly from Lemma 3.6 that $(a)$ holds with $R_{\lambda _k}>0$ large.

By $(f_2)$, for each $\eta >|V^-|_\infty$, there is $r_\eta >0$ such that $F(x,t)\ge \frac{1}{2}\eta t^2$ if $|t|\ge r_\eta$. For $u=v+w\in E_{\lambda _k}^-\bigoplus \mathbb {R}w_k$, we get

$$\begin{aligned} \int \limits _{\mathbb {R}^3}V^-(x)u^2dx=\int \limits _{\mathbb {R}^3}V^-(x)v^2dx+\int \limits _{\mathbb {R}^3}V^-(x)w^2dx \end{aligned}$$

by the orthogonality of $E_{\lambda _k}^-$ and $\mathbb {R}w_k$. Hence we obtain

$$\begin{aligned} \varphi _{\lambda _k}(u)&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}(|\nabla w|^2+\lambda _k V(x)w^2)dx+\frac{1}{4}\int \limits _{\mathbb {R}^3}K(x)\phi _uu^2dx-\int \limits _{supp V^-}F(x,u)dx\\&\le \frac{1}{2}\left( \mu _{j_k}(\lambda _k)-1\right) \lambda _k\int \limits _{\mathbb {R}^3}V^-(x)w^2dx-\int \limits _{supp V^-}\frac{1}{2}\eta u^2dx+\frac{1}{4}\bar{S}^{-2}\nu _6^4|K|_2^2\Vert u\Vert _{\lambda _k}^4\\&-\int \limits _{supp V^-,|u|\le r_\eta }\left( F(x,u)-\frac{1}{2}\eta u^2\right) dx\\&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}V^-(x)w^2dx-\frac{\eta }{2|V^-|_\infty }\int \limits _{\mathbb {R}^3}V^-(x)w^2dx +C_\eta +\frac{1}{4}\bar{S}^{-2}\nu _6^4|K|_2^2R_{\lambda _k}^4\\&\le C_\eta +1 \end{aligned}$$

for $u=v+w\in E_{\lambda _k}^-\bigoplus \mathbb {R}w_k$ with $\Vert u\Vert \le R_{\lambda _k}$ and $|K|_2<b_k:=2\bar{S}(\nu _6R_{\lambda _k})^{-2}$, where $C_\eta$ depends on $\eta$ but not $\lambda$. $\square$

Lemma 3.8

Suppose that $(V_3)$–$(V_4)$, $(K)$, $(f_1)$ and $(f_2)$ are satisfied. If $\Omega :=\text{ int }V^{-1}(0)$ is nonempty, then, for each $\lambda >\Lambda _0$, there exist $w\in E_\lambda ^+\bigoplus F_\lambda$, $R_\lambda >0$ and $b_\lambda >0$ such that for $|K|_{2} < b_{\lambda }$ (or$|K|_{\infty } < b_{\lambda }$),

• (a) $\sup \varphi _\lambda (\partial Q)\le 0$,

• (b) $\sup \varphi _\lambda (Q)$ is bounded above by a constant independent of $\lambda$,

where $Q=\left\{ u=v+tw:v\in E_\lambda ^-,t\ge 0, \Vert u\Vert \le R_\lambda \right\}$.

Proof

Choose $e_0\in C_0^\infty (\Omega )\backslash \left\{ 0\right\}$, then $e_0\in F_\lambda$. By Lemma 3.6, there is $R_\lambda >0$ large such that $\varphi _{\lambda }(u)\le 0$ whenever $u\in E^-_{\lambda }\bigoplus \mathbb {R}e_0$ and $\Vert u\Vert _\lambda \ge R_\lambda$.

For $u=v+w\in E_\lambda ^-\bigoplus \mathbb {R}e_0$, we obtain

$$\begin{aligned} \varphi _\lambda (u)&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}|\nabla w|^2dx+\frac{1}{4} \int \limits _{\mathbb {R}^3}K(x)\phi _uu^2dx-\int _{\Omega }F(x,u)dx\nonumber \\&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}|\nabla w|^2dx\!-\!\frac{\eta }{2}\int \limits _{\Omega }u^2dx\!-\!\int \limits _{\Omega , |u|\!\le \! r_\eta }\left( F(x,u)\!-\!\frac{\eta }{2}u^2\right) dx \!+\!\frac{1}{4}\bar{S}^{-2}\nu _6^4|K|_2^2\Vert u\Vert _{\lambda _k}^4\nonumber \\&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}|\nabla w|^2dx-\frac{\eta }{2}\int \limits _{\Omega }u^2dx+C_\eta +\frac{1}{4}\bar{S}^{-2}\nu _6^4|K|_2^2\Vert u\Vert _{\lambda _k}^4. \end{aligned}$$

(3.27)

Observing $w\in C_0^\infty (\Omega )$, one has

$$\begin{aligned} \int \limits _{\mathbb {R}^3}|\nabla w|^2dx=\int \limits _{\Omega }(-\Delta w)udx\le |\Delta w|_2|u|_{2,\Omega }\le d_0|\nabla w|_2|u|_{2,\Omega }\le \frac{d_0^2}{2\eta }|\nabla w|_2^2+\frac{\eta }{2}|u|_{2,\Omega }^2,\nonumber \\ \end{aligned}$$

(3.28)

where $d_0$ is a constant depending on $e_0$. Choosing $\eta \ge d_0^2$, we have $|\nabla w|_2^2\le \eta |u|_{2,\Omega }^2$, and it follows from (3.27) that

$$\begin{aligned} \varphi _\lambda (u)\le C_\eta +\frac{1}{4}\bar{S}^{-2}\nu _6^4|K|_2^2\Vert u\Vert _{\lambda _k}^4\le C_\eta +1 \end{aligned}$$

for all $u\in E_\lambda ^-\bigoplus \mathbb {R}e_0$ with $\Vert u\Vert \le R_\lambda$ and $|K|_2<b_\lambda :=2\bar{S}(\nu _6R_\lambda )^{-2}$. $\square$

Now we are in a position to prove Theorems 1.1 and 1.2.

Proof of Theorem 1.1

Case (i). It follows from Lemmas 3.5, 3.7 and Proposition 2.4 that, for $\lambda =\lambda _k$ and $|K|_2\in (0,b_k)$, $\varphi _{\lambda _k}$ has a $(C)_c$ sequence with $c\in [\alpha _{\lambda _k},\sup \varphi _{\lambda _k}(Q_k)]$. Setting $M:=\sup \varphi _{\lambda _k}(Q_k)$, then $\varphi _{\lambda _k}$ has a nontrivial critical point according to Lemmas 3.1 and 3.4.

Case (ii). The conclusion follows from Lemmas 3.1, 3.4, 3.5, 3.8 and Proposition 2.4. $\square$

Proof of Theorem 1.2

(Existence) Suppose $V\ge 0$. By Lemma 3.5, there exist constants $\alpha$, $\rho >0$ (independent of $\lambda$) such that

$$\begin{aligned} \varphi _\lambda (u)\ge \alpha \ \ \ \ \ \text{ for } u\in E_\lambda \text{ with } \Vert u\Vert _\lambda =\rho . \end{aligned}$$

(3.29)

Take $e_0\in C_0^\infty (\Omega )\backslash \left\{ 0\right\}$. Then, by $(f_1)$, $(f_2)$ and Fatou’s lemma,

$$\begin{aligned} \frac{\varphi _\lambda (te_0)}{t^4} \le \frac{1}{2t^2}\int \limits _{\Omega }|\nabla e_0|^2dx+\frac{1}{4}N(e_0)-\int \limits _{\left\{ x\in \Omega :e_0(x)\ne 0\right\} }\frac{F(x,te_0)}{(te_0)^4}e_0^4dx \rightarrow -\infty \end{aligned}$$

as $t\rightarrow +\infty$, which yields that $\varphi _\lambda (te_0)<0$ for $t>0$ large. Clearly, there is $C_1>0$ (independent of $\lambda$) such that

$$\begin{aligned} c_\lambda :=\inf _{h\in \Gamma }\max _{t\in [0,1]}\varphi _\lambda (h(t))\le \sup _{t\ge 0}\varphi _\lambda (te_0)\le C_1, \end{aligned}$$

(3.30)

where $\Gamma =\left\{ h\in C([0,1],E_\lambda ):h(0)=0, \Vert h(1)\Vert _\lambda \ge \rho ,\varphi _\lambda (h(1))<0\right\}$. By Proposition 2.3 and Lemma 3.3, we obtain a nontrivial critical point $u_\lambda$ of $\varphi _\lambda$ with $\varphi _\lambda (u_\lambda )\in [\alpha , C_1]$ for $\lambda$ large.

(Multiplicity) For each $k\in \mathbb {N}$, we choose $k$ functions $e_i\in C_0^\infty (\Omega )$ such that supp$e_i\cap$supp$e_j=\emptyset$ if $i\ne j$. Let

$$\begin{aligned} W_k=\text{ span }\left\{ e_1,e_2,\dots ,e_k\right\} . \end{aligned}$$

According to (3.29), Lemma 3.3 and Proposition 2.5, it suffices to show that $\sup \varphi _\lambda (W_k)$ is bounded above by a constant independent of $\lambda$.

For $u\in W_k$ and $\eta >0$, we have [cf. (3.28)]

$$\begin{aligned} \int \limits _{\mathbb {R}^3}|\nabla u|^2dx\le \frac{d_k^2}{2\eta }|\nabla u|_2^2+\frac{\eta }{2}|u|^2_{2,\Omega } \end{aligned}$$

($d_k$ is a constant depending on $W_k$). It follows that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}|\nabla u|^2dx\le \eta |u|_{2,\Omega }^2, \ \ \ \ \ \ \ \ \ \ \ \ \text{ if } \eta \ge d_k^2. \end{aligned}$$

(3.31)

Combining this with (2.4) and the Hölder inequality, we obtain

$$\begin{aligned} N(u)\le C_0\Vert u\Vert _\lambda ^4=C_0\left( \int \limits _{\Omega }|\nabla u|^2dx\right) ^2 \le C_0\eta ^2\left( \int \limits _{\Omega }u^2dx\right) ^2\le C_0\eta ^2|\Omega |\int \limits _{\Omega }u^4dx \hbox { for all } u\in W_{k}.\nonumber \\ \end{aligned}$$

(3.32)

By $(f_2)$, for each $\eta >d_k^2$, there is $r_\eta >0$ such that

$$\begin{aligned} F(x,t)\ge \frac{1}{2}\eta t^2+\frac{1}{4}C_0\eta ^2|\Omega |t^4,\ \ \ \ \ \ \ \ \forall x\in \mathbb {R}^3,\ \ |t|\ge r_\eta . \end{aligned}$$

(3.33)

Hence we obtain, using (3.31)–(3.33),

$$\begin{aligned} \varphi _\lambda (u)&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}|\nabla u|^2dx+\frac{1}{4}N(u)-\int \limits _{\Omega }F(x,u)dx\\&\le \frac{1}{2}\int \limits _{\mathbb {R}^3}|\nabla u|^2dx+\frac{1}{4}N(u)-\frac{\eta }{2}\int \limits _\Omega u^2dx-\frac{1}{4}C_0\eta ^2|\Omega |\int \limits _{\Omega }u^4dx\\&-\int \limits _{\Omega ,|u|\le r_\eta }\left( F(x,u)-\frac{\eta }{2}u^2 -\frac{1}{4}C_0\eta ^2|\Omega |u^4\right) dx\\&\le C_\eta \end{aligned}$$

for all $u\in W_k$, where $C_\eta$ is independent of $\lambda$. $\square$

4 Proof of Theorem 1.3

In this section, we are concerned with problem $(SP)_1$ with sublinear nonlinearity. We consider the functional $\varphi _1$ (denoted by $\varphi$ for simplicity) on $(E, \Vert \cdot \Vert )$:

$$\begin{aligned} \varphi (u)&= \frac{1}{2}\int \limits _{\mathbb {R}^3}(|\nabla u|^2+V(x)u^2)dx+\frac{1}{4}\int \limits _{\mathbb {R}^3}K(x)\phi _u u^2dx-\psi (u), \end{aligned}$$

where $\psi (u)=\int _{\mathbb {R}^3}F(x,u)dx$. Since the constant $\nu _s$ given in (2.1) is independent of $\lambda$, it still holds

$$\begin{aligned} |u|_s\le \nu _s\Vert u\Vert ,\ \ \ \ \ \ \ \ \forall u\in E. \end{aligned}$$

(4.1)

It follows from $(f_5)$ that

$$\begin{aligned} |F(x,u)|\le m(x)|u|^\sigma +h(x)|u|^\gamma ,\ \ \ \ \ \ \forall (x,u)\in \mathbb {R}^3\times \mathbb {R}, \end{aligned}$$

(4.2)

which, jointly with (4.1) and Hölder’s inequality, shows that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}F(x,u)dx&\le \int \limits _{\mathbb {R}^3}(m(x)|u|^\sigma +h(x)|u|^\gamma )dx\nonumber \\&\le |m|_{\frac{2}{2-\sigma }}|u|_2^\sigma +|h|_{\frac{2}{2-\gamma }}|u|_2^\gamma \nonumber \\&\le |m|_{\frac{2}{2-\sigma }}\nu _2^\sigma \Vert u\Vert ^\sigma +|h|_{\frac{2}{2-\gamma }}\nu _2^\gamma \Vert u\Vert ^\gamma \nonumber \\&< +\infty . \end{aligned}$$

(4.3)

Hence, $\psi$ and $\varphi$ are well defined. In addition, we have the following lemmas.

Lemma 4.1

Assume that $(V_3)$, $(V_4)$ and $(f_5)$ hold and $u_n\rightharpoonup u$ in $E$, then

$$\begin{aligned} f(x,u_n)\rightarrow f(x,u)\ \ \ \ \ \ \text{ in } L^2(\mathbb {R}^3). \end{aligned}$$

(4.4)

Proof

Since $u_n\rightharpoonup u$ in $E$, there is a constant $M>0$ such that

$$\begin{aligned} \Vert u_n\Vert \le M\ \ \ \ \ \ \text{ and }\ \ \ \ \ \Vert u\Vert \le M,\ \ \ \ \forall n\in \mathbb {N}. \end{aligned}$$

(4.5)

Up to a subsequence, we can assume that

$$\begin{aligned}&u_n\rightarrow u\ \ \ \ \ \text{ in } L_{loc}^2(\mathbb {R}^3),\nonumber \\&u_n(x)\rightarrow u(x)\ \ \ \text{ a.e. } x\in \mathbb {R}^3. \end{aligned}$$

(4.6)

By the properties of the functions $m$ and $h$, we have, for every $\varepsilon >0$, there exists $T_\varepsilon >0$ such that

$$\begin{aligned} \left( \int \limits _{|x|\ge T_\varepsilon }|m(x)|^\frac{2}{2-\sigma }dx\right) ^{\frac{2-\sigma }{2}}< \sqrt{\varepsilon }\ \ \ \ \ \text{ and }\ \ \ \ \left( \int \limits _{|x|\ge T_\varepsilon }|h(x)|^\frac{2}{2-\gamma }dx\right) ^\frac{2-\gamma }{2}<\sqrt{\varepsilon }. \end{aligned}$$

(4.7)

By (4.6), passing to a subsequence if necessary, we can assume that $\sum _{n=1}^\infty \int _{|x|\!\le \! T_\varepsilon }|u_n-u|^2dx<+\!\infty$. Taking ${w(x)=\sum _{n=1}^\infty |u_n(x)-u(x)|}$ for $|x|\le T_\varepsilon$, then $\int _{|x|\le T_\varepsilon }w^2dx<+\infty$. It follows from $(f_5)$ that, for all $n\in \mathbb {N}$ and $|x|\le T_\varepsilon$,

$$\begin{aligned} |f(x,u_n)-f(x,u)|^2&\le [m(x)(|u_n|^{\sigma -1}+|u|^{\sigma -1})+h(x)(|u_n|^{\gamma -1}+|u|^{\gamma -1})]^2\\&\le 4m^2(x)(|u_n|^{2\sigma -2}+|u|^{2\sigma -2})+4h^2(x)(|u_n|^{2\gamma -2}+|u|^{2\gamma -2})\\&\le 2^{2\sigma +1}m^2(x)(|u_n-u|^{2\sigma -2}+|u|^{2\sigma -2})\\&+2^{2\gamma +1}h^2(x)(|u_n-u|^{2\gamma -2}+|u|^{2\gamma -2})\\&\le 2^{2\sigma +1}m^2(x)(|w|^{2\sigma -2}+|u|^{2\sigma -2})\\&+2^{2\gamma +1}h^2(x)(|w|^{2\gamma -2}+|u|^{2\gamma -2}), \end{aligned}$$

and, using Hölder’s inequality,

$$\begin{aligned}&\int \limits _{|x|\le T_\varepsilon }\left[ 2^{2\sigma +1}m^2(x)(|w|^{2\sigma -2}+|u|^{2\sigma -2}) +2^{2\gamma +1}h^2(x)(|w|^{2\gamma -2}+|u|^{2\gamma -2})\right] dx\\&\quad \le 2^{2\sigma +1}|m|_{\frac{2}{2-\sigma }}^2\left[ \left( \int \limits _{|x|\le T_\varepsilon }w^2dx\right) ^{\sigma -1}+\left( \int \limits _{|x|\le T_\varepsilon }u^2dx\right) ^{\sigma -1}\right] \\&\qquad +2^{2\gamma +1}|h|_{\frac{2}{2-\gamma }}^2\left[ \left( \int \limits _{|x|\le T_\varepsilon }w^2dx\right) ^{\gamma -1}+\left( \int \limits _{|x|\le T_\varepsilon }u^2dx\right) ^{\gamma -1}\right] \\&\quad <+\infty . \end{aligned}$$

Hence, by Lebesgue dominated convergence theorem, we obtain

$$\begin{aligned} \int \limits _{|x|\le T_\varepsilon }|f(x,u_n)-f(x,u)|^2dx\rightarrow 0\ \ \ \ \ \text{ as }\ \ n\rightarrow \infty . \end{aligned}$$

(4.8)

On the other hand, using ($f_5$), (4.7), (4.5), (4.1) and the Hölder inequality, we have

$$\begin{aligned}&\int \limits _{|x|\ge T_\varepsilon }|f(x,u_n)-f(x,u)|^2dx\\&\quad \le \int \limits _{|x|\ge T_\varepsilon }[m(x)(|u_n|^{\sigma -1}+|u|^{\sigma -1})+h(x)(|u_n|^{\gamma -1}+|u|^{\gamma -1})]^2dx\\&\quad \le 4\int \limits _{|x|\ge T_\varepsilon }m^2(x)(|u_n|^{2\sigma -2}+|u|^{2\sigma -2})dx\\&\qquad +4\int \limits _{|x|\ge T_\varepsilon }h^2(x)(|u_n|^{2\gamma -2}+|u|^{2\gamma -2})dx\\&\quad \le 4\left( \int \limits _{|x|\ge T_\varepsilon }|m|^\frac{2}{2-\sigma }dx\right) ^{2-\sigma }(|u_n|_2^{2\sigma -2}+|u|_2^{2\sigma -2})\\&\qquad +4\left( \int _{|x|\ge T_\varepsilon }|h|^\frac{2}{2-\gamma }dx\right) ^{2-\gamma }(|u_n|_2^{2\gamma -2}+|u|_2^{2\gamma -2})\\&\quad \le 8 \varepsilon \left( \nu _2^{2\sigma -2}M^{2\sigma -2}+\nu _2^{2\gamma -2}M^{2\gamma -2}\right) . \end{aligned}$$

This, together with (4.8), shows that (4.4) holds. This completes the proof. $\square$

Lemma 4.2

Assume that $V\ge 0$, $(V_3)$, $(K)$ and $(f_5)$ hold. Then $\psi \in C^1(E,\mathbb {R})$ and $\psi ':E\rightarrow E^*$ (the dual space of $E$) is compact, and hence $\varphi \in C^1(E,\mathbb {R})$,

$$\begin{aligned}&\langle \psi '(u),v\rangle =\int \limits _{\mathbb {R}^3}f(x,u)vdx,\\&\langle \varphi '(u),v \rangle =\int \limits _{\mathbb {R}^3}\left( \nabla u\cdot \nabla v+V(x)uv+K(x)\phi _u uv-f(x,u)v\right) dx\nonumber \end{aligned}$$

(4.9)

for all $u,v\in E$. If $u$ is a critical point of $\varphi$, then the pair $(u,\phi _u)$ is a solution of problem $(SP)_1$.

Proof

In view of Lemma 4.1 and (4.1), the proof is standard and we refer to [23]. $\square$

Proof of Theorem 1.3

In view of Lemma 4.2 and the oddness of $f$, we know that $\varphi \in C^1(E,\mathbb {R})$ and $\varphi (-u)=\varphi (u)$. It remains to verify the conditions (i) and (ii) of Proposition 2.6. We follow an argument in [20].

Verification of $(i)$. Since $V\ge 0$, we get $F_\lambda =E_\lambda$. It follows from (4.3) that

$$\begin{aligned} \varphi (u)&\ge \frac{1}{2}\Vert u\Vert ^2-|m|_{\frac{2}{2-\sigma }}\nu _2^\sigma \Vert u\Vert ^\sigma -|h|_{\frac{2}{2-\gamma }}\nu _2^\gamma \Vert u\Vert ^\gamma ,\ \ \ \ \ \ \ \forall u\in E. \end{aligned}$$

Noting that $\sigma$, $\gamma \in (1,2)$, we have

$$\begin{aligned} \varphi (u)\rightarrow +\infty \ \ \ \ \ \text{ as }\ \ \Vert u\Vert \rightarrow \infty . \end{aligned}$$

(4.10)

Thus $\varphi$ is bounded from below.

Let $(u_n)\subset E$ be a (PS)-sequence of $\varphi$, i.e., $\left\{ \varphi (u_n)\right\}$ is bounded and $\varphi '(u_n)\rightarrow 0$ as $n\rightarrow \infty$. By (4.10), $(u_n)$ is bounded, and then $u_n\rightharpoonup u$ in $E$ for some $u\in E$. Recall that

$$\begin{aligned} (xy)^{1/2}(x+y)\le x^2+y^2,\ \ \ \ \ \ \ \forall x,y\ge 0. \end{aligned}$$

Hence we obtain, by (2.3) and Hölder’s inequality,

$$\begin{aligned}&\int \limits _{\mathbb {R}^3}K(x)(\phi _{u_n}u_nu+\phi _uu_n u)dx\\&\quad \le \left( \int \limits _{\mathbb {R}^3}K(x)\phi _{u_n}u_n^2dx\right) ^{1/2}\left( \int \limits _{\mathbb {R}^3}K(x)\phi _{u_n}u^2dx\right) ^{1/2}\\&\qquad +\left( \int \limits _{\mathbb {R}^3}K(x)\phi _uu_n^2dx\right) ^{1/2}\left( \int \limits _{\mathbb {R}^3}K(x)\phi _uu^2dx\right) ^{1/2}\\&\quad =\left( \int \limits _{\mathbb {R}^3}\nabla \phi _{u_n}\cdot \nabla \phi _udx\right) ^{1/2}\left( \Vert \phi _{u_n}\Vert _{\mathcal {D}^{1,2}}+\Vert \phi _u\Vert _{\mathcal {D}^{1,2}}\right) \\&\quad \le \left( \int \limits _{\mathbb {R}^3}|\nabla \phi _{u_n}|^2dx\right) ^{1/4}\left( \int \limits _{\mathbb {R}^3}|\nabla \phi _{u}|^2dx\right) ^{1/4}\left( \Vert \phi _{u_n}\Vert _{\mathcal {D}^{1,2}}+\Vert \phi _u\Vert _{\mathcal {D}^{1,2}}\right) \\&\quad =\Vert \phi _{u_n}\Vert _{\mathcal {D}^{1,2}}^{1/2}\Vert \phi _u\Vert _{\mathcal {D}^{1,2}}^{1/2} \left( \Vert \phi _{u_n}\Vert _{\mathcal {D}^{1,2}}+\Vert \phi _u\Vert _{\mathcal {D}^{1,2}}\right) \\&\quad \le \Vert \phi _{u_n}\Vert _{\mathcal {D}^{1,2}}^2+\Vert \phi _u\Vert _{\mathcal {D}^{1,2}}^2\\&\quad =\int \limits _{\mathbb {R}^3}K(x)(\phi _{u_n}u_n^2+\phi _uu^2)dx, \end{aligned}$$

which implies that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}K(x)(\phi _{u_n}u_n-\phi _uu)(u_n-u)dx\ge 0. \end{aligned}$$

Combining this with Lemma 4.1, we obtain

$$\begin{aligned}&\Vert u_n-u\Vert ^2=\langle \varphi '(u_n)-\varphi '(u),u_n-u\rangle -\int \limits _{\mathbb {R}^3}K(x)(\phi _{u_n}u_n-\phi _u u)(u_n-u)dx\\&\qquad \qquad \qquad +\int \limits _{\mathbb {R}^3}(f(x,u_n)-f(x,u))(u_n-u)dx\\&\le \Vert \varphi '(u_n)\Vert _{E^*}\Vert u_n\!-\!u\Vert \!-\!\langle \varphi '(u),u_n\!-\!u\rangle \!+\!\left( \int \limits _{\mathbb {R}^3}|f(x,u_n)\!-\!f(x,u)|^2dx\right) ^{1/2}\cdot |u_n\!-\!u|_2\\&\quad \rightarrow 0, \end{aligned}$$

that is, $u_n\rightarrow u$ $(n\rightarrow \infty )$. Hence the (PS) condition holds.

Verification of $(ii)$. For simplicity, we assume that $x_0=0$ in $(f_6)$. For $r>0$, let $D(r)$ denotes the cube

$$\begin{aligned} D(r)=\left\{ (x_1,x_2,x_3):0\le x_i\le r, i=1,2,3\right\} . \end{aligned}$$

Fix $r>0$ small enough such that $D(r)\subset B(0,\delta )$, where $\delta$ is the constant given in $(f_6)$. For arbitrary $k\in \mathbb {N}$, we shall construct an $A_k\in \Gamma _k$ satisfying $\sup _{u\in A_k}\varphi (u)<0$.

Let $m\in \mathbb {N}$ be the smallest integer such that $m^3\ge k$. We divide $D(r)$ equally into $m^3$ small cubes by planes parallel to each face of $D(r)$ and denote them by $D_i$ with $1\le i\le m^3$. We only use $D_i$ with $1\le i\le k$. Set $a=r/m$. Then the edge of $D_i$ has length $a$. We consider a cube $E_i\subset D_i$ $(i=1,2,\dots ,k)$ such that $E_i$ has the same center as that of $D_i$, the faces of $E_i$ and $D_i$ are parallel and the edge of $E_i$ has length $a/2$. Define $\zeta \in C_0^\infty (\mathbb {R},[0,1])$ such that $\zeta (t)=1$ for $t\in [a/4,3a/4]$, $\zeta (t)=0$ for $t\in (-\infty ,0]\bigcup [a,+\infty )$. Define

$$\begin{aligned} \xi (x)=\zeta (x_1)\zeta (x_2)\zeta (x_3),\ \ \ \ \ \ (x_1,x_2,x_3)\in \mathbb {R}^3. \end{aligned}$$

Then supp$\xi \subset [0,a]^3$. Now for each $1\le i\le k$, we can choose a suitable $y_i\in \mathbb {R}^3$ and define

$$\begin{aligned} \xi _i(x)=\xi (x-y_i),\ \ \ \ \ \ \forall x\in \mathbb {R}^3 \end{aligned}$$

such that

$$\begin{aligned} \text{ supp }\xi _i\subset D_i,\ \ \ \ \ \ \ \text{ supp }\xi _i\bigcap \text{ supp }\xi _j=\emptyset \ \ (i\ne j), \end{aligned}$$

(4.11)

and

$$\begin{aligned} \xi _i(x)=1\ \ (x\in E_i),\ \ \ \ \ \ \ 0\le \xi _i(x)\le 1\ \ (x\in \mathbb {R}^3). \end{aligned}$$

Set

$$\begin{aligned} V_k=\left\{ (t_1,t_2,\dots ,t_k)\in \mathbb {R}^k:\max _{1\le i\le k}|t_i|=1\right\} \end{aligned}$$

(4.12)

and

$$\begin{aligned} W_k=\left\{ \sum _{i=1}^kt_i\xi _i(x):(t_1,t_2,\dots ,t_k)\in V_k\right\} . \end{aligned}$$

Observing $V_k$ is homeomorphic to the unit sphere in $\mathbb {R}^k$ by an odd mapping, we get $\gamma (V_k)=k$. Furthermore, $\gamma (W_k)=\gamma (V_k)=k$ because the mapping $(t_1,\dots ,t_k)\longmapsto \sum _{i=1}^kt_i\xi _i(x)$ is odd and homeomorphic. Since $W_k$ is compact, there exists $C_k>0$ such that

$$\begin{aligned} \Vert u\Vert \le C_k,\ \ \ \ \ \ \ \ \forall u\in W_k. \end{aligned}$$

(4.13)

For $0<s<\varepsilon$ ($\varepsilon$ is the constant given in $(f_6)$) and $u=\sum _{i=1}^kt_i\xi _i(x)\in W_k$, we obtain

$$\begin{aligned} \varphi (su)&\le \frac{s^2}{2}\Vert u\Vert ^2+\frac{s^4}{4}\int \limits _{\mathbb {R}^3}K(x)\phi _uu^2dx -\int \limits _{\mathbb {R}_3}F\left( x,s\sum _{i=1}^kt_i\xi _i(x)\right) dx\nonumber \\&\le \frac{s^2}{2}C_k^2+\frac{s^4}{4}C_0C_k^4-\sum _{i=1}^k\int \limits _{D_i}F(x,st_i\xi _i(x))dx \end{aligned}$$

(4.14)

by (4.13), (4.11) and Lemma 3.5 $(i)$. Observing (4.12), there exists an integer $i_0\in [1,k]$ such that $|t_{i_0}|=1$. Then it follows that

$$\begin{aligned} \sum _{i=1}^k\int \limits _{D_i}F(x,st_i\xi _i(x))dx&= \int \limits _{E_{i_0}}F(x,st_{i_0}\xi _{i_0}(x))dx+\int \limits _{D_{i_0}\backslash E_{i_0}}F(x,st_{i_0}\xi _{i_0}(x))dx\nonumber \\&+\sum _{i\ne i_0}\int \limits _{D_i}F(x,st_i\xi _i(x))dx. \end{aligned}$$

(4.15)

Noting that $|t_{i_0}|=1$, $\xi _{i_0}\equiv 1$ on $E_{i_0}$ and $F(x,u)$ is even in $u$, we get

$$\begin{aligned} \int \limits _{E_{i_0}}F(x,st_{i_0}\xi _{i_0}(x))dx=\int \limits _{E_{i_0}}F(x,s)dx. \end{aligned}$$

(4.16)

By ($f_6$),

$$\begin{aligned} \int \limits _{D_{i_0}\backslash E_{i_0}}F(x,st_{i_0}\xi _{i_0}(x))dx+\sum _{i\ne i_0}\int \limits _{D_i}F(x,st_i\xi _i(x))dx\ge -a_2\text{ vol }(D(r))s^2,\quad \end{aligned}$$

(4.17)

where vol$(D(r))$ denotes the volume of $D(r)$, i.e. $r^3$. Combining (4.14)–(4.17), one has

$$\begin{aligned} \varphi (su)\le \frac{s^2}{2}C_k^2+\frac{s^4}{4} C_0C_k^4+a_2r^3s^2-\int \limits _{E_{i_0}}F(x,s)dx. \end{aligned}$$

Substituting $s=\varepsilon _n$ and using (1.2), we obtain

$$\begin{aligned} \varphi (\varepsilon _n u)\le \varepsilon _n^2\left[ \frac{C_k^2}{2}+\frac{\varepsilon _n^2}{4} C_0C_k^4+a_2r^3-\left( \frac{a}{2}\right) ^3M_n\right] . \end{aligned}$$

Since $\varepsilon _n\rightarrow 0^+$ and $M_n\rightarrow +\infty$ as $n\rightarrow \infty$, we choose $n_0$ large enough such that the right side of the last inequality is negative. Take

$$\begin{aligned} A_k=\varepsilon _{n_0}W_k. \end{aligned}$$

Then we have

$$\begin{aligned} \gamma (A_k)=\gamma (W_k)=k\ \ \ \ \ \ \ \text{ and }\ \ \ \ \ \sup _{u\in A_k}\varphi (u)<0. \end{aligned}$$

Consequently, Theorem 1.3 follows from Proposition 2.6. This completes the proof. $\square$

5 Concentration of solutions

In this section, we deal with problem $(SP)_\lambda$ with $\lambda =\lambda _k\rightarrow +\infty$.

Theorem 5.1

Suppose that $(V_3)$–$(V_4)$ and $(K)$ are satisfied, $V^{-1}(0)$ has nonempty interior $\Omega$ and there exist $a_3>0$, $p\in (2,2^*)$ such that

$$\begin{aligned} |f(x,t)|\le a_3(|t|+|t|^{p-1}),\ \ \ \ \ \ \ \ \ \forall (x,t)\in \mathbb {R}^3\times \mathbb {R}. \end{aligned}$$

(5.1)

Let $(u_k)\subset E$ be a solution of $(SP)_\lambda$ with $\lambda =\lambda _k$. If $\lambda _k\rightarrow +\infty$ and $\Vert u_k\Vert _{\lambda _k}\le C$ for some $C>0$ and all $k$, then, passing to a subsequence, $u_k\rightarrow \bar{u}$ in $L^s(\mathbb {R}^3)$ for $s\in (2,2^*)$, $\bar{u}$ is a weak solution of

$$\begin{aligned} \left\{ \begin{array}{ll} -\Delta u+\frac{1}{4\pi }\left( (K(x)u^2)*\frac{1}{|x|}\right) K(x)u=f(x,u)\ \ \ \ &{} \ \text{ in } \Omega ,\\ u=0\ \ \ \ &{} \text{ on } \partial \Omega ,\\ \end{array} \right. \end{aligned}$$

(5.2)

and $\bar{u}=0$ a.e. in $\mathbb {R}^3\backslash V^{-1}(0)$. If moreover $V\ge 0$ and $(f_1)$ is satisfied, then $u_k\rightarrow \bar{u}$ in $E$.

We note that $\bar{u}\in H_0^1(\Omega )$ if $V^{-1}(0)=\overline{\Omega }$ and $\partial \Omega$ is locally Lipschitz continuous (see [7]). Before proving the above theorem we point out some of its consequences.

Corollary 5.1

Let $(u_\lambda ,\phi _\lambda )$ be the solution obtained in Theorem 1.2 (existence result). Then $u_\lambda \rightarrow \bar{u}$ in $E$, $\phi _\lambda \rightarrow \phi _{\bar{u}}$ in $\mathcal {D}^{1,2}(\mathbb {R}^3)$ as $\lambda \rightarrow +\infty$, and $\bar{u}$ is a nontrivial solution of (5.2).

Proof

For $\lambda _k\rightarrow +\infty$, set $u_k:=u_{\lambda _k}$ be the critical point of $\varphi _{\lambda _k}$ obtained in Theorem 1.2. It follows from (3.30) that

$$\begin{aligned} C_1\ge c_{\lambda _k}=\varphi _{\lambda _k}(u_k)-\frac{1}{4}\langle \varphi _{\lambda _k}'(u_k),u_k \rangle =\frac{1}{4}\Vert u_k\Vert _{\lambda _k}^2+\int \limits _{\mathbb {R}^3}\mathcal {F}(x,u_k)dx\ge \frac{1}{4}\Vert u_k\Vert _{\lambda _k}^2. \end{aligned}$$

Hence $\left\{ \Vert u_k\Vert _{\lambda _k}\right\}$ is bounded. So the conclusion of Theorem 5.1 holds.

We show that $\bar{u}\ne 0$. Since $V\ge 0$ and $\langle \varphi _{\lambda _k}'(u_k),u_k\rangle =0$, we have

$$\begin{aligned} \Vert u_k\Vert _{\lambda _k}^2+N(u_k)=\int \limits _{\mathbb {R}^3}f(x,u_k)u_kdx\le \varepsilon |u_k|_2^2+C_\varepsilon |u_k|_p^p. \end{aligned}$$

If $\bar{u}=0$, then $u_k\rightarrow 0$ in $L^p(\mathbb {R}^3)$, and therefore

$$\begin{aligned} \Vert u_k\Vert _{\lambda _k}\rightarrow 0,\ \ \ \ \ \ \ N(u_k)\rightarrow 0\ \ \ \ \ \ \text{ as } k\rightarrow \infty \end{aligned}$$

(note $|u_{\lambda _k}|_2$ is bounded and $\varepsilon$ is arbitrary). Now it follows easily that $\varphi _{\lambda _k}(u_k)\rightarrow 0$, a contradiction with the fact $\varphi _{\lambda _k}(u_k)=c_{\lambda _k}\ge \alpha$. $\square$

Proof of Theorem 5.1

We adapt an argument in [7]. We divide the proof into three steps.

(1) Since $\Vert u_k\Vert \le \Vert u_k\Vert _{\lambda _k}\le C$, one has

$$\begin{aligned} u_k\rightharpoonup \bar{u}\ \ \text{ in } E,\ \ \ \ \ \ u_k\rightarrow \bar{u} \ \ \text{ in } L_{loc}^s(\mathbb {R}^3)\ \ (2\le s<2^*),\ \ \ \ \ \ u_k(x)\rightarrow \bar{u}(x)\ \ \text{ a.e. } x\in \mathbb {R}^3. \end{aligned}$$

For any $\psi \in C_0^\infty (\mathbb {R}^3)$, it follows from the fact $\langle \varphi _{\lambda _k}'(u_k),\psi \rangle =0$ that

$$\begin{aligned}&\left| \int \limits _{\mathbb {R}^3}V(x)u_k\psi dx\right| \\&\quad \le \frac{1}{\lambda _k}\left( \int \limits _{\mathbb {R}^3}|f(x,u_k)\psi |dx+\int \limits _{\mathbb {R}^3}|K(x)\phi _{u_k}u_k\psi |dx +\int \limits _{\mathbb {R}^3}|\nabla u_k\cdot \nabla \psi |dx\right) \\&\quad \le \frac{1}{\lambda _k}\left[ a_3(|u_k|_2|\psi |_2+|u_k|_p^{p-1}|\psi |_p)+|K|_2 |\phi _{u_k}|_6|\psi |_\infty |u_k|_3+|\nabla u_k|_2|\nabla \psi |_2\right] \\&\quad \le \frac{c}{\lambda _k}\longrightarrow 0\ \ \ \ \ \ \text{ as } k\rightarrow \infty , \end{aligned}$$

and hence

$$\begin{aligned} \int \limits _{\mathbb {R}^3}V(x)\bar{u}\psi dx=0,\ \ \ \ \ \ \ \forall \psi \in C_0^\infty (\mathbb {R}^3), \end{aligned}$$

which implies that $\bar{u}=0$ a.e. in $\mathbb {R}^3\backslash V^{-1}(0)$. Now for each $\psi \in C_0^\infty (\Omega )$, since $\langle \varphi _{\lambda _k}'(u_k),\psi \rangle =0$, it follows that

$$\begin{aligned} \int \limits _{\mathbb {R}^3}\nabla \bar{u}\cdot \nabla \psi dx+\int \limits _{\mathbb {R}^3}K(x)\phi _{\bar{u}}\bar{u}\psi dx=\int \limits _{\mathbb {R}^3}f(x,\bar{u})\psi dx, \end{aligned}$$

i.e., $\bar{u}$ is a weak solution of (5.2) by the density of $C_0^\infty (\Omega )$ in $H_0^1(\Omega )$.

(2) $u_k\rightarrow \bar{u}$ in $L^s(\mathbb {R}^3)$ for $2<s<2^*$. Arguing indirectly, by Lion’s vanishing lemma, there exist $\delta$, $\rho >0$ and $(x_k)\subset \mathbb {R}^3$ such that

$$\begin{aligned} \int \limits _{B_\rho (x_k)}(u_k-\bar{u})^2dx\ge \delta . \end{aligned}$$

It is easy to see that $|x_k|\mathop {\longrightarrow }\limits ^{k} \infty$. So meas$\left( B_\rho (x_k)\cap \left\{ x\in \mathbb {R}^3:V(x)<b\right\} \right) \rightarrow 0$, and

$$\begin{aligned} \int \limits _{B_\rho (x_k)\cap \left\{ V<b\right\} }(u_k-\bar{u})^2dx\le |u_k-\bar{u}|_3^2\left( \text{ meas }(B_\rho (x_k)\cap \left\{ V<b\right\} )\right) ^{1/3}\mathop {\longrightarrow }\limits ^{k}0. \end{aligned}$$

Thus,

$$\begin{aligned} \Vert u_k\Vert _{\lambda _k}^2&\ge \lambda _k b\int \limits _{B_\rho (x_k)\cap \left\{ V\ge b\right\} }u_k^2dx\\&= \lambda _k b \int \limits _{B_\rho (x_k)\cap \left\{ V\ge b\right\} }(u_k-\bar{u})^2dx\\&= \lambda _k b \left( \int \limits _{B_\rho (x_k)}(u_k-\bar{u})^2dx-\int \limits _{B_\rho (x_k)\cap \left\{ V<b\right\} }(u_k-\bar{u})^2dx\right) \\&\rightarrow +\infty , \end{aligned}$$

a contradiction with the boundedness of $\left\{ \Vert u_k\Vert _{\lambda _k}\right\} _k$.

(3) Suppose that $V\ge 0$ and $(f_1)$ holds. We show that $u_k\rightarrow \bar{u}$ in $E$. Since $\langle \varphi _{\lambda _k}'(u_k),u_k\rangle =0$ and $\langle \varphi _{\lambda _k}'(u_k),\bar{u}\rangle =0$, we have

$$\begin{aligned} \Vert u_k\Vert ^2_{\lambda _k}=\int \limits _{\mathbb {R}^3}f(x,u_k)u_kdx-\int \limits _{\mathbb {R}^3}K(x)\phi _{u_k}u_k^2dx \end{aligned}$$

(5.3)

and

$$\begin{aligned} (u_k,\bar{u})_{\lambda _k}=\int \limits _{\mathbb {R}^3}f(x,u_k)\bar{u}dx-\int \limits _{\mathbb {R}^3}K(x)\phi _{u_k}u_k \bar{u}dx. \end{aligned}$$

(5.4)

From (5.1) and $(f_1)$, for any $\varepsilon >0$, there exists $C_\varepsilon >0$ such that

$$\begin{aligned} |f(x,t)|\le \varepsilon |t|+C_\varepsilon |t|^{p-1},\ \ \ \ \ \ \forall (x,t)\in \mathbb {R}^3\times \mathbb {R}. \end{aligned}$$

Hence we obtain

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}f(x,u_k)(u_k-\bar{u})dx\right|&\le \varepsilon \int \limits _{\mathbb {R}^3}|u_k||u_k-\bar{u}|dx+C_\varepsilon \int \limits _{\mathbb {R}^3}|u_k|^{p-1}|u_k-\bar{u}|dx\nonumber \\&\le \varepsilon |u_k|_2|u_k-\bar{u}|_2+C_\varepsilon |u_k|_p^{p-1}|u_k-\bar{u}|_p\nonumber \\&= o(1) \end{aligned}$$

(5.5)

since $u_k\rightarrow \bar{u}$ in $L^p(\mathbb {R}^3)$ $(2<p<6)$, $(u_k)\subset E$ is bounded and $\varepsilon$ has been chosen arbitrarily. Similar to (2.7), we have

$$\begin{aligned} \left| \int \limits _{\mathbb {R}^3}K(x)\phi _{u_k}u_k(u_k-\bar{u})dx\right| \le |\phi _{u_k}|_6|u_k|_6\left( \int \limits _{\mathbb {R}^3}K(x)(u_k-\bar{u})^{3/2}dx\right) ^{2/3}\rightarrow 0. \end{aligned}$$

(5.6)

Using (5.3)-(5.6) and recalling $\bar{u}(x)=0$ if $V(x)>0$, we obtain

$$\begin{aligned} \Vert u_k\Vert ^2\le \Vert u_k\Vert _{\lambda _k}^2=(u_k,\bar{u})_{\lambda _k}+o(1)=\int \limits _{\mathbb {R}^3}\nabla u_k\cdot \nabla \bar{u} dx+o(1)=\Vert \bar{u}\Vert ^2+o(1). \end{aligned}$$

(5.7)

It follows from the weak lower semicontinuity that

$$\begin{aligned} \Vert \bar{u}\Vert ^2\le \liminf _{k\rightarrow \infty }\Vert u_k\Vert ^2, \end{aligned}$$

which, jointly with (5.7), shows that $u_k\rightarrow \bar{u}$ in $E$. The proof is complete. $\square$