Prediction of discharge coefficient of the trapezoidal broad-crested weir flow using soft computing techniques

Abstract

Weirs are hydraulic structures mostly used to measure the flow discharge and control the flow level in artificial or natural open channels. The ratio of the actual discharge to the theoretical discharge (discharge coefficient—C_d) must be known, in order to calculate the discharge of the channel having the weir. In this study, 91 experimental measurements are taken on seven trapezoidal broad-crested weirs with different upstream and downstream slopes. Experimentally measured flow properties are used to validate numerical models based on the computational fluid dynamics (CFD) methods. Two new weir geometries, not experimentally measured, are added in the numerical modeling, and 270 C_d values are calculated for nine weir geometries using numerical modeling. Theoretical C_d values are estimated using the artificial neural network (ANN), support vector machine (SVM), and M5Tree methods. In the models, the Froude number in the upstream region and dimensionless parameters of the flow are used as inputs. The performance of these methods has been examined to estimate the C_d values for eight cases. The performances of the methods are evaluated by the coefficient of determination (R²), root-mean-square error, mean absolute percentage error, and Nash–Sutcliffe model efficiency coefficient. The study results show that the Froude number significantly increases the performance of the models in estimating C_d values, and the ANN method is more successful in determining C_d than other methods.

1 Introduction

Hydraulic structures such as dams and weirs are built to benefit the most efficiently from water resources. Weirs are the oldest structures in hydraulic engineering. They are commonly used to control and regulate the flow, increase the water level, and measure discharge in the open channels (artificial or natural). Weirs can be classified according to their geometric shapes, such as ogee, piano, broad-crested and sharp-edged. Broad-crested weirs are mostly preferred to calculate the flow discharge and to determine the amount of water used in agricultural activities. Although it is possible to determine the flow discharge theoretically, conditions caused by the interaction of the flow with the structure are not considered in the calculation. The physical characteristics of the weir structure and flow conditions can cause separations in the weir crest, upstream, and downstream regions. In addition, a new boundary layer development begins when the flow field changes from the weir structure. In this case, the curvilinear flow can occur in the crest and upstream region of the weir, and the pressure distribution deviates from the hydrostatic pressure. Due to these reasons, the theoretical discharge is calculated as greater than the actual one. The theoretical discharge must be multiplied by a coefficient (discharge coefficient—C_d) to determine the actual discharge.

There are many studies in the literature to calculate the C_d for different weir types with empirical formulas using flow properties the experimentally measured [1,2,3,4,5]. In these studies, empirical formulas are suggested to determine the C_d based on the experiments performed for various weir types. In addition to empirical approach, advanced machine learning methods are frequently preferred to estimate the C_d in recent years. In the estimation, the parameters affecting the C_d are nondimensionalized and evaluated as input parameters. For instance, Salmasi, Yıldırım, Masoodi, Parsamehr [6] determined C_d values of the compound broad-crested rectangular weir with 39 experimental measurements. The effect of crest length and weir height on the C_d was investigated. In the study, the experimentally obtained the C_d results were calculated by using multiple regression equations based on dimensional analysis. The results of the regression were compared with genetic programming (GP) and artificial neural network (ANN) method results. According to the coefficient of determination (R²) and root-mean-square error (RMSE) parameters, it was seen that the GP was slightly more successful than the ANN method in determining the discharge coefficient. Hoseini and Afshar [7] evaluated the C_d of the rectangular broad-crested weir with the rounded upstream face for different flow conditions. They determined that the discharge coefficient was related to the water depth over the weir crest (h) in the upstream region, weir crest length (L), and channel width (b). Equations calculating C_d values were obtained by applying the multiple regression method. As a result, it was seen that the compatibility between the theoretical C_d and the C_d calculated with the proposed equation was high. Roushangar et al. [8] estimated the C_d of stepped spillways using the gene expression programming (GEP) and support vector machine (SVM) methods. Dimensionless geometric and hydraulic parameters of the spillway were used as inputs. As a result of the study, it was suggested that the GEP method can be used to determine the discharge coefficient of the spillway. Salmasi, Sattari [9] estimated the flow coefficient of broad-crested weirs, which they measured experimentally, with the M5Tree method. As a result of the study, they reported that the correlation between the M5Tree method and the experimental data was 0.95, and the RMSE value was 0.036. Li et al. [4] used ANN, SVM, and extreme learning machine (ELM) methods to estimate the C_d of the rectangular sharp-edged weir. Four statistical criteria were used to evaluate the success of the models, and C_d value was tried to be estimated in three different input combinations. Comparing the results of the estimation methods shows that the SVM method performed better than the other methods. Besides these works, there are many studies that used machine learning methods successfully in estimating the discharge coefficient [10,11,12,13,14]. Most of these studies estimated the C_d with a limited number of data due to the limitations caused by the experimental equipment. In addition, when these studies were examined, it was seen that the M5Tree, SVM, and ANN methods were frequently used, but there was no study in which they were used together to determine the C_d. For this purpose, it will also be investigated the performance of these methods in the same experimental set.

Moreover, the C_d estimation models, made for a single weir geometry, can be quite limited in using different geometries. However, this study aims to determine the C_d for the trapezoidal broad-crested weir, which has nine different upstream and downstream geometries. For this purpose, 91 C_d values are experimentally obtained from 13 discharges for the seven different weir geometries. Since the number of experimental measurements is insufficient to predict the C_d with artificial intelligence methods, numerical modeling based on computational fluid dynamics (CFD) methods has been carried out to increase the dataset. Due to the developments in computer technology, the use of CFD in the design and analysis of water structures has become widespread. Numerical modeling has given successful results in studies about the different flow-structure interactions, including weir flows [15,16,17,18,19,20,21]. However, numerical models need to be validated with experimental models before analyzing water structures. The main reason is that turbulence is defined by different approaches when solving the basic equations governing the flow. The previous studies show that turbulence kinetic energy and turbulent kinetic energy dissipation rate-based turbulence models give successful results in numerical modeling broad-crested weir flow [22,23,24,25,26,27].

Furthermore, there are also studies in which the C_d is determined using numerical simulations in the literature. For example, Kulkarni, Hinge [21] investigated C_d of the compound broad-crested weir with experimental and numerical models. The numerical model results were validated using the experimental results. In numerical models, the volume of fluids (VOF) method was used to determine the water–air interface, and the renormalization group (RNG) model was preferred to define turbulence in the basic equations. It was determined that the C_d values obtained experimentally and numerically were quite compatible. Thus, it is possible to evaluate a wider range of flow properties by increasing the experimentally obtained C_d using numerical models.

For this purpose, 91 experimental C_d values with a limited range due to the restrictions of the laboratory conditions are reproduced using the CFD techniques. Then, it was investigated how to determine these C_d values in cases of limited knowledge with the help of machine learning methods. Thus, practitioners will be able to easily calculate C_d values and, accordingly, flow discharge values using the results we have given in this present study for different weir and flow types.

The main motivation of this study is to solve the problems caused by the determination of the C_d coefficient, which is used for flow measurement in open channels in the laboratory environment over wide ranges. For this purpose, numerical models are created using the RNG turbulence model validated with 91 experimental measurements taken. Then, using the numerical model, two new weir geometries are added, and the number of weir geometries is raised to nine. In total, 270 C_d values are calculated according to 30 different discharges of each weir geometry. Thus, enough data could be obtained to estimate the C_d for a wide range. Finally, C_d values of the trapezoidal broad-crested weir are estimated using the ANN, SVM, and M5Tree methods with different input combinations. The estimation methods employed in this study use input combinations of dimensionless parameters of the weir and the flow properties because they are easily obtained in practice. In addition, how to estimate C_d values in the case of a limited number of inputs is also investigated within the scope of this study.

2 Data collection

2.1 Physical experiments

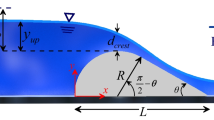
Experiments are carried out to determine the C_d for the trapezoidal broad-crested weir with different upstream and downstream slopes. These measurements are taken in the rectangular open channel, all surfaces of the channel are glass (Fig. 1). This open channel model has a length of 4 m, and width (b) and height of 0.35 m. The flow depth interacting with the trapezoidal broad-crested weir is measured with a 0.1 mm sensitivity digital limnimeter, and the flow discharge is obtained using an ultrasonic flow meter with a sensitivity of 0.01 m³/h. The trapezoidal broad-crested weir is placed in the open channel model at 1.40 m from the beginning of the model, and the measurements are taken when the open channel flow is ensured to be regular. The geometric properties of trapezoidal weirs with different slopes used in experimental and numerical modeling are given in Fig. 2. In the figure, L is the length of the weir crest, P is the weir height, α is the upstream slope, β is the downstream slope, and h is the water depth over the weir crest in the upstream region. The total weir head is defined as H₀ = h + V²/2 g, where V is the average velocity in the upstream region and g is gravity acceleration. In the experiments, L, P, and b are taken constant as 0.3 m, 0.1 m, and 0.35 m, respectively.

Fig. 1

Experimental setup

Fig. 2

Geometric properties of trapezoidal broad-crested weir

2.2 Numerical modeling

Numerical models based on the CFD method have many advantages compared to physical model studies, such as being economical, having the ability to be repeated, and requiring fewer human resources. In addition, numerical modeling does not require special measurement systems and equipment to obtain details about the flow properties or structure in physical experiments. To the reliability of the results of numerical modeling studies, which have many advantages, they should be validated with the results of physical model studies [21]. After the validation, numerical modeling studies can be used as an alternative to the physical model.

In this study, the basic equations (continuity and momentum) governing the motion of the two-dimensional, steady, turbulent, and incompressible open channel flow interacting with the trapezoidal broad-crested weir are solved with the ANSYS-Fluent software, which provides solutions based on the finite volume method. The water–air interface is determined by the VOF method. Additionally, the RNG turbulence model [28], based on the Boussinesq approach, is used in turbulence modeling. In this model, the turbulence stresses are solved by using turbulent kinetic energy and turbulent kinetic energy dissipation rate equations. It is stated that the RNG model is successful in modeling the open channel flows where boundary layer separations and secondary flows present [28]. Many researchers have reported that turbulence models (standard, realizable, and RNG) based on the solution of turbulent kinetic energy and turbulent kinetic energy dissipation rate are also successful in the numerical modeling of broad-crested weir flow [23, 25, 29].

2.3 Calculation of discharge coefficient (C _d)

The formulation of the discharge coefficient (C_d) is given in Eq. 1. C_d value is calculated by dividing the actual discharge by the theoretical [30].

$$C_{{\text{d}}} = \frac{{Q_{{{\text{actual}}}} }}{{b\sqrt {2gH_{o}^{3} } }}$$

(1)

In Eq. 1, Q_actual is the experimentally measured discharge, b is the channel width, g is the gravitational acceleration, and H_o is the total weir head.

3 Artificial intelligence methods

3.1 Support vector machine (SVM)

The support vector machine (SVM) method is a machine learning model that can be used for both classification and regression [31, 32]. It is accepted as a successful method for solving different learning problems such as classification, regression, transformation, and novelty detection [33]. The SVM theory is originally developed for classification purposes. Then it has acquired the ability to estimate quantitative output based on input values [34]. The regression with the SVM method first maps the input data to a high-dimensional feature space defined by the kernel function and obtains the optimum hyperplane that separates the training data with the maximum margin [35]. On the other hand, the method determines coefficients to minimize the effect of outliers on the regression equations; however, only residuals in absolute value greater than some positive constant are considered in the loss function [34, 36]. The SVM method uses e, insensitive loss functions, as shown in Eq. 2(e ≥ 0) [37]. Thus, if the difference between the predicted and observed values given in Fig. 3 is less than e, the loss is zero, and only data points with an absolute difference greater than e are considered lost.

$$\left| {y - f\left( x \right)} \right|_{e} = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {\quad {\text{if}}\;\;\;\left| {y - f(x)} \right| \le e} \hfill \\ {\left| {y - f(x)} \right| - e,\,} \hfill & {\quad {\text{if}}\;\;\,{\text{not}}\,} \hfill \\ \end{array} } \right\}$$

(2)

Fig. 3

Model parameters of support vector machines method

For multidimensional data (x₁, y₁),.….,(x_n, y_n) (x_i ∈ X ⊆ R_m, y_i ∈ Y ⊆ R), n is the number of samples in the training process. The approached multivariate regression function can be written as Eq. 3 [38].

$$f\left( x \right) = w \cdot \phi \left( x \right) + b$$

(3)

where ϕ(x) is the transformation from core to kernel space. The SVM method minimizes the e value while minimizing the difference between the predicted and desired outputs. The function approximation problem is transformed into an optimization problem shown in Eq. 4:

$$\min \frac{1}{2}\left| {\left| w \right|} \right|^{2} + C\sum\limits_{i = 1}^{n} {\left( {\xi_{i} + \xi_{i}^{*} } \right)}$$

(4)

$$\begin{aligned} & y_{i} - w \cdot \phi \left( {x_{i} } \right) - b \le e + \xi_{i}^{*} \quad i = 1, \ldots ,n \\ & w \cdot \phi \left( {x_{i} } \right) + b - y_{i} \le e + \xi_{i} \quad i = 1, \ldots n \\ & \xi_{i} ,\xi_{i}^{*} \ge 0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\quad i = 1, \ldots ,n \\ \end{aligned}$$

Here $\xi_{i}$ and $\xi_{i}^{*}$ are the resulting values to protect against outliers and smooth transition ($\xi_{i} ,\xi_{i}^{*} \ge 0$). C is a variable weight parameter that minimizes error. The quadratic optimization problem in Eq. 4 is solved with the Lagrangian equation shown in Eq. 5, where λ, λ*, α, and α* are positive real numbers.

$$\begin{aligned} L\,(w,b,\xi_{i} ,\xi_{i}^{*} ,\lambda ,\lambda^{*} ,\alpha ,\alpha^{*} ) & = \frac{1}{2}\left| {\left| w \right|} \right|^{2} + C\sum\limits_{i = 1}^{n} {\left( {\xi_{i} + \xi_{i}^{*} } \right)} \, + \sum\limits_{i = 1}^{n} {\alpha_{1}^{*} \left( {y_{i} - w.\phi (x) - b - e - \xi_{i}^{*} } \right)} \\ & \quad \, + \sum\limits_{i = 1}^{n} {\alpha_{i} \left( { - y_{i} + w.\phi (x) + b - e - \xi_{i} } \right)} - \sum\limits_{i = 1}^{n} {\left( {\lambda_{i} \xi_{i} + \lambda_{i}^{*} \xi_{i}^{*} } \right)} \\ \end{aligned}$$

(5)

For nonlinear regression, kernel functions k (…) are used to map the raw data to a higher-dimensional space to linearize it for higher accuracy (Eq. 6). The function approach is shown in Eq. 7.

$$k\left( {x_{i} ,x} \right) = \phi \,(x_{i} ) \cdot \phi \,(x)$$

(6)

$$f\left( x \right) = \sum\limits_{i = 1}^{{N_{SV} }} {\left( {\alpha_{i}^{*} - \alpha_{i} } \right)} \,k\left( {x_{i} ,x} \right) + b$$

(7)

Gaussian kernel function (Eq. 8) is used to define the kernel function term in Eq. 7 [39].

$$k\left( {x_{i} ,x} \right) = \exp \left( { - \sigma \left| {\left| {x_{i} - x} \right|} \right|^{2} } \right)$$

(8)

Kernel function parameters given in Eq. 8 are determined by the Bayesian optimization algorithm [40].

3.2 Artificial Neural Network (ANN)

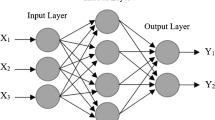
The artificial neural network (ANN) method is a conceptual technique widely used in different branches of science. Researchers frequently prefer the method because of its convenience in modeling problems without including analytical relationships [41,42,43]. The ANN models try to match the intrinsic nonlinear relationship between parameters to a complex problem. Figure 4 shows a typical ANN model with n neurons in the input layer (i), m neurons in the hidden layer (j), and one neuron in the output layer (k). The terms w_ij and W_jk given in Fig. 4 are the connection weights between the cell layers, and these values take random values during the model setup. However, they are constantly changed due to comparing the output values calculated during the training process with the desired output. Finally, the errors propagate backward until they converge to the link weight values, which will minimize the errors. In this study, the Levenberg–Marquardt algorithm is used to adjust the weights [44]. Levenberg–Marquardt (LM) algorithm requires less training time [45] and can converge even in highly complex optimization problems [46].

Fig. 4

Structure of artificial neural network method

Connection weights are used to connect the neurons of each layer to the neurons of the next layer. The sum of the weighted inputs and deviation as net inputs to the activation function in the hidden layer and the output layer is calculated according to Eqs. 9 and 10.

$$o_{j} = f({\text{net}}_{j} ) = f\left( {\sum\limits_{i = 1}^{n} {w_{ji} {\text{in}}_{i} } + \beta_{i} } \right)$$

(9)

$${\text{Out}} = f({\text{net}}_{{{\text{out}}}} ) = f\left( {\sum\limits_{i = 1}^{m} {w_{ji} io_{j} } + \beta_{j} } \right)$$

(10)

where o_j is the output of the hidden layer, Out is the output of the hidden layer, w_ji is the link weights between the input layer and the hidden layer, W_ji is the link weights between the hidden layer and the input layer, β_i and β_j are the bias values in the output layer and the hidden layer, f is the activation function (Sigmoid). The sigmoid activation function is shown in Eq. 11. In this study, n values are determined using the trial–error method. For this purpose, n is changed from 1 to 10, and the root-mean-square error (RMSE) is computed in every calculation. Then, the n value, which gives the minimum RMSE, is selected as the hidden layer neurons number of the ANN model, and in every case, this procedure is repeated. Besides, the maximum number of epochs, performance goal, and minimum performance gradient in training are selected as 1000, 10^–10, and 10^–100, respectively.

$$f\left( {{\text{net}}_{j} \left( {{\text{or}}} \right){\text{net}}_{{{\text{out}}}} } \right) = \frac{1}{{1 + {\text{e}}^{{ - {\text{net}}_{j} \left( {{\text{or}}} \right){\text{net}}{}_{{{\text{out}}}}}} }}$$

(11)

3.3 M5Tree

The M5Tree model, proposed by Quinlan [47], is based on the tree classification approach to show the relationship between dependent and independent variables. The M5Tree model, unlike the decision tree model for categorical data, may be utilized for both categorical and quantitative data. Contrary to standard regression models, which use just one equation to represent all data, the M5Tree regression tree model divides the data into subregions before assigning leaf labels. A linear regression equation is used to identify the nodes in the M5 model, allowing it to expect or forecast continuous numerical data [47]. The structure of a decision tree is like a tree with roots, branches, nodes, and leaves. The root is at the top level as the first node and is a chain of branches and nodes extending to the leaves. Each node belongs to a predictor variable, and a split occurs in the node. A numerical range leaves a parent node to reach a child node in a branch. Two branches branch off from each parent node in the M5Tree method.

The decision tree model is generated in two phases. The model is created in the first stage by separating the open data definition. Then, the M5Tree model's division criterion is optimized for the decrease in the data substandard node's deviation. The primary node is not divided, and the final node or leaf is attained when the standard deviation cannot be further decreased [48]. The corresponding equations are shown in Eqs. 12 and 13.

$$\sigma_{{\text{r}}} = \sigma (t) - \sum\limits_{i = 1}^{n} {\left( {\frac{{t_{i} }}{t}} \right)} \sigma \left( {t_{i} } \right)$$

(12)

$$\sigma = \sqrt {\frac{1}{n}\left[ {\sum\limits_{i = 1}^{n} {Y_{i}^{2} - \frac{1}{n}\left( {\sum\limits_{i = 1}^{n} {Y_{i}^{2} } } \right)} } \right]}$$

(13)

where σ_r is the reduction of the standard deviation at the sub-node, t is the input dataset to the parent node, t_i is a subset of the input data to the parent node, n is the number of datasets used, and σ is the standard deviation. Due to the division operation, the standard deviation at the sub-node is less than at the main node, leading to greater homogeneity [49].

3.4 Performance criteria

The coefficient of determination (R²), root-mean-square error (RMSE), mean absolute percentage error (MAPE), and Nash–Sutcliffe model efficiency coefficient (NSE) parameters are used to evaluate the performance of the models in estimating the C_d values. The equations of the R², RMSE, MAPE, and NSE parameters are given in Eqs. 14, 15, 16, and 17, respectively.

$$R^{2} = \left( {\frac{{\sum\limits_{i = 1}^{n} {\left( {T_{i} - \overline{{T_{i} }} } \right)\left( {P_{i} - \overline{{P_{i} }} } \right)} }}{{\sqrt {\sum\limits_{i = 1}^{n} {\left( {T_{i} - \overline{{T_{i} }} } \right)^{2} } } \sqrt {\sum\limits_{i = 1}^{n} {\left( {P_{i} - \overline{{P_{i} }} } \right)^{2} } } }}} \right)^{2}$$

(14)

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {T_{i} - P_{i} } \right)^{2} } }$$

(15)

$${\text{MAPE}} = \frac{100}{n}\sum\limits_{i}^{n} {\frac{{\left| {T_{i} - P_{i} } \right|}}{{\left| {P_{i} } \right|}}}$$

(16)

$${\text{NSE}} = 1 - \frac{{\sum\limits_{i = 1}^{n} {\left( {T_{i} - P_{i} } \right)^{2} } }}{{\sum\limits_{i = 1}^{n} {\left( {T_{i} - \overline{T}_{i} } \right)^{2} } }}$$

(17)

In the equations, T_i is the theoretical C_d, $\overline{{T_{i} }}$ is the mean theoretical C_d, P_i is the predicted C_d, $\overline{{P_{i} }}$ is the mean of the predicted C_d, and n is the total data number. The convergence of R² and NSE to 1 and RMSE and MAPE to 0 means that the forecasting model is successful.

4 Results

4.1 Experimental and numerical data collection

The determinate number of flow rates used in laboratory discharge coefficient studies also caused the obtained C_d values to be limited. The CFD methods mentioned in Sect. 2.2 were used to overcome this problem. This process was done in three stages. Firstly, seven different weir geometries (Models 1–7) and 13 C_d values for each weir geometry were measured in the laboratory. Upstream (α) and downstream (β) slopes of the weirs, water depth over the weir crest (h), total weir load (H_o), and ε (H_o/(H_o + L)) values obtained from the experimental are given in Table 1. Secondly, the numerical model is validated by means of all experimentally measured weir and flow conditions (13 discharges for each weir geometry). Flow conditions with the same characteristics as the experiments are modeled numerically, and the C_d values are determined depending on the numerical results. The mean absolute percentage error (MAPE) is used to determine the agreement between the experimental and numerical C_d values. The box plot of the MAPE values obtained in each weir geometry (called as model) is given in Fig. 5. The MAPE of C_d values calculated based on experimental and numerical model results are generally less than 10%. The mean MAPE values of each model are below 5%, except for Model 3. The fact that the mean MAPE values of the numerical and experimental C_d values are mostly less than 5% for different weir and discharge conditions means that the numerical model results are compatible with the experimental results.

Table 1 Geometric parameters and flow characteristics of the trapezoidal broad-crested weir

Fig. 5

MAPE values of experimental and numerical models

Finally, using CFD models validated with experimental data, 17 new analyses were carried out for each model, increasing the C_d number to 30. Moreover, a dataset was created by calculating 30 C_d values for two new weir geometries (Models 8 and 9), which could not be measured experimentally. Thus, the range of variation of the considered input parameters is quite wide. The calculated 270 C_d values for nine weir geometries with six upstream angles (α = 11.3°, 14.0°, 18.4°, 26.6°, 45°, and 90.0°) and five downstream angles (β = 11.3°, 14.0°, 18.4°, 26.6°, and 45°) vary between 0.35 and 0.43. Approximately 34% of the total 270 C_d values used in the study were obtained entirely from experiments, and the remaining part was obtained from the numerical models.

The variation of C_d value according to h/L, ε, and Fr values is given in Fig. 6. In the figure, the colors and shapes of the symbols represent the upstream slope (α) and the downstream slope (β) of the weir, respectively. The smallest C_d value is obtained in Model 4 (α = 90° and β = 18.4°), and the largest C_d value is obtained in Model 6 (α = 26.6° and β = 14.0°). As the h/L, Fr, and ε parameters increase, C_d value decreases in Models 3, 6, and 7, and increases in Models 1, 2, 4, 5, 8, and 9. In case the downstream slope remained the same, there is an increase in the C_d with the decrease in the upstream slope. In addition, Model 1 has larger C_d values when the h/L value, which increases with the rise of the discharge, varies between 0.3 and 0.35. A similar situation occurs when the Froude number varies between 0.20 and 0.25 and the ε value changes between 0.23 and 0.28. These results are consistent with those of Hager, Schwalt [30], Sargison, Percy [1], and Madadi, Hosseinzadeh Dalir, Farsadizadeh [50] are also compatible with the experimental results. These results reveal that numerically obtained C_d values can be evaluated like C_d values obtained by physical experiments. In this way, more discharge characteristics and different weir geometries can be also considered in numerical modeling. For this purpose, two new weir geometries are added to the seven weir geometries that are first physically measured. Moreover, the number of C_d, which is calculated experimentally, from 13 for each weir geometry has been increased to 30 with numerical modeling. Thus, after adding numerical experiments to the number of physical the number of C_d evaluated in the study becomes 270.

Fig. 6

Variation of the discharge coefficient with (a) h/L, (b) ɛ, and (c) Fr

4.2 Estimating C _d values

A dataset is created to estimate the C_d values from the physical and numerical data obtained for different weir models with the ANN, SVM, and M5Tree methods. Experimentally and numerically, a total of 270 C_d values are obtained for nine weir geometries. 70% of this dataset is in training, and 30% is used in the testing. The same number of data is randomly taken from each model for training and testing. Thus, the total data used in the training process are 189, 9 (Number of models)*21 (70% of each experimental set).

The distributions of the input (h/L, Fr, ε) and output (C_d) parameters used in the estimation models for training and testing are given in Fig. 7. Observations that are more than 1.5 interquartile range (IQR) below Q₁ or more than 1.5 IQR above Q₃ are considered outliers. The IQR describes the middle 50% of values when they are ranked from lowest to highest. As clearly shown in Fig. 7, although the distributions are different, there are no outliers in any input parameters. However, there are outliers in C_d values in both the training and testing processes. C_d values are generally within a specific range (0.380–0.390), but C_d values increase or decrease significantly, especially at very high and very low flow rates. Since this is hydraulically significant, these outliers have been preserved. In addition, the descriptive statistics values for the training and testing processes are given in Table 2. Here, Q₁, Q₂, and Q₃ denote the 1st, 2nd, and 3rd quartiles, respectively. As the 2nd quartile gives the median value, the max values also represent the 4th quartile. As given in Table 2, statistics in training and testing are generally close to each other. Although the value ranges of the variables in training are similar to those in testing, the most important difference is the C_d values. The maximum C_d values in training were higher than in testing.

Fig. 7

Amount of change of model parameters in the training and testing

Table 2 Basic statistics of input variables for training and testing

The input and output data distributions are especially important to be close to each other when creating the training and testing data. For example, the mean of h/L, ε, Fr, and C_d parameters in the training are 0.239, 0.149, 0.189, and 0.384, respectively. The mean of the h/L, ε, Fr, and C_d parameters in the testing are obtained as 0.246, 0.153, 0.193, and 0.384, respectively. A similar situation exists for the median, maximum, and minimum values. Thus, it is seen that the h/L, Fr, ε, and C_d parameters show a homogeneous distribution in the training and testing process. The input and output parameters of the cases created to be used in estimation methods are given in Table 3. In all cases, the h/L parameter is used as input. In the models, besides the h/L parameter, the weir's upstream (α) and downstream slopes (β) are added to examine the effect of the geometric features. In the first four cases, different combinations of h/L, α, β, and ε are used as input. On the other hand, in the last four cases, along with the h/L, α, β, and ε, the Froude number in the upstream region of the weir is used as the input.

Table 3 Input combinations used in forecasting models

The R², MAPE, RMSE, and NSE values obtained from ANN, SVM, and M5Tree methods for the training and testing of eight input combinations are given in Table 4. It is expected that the model success evaluated according to the performance criteria obtained in the training and testing processes will be consistent with each other, and the results will be supported according to all criteria. In addition, the success of the estimation methods is evaluated regarding these criteria obtained in the testing. The results presented in Table 4 show that Case 1 and Case 2 give low R² and NSE values in all methods. It is meaning that these cases are not suitable to be used to estimate C_d values. Besides, Case 2 with the M5Tree method has the worst performance in predicting C_d. In Case 3, where the upstream slope is used as an input, the highest NSE and R² values and the lowest RMSE and MAPE values are obtained with the ANN method. The SVM and M5Tree methods have similar results for Case 3. In Case 4, especially in the ANN and SVM methods, the R² and NSE values are above 0.9 and the MAPE value is below 1%. The M5Tree method is worse compared to the other two methods in Case 4. The results of the estimation methods are remarkable when the cases in which the Fr number is included (Cases from 5 to 8). In all estimation methods, Case 5, where only Fr and h/L values are input, gives very good results compared to the first four cases (From Case 1 to 4) in which Fr is not as input. For Case 5, the highest NSE and R² values are obtained as 0.9816 and 0.9811 with the ANN method, respectively. Although the SVM method gives slightly lower values, its results are similar to the ANN method. However, the NSE and R² values are obtained as a result of the estimation modeling for Case 5 with the M5Tree method are below 0.9 (about 0.87). In Case 6, prepared by adding the ε as a new input parameter to h/L and Fr, the most successful method is the SVM. Although there is little difference between the ANN and SVM methods and the R² and NSE values, they are very successful with a value of 0.999 in both training and testing. It is observed that the performance of the SVM method decreased, but the performance of the ANN and M5Tree methods increased in Case 7. It estimated the C_d values best among all models and cases with the ANN method in Case 8. The ANN method with Case 8 predicts almost perfectly the C_d values according to all performance criteria.

Table 4 R², RMSE, MAPE, and NSE values obtained with different methods and models

Figure 8 shows the distribution of the MAPE values calculated between the theoretical C_d values and the C_d values obtained with the ANN, SVM, and M5Tree methods for different cases in the testing. It is clearly seen that the MAPE values are high in all methods in cases not using the Fr number, but in cases using the Fr the mean MAPE values are low in ANN and SVM methods, and the distribution occurs in a very limited range. In particular, the maximum MAPE values are determined below 0.5% in Case 6 for the SVM method and in Case 7 and Case 8 for the ANN method.

Fig. 8

Change of MAPE values obtained in the testing for the different cases

The Taylor diagram is a graphical representation that provides a comparative evaluation of different models according to a reference point. This diagram presents the predictive value and its statistical relationship to the reference value. Three different statistical parameters, correlation coefficient, standard deviation, and root mean difference error (RMDE), can be seen simultaneously in the diagram. The most successful predicted model is coinciding with or closest to the reference point. Figure 9 shows Taylor diagrams of C_d values obtained in the different cases by the ANN, SVM, and M5Tree methods. Figure 9a shows that C_d values estimated using Cases 6, 7, and 8 from the Taylor diagram of the ANN method are quite close to the theoretical C_d values, also Case 8 almost coincides with the reference values. From the results of the SVM method, Case 6 is estimated quite close to the theoretical C_d value compared to the other cases (Fig. 9b). Case 7 is determined as the most successful case with the M5Tree method (Fig. 9c).

Fig. 9

Taylor diagrams of C_d values obtained with different cases and methods

The scatter plots of the theoretical and estimated C_d values of the testing for all cases are given for the ANN, SVM, and M5Tree methods in Figs. 10, 11, and 12, respectively. According to Fig. 10, the ANN method is insufficient to predict low C_d values (< 0.36) in Cases 1 and 2 and C_d values greater than 0.40 in Case 3. Although the ANN methods predict relatively better in Case 4 than the first three cases, it has been determined that the C_d values around 0.40 do not give very satisfactory results. In Case 5, it is seen that the estimated values converge to the theoretical C_d except for a few values, while in Cases 6, 7, and 8 almost all C_d values are estimated quite close. The SVM results given in Fig. 11 are generally similar to the ANN method results. Nevertheless, the SVM method, which predicted C_d values successfully, especially with Case 6, decreases estimation performance with Case 7. In Case 7, it is observed that the upstream slope (α) parameter added reduced the prediction success for the SVM method. The scatter plots obtained with M5Tree are in line with the performance criteria values in Table 4 and the Taylor diagram results. The M5Tree method with Case 7 is the most successful prediction among all cases. However, this method determined the C_d values are mostly above the theoretical C_d value. In general, it has been determined that using the upstream slope as an input in the estimation of C_d increases the model's success. Additionally, it is observed that the downstream slope does not contribute to the success of the model as much as the upstream slope.

Fig. 10

Scatter plots of C_d values theoretical and estimated with the ANN method in the testing

Fig. 11

Scatter plots of C_d values theoretical and estimated with the SVM method in the testing

Fig. 12

Scatter plots of C_d values theoretical and estimated with the M5Tree method in the testing

The results of the estimation methods show that if it is not possible to calculate the Fr number, it would be more appropriate to use the ANN method with Case 4. If it is possible, the ANN method with Case 8 would be more appropriate to calculate C_d values. The ANN is a black-box method, but it can be applied if the weight and bias values are known. For this purpose, the weight and bias values of Case 4 and Case 8 for the ANN method are given in Tables 5 and 6, respectively. In the tables, j is the number of hidden layers, and the values of w_ij, W_ji, and β_ij represent the terms in Eqs. 10 and 11.

Table 5 Model parameters of Case 4 for the ANN method

Table 6 Model parameters of Case 8 for the ANN method

5 Conclusions

In this study, the discharge coefficient of trapezoidal broad-crested weirs is investigated experimentally and numerically. The numerical model study is validated by using 91 experimental results in 13 different discharges in seven different weir geometries. Then, two new different weir geometries that do not investigate experimentally are added and 270 numerical models are carried out for nine different weir geometries. The C_d values obtained theoretically by using experimental and numerical model results are estimated with the ANN, SVM, and M5Tree methods with eight different input combinations. R², RMSE, MAPE, and NSE performance criteria are preferred in determining the success of the methods. The following main results are obtained,

• Among the models in which the Fr number is not used as an input, Case 4 (inputs: h/L, α, β, and ε) is the most successful in all methods according to all performance criteria.

• The models that used the Fr number give better results according to the models without the Fr number. The ANN method with Case 8 (inputs: h/L, α, β, ε, and Fr), the SVM method with Case 6 (inputs: h/L, ε, and Fr), and the M5Tree method with Case 7 (inputs: h/L, α, ε, and Fr) are most successful.

• Using the weir's upstream slope (α) as the input increases the success of the models more than using the downstream slope (β).

• The ANN method is most successfully determined to estimate C_d values than the SVM and M5Tree methods according to the performance criteria.

As a result of the study, it has been determined that if the upstream Froude number cannot be obtained, h/L, β, and α can be used as input parameters. However, if the Froude number can be acquired, the C_d values can be calculated by using the Fr, h/L, β, α, and ε parameters as inputs in the ANN method.

With the study results, it is possible to determine the C_d values in limited or full data cases by using the model parameters given in this article for the broad-crested weir and different flow types with different geometric properties. However, since the success of the estimation results obtained with limited inputs (Cases 1–4) is significantly lower than that obtained with the addition of other hydraulic parameters, new studies are required to increase the success of C_d estimation. It is evaluated that increasing the number of weir geometry and the C_d range will improve the performance of the C_d prediction models that would be developed.