1 Introduction

Maintaining the security of information transmission is important given the significant advances in network communication technologies. A serious challenge in cryptosystems is designing of substitution boxes (S-boxes) [1]. S-box designs are proposed based on mathematical structures, a group of theoretic approach [2]. S-box, performing confusion, has been widely employed in traditional cryptographic standards such as the Data Encryption Standard (DES) [3] and the Advanced Encryption Standard (AES) [4] for encryption and decryption process. Considering that the previous designs still do not have the highest score for the good S-box criteria, it is necessary to create a new S-box structure. In order to determine how efficient the S-box is, it has been examined in the form of a series of criteria such as nonlinearity (NL), linear approximation (LP), differential approximation (DP), strictly avalanche criteria (SAC), and bit independence criteria (BIC) [5, 6]. Therefore, if it reaches 120 in nonlinearity attacks [7], it will be one of the most ideal possible arrangements against nonlinearity attacks. The best-obtained value of SAC is 0.500 [8]. The best values so far obtained for BIC, LP, and DP are 112, 0.062, and 4, respectively [4]. Researchers have recently developed some algorithms for S-box design using the nonlinear properties of chaos. To use the chaotic space of nonlinear dynamic systems, a logistic map was used to design the S-box [9]. Subsequent studies have used maps such as three-dimensional Baker [8] or a combination of Baker and logistics [10] to develop the keyspace. Since hyper-chaotic systems have unique features, these systems were used in this article [11]. Studies on the use of chaos theory in the design of S-boxes have focused on the development of keyspace, and the use of chaotic boxes in nonlinear systems has not been considered in previous studies [12,13,14,15,16,17,18]. In ref. [19], the initial S-box was made with a spatiotemporal chaotic system, and then, its elements were randomly changed. The use of fractional derivatives as a superset of integer-order derivatives provides a more accurate description of natural phenomena [20,21,22,23]. Various applications of these derivatives have been found to solve problems such as mathematical biology [24,25,26], RC-electrical circuits [27], heat [28, 29], and fractal boundary value [30]. The fractional derivative of known equations such as the Fokker–Plank has better described the velocity of a particle in Brownian motion [31]. Solving nonlinear fractional models has been conducted even when the chaotic behavior has been studied [32,33,34]. Further, some attempts have been made to use the capabilities of fractional models combined with the chaotic properties of nonlinear systems to improve the designed S-boxes [35].

Optimization has been used to achieve stronger S-box. Optimization methods such as ant colony optimization [36], genetic algorithm optimization [37], firefly (FA) optimization [38], and teaching–learning-based optimization (TLBO) [39] have been used so far to increase the safety of designed S-boxes.

Russell Eberhart and James Kennedy (1995) devised particle swarm optimization [40]. PSO is a method based on swarm intelligence and solves optimization problems using optimized social behavior. The simplicity and simple implementation of PSO make it useful for signal processing and machine learning, neural networks, heat transfer, and so on [41,42,43]. In Ref. [44], one-dimensional and two-dimensional logistics and particle swarm optimization (PSO) were used to form the S-box. The random distribution capabilities of nonlinear dynamic systems can be used to reduce the required steps to achieve better results by the PSO method. Such a merger will improve the used PSO method [45].

Due to the increasing development of computational tools, it is necessary to review cryptographic methods and tools. The daily development of virtual network users has been accompanied by the need to increase keyspace. Considering the above-mentioned necessities, attention is paid to the forming and achieving of chaotic systems to meet these needs. Encryption algorithms with the help of S-box based on a strong chaotic system solve these problems while maintaining security. Increasing the complexity of the chaotic system used in the S-box has a significant effect on improving its criteria [46]. In order to improve the keyspace and the usable intervals of the map, another discrete map should be used to design the S-box.

In this study, the examples of Chebyshev polynomial of type one, two, their coupling, and hierarchy of rational-order maps were mentioned. Behavioral differences in these maps were used to improve PSO. Such differences can be seen again in the formation of the chaotic S-box. Finally, the performance of the produced chaotic S-boxes was optimized using the best results of improved PSO with two types of fitness. This study aimed to look for the best results by reviewing the available fitness (objective) functions.

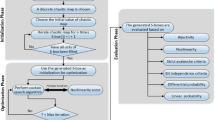
This study is organized as follows: Section 2 presents the model. Section 3 provides the improved PSO. Section 4 includes the design of the S-box. The S-box analysis is indicated in Sect. 5. The final section presents the conclusion.

2 The model

In the previous studies, the polynomial of chaotic maps is proposed [47,48,49]. The coupling of these maps will also increase the keyspace [50]. Such studies continued with the introduction of the hierarchy of rational-order chaotic maps from the same family of maps [51]. The above-mentioned maps are used in subsequent sections in the generation of improved PSO, chaotic S-box, and optimized chaotic S-box. The use of these ergodic maps increases the speed of achieving the desired model in the optimization.

2.1 One-parameter families of chaotic maps

The ratio of polynomials of degree N is considered as follows:

$$\begin{aligned} \varPhi (x, \alpha )=\frac{\alpha ^{2} F}{1+\left( \alpha ^{2}-1\right) F}, \end{aligned}$$

where F can be substituted with the Chebyshev polynomial of type one for \(\varPhi _{N}^{(1)}\) and Chebyshev polynomial of type two for \(\varPhi _{N}^{(2)}\). It should be noted that for certain value, the formed polynomial of type two is reduced to the logistic map. Using the first and second types of Chebyshev functions will lead to different types by this polynomial. In addition, the sentences of the odd and even present distinct behaviors. The chaotic interval is for even N and the first type in \(\alpha \in (0,N)\), while the second-type chaotic interval occurs in \(\alpha \in (1/N,\infty )\) [47]. Besides, for odd N, the chaotic interval is observed in \(\alpha \in (1/N,N)\).

The Kolmogorov–Sinai entropy and invariant measures of these maps are calculated in [47]. Three of these maps are given below:

$$\begin{aligned} \varPhi _{2}^{(1)}= & {} \frac{\alpha ^{2}(2 x-1)^{2}}{4 x(1-x) +\alpha ^{2}(2 x-1)^{2}}, \end{aligned}$$
(1)
$$\begin{aligned} \varPhi _{2}^{(2)}= & {} \frac{4 \alpha ^{2} x(1-x)}{1+4\left( \alpha ^{2}-1\right) x(1-x)}, \end{aligned}$$
(2)
$$\begin{aligned} \varPhi _{3}^{(1,2)}= & {} \frac{\alpha ^{2} x(4 x-3)^{2}}{\alpha ^{2} x(4 x-3)^{2}+(1-x)(4 x-1)^{2}}. \end{aligned}$$
(3)

Figure 1 indicates the time series diagram of Chebyshev polynomial of type one and Chebyshev polynomial of type two. The sensitivity of the maps to the partial change of their initial values is seen in these figures. In all of three figures, the control parameter \(\alpha =0.75\) is set, and the initial condition changes. Figure 1.1 is plotted for \(x_{0}=0.705\) and \(x_{0}=0.706\), indicating that despite a slight change in the initial value of \(x_{0}\), time series diagrams are obtained by a completely different way. Figure 1.2 is drawn for \(x_{0}=0.307\) and \(x_{0}=0.308\), and again with a slight change in the initial value of \(x_{0}\), we see two different time series charts. We plotted Fig. 1.3 for \(x_{0}=0.88899\) and \(x_{0}=0.88891\), where the difference between the time series charts for minor changes in \(x_{0}\) is evident.

Fig. 1
figure 1

The sensitivity of the chaotic map to initial conditions (1) \(\varPhi _{2}^{(1)}(x, \alpha )\) for \(x_{0}=0.705\) and \(x_{0}=0.706\), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\) for \(x_{0}=0.307\) and \(x_{0}=0.308\), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\) for \(x_{0}=0.88899\) and \(x_{0}=0.88891\) where the control parameter \(\alpha =0.75\), (4) the chaotic coupled map lattices for \(x_{0}=0.803\) and \(x_{0}=0.804\) where the control parameter \(a_{1}=1.5\), \(a_{2}=2.4\), \(N_{1}=6\), \(N_{2}=10\), \(\varepsilon =0.4\) and \(y_{0}=0.756\), (5) hierarchy of rational-order chaotic maps for \(x_{0}=0.0055\) and \(x_{0}=0.0056\) where the control parameter \(a_{1}=2.61\) and \(a_{2}=3.168\)

Full size image

Dependence on control parameter is quantified by Lyapunov exponent. In other words, the Lyapunov exponent of the chaotic system shows that neighboring orbits are exponentially separated. Positive Lyapunov exponent shows the chaotic area of the parameter and the measurability of system. In addition, a possible way to describe the keyspace may be in terms of positive Lyapunov exponents [52]. Lyapunov exponent curves for the maps of Eqs. 1, 2, 3 are shown in Figs. 2(1,2,3), respectively. It was obvious that in the various maps, the chaotic domains were different.

Fig. 2
figure 2

The variation of the Lyapunov characteristic exponent (1) \(\varPhi _{2}^{(1)}(x, \alpha )\) in terms of parameters \(a=\alpha \), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\) in terms of parameters \(a=\alpha \), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\) in terms of parameters \(a=\alpha \), (4) the chaotic coupled map lattices in terms of parameters a1, (5) hierarchy of rational-order chaotic maps in terms of parameters a1

Full size image

2.2 The chaotic coupled map lattices

The chaotic coupled map lattices were introduced and used in cryptography [50]. The form of these maps is as follows:

$$\begin{aligned} \varPhi _{{coupled}}(X_{n+1}, Y_{n+1})=\left\{ \begin{array}{l} {X_{n+1}=(1-\varepsilon ) f_{1}(x_{n})+\varepsilon f_{2}(y_{n})}, \\ {Y_{n+1}=(1-\varepsilon ) f_{1}(y_{n})+\varepsilon f_{2}(x_{n})}. \end{array}\right. \end{aligned}$$
(4)

Here, the strength of the coupling is shown with \(\varepsilon \). \(f_{1}\) and \(f_{2}\) are the chaotic trigonometric maps:

$$\begin{aligned} \left\{ \begin{array}{l} {f_{1}\left( x_{n}, a_{1}\right) =\frac{1}{a_{1}^{2}} \tan ^{2} \left( N_{1} \arctan \left( x_{n-1}^{\frac{1}{2}}\right) \right) }, \\ {f_{2}\left( x_{n}, a_{2}\right) =\frac{1}{a_{2}^{2}} \cot ^{2} \left( N_{2} \arctan \left( x_{n-1}^{-\frac{1}{2}}\right) \right) }, \end{array}\right. \end{aligned}$$

where a1 and \(a_{2}\) represent control parameters. Time series and Lyapunov exponent curve are shown in Figs. 1.4, 2.4, respectively. Figure 1.4 is plotted for constant parameter \(a_{1}=1.5\), \(a_{2}=2.4\), \(N_{1}=6\), \(N_{2}=10\), \(\varepsilon =0.4\) and \(y_{0}=0.756\) as well as variable initial value \(x_{0}=0.803\) and \(x_{0}=0.804\).

2.3 Hierarchy of rational-order chaotic maps

Hierarchy of rational-order chaotic maps was introduced in [51]. Numerical results and analytical calculations for Lyapunov exponent and Kolmogorov–Sinai entropy were obtained [51]. An example of this maps is:

$$\begin{aligned} x_{n+1}=\frac{a_{1}}{a_{2}} \times \frac{1-3 x_{n}^{2}}{3 x_{n} -x_{n}^{3}} \pm \sqrt{1+\left( \frac{a_{1}}{a_{2}} \times \frac{1-3 x_{n}^{2}}{3 x_{n}-x_{n}^{3}}\right) ^{2}}, \end{aligned}$$
(5)

where \(a_{1}\) and \(a_{2}\) represent control parameters. Figure 1.5 shows the corresponding time series diagram of dynamical system Eq. 5. Figure 1.5 is plotted for constant control parameter \(a_{1}=2.61\) and \(a_{2}=3.168\) as well as variable initial value \(x_{0}=0.03\) and \(x_{0}=0.030001\). Lyapunov exponent curve is shown in Fig. 2.5.

3 Improved PSO

Difficulty in well adjusting the global and local search capabilities and the possibility of being locked into stagnation are some of the problems that conventional PSO faces [53]. In order to solve this problem, the PSO algorithm was improved by chaotic behaviors. These algorithms included chaos initialization or updating step by chaotic map [45]. This section describes the PSO steps and how to use chaotic maps to determine its initial population and update its particle location and velocity. The best result of this section was used as an improved PSO for later designing of the S-box in sect. 4.

3.1 PSO algorithm

In PSO, the swarm comprises particles with position and speed, each one showing a possible solution in the optimization problems. PSO algorithms are divided into types such as the linearly decreasing inertia weight PSO (LDwPSO) [54], the nonlinearly decreasing inertia weight PSO [55], and chaotic inertia weight PSO [56], in terms of how the w parameter changes. This study used the linearly decreasing inertia weight PSO (LDwPSO). The steps of the PSO algorithm are as follows:

Step 1:

Defining the problem parameters

Cost function, number of decision variables (for example:\(\hbox {nVar}=10\)), size of decision variables matrix (for example:\(\hbox {VarSize}=[1\ \hbox {nVar}]\)), lower bound of variables (for example:\(\hbox {VarMin}=-10\);) and upper bound of variables (for example:\(\hbox {VarMax}= 10\)) is determined in this step.

Step 2:

Number the PSO Parameters

Maximum number of iterations (for example:\(\hbox {MaxIt}=1000\)), population size (for example:\(\hbox {nPop}=100\)), inertia weight (for example:\(\hbox {w}=1\)), inertia weight damping ratio (wdamp=0.99), personal learning coefficient (for example:\(\hbox {c}1=1.5\)), global learning coefficient (for example:\(\hbox {c}2=2.0\)) is determined.

Step 3:

Having initial population production using unifrnd function and call cost function for all primary particles and calculation of personal and global best for this population.

Step 4:

Updating the speed and position of its jth dimension at iteration t of each particle i using the following relationships and local and global search to achieve the best solution.

$$\begin{aligned} V_{i,j}(t+1)= & {} wV_{i,j}(t)+(c1)(r1)(BestX_{i,j}(t)-X_{i,j}(t))\nonumber \\&+(c2)(r2)(GlobalBest(t)-X_{i,j}(t)), \end{aligned}$$
(6)
$$\begin{aligned} X_{i,j}(t+1)= & {} X_{i,j}(t)+V_{i,j}(t+1), \end{aligned}$$
(7)

where \(V_{i,j}(t)\) represents a velocity of particle i at iteration t; \(X_{i,j}(t)\) represents a position of i particle at iteration t; r1 and r2 indicate two random number between (0,1); \(BestX_{i,j}(t)\) indicates the local best particle i in all swarm; and GlobalBest(t) indicates the leader of the swarm or global best position of all population.

Well-known benchmark function (minimization) was used to test the effectiveness of the given algorithm. Sphere function is:

$$\begin{aligned} {F_{\mathrm{{Sphere}}}} = \sum \limits _{i = 1}^n {x_i^2}, \end{aligned}$$

where \(- 10 \le {x_i} \le 10\). The minimum of this function was zero. In optimization, the goal was to get a minimum or maximum of a function. Applying the PSO algorithm with 1000 repetitions reached the number \(10^{-270}\), which was very close to zero. The result for sphere cost function is shown in Fig. 3. As can be seen, cost function approached the minimum value of the sphere function as the iteration increased. In the next subsections, this study attempted to get a better number in the same repetitions. Since the minimum of the sphere function was zero, the better the optimization result, the closer it was to this minimum. PSO works with the production of the initial population to make the S-box perform better. In other words, it improves the S-box.

Fig. 3
figure 3

The variation of the cost function (sphere) for PSO. This curve is plotted with number of decision variables(\(\hbox {nVar}=10\)), lower bound of variables(\(\hbox {VarMin}=-10\)), upper bound of variables(\(\hbox {VarMax}= 10\)), maximum number of iterations(\(\hbox {MaxIt}=1000\)), population size (for example:\(\hbox {nPop}=100\)), inertia weight (for example:\(\hbox {w}=1\)), inertia weight damping ratio(\(\hbox {wdamp}=0.99\)), personal learning coefficient(\(\hbox {c}1=1.5\)), and global learning coefficient(\(\hbox {c}2=2.0\))

Full size image

3.2 PSO initial population determination with chaotic map

All of the families of chaotic maps in Sect. 2 were used separately for the initialization value of PSO. These values for each map were selected based on their chaotic domain (positive Lyapunov exponent). Due to the similarity in quasi-code, this study included only one of them in this section, while the recorded results were compared for all maps.

In this subsection, the values of X in Eqs. 1, 2, 3, 4 and 5 are normalized in the range [0,1] to each decision variable in the n-dimensional space of optimization problem. By considering Lyapunov exponent curves, the parameters used here were \(\alpha =0.75\) for Eqs. 1, 2, 3, \(N_{1}=6, N_{2}=10, a_{1}=1.5, a_{2}=2.4, \varepsilon =0.4\) for Eq. 4, and \(a_{1}=2.61, a_{2}=3.168\) for Eq. 5. The function optimization problem with the continuous variable was defined as follows.

This study minimized f(x) (cost function) by finding \(X=[x_{1},x_{2},\ldots ,x_{n}]\). X represents the decision solution vector consisting of n variables, \(x_{i}\), bounded by lower \((L_{i})\) and upper limits \((U_{i})\). PSO initial population determination procedure with chaotic map can be illustrated:

Step 1:

Entering the initial conditions chaotic map. Set \(nPop=100, x(1)\), for Eq. 1.

Step 2:

Initializing the particle swarm position X by map function by Eq. 1:

figure a

The results for all the maps are shown in Fig. 4. As can be seen in all figures, the use of a chaotic map instead of unifrnd function had no significant effect on the cost function.

Fig. 4
figure 4

The variation of the cost function (sphere) for (1) \(\varPhi _{2}^{(1)}(x, \alpha )\), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\), (4) the chaotic coupled map lattices, (5) hierarchy of rational-order chaotic maps. These curves are plotted with number of decision variables(\(\hbox {nVar}=10\)), lower bound of variables(\(\hbox {VarMin}=-10\)), upper bound of variables(\(\hbox {VarMax}= 10\)), Maximum number of iterations(\(\hbox {MaxIt}=1000\)), population size (for example:\(\hbox {nPop}=100\)), inertia weight (for example:\(\hbox {w}=1\)), inertia weight damping ratio(\(\hbox {wdamp}=0.99\)), personal learning coefficient(\(\hbox {c}1=1.5\)) and global learning coefficient(\(\hbox {c}2=2.0\))

Full size image

3.3 Updating velocity with chaotic maps in PSO

As mentioned in the initialization value, all of the proposed maps in Sect. 2 were used to update velocity of PSO.

Update velocity with chaotic maps in PSO is as follows:

Step 1:

Entering the initial conditions chaotic map. Set \(nPop=100, MaxIt=1000, x(1)\), for Eq. 1.

Step 2:

Performing chaotic search by updating of the speed and position of each particle by using a subfunction derived from Eqs. 1–5 instead of r1 and r2:

figure b

The results for all the maps are shown in Fig. 5. All curves tended to a minimum with increasing repetition. Their difference speed toward zero corresponded to the maps. Graph 5.5 reached the number \(10^{-300}\) in the same repetitions of 1000. Hierarchy of rational-order chaotic maps reached the minimum with the least number of steps. As mentioned, Fig. 3 represents the variation in the cost function (sphere) for PSO. Compared to Fig. 5, the created number for the cost function in the same repetitions of 1000 (graph 5) was better \(10^{30}\) times.

Fig. 5
figure 5

The variation of the cost function (sphere) for (1) \(\varPhi _{2}^{(1)}(x, \alpha )\), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\), (4) the chaotic coupled map lattices, (5) hierarchy of rational-order chaotic maps. These curves are plotted with number of decision variables(\(\hbox {nVar}=10\)), lower bound of variables(\(\hbox {VarMin}=-10\)), upper bound of variables(\(\hbox {VarMax}= 10\)), maximum number of iterations(\(\hbox {MaxIt}=1000\)), population size (for example:\(\hbox {nPop}=100\)), inertia weight (for example:\(\hbox {w}=1\)), inertia weight damping ratio (\(\hbox {wdamp}=0.99\)), personal learning coefficient(\(\hbox {c}1=1.5\)), and global learning coefficient(\(\hbox {c}2=2.0\))

Full size image

4 The S-box design

Using chaos in the design of efficient S-boxes has been recently considered. This section describes the design of the S-box using the proposed chaotic maps. Then, these S-boxes are optimized by using improved PSO.

4.1 The chaotic S-box

Key is one of the fundamental pillars of any cryptography. Every algorithm is as secure as its key. For high levels of security, the key space size should not be less than \(2^{100}\) [57, 58]. The keyspace provided by the introduced maps to produce the S-box was vast. The order of complexity for decoding in our proposed maps was calculated as follows:

  1. 1-

    for the Chebyshev polynomial

    $$\begin{aligned} T(\alpha , {x_0}) = \theta (\alpha \times {x_0}), \end{aligned}$$
  2. 2-

    for the maps of Eq. 4

    $$\begin{aligned} T(N_{1}, N_{2}, a_{1}, a_{2}, \varepsilon , {x_0}, y_{0}) = \theta (N_{1} \times N_{2} \times a_{1} \times a_{2} \times \varepsilon \times {x_0} \times y_{0}), \end{aligned}$$
  3. 3-

    for the maps of Eq. 5

    $$\begin{aligned} T(a_{1}, a_{2},{x_0}) = \theta (a_{1} \times a_{2} \times {x_0}). \end{aligned}$$

As an example in the Chebyshev polynomial of type one to determine the keyspace, the keyspace will be over than \(10^{32}\) if the accuracy is \(10^{-16}\) by considering the map interval (0, 1) and chaotic region of the control parameter (0,2).

This keyspace was affected by the chaotic range of control parameters and their number. This space is more than \(10^{112}\) in the chaotic coupled map (Eq. 4) due to the increase in the number of control parameters (\({x_0}, y_{0} \in (0,1), \varepsilon \in (0,1), a_{1}, a_{2} \in (0.5,2), N_{1}\) and \(N_{2}\)). Hierarchy of rational-order chaotic maps was examined in the same way.

These spaces could resist all types of brute-force attacks. The best keyspace was for the chaotic coupled map lattices (Eq. 4).

From the mathematical perspective, an \(n*m\) S-box was a nonlinear mapping \(S : V_{n} \rightarrow V_{m}\), where \(V_{n}\) and \(V_{m}\) represent the vector spaces of n, m elements from GF(2). The steps for creating S-box are shown as follows:

Step 1:

Entering the initial conditions and control parameters by considering Lyapunov exponent curves (Fig. 2).

Step 2:

Repeating the map to 1000000 to pass the transition state.

Step 3:

Repeating the map to 700000 times and selecting the last number x(f).

Step 4:

Getting the first S-box from the following equation.

$$\begin{aligned} S(1)=x(f)*10^5 mod 256 \end{aligned}$$
Step 5:

Repeating the map and selecting the last number x(f).

Step 6:

The next S-box numbers were obtained from the following equation.

$$\begin{aligned} S(i)=x(f)*10^5 mod 256 \end{aligned}$$
Step 7:

If S(i) is in the S-box, the process continues from step 5.

Step 8:

Putting the obtained S(i) in the S-box table.

Step 9:

Repeating steps 5 through 8 until all 256 number S-boxes are filled.

The flowchart for creating S-box is shown in Fig. 6. Table 1 shows the best S-boxes generated from the maps of Eqs. 1, 2, 3, 4 and 5 presented in the model. This S-box is produced by the map of Eq. 3.

Table 1 Proposed S-box (16*16 matrix) from \(\varPhi _{3}^{(1,2)}(x, \alpha )\) in Eq. 3 for \(\alpha =0.75,\)
Full size table
Fig. 6
figure 6

S-box creation algorithm

Full size image

4.2 The chaotic S-box design with improved PSO

By considering the result of Sect. 3, this study improved PSO with the hierarchy of rational-order chaotic maps to optimize S-box. Various objective (fitness or cost) functions can be introduced in S-box optimization, including nonlinearity of the box and greater randomness of the box numbers. In this section, both cases are discussed in separate subsections.

4.2.1 The chaotic S-box design with improved PSO and nonlinearity fitness function

Many studies have considered nonlinearity as an objective function of optimization [37]. By considering this, the steps of the algorithm are as follows:

Step 1:

Entering initial conditions and control parameters related to the chaotic map of the objective function.

Step 2:

Entering improved PSO parameters.

Step 3:

Having initial population production using unifrnd function.

Step 4:

Creating of S-box with chaotic map (Sect. 4.1) and calculation of nonlinearity for all primary particles and calculation of personal and global best for this population.

Step 5:

Updating the speed and position of each particle using the hierarchy of rational-order chaotic maps and local and global search to achieve the best solution (subsection 3.3).

Step 6:

Saving the best nonlinearity and related S-box.

The flowchart for the optimized S-box design with improved PSO and nonlinearity fitness function is shown in Fig. 7. The results of all improved PSO algorithms for all the formed S-boxes in Sect. 4.1 are given in Fig. 8. The best-created S-boxes are shown in Table 2. This S-box is produced by the map of Eq. 4.

Table 2 Offered optimized S-box (16*16 matrix) from the chaotic coupled map lattices (Eq. 4) with nonlinearity fitness for \(N_{1}=6, N_{2}=10, a_{1}=1.5, a_{2}=2.4, \varepsilon =0.4\)
Full size table
Fig. 7
figure 7

Optimized S-box creation algorithm with nonlinearity fitness function

Full size image
Fig. 8
figure 8

Optimized S-box creation algorithm with P-value of mono-test fitness function

Full size image

4.2.2 The chaotic S-box design with improved PSO and mono-bit frequency test fitness function

Converting the outputs of the chaotic system to zero-one strings is one of the chaotic-based randomness production methods (entropy source) [59]. Here, six introduced maps are used to generate random numbers. The simplest and most effective ideals for statistical random measurement are the Chi-square test. The following formula was used to calculate:

$$\begin{aligned} \chi ^{2}=\frac{\left( \mathbf {n}_{0}-\mathbf {n}_{1}\right) ^{2}}{\mathbf {n}}, \end{aligned}$$

where \({n}_{0}\), \({n}_{1}\) represent the number of 0’s and 1’s in bit sequences, respectively [60]. This test is mono-bit frequency test. P-value was computed from the bit sequence for this test. If the P-value is greater than a predefined threshold 0.01, then sequence will pass the test successfully. Here, like Reference [61], the mono-bit test was selected as the optimization objective function. The steps of the algorithm are as follows:

Step 1:

Entering initial conditions and control parameters related to the chaotic map of the objective (fitness) function.

Step 2:

Entering improved PSO parameters.

Step 3:

Having initial population production using unifrnd function.

Step 4:

Creating S-box with chaotic map (Sect. 4.1).

Step 5:

Having the generated S-box as a \(16*16\) matrix. The rows were put together, and a \(1*256\) matrix was obtained.

Step 6:

Putting the numbers in pairs and converting the sums into binaries and then strings.

Step 7:

Calculating mono-bit frequency test for all primary particles and calculation of personal and global best for this population.

Step 8:

Updating the speed and position of each particle using the hierarchy of rational-order chaotic maps and local and global search to achieve the best solution (subsection 3.3).

Step 9:

Saving the best P-value of mono-bit frequency test and related S-box.

The flowchart for the optimized S-box design with improved PSO and P-value of mono-bit frequency test (fitness function) is shown in Fig. 9. The results of all improved PSO optimizations for all the formed S-boxes in Sect. 4.1 are given in Fig. 10. The best-created S-box is shown in Table 3. This S-box is produced by the map of Eq. 2.

Table 3 Offered optimized S-box (16*16 matrix) from \(\varPhi _{2}^{(2)}(x, \alpha )\) in Eq. 2 with P-value of mono-test fitness function for \(\alpha =0.75,\)
Full size table
Fig. 9
figure 9

Best nonlinearity of optimized S-box with nonlinearity fitness function for (1) \(\varPhi _{2}^{(1)}(x, \alpha )\) where \(\alpha =0.75,\), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\) for \(\alpha =0.75,\), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\) for \(\alpha =0.75,\), (4) the chaotic coupled map lattices for \(N_{1}=6, N_{2}=10, a_{1}=1.5, a_{2}=2.4, \varepsilon =0.4\), (5) hierarchy of rational-order chaotic maps for \(a_{1}=2.61, a_{2}=3.168\). Improved PSO based on hierarchy of rational-order chaotic maps for \(a_{1}=2.61, a_{2}=3.168\) is used. Other optimization conditions are: number of decision variables (\(\hbox {nVar}=9\)), lower bound of variables (\(\hbox {VarMin}=90\)), upper bound of variables (\(\hbox {VarMax}= 120\)), maximum number of iterations (\(\hbox {MaxIt}=10\)), population size (\(\hbox {nPop}=9\)), inertia weight (\(\hbox {w}=1\)), inertia weight damping ratio (\(\hbox {wdamp}=0.99\)), personal learning coefficient (\(\hbox {c}1=1.5\)), and global learning coefficient (\(\hbox {c}2=2.0\))

Full size image
Fig. 10
figure 10

Best P-value of optimized S-box with P-value of mono-test fitness function for (1) \(\varPhi _{2}^{(1)}(x, \alpha )\) where \(\alpha =0.75,\), (2) \(\varPhi _{2}^{(2)}(x, \alpha )\) for \(\alpha =0.75,\), (3) \(\varPhi _{3}^{(1,2)}(x, \alpha )\) for \(\alpha =0.75,\), (4) the chaotic coupled map lattices for \(N_{1}=6, N_{2}=10, a_{1}=1.5, a_{2}=2.4, \varepsilon =0.4\), (5) hierarchy of rational-order chaotic maps for \(a_{1}=2.61, a_{2}=3.168\). Improved PSO based on hierarchy of rational-order chaotic maps for \(a_{1}=2.61, a_{2}=3.168\) is used. Other optimization conditions are: number of decision variables (\(\hbox {nVar}=9\)), lower bound of variables (\(\hbox {VarMin}=0.01\)), upper bound of variables (\(\hbox {VarMax}=1\)), maximum number of iterations (\(\hbox {MaxIt}=10\)), population size (\(\hbox {nPop}=9\)), inertia weight (\(\hbox {w}=1\)), inertia weight damping ratio (\(\hbox {wdamp}=0.99\)), personal learning coefficient(\(\hbox {c}1=1.5\)), and global learning coefficient (\(\hbox {c}2=2.0\))

Full size image

5 The S-box analysis

Subsequently, the following important tests were applied to the generated S-box in Tables 1, 2, 3:

nonlinearity (NL), strict avalanche criterion (SAC), bit independence criterion (BIC), linear approximation probability (LP), and differential approximation probability (DP).

5.1 Nonlinearity

The degree of linearity of the S-box was given by nonlinearity test. Since the affine functions were weak in terms of cryptography, the similarity of the Boolean function variable of S-box was measured with the affine variable. The nonlinearity value was calculated using the following equation:

$$\begin{aligned} N = {2^{n - 1}} - \frac{1}{2}\mathop {\max }\limits _{a \in {B^n}} \left| {\sum \limits _{x \in {B^n}} {( - 1)}^{f(x) + a.x}} \right| , \end{aligned}$$

where \(B=\{0,1\}\), \(f:B^{n} \rightarrow B\), \(a\in {B^n}\) and a.x represents the dot product between a and x (see [62], for example). The highest theoretical limit of nonlinearity is 120 [7]. The best received value is 112 for the AES S-box [4]. For example, the nonlinearity of eight Boolean functions of offered optimized S-box for the map of Eq. 4 with nonlinearity fitness was 108, 104, 108, 106, 104, 108, 106, and 108. Therefore, the maximum and minimum and average values were 108, 104, and 106.5, respectively. This average was better than all the averages obtained with the chaotic S-box and their optimized S-box. The maximum and minimum and average values and comparing it with the results of previous work are given in Table 4.

Table 4 Nonlinearity values of offered S-box. The nonlinearity of eight Boolean functions of each offered S-box is calculated, and minimum, maximum, and average of them are shown in the table
Full size table

5.2 Strict avalanche criterion (SAC)

Webster and Tavares introduced another important measure (as strict avalanche criterion) that describing when one bit in the input of Boolean function changed, half of the output bits should be changed [1]. The dependence matrix for all the proposed S-boxes was calculated based on the reference [1] method. Table 5 shows that the minimum, maximum, and average values of dependence matrices. Further, comparing its results with the results of previous work is presented in this table. The best-obtained average value for SAC was 0.5. All obtained values for the proposed S-boxes were appropriate and very close to 0.500. The received value for the offered optimized S-box generated by the map of Eq. 5 with the P-value fitness( 0.499512) was the best-obtained value. The dependence matrix of this S-box is given in Table 6. The results were confirmed and improved compared to previous method.

Table 5 SAC values of offered S-boxes. Minimum, maximum, and average values of dependence matrices are shown
Full size table
Table 6 Dependence matrix of the offered optimized S-box for hierarchy of rational-order chaotic maps (Eq. 5) with the P-value fitness
Full size table

5.3 Bit independence criterion (BIC)

Webster and Tavares defined a desirable feature for any encryption transformation for S-box analysis, called the output bits independence criterion (BIC)[1]. The independence of the avalanche vectors sets was measured by the BIC. If one changed the inverse of input single bits, these sets would be created [63]. BIC-nonlinearity and BIC-SAC for all the proposed S-boxes were calculated based on the reference [1] method. Table 7 indicates the average values of BIC-nonlinearity and BIC-SAC. The numerical results of this test and comparing it with the results of previous work are depicted in Table 7. The amounts of BIC-nonlinearity and BIC-SAC were 112 and 0.5 for the AES S-box [4], which were the best-achieved values. The obtained average values of BIC-nonlinearity for the proposed S-boxes were between 102.071 and 104.429. The best was for the chaotic coupled map lattices (Eq. 4), being more than all of the obtained values in Table 7 references except for reference [39]. The best-obtained average value of BIC-SAC is 0.49986 for optimized S-box Chebyshev polynomial of type odd (Eq. 3) with nonlinearity fitness. This value was more than all of the obtained values in Table 7 references. BIC-nonlinearity and BIC-SAC of best proposed S-boxes are given in Tables 8 and 9.

Table 7 BIC values of offered S-boxes. These values are average
Full size table
Table 8 BIC-nonlinearity criterion for the offered S-box for the chaotic coupled map lattices (Eq. 4)
Full size table
Table 9 BIC-SAC criteria for the offered optimized S-box for \(\varPhi _{3}^{(1,2)}(x, \alpha )\) in Eq. 3 with nonlinearity fitness
Full size table

5.4 Linear approximation probability (LP)

The maximum value of imbalance in the event between input and output bits is called the linear approximation probability (LP). Mathematical definition of LP [64] is:

$$\begin{aligned} LP = \mathop {\max }\limits _{a,b \ne 0} \left| {\frac{{\# \{ x|x.a = f(x).b\} }}{{{2^n}}} - 0.5} \right| , \end{aligned}$$

where a, b represent the input and output masks, and the set x contains all the possible inputs, and \(2^n\) represents the number of its elements. If the S-box has low LP, it can resist linear attacks. The best LP results were from the AES S-box [4]. The LP obtained values were suitable for all suggested S-boxes. The most suitable value was for Chebyshev polynomial of type two (Eq. 2) and the hierarchy of rational-order chaotic maps (Eq. 5) (in optimized with P-value fitness). In addition, compared to previous works, it was less than references [8, 10, 18, 39, 65, 66], and [67] and similar to reference [17]. Table 10 shows the numerical results and compares the results of previous work.

Table 10 LP values of offered S-boxes
Full size table

5.5 Differential approximation probability (DP)

Biham and Shamir introduced a differential cryptanalysis method [68]. This method calculated XOR distribution between input and output bits of S-box was called DP. If this distribution is close between the input and output bits, S-box will be resistant to differential attacks. DP is defined as follows:

$$\begin{aligned} DP = \mathop {\max }\limits _{{\varDelta _x} \ne 0,{\varDelta _y}} (\# x \in X,{f_x} \oplus f(x + {\varDelta _x}) ={\varDelta _y}/{2^n}), \end{aligned}$$

where X shows the set of all possible input values, and \(2^n\) represents the number of its elements. The DP value for a strong S-box should be close to zero. The best result (\(\hbox {DP}=4\)) was for AES S-box [4]. All of the obtained values were suitable for the introduced S-boxes. The best DP (10) was for the chaotic coupled map lattices (Eq. 4) (in all recommended S-boxes) and Chebyshev polynomial of type two and hierarchy of rational-order chaotic maps (Eq. 5) (in both optimized modes) and Chebyshev polynomial of type one (Eq. 1) (in optimized with P-value fitness). Compared to the previous work, this result was similar to references [10, 39, 61, 66, 67, 69, 70] and [71]. Table 11 represents DP results for proposed S-boxes and compares the results of previous work.

Table 11 DP values of offered S-boxes
Full size table

6 Concluding remarks

S-boxes aim to provide the necessary confusion that Shannon is declared as the foundations of any cipher system. This study proposed a new methodology for designing S-box by introducing strong chaotic maps. In addition, it improved PSO with this map. Improved PSO results have been used to optimize chaotic S-boxes. This optimization was conducted with two fitness functions (nonlinearity and P-value of mono-test). This study considered the hierarchy of trigonometric maps with their composition. This family of chaotic maps has ergodic properties. Ergodicity is equivalent to the confusion property. The study incorporated in this study is enabled to open new ways in the construction S-boxes based on strong chaotic maps and improved PSO. The best chaotic S-box (Table 1) was obtained using Eq. 3 maps. Considering the results of Tables 4, 5, 6, 7, 8 for the S-boxes of Tables 2 and 3, it is better to use nonlinearity fitness function optimization. Testing the P-value was related to the randomness of the box, perhaps with considering reference [72], it needed to reexamine the chaotic property of the S-box. As future work, multi-objective particle swarm optimization (MOPSO) can be used instead of PSO for improved optimization, so that in addition to nonlinearity, all S-box analysis criteria can be optimized. Future studies can even use other optimizations, such as harmony search (HS) algorithm. Furthermore, the use of a series of Julia sets based on generalized Chebyshev polynomial of type two or quantum maps from well-known quantum systems such as the Dicke model leads to the production of S-boxes with various performances.

In future, we intend to examine the effect of this dynamic behavior on the generation of the S-box and will compare it with classical maps. Failure to meet the S-boxes ideal criteria indicates the need to create new S-boxes.