Optimal design of load frequency active disturbance rejection control via double-chains quantum genetic algorithm

Abstract

This paper tackles the design of active disturbance rejection controllers (ADRC) for load frequency control (LFC) of multi-area interconnected power systems. For the first time, the double-chains quantum genetic algorithm plays a role in tuning optimization of the parameters for ADRC. Not only is the proposed approach applied to the two-area reheat thermal power system, but it is also elongated to two-interconnected multi-source areas comprising thermal, hydro and gas units, two-area nonlinear non-reheat thermal power system with governor dead band in addition to three-area nonlinear reheat thermal power system with generation rate constraints. Comparison with other modern heuristic optimization strategies recently published proves the effectiveness and superiority of this method. The simulation results show that this robust approach can greatly shorten the stabilization time of the power system and meet the requirements of LFC with minimum transient deviation as well as steady-state performance indicators, which is worthy of application and promotion.

1 Introduction

Maintaining frequency stability is an essential indicator for measuring the operational performance of dynamic power systems [1]. Continuous load disturbances will lead to power imbalance and frequency deviation of the whole system. Consequently, LFC which can effectively suppress the adverse effects of load disturbances and uncertainties as well as maintain a balance between the power generation and the power demand is an indispensable mechanism for power system to eliminate deviations of frequency and power [2].

Since the LFC study of power systems was put forward in 1970 [3], various strategies have been applied to this important research proposition. Traditional proportional–integral (PI) [4] and proportional–integral-derivative (PID) [5] controllers owing to the advantages of clear principle, strong robustness and simple implementation are most frequently used in the field of LFC. They can restore the stability of the power system but are accompanied by poor performance, such as long stabilization time, many rebound overshoot phenomena and large transient frequency deviation [6].

In order to improve dynamic performance, LFC problems combined with advanced control algorithms have been extensively studied, such as neural network control [7], robust control [8], predictive control [9] and sliding mode control [10, 11], which have achieved dynamic response superior to traditional controllers and provide new solutions for LFC problems as well.

In recent years, as a new control method without depending on the precise model of the controlled object [12], ADRC has developed greatly in theory and applications relying on its small overshoot, high control accuracy, strong noise immunity, clear structure and easy digital implementation. However, it is difficult to manually tune numerous coupled parameters of the nonlinear ADRC controller, which brings restrictions to practical applications.

Intelligent algorithms have been widely studied after years of development, which have also been used for parameter tuning of LFC controllers taking in PI, PID and others owing to their achievement in handling optimization issues, such as genetic algorithms (GA) [13,14,15], particle swarm optimization (PSO) [16], artificial bee colony algorithm (ABC) [17], bacterial foraging optimization algorithm (BFOA) [18], differential evolution algorithm (DE) [19], antlion optimizer (ALO) [20], firefly algorithm (FA) [21, 22], mine blast algorithm (MBA) [23], differential evolution particle swarm optimization (DEPSO) [24], bacterial foraging optimization and particle swarm optimization (BFOA-PSO) [25], particle swarm optimization and pattern search algorithm (PSO–PS) [26] and so on. QGA [27] on the basis of GA and quantum calculation which has been wielded far and wide has better convergence speed, optimization ability and stability than most heuristic algorithms. DCQGA, as an improved QGA resting on real encoding and objective function gradient information, was proposed and executed to function extremes and neural network weight optimization to verify the effectiveness of the improved method in [28, 29]. The convergence of DCQGA was also proved in [30].

The prime contribution is to apply nonlinear ADRC controllers to interconnected LFC systems and to take advantage of DCQGA for the tuning of ADRC parameters for the first time in this paper. The strategy is applied to two areas containing only thermal turbines, two areas containing different units of thermal, hydro and gas turbines, as well as other two models that consider nonlinear constraints including GDB in the two-area power system and GRC in the three-area power system. By comparison of performance with other recently published methods and sensitivity analysis, the effectiveness of the proposed strategy has been confirmed, which also provides a more superior control strategy for the LFC system.

The rest contents are arranged as follows. Section 2 embraces dynamic models of related power systems. In Sect. 3, the design of the ADRC for LFC is proposed. The parameter optimization scheme of ADRC based on DCQGA is introduced in Sect. 4. For the simulation results of several common models and the sensitivity analysis of the controller, see Sect. 5. Finally, conclusions are made in the last section.

2 System description

2.1 Single-area power system

The linear model of the power system shown in Fig. 1 consists of governor, turbine, generator and load. The dynamic model of each part can be expressed as follows [7]. Especially, according to the usage scenario, there are three common forms to describe traditional turbines: non-reheat, reheat and hydro.

Fig. 1

Linear model of single-area power system

Governor with dynamics:

$$\begin{aligned} G_g(s)=\frac{1}{T_gs+1} \end{aligned}$$

(1)

where $T_g$ represents the time constant of the governor.

Non-reheat turbine with dynamics:

$$\begin{aligned} G_t(s)=\frac{1}{T_ts+1} \end{aligned}$$

(2)

where $T_t$ represents the time constant of the turbine.

Reheat turbine with dynamics:

$$\begin{aligned} G_t(s)=\frac{K_rT_rs+1}{(T_rs+1)(T_ts+1)} \end{aligned}$$

(3)

where $T_r$ represents the time constant of the reheat unit and $K_r$ is the reheat gain.

Hydro-turbine with dynamics:

$$\begin{aligned} G_t(s)=\frac{(T_Rs+1)(-T_ws+1)}{(T_2s+1)(0.5T_ws+1)} \end{aligned}$$

(4)

where $T_w$ denotes the time constant of the hydro-turbine, while $T_2$ and $T_R$ are the time constants of the compensator.

In addition, this paper also considers the gas turbine power plant [19], which is composed of value positioner, speed governor, fuel system and gas turbine. Its dynamic transfer function can be expressed as

$$\begin{aligned} G_{gas}(s)=\frac{1}{c_gs+b_g}\frac{X_cs+1}{Y_cs+1}\frac{-T_{CR}s+1}{T_Fs+1}\frac{1}{T_{CD}s+1} \end{aligned}$$

(5)

where $c_g$ and $b_g$ are the constants of valve positioner, $X_c$ and $Y_c$ are the leading and lagging time constant of the speed governor, respectively. $T_{CR}$ denotes the combustion reaction time delay of the gas turbine and $T_F$ is fuel time constant. $T_{CD}$ is the time constant of the compressor discharge volume.

Generator with dynamics:

$$\begin{aligned} G_p(s)=\frac{K_p}{T_ps+1} \end{aligned}$$

(6)

where $T_p$ and $K_p$ are the time constant and gain of the generator.

2.2 Multi-area power system

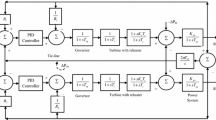
Figure 2 shows a dynamic model of area i in the multi-area power system which is composed of several single areas by tie-lines.

Fig. 2

Dynamic model of area i in multi-area power system

In Fig. 2, $T_{ij}$ stands for synchronization time constant between area i and area j, $R_i$ is the speed droop constant of area i, $B_i$ is the frequency response coefficient, $\varDelta P_{di}$ is the load disturbance of area i, $\varDelta f_{i}$ is the frequency deviation of area i, $\varDelta P_{tie,i}$ is tie-line power change connected with the frequency deviations through $\frac{2\pi }{s}$ and several synchronization coefficients, which can be expressed in the form of $\varDelta P_{tie,i}=\frac{2\pi }{s}\sum \nolimits _{j=1,j\ne i}^{n}T_ij(\varDelta F_i(s)-\varDelta F_j(s))$. What needs special explanation is $ACE_{i}$ which stands for control deviation of area i and is defined as $ACE_{i}=B_i\varDelta f_{i}+\varDelta P_{tie,i}$. Thus, the feedback control of area i can be expressed as $u_i=-K_i(s)ACE_{i}$, where $K_i(s)$ is the representation of the controller in area i. Thus, when the system is stable, there are $ACE_{i}=0, \varDelta f_{i}=0, \varDelta P_{tie,i}=0$.

3 Design of load frequency active disturbance rejection controller

3.1 Representation of ADRC

As a known control technique to estimate and compensate for uncertainties, ADRC consists of tracking differentiator (TD), extend state observer (ESO) and state error feedback (SEF) [12], of which structural schematic diagram is shown in Fig. 3.

Fig. 3

Structural schematic diagram of ADRC

In Fig. 3, the uncertain nth order plant affected by unknown external disturbances d(t) can be expressed as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ \vdots \\ {\dot{x}}_{n-1}=x_n\\ {\dot{x}}_{n}=f(x_1,x_2,\cdots ,x_{n-1},t)+d(t)+bu(t)\\ y=x_1 \end{array} \right. \end{aligned}$$

(7)

where x is the system vector, $f(x_1,x_2,\cdots ,x_{n-1},t)$ is the uncertain function, u(t) represents the control input and y is the system output.

TD which has the advantage of arranging the transition process and extracting the differential signals of each order of the reference input as well as suppress the noise amplification effect in the input signal can be described as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{v}}_1=v_2\\ {\dot{v}}_2=v_3\\ \vdots \\ {\dot{v}}_{n-1}=v_n\\ {\dot{v}}_{n}=r^n\varphi (v_1-v_0,\frac{v_2}{r},\cdots ,\frac{v_n}{r^{n-1}}) \end{array} \right. \end{aligned}$$

(8)

where $v_0$ is the reference input, $v_i(i=1,2,\cdots ,n)$ represents the trace output. When the parameter r is large enough, there are, $v_1\rightarrow v_0$, $v_i\rightarrow \frac{d^{(n-1)}v_0}{dt^{(n-1)}}\,(i=2,3,\cdots ,n)$.

ESO which can estimate uncertainties and disturbances can be expressed by the following equation:

$$\begin{aligned} \left\{ \begin{array}{l} e=z_1-y\\ {\dot{z}}_1=z_2-\beta _{01}e\\ {\dot{z}}_2=z_3-\beta _{02}fal(e,0.5,\delta )\\ \vdots \\ {\dot{z}}_n=z_{n+1}-\beta _{0n}fal(e,\frac{1}{2^{n-1}},\delta )+b_0u\\ {\dot{z}}_{n+1}=-\beta _{0n+1}fal(e,\frac{1}{2^{n}},\delta ) \end{array} \right. \end{aligned}$$

(9)

where $z_i\,(i=1,2,\cdots ,n)$ are the estimated values of the system state variables $x_i\,(i=1,2,\cdots ,n)$, $z_{n+1}$ is a new state variable that is expanded from the real-time action of the uncertainty function $f(x_1,x_2,\cdots ,x_{n-1},t)$ and external disturbances d(t), as long as the parameter b is known, the control variable can be taken as $u=(u_0-z_{n+1})/b_0$. So that the nonlinear object (7) becomes the form of linear integrator as:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ \vdots \\ {\dot{x}}_{n-1}=x_n\\ {\dot{x}}_{n}=bu_0(t)\\ y=x_1. \end{array} \right. \end{aligned}$$

(10)

This process is called dynamic compensation linearization. $\beta _{0i}(i=1,2,\cdots ,n,n+1)$ represent the gains. $fal(e,\alpha ,\delta )$ which reflects the control idea of using a small gain when there is a large error and using a large gain when there is a small error has the expression as

$$\begin{aligned} fal(e,\alpha ,\delta )= \left\{ \begin{array}{l} e/\delta ^{\alpha -1},\qquad \quad |e|\le \delta \\ |e|^{\alpha }sign(e), \quad |e|> \delta. \end{array} \right. \end{aligned}$$

(11)

SEF takes advantage of the nonlinear combination structure of feedback error information to replace the single linear weighted form in traditional control. To a certain extent, it improves the information processing ability of the system. The expression of SEF is

$$\begin{aligned} \left\{ \begin{array}{l} e_i=v_i-z_i, i=1,2,\cdots ,n\\ u_0=\sum _{i=1}^{n}\beta _ifal(e_i,\alpha _i,\delta _0)\\ u=(u_0-z_{n+1})/b_0 \end{array} \right. \end{aligned}$$

(12)

where $u_0$ represents virtual control input after dynamic compensation linearization, $\beta _i$ represents the gains of SEF, $\alpha _i(i=1,2,\cdots ,n)$,$\delta _0$ are adjustable parameters.

According to the constitution and schematic diagram, ADRC completes the real-time state estimation and compensation of the control plant based on its core expanded state observer and dynamic compensation linearization. It is a control mechanism with both feedback and feedforward.

3.2 Design of ADRC controller for LFC

According to the distributed LFC method for the multi-area power system proposed in [5], which means assuming $\varDelta P_{tie,i}=0$ first, and then designing a controller for each area separately. Taking the power system area composed of Eqs. (1), (2) and (6) as an example, the steps for designing an ADRC controller are as follows:

Step 1 Determine the order of ADRC. The open-loop transfer function of the system can be expressed as

$$\begin{aligned} G(s)=\frac{\varDelta f(s)}{u(s)}=\frac{K_p}{(T_gs+1)(T_ts+1)(T_ps+1)+K_p/R}. \end{aligned}$$

(13)

It is expressed in the form shown in Eq. (7) as

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{x}}_1=x_2\\ {\dot{x}}_2=x_3\\ {\dot{x}}_{3}=a_1x_1+a_2x_2+a_3x_3+bu(t)\\ y=x_1 \end{array} \right. \end{aligned}$$

(14)

where $a_1=-\frac{R+K_p}{RT_pT_tT_g}$, $a_2=-\frac{T_p+T_t+T_g}{T_pT_tT_g}$, $a_3=-\frac{T_pT_t+T_tT_g+T_gT_p}{T_pT_tT_g}$, $b=-\frac{K_p}{T_pT_tT_g}$. The relative order is 3, so the third-order ADRC can be used.

Step 2 Determine the form of TD. Since the control goal is to make ${ACE_i(t)=0}$ at steady state, $v_0 = 0$ is needed. However, the tracking differentiator will lose its effect at this time. Therefore, TD design is negligible.

Step 3 Determine the form of ESO. The order of ESO is 4 according to step 1. $ACE_i$ is the input of ESO and set $\delta = 0.0005$. Thus, the form of ESO is:

$$\begin{aligned} \left\{ \begin{array}{l} e=z_1-ACE_i\\ {\dot{z}}_1=z_2-\beta _{01}e\\ {\dot{z}}_2=z_3-\beta _{02}fal(e,0.5,0.0005)\\ {\dot{z}}_3=z_{4}-\beta _{03}fal(e,0.25,0.0005)+b_0u\\ {\dot{z}}_{4}=-\beta _{4}fal(e,0.125,0.0005) \end{array} \right. \end{aligned}$$

(15)

Step 4 Determine the form of SEF. $\delta _0 = 0.001$, $\alpha _1=0.3$, $\alpha _2=0.8$, $\alpha _3=1.2$ are set. Then, SEF is described as

$$\begin{aligned} \left\{ \begin{array}{l} e_i=v_i-z_i, i=1,2,3\\ u_0=\beta _1fal(e_1,0.3,0.001)+\beta _2fal(e_2,0.8,0.001)\\ \qquad +\beta _3fal(e_3,1.2,0.001)\\ u=(u_0-z_4)/b_0 \end{array} \right. \end{aligned}$$

(16)

After that, 8 parameters, which consist of $\beta _{01}$, $\beta _{02}$, $\beta _{03}$, $\beta _{04}$ in ESO, $\beta _{1}$, $\beta _{2}$, $\beta _{3}$, $b_{0}$ in SEF, wait to be tuned. It is extremely difficult to tune manually, so optimization with intelligent algorithms is required.

4 Design of DCQGA for optimizing the parameters of ADRC

4.1 Basics of QGA

QGA is an intelligent optimization algorithm that introduces quantum concepts such as quantum states, quantum gates and probability amplitudes to GA, resulting in stronger parallel processing capability and faster convergence speed than GA.

4.1.1 Qubit encoding

QGA utilizes qubit encoding that is different from traditional binary encoding. Each bit marked as $|\psi =\alpha |0\rangle +\beta |1 \rangle$ is not a fixed ‘0’ or ‘1’ state, but an arbitrary superposition state between the two. $\alpha$ and $\beta$ are complex constants, representing probability amplitudes at state ‘0’ and ‘1,’ respectively, which satisfy $\alpha ^2+\beta ^2=1$. Therefore, an individual in QGA can be coded as

$$\begin{aligned} q^t_j= \left( \begin{array}{c|c|c|c|c|c|c|c|c|c} \alpha ^t_{11} & \alpha ^t_{12} & \cdots & \alpha ^t_{1k_1}&\alpha ^t_{21} & \alpha ^t_{22} & \cdots & \alpha ^t_{2k_2}& \cdots & \alpha ^t_{mk_m}\\ \beta ^t_{11} & \beta ^t_{12} & \cdots & \beta ^t_{1k_1}&\beta ^t_{21} & \beta ^t_{22} & \cdots & \beta ^t_{2k_2}& \cdots & \beta ^t_{mk_m}\\ \end{array} \right) \end{aligned}$$

(17)

where $q^t_j$ represents the t-th generation and the j-th individual, k is the length of qubits for each parameter, and m represents the totality of optimized parameters.

4.1.2 Quantum revolving gate

QGA chooses the quantum revolving gate as the implementation mechanism for the renewal of quantum evolution. The renewal process is

$$\begin{aligned} \left[ \begin{array}{c} \alpha ^{t+1}_{i} \\ \beta ^{t+1}_{i} \end{array} \right] =U(\varDelta \theta _i)\left[ \begin{array}{c} \alpha ^{t}_{i} \\ \beta ^{t}_{i} \end{array} \right] =\left[ \begin{array}{ll} \mathrm{cos}(\varDelta \theta _i)& \quad -\mathrm{sin}(\varDelta \theta _i)\\ \mathrm{sin}(\varDelta \theta _i)& \quad \mathrm{cos}(\varDelta \theta _i) \end{array} \right] \left[ \begin{array}{c} \alpha ^{t}_{i} \\ \beta ^{t}_{i} \end{array} \right] \end{aligned}$$

(18)

where ($\alpha ^{t}_{i}$, $\beta ^{t}_{i}$) and ($\alpha ^{t+1}_{i}$, $\beta ^{t+1}_{i}$) represent the qubits before and after the renewal process, respectively. $U(\varDelta \theta _i)=\left[ \begin{array}{ll} \cos (\varDelta \theta _i)& \quad -\mathrm{sin}(\varDelta \theta _i)\\ \sin (\varDelta \theta _i)& \quad \mathrm{cos}(\varDelta \theta _i) \end{array} \right]$ stands for the tuning operation of a quantum revolving gate, $\varDelta \theta _i$ is the rotation angle. The adjustment principle of $\theta _i$ is to compare the fitness of the best individual $f(b_i)$ with the current one’s fitness $f(x_i)$, if $f(x_i)>f(b_i)$, then update ($\alpha ^{t}_{i}$, $\beta ^{t}_{i}$) in the direction that favors $x_i$; Otherwise, update in the direction in favor of $b_i$. The specific adjustment rules $\varDelta \theta _i=|\varDelta \theta _i|s(\alpha _i, \beta _i)$ are shown in Table 1.

Table 1 Adjustment rules of rotation angle $\varDelta \theta _i$

4.2 DCQGA

In view of the complexity of determining the rotation angle of the quantum gate in the QGA, and the premature phenomenon is prone to multi-parameter function optimization problems, DCQGA capitalizes on the gradient information of the objective function to generate rotation angles. At the same time, DCQGA treats both the real-coding probability amplitudes of qubits as genetic loci, thereby enhancing the traversal of the search space under the same population size condition, and also further speeding up the optimization process and enhancing the global optimal solution probability.

4.2.1 Real double-chain encoding

The quantum encoding scheme used by DCQGA is

$$\begin{aligned} q^t_j= \left( \begin{array}{c|c|c|c} \cos \theta _{j1} & \cos \theta _{j2} & \cdots & \cos \theta _{jm}\\ \sin \theta _{j1} & \sin \theta _{j2} & \cdots & \sin \theta _{jm}\\ \end{array} \right) \end{aligned}$$

(19)

where $\theta$ is the probability amplitude angle as well as a random number between $[0, 2\pi ]$, m is the totality of optimized parameters.

The probability amplitude ($\cos \theta$, $\sin \theta$) of each qubit can be regarded as a pair of parallel genes which is no longer a 0/1 value after collapsing like in QGA, but a real number in the range of [0, 1]. Each individual simultaneously represents 2 feasible solutions in the search space, i.e., two rows of matrix $q^t_j$. Since the two solutions are updated simultaneously in each optimization step, this encoding scheme can expand the search range and speed up the optimization process for the same population size as common QGA. The sine and cosine values are calculated from the corresponding $\theta$ randomly generated by each parameter. When generating the initial population, and then use Eq. (20) to map to the solution space.

$$\begin{aligned} \left\{ \begin{array}{l} p_{ic}^j=\frac{1}{2}[b_i(1+\cos \theta _{ji})+a_i(1-\cos \theta _{ji})]\\ p_{is}^j=\frac{1}{2}[b_i(1+\sin \theta _{ji})+a_i(1-\sin \theta _{ji})] \end{array} \right. \end{aligned}$$

(20)

where $p_{ic}^j$ and $p_{is}^j$ represent the cosine solution and sine solution of the i-th parameter of the j-th individual; $b_i$ and $a_i$ are upper and lower bounds.

4.2.2 Adjustment of the quantum revolving angle

The rotation is to shift each individual’s qubits phase to the qubit phase of the globally optimal individual. The direction and size of the rotation angle $\varDelta \theta _ {ij}$ are critical, which directly affects the convergence speed and search efficiency of the algorithm. Note

$$\begin{aligned} A=\left[ \begin{array}{ll} \cos \theta _0& \quad \cos \theta _i\\ \sin \theta _0& \quad \sin \theta _i \end{array} \right] \end{aligned}$$

(21)

where $\theta _0$ is the probability amplitude angle of the current population’s optimal solution for a qubit, and $\theta _i$ is the probability amplitude angle of the current solution’s corresponding qubit. In DCQGA, the method of changing the trend of the fitness function of the search point (single gene chain) is applied to the design of the rotation angle calculation function. If the change rate of the fitness function of a search point is greater than that of others, the rotation angle will be reduced appropriately. Otherwise, the rotation angle will increase appropriately. Such a method can make each chromosome step in the search process stable, thereby accelerating the convergence and slow progress of the search process to avoid the loss of the global optimal solution. Li et al.  [31] The angle direction is $-sgn (A)$ when $A \ne 0$; otherwise, it can be positive or negative. The angle step function is determined as

$$\begin{aligned} |\varDelta \theta _{ij}|=-sgn (A) \varDelta \theta _0\times \exp \left( -\frac{|\bigtriangledown fit(p^j)|-\bigtriangledown fit_{\min }^j}{\bigtriangledown fit_{\max }^j-\bigtriangledown fit_{\min }^j}\right) \end{aligned}$$

(22)

where $\varDelta \theta _0$ is the initial iteration value of $0.01\pi$ in this paper and $fit(p^j)$ is the fitness value of the solution $p^j$. And

$$\begin{aligned}&\bigtriangledown fit(p^j)=fit(p_{par}^j)-fit(p^j) \end{aligned}$$

(23)

$$\begin{aligned}&\bigtriangledown fit_{\max }^j=\max \left\{ \begin{array}{l} |fit(p_{par}^1)-fit(p^1)|,\cdots ,\\ |fit(p_{par}^j)-fit(p^j)|,\cdots ,\\ |fit(p_{par}^m)-fit(p^m)| \end{array} \right\} \end{aligned}$$

(24)

$$\begin{aligned}&\bigtriangledown fit_{\min }^j=\min \left\{ \begin{array}{l} |fit(p_{par}^1)-fit(p^1)|,\cdots ,\\ |fit(p_{par}^j)-fit(p^j)|,\cdots ,\\ |fit(p_{par}^m)-fit(p^m)| \end{array} \right\} \end{aligned}$$

(25)

where $p_{par}^j$ s is the previous generation solution of $p^j$.

4.2.3 Quantum mutation

DCQGA introduces quantum not-gate to chromosome mutation. Several quantum chromosomes are randomly selected according to the mutation probability $p_m$, and quantum not-gate is used to apply transformations to the qubits of the chromosome to interchange the two probability amplitudes of the qubit, that is, the current qubit amplitude angle $\theta _i$ becomes $\pi /2-\theta _i$, thereby both strands are mutated at the same time.

4.2.4 Description of DCQGA

The implementation process of DCQGA can be described as follows.

Step 1 Set $\varDelta \theta _0$ and $p_m$.

Step 2 randomly generate an initial population according to Eq. (19).

Step 3 Map the population to the solution space according to Eq. (20), and calculate the fitness value of each chain of each individual. Then, update the global optimal solution individual $X_0$ and the corresponding optimal chain $p_0$.

Step 4 For the qubits of each chain of the non-current global optimal solution in the population, use Equation (21) to obtain the rotation angle with each qubit of the optimal chain $p_0$ as the target, and use Equation (17) to update these chains.

Step 5 Use $p_m$ as the mutation probability to perform quantum mutation on all the chains in the population.

Step 6 Go back to Step 3, until the number of iterations or algorithm convergence is reached.

4.3 Parameters optimization of DCQGA-based ADRC for LFC

The schematic diagram of the design principle of the load frequency ADRC based on the DCQGA algorithm is shown in Fig. 4. The specific implementation process for the N-interconnected power system is as follows.

Fig. 4

Schematic diagram of the design principle for the load frequency active disturbance rejection controller based on the DCQGA algorithm

• (1) Determination of the objective function

Aiming at obtaining relatively superior controller parameters, the fitness function reflecting the performance of the controller is imperative to be reasonably determined first. Time-weighted integral of absolute error (ITAE) of which concrete expression is $ITAE=\int _{0}^{\infty } t|e(t)| dt$ is the most customarily used criterion and has a great effect on practical application. Therefore, the objective function used for LFC can be expressed as

$$\begin{aligned} Minimize\,J=ITAE=\int _{0}^{t_{\max }}\left( \sum _{i=1}^{N}|\varDelta f_i|+\sum _{i=1}^{N}\sum _{j=1}^{i-1}|\varDelta P_{tie,ij}|\right) t\mathrm{d}t. \end{aligned}$$

(26)

• (2) Limitation of parameter range

According to the meaning of parameters and multiple debugging results, the ranges of parameters of ADRC for LFC can be given by:$\beta _{01}\in [0,400]$, $\beta _{02}\in [0,8000]$, $\beta _{03}\in [0,80000]$, $\beta _{04}\in [0,800000]$ $\beta _{1}\in [0,1000]$, $\beta _{2}\in [0,1000]$, $\beta _{3}\in [0,2500]$, $b_{0}\in [1,5000]$.

• (3) Parameter optimization of DCQGA

DCQGA runs according to the flowchart shown in Fig. 5 to obtain optimized parameters, where the population size is 40, and the maximum iteration amount $t_{max}$ is 200. The fitness function takes $fitness=1/J$.

Fig. 5

Flowchart of DCQGA

5 Numerical analysis

5.1 Two-area reheat thermal power system

It is considered that the steam turbines are reheat turbines in Fig. 2, and the two areas of the interconnected system have the same model parameters [16] as shown in Appendix A.

5.1.1 Nominal parameters response analysis

Each area of the interconnected power system adopts an ADRC controller, of which parameters are optimized by DCQGA. Step load perturbation (SLP) $\varDelta P_{L1}= 0.01pu$ is applied only in area 1. The parameters after optimization are shown in Table 2.

Table 2 Optimized ADRC controller parameters for LFC of the two-area reheat thermal power system by DCQGA and QGA

Fig. 6

Dynamic response of the two-area reheat thermal power system for $\varDelta P_{L1} = 0.01$ pu

The transient performance of the proposed DCQGA tuned ADRC controller for an SLP of 0.01 pu in area l is shown in Table 3. Results are compared with QGA tuned ADRC controller, DCQGA tuned PID controller, MBA tuned fuzzy PID controller [23], DE–PSO tuned fuzzy PID controller [24], DE tuned fuzzy PID controller [24], PSO tuned fuzzy PID controller [24], PSO–PS tuned fuzzy PID controller [26], ABC tuned PI/PID controllers [17] and PSO tuned PI controller [16] for the same model to demonstrate the superiority of the method of this paper. As seen in Table 3, the best system performance is obtained with the proposed DCQGA tuned ADRC controller, where $O_{sh}$ and $U_{sh}$, respectively, indicate the maximum overshoot and the maximum undershoot, and $t_s$ indicates the settling time (for $5\%$ band for PI controller and $0.005\%$ for others).

Table 3 Transient performance of $\varDelta {f_1}$, $\varDelta {f_2}$ and $\varDelta {P_{tie}}$ under different controllers optimized by different algorithms for LFC of the two-area reheat thermal power system for $\varDelta P_{L1} = 0.01$ pu

Figure 6 shows the dynamic response of the frequency deviation $\varDelta {f_1}$, $\varDelta {f_2}$ and the tie-line power change $\varDelta {P_{tie}}$ with the proposed DCQGA tuned ADRC controller when $\varDelta P_{L1}= 0.01$ pu, $\varDelta P_{L2}= 0$. The responses under the action of other controllers are shown in Fig. 6 as well. What can be seen from the dynamic response and transient performance is that the proposed controller restores the system frequency and power to a stable preset value with the smallest overshoot in the shortest settling time (for example, 0.2878 s of $\varDelta {f_1}$, $49.2\%$ of the second smallest 0.5852 s of QGA-ADRC) and has a steady-state performance index with the smallest error (13.158, $24.0\%$ of the second smallest 50.697 of QGA-ADRC), showing better optimization efficiency of DCQGA than QGA and better disturbance suppression ability of proposed DCQGA tuned ADRC than other approaches, which proves the effectiveness and superiority of the proposed approach.

5.1.2 Sensitivity analysis

So as to investigate the sensitivity of the system to uncertain factors, simulation researches are carried out under conditions where the system parameters and workload conditions are under of change. Besides increasing $\varDelta P_{L2}\not =0$, the system parameters and workload conditions change within $\pm 50\%$ of the nominal value, while only one variable is changed at a time. Table 4 shows the transient performance indicators of the system under different conditions when parameters of proposed DCQGA tuned ADRC controllers remain consistent as shown in Table 2.

Table 4 Transient performance of the two-area reheat thermal power system controlled by DCQGA-ADRC for sensitivity analysis

Fig. 7

Dynamic response of the two-area reheat thermal power system when changing $T_g$ in the range of $\pm 50\%$

Fig. 8

Dynamic response of the two-area reheat thermal power system under change of load disturbance: at t = 0–5 s, $\varDelta P_{L1}=0.01$ pu, $\varDelta P_{L2}=0$; at t = 5–10 s, $\varDelta P_{L1}=0$, $\varDelta P_{L2}=0.01$ pu; t = 10–20 s, $\varDelta P_{L1}=0.01$ pu, $\varDelta P_{L2}=0.01$ pu

As an example, Fig. 7 shows the dynamic response of the system when changing $T_g$. Figure 8 illustrates the output response of the system to different load disturbances under the control of the proposed method, QGA-ADRC and MBA-Fuzzy-PID, where, at t = 5–10 s, $\varDelta P_{L1}=0$, $\varDelta P_{L2}=0.01$ pu; t = 10–20 s, $\varDelta P_{L1}=0.01$ pu, $\varDelta P_{L2}=0.01$ pu. It is clear that the frequency deviation and the tie-line power change are within the neighborhood of the system’s nominal parameter curve under the change of system parameters and operating conditions. According to this, it can be said that the limit value reached by the transient response of the power system is within an acceptable range, and the power system is robust to load disturbances and system parameter fluctuations under the proposed approach.

5.2 Extension to other power systems

This section investigates the control capabilities of the proposed DCQGA-ADRC-LFC in a multi-source interconnected power system, a two-area power system with GDB nonlinearity and a three-area power system with GRC nonlinearity.

Fig. 9

Model of the two-area six units thermal, hydro and gas power system

5.2.1 Two-area six units thermal, hydro and gas power system

Figure 9 demonstrates the schematic diagram of this system model. See Appendix B for model parameters [18]. Each area is comprised of thermal, hydro and gas units, where the hydro and gas units contain minor non-minimum phase links as shown in Eqs. (4) and (5). So as to eliminate the frequency deviation and tie-line power changes caused by load disturbances, each unit in this section utilizes an ADRC controller to complete the LFC. Table 5 shows the best ADRC parameters after applying SLP $\varDelta P_{L1}=0.01$ pu in area 1 after 50 runs of DCQGA optimization.

Table 5 Optimized ADRC controller parameters for LFC of the two-area six units thermal, hydro and gas power system by DCQGA

Fig. 10

Dynamic response of the two-area six units thermal, hydro and gas power system for $\varDelta P_{L1} = 0.01$ pu

The transient performance of the proposed DCQGA tuned ADRC controller in this case is shown in Table 6. For comparison, Table 6 also gives the performance index values of FA tuned fuzzy PID controller [21], DCQGA tuned PID controller and DE tuned PID controller [19]. The dynamic response curve of frequency deviation $\varDelta {f_1}$, $\varDelta {f_2}$ and tie-line power change $\varDelta {P_{tie}}$ in each area is shown in Fig. 10.

Table 6 Transient performance of $\varDelta {f_1}$, $\varDelta {f_2}$ and $\varDelta {P_{tie}}$ under different controllers optimized by different algorithms for LFC of the two-area six units thermal, hydro and gas power system for $\varDelta P_{L1} = 0.01$ pu

According to the data in Table 6 and Fig. 10, compared with several other algorithms, the LFC system with the participation of DCQGA tuned ADRC has the smallest error steady-state performance index and minimizes the settling time for the frequency and tie-line power to recover the set value with minimal transient deviation and less inversion and overshoot phenomenon, which means that the method proposed in this paper can better realize the LFC of multi-source interconnected power systems.

5.2.2 Two-area non-reheat thermal power system with GDB nonlinearity

So as to further evaluate the effect of the proposed method, inherent requirements and basic constraints of physical system dynamics are necessary to be taken into account [7]. GDB which makes the system oscillate violently, will be considered in this section. The transfer function of governor with GDB nonlinearity which is a nonlinear problem with hysteresis in general is given by

$$\begin{aligned} G_g(s)=\frac{0.8-(0.2/\pi ) s}{T_gs+1}. \end{aligned}$$

(27)

Relevant parameters [25] are shown in Appendix C.

Fig. 11

Dynamic response of the two-area non-reheat thermal power system with GDB nonlinearity for $\varDelta P_{L1} = 0.01$ pu

For the two-area power system with GDB nonlinearity, SLP $\varDelta P_{L1}=0.01pu$ was applied to area 1 at time t = 0, and the optimal parameters of the ADRC controller optimized by DCQGA in 50 running results are shown in Table 7. Table 8 shows the transient performance of the proposed method compared with other algorithms. The dynamic response process is shown in Fig. 11.

Table 7 Optimized ADRC controller parameters for LFC of the two-area non-reheat thermal power system with GDB nonlinearity by DCQGA

Table 8 Transient performance of $\varDelta {f_1}$, $\varDelta {f_2}$ and $\varDelta {P_{tie}}$ under different controllers optimized by different algorithms for LFC of the two-area non-reheat thermal power system with GDB nonlinearity for $\varDelta P_{L1} = 0.01$ pu

It can be seen that the proposed method still has a fairly good control effect on the LFC system with GDB nonlinearity, which is specifically embodied as follows: the system recovery stability time is only 6.2119 s, 61.31% of the second shortest stabilization time 10.1328 s of PSO–PS-FUZZY-PID controller, while the maximum transient deviation is $88.9820\times 10^{-4}$ Hz, which is one order of magnitude less than other algorithms and the steady-state error performance index is $1.271\times 10^{-2}$, which is much less than other algorithms. It can be concluded that the proposed method is also applicable to this nonlinear system, which further validates the effectiveness and superiority of the proposed method.

5.2.3 Three-area reheat thermal power system with GRC nonlinearity

GRC is an important nonlinear condition common in actual power systems, which is difficult to linearize. The model diagram is shown in Fig. 12. Reference [32] pointed out that GRC has a huge impact on the system dynamic response, which will make the overshoot of the system too large and the settling time too long. Moreover, due to the uncertainty of the system parameters, the entire system will become unstable when disturbances occur . In order to further evaluate the control ability of the proposed method on multi-area power systems, the three-area power system considering GRC nonlinear constraints will be studied in this section, each area considers $3\%$ of GRC constraints, and other model parameters [23] are given in Appendix D.

Fig. 12

Model of the GRC nonlinearity

Table 9 Optimized ADRC controller parameters for LFC of the three-area reheat thermal power system with GRC nonlinearity by DCQGA

Assuming a perturbation of SLP $\varDelta P_{L1}=0.01$ pu is applied in area 1, the obtained optimal parameters of ADRC tuned by DCQGA are given in Table 9. The dynamic response curves of the load frequency deviations and tie-line power changes in the closed-loop three-area power system considering GRC are shown in Fig. 13. The system response curves under the MBA-FUZZY-PID controller mentioned in [23] are plotted in Fig. 13 as well. The performance index comparison of the power system under the control of the proposed method and other algorithms is quantified in Table 10.

Fig. 13

Dynamic response of the three-area reheat thermal power system with GRC nonlinearity for $\varDelta P_{L1} = 0.01$ pu

Table 10 Transient performance of frequency deviations and tie-line power changes under different controllers optimized by different algorithms for LFC of the three-area reheat thermal power system with GRC nonlinearity for $\varDelta P_{L1} = 0.01$ pu

According to the simulation data shown in Fig. 13 and Table 10, it could be derived that using the DCQGA to optimize the parameters of the ADRC controllers can make the system obtain better dynamic characteristics. The frequency deviation and tie-line power change of the system quickly stabilize to zero with small overshoot. The settling time of the power system is shortened to 5.3342 s (the best of others is 9.789 s). It shows this method is effective and superior to achieve the purpose of load frequency control. It also further proves that the DCQGA to optimize the parameters of the ADRC controllers still has a good control effect on the nonlinear multi-area power system.

6 Conclusion

A load frequency active disturbance rejection control method based on DCQGA parameter optimization is proposed in this paper. Firstly, the method is applied to a two-area reheat thermal power system and compared with the results of other recently published algorithms. Then, the sensitivity of the proposed method is analyzed based on the system. After that, the simulation of the multi-source two-area power system under the proposed approach is carried out. Finally, the designed algorithm is applied to two-area with GDB and three-area with GRC power systems to detect the ability of this method to deal with nonlinear constraints so that it can be applied to actual systems. The results show that the proposed approach with the advantages of smaller error, shorter stabilization time and good robustness is effective and superior to cope with LFC problems.

Appendices

Appendix A: Parameters of the two-area reheat thermal power system [16]

$B_1=B_2=0.425$ pu; $R_1=R_2=2.4$ Hz/pu; $T_{g1}=T_{g2}=0.08$ s; $T_{t1}=T_{t2}=0.3$ s; $T_{r1}=T_{r2}=10$ s; $K_{r1}=K_{r2}=0.5$; $T_{p1}=T_{p2}=20$ s; $K_{p1}=K_{p2}=120$ Hz/pu; $T_{12}=0.086$ s.

Appendix B: Parameters of the two-area six units thermal, hydro and gas power system [18]

$B_1=B_2=0.4312$ pu; $R_1=R_2=R_3=2.4$ Hz/pu; $T_{p}=11.49$ s; $K_{p}=68.9566$ Hz/pu; $T_{12}=0.086$ s; $T_{g1}=T_{g2}=0.08$ s; $T_{t}=0.3$ s; $T_{r}=10$ s; $K_{r}=0.3$; $T_w=1$ s; $T_R=5$ s; $T_2=28.75$ s; $b_g=0.05$; $c_g=1$; $X_c=0.6$ s; $Y_c=1$ s; $T_{CR}=0.01$ s; $T_F=0.23$ s; $T_{CD}=0.2$ s; $K_T=0.543478$; $K_H=0.326084$; $K_G=0.130438$.

Appendix C: Parameters of the two-area non-reheat thermal power system with GDB nonlinearity [25]

$B_1=B_2=0.425$ pu; $R_1=R_2=2.4$ Hz/pu; $T_{g1}=T_{g2}=0.2$ s; $T_{t1}=T_{t2}=0.3$ s; $T_{p1}=T_{p2}=20$ s; $K_{p1}=K_{p2}=120$ Hz/pu; $T_{12}=0.0707$ s.

Appendix D: Parameters of the three-area reheat thermal power system with GRC nonlinearity [23]

$B_1=B_2=B_3=0.425$ pu; $R_1=R_2=R_3=2.4$ Hz/pu; $T_{g1}=T_{g2}=T_{g3}=0.08$ s; $T_{t1}=T_{t2}=T_{t3}=0.3$ s; $T_{r1}=T_{r2}=T_{r3}=10$ s; $K_{r1}=K_{r2}=K_{r3}=0.5$; $T_{p1}=T_{p2}=T_{p3}=20$ s; $K_{p1}=K_{p2}=K_{p3}=120$ Hz/pu; $T_{12}=T_{13}=T_{23}=0.086$ s.