1 Introduction

Astrophysicist Lane [1] and Emden [2] first time introduced nonlinear singular Lane–Emden model working on thermal performance of a spherical cloud of gas and classical law of thermodynamics [3]. The singular models designate a variety of phenomena in physical science [4], density profile of gaseous star [5], catalytic diffusion reactions [6], isothermal gas spheres [7], catalytic diffusion reactions [6], stellar structure [8], electromagnetic theory [9], mathematical physics [10], classical and quantum mechanics [11], oscillating magnetic fields [12], isotropic continuous media [13], dusty fluid models [14] and morphogenesis [15]. To find the solution, these singular models are always very challengeable and hard to handle due to the singularity at the origin. The generic form on of such model represented with third-order nonlinear Emden–Fowler equation is written as [16]:

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{2p}{t}} \right)y^{{\prime \prime }} (t) + \frac{p(p - 1)}{{t^{2} }}y^{{\prime }} (t) + f(t)g(y) = 0, \\ & y(0) = y_{0} ,\,\,y^{{\prime }} (0) = 0,\,\,\,y^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(1)

There are only few numerical and analytic existing techniques to tackle such nonlinear singular models (1). To mention few reported techniques to solve the singular models represented with differential equations include Shawagfeh [17] used the Adomian decomposition method (ADM), Wazwaz [18] also applied ADM to avoid the difficulty of singularity, Liao [19] applied an analytic algorithm to avoid the singularity, He and Ji [20] developed a numerical scheme based on Taylor series, Nouh [21] applied power series solution by using Pade approximation technique as well as Euler-Abel transformation and Mandelzweig and along with Tabakin [22] developed Bellman and Kalabas quasi-linearization method. All these techniques have their own performance, accuracy and efficiency, as well as inadequacies over one another. Beside these deterministic procedures, numerical solvers based on heuristic computing paradigm look promising to be incorporated in the domain of nonlinear singular systems.

The considerable potential of heuristic computing paradigm based on stochastic numerical solvers is exploited for solving linear/nonlinear systems by manipulating the universal approximation competency of artificial neural networks (ANNs) optimized with local/global search methodologies [23,24,25]. Few recent applications of paramount significance include Thomas–Fermi atom’s model [26], prey-predator models [27], plasma physics problems [28], models of fractional ordinary differential equations [29], model of heartbeat dynamics [30], linear fractional cable equation [31], machines [32], control systems [33], cell biology [34], power [35] and energy [36]. The intention of the present study is to present the detail study of the singular Emden–Fowler model along with numerical results for better system understanding using the stochastic technique.

The aim of the present study is to find the solution of Eq. (1) by integrated intelligent computing paradigm based on the artificial neural networks (ANNs) optimized with genetic algorithms (GAs) refined by the active-set algorithm (ASA), i.e., ANN–GA–ASA. The major features of the proposed solver ANN–GA–ASA are briefly given below:

  • A novel application of integrated intelligent computing paradigm ANN–GA–ASA is presented for finding the solution of nonlinear multi-singular models governed with third-order nonlinear Emden–Fowler equation.

  • Consistently matching outcomes of the proposed ANN–GA–ASA with reference solutions for different variant of nonlinear Emden–Fowler system established the worth of the solver in terms of accuracy and convergence.

  • Validation of the performance is ascertained through statistical observations on multiple execution of ANN–GA–ASA in terms of mean absolute deviation (MAD), Theil’s inequality coefficient (TIC) and Nash–Sutcliffe efficiency (NSE) performance indices.

  • Beside provision of accurate solution of nonlinear Emden–Flower differential system, smooth implementation, ease in understanding, stability, applicability and robustness are other valuable promises.

Rest of the paper is organized as follows: proposed framework of stochastic solver ANN–GA–ASA is presented in Sect. 2, performance measures are listed at Sect. 3, result with discussions is presented in Sect. 4, while conclusions with future related works are listed Sect. 5.

2 Proposed methodology

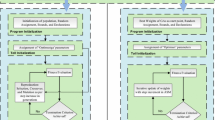
The proposed framework as shown in Fig. 1 for presenting the solution of model (1) is divided in two portions. Firstly, by introducing the procedure for formulation of an error-based fitness function and secondly, the combination of GA-ASA is presented to optimize the fitness function for system (1).

Fig. 1
figure 1

Framework of proposed methodology to solve nonlinear Emden–Fowler model

Full size image

2.1 ANN modeling

The variety of ANN models are introduced by research community for the solutions of nonlinear systems arising in application of broad fields [37,38,39]. The feed-forward ANN models-based procedure for approximating solutions and their respective mth order derivatives are mathematically presented as:

$$\hat{y}(t) = \sum\limits_{j = 1}^{n} {\alpha_{j} h(\delta_{j} t + \beta_{j} )} ,$$
(2)
$$\hat{y}^{(m)} (t) = \sum\limits_{j = 1}^{n} {\alpha_{j} h^{(m)} (\delta_{j} t + \beta_{j} )} ,$$
(3)

where \(\alpha_{j}\), \(\delta_{j}\) and \(\beta_{j}\) are the respective jth components of \(\varvec{\alpha ,}\,\,\varvec{\delta}\) and \(\varvec{\beta}\) vectors, while m shows the derivative order. The log-sigmoid expression \(h\left( t \right) \, = \left( {1 + \exp ( - t)} \right)^{ - 1}\) and its derivative are used as an activation/transfer functions in the networks. The updated form of the above network is written as follows:

$$\hat{y}(t) = \sum\limits_{j = 1}^{n} {\alpha_{j} \left( {1 + e^{{ - (\delta_{j} t + \beta_{j} )}} } \right)^{ - 1} } ,$$
(4)
$$\hat{y}^{(m)} (t) = \sum\limits_{j = 1}^{n} {\alpha_{j} \frac{{d^{m} }}{{dt^{m} }}\left( {\left( {1 + e^{{ - (\delta_{j} t + \beta_{j} )}} } \right)^{ - 1} } \right)} .$$
(5)

In case of Emden–Fowler Eq. (1), the expression for high order derivative in ANN formulations is given as:

$$\tilde{y}^{{{\prime \prime \prime }}} (t) = \sum\limits_{j = 1}^{n} {\alpha_{j} \delta_{j}^{3} \left( {\frac{{6e^{{ - 3(\delta_{j} t + \beta_{j} )}} }}{{\left( {1 + e^{{ - (\delta_{j} t + \beta_{j} )}} } \right)^{4} }} - \frac{{6e^{{ - 2(\delta_{i} t + \beta_{i} )}} }}{{\left( {1 + e^{{ - (\delta_{j} t + \beta_{j} )}} } \right)^{3} }} + \frac{{e^{{ - (\delta_{i} t + \beta_{i} )}} }}{{\left( {1 + e^{{ - (\delta_{j} t + \beta_{j} )}} } \right)^{2} }}} \right)} \,$$
(6)

The networks (4) to (6) are arbitrarily combined to form the ANN architecture for nonlinear Emden–Fowler equation as shown in Fig. 2. The combination of Eqs. (4) to (6) is exploited for the fitness function formulation of Eq. (1) in mean squared error sense as:

$$\varepsilon = \varepsilon_{1} + \varepsilon_{2} ,$$
(7)
$$\varepsilon_{1} = \frac{1}{N}\sum\limits_{k = 1}^{N} {\left( {\hat{y}_{k}^{{{\prime \prime \prime }}} + 2pt_{k}^{ - 1} \hat{y}_{k}^{{\prime \prime }} + p(p - 1)t_{k}^{ - 2} \hat{y}_{k}^{{\prime }} + f_{k} g(\hat{y}_{k} )} \right)}^{2} ,$$
(8)
$$\varepsilon_{2} = \frac{1}{2}((\hat{y}_{0} - A)^{2} + (\hat{y}_{0}^{{\prime }} )^{2} + (\hat{y}_{0}^{{\prime \prime }} )^{2} ),$$
(9)

where \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are the fitness/error functions associated with main body of Eq. (1) and its initial conditions, respectively, while \(N = 1/h,\,\,\,\hat{y}_{k} = \hat{y}\left( {t_{k} } \right),\)\(\,t_{k} = kh,\,\,\,f_{k} = f\left( {t_{k} } \right).\) An appropriate optimization procedure is adopted for learning of weight vector \(W = [\varvec{\alpha},\;\varvec{\delta},\;\varvec{\beta}]\), such that error-based fitness function (7) approaches to optimal zero value.

Fig. 2
figure 2

ANN architecture for nonlinear third-order singular Emden–Fowler model

Full size image

2.2 Optimization procedure

The weights of ANNs are trained by manipulating the strength of integrated meta-heuristic computing procedure based on GAs supported with ASA, i.e., GA-ASA. The graphical abstract of present designed methodology for solving Eq. (1) is presented in Fig. 1.

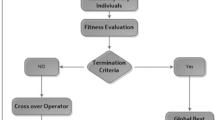
Global search efficacy of GAs, introduced by Holland in early 1970’s [40, 41], is exploited for finding the weight vector W of ANN. Population formulation with candidate solution or individual in GAs is performed using the bounded real numbers. While, each candidate solution or individual has elements equal to unknown weights in ANN models. GAs operate with its fundamental operators based on selection, crossover, mutation and elitism procedures and has been used in many applications recently, for instance, solving nonlinear electric circuit models [42], emergency humanitarian logistics scheduling [43], dynamics of nonlinear Troesch’s problem [44], traveling salesman problem [45], parameter estimation [46], fecal coliform predictive model [47], nonlinear nanofluidic model [48], optimization of wireless sensor network in smart grids [49], nonlinear micropolar fluid flow systems [50], recommendation systems [51] and prediction of thermal conductivity [52].

The optimized parameters of GA converge faster by the hybridization procedure with the appropriate local search method by taking global best of GAs as initial weights. Therefore, efficient local search method based on active-set algorithm (ASA) is used of rapid fine tuning of parameters. Recently, ASA-based optimization is used in many applications, e.g., water distribution systems [53], solution of optimal control problems [54], distributed model predictive control [55], transportation of discrete network design bi-level problem [56] and solution of ball/sphere constrained optimization problems [57]. In the present study, the hybrid scheme based on GA-ASA is used in order to tune the decision variables for solving the third-order singular model (1). The detailed pseudocode of GA-ASA is tabulated in Table 1

Table 1 Workflow of optimization scheme GA-ASA in pseudocode
Full size table

Stability of proposed stochastic solver ANN–GA–ASA based on neural networks with arbitrary weights, that dependent on number of neurons in the hidden layers, is mainly carried out with the help of two procedures, i.e., theoretical analysis and stochastic analysis. In theoretical analysis, appropriate global and local conditions are derived generally with the help of problem specific Lyapunov functions [58,59,60], while in stochastic analysis, Monte Carlo simulation is conducted with different set of the parameters of the neural networks and results of statistical observations are used to evaluate the stability [61,62,63].

3 Performance measures

The performance measures of MAD, NSE and TIC are incorporated for the analysis in this study.

The mathematical expression of MAD, TIC and NSE by means of the exact/true solution \(y\) and approximate/calculated solution \(\hat{y}\) are provided below:

$${\text{MAD = }}\frac{1}{n}\sum\limits_{m = 1}^{n} {\left| {y_{m} - \hat{y}_{m} } \right|} ,$$
(10)
$$\begin{aligned} {\text{TIC = }}\frac{{\sqrt {\frac{1}{n}\sum\nolimits_{m = 1}^{n} {\left( {y_{m} - \hat{y}_{m} } \right)}^{2} } }}{{\left( {\sqrt {\frac{1}{n}\sum\nolimits_{m = 1}^{n} {y_{m}^{2} } } + \sqrt {\frac{1}{n}\sum\nolimits_{m = 1}^{n} {\hat{y}_{m}^{2} } } } \right)}} \hfill \\ \hfill \\ \end{aligned}$$
(11)
$${\text{NSE = }}\left\{ {1 - \frac{{\sum\nolimits_{m = 1}^{n} {\left( {y_{m} - \hat{y}_{m} } \right)}^{2} }}{{\sum\nolimits_{m = 1}^{n} {\left( {y_{m} - \bar{y}_{m} } \right)}^{2} }}} \right.,\quad \bar{y}_{m} = \frac{1}{n}\sum\nolimits_{m = 1}^{n} {y_{m} }$$
(12)
$${\text{E}}_{NSE} = 1 - {\text{NSE}}$$
(13)

4 Results and discussion

The detailed results of proposed ANN–GA–ASA along with necessary interpretation are presented for five cases of nonlinear singular Emden–Fowler system (1) in this section. The stability of the proposed stochastic solver ANN–GA–ASA based on neural networks is evaluated on stochastic analysis which is performed on 100 independent runs of ANN–GA–ASA to solve nonlinear multi-singular third-order Emden–Fowler equations. Additionally, the accuracy, convergence, stability and robustness of the proposed stochastic solver ANN–GA–ASA are examined with the help of statistical observations on different performance metrics, MAD, TIC, ENSE and their global variants GMAD, GTIC and GENSE based on 100 number of independent runs of the solver. The five cases of the nonlinear singular Emden–Fowler system (1) are narrated as follows.

Case I

Consider the nonlinear Emden–Fowler equation by putting \(p = 1\) and \(f(t)g(y) = - \frac{9}{8}(t^{6} + 8)y^{ - 5}\) in Eq. (1), then we have:

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{2}{t}} \right)y^{{\prime \prime }} (t) - \frac{9}{8}(8 + t^{6} )y^{ - 5} = 0 \\ & y(0) = 1,\,\,\,y^{{\prime }} (0) = 0,\,\,\,y^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(14)

The exact/true form of the solution of (14) is \(\sqrt {1 + t^{3} }\), and the fitness/error function for (14) is given below:

$$\varepsilon = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {8t_{m} \hat{y}^{\prime\prime\prime}(t_{m} ) + 16\hat{y}^{\prime\prime}(t_{m} ) - 9t_{m} (t_{m}^{6} + 8)\hat{y}^{ - 5} } \right)^{2} } + \frac{1}{3}\left( {\left( {\hat{y}_{0} - 1} \right)^{2} + \left( {\hat{y}^{\prime}_{0} } \right)^{2} + \left( {\hat{y}^{\prime\prime}_{0} } \right)} \right)$$
(15)

Case II

Consider the third-order Emden–Fowler model by using \(p = 2\) and \(f(t)g(y) = - 9(3t^{6} + 10t^{3} + 4)y\) in Eq. (1), then we have

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{4}{t}} \right)y^{{\prime \prime }} (t) + \left( {\frac{2}{{t^{2} }}} \right)y^{{\prime }} (t) - 9(4 + 10t^{3} + 3t^{6} )y = 0 \\ & y(0) = 1,\,\,\,y^{{\prime }} (0) = 0,\,\,\,^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(16)

The exact/true solution of Eq. (16) is \(e^{{t^{3} }}\), and the fitness/error function of above equation is given below:

$$\begin{aligned} \varepsilon & = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {t_{m}^{2} \hat{y}^{{{\prime \prime \prime }}} (t_{m} ) + 4t_{m} \hat{y}^{{\prime \prime }} (t_{m} ) + 2\hat{y}^{{\prime }} (t_{m} ) - 9t_{m}^{2} (4 + 10t_{m}^{3} + 3t_{m}^{6} )\hat{y}} \right)^{2} } \\ & \quad + \frac{1}{3}\left( {\left( {\hat{y}_{0} - 1} \right)^{2} + \left( {\hat{y}_{0}^{{\prime }} } \right)^{2} + \left( {\hat{y}_{0}^{{\prime \prime }} } \right)} \right) \\ \end{aligned}$$
(17)

Case III

Using \(p = 3\) and \(f(t)g(y) = - 6(10 + 2t^{3} + 6t^{6} )e^{ - 3y}\) in Eq. (1). The nonlinear Emden–Fowler equation takes the form as:

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{6}{t}} \right)y^{{\prime \prime }} (t) + \left( {\frac{6}{{t^{2} }}} \right)y^{{\prime }} (t) - 6(10 + 2t^{3} + 6t^{6} )e^{ - 3y} = 0 \\ & y(0) = 0,\,\,\,y^{{\prime }} (0) = y^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(18)

The exact/true solution of Eq. (18) is \(\log (1 + t^{3} )\), and the fitness formulation of above case is written as:

$$\begin{aligned} \varepsilon & = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {t_{m}^{2} \hat{y}^{{{\prime \prime \prime }}} (t_{m} ) + 6t_{m} \hat{y}^{{\prime \prime }} (t_{m} ) + 6\hat{y}^{{\prime }} (t_{m} ) - 6t_{m}^{2} (10 + 2t_{m}^{3} + 6t_{m}^{6} )e^{{ - 3\hat{y}}} } \right)^{2} } \\ & \quad + \frac{1}{3}\left( {\left( {\hat{y}_{0} } \right)^{2} + \left( {\hat{y}_{0}^{{\prime }} } \right)^{2} + \left( {\hat{y}_{0}^{{\prime \prime }} } \right)} \right) \\ \end{aligned}$$
(19)

Case IV

Take \(p = 4\), \(g(y) = y^{m}\) and \(f(t) = 1\) in Eq. (1) using \(m = 0\). The Lane–Emden Eq. (1) becomes in this case as:

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{8}{t}} \right)y^{{\prime \prime }} (t) + \left( {\frac{12}{{t^{2} }}} \right)y^{{\prime }} (t) + y^{m} = 0, \\ & y(0) = 1,\,\,\,y^{{\prime }} (0) = 0,\,\,\,\,y^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(20)

The true solution of the model (20) is \(1 - \frac{1}{90}t^{3}\), and error function becomes as:

$$\varepsilon = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {t_{m}^{2} \hat{y}^{{{\prime \prime \prime }}} (t_{m} ) + 8t_{m} \hat{y}^{{\prime \prime }} (t_{m} ) + 12\hat{y}^{{\prime }} (t_{m} ) + t_{m}^{2} \hat{y}^{m} } \right)^{2} } + \,\frac{1}{3}\left( {\left( {\hat{y}_{0} - 1} \right)^{2} + \left( {\hat{y}^{{\prime }} } \right)^{2} + \left( {\hat{y}_{0}^{{\prime \prime }} } \right)^{2} } \right)$$
(21)

Case V

By taking \(p = 4\) and \(g(y) = - (10 + 10t^{3} + t^{6} )y\) in Eq. (1), the Emden–Fowler equation takes the form as

$$\begin{aligned} & y^{{{\prime \prime \prime }}} (t) + \left( {\frac{4}{t}} \right)y^{{\prime \prime }} (t) - (t^{6} + 10t^{3} + 10)y = 0, \\ & y(0) = 1,\,\,\,y^{{\prime }} (0) = 0,\,\,\,y^{{\prime \prime }} (0) = 0. \\ \end{aligned}$$
(22)

The true solution of Eq. (23) is \(e^{{{{t^{3} } \mathord{\left/ {\vphantom {{t^{3} } 3}} \right. \kern-0pt} 3}}}\), and error function becomes as:

$$\varepsilon = \frac{1}{N}\sum\limits_{m = 1}^{N} {\left( {t_{m} \hat{y}^{\prime \prime \prime } (t_{m} ) + 4\hat{y}^{\prime \prime } (t_{m} ) - t_{m} (10 + 10t_{m}^{3} + t_{m}^{6} } \right)^{2} } \hat{y} + \frac{1}{3}\left( {\left( {\hat{y}_{0} - 1} \right)^{2} + \left( {\hat{y}_{0}^{\prime } } \right)^{2} + \left( {\hat{y}_{0}^{\prime \prime } } \right)^{2} } \right)$$
(23)

Optimization is performed for all five cases of Emden–Fowler equation for the trained inputs between 0 and 1 with step 0.1 by the hybrid procedure GA-ASA for 100 independent trails. Optimized weights of ANNs for each case of the system are presented in Fig. 3, and these weights presented in Fig. 3a–e can be used in Eq. 4 to find the approximate results of proposed ANN–GA–ASA in the trained interval [0, 1] for solving cases 1, 2, 3, 4 and 5 of the nonlinear singular Emden–Fowler system (1), respectively. The solutions of proposed ANN–GA–ASA are determined using weight in Fig. 3 in (4) for both trained input grid, i.e., [0. 0.1, 0.2, …, 1] and testing input grid [0.05, 0.15, …, 0.95], and results are illustrated in Fig. 4a–d, f along with the reference exact solutions for cases 1, 2, 3, 4 and 5 of Emden–Fowler system (1), respectively.

Fig. 3
figure 3

Set of weights by proposed ANN–GA–ASA for nonlinear third-order Emden–Fowler equation for all cases

Full size image
Fig. 4
figure 4

Comparison of results for training and testing of proposed ANN–GA–ASA with exact solution for nonlinear third-order Emden–Fowler equation for all five cases

Full size image

The results of ANN–GA–ASA are consistently overlapping with exact solution for both training and testing points for each case of the system. In order to show the level of precision achieved, the values of absolute error (AE) from reference exact solutions are determined for both training and testing input grids and results are presented in Fig. 5 on semi-logarithmic scale. The absolute error plots are shown in Fig. 5a–d, e of proposed ANN–GA–ASA for nonlinear third-order Emden–Fowler equation for all respective five cases. The value of AE lies in the range 10−09–10−06, 10−06–10−04, 10−05–10−07, 10−09–10−07 and 10−06–10−09 for both train and test points of cases 1, 2, 3, 4 and 5, respectively. No noticeable difference exists between training and testing results established the worth of the ANN–GA–ASA for solving Emden–Fowler equation.

Fig. 5
figure 5

Comparison of results for training and testing of proposed ANN–GA–ASA for nonlinear third-order Emden–Fowler equation for all five cases

Full size image

Hundred trials of ANN–GA–ASA are conducted for finding the solution of Emden–Fowler Eq. (1) for all five cases. The best solutions with minimum value of error-based fitness, mean solutions and reference exact results are plotted in Fig. 6 for all five cases of model (1). It is clear from all five Fig. 6a–e that the best and mean solutions are overlapped with the true solutions for all cases. The comparison of the performance is conducted on the basis of best, worst and mean values of the absolute error from all 100 independent executions of proposed ANN–GA–ASA, and results are presented in Fig. 7 which have five subfigures and Table 2 for all five variations of Emden–Fowler system (1).

Fig. 6
figure 6

The best and mean values of approximate solutions of proposed ANN–GA–ASA and their comparison with exact results for all five cases

Full size image
Fig. 7
figure 7

The best, mean and worst values of absolute error for the proposed ANN–GA–ASA for all five cases

Full size image
Table 2 Statistics results for all cases of singular model
Full size table

Additionally, the values of performances metrics MAD, TIC and ENSE are calculated for best, worst and mean values of the absolute error from all 100 independent executions of proposed ANN–GA–ASA and results are presented in Fig. 8 for all five variations of nonlinear third-order Emden–Fowler model.

Fig. 8
figure 8

The MAD, TIC and ENSE values of the performance indices for the proposed ANN–GA–ASA for all five cases

Full size image

One may observe from results presented in Fig. 7 and Table 3 that the values of AE lie around 10−06–10−07, 10−04–10−05, 10−06–10−08, 10−06–10−09and 10−07–10−09 for the best solutions for cases 1–5, respectively, while respective average values are 10−02–10−03, 10−01–10−02, 10−02–10−03, 10−02–10−04 and 10−04 to 10−05. The statistical analysis presented in the terms of minimum (Min), mean (Mean) and standard deviation (SD) in Table 2 shows that Min values lie in the ranges of [10−07, 10−08] for case 1, [10−05, 10−06] for case 2, [10−06, 10−08] for case 3, [10−08, 10−10] for case 4 and [10−07, 10−09] for case 5, whereas the mean values mostly lie in the ranges of [10−02, 10−03] but in some cases range [10−05, 10−06] as well. Moreover, the SD values in small ranges for all the cases. These results further endorsed the consistent reasonable precision of all three performance metrics MAD, TIC and ENSE for proposed ANN–GA–ASA.

Table 3 Global performance results for all five cases
Full size table

Analysis on the performance of ANN–GA–ASA is further examined on the basis of histograms studies. The values of the fitness, MAD, TIC and ENSE are illustrated graphically in Figs. 9, 10, 11 and 12, respectively. The presented results show that respective MAD, TIC and ENSE values for cases 1–5 lie around 10−06–10−08, 10−04–10−06, 10−04–10−06, 10−06–10−08 and 10−05–10−07, 10−10–10−12, 10−08–10−10, 10−08–10−09, 10−11–10−12 and 10−12–10−14, 10−09–10−10, 10−09–10−10, 10−11–10−12 and 10−13–10−15. The mean values of MAD lie around 10−02–10−04, 10−02–10−04, 10−02–10−03, 10−02–10−04 and 10−01–10−03. The histogram plotted for all four performances measure show the consistence of the convergence and the precision of ANN-GA-AS on the basis of fitness, TIC, MAD and ENSE.

Fig. 9
figure 9

The comparison on fitness through histogram studies for the proposed ANN–GA–ASA for all five cases

Full size image
Fig. 10
figure 10

The comparison on MAD values through histogram studies for the proposed ANN–GA–ASA for all five cases

Full size image
Fig. 11
figure 11

The comparison on TIC values through histogram studies for the proposed ANN–GA–ASA for all five cases

Full size image
Fig. 12
figure 12

The comparison on ENSE values through histogram studies for the proposed ANN–GA–ASA for all five cases

Full size image

The results of global performance operators, i.e., GFIT, GMAD, GTIC and GENSE being the average values of fitness, MAD, TIC and ENSE, for 100 executions of ANN–GA–ASA are tabulated in Table 3 for all five cases of third-order nonlinear Emden–Fowler model. The magnitude (Mag) and SD of these global operators show reasonable precision for all four global statistical operators [GFIT, GMAD, GTIC and GENSE] for each scenario of the problem.

5 Conclusion

The motivation behind this study is to solve third-order nonlinear singular differential model by exploiting the strength of integrated intelligent computing paradigm based on artificial neural network models optimized with genetic algorithm hybrid with active-set technique. Some of the key findings are summarized below

  • Artificial neural network is successfully applied to solve the third-order nonlinear singular differential model.

  • The accuracy and convergence of the present method are analyzed through the outcomes of statistical measures based on 100 independent runs to solve five cases of third-order nonlinear singular differential model.

  • The best AE values lie up to 10−05–10−09. However, the worst solution of AE also lies up to 10−01–10−05.

  • The global FIT, MAD, TIC and ENSE are presented with good agreements with their optimal gauges.

The presented scheme ANN–GA–ASA looks promising to be exploited for solving the higher order nonlinear singular systems represented with differential equations involving both integer and fractional order derivatives.