1 Introduction

With the introduction of the smart grid concept, integration of renewables into power systems is getting more attention day by day. Several different topologies of MLIs and their implementations in renewable technologies can be found in [1]. As it is known, the outputs of the photovoltaics (PVs) are dependent on the weather parameters, and they have a fluctuating nature especially in cloudy days. These fluctuations may be mitigated by using inverters; hence, new standards are employed. For efficient operation of power distribution systems, IEEE 1547 [2] standard has been developed. In the USA, California state started using Rule 21 [3], which makes it mandatory for PV panel owners to have inverters. Importance of MLIs was signified before. For instance in [4], it was stated that switching losses can be reduced due to lower switching frequency. Hence, they can be used together with renewables with less voltage fluctuation problems.

If switching angles of MLIs are selected properly, total harmonic distortion (THD) can be minimized. Development of methods for the elimination of higher-order terms of harmonics in MLIs goes back to 70s [5]. For canceling higher-order terms of harmonics, [6] used the resultant theory. Optimum switching angles were determined; however, it was not easy to solve high-order polynomials when the number of MLI levels increased. In a recent study [7], the authors determine optimum switching angles by using Groebner bases and symmetric polynomials theory. However, the computations have to use symbolic computation toolboxes and cannot be easily implemented on microcontrollers. To overcome this problem, another two-level algorithm was developed in [8]. Other than analytical-based methods, numerical methods such as Newton–Raphson method and sequential quadratic programming were also used to find optimal switching angles of the MLIs [9, 10]. MATLAB’s fsolve function-based numerical method was used in [11]. Apart from derivative-based numerical methods, non-derivative-based methods were also used. Population-based ones such as genetic algorithms [4, 12], bee algorithm [13], harmony search method [14, 15], particle swarm optimization (PSO) [16,17,18] and non-population-based ones such as generalized pattern search algorithm [19] were used in optimization problems in MLIs. A more detailed review on solution algorithms used for MLIs can be found in [20]. More specifically, review on implementation of meta-heuristic methods on converter problem is detailed in [21] and in [22]. There are also more recent studies available in the literature. One of them uses the modified version of grey wolf optimization (GWO) algorithm to minimize harmonics in hybrid MLIs [23]. Selective harmonics elimination problem is solved by using whale optimization algorithm (WOA) in [24]. The authors of [25] use a modified version of WOA in solving hybrid cascaded MLI. The impact of DC sources on selective harmonic elimination is optimally determined in MLIs by using teaching–learning-based optimization method [26]. Moreover, [27] aims to design a MLI topology with minimum switch counts.

It is known that numerical optimization methods based on derivative information may reach the optimal solutions faster compared to heuristic optimization methods. However, the derivatives of the analytical functions are not always possible to obtain. Thus, numerical optimization problems may face convergence problems. Hence, population-based optimization methods have become popular. These type of methods generally mimick processes from nature [28]. The interactions of the members of the swarms help to solve optimization problems [29, 30]. Initial step of these algorithms includes creating random solution candidates. Next step calculates the objective function values of these solution candidates. Hence, better solutions are obtained by applying some evolutionary techniques such as crossover, mutation and so on [28]. One of the population-based non-derivative methods is PSO. Having observed the behaviors of flocks of the species, the method simulates the food searching process [31]. PSO has been very popular due to success in solving problems and application simplicity. In recent years, there are more attempts to develop new heuristic optimization algorithms. One of them is moth-flame optimization (MFO) method [32] and has been applied in the multilevel inverter optimization problem [33]. Based on the white hole, black hole, wormhole properties of multi-verse physics, multi-verse optimization (MVO) algorithm [34] was developed. MVO is applied to some real problems such as load frequency control [35] and optimization of electricity generation systems [36]. Moreover, combined with neural networks it is successfully applied in intrusion detection systems for computer networks [37]. Another recent application concentrates on solving feature selection problems [38]. Another recent algorithm uses behaviors of salp swarms: salp swarm algorithm (SSA) [39]. Even recently developed, SSA can solve several real-life problems from several different areas. For example, in image processing area, an improved version of SSA is proposed to solve image segmentation problem [40]. Histopathology images were used to detect prostate cancers utilizing a fuzzy-integrated SSA in [41]. Soil water retention curve parameters were determined and compared to those of differential evolution (DE) and PSO, and it was found that SSA provided the smallest sum of squared errors [42]. An application related to mining and geotechnical engineering focuses on hyper-parameter optimization of SVM models for fiber-reinforced cement paste backfilll (CPB) datasets [43] recently. A wrapper-based kernel extreme learning machine is utilized with SSA to classify the digital mammograms in an efficient and optimized way in [44]. In [45], the authors have optimized the artificial neural network (ANN) algorithm that estimates the compressive strength of concretes that contain a supplementary cementitious material named as ground granulated blast furnace slag using a multiobjective SSA. Another application is to cloud computing area by proposing a combination of SSA and sine–cosine algorithm-based multiobjective optimization algorithm to optimally place virtual machines [46]. In electrical power systems area, SSA is used to optimally determine the parameters of photovoltaic cells [47]. A modified version is developed and is applied to improve the maximum power point tracking and ride-through ability of variable speed generators in [48]. Another application area is smart grids: The authors of [49] determined the size and capacity of distributed generators on distribution systems using SSA. Optimal load frequency control problem of renewable power systems is also solved by SSA [50]. Furthermore, with the help of SSA, hydrogen consumption of super-capacitors is recently minimized under fluctuated load conditions [51]. As given in [52], SSA has many advantages and few disadvantages compared to other methods such as genetic algorithms [53], differential evolution method [54], cuckoo search algorithm [55] and so on. From these, one may find the followings more significant. The SSA needs to tune less parameters. It has powerful neighborhood search capability, and the implementation of the algorithm is easy.

As the literature review states, the performances of the MVO and SSA in dealing with engineering problems are remarkable. Hence, this paper extends a previous study [33] both in terms of the used model and the applied methodology. It uses SSA and MVO aiming to eliminate harmonics and to minimize total harmonic distortion (THD) in multilevel converters. Several numerical simulation results of seven-level, 11-level and 15-level MLIs using MVO and SSA are calculated and compared to each other. For comparison, simulations are also performed using PSO which is a well-known population-based optimization method. The results of the numerical calculations are verified by using MATLAB/Simulink models. In brief, the contributions of this study can be summarized as follows:

  • An optimization model that aims to eliminate the harmonics and to minimize THDs is solved.

  • SSA and MVO are implemented to solve the optimization model. The numerical results of performed simulations of the 7-, 11-, and 15-level MLIs are compared both in terms of numerical accuracy and quality. Moreover, the numerical results obtained using MVO and SSA are compared to the solutions obtained by using PSO.

  • MATLAB/Simulink model for seven-level MLI is built. THD values are calculated using FFT tool to compare to the ones obtained by using the heuristic optimization methods.

The organization of the paper is briefly given as follows: Sect. 2 gives information on cascaded H-bridge MLIs. Then, the working principles of MVO, SSA and PSO are explained. Numerical results of the calculations are provided by using different modulation indexes, and the results are illustrated. Then, simulations are performed by using developed MATLAB/Simulink models. The final section concludes the paper.

2 Cascaded H-bridge multilevel inverters

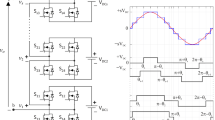
Figure 1 shows simple illustration of a cascaded H-bridge MLI with seven levels. Note that DC sources have equal magnitudes and are connected to a single-phase full-bridge or H-bridge inverter. Here, each inverter level produces \(+V_{\mathrm{dc}}\), 0, or \(-V_{\mathrm{dc}}\) depending on the connections of the DC sources to AC outputs. It should be noted that the combinations of the switches \(S_i\) are important in outputs [56].

Fig. 1
figure 1

Single-phase, seven-level cascaded H-bridge MLI

Full size image

For the seven-level inverter, stepped output voltage graph of seven-level inverter and its corresponding conducting angles are shown in Fig. 2.

Fig. 2
figure 2

Voltage output of seven-level cascaded H-bridge MLI

Full size image

The number of output voltage levels is a function of separate DC sources and may be given as \(2\times \mathbf{k }+1\) where k is the number of separate DC sources. Fourier transform of stepped waveform with s steps is shown below [56]:

$$\begin{aligned} V(\omega t)= & {} {{4V_{\mathrm{dc}}}\over {\pi }}\sum _{n}\left[ \cos (n\theta _1) + \cos (n\theta _2)+\cdots + \cos (n\theta _s)\right] \sin \left( {{n\omega t}\over {n}}\right) , \\&\quad n=1,3,5,7, \ldots \end{aligned}$$
(1)

In Eq. (1), \(\omega\) and \(V_{\mathrm{dc}}\) represent the angular velocity and the voltage magnitude of the DC source, respectively. Note that \(\theta _i\) shows the conducting angle of step i. After normalization according to \(V_{\mathrm{dc}}\) is applied, the magnitudes of the coefficients of Eq. (1) can be determined by using the following expression [56]:

$$\begin{aligned} H(n)={{4}\over {n\pi }}\sum _{n}\left[ \cos (n\theta _1) + \cos (n\theta _2)+\cdots +\cos (n\theta _s)\right] \quad n=1,3,5,7, \ldots \end{aligned}$$
(2)

where the switching angles \(\theta _1, \theta _2, \ldots , \theta _n\) must satisfy the constraints given below:

$$\begin{aligned} \theta _1 \le \theta _2 \le \cdots \le \theta _n \le {\pi \over 2} \end{aligned}$$
(3)

Total harmonic distortion (THD) is the ratio of the summation of voltage magnitudes with odd indexes to the main voltage component and can be mathematically shown as:

$$\begin{aligned} {\text {THD}}={{\sqrt{(\sum _{n=3,5,7\ldots }^{n=49}V_{n}^{2})}}\over {V_{1}^2}} \end{aligned}$$
(4)

Conventionally, the optimization models aim to minimize lower-order odd harmonics. This approach is briefly summarized as follows. The number of harmonics that is possible to be eliminated is less than the number of H-bridges (HBs). For example if a MLI with three HBs is considered, then two lower-order harmonics can be eliminated by solving the equations given in [33]:

$$\begin{aligned} F(n)&= \cos (\theta _1) + \cos (\theta _2)+ \cos (\theta _3)-3m_1 \\ F(5n)&= \cos (5\theta _1) + \cos (5\theta _2)+ \cos (5\theta _3) \\ F(7n)&= \cos (7\theta _1)+ \cos (7\theta _2)+ \cos (7\theta _3) \end{aligned}$$
(5)

In (5), \(m_1\) is the modulation index defined as \(V_{L}^{*}\over {V_{\mathrm{Lmax}}}\). Note that \(V_{L}^*\) represents the amplitude command of the inverter for a sine wave output phase voltage and \(V_{\mathrm{Lmax}}\) represents the maximum attainable amplitude of the inverter [56]. F(k) functions should be equal to 0 to cancel the odd harmonics.

However, since IEEE 519 standard forces to minimize the first fifty harmonics [57, 58], this paper uses the following models to optimize seven, 11 and 15 MLIs:

$$\begin{aligned} \begin{aligned}&{\text {minimize}} \sqrt{\sum _{n=3,5,7 \ldots }^{n=49}{{V_{n}^2}}\over {{V_1}}}+ | \cos (\alpha _1)+\cos (\alpha _2)+\cdots +\cos (\alpha _k)-km| \\&{\text {subject to}} \qquad \theta _1\le \theta _2 \le \cdots \theta _k \le 90^{\circ } \end{aligned} \end{aligned}$$
(6)

Note that k is 3, 5 and 7 for seven-, 11- and 15-level MLIs in Eq. 6, respectively.

3 Heuristic methods

This section explains the used heuristic methods for THD minimization problem. The first subsection briefly explains MVO algorithm and details the application of THD minimization problem step by step. Then, similarly, SSA and PSO methods are briefly given in the next subsections. Application of the methods to THD minimization problem is detailed by giving the algorithms and flowcharts.

3.1 Multi-verse optimization

Heuristic methods mimick behaviors from natural processes. Similar to those, MVO uses multi-verse theory in physics. Thus, the optimization process includes mathematical models of white hole, black hole and wormhole [34]. The algorithm assumes that there may exist multiple universes which may have interactions with each other through white holes, black holes and wormholes. In the algorithm, each variable set forms a universe, and each variable in the universe is an object. Then, their corresponding inflation rates, in other words their fitness function values, are calculated. If the inflation rates are high, then the chance of having white holes is high, but the possibility of having black holes is low. This means that the objects with higher inflation rates can send objects by using white holes, and the ones with lower rates can receive objects by using black holes. Then, the roulette wheel chooses white holes in each step by using the following equation:

$$\begin{aligned} x_{i}^{j}={\left\{ \begin{array}{ll} x_{k}^{i} \qquad r_1< {\text {NI}}(U_i)\\ x_{i}^{j} \qquad r_1\ge {\text {NI}}(U_i) \end{array}\right. } \end{aligned}$$
(7)

where \(x_{i}^{j}\), \(x_{k}^{j}\) and \({\text {NI}}(U_i)\) represent the jth object in the universe i, the jth object in the universe k selected by roulette wheel mechanism and the normalized inflation rate of universe i, respectively. Random movements are also needed. This is provided by using wormholes independently from the inflation rates.

The algorithm uses wormhole existence probability (WEP) and travelling distance rate (TDR) to change solutions in the iterations. These parameters are given as follows [34]:

$$\begin{aligned} \text {WEP} &= a+t\times {(b-a)\over {T}} \end{aligned}$$
(8)
$$\begin{aligned} \text {TDR} &= 1-{t^{1\over p}\over {T^{1\over p}}} \end{aligned}$$
(9)

where a and b represent a predefined minimum and a maximum number such as 0.1 and 1, respectively. T shows the maximum number of iterations, and t represents the current iteration. p is a constant called as exploitation factor. Note that the accuracy and the speed of the local search of the algorithm increase as the chosen p value increases.

The equation that defines the movements between the universes is given as follows:

$$\begin{aligned} {x_{i}}^{j}&=\left\{ \begin{array}{ll} \left\{ \begin{array}{ll} x_j + {\text {TDR}} + (({\text {ub}}_j - {\text {lb}}_j) * r_4 + {\text {lb}}_j)) &{} {\text { if }}\quad r_3<0.5 \\ x_j - {\text {TDR}} + (({\text {ub}}_j - {\text {lb}}_j)* r_4 + {\text {lb}}_j)) &{} \text { if }\quad r_3\ge 0.5 \end{array}\right. &{} {\text { if }} r_2< {\text {WEP}} \\ x_{\mathrm{RouletteWheel}}^j &{} {\text { if }} r_2 \ge {\text {WEP}} \end{array}\right. \end{aligned}$$
(10)

where \({\text {ub}}_j\), \({\text {lb}}_j\) and \(r_i\) represent the upper and lower bounds for the variables and random number between 0 and 1, respectively.

A sample solution candidate set (universes) may look as given below:

$$\begin{aligned} u_1&= a_1, a_2, a_3, a_4, \ldots , a_{d-2}, a_{d-1}, a_{d} \\ u_2&= b_1, b_2, b_3, b_4, \ldots , b_{d-2}, b_{d-1}, b_{d} \\ u_3&= c_1, c_2, c_3, c_4, \ldots , c_{d-2}, c_{d-1}, c_{d} \\ \vdots \\ u_{n-1}&= x_1, x_2, x_3, x_4, \ldots , x_{d-2}, x_{d-1}, x_{d} \\ u_{n}&= y_1, y_2, y_3, y_4, \ldots , y_{d-2}, y_{d-1}, y_{d} \end{aligned}$$
(11)

Here, \(u_i\) represents the ith universe, \(a_i, \ldots , y_i\) represents the objects in the universes, and d shows the number of objects. In this representation, it is assumed that the objective functions are evaluated and sorted accordingly. Then, after moving objects through white/black holes and wormholes, the new representation may look as follows:

$$\begin{aligned} u_1&= a_1, a_2, a_3, a_4, \ldots , a_{d-2}, a_{d-1}, a_{d} \\ u_2&= b_1, a_2, z_3, a_4, \ldots , a_{d-2}, b_{d-1}, b_{d} \\ u_3&= a_1, c_2, b_3, c_4, \ldots , z_{d-2}, c_{d-1}, a_{d} \\ \vdots \\ u_{n-1}&= a_1, g_2, x_3, k_4, \ldots , b_{d-2}, x_{d-1}, b_{d} \\ u_{n}&= b_1, f_2, x_3, y_4, \ldots , e_{d-2}, y_{d-1}, a_{d} \end{aligned}$$
(12)

Note that \(z_i\) represents the object values obtained by transfer operation using wormholes.

3.1.1 Implementation of MVO to MLI optimization problem

To apply MVO method in cascaded H-bridge MLI optimization problem, the process is given as follows:

  1. 1.

    The solution process is started by creating random universes in the allowed ranges: \(0 \le \theta _i \le {\pi \over 2}\). Note that each universe is composed of d variables. For seven-level, 11-level and 15-level MLI, d is 3, 5 and 7, respectively. Hence, initial step is creating an N by 3 (for seven-level MLI), N by 5 (for 11-level MLI) and N by 7 (for 15-level MLI) random solution candidates. Note that N is the size of the number of the universes.

  2. 2.

    Then, the universes are sorted according to the numerical results of the evaluations of the fitness function given in Eq. (6). Note that each solution candidate should comply with \(\theta _1 \le \theta _2 \le \cdots \theta _n\).

  3. 3.

    WEP and TDR are calculated using Eqs. (8) and (9), respectively.

  4. 4.

    The universes exchange transfer objects according to the roulette wheel selection process given as follows. For each object in each universe, a random number \(r_1\) is created. If this number is less than normalized inflation rate of the corresponding universe, then an object from kth universe is selected based on the roulette wheel mechanism described in [59]. Otherwise, the object’s location does not change.

  5. 5.

    The best solution in the solution candidate set is found, and its position is set as \(p_i^t\).

  6. 6.

    The positions of the solution candidates are updated.

  7. 7.

    To stop, the algorithm either checks the differences of best solutions of predefined number of iterations or checks the maximum number of iterations. If a stopping decision is not given, the algorithm goes to the second step.

3.1.2 Flowchart of MVO implementation on MLI optimization problem

The flowchart of implementation of MVO to MLI optimization problem is given in Fig. 3.

Fig. 3
figure 3

MVO flowchart

Full size image

3.2 Salp swarm optimization

SSA mimicks the swarming behavior of salps in the optimization process [39]. To obtain better movement abilities and hence reaching food sources easier, the salps form salp chains. Similar to other heuristic methods, good solutions have more importance in obtaining solutions. Therefore, the best salp, called the leading salp in the chain, is followed by the others. The leading salp aims to move to the food source or in other words to the optimal solution. Hence, all members of the salp population are expected to move to the optimal solution in the end of the process.

The position changes of the leading salps and the followers are performed based on Eqs. (13) and (15) which are given below [39]:

$$\begin{aligned} {x_j}^1 = {\left\{ \begin{array}{ll} F_j+c_1({\text {ub}}_j-{\text {lb}}_j)c_2 + {\text {lb}}_j) &{} c_3 \ge 0 \\ F_j-c_1({\text {ub}}_j-{\text {lb}}_j)c_2 + {\text {lb}}_j) &{} c_3 \ge 0 \end{array}\right. } \end{aligned}$$
(13)

where \(x_j^1\) represents the leader salp, \(F_j\) is the position of the food source, ub and lb represent the upper and lower values, respectively, and \(c_1\), \(c_2\) and \(c_3\) are random numbers.

Parameter \(c_1\) is defined as follows [39]:

$$\begin{aligned} c_1=2e^{-({{4l}\over {L}})^2} \end{aligned}$$
(14)

where l and L represent the current iteration number and the maximum iteration number. The follower salps use Newton’s law of motion for updating their positions [39]:

$$\begin{aligned} x_j^i={1\over 2}{V_{\mathrm{par}}}t^2+v_0 t \end{aligned}$$
(15)

Here, \(v_0\) is the initial speed and \(V_{\mathrm{par}}\) is calculated by dividing the final speed to initial speed.

3.2.1 Implementation of SSA to MLI optimization problem

Steps of SSA method to solve MLI optimization problem are given as follows:

  1. 1.

    This step initializes the salps. Each entry in each salp corresponds to the switching angles. They are initialized randomly in the allowed variable ranges. In other words, the number of salps is \(N_s\) and each salp consists of s elements ranging from 0 to \({\pi \over 2}\) satisfying the following condition: \(0 \le \theta _i \le {\pi \over 2}\). The number of the variables of each salp will be different for seven-, 11- and 15-level MLIs. The number of variables for the seven-, 11- and 15-level inverter cases is 3, 5 and 7, respectively.

  2. 2.

    Each salp’s entries are given as inputs to Eq. (6), and the fitness value of each salp is calculated.

  3. 3.

    The best solution of the solution candidates is called the leader. It is found by sorting the salps according to the results of the objective function evaluations. The other solutions, namely the followers, are expected to follow the leader. The position of the leader is updated using Eqs. (13) and (14).

  4. 4.

    The positions of the followers are updated by using Eq. (15).

  5. 5.

    This step decides whether the algorithm stops or continues. It either checks the differences of best solutions of predefined number of iterations or checks the maximum number of iterations. If the algorithm does not stop, it goes to step 2.

3.2.2 Flowchart of SSA implementation on MLI optimization problem

The flowchart of implementation of SSA to MLI optimization problem is given in Fig. 4.

Fig. 4
figure 4

SSA flowchart

Full size image

3.3 Particle swarm optimization

PSO is developed based on the swarm behavior of the bird flocks while searching for food. The algorithm uses the information of the local and global best values to update the positions of the particles. Thus, the particles are expected to move to the locations that are close to optimal points. In each iteration, the update process of the positions is performed according to the equations given below:

$${\text{Spd}}: = w \times {\text{Spd}} + l_{1} \times {\text{random}}\;{\text{number}} \times ({\text{local}}\;{\text{best}} - {\text{loc}})\quad + l_{2} \times {\text{random}}\;{\text{number}} \times ({\text{global}}\;{\text{best}} - {\text{loc}})$$
(16)

In Eq. (16), \(l_1\) and \(l_2\) are the learning factors, and Spd and loc represent the velocity and the position of the particle, respectively. As stated above, the local and global best values are used to update the velocity. They are represented as the “\({\mathrm {local\,best}}\)” and “\({\mathrm {global\,best}}\),” respectively.

After determination of the velocities, the locations are updated simply by using the following equation:

$$\begin{aligned} {\text {loc}}:= {\text {loc}} + {\text {Spd}} \end{aligned}$$
(17)

3.3.1 Implementation of PSO to MLI optimization problem

Steps of PSO method to solve MLI optimization problem are summarized as follows:

  1. 1.

    Initialization step comprises of choosing the control parameters and initialization of the particles. The control parameters are the number of particles and the learning factors \(l_1\) and \(l_2\). Each particle is composed of 3, 5 or 7 entries depending on the level of MLI being investigated. Thus, the elements of each particle should satisfy the following condition: \(0 \le \theta _i \le {\pi \over 2}\).

  2. 2.

    Each particle’s fitness values is computed using Eq. (6). Then, the local and global best values are found.

  3. 3.

    The velocities of the particles are updated using the learning parameters and the local and the global best values using Eq. (16). Then, locations are updated using Eq. (17).

  4. 4.

    The updated particles and their corresponding switching angles are evaluated in Eq. (6). The results are compared to the results obtained in the previous iteration. The better particles are stored.

  5. 5.

    The local and global best values are updated.

  6. 6.

    This step decides whether the algorithm stops or continues. The stopping criterion either checks reaching the number of maximum iterations, or it checks the numerical differences of the best values obtained so far to the ones obtained, i iterations ago. If the decision is stop, the algorithm gives the switching angles as outputs; otherwise, it goes back to the third step.

3.3.2 Flowchart of PSO implementation on MLI optimization problem

The flowchart of PSO to solve MLI optimization problem is given in Fig. 5.

Fig. 5
figure 5

PSO flowchart

Full size image

4 Tests and results

The tests are performed for seven-level, 11-level and 15-level MLIs. Numerical calculations are done on a laptop with the following specifications: 2.40 GHz, Quad Core CPU and 8.00-GB RAM. As specified above, SSA, MVO and PSO were used for simulation purposes. SSA-, MVO- and PSO-based MATLAB-based source codes provided in [60, 61] are modified and used in solving optimization problem of MLIs.

Simulations are performed 100 times for each modulation index in each case. The control parameters of MVO-, SSA- and PSO-based optimization algorithms are selected experimentally as follows. For MVO, the number of universes is selected as 30. The initial value of WEP is set as 0.2, and this value is linearly increased up to 1. Hence, the chance of obtaining a wormhole increases as iterations increase. Maximum number of iterations is set as 1000. TDR ranges from 0.6838 to 0; thus, the accuracy of local search improves over iterations. For SSA, the number of salps and the number of iterations are chosen as 30 and 1000, respectively. SSA uses control parameter \(c_1\) which is used to balance the exploration and exploitation. This parameter decreases according to Eq. (14), as the iterations evolve. The number of particles for PSO is selected as 30. Both learning factors, \(l_1\) and \(l_2\), are chosen as 2. Inertia factor w is not changed through the iterations and selected as 0.8. Finally, maximum iterations for PSO are set as 1000.

Due to limited space, modulation indexes ranging from 0.4 to 1 with 0.1 increments, their respective switching angles and THDs are given in the following tables. Note that all the quantities given in the tables are the mean of the results of 100 simulations. In Table 1, near optimal switching angles found by MVO, SSA and PSO and their respective THDs are shown for seven-level MLI. It is observed that mean of switching angles and their respective THDs calculated using three methods are found to be very close for this system. Minimum THDs are obtained as \(10.43\%\) for modulation index value of 0.84 for all three methods. Near optimal angles are \(8.613^{\circ }\), \(27.837^{\circ }\), \(49.684^{\circ }\) for SSA \(8.597^{\circ }\), \(27.801^{\circ }\), \(49.709^{\circ }\) for MVO and \(8.613^{\circ }\), \(27.841^{\circ }\), \(49.682^{\circ }\) for PSO for this modulation index.

Table 1 Mean values of switching angles, modulation indexes and THDs for seven-level cascaded H-bridge MLI
Full size table

Similarly, Table 2 shows the mean values of the optimal switching angles and their respective THDs for 11-level cascaded H-bridge MLI. Similar to the previous test case, the simulation results are close to each other with slight differences. Using SSA, minimum THD is calculated as \(6.14\%\) for 0.82 modulation index. The switching angles are \(5.422^\circ\), \(16.541^\circ\), \(28.512^\circ\), \(41.394^\circ\) and \(58.869^{\circ }\). MVO finds the minimum THD similarly for modulation index value of 0.82 with a small difference: \(6.15\%\). Near optimal switching angles for this case are \(5.485^{\circ }\), \(16.485^{\circ }\), \(28.591^{\circ }\), \(41.445^{\circ }\) and \(58.797^{\circ }\). PSO finds the minimum THD for the same modulation index. A THD value of \(6.14\%\) is found with corresponding mean switching angles: \(5.432^{\circ }\), \(16.535^{\circ }\), \(28.512^{\circ }\), \(41.403^{\circ }\) and \(58.865^{\circ }\).

Table 2 Switching angles, modulation indexes and THD values for 11-level cascaded H-bridge MLI
Full size table

Simulation results of 15-level cascaded H-bridge MLI are shown in Table 3. This time, the differences of the numerical simulation results are not as close as the previous cases. It is seen in the table that THDs found by MVO and PSO are closer to each other; however, smaller compared to those of SSA. For instance, the maximum difference of THDs of three methods is even approximately \(10\%\) for modulation index of 1. SSA may not be able to escape local optimum trap for this case for previously set maximum iteration value of 1000. Both MVO and PSO methods find the lowest THD as \(4.311\%\) for modulation index value of 0.8. Switching angles for this case are found as \(3.930^\circ\), \(11.534^\circ\), \(19.980^\circ\), \(30.302^\circ\), \(38.874^\circ\), \(51.091^\circ\) and \(65.616^\circ\) by using MVO and \(3.879^\circ\), \(11.670^\circ\), \(19.489^\circ\), \(30.419^\circ\), \(38.746^\circ\), \(51.193^\circ\) and \(65.715^\circ\) by using PSO. Minimum THD using SSA is found at the same modulation index level. However, a higher value compared to those of MVO and PSO: \(4.420\%\). Switching angles are \(4.969^\circ\), \(12.667^\circ\), \(20.794^\circ\), 29.779º, \(38.868^\circ\), \(50.964^\circ\) and \(65.290^\circ\).

Table 3 Switching angles, modulation indexes and THD values for 15-level cascaded H-bridge MLI
Full size table

Figure 6 illustrates the obtained near optimal switching angles using SSA for seven-level, 11-level and 15-level MLIs. From Fig. 6, one may observe the mean values of THDs for three different test systems. In the figure, shaded areas show the standard deviations of the obtained simulation results. It is seen from the figure that for seven- and 11-level MLIs, the standard deviations is low; however for 15-level MLI, modulation indexes higher than 0.8 produce high standard deviations for SSA. When THDs of three tests systems are compared, for most of the modulation indexes, 15-level MLI produces lower values. However, for modulation indexes higher than 0.8 and around 0.5, THDs of 11-level MLIs are better due to high standard deviations obtained for 15-level MLI. THD of seven-level MLI is the worst until a modulation index value is close to 0.9. After that modulation index, THDs of three test cases behave similar. For modulation index of 1, seven-level MLI produces the smallest THD percentage.

Fig. 6
figure 6

Near optimal angles obtained with SSA for seven-, 11- and 15-level MLIs and THD values

Full size image

Similarly, Figs. 7 and 8 show the obtained near optimal switching angles for seven-level, 11-level and 15-level MLIs using MVO and PSO, respectively. One can easily see from three figures that standard deviations of switching angles calculated using MVO, PSO and SSA are slightly different for seven- and 11-level MLIs. However, the standard deviations of the simulation results of the 15-level MLIs calculated using SSA are worse than the ones obtained with MVO and PSO. But, there is not a significant difference in terms of the standard deviations obtained by MVO and PSO. Thus, MVO- and PSO-based optimization simulation results are more robust.

Figures 7 and 8 also illustrate the mean values of THDs for three test systems. For seven- and 11-level MLIs, the THDs calculated by using three methods are very close to each other. This is different for 15-level MLIs. SSA produces higher standard deviations for modulation indexes between 0.8 and 0.9 compared to those of MVO and PSO. Standard deviations found by using three methods for remaining modulation indexes have slight differences.

Fig. 7
figure 7

Near optimal angles obtained with MVO for seven-, 11- and 15-level inverters and THD values

Full size image
Fig. 8
figure 8

Near optimal angles obtained with PSO for seven-, 11- and 15-level inverters and THD values

Full size image

Table 2 shows the obtained mean switching angles for different modulation indexes for 11-level MLI. According to [56], for modulation index 0.8, the following switching angles were obtained: \(\theta _1=6.57^{\circ }\), \(\theta _2=18.94^{\circ }\), \(\theta _3=27.18^{\circ }\), \(\theta _4=45.14^{\circ }\), \(\theta _5=62.24^{\circ }\). Previously, using MFO algorithm [33] for same modulation indexes the following switching angles were computed: \(\theta _1=5.96^{\circ }\), \(\theta _2=18.83^{\circ }\), \(\theta _3=25.97^{\circ }\), \(\theta _4=43.86^{\circ }\),\(\theta _5=61.64^{\circ }\). SSA calculated these values as \(\theta _1=5.59^{\circ }\), \(\theta _2=17.26^{\circ }\), \(\theta _3=29.73^{\circ }\),\(\theta _4=43.35^{\circ }\), \(\theta _5=62.98^{\circ }\), respectively. The switching angles found by MVO are as follows: \(\theta _1=5.53^{\circ }\), \(\theta _2=17.21^{\circ }\), \(\theta _3=29.72^{\circ }\), \(\theta _4=43.37^{\circ }\), \(\theta _5=62.99^{\circ }\). PSO calculated these switching angles as \(\theta _1=5.58^{\circ }\), \(\theta _2=17.25^{\circ }\), \(\theta _3=29.72^{\circ }\), \(\theta _4=43.37^{\circ }\), \(\theta _5=62.99^{\circ }\). From these five sets of different solutions, the THDs found by [56], MFO [33], SSA, MVO and PSO are, \(6.8490\%\), \(6.8698\%\), \(6.1856\%\), \(6.1860\%\) and \(6.1901\%\), respectively. From these results, it is seen that SSA provides a slightly better THD compared to MVO and PSO. The worst THD is obtained by using MFO.

4.1 MATLAB/Simulink results

To further verify the simulation results, a seven-level MLI is built in MATLAB/Simulink as shown in Fig. 9.

Fig. 9
figure 9

Simulink model for seven-level cascaded H-bridge MLI

Full size image

Then for \(m=0.7\) and \(m=0.8\) modulation indexes, THD values are calculated by using the switching angles found by using the numerical simulation results of SSA given in Table 1: For \(m=0.7\), \(\theta _1=10.533\), \(\theta _2=35.546\) and \(\theta _3=72.350\), and for \(m=0.8\), \(\theta _1=9.803\), \(\theta _2=30.000\) and \(\theta _3=56.733\). Figures 10 and 11 show the stepped voltage waveform of the seven-level MLI using two different modulation indexes and near optimal switching angles. Figures 12 and 13 show the THDs of those configurations using FFT Analysis Tool. It is seen from the figures that for \(m=0.7\), and for \(m=0.8\), THD values of 16.99% and 12.02% are obtained. Compared to the numerical simulation results, 16.05% and 11.01%, the differences are around 1%.

Fig. 10
figure 10

Voltage magnitudes obtained for \(m=0.8\)

Full size image
Fig. 11
figure 11

Voltage magnitudes obtained for \(m=0.7\)

Full size image
Fig. 12
figure 12

Obtained THD results for \(m=0.8\) using Simulink model

Full size image
Fig. 13
figure 13

Obtained THD results for \(m=0.7\) using Simulink model

Full size image

5 Conclusion and future work

This study approaches harmonic elimination and THD minimization problem for cascaded H-bridge MLIs by using three intelligent optimization algorithms. Two of these algorithms are recently developed intelligent optimization methods: SSA and MVO. For comparison purpose, a more popular algorithm PSO is also implemented. Numerical simulations are performed on seven-level, 11-level and 15-level MLIs. Optimum switching angles by using all methods are calculated and illustrated for modulation indexes ranging from 0.4 to 1. Moreover, THD values are calculated and illustrated as well. Numerical simulations show that both SSA and MVO algorithm are as successful as PSO in solving harmonic elimination problem. However, MVO gives more consistent numerical simulation results with less standard deviation compared to SSA. Moreover, to verify the simulation results, MATLAB/Simulink model for seven-level cascaded H-bridge MLI is developed, and voltages obtained using near optimal switching angles for two representative cases are illustrated. THD values of those cases were also calculated using FFT Analysis Tool. It was observed that the numerical values obtained using the simulated cases and MATLAB/Simulink model provide similar results giving an approximate difference of 1%. In future, the study is planned to be extended by including MLIs with unequal DC sources to model PVs with different outputs. Moreover, hybridization of the optimization methods will be implemented to further improve the performance.